Abstract
Ion mobility spectrometry (IMS) coupled to orthogonal time-of-flight mass spectrometry (oTOF) has shown significant promise for the characterization of complex biological mixtures. The enormous complexity of biological samples (e.g. from proteomics) and the need for both biological and technical analysis replicates imposes major challenges for multidimensional separation platforms in regard to both sensitivity and sample throughput. A major attraction of the IMS-TOF MS platform is separation speeds exceeding that of conventional condensed-phase separations by orders of magnitude. Known limitations of the IMS-TOF MS platforms include the need for extensive signal averaging due to factors that include significant ion losses in the IMS-TOF interface and an ion utilization efficiency of less than ~1% with continuous ion sources (e.g. ESI). We have developed a new multiplexed ESI-IMS-TOF mass spectrometer that enables lossless ion transmission through the IMS-TOF as well as a utilization efficiency of >50% for ions from the ESI source. Initial results with a mixture of peptides show a ~10-fold increase in signal-to-noise ratio with the multiplexed approach compared to a signal averaging approach, with no reduction in either IMS or TOF MS resolution.
Keywords: Electrospray ionization, multiplexing, ion mobility spectrometry, time-of-flight mass spectrometry
INTRODUCTION
Since its introduction as an analytical technique in early 1970s1, ion mobility spectrometry (IMS) has been increasingly applied to the characterization of gas-phase ions in a number of applications, including quality control in semiconductor manufacturing processes2, environmental monitoring of air and water3, detection of explosives4, and chemical warfare agents and toxins.5,6 IMS is based on spatial separation of gas-phase ion species due to differences in their mobilities, analogous to capillary electrophoresis (CE) in the condensed phase.
Coupling of electrospray ionization (ESI) and matrix-assisted laser desorption ionization (MALDI) to IMS has provided an impetus for expanding the realm of IMS capabilities to proteomics and other system biology applications.7,8 The enormous complexity of biological systems, e.g. >20,000 different proteins may be expressed at detectable levels by a mammalian system,9 has challenged the separation and analysis power of existing approaches, and to this point has been most effectively addressed by combinations of orthogonal fractionation and separation techniques combined with mass spectrometry (MS) as a final separation stage due to its high sensitivity, resolution, broad dynamic range and accurate mass measurement capability. Protein detection and identification in a variety of important biomedical applications, including discovery of candidate biomarkers in human blood plasma for early cancer detection, represents a significant analytical challenge for condensed-phase multidimensional separations coupled to MS, as many proteins of interest are expected at abundance levels far below that of higher abundance proteins.10 The large dynamic range of interest (>1010), coupled with issues that derive from biological variation, has greatly hindered proteomic approaches for effectively discovering low level candidate biomarkers in such biological fluids. Liquid chromatography (LC)-MS based proteome analysis of human blood plasma has generally involved the coupling of a high abundance protein depletion step with intensive protein and/or peptide level fractionation/separation techniques to obtain a greater analytical “depth of coverage”. This approach effectively transforms each sample into many samples, and thus reduces the number of individual samples that can be analyzed. At present, for example, it is not practical to perform an in-depth proteomic studies involving several hundred individual human blood plasma samples. This throughput versus proteome analysis coverage tradeoff can be addressed by either increasing the depth of coverage in a single analysis or the throughput of current approaches. Since gas-phase ion separations are typically two to three orders of magnitude faster (~10-–100 ms) than fast reverse-phase (RP) LC separations of comparable separation power (~5–10 min), IMS represents an attractive complementary orthogonal separation approach. When introduced between the condense phase separation and MS analysis, IMS can potentially increase the total effective peak capacity provided e.g. a fast RPLC-MS platform by over an order of magnitude without affecting the overall analysis speed, and thus help in addressing both the depth of coverage and throughput needs.
IMS, in turn, benefits from coupling with fast MS detection capable of acquiring the entire mass spectrum in a single scan. Young et al. first coupled a lower-pressure IMS to an orthogonal time-of-flight (TOF) analyzer to measure the formation and decomposition rates of hydrates of hydronium ion. More recently, this approach was used in combination with ESI for characterization of different biochemical compounds.12,13 Despite its attractiveness for higher throughput proteomic studies, the application of IMS-MS has been limited by low sensitivity primarily arising from ion losses at the IMS-MS interface and low duty cycle. Tang et al. have recently reported on ion lossless IMS-MS separations with an IMS drift tube incorporated between two electrodynamic ion funnels.14 In that experiment, ions were trapped in an “hourglass” ion funnel for 50 to 100 ms at an elevated pressure of 4 torr and then gated into the IMS drift tube in short 50 μs pulses. At the exit of the IMS drift tube, ion packets, spatially dispersed mainly due to thermal diffusion15, were captured by a regular ion funnel followed by a short collisional quadrupole. These developments have also recently been adopted by Clemmer and coworkers.16 Though ion transmission drastically improved as compared to earlier implementations of IMS-oTOF design,17 we also note that lower efficiency of ion trapping/accumulation in the ion funnel still limits the ion utilization efficiency or duty cycle.
The duty cycle of IMS with a continuous ion source can be improved using a Fourier transform (FT) approach.18,19 Using two gates were used at the entrance and the exit of the drift region, allows the “front” and “exit” gate opening and closing voltages to be correlated with the drift time for ions of interest. This approach provided a 3- to 5-fold increase in the signal-to-noise ratio (SNR) for the ions of a specific drift time at any given moment. Obtaining improved sensitivity for all species in a single IMS separation, requires a multiplexing technique, such as the Hadamard transform (HT). HT has been extensively used in optical spectrometry for over five decades.20 The concept of measuring different bundles of objects by weighing them in groups rather than individually was first proposed by Fellgett, and the resulting increase in accuracy is sometimes called the Felgett or multiplex advantage.21,22 If spectral line intensities are simultaneously detected in N measurements, the theoretical increase in SNR over a single measurement is then expected to be . Decker has experimentally demonstrated such an SNR gain by comparing the mercury vapor emission spectra obtained both with a monochromator and a Hadamard transform spectrometer.23 HT has been successfully applied to TOF MS and capillary electrophoresis (CE), yielding an increase in the duty cycle up to 50%. In CE experiments with fluorescence detection, Kaneta et al.24 have experimentally demonstrated an SNR increase by a factor of 8, which was in excellent agreement with the theoretically predicated value of 8.02. CE multiplexing was achieved by photo-degradation of a light-absorbing analyte, an approach that would be difficult to implement with a complex biological sample. For an HT on-axis TOF MS a proof-of-principle has been demonstrated using both direct infusion25 and CE26, although no comparison with conventional signal averaging was reported. A 5- to 6-fold increase in sensitivity has recently been reported in HT measurements using atmospheric-pressure IMS separations (without MS).27,28 This improvement, however, falls short of the theoretically expected gain of 15 to 45 (the theoretical gain for a 13-bit sequence is ). The discrepancy can be explained, in part, by the fact that the encoding pseudo-random binary sequence used in these multiplexing experiments exceeded the ion mobility drift times by almost two orders of magnitude. As a result, only a small fraction of the sequence contributed to any SNR enhancement as compared to that of a conventional averaging approach.
Here we describe the first implementation of the multiplexed ion mobility spectrometry combined with orthogonal TOF mass spectrometry incorporating an ESI interface. The high transmission efficiency, increased sensitivity, high throughput and resolving power achievable make this technology a potential basis for incorporation in an advanced proteomics platform.
EXPERIMENTAL SECTION
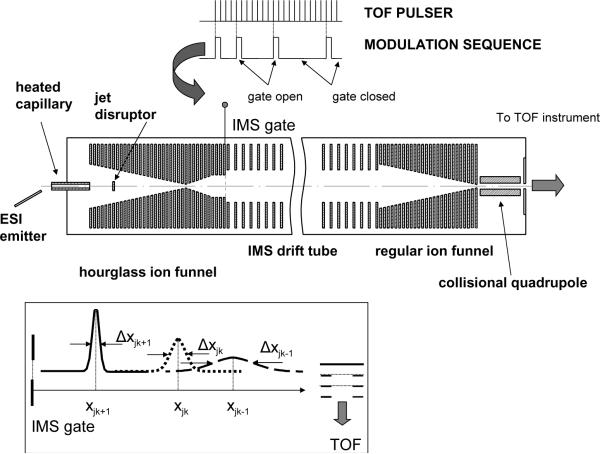
The multiplexed IMS-TOF MS approach has been implemented using two commercial orthogonal TOF instruments; a Q-Star Pulsar (Sciex, Toronto, Canada) and an Agilent TOF (Agilent, Santa Clara, CA) (Figure 1). The design of an ESI source and IMS drift tube coupled to both TOF spectrometers has been described elsewhere.14 The ESI source incorporated a 50-um-i.d. fused silica tip electrospraying into a 64 mm-long 430-um i.d. heated inlet capillary operating at a temperature of ~120 °C. The ESI emitter was mounted on a 2D translation stage enabling fine position adjustment with respect to the inlet. All voltages in the ESI source were referenced to a 4 kV potential applied to the IMS drift tube.
Figure 1.
Schematic of the ESI multiplexed IMS-TOF MS instrumentation.
Following droplet desolvation in the inlet capillary, intact ions were introduced into an “hourglass” ion funnel at 4 Torr for further trapping and accumulation. The hourglass ion funnel consisted of 0.5 mm-thick 100 ring electrodes, separated by 0.5 mm-thick Teflon spacers. The front section of the funnel incorporated a tapered converging assembly of 42 electrodes whose diameter was linearly decreasing from 25.4 mm to 2 mm. The exit diverging section of the hourglass ion funnel encompassed a set of 10 electrodes of 25.4-mm in diameter (20-mm in diameter for the funnel coupled to Agilent TOF), with a 20 lines/inch mesh (Buckbee-Mears, St.Paul, MN) mounted on the exit funnel plate. The first and the last but one electrodes of the straight exit section of ion funnel were independently driven at a potential of 40 V, while the potential at the exit electrode was switched between 60 V and 28 V, enabling ion accumulation and gating into the IMS drift tube, respectively. Ion packet multiplexing was conducted by encoding the gating potential (i.e., a potential applied to the funnel exit electrode) with a pseudo-random binary sequence (PRS). Switching potentials on the ion funnel floating at 4 kV potential was implemented with a fiber-optic triggering circuitry. Similar to the conventional ion funnel,29 an alternating rf potential at a frequency of 500 kHz and a peak-to-peak amplitude of 90 V was applied to all funnel plates except for the last dc-only plate, and a dc gradient of 24 V/cm was produced to assist ion transmission in the axial direction.
An IMS drift tube, coupled to the TOF Q-Star Pulsar, consisted of 55-mm–i.d. 80-mm o.d. 210 copper electrodes separated by 10 mm-long tubular plastic spacers, establishing a 2100-mm-long separation region. Pressure in the drift region was ~4 torr and the electric field strength was ~ 2 kV/m. An 840-mm long IMS drift tube interfaced to Agilent TOF was operated under identical pressure and electric field strength as that used in the IMS-Q-Star instrument.
To capture all ions exiting the IMS separation region, an additional 100-mm-long ion funnel was employed. This funnel was driven at the same rf and dc fields as the front-end hourglass funnel, and then coupled to a 25 mm-long collisional quadrupole operating at a frequency of 2 MHz and a peak-to-peak amplitude of 200 V. The quadrupole manifold was evacuated by a mechanical pump (Alcatel 2033, 12.8 L/s) to provide a pressure drop to ~140 mTorr and an interface for the IMS drift region to the lower-pressure rf ion guides of the commercial TOF instruments.
Both the Q-Star Pulsar and Agilent TOF were coupled to a 10 GHz time-to-digital converter, TDC (Ortec 9353, Oak Ridge, TN). Timing sequences were set by an I/O control board PCI-6711 (National Instruments, Austin, TX) installed in a Dell PC running on Windows XP operating system. Data acquisition software was developed in-house using Visual C# and implemented on top of the active × controls running Ortec hardware. To synchronize IMS and MS operations, the IMS pulsing period was made divisible by the TOF acquisition period and user-defined from the data acquisition software. Once desired sequence for multiplexing was programmatically generated, the PRS was uploaded to PCI-6711 that was triggered by a TOF pusher pulse. In this approach, a sub-ns jitter was achieved between the onset of TOF spectrum acquisition and triggering signal employed for opening or closing an IMS gate. The IMS gate opening time in both standard and multiplexed experiments was 100 μs. A typical IMS separation and TOF scan durations were 127 ms and 100 μs, respectively. Each TOF mass spectrum acquisition was digitized at 1.6 ns resolution (i.e., 2N × 0.1 ns, where N =4), yielding 62,500 TOF bins per TOF scan and ~8 × 109 bins per single IMS separation.
Peptides used in this study were purchased from Sigma Aldrich (St. Louis, MO) and further analyzed without additional purification. Samples diluted in water : methanol : acetic acid buffer (79.64 : 20 : 0.36 v%) were introduced into the instrument at a flow rate of 0.4 μL/min by a syringe pump (KD Scientific, Holliston, MA).
RESULTS AND DISCUSSION
We extensively modeled the reconstruction of the signal generated by a multiplexed IMS-TOF MS instrument using Microsoft Visual C++, and only a small portion of that work is presented here. Modeling was performed assuming that i) ion packet broadening in the IMS drift tube is mainly driven by thermal diffusion, facilitating independent ion packet dispersion, and ii) the spatial distribution of an ion cloud is governed by the central limit theorem, resulting in a Gaussian ion density profile along the IMS drift axis. Although space charge effects contribute to the overall expansion of an ion cloud in the IMS drift tube,30 the estimations indicated they contributed <5% of that exerted by the thermal diffusion under our experimental conditions, which account for ~1 nA pulsed ion current resulting from ion accumulation in the funnel.
Ion motion in the IMS drift tube is determined by the ion mobility constant, K, whose equation was originally derived by Revercomb and Mason31
| (1) |
where Ze is the ion charge, N is the number density of the gas, m and M are the masses of the drift gas and analyte, respectively, k is Boltzmann's constant, T is the absolute temperature of the drift gas, and Ω0 is the diffusion collision integral. The drift velocity, vd, in the lower electric field of intensity E is determined by the field-independent ion mobility constant, K, as follows:
| (2) |
We first consider identical ion species whose gating into the IMS drift tube is determined by a PRS. Since ion packets disperse along the drift axis independently of each other, the temporal and spatial spread of an ion packet within the IMS drift tube can be estimated as:
| (3) |
| (4) |
| (5) |
| (6) |
| (7) |
where j is the temporal step index, k is the modulation bin index within PRS, PRSk is the digital `1' or `0' event, which represents an “on” or “off” gate status, t_TOF x j is the elapsed time synchronized with the PRS onset, t_offsetk is the temporal offset of the ion packet gated into the IMS drift tube in k-th modulation bin relative to the PRS onset, tj,k is the drift time of the ion packet gated into the IMS drift tube in k-th modulation bin, tg is the gate opening time, t_TOF is the spectrum acquisition rate with a TOF mass spectrometer, Rd is the diffusion-only resolving power,31 and Ld is the length of the IMS drift tube. Equation 3 is similar to that reported previously,31,32 except for the dependence of the drift time on the modulation bin number, a difference that can be better understood by examining a snap-shot of IMS separation at the end of the encoding sequence. In this case, an ion packet launched into the IMS drift tube by the first “gate on” event would approach the end of the drift region and exhibit the full dispersion due to thermal diffusion, while the temporal spread of an ion packet gated into the drift region just before taking the snap-shot would be characterized only by the gate opening time, tg. At a given elapsed time, the spatial distribution of ions within different ion packets would depend on ion packet position along the drift tube.
The number of ions as a function of their position along the IMS drift tube can be then evaluated
| (8) |
| (9) |
| (10) |
where i is the spatial step index, step is the spatial step, xj,k position of the center of kth ion packet at time tj, N0 is the total number of ions in a given packet, Ni,j,k is the number of ions within a spatial interval of ⌊xj,k, − step × i; xj,k + step × i⌋, and N_ions_IMSi,j,k is the number of ions within a spatial interval of ⌊xj,k, + step × i; xj,k + step × (i + 1)⌋ along the IMS drift tube. Note, that N0 is considered to be a time-independent constant that is a first-order approximation for a relatively stable continuous ion source, such as from ESI. A three-dimensional integral, N_ions_IMSi,j,k, interpolated with Chebyshev's polynomials in the software, defines the spatial distribution of all ion packets along the IMS drift axis at any given time.
To convert the spatial distribution of ions in the IMS drift tube to the number of ions to be extracted into the orthogonal TOF MS flight tube, ion signals from all the ion packets in the IMS drift tube that contribute to the ion distribution inside the TOF extraction region were summed for each TOF mass spectrum acquisition. Importantly, since the PRS is synchronized with a TOF pulser (see Equations 5–6), each summation corresponded to the number of ions that were gated into the TOF flight tube. Modeling also allowed for the over-sampling of the modulation bins, so that a modulation bin width could be a multiple of several TOF acquisitions. Given an ion's mass-to-charge ratio, (m/z)n, and a calibration coefficient, slope, a TOF function, TOFn
| (11) |
was then added to the total IMS drift time and the ion arrival time at the detector was obtained.
Typical parameters used for ion mobility modeling included an IMS drift tube length of 2 m, an IMS drift tube pressure of 4 torr, and an electric field strength in the IMS drift region of 2 kV/m, corresponding to 4 kV potential applied to the first IMS electrode. TOF parameters in the reflectron mode were chosen such that m/z 500 would arrive at the TOF detector 50 us following the extraction pulse. The length of the TOF extraction region (where signals from all ion packets encoded by the PRS were summed) was 30 mm. The encoding 9-bit sequence comprised 511 modulation bins that were each 200 us-long], giving rise to an IMS separation time of ~100 ms. Each modulation bin was synchronized with a 100 us-long TOF mass spectrum acquisition, that, in turn, incorporated 103 TOF detector bins. The TOF detector bin width of 100 ns was limited only by a PC SDRAM, and was considered to be adequate for multiplexed IMS-TOF modeling. Given the TOF acquisition rate, signal reconstruction was performed at an over-sampling rate of >103. The principle of signal reconstruction using inverse transform with a generalized inverse matrix under the conditions of major over-sampling (> 105) has been reported elsewhere33 and successfully implemented in experiments using multiplexed orthogonal TOF.34 In general, given an inverse matrix of N × N elements, S−1, and a detected signal vector of M elements, y, where M is a multiple of N and M>> N, the latter is split into N bins to enable deconvolution of the original M-element signal vector, z, in M/N inverse transforms.
The details of the multilayer signal reconstruction where a modulation bin comprises multiple TOF mass spectra that, in turn, encompass ~105 TOF bins are given in the Appendix. Importantly, the compression of the experimental multiplexed IMS-TOF signal (i.e., removal of zero entries from TOF spectra) yielded a fully reconstructed 2D separation in less than minute, an attractive feature e.g. for on-line LC fractionation coupled to a multiplexed IMS-TOF MS instrument.
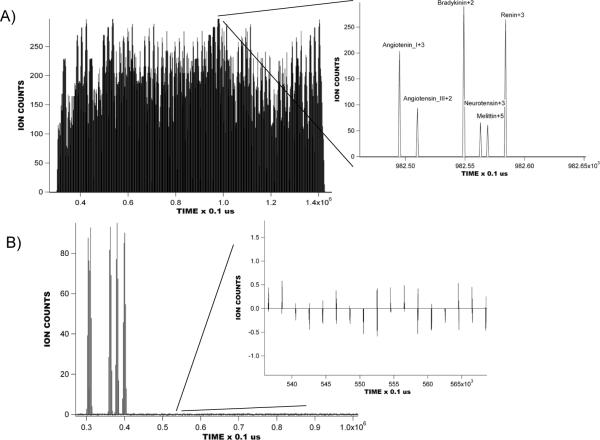
Figure 2A shows the modeled raw signal obtained with an equimolar mixture of six peptides. To generate this signal, 100 ions for each peptide were introduced into the IMS drift tube during each 200 us-long “gate open” event in a 9-bit modulation sequence. The modeling assumed ideal ion transmission; i.e. all ions gated into the IMS region reach the MS detector. A significant intermingling of ion packets is observed in the IMS drift tube. An inset to Figure 2A shows the MS signal from a portion of the IMS separation corresponding to one TOF mass spectrum. Figure 2B shows an IMS-TOF MS signal reconstructed by inverse transformation of a 511 × 511 simplex matrix. A characteristic feature of this reconstruction is the mathematical pseudo-noise observed at the background level, as shown in the inset. Similar background noise has been observed in HT-TOF MS measurements, and Poissonian statistics for the arrival times of ions at the detector have been employed to estimate the magnitude of the baseline noise as a function of mass spectral features and acquisition conditions.35 The magnitude of the pseudo-noise was found to be dependent on the temporal separation between two adjacent packets and represents the overlapping of spatial distributions of ion packets launched in different modulation bins. In extremes case, ion packet broadening due to thermal diffusion results in a significant increase in the pseudo-noise, making multiplexing impractical. Therefore, thermal diffusion imposes a fundamental limitation on the encoding sequence length (i.e., the number of bins in a sequence), and sets the minimum interval desirable between two adjacent gate pulses. On the other hand, the sequence length must not exceed the time scale of an IMS separation in the standard averaging mode as no SNR improvement can be gained on the timescale longer than that of a single signal averaging experiment. To understand this one can compare signal averaging against multiplexing, where two acquisitions in the multiplexed mode are performed on a timescale of one acquisition in signal averaging mode. The SNR improvement obtained using the multiplexed approach is compared to signal averaging; four acquisitions in the multiplexed mode provide a factor of 2 gain, while signal averaging would result in gain. The obtainable gain thus depends on the number of multiplexed acquisitions made on the timescale of a single signal averaging experiment; the advantage of multiplexing is that one can perform multiple acquisitions in the multiplexed mode on the timescale of the signal averaging experiment. In the above example, the signal averaging approach would provide the same SNR if performed on a time scale twice-longer than that of the multiplexed experiment. Multiplexing provides the basis (due to the encoding-decoding algorithm) for more acquisitions on the timescale of a single signal averaging experiment, and the benefits of multiplexing would only be realized for a portion of the encoding sequence that corresponds to the duration of the IMS separation in signal averaging mode. (correct)
Figure 2.
A) Modeled multiplexed IMS-TOF MS raw data signal obtained with an equimolar mixture of Angiotensin_I +3 (m/z 432.89), Angiotensin_III +2 (m/z 459.25), Bradykinin +2 (m/z 530.78), Neurotensin +3 (m/z 558.314), N-acetyl renin +3 (m/z 600.994), Melittin +5 (m/z 570.15). 100 ions of each peptide were introduced into the IMS drift tube during PRS gating pulses. B) Reconstructed modeled multiplexed IMS-TOF spectrum of the equimolar mixture of peptides used in Figure 2A. Reconstruction was performed at a resolution of 100 ns.
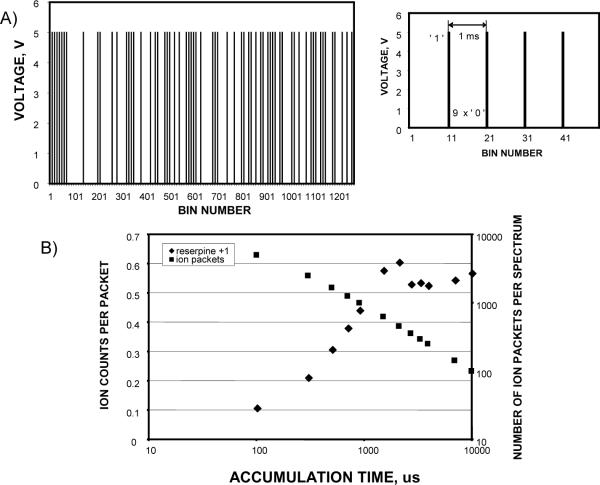
Our experimental implementation of multiplexed IMS-TOF measurements has been guided by these modeling results and using similar signal reconstruction routines. Figure 3A shows the encoding sequence used for the multiplexed IMS-TOF MS experiments. The important difference between this sequence and the conventional encoding sequences used in HT photospectrometry,20 HT-TOF MS,25 HT-CE24 and HT-IMS27 is that the adjacent digital `1' events (i.e., “gate open” events) in our sequence are separated by `0' events (i.e., “gate closed” events), while a typical encoding sequence in HT experiments has combinations of consecutive `1' events.
Figure 3.
A) Experimental extended 7-bit maximum length pseudo random sequence. Each pulse corresponds to the ion gating into the IMS drift tube. Inset shows a portion of the sequence. The gating pulse duration was 100 μs. The shortest interval between the gating pulses was 900 μs and the longest was 6900 μs. To perform signal reconstruction the extended 1270-element sequence was folded into a 127-element weighed vector, with each element obtained by summing 10 preceding elements. B) Dependence of the 1 μM reserpine signal per single TOF scan on the ion accumulation time in the hourglass ion funnel. Data were acquired with IMS- TOF (Q-Star Pulsar) MS operated in the signal averaging mode.
Three objectives were achieved by introducing delays between two adjacent ion releases into the IMS drift tube. First, extending the timing interval between two neighboring ion packets reduced the detrimental effects of diffusion-driven ion dispersion upon signal reconstruction, thus decreasing the mathematical noise upon signal reconstruction. Second, the constant short gate opening time (~100 μs, see inset) minimized peak broadening due to the gating term, tg, in Equation 3. For comparison, in HT-IMS experiment with a conventional 13-bit PRS27 implemented at a rate of 150 μs per modulation bin, the longest gate open event would be ~2 ms. As a result, the gate opening time would on average exceed that of the signal averaging mode by ~3–4 fold, resulting in peak broadening. Third, ions delivered to the ion funnel from a continuous source can better be efficiently accumulated between two adjacent releases for the shorter periods without exceeding the level at which space charge effects would be problematic, and resulting in a increase in the charge density per ion cloud released to the IMS drift tube. To perform signal reconstruction, 1270 element modulation sequence was folded into a 127-element vector, such that each vector element was a sum of the 10 preceding elements in the modulation sequence. As a result, a weighed 127-element PRS was obtained to be used for generation of a generalized weighed matrix and inverse transform.
Since both standard and multiplexed modes incorporated ion accumulation between adjacent gate pulses, the ion signal intensity for one TOF mass spectrum was examined. The interval between two adjacent pulses in the experimental PRS, shown in Figure 3A, varied between 1 ms and 7 ms, while standard IMS was conducted using one ion packet ejected from the ion accumulation trap every 127 ms. Figure 3B shows the charge density of a trapped ion cloud as a function of the accumulation time. This dependence revealed ion signal saturation from ESI of a 1 μM sample of reserpine for an accumulation time of ~1 ms. Therefore, when comparing the multiplexed versus standard IMS modes of operation, no signal enhancement using the standard IMS mode could be achieved for accumulation events longer than 1 ms with the current design of the ion funnel (presumably due to space charge constraints), and SNR improvement will only be attained via the multiplexing gain or mechanisms other than ion accumulation in the ion funnel trap e.g. the overlapping of ion packets in the TOF extraction region.
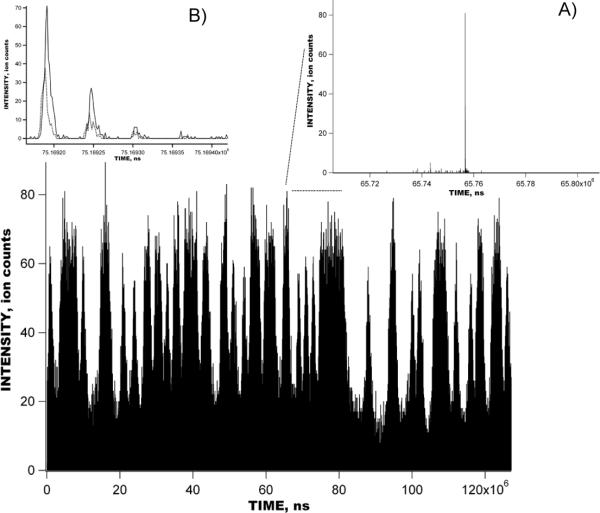
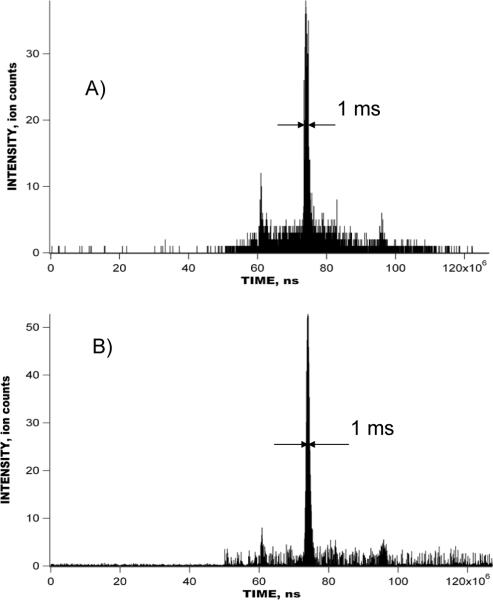
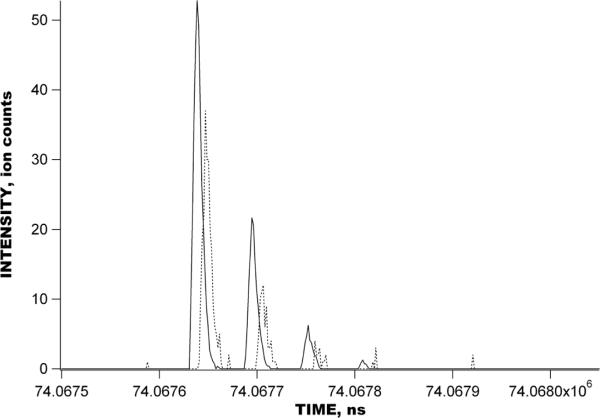
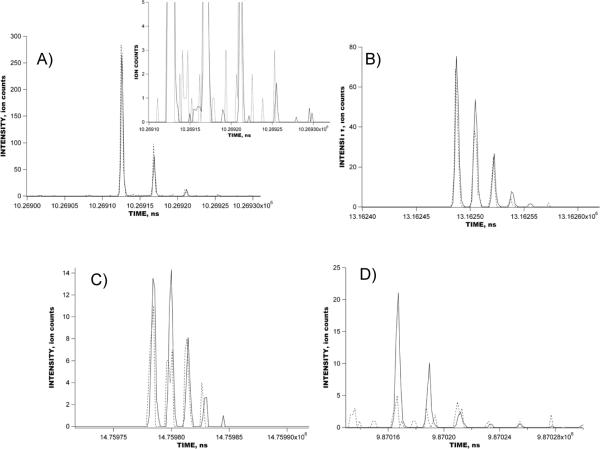
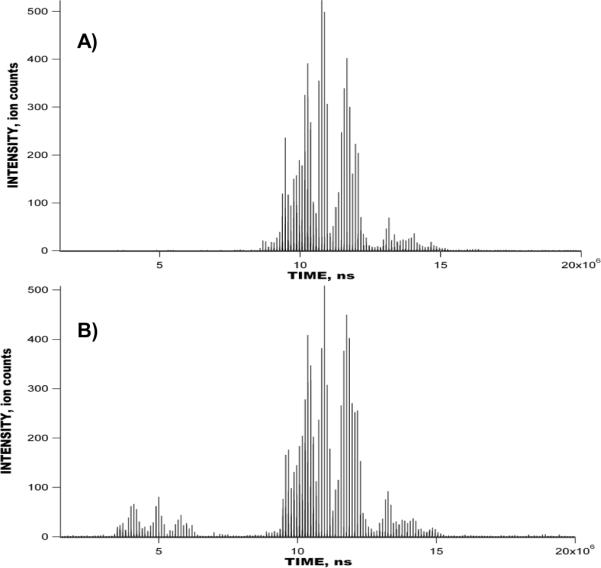
Figures 4 shows the raw signal obtained with a 1 uM reseprine solution using the IMS-TOF Q-Star Pulsar mass spectrometer in the multiplexed mode. IMS-TOF analysis in Figure 4 encompasses 1270 concatenated TOF spectra acquired at a resolution of 1.6 ns, each spectrum being a sum of 1000 TOF mass spectra. The inset shows the detected signal during a small portion of the IMS separation corresponding to a single mass spectrum. The total number of ion packets in the IMS drift tube during a single IMS separation was 64 and each IMS separation was conducted in 127 ms. Figure 5 shows the comparison between the reconstructed signal acquired in the multiplexed experiment in Figure 4 and that acquired in the signal averaging mode. The IMS-TOF MS was operated under conditions identical to those in Figure 4, so that each IMS separation was performed in 127 ms and comprised 1270 TOF mass spectra. Both multiplexed and signal averaging mode separations were acquired over a period of 127 s, corresponding to 1000 IMS acquisitions. Signal reconstruction in Figure 5B was performed at a resolution of 1.6 ns. The only difference between IMS-TOF separations in Figure 5A–B was the number of ion packets present in the IMS drift tube at a given time. In the experiment conducted in the signal averaging mode (Figure 5A), only one ion packet was injected into the drift tube in the course of the entire 127-ms long IMS separation, while, in the multiplexed experiment, 64 ion packets were present in the IMS drift region at the end of each IMS separation. Figure 6 shows a small portion of both the multiplexed and signal averaging IMS-TOF analyses from Figure 5 representing a small segment of one TOF mass spectrum and showing peaks due to reserpine ions. When compared to the data obtained with the IMS-TOF in signal averaging mode, a ~10-fold SNR increase was observed for the reserpine signal in the multiplexed experiment, exceeding the theoretical multiplexing gain of 5.6 for a sequence of 127 elements (see discussion below). Figure 7 shows the raw multiplexed data obtained with a 1 uM mixture of bradykinin, angiotensin I, fibrinopeptide and neurotensin in the multiplexed experiments using a IMS-Agilent TOF MS instrument. The inset shows a portion of the IMS separation corresponding to a single TOF spectrum. Signal acquisition parameters, including TOF scan and IMS separation durations, TOF digitization rate, and the number of IMS acquisitions were the same as for the multiplexed IMS-TOF (Q-Star) MS measurements (see Figure 5–6). Figure 8 shows a comparison of data acquired in the multiplexed and signal averaging modes. Figure 8A demonstrates the IMS-TOF (Agilent) signal acquired in the signal averaging mode, while Figure 8B shows the reconstructed signal obtained in the multiplexed experiment in Figure 7. Similar to Figure 5, both measurements used identical experimental conditions. The TOF spectrum and IMS spectrum acquisition rates were 100 μs and 127 ms, respectively, and each dataset represents a sum of 1000 IMS acquisitions. Signal reconstruction was performed with a single TOF bin resolution of 1.6 ns. (The IMS-TOF signal at drift times of about 5 ms was due chemical noise variation and was not related to signal reconstruction algorithm.) A detailed comparison of signal averaging and multiplexed datasets is shown in Figure 9, where small portions of the TOF mass spectra, corresponding to the detected peptides from both the multiplexed and signal averaging experiments, are superimposed. Interestingly, reconstructed multiplexed spectra exhibited SNR improvements both for higher (e.g., bradykinin in Figure 9A) and lower abundance species (e.g., neurotensin in Figure 9C and angiotensin I in Figure 9D). For the signal averaging mode, the noise level corresponds to single ion counts, thus a SNR of ~300 is obtained for bradykinin signal in Figure 9A (Figure 9A, dashed line). The corresponding noise level for the multiplexed measurement was ~0.1 (Figure 9A, solid line), resulting in ~10-fold greater SNR for the same peptide. The order of magnitude increase in the SNR for lower abundance species (Figure 9C, 9D) is evident in the isotopic distributions detected in the multiplexed vs. signal averaging experiments.
Figure 4.
Experimental raw data signal obtained with 1 μM solution of reserpine in multiplexed IMS-TOF MS (Q-Star Pulsar) experiment. Multiplexed IMS-TOF raw signal was acquired at 1.6 ns resolution and summed over 1000 IMS acquisitions, corresponding to 127 s. Inset shows a small portion of the multiplexed IMS-TOF MS measurement corresponding to single a mass spectrum.
Figure 5.
A) 1 uM reserpine signal acquired with the IMS-TOF MS (Q-Star MS Pulsar) instrument operated in the signal averaging mode. Experimental conditions were identical to that in Figure 5A. B) Reconstructed 1 uM reserpine signal acquired in the multiplexed experiment with the IMS-TOF MS in Figure 4. Temporal resolution of the reconstructed signal is 1.6 ns. Each IMS separation comprises 1270 TOF scans, and a total of 1000 IMS separations were summed both in the multiplexed and signal averaging modes.
Figure 6.
A portion of the reconstructed multiplexed IMS-TOF separation in Figure 5A (solid line) superimposed with that of IMS-TOF separation conducted in the signal averaging mode in Figure 5B (dashed line). Noise level in the conventional IMS-TOF separation corresponds to single ion counts.
Figure 7.
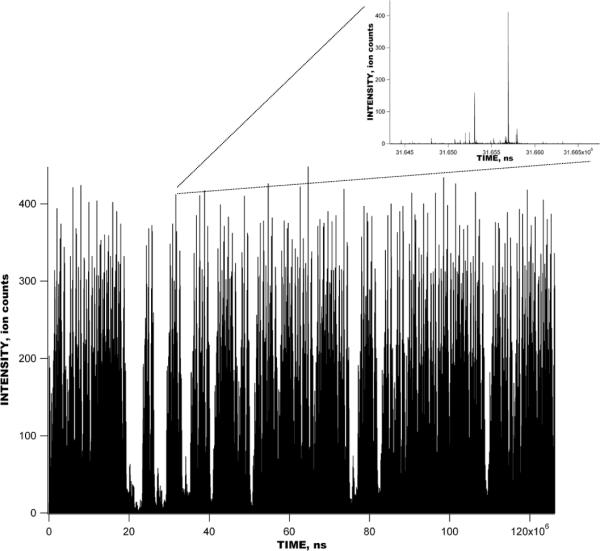
Experimental raw data signal acquired in the multiplexed IMS- TOF MS (Agilent) measurement with 1 μM solution of bradykinin, angiotensin I, fibrinopeptide and neurotensin. Multiplexed IMS-TOF raw signal was acquired at 1.6 ns resolution and summed over 1000 IMS acquisitions, corresponding to 127 s. Multiplexed IMS separation encompasses 1270 TOF spectra. Inset shows a small portion of the multiplexed IMS-TOF separation corresponding to a single mass spectrum.
Figure 8.
A) Signal obtained with the peptide mixture in Figure 7 using IMS-TOF MS (Agilent) instrument operated in the signal averaging mode. Experimental conditions were identical to those used in Figure 7. B) Reconstructed IMS-TOF signal from the multiplexed experiment in Figure 7. Each IMS separation in Figure 8A–B comprises 1270 TOF mass spectra, and a total of 100 IMS separations were summed.
Figure 9.
Superimposed portions of the IMS-TOF MS separations performed in the multiplexed (solid line) and signal averaging modes (dashed line) in Figure 8. The IMS-TOF MS (Agilent) instrument was operated under the conditions described in Figure 7. A) A portion of one out of several TOF mass spectra corresponding to bradykinin signal; B) fibrinopeptide signal; C) neurotensin signal, and D) angiotensin I signal.
An important characteristic that distinguishes the current approach from the earlier implementations of the HT-IMS27,28 is the combination of ion accumulation with multiplexing. In the ideal scenario, the ion trapping efficiency would remain constant for accumulation times extending to >10 ms. Given a 1 ms-long modulation bin comprising 10 sub-modulation bins (as in the current approach) and a gate opening time of 100 μs, an average weighed accumulation time for a 7-bit sequence would be ~2 ms, resulting in a ~20-fold (2 ms/ 100 us) increase in the ion cloud charge density. Therefore, an expected SNR increase, SNR_mult, would be:
| (12) |
| (13) |
where Efficiencytrap is the charge density increase due to ion accumulation as compared to that of the continuous beam, Gainmult is the multiplexing gain, and N is the number of PRS bits. If HT-IMS is operated at higher modulation rate based on e.g. a 10-bit sequence, an SNR increase would be limited to a multiplexing gain of ~16. The drawback of running the instrument at higher modulation rate would be an increase in mathematical pseudo noise due to diffusion-driven ion cloud overlap and the loss of multiplexing advantage
In measurements using a 1 μM solution of reserpine, a charge collector positioned immediately downstream of the hourglass ion funnel gave rise to an ion current of ~50 pA. This current translates to the maximum of ~3 × 105 singly charged ions that could be accumulated in the ion funnel trap in 1 ms. Figure 3B shows that charge density per ion packet doesn't increase with an increase in ion accumulation times longer than ~ 2 ms. Therefore, the charge capacity of the ion funnel trap under current experimental conditions was limited to ~ 106 ions. Based on the balance of Coulombic repulsion and effective potential forces, the theoretical charge capacity of the present ion funnel trap has earlier been estimated as >107 elementary charges,36 exceeding the present experimental situation by more than an order of magnitude An increase in the ion funnel effective potential due to an increase in the rf frequency and amplitude can potentially bridge this gap between theory and experiment. Based upon Equation 12, the accumulation of greater ion populations (e.g. by extending the linear dynamic range of our ion funnel trap to enable a linear increase in ion populations at accumulation times to >10 ms) could potentially result in a further >10-fold SNR improvements as compared to that experimentally achieved, and an increase in the duty cycle to ~95 % for ion utilization.
The experimental observation of an SNR increase greater than the multiplexing gain (see Figures 6 and 9) needs further explanation. Since both conventional and multiplexed IMS-TOF measurements were performed using the ion trapping mode, and there was no increase in the ion packet charge density for accumulation times greater than 1 ms (see Figure 4), we infer that the SNR improvement is due to the multiplexing gain. This would be the case for one-dimensional multiplexed IMS separations, where the experimental gain could never exceed the theoretical multiplexing gain. However, in two-dimensional separations, an overlap of the ion clouds in TOF extraction region due to thermal diffusion (see raw multiplexed data in Figures 4 and 6) increases the number of ions to be pulsed to the mass spectrometer in a single scan as compared to that of the standard IMS separation. This is also confirmed in modeled data (see Figure 2A), so that peak intensities of ~300 ions were observed with only 100 ions introduced per packet into the IMS drift tube. In these measurements both the number of TOF packets with ions, as well as the number of ions per TOF packet are increased, resulting in an SNR increase greater than the multiplexing gain. Thus, a significant part of the multiplexing gain with IMS-TOF measurements arises from second separation dimension (i.e., the MS).
Finally, a multiplexed IMS-TOF resolution in the IMS dimension (~70 for the IMS-Q-Star and ~45 for the IMS-Agilent TOF MS) was found to be similar to that for the conventional IMS-TOF (see Figures 5 and 8), implying a weak dependence of ion drift times on the space charge in the multiplexing experiments. Unlike atmospheric pressure HT-IMS where IMS resolution is primarily dependent on the gate opening time, in a lower pressure (~4 torr) IMS separation, a separation peak width (~1 ms fwhm for the IMS-QStar TOF MS platform) is primarily determined by thermal diffusion (see Equation 3). Further increases in the pressure and electric field strength are projected to facilitate an increase in the multiplexed IMS resolution, since the thermal diffusion term will be reduced while the gate opening time would remain constant (see Figure 3).
CONCLUSIONS
A newly developed multiplexed IMS-TOF MS approach has been modeled and experimentally implemented with an ESI source. We have found that previous results using Hadamard IMS have been limited by diffusion phenomena. Data reconstructed in the multiplexed IMS-TOF MS experiments using the new approach, and proper selection of the encoding sequence, showed a ~10-fold increase in SNR as compared to that of the IMS-TOF MS instrument operating in the conventional signal averaging mode for a mixture of peptides. Further sensitivity improvements should be attainable by increasing the charge capacity of the ion accumulation trap and the efficiency of ion ejection from the trap with shorter gate pulses. Such an implementation could completely eliminate ion losses in the ESI-IMS interface, resulting in >95% ion utilization efficiency. Since a multiplexed IMS-TOF MS separation is performed on a time scale of ~100 ms, it provides a potential basis for extremely high-throughput and sensitive platform for proteomics and system biology applications. Integration of the multiplexed IMS-TOF MS platform with on-line RPLC fractionation would potentially enable complete sample analysis in a 3D separation with substantially increased throughput compared to LC-MS, making such an approach highly attractive for clinical applications.
ACKNOWLEDGEMENTS
The authors are grateful to Drs. Alexander Shvartsburg and Brian Clowers for helpful discussions and also thank the NIH National Center for Research Resources (RR18522) for supporting portions of this research. Pacific Northwest National Laboratory is operated by the Battelle Memorial Institute for the U.S. Department of Energy through Contract DE-AC05-76RLO1830.
APPENDIX
An essential part of signal reconstruction is the ability to perform an inverse transform with a generalized weighed matrix under the conditions of significant over-sampling. An example of such over sampling is represented by the experimental maximum length pseudo random sequence (PRS) shown in Figure 3A. The total number of modulations bins in the experimental PRS is 127, with each modulation bin incorporating 10 sub-modulation bins. The number of TOF bins in each sub-modulation bin is 62,500. The durations of experimental modulation, sub-modulation and TOF bins are 1 ms, 100 μs, and 1.6 ns, respectively. An extended 127-ms-long PRS incorporates 1270 elements (i.e, the number of submodulation bins in the sequence, 127 × 10 =1270). As described in the text, adjacent 100-μs long gate pulses (i.e., digital `1's in the extended sequence) are separated by “accumulation” sub-modulation bins (i.e., digital `0's) to enable ion accumulation between ion releases into the IMS drift tube, minimize ion cloud overlap due to thermal diffusion and maintain short fixed gate opening time. To perform signal reconstruction, the extended PRS was folded into a weighed PRS, such that the number of consecutive “accumulation” sub-modulation bins constitutes the sequence weight.
where i the modulation bin number, j is the sub-modulation bin number, M is the number of sub-modulation bins within a modulation bin, PRS_extended_zerosij is the counter that corresponds to the number of digital `0's in the extended PRS sequence, and PRS_weighedi is the element of the folded weighed PRS.
For instance, if two adjacent `1's in the extended sequence are separated by 9 consecutive `0's, the modulation bin would then be represented in the folded sequence with a weight of 9. If all sub-modulation bins within a particular modulation bin were `0's, the weighed element in the folded sequence would be 0. Weighing approach could also be described by generation of a 7-bit maximum length PRS using a shift register approach. The sequence would be then stretched, so that each `1' would become a series of `0000000001', while each `0' would be represented as `0000000000'. The extended PRS was used for data acquisition and then folded with weights, as described above, to generate an inverse matrix and perform signal reconstruction. Folding, down-shifting and taking a matrix inverse brought about a 127× 127 element inverse matrix.
Let one consider an extended PRS that consists of N-modulation bins, each encompassing M sub-modulation bins. Each of these sub-modulations bins, in turn, includes L time-of-flight (TOF) bins. If an inverse matrix S−1 is obtained with the weighed PRS, the signal reconstruction would then be performed as follows:
| (14) |
where n is the row index of the inverse matrix, n ∈ [0, N − 1], i is the column index of the inverse matrix, i ∈ [0, N − 1], j is the sub-modulation bin number, j ∈ [0, M − 1], and k is the TOF bin number, k ∈ [0, L − 1] sni is the inverse matrix element, yijk and znjk are the detected and reconstructed signals, respectively, corresponding to a single TOF bin. Importantly, to enable inverse transform, the number of rows and columns of the inverse matrix must be equal to the number of modulation bins. Following Equation 14, signal reconstruction is performed independently for each sub-modulation bin, and the total of M transforms is needed to complete the algorithm. It's noteworthy that no averaging or/and summing is performed to obtain the original data vector with the inverse transform of the generalized weighed matrix S−1 and reconstruction resolution is equal to a TOF bin width.
REFERENCES
- 1.Karasek FW. Anal. Chem. 1974;46:710A–717A. doi: 10.1021/ac60345a031. [DOI] [PubMed] [Google Scholar]
- 2.Carr TW. Thin Solid Films. 1977;45:115–122. [Google Scholar]
- 3.Eiceman GA, Garcia-Gonzalez L, Wang Y-F, Pittman B. Talanta. 1992;39:459–467. doi: 10.1016/0039-9140(92)80165-a. [DOI] [PubMed] [Google Scholar]
- 4.Lawrence AH, Neudorfl P. Anal.Chem. 1977;50:152–155. [Google Scholar]
- 5.Kientz Ch.E. J.Chrom. A. 1998;814:1–23. doi: 10.1016/s0021-9673(98)00338-0. [DOI] [PubMed] [Google Scholar]
- 6.Hill HH, Siems WF, Louis R.H.St., McMinn DG. Anal.Chem. 1990;62:1201A–1209A. doi: 10.1021/ac00222a001. [DOI] [PubMed] [Google Scholar]
- 7.Wittmer D, Chen YH, Luckenbill BK, Hill HH. Anal. Chem. 1994;66:2348–2355. [Google Scholar]
- 8.Gillig KJ, Ruotolo B, Stone EG, Russell DH, Fuhrer K, Conin M, Schultz AJ. Anal. Chem. 2000;72:3965–3971. doi: 10.1021/ac0005619. [DOI] [PubMed] [Google Scholar]
- 9.Aebersold R, Mann M. Nature. 2003;422:198. doi: 10.1038/nature01511. [DOI] [PubMed] [Google Scholar]
- 10.Anderson NL, Anderson NG. Mol. Cell. Proteomics. 2002;1:845–867. doi: 10.1074/mcp.r200007-mcp200. [DOI] [PubMed] [Google Scholar]
- 11.Young CE, Edelson D, Falconer WE. J. Chem. Phys. 1970;53:4295–4302. [Google Scholar]
- 12.Guevremont R, Siu KWM, Wang J, Ding L. Anal. Chem. 1997;69:3959–3965. doi: 10.1021/ac970359e. [DOI] [PubMed] [Google Scholar]
- 13.Hoaglund CS, Valentine SJ, Counterman AE, Clemmer DE. Anal. Chem. 1998;70:2236–2242. doi: 10.1021/ac980059c. [DOI] [PubMed] [Google Scholar]
- 14.Tang K, Shvartsburg AA, Lee H-N, Prior DC, Buschbach MA, Li F, Tolmachev AV, Anderson GA, Smith RD. Anal. Chem. 2005;77:3330–3339. doi: 10.1021/ac048315a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Spangler CE, Colins CL. Anal. Chem. 1975;47:403–407. [Google Scholar]
- 16.Koeniger SL, Merenbloom SI, Valentine SJ, Jarrold MF, Udseth HR, Smith RD, Clemmer DE. Anal.Chem. 2006;78:4161–4174. doi: 10.1021/ac051060w. [DOI] [PubMed] [Google Scholar]
- 17.Hoaglund-Hyzer CS, Clemmer DE. Anal. Chem. 2001;73:177–184. doi: 10.1021/ac0007783. [DOI] [PubMed] [Google Scholar]
- 18.Knorr FJ, Eatherton RL, Siems WF, Hill HH., Jr. Anal. Chem. 1985;57:402–406. doi: 10.1021/ac50001a018. [DOI] [PubMed] [Google Scholar]
- 19.St. Louis RH, Siems WF, Hill HH. Anal. Chem. 1992;64:171–177. [Google Scholar]
- 20.Harwit M, Sloane NJ. Hadamard Transform Optics. Academic Press; New York: 1979. [Google Scholar]
- 21.Felgett P. PhD thesis. Cambridge University; The theory of infrared sensitivities and its application to investigations of stellar radiation in the near infrared. [Google Scholar]
- 22.Fellgett P. J.de Physique. 1967;28:165–171. [Google Scholar]
- 23.Decker JA. Appl. Opt. 1971;10:510–514. doi: 10.1364/AO.10.000510. [DOI] [PubMed] [Google Scholar]
- 24.Kaneta T, Yamaguchi Y, Imasaka T. Anal.Chem. 1999;71:5444–5446. doi: 10.1021/ac990625j. [DOI] [PubMed] [Google Scholar]
- 25.Brock A, Rodriguez N, Zare RN. Anal. Chem. 1998;70:3735–3741. [Google Scholar]
- 26.Fernandez FM, Vadillo JM, Kimmel JR, Weterhall M, Markides K, Rodriguez N, Zare RN. Anal. Chem. 2002;74:1611–1617. doi: 10.1021/ac015673u. [DOI] [PubMed] [Google Scholar]
- 27.Clowers BH, Siems WF, Hill HH, Massick SM. Anal.Chem. 2006;78:44–51. doi: 10.1021/ac050615k. [DOI] [PubMed] [Google Scholar]
- 28.Szumlas AW, Ray SJ, Hieftje GM. Anal. Chem. 2006;78:474–4471. doi: 10.1021/ac051743b. [DOI] [PubMed] [Google Scholar]
- 29.Belov ME, Gorshkov MV, Udseth HR, Anderson GA, Smith RD. Anal.Chem. 2000;72:2271–2279. doi: 10.1021/ac991360b. [DOI] [PubMed] [Google Scholar]
- 30.Spangler GE. Anal. Chem. 1992;64:1312. [Google Scholar]
- 31.Revercomb HE, Mason EA. Anal.Chem. 1975;47:970–983. [Google Scholar]
- 32.Asbury GR, Hill HH. J. Microcolumn Separations. 2000;12:172–178. [Google Scholar]
- 33.Belov ME, Fancher CA, Foley P. U.S. Patent 6,900,431. 2005
- 34.Belov ME, Foley P. Proceeding of the 52nd ASMS Conference; Nashville, TN. 2004. [Google Scholar]
- 35.Kimmel JR, Yoon OK, Zuleta IA, Trap O, Zare RN. J. Am. Soc. Mass Spectrom. 2005;17:1117–1130. doi: 10.1016/j.jasms.2005.07.025. [DOI] [PubMed] [Google Scholar]
- 36.Tolmachev AV, Udseth HR, Smith RD. Anal.Chem. 2006;72:972–978. doi: 10.1021/ac990729u. [DOI] [PubMed] [Google Scholar]