Unassisted Transport of N-acetyl-L-tryptophanamide through Membrane: Experiment and Simulation of Kinetics

Abstract

Cellular transport machinery, such as channels and pumps, is working against the background of unassisted material transport through membranes. The permeation of a blocked tryptophan through a 1,2-Dioleoyl-sn-glycero-3-phosphocholine (DOPC) membrane is investigated to probe unassisted or physical transport. The transport rate is measured experimentally and modeled computationally. The time scale measured by Parallel Artificial Membrane Permeation Assay (PAMPA) experiments is ~8 h. Simulations with the Milestoning algorithm suggest Mean First Passage Time (MFPT) of ~4 h and the presence of a large barrier at the center of the bilayer. A similar calculation with the solubility-diffusion model yields MFPT of ~15 min. This permeation rate is nine orders of magnitude slower than the permeation rate of only a tryptophan side chain (computed by us and others). This difference suggests critical dependence of transport time on permeant size and hydrophilicity. Analysis of the simulation results suggests that the permeant partially preserves hydrogen bonding of the peptide backbone to water and lipid molecules even when it is moving closer to the bilayer center. As a consequence, defects of the membrane structure are developed to assist permeation.

1. INTRODUCTION

Biological membranes separate life from mere solutions. They sustain concentration differences of biomaterials in cells compared to their immediate external surrounding. The concentration gradients make it possible to respond to cellular needs and conduct necessary biochemical reactions. However, the separation cannot be absolute. Communication between intra and inter cellular environments must be established to make it possible to absorb new substrates, to get rid of waste products, to receive and submit signals, and to respond by (for example) adjusting incoming and outgoing fluxes of materials.

Membrane proteins control many of these processes in modern cells. In contemporary membranes one finds numerous signal proteins, channels and pumps, allowing for significant cellular control on exchanges with the exterior environment. However, materials are also transported directly through membranes, a permeation process that we call physical or unassisted permeation.

We anticipate significant dependence of permeation properties on permeant characteristics such as size and we therefore review some past investigations. Quantitative computational studies illustrate that physical transport of small molecules such as water, oxygen, and nitric oxide is sufficiently rapid to make a significant contribution in modern cells^1–6. Permeation of these small molecules does not impact membrane integrity in a significant way and can be made directly, retaining the average structure of the membrane, which simplifies the calculations. Studies of time-scales of permeation of small molecules are usually separated into steps. A reaction coordinate (RC) is assumed which typically consists of permeant displacement normal to the surface of the membrane (its z coordinate). Then, constrained dynamics is used to sample configurations along the RC. The potential of mean force (PMF) and the diffusion-constant along the RC are calculated and used in a formula for the permeability coefficient^2,3,7:

$$P={\left[\underset{z_1}{\overset{z_2}{\int }}\frac{\exp \left(\beta \Delta G\left(\mathcal{z}\right)\right)}{D\left(\mathcal{z}\right)}d\mathit{z}\right]}^{-1}$$ (1)

where ΔG(z) is the free energy difference as a function of the position of the permeant along the membrane normal, D(z) is a position dependent diffusion constant and β = 1/kT. More details about the implementation are provided in the Theory section.

More studies on water permeation have been published compared to any other small permeant^3,4,8. Most computational investigations have found a free energy barrier for permeation through different lipids of ~ 6 kcal/mol. The permeation time for such a barrier is in the microsecond range. For other small polar solutes with ability to form a few hydrogen bonds (such as acetamide and methanol) the barrier to permeation is similar to water. More hydrophilic and amphiphilic compounds have slower permeation. These compounds usually have a minimum in the free energy at the interface of the headgroup and hydrophobic tail regions of the lipid due to their amphiphilicity, and a maximum at the hydrophobic bilayer center. For example, Wei and Pohorille^9,10 investigated the permeation of several riboses and two different nucleosides through a palmitoyloleoylphosphatidylcholine (POPC) bilayer. The free energy differences for the nucleosides to transfer to the center of the bilayer was 10 and 12 kcal/mol, respectively, and that make their permeability about 4 orders of magnitude smaller than water.

Another class of permeants that has received considerable attention is of amino acids and small peptides. Studies of physical transport of amino acids and small peptides could provide some insight into the onset of membrane machinery. Larger peptides may become channels, transporters, or leading peptides assisting the permeation of bigger objects¹¹ (depending of course on their amino acid composition). Permeation studies of peptides with experiments and simulations could be used to determine what is the minimal size of a peptide that can permeate a membrane efficiently. Also, examining the permeation of amino acids and small peptides may be an initial step in the design of membrane proteins.

Previous studies have addressed the partitioning of amino acid side chains into membranes^12–18, or the coupling of membrane defects to their transport, as was observed in studies of permeation of helical peptides^11,19–25. Water fingering²⁶ into the membrane was also observed in transport of charged entities²⁷. An interesting class of peptides that has been studied by others is of the highly cationic and hydrophilic cell penetrating peptides (for reviews see^28–30). These insightful studies on amino acids and small peptides permeants focused on thermodynamics and qualitative understanding of transport mechanisms rather than kinetics.

Here, we investigate the time scales and mechanisms of unassisted transport of a neutral, amphiphilic and hydrophilic molecule, a blocked tryptophan, using experiments and simulations. The focus of the present investigation is on kinetics. Time scales are critical in biology since most cellular processes are kinetically and not thermodynamically controlled. To understand events that occur in conditions far from equilibrium, and to build adequate models of systems-biology, material transport into and out of cells should be considered.

A blocked tryptophan (Figure S1, Supporting Information), is particularly intriguing since tryptophan side chains are frequently found at membrane-water interfaces and have the dual capacity for hydrogen bonding and hydrophobic interactions. Previous simulations of analogs of tryptophan and other amino acids focused on the determination of the free energy of solvation and analysis of their distributions inside the bilayer. The use of side-chain analogs reduces the size and amphiphilic character of the permeant and diminishes the disturbance of the membrane. Calculations of the PMF for permeation of the tryptophan analog gave a barrier of about ~ 4 kcal/mol in a DOPC membrane and ~5 kcal/mol in a dimyristol phosphatidylcholine (DMPC) membrane^12,17. Permeation times in the microsecond range are expected.

Here, we report experimental data that indicates that a block tryptophan take hours (!) to permeate completely through a bilayer membrane, under unassisted condition. What is the reason for this huge difference in time scales of permeation between the protected tryptophan with peptide backbone and its side chain only? The answer of this question is the main motivation of this work.

To address computationally the prediction of time scale and mechanism of this long-time process the use of Milestoning^31–35 or Directional Milestoning^36,37 seems appropriate. Milestoning is a theory and algorithm that accumulate short time trajectories to estimate the overall kinetics and thermodynamics of a complex system. It can be applied for arbitrary dynamics (not only over damped Langevin) and is not restricted to one-dimensional coordinate. Nevertheless, because the blocked tryptophan is still a small molecule, the solubility-diffusion model can be used as a reference and alternative computational approach to obtain the PMF and permeability estimates with the use of equation (1). The solubility-diffusion model accounts for the permeation rate of small molecules like water, diatomic neutral gas molecules and even some small polyatoms. Indeed numerous investigations compute the potential of mean force and the average permeation rate using equation (1) and variants (for a review see⁷).

Equation (1) assumes that there is only one slow variable in the system (the position of the center of mass of the permeant along the normal to the membrane plane - z). While this choice is probably appropriate for small molecules like water and even the blocked tryptophan that we consider here, it is unlikely to prevail for peptides of considerable length. For larger permeants, orientational, translational and internal motions will become important for permeation. Those motions will be increasingly slower, more complex, and coupled more strongly to the membrane motions with permeant size. The use of a more general approach than solubility-diffusion model such as Milestoning will be necessary to study permeation of more complex systems.

In this work, we use Milestoning in one dimension (z) to study the permeation process of the blocked tryptophan through a DOPC lipid bilayer. While Milestoning can be used with a large number of coarse variables the present set-up is appropriate for this small permeant and allows us to make direct comparison with the solubility-diffusion model based on Equation (1), which is restricted to one dimension. Milestoning is a more detailed theory even in one dimension because it is not restricted to over damped kinetics. To further test our computational estimates for the mean first passage time we measure experimentally the unassisted permeation rate of N-acetyl-L-tryptophanamide (NATA) through DOPC and egg phosphatidylcholine (EPC) membranes using the PAMPA method³⁸ with the fluorescence intensity of NATA as a probe. Experiments and Milestoning results show permeation times in hours. This slow permeation is explained by unsatisfied hydrogen bonds that create a large barrier at the center of the membrane.

2. THEORY

2.1 Solubility-diffusion model

From simulations in which the permeant is constrained to particular membrane depth, z, the PMF can be computed according to:

$$\Delta G\left(\mathcal{z}\right)=-\underset{\mathrm{water}\mathrm{phase}}{\overset{\mathcal{z}}{\int }}\langle F_{\mathcal{z}}(\mathcal{z}\prime )\rangle d\mathcal{z}\prime$$ (2)

where $\langle F_{\mathcal{z}}\left(\mathcal{z}\right)\rangle$ is the average over the simulation time of the force along the z axis acting on the permeant molecules that keep them constrained at different $\mathcal{z}$ depths in the bilayer. The permeability coefficient P is obtained using the solubility-diffusion model (Equation (1)) where $D\left(\mathcal{z}\right)$ is the local diffusion of the permeant at depth $\mathcal{z}$ given by

$$D\left(\mathcal{z}\right)=\frac{{\left(RT\right)}^2}{{\int }_0^{\infty }\langle \Delta F_{\mathcal{z}}(\mathcal{z},t)\cdot \Delta F_{\mathcal{z}}(\mathcal{z},0)\rangle dt}$$ (3)

where $\Delta F_{\mathcal{z}}(\mathcal{z},t)$ is the instantaneous deviation of the force $F_{\mathcal{z}}(\mathcal{z},t)$ from the average force $\langle F_{\mathcal{z}}\left(\mathcal{z}\right)\rangle$.

Rather than comparing permeation coefficient, we prefer to consider the permeation time-scale. We can estimate the high friction limit of the mean first passage time τ, appropriate for the solubility-diffusion model, of diffusive motion from points a and b along the $\mathcal{z}$ coordinate with the following expression^39,40:

$$\langle \tau \rangle ={\int }_a^{b}d\mathcal{z}(\exp \left(\beta \Delta G\left(\mathcal{z}\right)\right)∕D\left(\mathcal{z}\right)){\int }_a^{z}d\mathcal{z}\prime \exp (-\beta \Delta G(\mathcal{z}\prime ))$$ (4)

2.2 Milestoning

Milestoning^{31,33–35,41} and Directional Milestoning^36,37 are a theory and an algorithm developed to enable the microscopic calculations of time scales and rates in complex systems. Among large systems investigated with Milestoning we find: (i) allosteric transition in Scapharca hemoglobin³³ and (ii) the recovery stroke in myosin⁴¹. The time scale investigated varies from nanoseconds³¹, to microseconds³³, and to milliseconds^41,42.

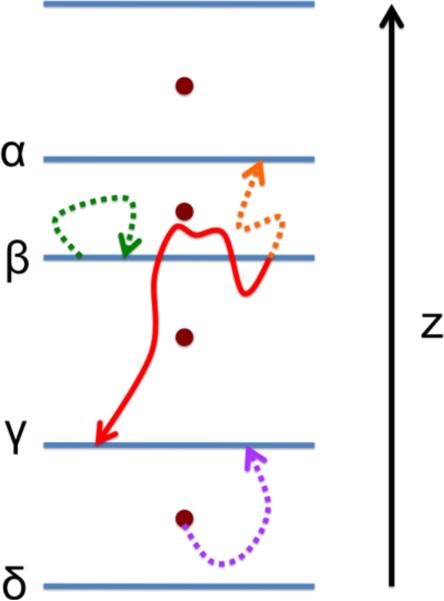
A Milestoning calculation starts with the identification of anchors. Anchors are sets of points in phase space that provide a coarse coverage of the accessible configurations and momenta for the system at hand^36,37. With anchors at hand, which in our case are distributed along the normal to the membrane (Figure 1), we are ready to define Milestones, M.

Figure 1.

A schematic representation of Milestoning along a single dimension (z axis). The circles denote anchors, the blue lines between them denote milestones, and the curves are trajectory fragments between milestones. The purple curve represents a trajectory in which the bottom anchor enters the γ milestone. The green, orange and red curves represent the kind of trajectories that were used in the present work. The green curve represents an unsuccessful trajectory for milestone β (it is not a first hitting point). The orange curve is a first hitting point trajectory because it reaches a neighbor milestone (α in this case) before hitting the originating milestone. A forward trajectory (red curve) is launched by reversing the velocity of the orange trajectory. A forward trajectory is stopped when a neighbor milestone is hit. Notice that a forward trajectory is not terminated when crossing the originating milestone.

Milestones are directional interfaces separating anchors. A Milestone between anchors i and j is the set of points Y such that

$$M_{\alpha }(i\to j)=\left\{Y\mid d{(Y,Y_i)}^2=d{(Y,Y_j)}^2+{\Delta }^2\mathrm{and}\forall kd(Y,Y_j)\le d(Y,Y_k)\right\}$$ (5)

The vector Y is defined in a coarse grained space^36,37. In the present application it is simply z. The distance is defined as $d(Y,Y_k)=\sqrt{\sum _l{[y_l-y_{lk}]}^2}$ (y_l is an element of the vector Y). For brevity we also use a single Greek letter to denote a Milestone (e.g. M_α is the Milestone α). The parameter Δ was introduced to avoid crossing of interfaces^36,37. It is not important when the milestones are exactly parallel to each other and therefore never cross, which is the present case with y=z. In Milestoning theory we assume de-correlation of fluxes between interfaces (milestones). If the Milestones cross, trajectories initiated near the crossing domain can be exceedingly short and violate the de-correlation condition. In the present investigation the interfaces are non-crossing by construction (Figure 1) and Δ was set to zero.

In Milestoning we consider the transition kernel between Milestones, K_αβ (t). It is the probability that a trajectory initiated at Milestone α will reach for the first time another Milestone β at time t (Figure 1). It is estimated from a set of trajectories as K_αβ (t) ≅ n_αβ (t)/n_α where n_α is the number of trajectories initiated at interface α (sampled from a first hitting distribution, see Section 3.2 and References³⁶,³⁷ for more details) and n_αβ(t) is the number of trajectories initiated at α that reached interface β at time t. Note that because the Milestones are close to each other these trajectories are much shorter than the overall time scale of the physical process under consideration. We typically use picosecond trajectories combined by the theory below to estimate very long time scales. A millisecond time scale was estimated for myosin⁴¹ and hours for membrane permeation (see below).

With the transition kernel at hand we solve coupled integral equations for the fluxes through the interfaces:

$$q_{\alpha }\left(t\right)=p_{\alpha }\left(0^{+}\right)\delta \left(t\right)+\underset{0}{\overset{t}{\int }}\sum _{\beta }{q}_{\beta }(t\prime )K_{\beta \alpha }(t-t\prime )dt\prime$$ (6)

The function p_α(t) is the probability that at time t the last interface that was passed is α, and q_α is the flux through interface α. Moments of K_βα (t) are the only entities that we estimate from short Molecular Dynamics trajectories.

A schematic view of anchors, Milestones, and trajectories between interfaces is shown in Figure 1.

A closed form solution to the integral equations can be found for the overall mean first passage time and for the stationary distribution^36,43 by solving Equation 6 analytically

$${\mathbf{q}}_{\mathit{stat}}(\mathbf{I}-\mathbf{K})=0p_{\alpha ,\mathit{stat}}=q_{\alpha ,\mathit{stat}}\cdot \langle t_{\alpha }\rangle \langle \tau \rangle =\mathbf{p}\cdot {(\mathbf{I}-\mathbf{K})}^{-1}\langle t\rangle$$ (7)

where q_stat is a vector of stationary fluxes at the Milestones (vector with components q_α ≡ (q)_α), I is the identity matrix, K is the matrix of the time-integrated local transitions between Milestones: ${\left(\mathbf{K}\right)}_{\alpha \beta }\equiv \underset{0}{\overset{\infty }{\int }}{K}_{\alpha \beta }(t\prime )dt\prime$ and 〈t_α〉 is the average time that takes a trajectory initiated at Milestone α to reach for the first time another Milestone $\langle t_{\alpha }\rangle \equiv \underset{0}{\overset{\infty }{\int }}\sum _{\beta }t{K}_{\alpha \beta }\left(t\right)dt$. 〈t〉 is a vector of all the average life-times of different Milestones (〈t_α ≡ 〈t〉_α), and 〈τ〉 is a vector of the overall mean first passage times of the system starting from each of the Milestones and reaching the product (absorbing) state. If the system obeys first-order exponential kinetics the inverse of 〈τ〉 from the Milestones of the reactant is the rate constant. The theory also allows to compute higher moments of the overall mean first passage time and to explore non-exponential kinetics^34,36,43.

Equation (7) is a central result of the Milestoning theory. It makes it possible to obtain the stationary probabilities, the logarithms of which (if the system is in equilibrium) corresponds to the free energy profile. This relationship is important here since it allows us to compare and test Milestoning with respect to other well-established techniques, such as the solubility-diffusion model, that compute thermodynamic properties (but are not as general as Milestoning for the calculations of kinetics).

3. SIMULATIONS

3.1 The set-up of the system

The simulated bilayer system contained 40 DOPC lipid molecules, 1542 water molecules and 2 NATA (N-acetyl-L-tryptophanamide) molecules. For reference purpose we also simulated side chains of tryptophan patched with a hydrogen atom at the dangling bond, pointing to the C_α position, and replacing the NATA molecules. The size of the simulation cell is 37 × 37 × 75 Å, with the z axis perpendicular to the bilayer surface. This small simulation box is appropriate for permeation of a single amino acid. The side chain and backbone atoms of NATA are modeled with the OPLS united-atom force field⁴⁴ and the Berger force field⁴⁵ parameters were used for the lipid molecules. Water molecules were represented with the SPC model⁴⁶. Periodic boundary conditions were applied in the three spatial directions. The long-range component of the electrostatics interaction was calculated using the smooth Particle Mesh Ewald method⁴⁷ with a grid of 32 × 32 × 64 as implemented in our program MOIL⁴⁸. The simulations were conducted on a newly optimized version of MOIL that is able to exploit the power of graphic processing units (GPU)⁴⁹. The sampling for the potential of mean force calculation and starting points for Milestoning were conducted on a local cluster of GPUs. The real space cutoff for the electrostatics and the van der Waals interactions was set to 9.0 Å. In all the simulations we constrain water bond lengths and angle with a matrix version⁵⁰ of the SHAKE algorithm⁵¹, and r-RESPA⁵² was used to have a dual time stepping; the reciprocal-space component of the Ewald sum was evaluated every 4 fs and the rest of the forces were evaluated every 1 fs.

The initial coordinates for the lipid/water system were taken from a larger pre-equilibrated DOPC box (with 128 lipid molecules) from Siu et al.⁵³. After reducing the number of molecules of the system, a short minimization with a conjugate gradient method was performed followed by four 500 ps MD simulations to heat the system to 300K and equilibrate it under the smaller box conditions described above.

After 2 ns of membrane equilibration time, we added two NATA molecules into the system (one in each layer) and performed umbrella sampling simulations (Figure 2). The two molecules are sufficiently separated from each other and their correlation can be ignored.

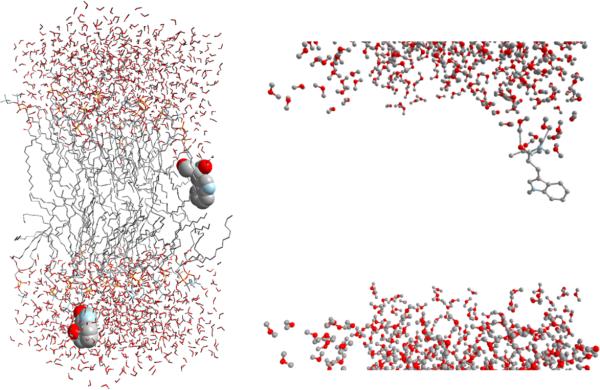
Figure 2.

A molecular snapshot from one of our simulations. Space-filling is used to represent the two NATA molecules. Carbon and hydrogen atoms are in grey, phosphorus atoms in yellow, nitrogen atoms in blue, and oxygen atoms in red. The bilayer center is at z = 0. The permeant in the top lipid layer is located at z = 3.5 Å and the one in the bottom layer at z = −28.5 Å. The former orients such as the backbone atoms point to the aqueous phase at the top and the aromatic ring points to the center of the bilayer. Note the water molecules wetting the backbone side of this molecule. This can be seen better in the close-up view on the right (the lipid atoms were removed to facilitate the view of the hydrogen bonds formed by three water molecules). See section 5 for further discussion.

Using two molecules makes it possible to obtain more statistics and/or evaluate the convergence of the results. In the umbrella sampling simulations, we applied a harmonic restraining force of 7 kcal/mol to each molecular center of mass to keep them at different positions along the normal of the bilayer. The location of the biasing potential in consecutive windows was separated by 1 Å. In each simulation, the centers of the two NATA molecules were separated by Δz = 32 Å to minimize their interaction. The use of two NATA molecules allowed us to cover the range of z = −32 Å to z = 32 Å with only 33 milestones. Each of these simulations was run for 50 ns and structures were saved every 1 ps. Only the last 20 ns structures were used for further analysis and as starting spatial configurations for the Milestoning simulations. Such lengthy simulations at each window were absolutely necessary to obtain converged properties and are a clear evidence for the existence of other slow variables at the nanoseconds time scale. A few additional constrained simulations were performed at half Angstroms location (3.5, 6.5, 9.5, and 12.5 Å from the center of the bilayer) to improve statistics in the Milestoning calculations (see below). Finally we also extend the calculations near the top of the barrier (z= −2, −1, 0, 1, 2 Å) to 100 ns instead of 50 ns to further examine the convergence of the simulations.

All the simulations were performed at constant volume and energy. The NVE ensemble is the most appropriate for simulation of time dependent properties using microscopic atomically detailed models. The volume of the cell has an area per lipid of 68.5 Ų, close to the experimental value of 72.1 Ų. The umbrella sampling simulations were performed in GPU-equipped computers with a newly developed MD code that has been especially calibrated to minimize the total energy drift in long MD trajectories. The typical relative deviation of the energy after 50 ns simulations was less than 0.05%. The initial velocities were drawn from a Maxwell distribution of velocities at 300 K. No temperature drifts occurred during the simulations and the standard deviation was ±2.7 K. Hence our NVE ensemble mimics well (due to the large box size) the NVT ensemble.

To compare Milestoning to another approach (the solubility-diffusion model^2,3) we conduct Milestoning calculations along the one dimension of the normal to the membrane plane. We use planes normal to the bilayer surface as Milestones with the location of each plane corresponding to one of the locations of the harmonic restraining potential used in the umbrella sampling calculations. Initial configurations were taken from the last 20 ns of each umbrella sampling simulations.

3.2 Milestoning simulations

The distance separating the Milestoning hypersurfaces varies depending of their location with respect to the center of the bilayer. Milestones close to the bilayer center are separated by 1.5 Å while the separation is 2 Å for milestones more than 14 Å away from the center. These changes were done to increase the statistics for the number of trajectories moving to the center of the bilayer where a barrier is located (Section 5.2.2) and are typical in Milestoning calculations in which the exact position of the interfaces can be adjusted (with respect to uniform) to maximize efficiency.

The system set-up for the Milestoning calculations was similar to the one described before for the umbrella sampling simulations. The only difference is that in order to calculate the transition kernel K_αβ (t) for a given Milestone α, the harmonic restraint was removed for the permeant located at Milestone α but it was kept on the second permeant.

The Milestoning protocol that we followed has two stages (see Figure 1). In the first stage, we check if the initial spatial configurations (from the umbrella sampling simulations) and velocities (assigned according to a Maxwell distribution at 300K) correspond to a first hitting point for the milestone of interest^36,37. This was done by performing a molecular dynamics simulation and checking if the center of the free NATA molecule hits a neighboring milestone before hitting its starting milestone. If that happened, the attempt was considered successful and the phase point information was saved for the second stage.

In the second stage, we launch new MD trajectories using the first hitting points generated in the first stage. The particle velocities of the second stage are reversed with respect to the saved velocities of the first stage. These trajectories are stopped when the center of the free NATA hits a neighboring milestone regardless if the initial milestone is crossed or not. The information needed for the Milestoning equations (Equation 7) to estimate the equilibrium density and the overall mean first passage time is then extracted. Those are the identity of the milestone hit and the time it takes to hit a neighboring milestone. These entities correspond to the zero and first time moments of transition kernel K_αβ (t) and we need these moments for all αβ pairs of nearby milestones.

Thirty-five milestones were used in the calculations (17 for each lipid layer plus the milestone at the center of the bilayer). The total number of trajectories launched at each milestone varied but a typical number was 400. This set of trajectories was used to compute the corresponding transition kernel. The length of the trajectories varies from tens to hundreds of picoseconds. A rough estimate of the total simulation time required for the Milestoning calculation is about 4 microseconds, much slower than the hour time scale that we predict for the permeation process, and significantly easier to compute (due to trivial parallelization of many trajectories) than a single 4 microsecond trajectory. Therefore results can be obtained in days (instead of weeks) using available clusters.

4. EXPERIMENTAL SET-UP

4.1 Material

Egg yolk phosphatidylcholine (lecithin; L-α-phosphatidylcholine; EPC) and DOPC (1,2-Dioleoyl-sn-glycero-3-phosphocholine) were purchased from Avanti Polar Lipids (Alabaster, AL). The protected and unprotected amino acids, sodium acetate, sodium phosphate monobasic, sodium phosphate dibasic, phosphate buffered saline tablets (P-4417), 1,9-decadiene (Aldrich 118303), cresyl blue, and lucifer yellow were purchased from Sigma (St. Louis, MO). Hydrophobic filter plates (0.45 μm PVDF Membrane without underdrain; MAIPNTR10) and the 96-well disposable transport receiver plates (MATRNPS50) were purchased from Millipore Corporation (Billerica, MA).

4.2 Experimental procedures

The parallel artificial membrane permeation assay (PAMPA) was proposed by Kansy et al. in 1998³⁸. This procedure has provided a straightforward approach to measure unassisted permeation and has been widely used to study oral absorption, blood-brain barrier penetration, and skin permeation. The PAMPA was used as it has been published previously^38,54–60. N- and C- termini protected L-tryptophan (NATA) and unprotected (charged) L-tryptophan (TRP) were prepared at a concentration of 180 μM for all of these measurements. Samples were prepared by dissolving the powdered form of NATA and TRP in 20 mM sodium acetate buffer for a pH 4.8, and 20 mM sodium phosphate buffer for a pH 7.2. Lipid solutions (5% w/v) of EPC and DOPC were prepared in 1,9-decadiene. Very careful sonication was applied to EPC and DOPC to ensure complete dissolution. A 96-well receiver microplate (acceptor compartment) was filled with 280 μL of the corresponding buffer, and the PCC filter plate (donor compartment) was fused on the buffer-filled acceptor plate. The measurements were carried out at both 310 K and 296 K. The lipid solutions (5 μL) were carefully added onto the filter surface avoiding pipette tip contact with the filter. Immediately after, the corresponding amino acid samples (150 μL per each well) were applied to the filter plate. Samples and lipid were pipetted on every 3 hours and the experiment was terminated at 30 hours. The fluorescence intensity of the sample was monitored with a Fluorolog (Horiba Jobin Yvon Inc., Edison, NJ) with the excitation wavelength set to the 280 nm for NATA. Membrane integrity was tested with Lucifer yellow and Cresyl blue.

5. RESULTS AND DISCUSSION

5.1 Experiment

The translocation of NATA was determined across DOPC and EPC lipids over a 30 hour time period. The rate of translocation was determined by fitting the curve produced by the fluorescence intensity change as a function of time. These experiments were performed at 296 K and 310 K. Lucifer yellow and Cresyl blue were used as positive and negative controls, respectively. The integrated fluorescence intensities were plotted against time in order to obtain the rate of translocation in each case (Figure 3).

Figure 3.

Observed rate of membrane permeation of N-acetyl-L-Tryptophan-Amide (NATA) at two different pHs (pH 4.8, pH 7.2), two different temperatures (296 K, 310 K) and through two different lipid bilayers (DOPC, EPC). Integrated fluorescence intensities of NATA as a function of time are shown at 310 K (X) and 296 K (•) in DOPC and in EPC. (A) NATA in DOPC at pH 4.8, (B) NATA in DOPC at pH 7.2, (C) NATA in EPC at pH 4.8, and (D) NATA in EPC at pH 7.2. Repeating the measurements three times tests the reproducibility of the measurements.

The observed rates are in hours with moderate dependence on temperature. There is a measurable dependency of the time scale on lipid type and pH, but the overall permeation does not deviate significantly from the hour time scale.

The translocation of TRP was determined in an identical manner across DOPC and EPC lipids over a period of 30 hours. However, these experiments have proven to be difficult to converge and interpret. The fluorescence intensity of the permeated molecules is about 1,000 times weaker compared to the ones reported for NATA. We were unable to reach curve saturation in 30 hours of experiment and the population growth is clearly non-exponential. The difficulty in the interpretation of experimental observations prevent us at this time to report the results in greater detail, with the exception of the qualitative observation that the charged amino acid permeates much more slowly that the neutral molecule.

5.2 Simulations

In Figure S2 (Supporting Information), we consider the structural properties of the lipid membrane to test that the simulation is sound and producing distributions similar to experiments and other simulations. Here we consider the impact of the permeant on the structure of the membrane, discuss the origin of this perturbation, and then compare the MFPT and free energy profiles obtained by Milestoning and the solubility-diffusion model.

5.2.1 Bilayer structure and solute perturbation

A detailed analysis of the density profile changes when the permeant is added (Figure S3, Supporting Information) shows distortions of the membrane structure that becomes maximal when NATA is ~4 Å away from the membrane center. It is observed that the phosphate and glycerol groups tend to move closer to the center of the bilayer as the permeant gets deeper. Perturbations of the hydrocarbon distribution are also observed because several CH₂ groups are displaced by these phosphate and glycerol groups that are moving away from their normal positions. These perturbations diminish when the permeant is at the center of the bilayer. The center is low in density and that reduces the impact of the permeant at that position.

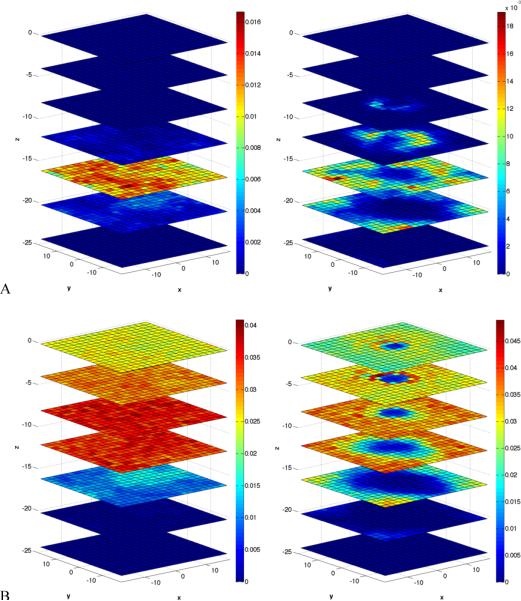
A detailed view of the spatial locations of the defects caused by the permeant is illustrated by a series of 2D density slices along the z axis (Figures 4 and 5). We compare the surfaces in the absence of the permeant to a system where the permeant is placed at the location of maximal perturbation according to the density profiles of Figure S3. The perturbations of the densities of the hydrocarbon chains, phosphate, and glycerol are striking as well as the tendency of water to penetrate closer to the location of the permeating NATA. This hydrating finger is not only formed by a water column (Figure 4A) but it also contains contributions from the phosphate (Figure 4B) and glycerol (Figure 5A) groups. The presence of this finger distortion creates a distinctive hole in the hydrocarbon density closer to the permeant (Figure 5B).

Figure 4.

Cross sections in the xy plane of the water (A) and phosphate group (B) densities. Left side (no permeant) and right side with permeant at z = −4 Å. Blue means no density and red maximum density. The separation between the planes is 4 Å. The top cross section corresponds to the center of the bilayer (z = 0 Å). The cross section z = −4 Å is the second from top. Note that the density is computed in a domain not perturb by the second permeant. Configurations were obtained from the last 20 ns of the corresponding umbrella sampling simulation with the permeant located at the center of the xy plane for this analysis.

Figure 5.

Cross sections in the xy plane of the glycerol group (A) and CH₂ (B) densities. Left side (no permeant) and right side with permeant at z = −4 Å. For more details see caption of Figure 4.

What is the reason for the formation of these defects? NATA is stabilized in aqueous solution by the formation of hydrogen bonds. It can donate towards hydrogen bonding 3 hydrogen atoms and provide acceptors to 5 polar hydrogen atoms. During the permeation, the permeant tries to preserve as much as possible these hydrogen bonds as it progresses more deeply into the bilayer. Only when NATA is close to the center (z < 3 Å away) are most of the hydrogen bonds dropped (Figure 6). Nevertheless, even at the membrane center the average number of hydrogen bonds to water molecules is still not zero. In the range between 7–16 Å there is a similar contribution of water and lipid molecules to the formation of hydrogen bonds with the permeant. Outside of that range water molecules have a bigger contribution. The mechanistic picture suggested by these results (see also figures 4 and 5) is that water molecules assist in the permeation process of NATA providing needed hydrogen bonding. Glycerol groups and (with less extent) phosphate groups also have a contribution toward hydrogen bond formation to the permeant. These groups can also contribute to the stabilization of the water fingerings observed during the simulations (Figure 2). For example, Figure 5A shows that glycerol atoms partially surround the water finger.

Figure 6.

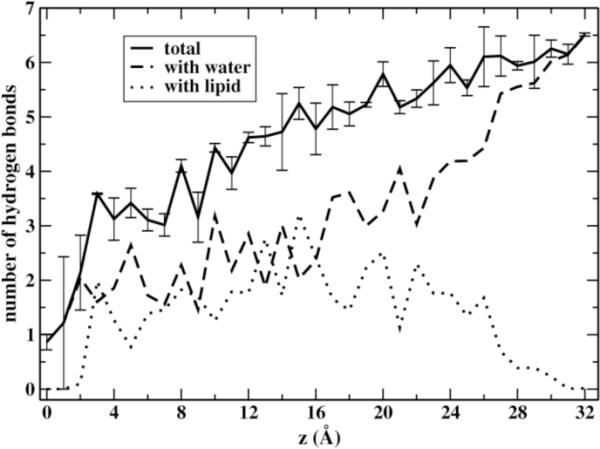
Changes in the number of hydrogen bonds accessible to the permeating blocked tryptophan. Shown are the total number of hydrogen bonds (solid line), hydrogen bonds with water molecules (dashed line) and with lipids (dotted line). These are averages over the two layers. Error bars for the total number of hydrogen bonds are estimated from the values in each layer.

Formation of water fingers was described before for permeation of polar amino acid analogous such as the side chain of asparagine (acetamide)¹⁷. They observed that when the permeant was at the center of the bilayer the water defects dissipate. In our case, the water defects are observed transiently when the blocked tryptophan is at the membrane center. When the permeant is slightly displaced from the center the water perturbation becomes permanent on the average. The identity of the water molecules present in the water finger is constantly changing. The residence time in the finger can vary from a few tens of ps to 5 ns, and even longer (Figures S4 and S5, Supporting Information). The presence of the permeant and water fingers seems to increase the probability of water permeation through the membrane. In the absence of permeant we did not observe any translocation of water during the last 20 ns of a MD simulation. But when the permeant was in the center, the results of two independent simulations produce 3 and 2 water permeation events. The statistics is poor but it suggests that the presence of the permeant perturbs the local integrity of the membrane and increases the probability that water explores deeper regions of the membrane.

To further examine the convergence of transient water permeation into the membrane we compute the number of water molecules close to the membrane center as NATA permeates. We compare the results for both layers in Figure 7.

Figure 7.

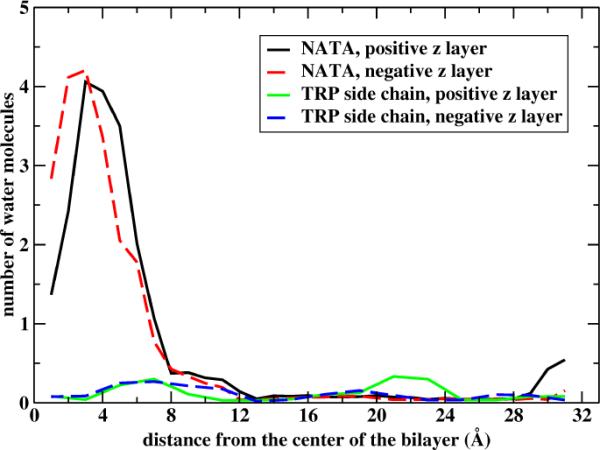
The number of water molecules permeating to the membrane. The number of water molecules within 10 Å from the membrane center is shown as a function of the center of mass position of NATA (black and red curves for the two layers of the membrane) and of the tryptophan side chain (blue and green lines for the two layers of the membrane).

The significant permeation of water molecules that follow a neutral molecule is surprising. We therefore want to compare our NATA results to yet another molecule for which other simulations are available. We simulate the permeation of tryptophan side chain using the same protocol as NATA in which 50 ns are used for each umbrella window. As is clear in figure 7 the side chain of the tryptophan is unsuccessful in bringing water molecule to the membrane center.

For an exact average the black and red (and blue and green) curves of Figure 7 should be identical. The statistical errors are, however, not large. Note also the striking difference between NATA and the side chain (only) of the tryptophan molecule. The blue and green lines of the side chain show almost no water permeation to the membrane. The water permeation is assisted by hydrogen bonding to the backbone of the tryptophan molecule, hydrogen bonding which is missing for the side chain.

We further examine the properties of permeant-assisted water translocation in figure 8 in which we show the fluctuations of the number of water molecules coming within 10 Å from the bilayer center as a function of time when the permeant is fixed at 4 Å from the membrane center.

Figure 8.

Following the number of water molecules that permeate the membrane in the presence of each of the two permeants, NATA and the side chain of tryptophan. The permeants are fixed at two locations z=−4 Å and z=4 Å to check statistical convergence. The number of water molecules fluctuates significantly, however, the fluctuations are similar after about 10 nanoseconds. Note that the water permeation is smaller for the side chain.

To help the formation of these favorable hydrogen bond interactions the permeant adopts an orientation such that the more polar backbone atoms point to the aqueous phase (Figure 2). This impacts also the orientation preferences of the amino acid as a function of membrane penetration. In figure 9 we illustrate that the permeating molecule favors this orientation at the two sites of the barrier. This type of orientational preference driven by hydrogen bonding was also suggested by Bemporad et. al⁶¹ in their simulations of three drugs but at a shorter time scale (2 ns) where equilibration of these motions was more difficult to attain. Our results of 50 ns of simulation time were also not always enough to adequately sample this degree of freedom of the permeant (see the large error bars when the permeant is at z = 6 Å).

Figure 9.

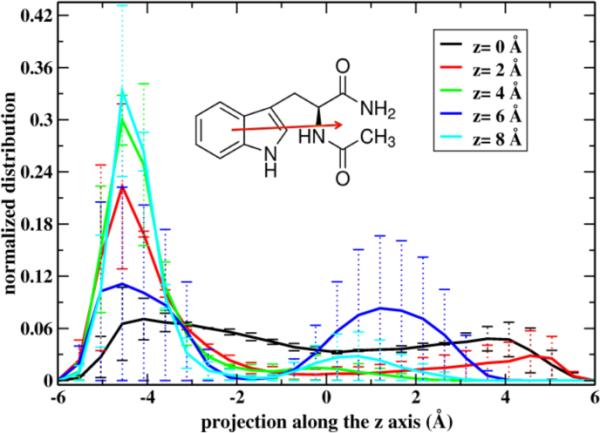
The distribution of the projection of the orientation vector of NATA with respect to the membrane normal. The orientation vector is defined as a vector connecting the center of masses of the side chain and backbone atoms of the amino acid (inset).

When the projection is negative the polar groups are pointing in the direction of the closest water layer. The solid lines are the averages over the two layers. The legend shows the distance of the permeant from the center.

5.2.2 Mean First Passage Time (MFPT) and free energy barrier

The overall mean first passage time for permeation through the bilayer center is estimated with the Milestoning calculations to be 3.8 hours. This is an average over the two NATA molecules and the two layers. The results for the individual layers are 7.5 (negative z layer) and 0.05 (positive z layer) hours so the uncertainty is large. The permeability-diffusion model gives 0.23 hours (0.41 and 0.05 hours for the negative and positive z layers, respectively). Increasing the sampling at the top of the barrier z=(−2, −1, 0, 1, 2 Å) decreases slightly the difference between the two layers. Estimating corresponding times from the experimental curves of Figure 3 suggests ~8 hours for the transition.

The time scale for downhill permeation (from the center of the bilayer to the aqueous solution) obtained with Milestoning is 1.6 μs (negative z layer) and 265 μs (positive z layer). The solubility-diffusion model gives 0.6 μs and 13 μs, respectively. So even a downhill calculations by straightforward Molecular Dynamics is a significant challenge.

It is shown in Figure 10 a comparison between the free energy profiles using Milestoning and the solubility-diffusion model. The agreement is remarkable considering that the two approaches are very different. In Milestoning the thermodynamic data is computed by estimating the long-time limit of a Generalized Master Equation³⁵, a kinetic model. The calculation with umbrella sampling does not involve kinetics and is based on the integration of a force at a fixed z position that is thermodynamically averaged (Equation (2)). An important difference between the two profiles is at the top of the barrier where the permeant flips its orientation and convergence is slow (see also Figure 9). In this case, the strategy described by Wei and Pohorille¹⁰, or Directional Milestoning^36,37 is likely to improve the sampling and make the free energy profiles computed by both methods more similar. Still, computing permeation times with the solubility-diffusion model is not equivalent to Milestoning. In the first method a diffusion constant is estimated, and over damped dynamics is assumed (Eq. (4)). In Milestoning transitional trajectories (with Newtonian mechanics) are computed explicitly.

Figure 10.

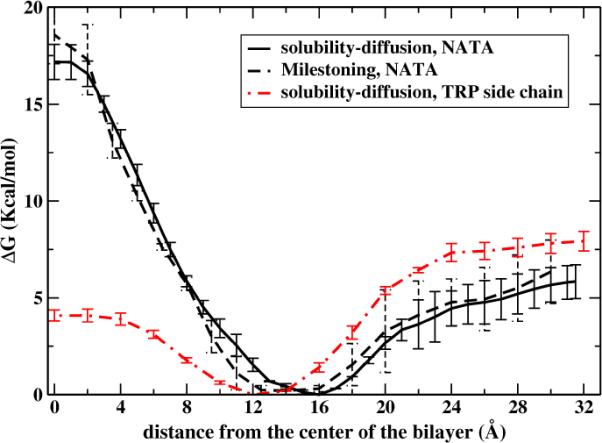
A comparison between the potential of mean force for NATA permeation obtained with the solubility-diffusion model (solid line) or with Milestoning (black dashed line). The zero z position is the center of the membrane. The potential is an average over the two layers, and the error bars are estimated from the values of each layer. Also shown is the potential of mean force computed for the permeation of tryptophan side chain. The last calculation compares favorably with the results of other simulations¹⁷.

MacCallum et al.¹⁷ used umbrella sampling simulations to determine the distribution of methylindole (an analogue to the tryptophan side chain) permeating through a DOPC lipid bilayer at 298 K. Using our simulation set-up we also computed the PMF for this TRP side chain analogue. Comparison of the free energy profile of methylindole (figure 2C of that paper, and red plot in our Figure 10) and the NATA results show a similar preference to occupy the region 12–16 Å away from the bilayer center that contains both hydrophobic groups and the edge of the lipid headgroups. The amphiphilic NATA and methylindole fit well in that region. The most notable difference is the large barrier at the center observed with NATA (~18 kcal/mol in our Milestoning calculation) compared to methylindole (~4 kcal/mol). The bigger structural difference between both permeants is the presence of more atoms with hydrogen bond capabilities in NATA. To satisfy those hydrogen bonds NATA is forced to adapt preferential orientations and when it gets closer to the bilayer center the structure of the lipid is distorted to help in the formation of these hydrogen bonds. The permeation process becomes very rare but still possible to study with Milestoning.

It is shown in Figure 11 local first passage time distributions for two Milestones. The time distributions for trajectories starting at the membrane center (top figure) is symmetric as expected for trajectories going to the neighboring milestones at z = −2 and 2 Å. The agreement between both distributions also confirms that the effect of the constrained permeant in the Milestone simulations of the mobile permeant was negligible. The residence time is short (27.6 ps for the black distribution and 28.6 ps for the red distribution). The distributions are different when the Milestone is at the steep part of the barrier (|z| = 8 Å). In that case more than 90% of the trajectories reach milestone at |z| = 9.5 Å before milestone at |z| = 6.5 Å. The average times of transitions to |z| = 9.5 is 46 ps and for transitions to |z| = 6.5 is 65 ps. If the local transition process were Markovian the transition kernel would be of the form (K)_αβ ∞ exp(−k_αt). If the analogy is pursued further, the formula below defined the rate coefficients for the Master equation:

$$\begin{array}{cc}\hfill \frac{d{P}_{\alpha }}{dt}& =\sum _{\beta \ne \alpha }{k}_{\alpha \beta }{P}_{\beta }-\sum _{\beta \ne \alpha }{k}_{\beta \alpha }{P}_{\alpha }\hfill \\ \hfill k_{\alpha \beta }& =\frac{{\int }_0^{\infty }{K}_{\alpha \beta }(t\prime )dt\prime }{{\int }_0^{\infty }\sum _{\beta }t\prime K_{\alpha \beta }(t\prime )dt\prime }\equiv \frac{K_{\alpha \beta }}{\langle t_{\alpha }\rangle }\sum _{\beta }{k}_{\alpha \beta }=k_{\alpha }=\frac{1}{\langle t_{\alpha }\rangle }\hfill \end{array}$$ (9)

Figure 11.

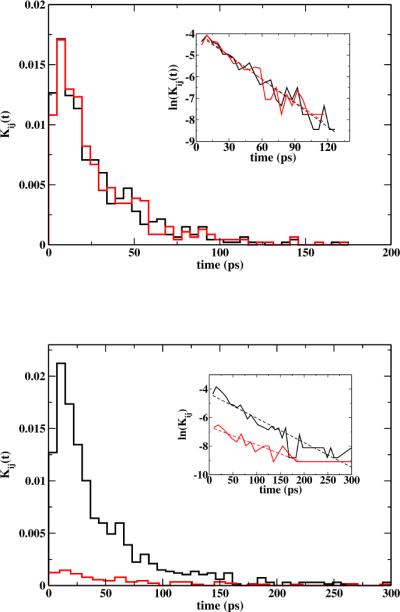
Local first passage time distributions for milestones located at (top) and z = 0 z = 8 Å (bottom). In the top figure, the time distributions for trajectories that reach milestone Å are in black and z = 2 z = −2 Å in red. In the bottom figure, black correspond to the time distributions for trajectories ending at z = 9.5 Å and red for the ones ending at z = 6.5 Å. The insets show corresponding linear fitting of ln K_ij versus time. For the fitting, we remove points with K_ij = 0 and outliers at the long tails. Correlation coefficients for the fitting were bigger than 0.94 in all cases but the red plot at the bottom that has correlation coefficient of 0.90.

It should be noted though that this formulation of the Master equation^34,62 is different from the common implementation of Markov State Models (MSM)^63–65. Milestoning uses interfaces, MSM uses states, though a unification of some of the ideas of the two formulations have been made⁶⁶. The observation that the decay in time of K_αβ (t) depends only on a single time constant can be put into a test. If correct we should have the same time-decay constant for K_αβ (t) namely k_α. For the central milestone, with (K)_αβ ≈ 0.50 the two rate coefficients extracted from an exponential fitting, k_0→2 = 3.7 ×10⁻² ps⁻¹ and k_0→−2 = 3.5 ×10⁻² ps⁻¹ are similar and satisfy this relation. The fitted value of 〈t_α〉 = 27.8 ps is in agreement with the residence time from the distribution (28.1 ps). Trajectories leaving the milestone at |z| = 8 Å, where K_8→9.5 = 0.91 the two rate constants obtained by the exponential fitting were k_8→9.5 = 1.7 ×10⁻² ps⁻¹ and k_8→6.5 = 1.2 ×10⁻² ps⁻¹. Hence, the Markovian assumption is less satisfactory in this case.

The experimental results reported above are in qualitative agreement with the experiments of Chakrabarti and Deamer^21,67 in the sense that the charged amino acid permeates a lot slower than the neutral molecule. However, quantitatively the results are different. The permeation coefficient for the neutral molecule in Chakrabarti and Deamer's experiment is close to the permeation coefficient of water (P = 10⁻² cm sec⁻¹) while our's is considerably slower (P~10⁻⁷ cm sec⁻¹). It is not clear why the permeation of NATA is comparable to permeation of a water molecule. They use unilamellar vesicles and not a planar membrane. Our experiments consider only a concentration gradient. Their experiments were conducted under pH transmembrane gradients. However, the five order of magnitude difference in the experimental results is unlikely to be explained by these differences. We anticipate that more experiments using different experimental techniques will be required to solve this discrepancy.

We further comment that the experimental measurements are consistent with the simulations presented here. The same simulation protocol was also used to study the potential of mean force of the tryptophan side chain and yields a central barrier of ~4kcal/mol in agreement with other simulations¹⁸. Hence our surprising experimental and computational result that neutral molecules can permeate extremely slowly is supported by further experimental evidence and consistency checks of the simulation protocol.

The dramatic difference between tryptophan side chain and NATA suggests a significant role of unsatisfied backbone hydrogen bonds that create a membrane barrier. Water fingers somewhat reduce the permeation time scale but the overall mean first passage time remains very high.

6. CONCLUSIONS

In the present paper we consider a permeation process of a midsize molecules (NATA) through a DOPC membrane bilayer. Both experiments and simulations were conducted, illustrating a strikingly slow process with a time scale of hours. The overall agreement between kinetic experiment and the two computational methods increases our confidence in the results. The result is particularly intriguing since investigations of the permeation of the side chain alone (and repeated by us) reveal a free energy barrier¹⁷ smaller by at least a factor of 4. The importance of hydrogen bonds of the backbone is clearly illustrated. This requirement makes it necessary for the peptide chain to exceed critical size (such that most of the hydrogen bonds are satisfied internally) before permeation can be conducted rapidly. Investigations of the critical size of membrane permeating peptides will be a topic of future work. For more complex systems the inclusion of additional coarse-grained variables, besides the z coordinate used in this work, will be necessary. We expect that in these cases that go beyond the approximations used by the solubility-diffusion model, Milestoning will provide meaningful estimates of the permeation rate and insights into the unassisted permeation process.