Differential confounding of rare and common variants in spatially structured populations

Abstract

Well-powered genome-wide association studies, now possible through advances in technology and large-scale collaborative projects, promise to reveal the contribution of rare variants to complex traits and disease. However, while population structure is a known confounder of association studies, it is unknown whether methods developed to control stratification are equally effective for rare variants. Here we demonstrate that rare variants can show a systematically different and typically stronger stratification than common variants, and that this is not necessarily corrected by existing methods. We show that the same process leads to inflation for load-based tests and can obscure signals at truly associated variants. We show that populations can display spatial structure in rare variants even when F_ST is low, but that allele-frequency dependent metrics of allele sharing can reveal localized stratification. These results underscore the importance of collecting and integrating spatial information in the genetic analysis of complex traits.

Introduction

Quantifying the contribution to of rare variants to the heritability of different traits is an important and open question in complex trait genetics¹. While there is no universally accepted definition of what constitutes a ‘rare’ variant, a minor allele frequency (MAF) of 1% is the conventional definition of polymorphism². At this frequency, the power of the current generation of genome wide association studies (GWAS) is negligible for modest effect sizes³. Therefore, although a small number of associations with rare variants have been reported, for example with type 1 diabetes⁴ and cholesterol levels^5,6, it has not been possible to test the hypothesis that rare variants account for a significant proportion of the missing heritability for most complex traits. Recently, however, four factors have combined to make the direct investigation of rare variants possible. First, the increasing size of GWAS samples and meta-samples, now approaching cohort sizes of 100,000 through large-scale international collaborations, boosts power. Second, the ascertainment of many rare variants through the 1000 Genomes project⁷, has enabled imputation of millions of rare and low frequency variants and led to the development of a new generation of low-cost genotyping platforms that interrogate rare variants directly. Third, the decline in the cost of sequencing technology has enabled large scale sequencing studies to be performed which in principle allow the detection of all variants in a sample. Finally, the recent development of new statistical tests for association aimed at rare variants^8-13 (reviewed in ref. 14) potentially provides power to detect genes or pathways harbouring multiple rare variants for which there would be individually low power to detect association.

The large sample sizes required for such studies typically require combining information across multiple geographic locations, within and across countries. Population structure, which can lead to spurious correlations between allele frequencies and non-genetic risk factors, has long been known to be a major potential confounding factor for association studies^15-17. The effects of stratification have been studied extensively^18-20 and testing and correcting for structure is now standard practice in GWAS through methods such as genomic control (GC)^21,22, principal component analysis (PCA)²³ and mixed models²⁴. However, analyses of these methods have typically concentrated on common variants and there has been little investigation of the effect that structure might have specifically on rare variants. Informally, rare variants, through being typically recent, may tend to have different geographic distributions than more common and typically older variants.

We therefore set out to investigate (a) under what conditions population structure will lead to differential test-statistic inflation for variants of different frequencies, (b) whether methods effective for controlling stratification of common variants are also appropriate for rare variants, (c) whether different ways of analyzing rare variants (single-marker versus aggregating) are equally affected by structure and (d) how best to measure population structure in empirical data in a manner that is informative about differential stratification. We used a simple lattice model to approximate population structure across a geographical region and investigated the interaction between the spatial distribution of non-genetic risk and inflation of standard association tests under the null model of no genetic risk (Online methods). We contrasted the situation where non-genetic risk is smoothly distributed (for example, a latitudinal effect) with the situation where the same overall risk is concentrated into one or more small, sharply defined regions (for example, localized environmental pollution).

Results

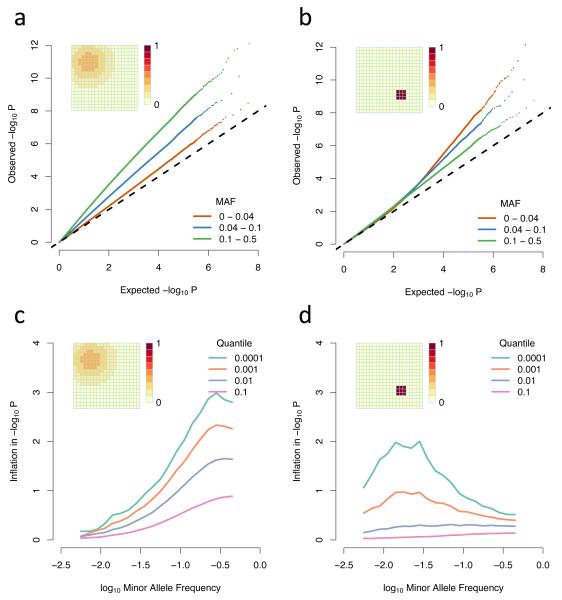
As is well documented, population structure leads to inflation of association test statistics under the null and hence systematic underestimation of P-values. When the risk has a wide and smooth distribution, rare variants show less inflation than common variants (Fig. 1a, c). In contrast, when the risk has a small, sharp spatial distribution, rare variants show more inflation than common variants, particularly for small P-values (Fig. 1b, d). The magnitude of inflation increases as the P-value decreases in both scenarios and the greatest inflation is for variants with frequency approximately equal to the fraction of the area with elevated risk (Fig. 1c, d). As the size or smoothness of the area of risk increases, the inflation is spread over a wider range of P-values (Supplementary Fig. 1 and 2).

Figure 1. Differential inflation of rare and common variants.

(a-b) QQ plots of association test P-values, broken down by allele frequency for (a) a broad, smoothly (Gaussian) varying non-genetic risk factor and (b) a small, sharply defined region of constant non-genetic risk; (c-d) Inflation plots showing the amount by which the observed −log₁₀ P-value exceeds the expected value across allele frequencies. Different lines represent different levels of significance, with −log₁₀ P-value equal to 1,2,3 or 4; The grids in the top left of the pictures represent the spatial distribution of risk and the scale indicates by how many standard deviations the phenotypic mean is shifted in each grid square. The populations simulated here are uniformly distributed over the grid, with two individuals in each square, and a migration rate of 0.01.

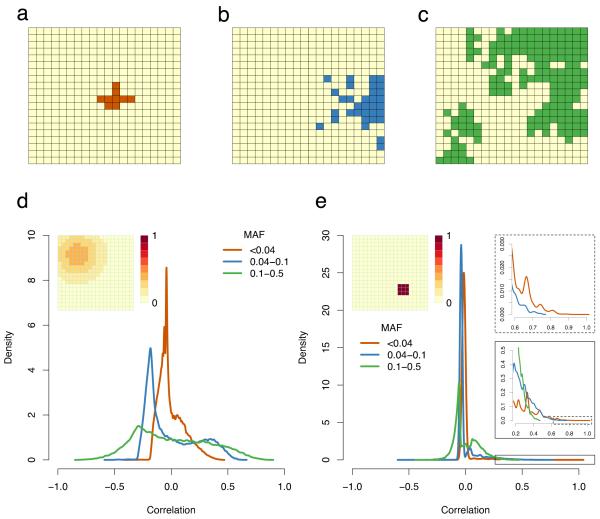
Such differential behaviour can be understood as a result of the interaction between the spatial distribution of risk and the spatial distribution of variants. Small P-values occur when a variant shows strong correlation with the non-genetic risk. Rare variants, through being recent, tend to show greater geographic clustering than common ones (Fig. 2a-c). When non-genetic risk varies on a large scale, rare variants cannot be highly correlated with it (Fig. 2d). In contrast, when non-genetic risk varies on a small scale, although most variants are uncorrelated with the risk, rare variants have a tail of highly correlated variants (Fig. 2e), which drive the inflation

Figure 2. Spatial distribution of rare and common variants.

(a-c) Examples from simulations of the spatial distribution of (a) rare, (b) low frequency and (c) common variants. In each case, grid squares where the allele is present are in colour; (d-e) The distribution of the correlation coefficient between genotypes and non-genetic risk for rare, low frequency and common variants. These are kernel density estimates of the distribution of the correlation between genotypic value (0/1) and associated environmental risk for individuals from the simulations described in Figure 1; (d) Gaussian risk; (e) Small, sharply defined risk. The inset panels in e show successive enlargements of the boxed areas in the tail of the distribution. All parameters are the same as in Figure 1. Abbreviations: MAF: minor allele frequency.

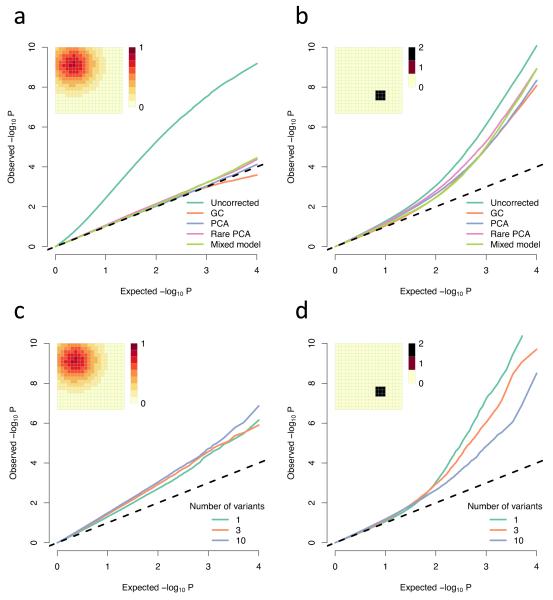
Several methods for correcting for population stratification in GWAS have been developed. The most popular are genomic control (GC)^21,22, principal component analysis (PCA)²³ and linear mixed models²⁴. These corrections are known to be effective in the standard GWAS setting and we find they are all effective when non-genetic risk has a large and smooth distribution (Fig. 3a). However, none of them are effective for the small, sharp distribution of risk (Fig. 3b). GC fails in this case because most variants, even rare ones, have correlation with the non-genetic risk of close to 0 (Fig. 2e). PCA and mixed models fail because they effectively try to correct based on linear functions of relatedness. In the simulations, the first few principal components always include the axes of the grid, so can correct for any non-genetic risk which can be expressed as a linear function of these axes. However, the small, sharp region of risk would require a highly non-linear function to be expressed in these terms, which cannot be achieved simply by including the top components. Ultimately, including a large enough number of principal components will remove virtually all stratification (here, between 20 and 100 PC’s is sufficient; Supplementary Fig. 3), but it is not possible to know how many are required and inclusion of many components will lead to substantial reduction in power to detect true associations.

Figure 3. Comparison of methods for correcting for population structure.

(a-b) QQ plots of −log₁₀ P-values showing the uncorrected values and the values under different corrections; (c-d) Simulated rare variant load tests (Online methods); All parameters are the same as in Figure 1, except the non-genetic risk is doubled so for the Gaussian risk a and c the phenotypic mean is shifted by at most 0.8 standard deviations, while for the small, sharp risk in b and d it is shifted by at most 2 standard deviations; These are both averaged over multiple simulations in order to show the average effect. Individual experiments may vary due to the sampling variance of the trait. (a-b) averaged over 100 simulations, each testing one trait at 10,000 loci in total (10 loci on each of 1000 genealogies, representing independent genomic regions). (c-d) averaged over 10 simulations, each one testing 10,000 genealogies with either 1,3, or 10 variants in each; Abbreviations: GC, genomic control; PCA principal component analysis, using the first 10 principal components; Rare PCA, as PCA but using only variants with MAF < 4%.

Where variants are sufficiently rare that they are unlikely to be observed in more than a few samples, adequate power to detect true association can only be obtained by combining information across multiple variants within a gene, though this can be approached in many ways^8-14. To assess the effects of stratification of such aggregating tests, we considered one of the simplest ‘load-based’ tests¹¹, which tests association with the number of rare variants carried in a region, typically a gene. For smoothly-varying Gaussian risk, test-statistic inflation is largely independent of the number of variants considered (Fig. 3c). For sharply-defined risk, test-statistic inflation is reduced as more variants are considered, but still increases sharply for low P-values (Fig. 3d). Given that some versions of these tests cannot easily accommodate relatedness information and that the problems of spatial structure will increase as allele frequency decreases, these results suggest that similar care need be taken when interpreting enrichment of either single or multiple variants within cases or controls.

The results discussed so far relate to inflation under the null. However, another implication of differential structure is that causal rare variants may be geographically localized. Thus even when there is no spatial structure to non-genetic risk, test-statistic inflation will be observed. When there are many loci with rare variants contributing to the background genetic effect, inflation is typically stronger for common variants and will be corrected for by standard approaches. However, when there are only a few loci driving risk, inflation is greater for rare variants (Supplementary Fig. 4). Consequently, if genetic risk is driven by small numbers of rare variants, then true signals are more likely to be obscured by rare variants that show association even though they are not physically linked to the causal variants.

Discussion

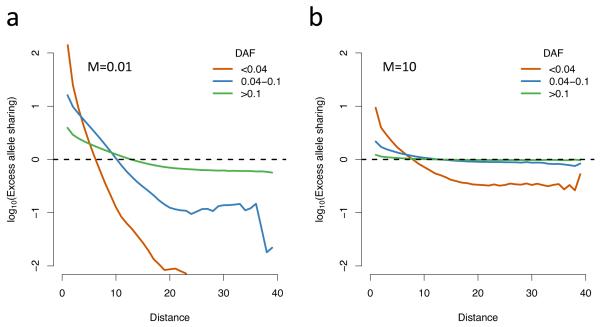
We have demonstrated that under certain conditions rare and common variants exhibit differential patterns of stratification. However these results are qualitative and we must also ask whether these conditions are likely to be met in practice. While the data that would be required to investigate this effect directly are not yet available, we can nonetheless consider metrics that could be used to relate our simulations to real populations. Historically, approaches to summarizing population structure in genetic data have focused on simple statistics, such as Wright’s fixation index F_ST, which measures the proportion of overall genetic variation that results from between-population variation. Among human populations, F_ST is typically estimated to be <0.1 (for example, 0.071 between the 1000 Genomes CEU and YRI populations⁷ and typically <0.02 within Europe²⁵). Dividing the simulated grid into two equal sub-populations, for the migration parameter used for Figure 1 (M=0.01) F_ST is approximately 0.1, which is comparable to a worldwide sample. Within a European sample, a more appropriate migration parameter might be M=10, which gives F_ST<0.01, a value which would be considered negligible. However, F_ST estimates are driven by common variants, and also depend on the relative sizes and number of the sub-populations (Supplementary Fig. 5). Analysis of allele sharing by distance as a function of distance shows that while common variants show effectively no excess allele sharing at short ranges, even with M=10 rare variants still show excess clustering (Fig. 4) and although stratification is much reduced compared to a low migration rate, it is still greatest for rare variants (Supplementary Fig. 6). These results are consistent with empirical observations that show very low rare-allele sharing even between very closely related human populations²⁶. The fact that excess allele sharing increases as frequency decreases implies that even for relatively unstructured populations, this effect will be observed below some, sufficiently low, variant frequency. These results highlight the need for methods for explicitly showing spatial structure, such as the allele-sharing plot (Fig. 4) or other spatial correlation measures such as Moran’s I statistic²⁷, which provides a much richer and more informative representation than any single statistic.

Figure 4. Excess allele sharing.

A ratio measuring how much more likely two individuals at a given spatial distance are to share a derived allele, compared to what would be expected in a homogenous population (Methods). The parameters are the same as those used in Figure 1, apart from migration rate, which is (a) M=0.01, (b) M=10; In a, F_ST=0.1 and in b, F_ST<0.01; Abbreviations: DAF: derived allele frequency.

There are three ways in which non-genetic risk might show sharply-defined boundaries of the type for which we have shown differential inflation. First, localized environmental exposure may be highly patchy, for example associated with urban areas. Second, there may be systematic measurement bias at a single recruitment centre. Third, and more subtly, there may be local variation in recruitment policy or rates of misclassification (the effect of which can be thought of as changing the background disease risk). Although we have simulated quantitative trait data, case-control studies are subject to the same issues of population structure and a case-control study that randomly misclassifies cases and controls will bias effect size estimates²⁸. When this misclassification is restricted to a particular spatial area, for example a single recruitment center in a large study, it will produce the effects described here. In fact, if we add additional disconnected small areas of risk of the same size as the first, the inflation in P-value has the same distribution with respect to frequency (Supplementary Fig. 7) so this observation would extend to the case where multiple collection centers were making biased measurements or random misclassifications. Because the extent and clustering of non-genetic risk will differ between phenotypes and study designs, it is not possible to predict any general influence of differential stratification. The principal problem with trying to account for known non-genetic risk (i.e. to include these as covariates within the analysis) is that while information about broad-scale risk factors may be available, typically, the more localized a risk factor is, the less we are likely to know about it and the greater effect this will have on rare variants.

Given that existing methods can fail to correct for rare variant stratification, what approaches can be taken to guard against its effects? One approach is to use methods that are robust to stratification (though at a cost to power and ease of experimental design), such as family-based association, perhaps only for replication. Another is to adapt existing methods to work better with rare variants. For example, although PCA with rare variants does not effectively control inflation if we linearly correct using the top components (Fig. 3b), in principal, more sophisticated methods for selecting non-linear functions of components could correct appropriately.

Alternatively, we might look to the development of new measures of relatedness more sensitive to recent ancestry and fine-scale structure. Whichever approach is taken, it is likely to require fine-grained information about the geographic origins and recruitment path of each sample. The collection of such information must be an important consideration in the design of future studies.

Appendix

Online Methods

Simulations of association studies

We simulate genotypes and quantitative traits by starting with a number of individuals and their locations on the grid and work backwards in time to generate random genealogical events. Each event is either a coalescence of two lineages or a migration of a single lineage from one square to another. The relative rates of coalescence and migration depend on the population-scaled migration rate M and the number and distribution of lineages on the grid.

More precisely, suppose we have a K × K grid and we wish to simulate a sample of C = cK² individuals where c is the number of individuals in each grid square. We simulate L loci on each of G genealogies for a total of LG loci. Each genealogy represents an independent genomic region, with no recombination inside each region. Index the grid squares by i, j and denote the number of lineages in grid square i, j at time t by $n_{i,j}^t$. Let s_{i, j} represent the number of grid squares adjacent to i, j in a Manhattan sense, so $s_{i,j}\in \left\{2,3,4\right\}$.

Now we start at t = 0 and repeat the following steps until only one lineage remains:

1. At time t, the rate of coalescence within grid square i, j is ${\lambda }_{i,j}^t=\frac{n_{i,j}^t\left(n_{i,j}^t-1\right)}{2}$ and the total rate of coalescence is ${\lambda }_{•,•}^t=\sum _{i,j}\frac{n_{i,j}^t\left(n_{i,j}^t-1\right)}{2}$ where we use dots to represent summation over indices. The rate of migration for each grid square is ${\mu }_{i,j}^t=\frac{M{n}_{i,j}^t{s}_{i,j}}{2}$ and the total rate of migration is ${\mu }_{•,•}^t$. The next event occurs at time t + T where $T~Exp({\lambda }_{•,•}^t+{\mu }_{•,•}^t)$. It is coalescence with probability $\frac{{\lambda }_{•,•}^t}{{\lambda }_{•,•}^t+{\mu }_{•,•}^t}$ and migration with probability $\frac{{\mu }_{•,•}^t}{{\lambda }_{•,•}^t+{\mu }_{•,•}^t}$.

2. If the next event is coalescence, it occurs in grid square i, j with probability $\frac{{\mu }_{i,j}^t}{{\mu }_{•,•}^t}$. In this grid square, choose two lineages uniformly, and join them together. Return to 1) with t replaced by t + T.

3. If the next event is migration, it occurs in grid square i, j with probability $\frac{{\mu }_{i,j}^t}{{\mu }_{•,•}^t}$. In this grid square, choose one lineage uniformly, and move it uniformly to one of the adjacent grid squares. Return to 1) with t replaced by t + T.

Once we have simulated a single instance of the genealogy, we generate genotypes at L random loci by sampling L nodes from the genealogy with replacement, selecting each node with probability proportional to the length of the branch above that node, and setting each individual’s genotype to 0 or 1 at each locus according to whether they are descended from that node or not so that a genotype of 0 represents an ancestral allele and a genotype of 1 represents a derived allele.

We generate quantitative traits for each locus, for each individual by sampling from a standard normal distribution. We shift the mean of the distribution for each individual according to the non-genetic risk in the square that that individual came from. Let $\varphi :\left[1,C\right]\to \left[1,K\right]\times \left[1,K\right]$ be a function which maps each individual to the grid square which they originated in. Then, for individual k , the trait value $Y_k~N\left(R_{\varphi \left(k\right)},1\right)$ where R_{i, j} is the non-genetic risk in grid square i, j . In a real experiment, each individual would have one value of Y_k which would be tested against every locus, but to reduce the uncertainty due to sampling error, in our simulations, we resample the trait independently for each locus, except where that would be inappropriate, for example when testing corrections, in which case we average the results over many experiments instead.

We perform association tests for this locus by fitting a simple linear model $Y_k^{l,g}={\mu }^{l,g}+{\beta }^{l,g}{X}_k^{l,g}+{\epsilon }_k^{l,g}$ where ${\epsilon }_k^{l,g}~N(0,{\sigma }_{l,g}^2)$ IID for some σ_l,g and computing the P-values of the beta estimates. We then repeat this for l = 1… L and g =1… G.

The results in Figure 1 use the following parameters; K = 20, c = 2 so C = 800, M = 0.01, G =100,000 and L =1000. This gives us 10⁸ points in each QQ plot. The maximum non-genetic risk for the Gaussian risk was 0.4 standard deviations and 1 standard deviation for the small, sharp risk. We computed the statistic $Q=\frac{\mathrm{var}\left(R_{\varphi \left(k\right)}\right)}{\mathrm{var}\left(Y_k\right)}$, which is the proportion of the phenotypic variance explained by the non-genetic risk, and was equal to 1.4% for the Gaussian risk and 2.2% for the small, sharp risk.

Correcting for stratification

In order to investigate the effect of corrections for population structure, we sample genotypes for multiple loci and genealogies as described above. However now we sample only one realization of the quantitative trait $Y_k~N\left(R_{\varphi \left(k\right)},1\right)$ to use for every l,g. We compute single marker test statistics as described above, and then perform the following corrections

1. Genomic control. We take the P-values for each locus p^l,g and compute chi-squared statistics ${\mathrm{X}}^{l,g}=F_{{\chi }^2}^{-1}(1-p^{l,g})$ where F_χ² is the cumulative distribution function of the chi-squared distribution with one degree of freedom. We then compute adjusted test statistics ${\tilde{X}}^{l,g}=\frac{X^{l,g}}{\lambda }$ where the genomic inflation constant $\lambda =\frac{\langle X^{l,g}\rangle }{F_{{\chi }^2}^{-1}\left(0.5\right)}$ and 〈•〉 represents the median and compute adjusted P-values ${\tilde{p}}^{l,g}=1-F_{{\chi }^2}\left({\tilde{X}}^{l,g}\right)$.

2. Principal component analysis. We compute the principal components of the LG × C genotype matrix $X=\left\{X_k^{l,g}\right\}$, say P¹,…,P^N and then fit the linear model $Y_k={\mu }^{l,g}+{\beta }^{l,g}{X}_k^{l,g}+\sum _{i=1}^{10}{\gamma }_i^{l,g}{P}_i+{\epsilon }_k^{l,g}$ where ${\epsilon }_k^{l,g}~N(0,{\sigma }_{l,g}^2)$ for some ${\sigma }_{l,g}^2$. We test the significance of the beta estimates as before. We also tried PCA, but calculating the principal components only from rare markers with MAF<4%.

3. Mixed model analysis. The linear mixed model has the form Y = μ + βX + ε_G + ε_R where ε_G ~ MVN(0, ${\sigma }_G^{2}R$) and ε_R ~ MVN(0, ${\sigma }_R^{2}I$) for some ${\sigma }_G^2$ and ${\sigma }_R^2$ and where R is the fixed kinship matrix. Here we used the correlation matrix of the genotype vectors as an approximation to the kinship matrix.

We fitted the model using software kindly provided by Matti Pirinen. This fits the same model as the EMMA package²⁴, but with a more efficient numerical algorithm (Matti Pirinen, Peter Donnelly and Chris Spencer; Efficient Computation with a Linear Mixed Model on Large-scale Data Sets with Applications to Genetic Studies; Manuscript in revision).

Because we are sampling a single trait for all loci, there is some variance in the amount of inflation and the effectiveness of the corrections, mainly because of the sampling variance of the phenotype. So that we give an accurate idea of the overall effect, we perform these simulations 100 times and show the pointwise average of the QQ plots.

Load based test

We implement a test for association of a quantitative trait with rare variant load (sometimes described as a “collapsing” or “burden” test) as described in reference ¹¹.

We simulate variants $X=\left\{X_k^{l,g}\right\}$ as described above, but include only rare variants (MAF<4%). We imagine that each genealogy represents an independent genomic region (say, a gene) and that each of the L variants on that genealogy represents a rare variant that segregates in the population. We then compute the rare variant load (or “burden”) $B_k^g$ for each individual for each region by counting the number of derived alleles at each locus so that $B_k^g=X_k^{•,g}$. We simulate traits as described above and test association with the rare variant load by fitting the model $B_k^g={\mu }^g+{\beta }^g{B}_k^g+{\epsilon }_k^g$ where ${\epsilon }_k^g~N(0,{\sigma }_g^2)$.

Excess allele sharing by distance

We calculate the probability that two individuals at a given distance share an allele, compared to what would be expected from a randomly mating population.

Specifically, given the LG × C genotype matrix $X=\left\{X_k^{l,g}\right\}$, we first divide the variants into rare, low frequency and common variants based on their allele frequencies. Suppose there are R rare variants in an R × C genotype matrix $\tilde{X}=\left\{{\tilde{X}}_k^r\right\}$ with allele frequencies $f_r=\frac{{\tilde{X}}_{•}^r}{C}$ and the spatial distance between individuals i and j is given by D_i,j. Then we compute the excess allele sharing at distance d, Q_d as:

$$Q_d=\frac{1}{R}\sum _{r=1}^R\frac{\sum _{i=1}^c\left[\chi \{{\tilde{X}}_r^i=1\}\sum _{j>1}\chi \{({\tilde{X}}_r^j=1)\cap (D_{i,j}=d)\}\right]}{f_r\sum _{i=1}^C\left[\chi \{{\tilde{X}}_r^i=1\}\sum _{j>i}\chi \left\{(D_{i,j}=d)\right\}\right]}$$

Where χ{A} is the indicator function of the event A and recalling that ${\tilde{X}}_k^r\in \{0,1\}$ with 0 and 1 representing the ancestral and derived alleles respectively. So for a given distance, for each derived allele, we count the number that are shared at a given distance, and divide by the total number of individuals at that distance to get the allele sharing probability. We then divide by the allele frequency, which is the allele sharing probability in an infinite homogenous population, to get the excess allele sharing probability. Figure 3c-d shows log₁₀ Q_d for rare, low frequency and common variants, with simulation parameters described in the figure legend.