Revisiting detrended fluctuation analysis

Abstract

Half a century ago Hurst introduced Rescaled Range (R/S) Analysis to study fluctuations in time series. Thousands of works have investigated or applied the original methodology and similar techniques, with Detrended Fluctuation Analysis becoming preferred due to its purported ability to mitigate nonstationaries. We show Detrended Fluctuation Analysis introduces artifacts for nonlinear trends, in contrast to common expectation, and demonstrate that the empirically observed curvature induced is a serious finite-size effect which will always be present. Explicit detrending followed by measurement of the diffusional spread of a signals' associated random walk is preferable, a surprising conclusion given that Detrended Fluctuation Analysis was crafted specifically to replace this approach. The implications are simple yet sweeping: there is no compelling reason to apply Detrended Fluctuation Analysis as it 1) introduces uncontrolled bias; 2) is computationally more expensive than the unbiased estimator; and 3) cannot provide generic or useful protection against nonstationaries.

An observed time series is generally considered to be decomposable into a signal, corresponding to the state of a process describing the system of interest, and noise. For time series dominated by stochastic properties, Hurst introduced a simple means of characterizing the dependence of observations separated in time. Hurst's heuristic Rescaled Range (R/S) Analysis¹ splits a time series into adjacent windows and inspects the range R of the integrated fluctuations, rescaling by the standard deviation S as a function of window size (acting as a characteristic ruler). In other words, by treating the time series as noise driving a (possibly correlated) random walk, it can be characterized by measuring the dispersion on a scaling support. Empirically, it is found that the R/S statistic is approximately related to the window size by a power law: as a point of reference, the (Hurst) exponent of this power law is 0.5 for white noise. Many natural systems display long-range dependence (often interpreted as correlated noise) with a Hurst exponent near 0.7².

It is simple to apply R/S Analysis to a time series. However, the records one is confronted with are often poor, brutish, and short. Further compounding this unfortunate situation, the tools available to study time series are typified as being only asymptotically correct, and cannot be expected to be robust in the presence of measurement noise or, worse, nonstationaries resulting from a time series being short relative to the characteristic times of the generating processes, or the measurement being polluted by an external signal.

Detrended Fluctuation Analysis (DFA) is a technique for measuring the same power law scaling observed through R/S Analysis. It was introduced specifically to address nonstationaries³. Like R/S Analysis, a synthetic walk is created, however a detrending operation is performed where a polynomial (originally, and usually, linear) is locally fit to the walk within each window to identify the trend, and then that trend is subsequently removed. DFA is typically described as enabling correct estimation of the power law scaling (Hurst exponent) of a systems' signal in the presence of (extrinsic) nonstationaries while eliminating spurious detection of long-range dependence. This purported protection against nonstationaries effects is attributed to the “detrending” operation performed and is thought to provide an important distinction from spectral or other approaches. Empirically, it has been found that when estimating scaling in well-defined test cases, such as fractional Brownian noise⁴, DFA performs well compared to other heuristic techniques, including R/S Analysis, and is competitive, in the limit of large window sizes, with theoretically justified estimators such as the local Whittle method⁵. The combination of DFA being specifically designed to seamlessly deal with nonstationaries (intent) and its relatively good performance on simple test cases (observation) has solidified the opinion that DFA is effectively a turn-key approach: one can simply feed data in and obtain a meaningful parameterization as embodied by the scaling parameter (Hurst exponent). As a result, DFA is a popular approach, and is specifically chosen if nonstationaries are either suspected or known to exist.

However, as the analyzed walk is generated from the noise there is a clear and necessary relation to spectral methods; the only difference between analysis of the noise and its walk is due to the structure of the algorithm used. This structure may tease out information (i.e., is more or less correct, relying on a constraining parametric structure built into the algorithm) or induce bias (i.e., artifacts, or incorrect parametric structure inadvertently introduced by the algorithm). Indeed, independent studies⁶,⁷ assert that, via formal manipulations, DFA can be directly mapped to the spectrum. In Ref.6 the relationship was formed using an approximation of the spectrum, and the authors conclude there is no reason to recommend DFA over spectral analysis. In Ref.7, it was determined that the detrending operation in DFA effectively creates frequency-weights, making DFA equivalent to a weighted spectral measure. The authors also conclude that it is not tenable to believe that DFA is unique from spectral analysis. The precise meaning and suitability of the weights were not discussed; however, unless weights can be justified on theoretical grounds, they are likely to introduce bias. Both basic considerations and detailed investigations dictate that the spectral and DFA approaches are strongly related, suggesting that the ability of DFA to account for nonstationaries is overestimated.

Such considerations indicate that DFA can, at best, only deal with a limited subset of the possible nonstationaries. Empirical investigations of specific trends demonstrate that even very simple nonstationaries, such as sinusoidal periodicities or monotonic global trending⁸,⁹, affect DFA estimates. In a related publication¹⁰, more complex nonstationaries are considered with the same finding: DFA is affected in a significant and detrimental manner (we note that rather than shattering the belief DFA can effectively detrend, these works⁸,⁹,¹⁰ are widely cited as demonstrating efficacy). Additionally, formal asymptotic analysis suggests that DFA is “not robust at all and should not be applied for trended processes”¹¹. These considerations have led some practitioners to hold a more nuanced view that DFA cannot eliminate the effects of all nonstationaries and that some “preprocessing” may be required¹⁰. However, the prevailing anchor belief is that DFA can mitigate nonstationaries – possibly requiring the use of higher order polynomials⁸, or some other improved detrending scheme.

The aim of this short report is to critically examine the algorithmic structure of DFA in order to determine to what extent DFA can be expected to mitigate effects due to nonstationaries. We show the source of spurious curvature empirically and ubiquitously observed in DFA and R/S plots arises out of small sample effects induced by the scheme used to segment and measure the data, as a result serious spurious curvature will always be introduced. Furthermore, as DFA partitions data by sweeping through differing window sizes and then performs local regression within the segmentation windows, additional spurious curvature will be induced for any smooth nonlinear trend: i.e. rather than mitigating nonstationaries, DFA will introduce uncontrolled artifacts in the presence of nonlinear trends. The result is that DFA cannot be expected to provide meaningful protection against smoothly varying nonstationaries.

We focus on a comparison between standard diffusion analysis, also known as Fluctuation Analysis (FA), and DFA. Despite DFA being specifically crafted to improve upon and replace FA, and in stark contrast to prevailing opinion, it appears FA is a more compelling approach.

Results

Detrended fluctuation analysis: basic algorithm

DFA consists of two steps:

1. the data series B(k) is shifted by the mean and integrated (cumulatively summed), 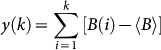, then segmented into windows of various sizes Δn; and

2. in each segmentation the integrated data is locally fit to a polynomial y_Δn(k) (originally, and typically, linear) and the mean-squared residual F(Δn) (“fluctuations”) is found:

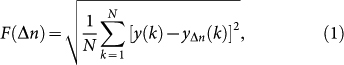
where N is the total number of data points. Note that F²(Δn) can be viewed as the average of the summed squares of the residual found in the windows. The n-th order polynomial regressor in the DFA family is typically denoted as DFAn, with unlabeled DFA often referring to DFA1.

This procedure tests for self-similarity (fractal properties) as it performs a measure (the dispersion of the residual of integrated fluctuations about a regressor) at different resolutions (window sizes). If power law scaling is present then a double logarithmic (“log-log”) plot of F(Δn) versus Δn, often termed the fluctuation plot, is expected to be linear 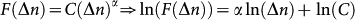, with C being a constant) and a scaling exponent α can be estimated from a least-squares fit. This scaling exponent α is a measure of correlation in the noise and is simply an estimate of the Hurst exponent H.

The standard view, following the original reasoning³, is that by removing local polynomials nonstationaries can be “detrended”.

Measuring diffusion: fluctuation analysis

In DFA a heuristic measure of an integrated walk is made: for a given segment size (time window), the dispersion of the walk around a regressor is measured. As walks are characterized by the effective diffusion rate, which DFA attempts to estimate in an ad hoc manner, a related and conceptually grounded measure is the rate an ensemble of realized walks disperses. Measuring the diffusional spreading of a stochastic process as a function of (scaling) time frames leads to an approach that is similar to DFA methodology. The standard diffusion scheme is a natural starting point, and is also known as FA¹².

FA is simple to set up: the ergodic theorem¹³ connects a single trajectory and the statistics of an ensemble of independently realized trajectories. By segmenting the data into windows of Δn steps, an ensemble of walks can be created and the scaling of the differences between start and end points (e.g. walk distances) characterize the walk. The square root of the second order structure function¹⁴ S₂ can be used to determine the diffused distance. The square root of the second order structure function reduces to the Mean Square Distance (MSD), a standard measure used to inspect single particle trajectories:

where the angular brackets denote averaging, y_i is the i-th position on the walk created by cumulatively summing a realization of a noise process, and Δn determines the time separation. As regression is not required, and as only end points of a window are inspected, FA is computationally light, relative to DFA. This is not a significant advantage for most data sets encountered in practice (i.e. small), but becomes notable for simulation data or large experimental data sets. A double logarithmic plot of the diffused distance relative to the elapsed time (Δn·t_s, where Δn is the window size and t_s is the sampling period) will be linear if power law scaling occurs.

It is clear that FA should work well for stationary signals and that it will not protect against nonstationaries.

Fractional brownian noise

Fractional Brownian noise (fBn), also known as fractional Gaussian noise, is a generalization of random Gaussian noise to include correlation⁴. The correlation is described by the Hurst exponent H, which is in the range 0 < H < 1, with H = 0.5 corresponding to no correlation. Anticorrelation exists for H < 0.5 and correlation for H > 0.5. Due to the ability to generate fBn series with well-defined properties¹⁵,¹⁶, this process has become a useful and popular operational model. While approximate methods, such as the spectral method¹⁶, are fast they introduce error undercutting the ability of fBn to act as a test case. Exact fBn is used here in order to create noise with well-defined correlation¹⁵.

Comparison of DFA and FA on fBn

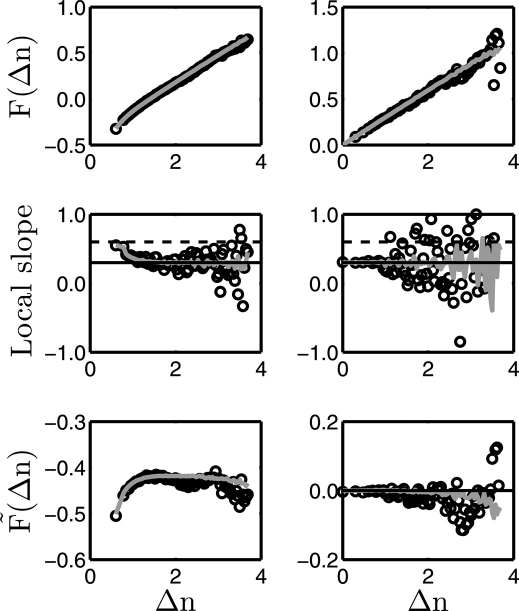
Visual inspection of DFA and FA fluctuation plots for realizations of fBn shows that, in contrast to the dictated linearity, DFA displays significant curvature on log-log plots for short time windows while FA is linear; see Figure 1 for the H = 0.3 case. The spurious curvature has long been known, being noted already in the original reference³. Observed curvature appears mild, however, fluctuation plots are graphically weak due to the logarithmic transformation with nonlinearity of the transformed variables and scatter often appearing mild even when significant. Despite the apparent mild curvature, as in the top row of Figure 1, looking at the local slope of the fluctuation plot, middle row of Figure 1, reveals that the estimate there is biased up to approximately twice the set value (dashed line in the figure). Use of the local slope provides a more powerful visual tool, with the advantage of providing a direct estimate of the Hurst exponent; however, the local slope, being a numerical derivative, may be numerically unstable for short data sets making inspection of a normalized fluctuation plot (scaled by a nominal power law fit) more suitable in such cases (bottom row of Figure 1). Normalization by a nominal power law fit effectively rotates the fluctuation plot, reducing the range taken by fluctuations allowing inspection on a finer scale and thereby increasing visual power. While common practice is to focus on the raw fluctuation plot, use of local slope or normalization suppresses less information.

Figure 1. Fluctuation plots.

DFA (left column), and FA (right column) characterize a signal by integrating a fluctuating signal and analyzing the resulting integrated walk. The top row shows the fluctuation plots (diffused distance) for fBn with H = 0.3; significant curvature for small time windows can be seen for DFA. Unfortunately, this regime provides the most statistics. The local slope (middle row) corresponds to the estimated Hurst exponent; the black line indicates the specified value and the dashed line 2X this value. In the bottom row, the fluctuation plot is scaled by the nominal power law fit resulting in a normalized fluctuation plot. The superimposed grey lines are values averaged over 50 trials.

Due to the initial bias, removal of the short time window region is necessary to obtain “reasonable” fits, with ad hoc thresholds selected in practice. The evolution of this practice indicates both the prevalence and seriousness of the bias, it will be seen below that the bias is due to inadvertently induced finite-size effects and will always be present.

Fundamental issue: estimating from small samples

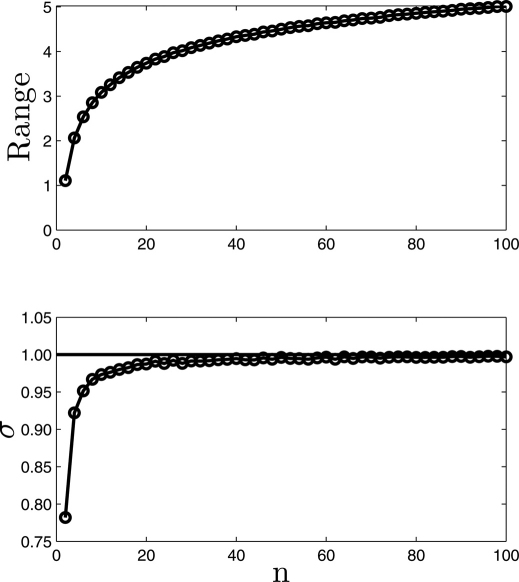
As the number of data points used to estimate dispersion decreases, one is effectively sampling from an artificially “light tailed” distribution as the tails are unlikely to be sampled, resulting in a bias towards systematic underestimation of the true dispersion (see Figure 2).

Figure 2. Source of fluctuation plot curvature.

The range (top panel) and standard deviation (bottom panel) for uncorrelated (H = 0.5) unit Gaussian noise display rapid decay with significant underestimation of the dispersion as the sample size becomes small and falls towards zero. This sample size dependent bias induces curvature in fluctuation plots. Note that the curvature is more pronounced in the range and does not saturate; this is reflected in the empirically noted improvement of DFA (which uses the standard deviation) over R/S Analysis (range).

For DFA, the magnitude of this effect diminishes with increasing time window (and hence sample) size and the result is the spurious curvature seen in DFA curves (for example, as in Figure 1). In applying FA, the curvature due to insufficient samples to accurately gauge the dispersion is induced on the opposite end of the fluctuation plot, as is seen in Figure 1. Here data truly is lacking as there are fewer far separated points. The curvature induced in DFA at small window size is due to too few samples within a window. Combining estimates over all widows does not rectify the problem – averaging poor and systematically biased estimates can provide little improvement. The lack of curvature displayed by DFA at large window size is induced by measuring over the entire time interval, artificially increasing the number of samples available.

As the problem arises due to the fundamental framework of DFA, which uses a partitioning and measuring scheme which induces substantial finite-size effects, there is no clear route to eliminating the curvature. For example, while there are empirical means that attempt to correct for the observed spurious curvature in DFA⁹, such an approach relies on creating a set of surrogate data to characterize the average curvature allowing normalization. The proposed correction⁹ also requires selection of a control parameter and retains visibly mild curvature (largely reduced, and concave up rather than concave down) discernable by eye (e.g. sizeable) in the (partially) corrected fluctuation plots investigated.

For FA the removal of a mean (or trend) is under the practitioners complete control, thus in principle the mean can be found and removed in a well-defined manner. Further, the empirical sample mean is a fairly efficient estimate of the true mean, even for correlated data¹⁷. However, it should be emphasized that for short time series the estimated mean can poorly represent the limiting value (despite being a better and a more efficient estimate than the dispersion, significant error can arise; for example for n = 1000 and H = 0.8 it is not unusual to find a mean with magnitude greater than 0.3 for fBn of unit variance and a true mean of zero). Without additional information to estimate the true mean, bias will almost surely be introduced and extra care is required. This is a fundamental difficulty: with few samples one cannot ensure good estimates.

Nonlinear structure and (in)ability to detrend

There is a detrimental aspect to the DFA algorithmic core regression scheme: it ensures that incorrect scaling will be obtained in the presence of smooth, nonlinear structure within a time series.

Perhaps the simplest nonstationary is a trend with a noise process additively riding on the (changing) background. Consider the case where the trend is dominant, and further consider smooth trends which are nonlinear under integration. The integrated process associated with such a time series will be a smooth nonlinear function, with a small amount of scatter around the global trend. Locally a nonlinear function behaves like its derivative, and as one partitions with finer (smaller) windows a linear approximation improves in quality. The same is true of n-th order polynomials (as leveraged by Taylor approximations). Thus one might expect DFA to “detrend” in the limit of small window size, albeit with the limit being cutoff by the minimum achievable window size which will restrict achievable accuracy. However, the fidelity of the approximation will depend on the partition in an unclear manner: the differing partitions will have residuals which depend on the specific partition size, the functional form of the trend, and the polynomial order selected for fitting. As a result of changing fidelity, curvature will be induced in the fluctuation plot. In principle, one can account for this changing fidelity. However, in practice, it is a hard inverse problem. Characterizing the changing fidelity of the DFA fitting is ill posed, without knowledge of the specific nonlinear function, while if one does have such knowledge then explicit detrending is available. Additionally, it is precisely in the limit of small window sizes that spurious curvature is induced by DFA due to finite size effects, thus compounding the problem: removing spurious curvature due to the interaction between DFA and a nonlinear trend seems intractable. This general argument rationalizes the empirical findings indicating that DFA fails to detrend for periodic, power law, and even linear (quadradic under integration) trends⁸,⁹ – all being specific examples of nonlinear smooth functions.

It should be emphasized that smooth nonlinear trends make up a huge class of possible trends, this class embodying many trends one would like to remove in practice (any nontrivial slowly varying nonstationarity falls under this class). Smooth nonlinear trends are also those best capturable by polynomial approximation, so it is not clear that trends of other classes would be more effectively dealt with by DFA; for example, removing pollution of a signal by spikes or other noise processes, dealing with data sets with deletions, or the like, would seem even more difficult to perform due to even less constraints on the mixture and difficulty for polynomials to follow sharp movements, an impression supported by empirical study¹⁰. Despite widespread statements attesting to DFA's ability to detrend, we are unaware of any nontrivial trend type specifically studied and found to be effectively detrended by DFA, nor does it appear that DFA can be readily modified to enable detrending of nontrivial trends (however, see Ref.18 for an alternative view).

On the limits of H

The observation that FA can only find H in the region (0,1), while DFA can find values for H > 1, is often thought to provide evidence that DFA is superior and is considered to be a serious drawback of FA. It should be emphasized that for a stationary univariate noise process, H is in the domain (0,1). This constraint is related to the celebrated identity¹⁹ linking the Hurst exponent to the fractal dimension for self-affine objects: H + D = d + 1, with H being the Hurst exponent, the fractal dimension D in domain [d, d+1), and d is the dimension the mathematical object is embedded in (d = 2 for standard univariate time series). That FA returns a value in (0,1) is consistent with FA working correctly, provided that the input signal is stationary. As DFA is claimed to “detrend” the signal, leading to a stationary aspect which is then characterized by the estimated H value, an estimate of an H outside the domain (0,1) is direct evidence that the purported detrending was not successful. Rather than providing evidence that DFA is superior to FA due to detrending of nonstationaries, the observed bounds on FA estimates of H and estimates made by DFA with H > 1 provides powerful evidence of the opposite.

DFA of DNA sequences

DFA was originally created specifically to address the question of power law scaling in DNA sequences³, where patches of nucleotide rich regions (nonstationaries) exist making the discrimination between long range correlated noise and the effects of nonstationaries an important question (both can lead to similar heavy-tailed spectra following a nominal 1/f ^β scaling).

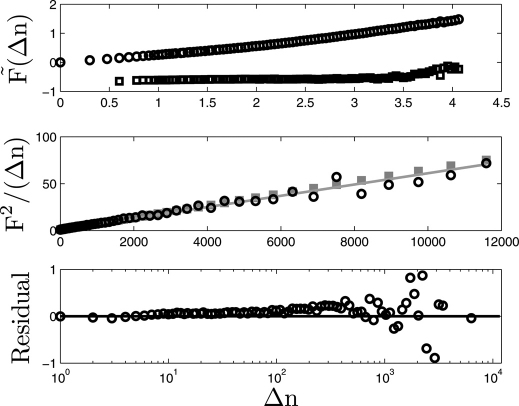
Diffusion analysis, termed FA, was introduced and used to test for power law scaling in DNA sequences¹², and it was reported that power law scaling occurs with a random walk (H = 0.50 ± 0.01) characterizing exon sequences and correlated power law scaling characterizing intron sequences (H = 0.61 ± 0.03). A clear distinction between intron and exon sequences was reported and the fluctuation plots shown displayed excellent linearity on the log-log plot. The findings, however, were called into question when several groups working with the same tools and data²⁰,²¹ were unable to reproduce either the depicted linearity underlying the validity of a single parameter (H) characterizing the sequences, nor the clear separation between the sequence types. In addition it was pointed out that the findings were consistent with patches of biased walk regions existing in exons and unbiased walks in intron regions²²,²³ and the implicit stationary assumption made¹² was questioned. It was shown²³ that curvature rather than linearity empirically depicts fluctuation plots for exon sequences and a model based on the known mosaic (patch) structure in such sequences was constructed, which demonstrated that such curvature is expected. In response the authors¹² created DFA³ and the data were reanalyzed, with the clear separation between exons and introns, as well as the H values initially reported (H ∼ 0.5 and H ∼ 0.6, for exons and introns, respectively), being reported as upheld; and with strong linearity displayed in fluctuation plots of sequences investigated by DFA. An exon sequence was shown to display power law scaling with H ∼ 0.5 when inspected with DFA, while strong (concave up) curvature was shown in the fluctuation plot for FA (see Figure 5 in the original DFA work³, and Figure 3 here, where the λ-DNA sequence is shown).

Figure 3. Fluctuation plots for λ-DNA.

Following Ref.12 the FA (dots) and DFA (squares) fluctuation plots are shown, normalized here by (Δn)^0.5 (top panel). Note the concave up curvature of the FA results, and the approximately flat DFA results. Karlin & Brendel model predictions (here recast into linear form, 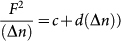) for λ-DNA (middle, lower panels) are close to the observed FA measured fluctuations (dots). A linear fit (grey line) indicates the Karlin & Brendal model is suitable; for two patch types an analytic prediction of fluctuations (grey squares) captures the observed λ-DNA fluctuations (black dots) surprisingly well, where the patch biases required for prediction are empirically estimated from the sequence. Some short-range structure, visible when inspecting the residual between the model and the data (bottom panel), is not accounted for by the two-type patch model, and is attributable to a notable short-range correlation in the DNA sequence, where base-pairs which are separated by two others are (positively) correlated.

Given the now well-known and ubiquitously observed spurious curvature induced by DFA, which, as seen here, arises from severe finite-size effects, it is worth reconsidering the findings. In particular, some curvature is visible for the DFA fluctuation plot of exon sequences, as well as for intron sequences in the raw fluctuation plot³. Importantly, as it is known that DFA induces downward (spurious) curvature on fluctuation plots and as the FA fluctuation plot of the sequence is concave up, the linearization obtained may be not due to (only) detrending, but instead be (at least in part) an artifact.

The Karlin & Brendel model²³ can provide some insight. Briefly: for DNA sequences, investigation of patch effects is facilitated by a first approximation model, which makes use of an Analysis of Variance (ANOVA) style approach. The resulting Karlin & Brendel model estimates intra-patch fluctuation variance to be of order Δn and inter-patch fluctuation variance of order (Δn)². As such a qualitative upward curvature is expected. However, for λ-DNA it turns out that quantitative predictions can be made by the Karlin & Brendel approach, and we find good agreement between the model and the FA results (see Figure 3).

Recasting the Karlin & Brendel model into linear form facilitates visual inspection and gives 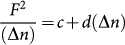, where F is the measured fluctuations, (Δn) is the window size, and c and d are model parameters. In a footnote, they explicitly consider the simple case of two patch types and derive analytical expressions for the model parameters (see their footnote 22, which addresses this special case²³; 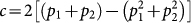and d = (p₁−p₂)², where p₁ and p₂ are the probability of positive steps in patches of type 1 and 2). Inspection of the empirically estimated bias suggests λ-DNA can be so approximated, with biases of 0.456, 0.536, and 0.457 found for the respective patches. Taking the patches to be of types described by biases of 0.46 and 0.54 describes the fluctuation data of λ-DNA quite well, considering the sensitivity in estimating d due to squaring a difference (we find that, for example, using biases of 0.456 and 0.54 gives better results (not shown here), with the small error in slope corrected; we initially used those values in preliminary investigations, optimization could very well improve upon the results). Short-range structure appears in the data, which is not captured by the model, and which can be attributed to the short-range correlation of sequence elements observed here (likely the codon “on-off-off” repeat structure²⁴).

Despite being an approximate first pass model, the Karlin & Brendel model appears to capture the main behavior of the observed DNA sequence, demonstrating that theoretical treatments can make meaningful contact with FA results. While inspection of the Karlin & Brendel model supports usage of FA, for example estimating sequence c and d parameters may enable meaningful characterization and classification of sequences, it cannot speak to DFA's ability to detrend in this patchy case (piecewise constant bias patches). It may well be true that DFA can detrend patchy sequences, however some care is required in generalizing. Large offsets cannot be so captured (as sudden large jumps cannot be captured by low order polynomials using standard regression), and the DFA induced curvature complicates interpretation (is apparent linearity mainly due to successful detrending, indicating underlying power law scaling, or significantly spurious, with apparent linearity arising from interaction between true upward curvature and induced downward curvature?).

Discussion

It appears that the only nonstationary that DFA can arguably address is (possibly piecewise) constant offsets, however, due to spurious curvature resulting from the severe finite-size effects introduced, some problems in interpretation remain.

A seemingly puzzling aspect should be clearly pointed out: empirical tests can find that DFA performs perfectly adequately and even superior to many other alternative (albeit typically heuristic) measures⁵, which appears to conflict with the general arguments laid out here. Note, however, that such tests involve (ad hoc) selection of a threshold, with only windows above considered. It is precisely in this limit of large windows where (1) DFA does not suffer serious finite-size effects yet (2) its polynomial fit and detrend scheme can not be expected to “detrend” in this limit: thresholded estimates supplied are therefore suitable for stationary signals (which provide the known cases DFA is tested against), given sufficient data. In other words, it is empirically found that DFA asymptotically provides good results for stationary time series, however it appears that DFA cannot provide protection against nonstationaries (but rather aggravates their effects, for nonlinear trends) while its partitioning scheme ensures DFA imparts serious bias for short data sets.

In addition to the spurious curvature introduced, the fact that DFA can estimate H > 1 reveals that, in such cases, detrending is not actually performed. Despite the seemingly negative conclusion that DFA is fundamentally flawed, and cannot provide meaningful detrending, there is significant good news. In contrast to the mystery surrounding the action and interpretation of DFA, use of FA or spectral methods is straightforward and interpretable (with strong theory and good – robust, fast – computational implementations). In practice, DFA is highly nonrefutable with no detrended signal to inspect. Explicit detrending reintroduces refutability to analysis, allowing for visual inspection to assess sensibility, sensitivity on a proposed detrend to be estimated, and quantitative probes to be applied. Explicit detrending enables data characteristics to guide detrending choices. For example, if sudden discrete jumps between levels are expected, wavelet thresholding is quite reasonable²⁵.

Finally, it should be noted that while FA offers a (more) compelling means of analysis there remain well-known issues – least-square fits of logarithmically transformed data are inherently problematic²⁶, while the (often highly) limited data available further reduces confidence and recommends, for example, making use of surrogate data²⁷ to strengthen conclusions and probe finite sample size effects.

Methods

Figure 1 details: 50 sets of 20,000 data point realizations were created using the (exact) Davies-Harte algorithm¹⁵.

Figure 2 details: from 10,000 realizations the average range and standard deviation were found.

Figure 3 details: a symbolic walk was generated for λ-DNA (Genbank: LAMCG), with steps of +1 for pyrimidines and -1 for purines. Weighted (number of windows) least-squares was performed for linear fitting. Breakpoints were roughly estimated, by eye, to be at positions 22,550 and 37,980; in each of these patches the bias was estimated.

In all cases adjacent, rather than sliding, windows were used in calculating FA, as a result the finite size error induced scatter is not artificially smoothed away in the figures.

Author Contributions

RMB conceived, designed, and performed the study. Both authors wrote the paper and reviewed the manuscript.