The Hydrogen Catalyst Cobaloxime – a Multifrequency EPR & DFT Study of Cobaloxime’s Electronic Structure

Abstract

Solar fuels research aims to mimic photosynthesis and devise integrated systems that can capture, convert, and store solar energy in the form of high-energy molecular bonds. Molecular hydrogen is generally considered an ideal solar fuel as its combustion is essentially pollution-free. Cobaloximes rank among the most promising earth-abundant catalysts for the reduction of protons to molecular hydrogen. We have used multifrequency EPR spectroscopy at X-band, Q-band, and D-band combined with DFT calculations to reveal electronic structure and establish correlations between structure, surroundings and catalytic activity of these complexes. To assess the strength and nature of ligand cobalt interactions, the BF₂-capped cobaloxime, Co(dmgBF₂)₂, was studied in a variety of different solvents with a range of polarities and stoichiometric amounts of potential ligands to the cobalt ion. This allows the differentiation of labile and strongly coordinating axial ligands for the Co(II) complex. Labile, or weakly coordinating, ligands like methanol result in larger g-tensor anisotropy than strongly coordinating ligands like pyridine. Additionally, a coordination number effect is seen for the strongly coordinating ligands with both singly-ligated LCo(dmgBF₂)₂ and doubly-ligated L₂Co(dmgBF₂)₂. The presence of two strongly coordinating axial ligands leads to the smallest g-tensor anisotropy. The relevance of the strength of the axial ligand(s) to the catalytic efficiency of Co(dmgBF₂)₂ is discussed. Finally, the influence of molecular oxygen and formation of Co(III) superoxide radicals LCo(dmgBF₂)₂O₂^• is studied. The experimental results are compared with a comprehensive set of DFT calculations on Co(dmgBF₂)₂ model systems with various axial ligands. Comparison with experimental values for the “key” magnetic parameters like g-tensor and ⁵⁹Co hyperfine coupling tensor allows the determination of the conformation of the axially ligated Co(dmgBF₂)₂ complexes. The data presented here are vital for understanding the influence of solvent and ligand coordination on the catalytic efficiency of cobaloximes.

Introduction

The production of carbon-neutral and sustainable fuel sources by solar energy conversion is considered to be a vital component of our future energy landscape.^1,2 Biology provides several examples for processes necessary to transform abundant solar energy to energy stored in the form of chemical bonds in small, energy-dense molecules, such as molecular hydrogen. Molecular hydrogen is generally considered as an ideal energy carrier, since its combustion is essentially pollution-free. A major goal in the field of solar H₂ production is to generate molecular systems which ideally have both a high turnover number (stability of the molecular device) and high turnover frequencies (efficiency of catalyst) using earth-abundant first-row transition metals rather than unsustainable precious metals. A variety of different catalysts designed towards this goal have been structurally and mechanistically characterized for the reduction of protons to molecular hydrogen (reviewed in ^2,3). However, both the efficiency and stability of these devices still need significant improvement. The development of an efficient system for hydrogen generation driven by sunlight has even been termed a “Holy Grail” of solar-driven water splitting.³ Among currently known complexes, cobaloxime compounds (cobalt macrocycles with di-glyoxime ligands) have been emerged as productive electrocatalysts for the reaction 2H⁺ + 2e⁻→ H₂ with low overpotential in the presence of a proton source in organic solvents. Cobaloximes are not only among the best synthetic transition metal complexes known for H₂ production, they are also relatively easy to synthesize, oxygen tolerant, are amenable for coupling to natural and artificial photosynthetic systems,^3,4 and rely only on earth-abundant materials. The pseudo-macrocyclic cobaloxime compounds were originally developed and investigated as vitamin-B₁₂ analogs,^5,6 and have been extensively studied as a model system for vitamin B₁₂.^7–9 About twenty years later, Connolly & Espenson found that difluoroboryl-cobaloxime Co(dmgBF₂)₂ catalyzes proton reduction in acidic media.¹⁰ The urgent need for earth-abundant materials capable of solar energy conversion has prompted renewed interest in the catalytic properties of cobaloxime compounds. Both electrocatalytical systems for hydrogen evolution which utitilize cobaloxime as well as systems using photosensitizers were reported.^3,11–18 Recently, the first photocatalytic supramolecular assemblies based on pyridyl coordination of a variety of photosensitizers to the Co(II) center of the cobaloxime macrocycle have been described.^4,19–22 However, a significant problem for many cobaloxime compounds is their low stability at low pHs and rapid decomposition, which limits their general utility for hydrogen catalysis, while the (BF₂-capped) difluoroboryl-cobaloximes –like Co(dmgBF₂)₂ (Figure 1) – have been found to be more resistant toward acidic hydrolysis than H-capped cobaloxime compounds.^3,10,23 In addition, the reduced nucleophilicity of its hydride derivative limits undesired hydrogenation reactions. Furthermore, for the BF₂-capped cobaloxime, the ground state is more easily reduced with its Co(II)/Co(I) potential about 0.5 V more positive than the H-capped cobaloxime.³ Another benefit is that the presence of a conjugated bridging ligand facilitates the transfer of electrons to the cobalt ion. The BF₂-capped cobaloxime Co(dmgBF₂)₂ studied here is quite resistant to the oxidation by molecular oxygen and the ensuing degradation of the cobalt macrocycle. These factors make it a better model system for studying the interaction of the cobalt complex with molecular oxygen, as compared to H-capped cobaloxime.²⁴

Figure 1.

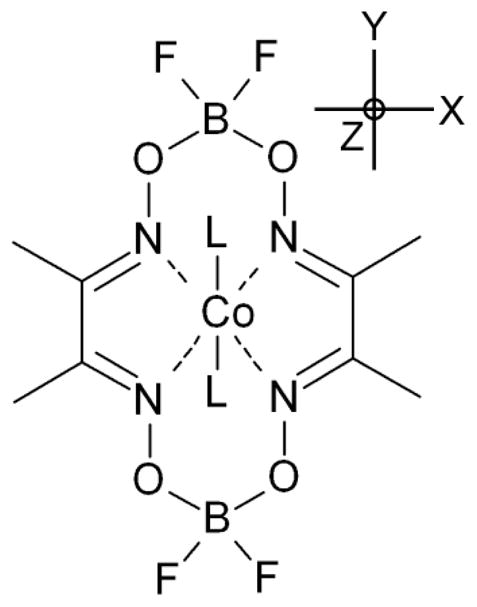
Molecular structure of the BF₂-capped cobaloxime Co(dmgBF₂)₂ investigated in this work. The molecular axes system is also depicted. The g-tensor principal axes and the principal axes of the ⁵⁹Co hyperfine coupling tensor (A-tensor) are expected to be collinear to the molecular axes system unless molecular oxygen is bound.

The catalytic efficiency is determined to a large extent by the electronic structure of the cobaloxime. The electronic structure in turn is strongly influenced by the macrocycle’s surroundings and in particular by the ligand(s) directly bound to the central metal ion. Also, other secondary interactions, such as hydrogen bonding to the fluorine atoms and the dielectric properties of the medium cannot be neglected. An excellent illustration of the importance of the surroundings is the redox potential. The cobaloxime Co(II)/(I) reduction potential is sensitive to its coordination environment and shifts significantly on pyridyl coordination to the Co(II) center.^3,4,21 Thus, the knowledge of the electronic properties is essential for an understanding of the catalytic properties of the complex.

So far, only cursory experimental data regarding changes in the electronic structure as a result of axial coordination are available. The resting state of cobaloxime’s catalytic cycle is 3d⁷ low spin Co(II).²⁵ Since the highest occupied molecular orbital (HOMO) of the Co(II) complex, which carries a single unpaired electron, has mainly d_z2 character, the effect of axial coordination by fifth and sixth ligands to the cobalt ion is crucial for the function of cobaloxime, and particularly in catalytic processes involving axial ligand exchange. Electron paramagnetic resonance (EPR) spectroscopy is an excellent tool to characterize any changes in electronic structure which result from changes to the surrounding environment or properties of the orbital carrying the unpaired electron. Changes in the electronic properties can then be correlated with different catalytic efficiencies of cobaloxime.

Several EPR studies on cobaloxime compounds exist but there are number of inconsistencies and gaps in the published data, e.g. refs ^24–35. First, almost all studies focus on H-capped cobaloxime and to the best of our knowledge, there has been only one previous cursory EPR study of Co(dmgBF₂)₂.²⁵ The second drawback is that most previous cobaloxime EPR studies (including the one by Bakac and co-workers on Co(dmgBF₂)₂) performed EPR spectroscopy only at the conventional X-band frequency (9–10 GHz). In most cases, the X-band spectra are very congested, with g-tensor anisotropy and ⁵⁹Co hyperfine interaction having the same order of magnitude, which makes it difficult to determine the principal components of the g-tensor, leaving one of the most important parameters far from precisely determined. In fact, in many studies both g-tensor and the ⁵⁹Co A-tensor were reported as axial, whereas it is shown in our study that in nearly all cases both tensors are essentially rhombic. Furthermore, the previous studies were either lacking quantum mechanical calculations completely or the treatment was restricted to Hückel theory.

Here we use EPR spectroscopy at X-band (9 GHz), Q-band (34 GHz), and D-band (130 GHz) microwave frequencies to distinguish clearly between field-dependent and field-independent parameters. The multifrequency approach allows us to determine g-tensor anisotropy and hyperfine splitting due to the central metal (⁵⁹Co) and coordinating solvents molecules/ligands (L) that have ¹⁴N, ¹⁵N, or ³¹P magnetic nuclei. A variety of different solvents from different groups are studied, including (i) polar protic solvents, (ii) polar aprotic solvents, (iii) non-polar solvents, and with and without potential ligands to the central cobalt ion. The experimental investigation were accompanied by an extensive Density Functional Theory (DFT) study on the cobaloxime, taken into account a variety of different possible conformations of the cobaloxime macrocycle and ligand/solvent molecules.

The catalytically relevant ligands studied both in experiment and calculation include the “small and simple” ligand pyridine as well as two rather bulky organic molecules, N-cyclohexyl-N′-4-pyridyl-1,7-dipyrrolidinylperylene-3,4:9,10-tetracarboxylic acid bisimide (PDI) and triphenylphosphane (PPh₃) (Figure S1). The PDI scaffold is widely used in many light-harvesting applications due to its high extinction coefficient, broad absorbance and redox tunability, exceptional structural integrity, and thus presents an attractive alternative to other photosensitizers which contain precious metals. PDI derivatives are most often employed as acceptor fragments in donor-bridge-acceptor constructs.³⁶ A supramolecular cobaloxime assembly was recently reported with a pyridyl-functionalized PDI molecule coordinated to cobaloxime, acting as a photosensitizer.²¹ Triphenylphosphine (PPh₃) is the second bulky ligand studied. The central phosphorous atom acts as the ligating atom of PPh₃ where the ³¹P nuclear spin of I = ½ allows the hyperfine interaction of the phosphorus atom with the unpaired electron to be monitored. Interaction of cobaloximes with molecular oxygen were studied on the example of a O₂: Co:PPh₃ complex which efficiently formed a stable, but reversible, paramagnetic adduct. The oxygenation is found to dramatically change the EPR spectrum of cobaloxime, resulting in a pronounced reduction of g-tensor anisotropy and decrease in both ³¹P and ⁵⁹Co hyperfine interaction, which is consistent with a pronounced shift of electron spin density to molecular oxygen. We anticipate that this comprehensive study of the changes in the electronic properties in response to a variety of environmental factors can be correlated with demonstrated catalytic efficiencies of cobaloxime and eventually provide a predictive tool for the design of new cobaloxime catalyst structures.

Experimental Procedures

Sample preparation

All commercial reagents including organic solvents were of ACS grade and purchased from Sigma-Aldrich unless otherwise noted. ¹H NMR (500 MHz) was performed on a Bruker DMX 500 spectrometer and referenced to TMS or residual solvent peak as an internal standard. ESI-MS was conducted on a ThermoFisher LCQ Fleet from dilute acetonitrile or methanol solutions. UV-Vis absorbance measurements were performed on a Shimadzu UV-1601 spectrophotometer. The synthesis of the cobaloxime Co(dmgBF₂)₂•H₂O was carried out as previously described and matched all characterization methods.²³ Solvents were methanol, glycerol/H₂O, acetone, toluene, dichloromethane (CH₂Cl₂), and dimethylformamide (DMF). The synthesis of N-cyclohexyl-N′-4-pyridyl-1,7-dipyrrolidinylperylene-3,4:9,10-tetracarboxylic acid bisimide (PDI) was described previously.^{21 15}N-labeled pyridine was obtained from Cambridge Isotope Laboratories (Andover, MA). Co(dmgBF₂)₂•H₂O was dissolved in the respective solvent (or solvent mixture, possibly containing potential ligand molecules) to yield a 1–3 mM solution. The solutions were thoroughly purged with N₂ before filling the quartz tubes used for the EPR measurements under nitrogen atmosphere in a dry box. The samples were then frozen quickly in liquid nitrogen. The samples of the oxygen adduct LCo(dmgBF₂)₂O₂, were prepared outside the dry box under aerobic conditions and frozen quickly in liquid nitrogen.

EPR spectroscopy

CW X-band (9 GHz) EPR experiments were carried out with a Bruker ELEXSYS E580 EPR spectrometer (Bruker Biospin, Rheinstetten, Germany), equipped with a TE₁₀₂ rectangular EPR resonator (Bruker ER 4102st) and a helium gas-flow cryostat (Air Product, Allentown, PA). The temperature was controlled by a Lakeshore cryogenic temperature controller (Westerville, OH).

Pulse X-band experiments were performed on the same spectrometer, using a Flexline dielectric ring resonator (Bruker ER 4118X-MD5 or Bruker EN 4118X-MD4-W1) and a helium gas-flow cryostat (CF935, Oxford Instruments, UK). The temperature was controlled by an ITC (Oxford Instruments, UK).

CW Q-band (34 GHz) EPR experiments were carried out with the same EPR spectrometer, equipped with a Q-band bridge (Bruker ER 051 QG) a cylindrical EPR resonator (Bruker ER 5106 QT-W) and a helium gas-flow cryostat (CF935, Oxford Instruments). The temperature was controlled by an ITC (Oxford Instruments, UK). The microwave (MW) frequency was monitored by a frequency counter (5352B, Hewlett Packard).

High frequency EPR measurements were performed on a home-built D-band (130 GHz) spectrometer equipped with a single mode TE₀₁₁ cylindrical cavity.³⁷ EPR spectra of the samples were recorded in pulse mode in order to remove the microwave phase distortion due to fast-passage effects. The absorption line shape of the EPR spectra was recorded by monitoring the electron spin echo (ESE) intensity from a two microwave pulse sequence as a function of magnetic field. The duration of a π/2 microwave pulse was 40–60 ns, and typical separation times between microwave pulses were 150–300 ns. All D-band spectra have been pseudo-modulated to facilitate comparison with the respective X- and Q-band spectra.³⁸

Data processing was done using Xepr (Bruker BioSpin, Rheinstetten) and Matlab^™ 6.5 (MathWorks) environment. The magnetic parameters were obtained from theoretical simulation of the EPR and ENDOR spectra. The simulations were performed using the EasySpin software package (version 3.1.7).³⁹ Quadrupole interactions were not included since within the first order of perturbation theory they do not contribute to the EPR spectra. Several simulations were repeated with the program SIMFONIA Version 1.25 (Bruker BioSpin, Rheinstetten, 1996), using second order perturbation theory, and delivered virtually identical parameters. The accuracy in determination of the electronic g-tensor for the set of multifrequency EPR spectra is estimated to be ±0.001.

Density Functional Theory calculations

Starting structures for all geometry optimizations presented in this paper were obtained from the coordinates of the crystal structure of Co(dmgBF₂)₂ with acetonitrile as axial ligands, provided in the Supplementary Information. This structure is very similar to the one described by Bakac et al. for Co(dmgBF₂)₂ with methanol as axial ligands. The geometry optimizations were carried out using density functional theory (DFT) with the B3LYP functional^40–42 using the 6–31G* basis set, as implemented in PQSMol.⁴³ All structures were first optimized in the gas phase and the resulting structures were re-optimized with solvent effects included by employing the continuum solvation model COSMO with a dielectric constant set to 80.⁴⁴ Geometry optimizations were also performed with lower dielectric constants and led to nearly identical structures. In addition, a selected set of geometry optimizations were performed using larger basis sets with the program package ORCA.⁴⁵ These geometry optimizations again led to nearly identical structures and subsequently g-values. After confirming by the absence of imaginary frequencies that the stationary points obtained were minima, the spectroscopic parameters were obtained via single point DFT calculations, performed with the program package ORCA.⁴⁵ For all calculations of magnetic parameters, the program ORCA with the B3LYP functional was used in combination with the TZVP triple-ζ basis set of Ahlrichs and co-workers on all atoms except cobalt.^46,47 For the transition metal ⁵⁹Co, the Wachters basis set, developed for third row transition metals, was used.^48,49 The Wachters basis set has proven quite successful for transition-metal compounds and is well suited for the description of structures, energies, and other properties, see e.g. ^50,51 These single point calculations also employed COSMO to account for the dielectric screening of surrounding molecules. The principal g-values were calculated employing the coupled-perturbed Kohn-Sham equations,⁵² in conjunction with a parameterized one electron spin-orbit operator. The magnetic dipole and the isotropic Fermi contact contributions to the hyperfine coupling were calculated for all atoms, while for ⁵⁹Co second order spin-orbit hyperfine contributions were also calculated.

In an additional set of calculations, the effect of the displacement of the central cobalt ion from the plane was systematically investigated. The complex contained a single pyridine molecule as the axial ligand in the “boat towards pyridine” conformation. A restricted geometry optimization was performed with the cobalt ion being pushed/pulled systematically in and out of the plane of the macrocycle using a torsion constraint (Co-N-N-N, Figure 1). The planar nature of the macrocycle portion of the complex was maintained by constraining the nitrogen atoms to remain in plane via constraining the torsion angle of the four nitrogen atoms to the initial, unconstrained value of −0.0158°. The spectroscopic parameters were obtained via single point DFT calculations as described above.

Results & Discussion

Experimental Results - EPR under anaerobic conditions

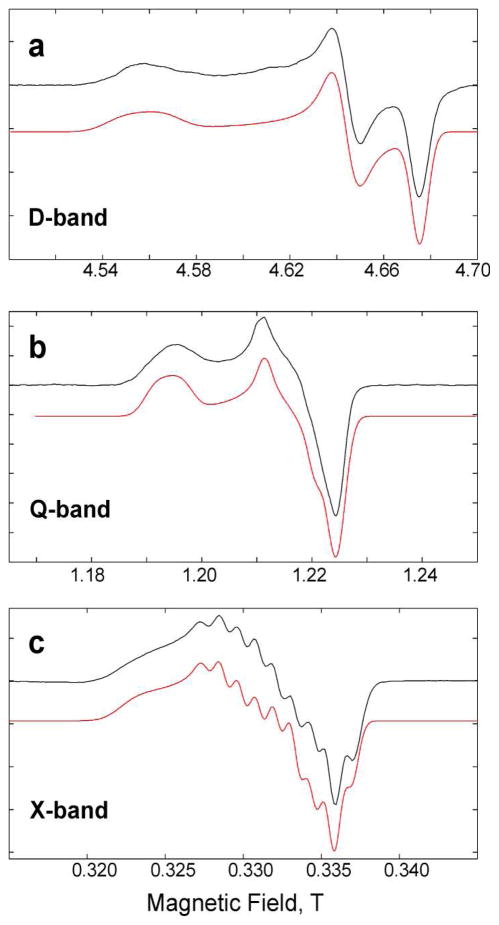
Figure 2 shows selected EPR spectra of the cobaloxime Co(dmgBF₂)₂ in several different solvents or solvent mixtures under anaerobic conditions, recorded at X-band (9–10 GHz), Q-band (34 GHz), and D-band (130 GHz) microwave frequencies. The multifrequency approach allows us to clearly distinguish between magnetic field-dependent parameters (electronic g-tensor) and magnetic field-independent parameters (hyperfine coupling tensors, A-tensors).

Figure 2.

EPR spectra of the cobaloxime Co(dmgBF₂)₂ in different solvents recorded at different microwave frequencies (D-band, Q-band, X-band) at cryogenic temperatures. The field-swept ESE-detected D-band spectra have been pseudo-modulated. Q-band and X-band spectra are CW EPR spectra. From the spectrum of cobaloxime in methanol with pyridine:Co in 1:1 ratio a minor contribution of the non-pyridine coordinated species has been subtracted. Simulations are depicted in red. Figure S2 (Supplementary Information) provides these D-band spectra and additional D-band spectra without pseudo-modulation.

We will first discuss the D-band spectra since their analysis is clearest. At D-band, the g-tensor anisotropy of Co(dmgBF₂)₂ is by far larger than the other magnetic interactions, i.e. any hyperfine interaction, and the line width. All our frozen solution D-band EPR spectra show a substantial g-tensor anisotropy (g_x–g_z > 0.18) and are typical for a low-spin d⁷ (S = ½) electron configuration of ⁵⁹Co. This is in complete agreement with previous investigations of several cobaloximes and related compounds.^25,30,33,53 Hence, the (pseudomodulated) D-band spectra allow a straightforward determination of the three principal values of the electronic g-tensor, which was found in all cases to be rhombic. In contrast, many previous studies of cobaloxime at lower magnetic fields approximated the g-tensor to be axial. The values obtained from analysis of the D-band spectra were used as constraints in the simulation of X-band and Q-band data. In the following, we will refer to the principal g-values as g_x (for g_max), g_y (for g_mid), and g_z (for g_min). In all cases, the smallest principal g-value g_z is found to be close to the value of a free electron (g_e). This result is expected for a complex where the unpaired electron resides preferentially on the d_z2 orbital (see below for a more detailed discussion). The largest g-tensor anisotropy (g_x–g_z > 0.34) is found in the case of a 1:1 ratio of PDI:Co (see Table 1). The presence of PDI in the toluene solution could result in a mixture of doubly-ligated, singly-ligated, and non-ligated cobaloxime complexes, depending on the free enthalpy of the respective complexes. Since Co(dmgBF₂)₂ is minimally soluble in neat toluene, at least one PDI molecule must be ligated to a cobaloxime in solution. The spectrum shows no indication of the presence of several paramagnetic species, demonstrating that only cobaloxime with one axial ligand is present. This conclusion is clearly verified by analysis of the ligand superhyperfine structure (¹⁴N) at lower magnetic fields (see below). The presence of triphenylphosphine (PPh₃) in a solution of CH₂Cl₂:toluene (1:1) results in a slightly lower g_x-value than observed for PDI in toluene. This value is similar to that in methanol and several other neat solvents without strong axial ligand, which have g_x -values around 2.26–2.28 (see Table 1 & Figure S2). Interestingly, the g_y-value is much smaller than in these other solvents, a property which has been also detected for H-capped cobaloxime.^29,33 The unusual ratio of g_x/g_y has been explained as a PPh₃ -induced distortion of the macrocycle.²⁹ The possible PPh₃ -induced distortion of the macrocycle is discussed below in more detail. Smaller g-tensor anisotropy is found when pyridine is present in slight stoichiometric excess as compared to the cobaloxime. The smallest g-tensor anisotropy (g_x–g_z ≈ 0.18) is found in the case of a large pyridine ligand excess with respect to the cobaloxime. The spectrum shows no sign of the presence of multiple species, indicating that two pyridine molecules act as axial ligands. In all D-band spectra, the hyperfine structure of ⁵⁹Co (I = 7/2) is resolved only at g_z orientation (high-field edge) resulting in a splitting into 2I+1= 8 lines. In case of PPh₃ as axial ligand, the ⁵⁹Co hyperfine structure is not resolved even at the high-field edge. This is be due to the substantial ³¹P hyperfine interaction in addition to the ⁵⁹Co hyperfine interaction (see Table 1 & discussion below).

Table 1.

EPR simulation parameters for the cobaloxime Co(dmgBF₂)₂ in different solvents. The same set of parameters was used to simulate X-band, Q-band, and D-band spectra. Note, that the signs of the hyperfine coupling constants A_x, A_y, and A_z could not be determined by analysis of the EPR spectra. Thus, only the magnitude is given. The ¹⁴N hyperfine coupling constants refer to the axial ligands, not to the macrocycle (equatorial) nitrogen atoms.

Solvent/Ligand(s)	gx	gy	gz	|A|(59Co) [MHz]	|A|(14N) [MHz]	|A|(31P) [MHz]
Glycerol: H2O 60:40 (v/v)	2.2750	2.1785	2.0065	15, 15, 329*	n/a	n/a
Methanol	2.2840	2.1820	2.0080	53, 20, 338*	n/a	n/a
Dimethylformamide (DMF)	2.2600	2.1695	2.0077	60, 50, 302*	n/a	n/a
Toluene PDI:Co 1:1	2.3473	2.1815	2.0000	85, 10, 306*	30, 30, 40	n/a
Methanol Pyridine:Co 1:1	2.2380 2.2610	2.1530	2.0058	10, 10, 285*	33, 36, 43	n/a
Methanol Pyridine:Co 10:1	2.1910	2.1270	2.0080	105,148,242	36, 39, 48	n/a
Acetone:Pyridine 1:1 (v/v)	2.1895	2.1278	2.0077	110, 148, 243	36, 39, 48	n/a
CH2Cl2:Toluene:1:1 (v/v) with PPh3	2.3000	2.1425	1.9995	36,10,249*	n/a	300, 300, 358
CH2Cl2:Toluene 1:1 (v/v) with PPh3 & O2	2.0390	2.0014	1.9879	28*, 32, 13	n/a	20, 37, 37

The accuracy in determination of the electronic g-tensor for the set of multifrequency EPR spectra is estimated to be ±0.001.

^*In these cases, the hyperfine coupling constants A_x and A_y were estimated from the linewidth.

At Q-band frequency the g-tensor anisotropy is resolved in most cases, while at X-band frequency the g-tensor anisotropy is generally unresolved, since the cobalt hyperfine interaction is of comparable magnitude. As in the D-band spectra, the cobalt hyperfine structure is resolved only for g_z, while for the A_x- and A_y- components of the ⁵⁹Co A-tensor only an upper limit can in most cases be estimated by line broadening. The accuracy of determination of A_x and A_y is thus lower than for A_z. To determine A_x and A_y more precisely, we performed pulsed ENDOR and pulsed ELDOR-detected NMR experiments at X-band frequency on cobaloxime in methanol. Unfortunately, we were not able to detect signals of ⁵⁹Co in ELDOR-detected NMR experiments. Only weak and broad ENDOR signals were detected, which we attribute to ⁵⁹Co (Figure S4). The strongly anisotropic ⁵⁹Co A-tensor and the non-negligible quadrupolar coupling are most probably responsible for this.

The chemical nature and number of axial ligands can in many cases not be determined by inspection of the EPR spectra. However, if the coordinating atom of the axial ligand molecule possesses a magnetic nucleus (I ≠ 0), the hyperfine interaction with the unpaired electron of the cobalt ion can deliver the necessary information. For pyridine or PDI with their nitrogen (I(¹⁴N) = 1) atom as ligand, a superhyperfine structure can be observed, at least in the high-field part, of the X-band and Q-band EPR spectra. For the samples with a stoichiometric ratio of PDI to Co(dmgBF₂)₂, each resolved cobalt hyperfine line is split in three lines with equal intensity (1:1:1) and demonstrates the presence of one nitrogen axially coordinating the Co(II) ion. The same superhyperfine structure is observed for 1:1 pyridine:Co, indicating that also here only one nitrogen is axially coordinating the cobalt ion. In contrast, in the case of a large excess of pyridine, the superhyperfine structure observed consists of five lines with an intensity ratio of 1:2:3:2:1. This pattern is indicative for two magnetically equivalent nitrogen atoms that are interacting with the same paramagnetic cobalt ion. A smaller excess of pyridine (<10:1) results in a mixture of doubly- and singly-coordinated complexes. Similar results have been obtained for H-capped cobaloxime.^28,35 To exclude the possibility that the strongly interacting nitrogen atoms(s) responsible for the superhyperfine structure are from the equatorial dimethylglyoxime ligands, we performed these measurements also with ¹⁵N-labeled (I = ½) pyridine instead (Figure S3). The superhyperfine structure changed with respect to the ¹⁴N-labeled pyridine, exhibiting a pattern of 1:1 for singly-ligated cobaloxime and 1:2:1 for doubly-ligated cobaloxime. This proves unequivocally that the resolved superhyperfine structure is due to the axial ligand(s). We did not observe in any case resolved hyperfine structure from the equatorial (macrocycle) nitrogen atoms, indicating that their hyperfine couplings are rather small, at least for A_z (assuming that the A-tensor is close to collinear to the g-tensor). This is in agreement with previous studies of H-capped cobaloximes, where also hyperfine coupling constants of the equatorial nitrogen atoms could not be determined from the EPR spectra.^29,32 The quantitative appearance of cobaloxime complexes singly-ligated by PDI or pyridine in samples with a 1:1 stoichiometric ratio demonstrates the far higher affinity of the nitrogen-containing pyridine bases and derivatives to the central Co(II) ion as compared to the oxygen-containing polar (e.g. acetone) or polar and protic (e.g. methanol) solvents, which are readily replaced as axial ligands.

Somewhat different results were obtained for PPh₃ as axial ligand. In the case of the bulky ligand PPh₃, the same EPR spectrum was found for different stoichiometric ratios of cobalt and PPh₃, as long as PPh₃: Co(dmgBF₂)₂ >1 (Figure 2). This is a clear sign of the stability of the five-coordinated complex, if compared to pyridine as the axial ligand, where a tenfold stoichiometric excess results mostly in doubly-ligated cobaloxime complexes. Our observation is in agreement with previous results obtained in a study of H-capped cobaloxime,^26,29 where no doubly-ligated cobaloxime was observed when PPh₃ or related compounds were present. All these results indicate that the binding of a second PPh₃ molecule is not as thermodynamically favorable as it is for pyridine, and that the singly-ligated PPh₃: Co(dmgBF₂)₂ complex is rather stable. A possible reason for this behavior is that the binding of the first bulky ligand molecule results in a displacement of the cobalt ion from the equatorial plane of the macrocycle, possibly including a deformation of the macrocycle. This would make the binding of a second bulky ligand thermodynamically unfavorable and also lower the accessibility of the cobalt ion for catalytic reactions. Since the Co(II)-coordinating part of PDI is identical to pyridine, we consider the explanation that PDI directly causes a much more pronounced cobalt displacement or macrocycle distortion unlikely. A more detailed discussion is given below. In a study of H-capped cobaloxime, Baumgarten et al. observed a larger g-anisotropy when using a toluene:THF mixture instead of methanol.³³ For our BF₂-capped cobaloxime the increase of g-tensor anisotropy is even larger in neat toluene with PDI. It should be mentioned, that the experimental data do show a large increase of g_x as compared to pyridine, but the ⁵⁹Co hyperfine interaction stays similar in magnitude. The effect of cobalt displacement from the plane is discussed in more detail in the DFT section, where we performed a systematic study of the dependence of magnetic parameters on the Co(II) out-of-plane distance.

Correlation Dependence of g- and A-tensors

For simulation of the EPR spectra it has been assumed that the g-tensor principal axes and the principal axes of the ⁵⁹Co A-tensor are collinear. The ligand superhyperfine principal axes (¹⁴N, ³¹P) were assumed to be collinear to the g-tensor principal axes as well. A rotation of the A-tensor with respect to the g-tensor did not lead to an improved fit. The assumption that the g-tensor principal axes and the ⁵⁹Co A-tensor principal axes are close to collinear is also justified on basis of the theoretical DFT calculations (see below). A similar observation concerning the collinearity of g-tensor and ⁵⁹Co A-tensor has also been made for H-capped cobaloxime.^27,33

Figure 3a shows a plot of the g_y-values vs. g_x values. Ignoring the large, bulky ligands PDI and PPh₃, there exists a linear relation between g_y and g_x. A linear interpolation to smaller g_x -values intersects the point where both g_x and g_y are near free electron g-value, g_e (g_x, g_{y ~} g_e). This linear dependence can be justified on the basis of the simplified Stone formula as a first approximation for the prediction of g-tensor anisotropy due to spin-orbit coupling:

$$\mathrm{\Delta }\text{g}\sim (\rho \ast \zeta )/\mathrm{\Delta }\text{E}$$ (Eq. 1)

where Δg is the deviation from g_e; ζ is the spin-orbit coupling constant for the respective atom; ρ is the unpaired spin density in the particular atomic orbital containing the unpaired electron; ΔE is the energy difference between the orbital containing the unpaired electron and lower or higher laying orbitals.⁵⁴ According to Stone’s theory of g-values, negative deviation of g-values from the free electron value is due to spin-orbit coupling with empty higher laying orbitals while spin-orbit coupling with lower laying occupied orbitals leads to positive deviations. The difference between Δg_x and Δg_y is related to the symmetry properties of the particular atomic orbitals. Total deviation of the g-values is a sum of the deviations induced by each atom in the molecule. As Co(II) in 3d⁷ configuration has the biggest spin-orbit coupling constant, 515 cm^•1, as compared to other atoms in the molecule,⁵⁵ the analysis can be simplified by taking into account only Co orbitals. Thus, if the electronic structure of the cobaloxime does not change substantially upon change of the axial ligand, i.e. the molecular orbitals are in the first order approximation the same combination of the atomic orbitals, the plot of g_y vs. g_x should demonstrate linear dependence. As it was shown previously,^53,56,57 the complete absence of axial ligands results in very large g-tensor anisotropy and very large ⁵⁹Co hyperfine coupling constants, much larger than observed in our study. We thus conclude that we always have at least a weak axial ligation of the Co(II) ion. According to Eq. 1 the same linear behavior should hold for the plot of A_z vs. g_x or g_y, as A_z is proportional to the spin density of the unpaired electron within the first order of approximation. Indeed, the plot of A_z vs. g_x (Figure 3b) shows also linear dependence. This is important, since the slopes of the lines on Figure 3 are sensitive characteristics of the electronic structure of the compound and might be a reference point for testing the validity of DFT calculations along with g- and A-tensors.

Figure 3.

Plots of g_y and |A_z| (⁵⁹Co) vs. g_x for the cobaloxime Co(dmgBF₂)₂ in different solvents. All data are obtained from experiments.

A large g-tensor anisotropy for Co(dmgBF₂)₂ is observed for “weakly” coordinating ligands like alcohols, acetone or DMF where an oxygen atom is involved in coordination of the cobalt ion. Ligands termed “weakly coordinating or labile” can be easy replaced by small amounts of another type of ligands referred to as “strongly coordinating”. Two general types of “strong” Co(II) coordination can be distinguished. In the six-coordinated L₂Co(dmgBF₂)₂, complex two strong axial ligands like pyridine are bound to the central cobalt ion. In the five-coordinated LCo(dmgBF₂)₂ only one strong axial ligand is present. If in the case of one strong axial ligand like pyridine a second, weak ligand like methanol or acetone binds at the open axial coordination site can not be verified on basis of our experimental results.

In both cases (singly- or doubly-ligated by pyridine) the g-tensor anisotropy is significantly smaller than for the weakly coordinating solvents like methanol. The doubly-ligated pyridine:cobaloxime complex exhibits even smaller g-tensor anisotropy than the singly-ligated cobaloxime. Since cobaloxime in a solvent of “weak” ligand molecules has most probably two axial ligands, the g-tensor anisotropy is unlikely to be predominantly caused by displacement of the Co(II) ion from the equatorial plane. More likely, the interaction strength with ligand molecules leads to reduced g-tensor anisotropy. The relative small hyperfine interaction with the pyridine nitrogen atoms contradicts the assumption of a substantial shift of unpaired spin density from Co(II) to the ligand molecules, which is supported by the DFT calculations (see below). Concomitantly to the reduced g-tensor anisotropy a reduction of the ⁵⁹Co A_z-value is found, while A_x and A_y both increase in magnitude. The main effect of axial ligand field could be a modification of ΔE term in Eq. 1 and/or a reduction of spin density in the d_z2 orbital, which seems unlikely. A direct determination of relative orbital energies is complicated, since multiple parameters influence the relation between magnetic properties and orbital energies.⁵⁷

So far, the two bulky ligands PDI and PPh₃, which do not fit into the rather simple model described above, have not been discussed. Unfortunately, due to the hydrophobic nature of there ligands, their complexes with cobaloxime can exist only in non-polar solvents such as toluene or CH₂Cl₂/toluene mixture. On the other hand the hydrophilic nature of cobaloxime does not allow existence of pyridine:cobaloxime complexes in strongly non-polar solvents, thus prevents from the direct comparison of magnetic resonance parameters with bulky hydrophobic ligands in the same solvents. These two bulky ligands in combination with the non-polar solvents also exhibited different thermodynamic properties, showing a lower affinity for a second molecule to ligate the Co(II) ion. This matter will be further addressed in the DFT section.

Experimental Results - EPR under aerobic conditions

It is well known that many Co(II) complexes including cobaloximes form adducts with molecular oxygen.^{24,25,58–60} The BF₂-capped cobaloxime Co(dmgBF₂)₂ studied here is expected to be quite resistant against the oxidation by molecular oxygen and subsequent degradation of the cobalt macrocycle.³ This makes it the ideal cobaloxime for studying the interaction of the complex with molecular oxygen, as compared to previous studies of the H-capped cobaloxime. A certain resistance against oxidation and degradation by molecular oxygen is also desirable for any catalyst involved in hydrogen production.

Bakac and co-workers already observed the reversible binding of molecular oxygen by Co(dmgBF₂)₂ in a variety of different solvents, including water, methanol, acetonitrile, and acetone.²⁵ Schrauzer & Lee studied H-capped cobaloxime, using different bases as axial ligands.²⁴ The EPR spectra changed dramatically upon oxygenation, indicating a strong change of the electronic structure of the complex. “Unspecific” oxidation of the macrocycle could be excluded, since the process was reversible and could be repeated multiple times, if water was carefully removed from the solution.²⁴ Lubitz and co-workers studied oxygen adducts of H-capped cobaloxime in a zeolite matrix.⁶¹ However, the X-band spectra presented previously exhibited rather low g-tensor resolution and did not allow a unique determination via magnetic parameters. Here we used the multifrequency approach described above to study the oxygenation of Co(dmgBF₂)₂. We choose a solvent mixture of toluene and CH₂Cl₂, which is known to solubilize Co(dmgBF₂)₂ well without exerting strong interactions on the cobalt center, and also generates a good glass at cryogenic temperatures. These solvents have been previously used to study the oxygenation of cobalt complexes.^58–60 A small amount of PPh₃ was added to act as axial ligand for multiple reasons. In general, cobalt complexes without strong axial ligand are poor oxygen binders, while the presence of one strong axial ligand allows binding of molecular oxygen even at ambient pressures.⁵⁸ As mentioned above and observed previously,^26,29 the presence of PPh₃ in slight excess in the solution results exclusively in a singly-ligated cobaloxime complex, displacing weakly interacting solvent molecules from one binding site and leaving the other coordination site open for another small ligand like molecular oxygen. For a 2:1 ratio of PPh₃:cobaloxime investigated here, we observed quantitative binding of molecular oxygen as shown by the almost complete disappearance of the EPR signal typical for anaerobic cobaloxime samples and appearance of an intense signal from the superoxide. This species was efficiently generated and rather stable in the presence of PPh_3, which is similar to the findings of Schrauzer & Lee for H-capped cobaloxime,²⁴ while the use of other axial ligands resulted in much lower yields of this paramagnetic species. Subsequent bubbling of the solution containing oxygenated cobaloxime with nitrogen gas largely restored the “original” signal as shown in Figure 2. These findings exclude the possibility that the cobaloxime has undergone unspecific oxidation of the macrocycle, which would instead show irreversible spectral changes. Prolonged incubation of the solution for days under aerobic conditions and ambient temperature lead to a steady decrease of the EPR signal, indicating slow degradation of the complex and built-up of possible diamagnetic di-nuclear Co-O₂-Co complexes.^24,58 The presence of ³¹P with a nuclear spin of I = ½ as the ligating atom of PPh₃ also provides the advantage to monitor changes in the spin density distribution via ³¹P hyperfine interaction with the unpaired electron(s) of the cobaloxime, while a possible shift of spin density to or from an axial ligand coordinating via an oxygen atom, i.e. acetone, methanol, or THF - can not easily be observed.

The EPR spectra of oxygen-exposed Co(dmgBF₂)₂ recorded at the three different microwave frequencies are depicted in Figure 4. They are well resolved and could be simulated with the same set of parameters, indicating the presence of only one paramagnetic species. The D-band EPR spectrum (Figure 4a) is rather narrow (<0.15 T) as compared to the spectra of the Co(II) cobaloxime under anaerobic conditions (Figure 2). It exhibits the typical shape for a S = ½ system with a rhombic g-tensor. In the following, we will keep the nomenclature introduced above to name the principal g-values as g_x (for g_max), g_y (for g_mid), and g_z (for g_min). Note, that different nomenclatures have been used previously.^60–62 In contrast to the spectra of the Co(II) cobaloxime recorded under anaerobic conditions, resolved hyperfine structure is not visible. The absence of the prominent cobalt hyperfine structure at the high-field part of the spectrum is a further indication of the significant electronic changes experienced by the cobalt ion upon binding of oxygen. The principal values of the g-tensor can be directly determined from the spectrum, as 2.0390, 2.0014, and 1.9879. The g-values determined by Bakac et al. for acetone ligated cobaloxime and by Schrauzer & Lee do not agree well with our findings.^24,25 This could be due to the difference in one of the axial ligand, however, the poorly resolved X-band EPR spectra reported previously might have resulted in an erroneous determination of the g-tensor. The pronounced reduction of the g-tensor anisotropy is typical for Co(II) low spin complexes singly-ligated by molecular oxygen.^58–60 At Q-band frequencies (Figure 4b), the spectrum is less than 40 mT wide, and the three principal g-values are still resolved, confirming the absence of any large hyperfine interaction. However, a clear broadening of the g_y component can be observed, which can be attributed to unresolved hyperfine interaction.

Figure 4.

EPR spectra of the complex PPh₃: Co(dmgBF₂)₂ in a CH₂Cl₂:toluene 1:1 mixture under aerobic conditions recorded at different microwave frequencies (D-band, Q-band, X-band). The field-swept ESE-detected D-band spectra have been pseudo-modulated. Q-band and X-band spectra are CW EPR spectra. Simulations are depicted in red.

At X-band frequency, the whole spectrum is about 20 mT wide. Its appearance resembles many X-band spectra of oxygenated forms of related cobalt complexes and cobaloximes, see e.g.^60,63,64 A well-resolved hyperfine structure is visible around g_y, although the hyperfine structure around g_x is not resolved. This is in contrast to vitamin B₁₂ complexes where the hyperfine structure at low field is typically well resolved.^61,64,65 The number of lines could only be reproduced in the spectral simulation by the assumption of significant hyperfine interaction of one phosphorus nucleus and one cobalt nucleus, both being very similar in magnitude, around 35 MHz. The presence of substantial ³¹P hyperfine interaction was confirmed by additional experiments. The use of PDI instead of PPh₃ as axial ligand resulted in a decrease of hyperfine lines from 9 to 8 (see Figure S7). The absence of a visible hyperfine structure at g_x allows no reliable estimation of A_x neither for ⁵⁹Co nor ³¹P. The EPR signals arising from g_z severely overlap with the hyperfine structure of g_y. The A_x and A_z values used for the simulation thus bear a rather large error. The much lower magnitude of the ³¹P hyperfine interaction as compared to the deoxygenated cobaloxime is in line with the observed dramatically reduced ⁵⁹Co A-values due to the lower spin density on the coordinated cobalt ion. In this type of complex, the ⁵⁹Co A-tensor and ³¹P A-tensor are expected not be collinear anymore with the g-tensor.⁶⁰ Lifting the assumption of collinear axes systems and using similar angles as in studies of related cobalt oxygen adducts^60,63,65 lead only to minor changes in the spectral simulations. Schrauzer & Lee estimated for the H-capped cobaloxime a reduction of unpaired spin density at the cobalt by at least a factor of 5 on the basis of the ⁵⁹Co isotropic hyperfine coupling. Even larger reductions have been estimated for H-capped cobaloxime ⁶¹ and related compounds.^63,65

Cobalt complexes can form several different complexes with molecular oxygen, see e.g. ⁵⁸. One complex which may be formed by cobaloximes dissolved in organic solvents in the presence of molecular oxygen are dinuclear μ-peroxides, as shown previously for H-capped cobaloxime.²⁴ This type of dinuclear complex is diamagnetic and thus not detectable by EPR spectroscopy. A paramagnetic μ-superoxo radical cation L-Co(dmg₂H₂)-O₂-Co(dmg₂H₂)-L⁺ with a characteristic 15-line signal in liquid solution was also observed. This signal is due to the interaction of two magnetically equivalent cobalt nuclei with the unpaired electron symmetrically delocalized over the Co-O₂-Co moiety.²⁴ We did not observe the dinuclear μ-superoxo radical under our experimental conditions. Mononuclear superoxide complexes can be described as L-Co(dmg₂H₂)-O₂^•and characterized by a hyperfine splitting multiplicity of eight, indicative of the presence of only one cobalt ion in the complex. This complex was obviously observed in our study. The frozen solution spectra reported here show no indication of S > ½. As Co(II) has one unpaired electron in the non-oxygenated complex, and molecular oxygen is a ground state triplet (S = 1) due to two unpaired electrons, the resultant spin is S = ½. The coordination environment in Co(II) Schiff base compounds resembles that of cobaloxime, and a qualitative interpretation of the EPR spectra of these compounds binding molecular oxygen has been given by Hoffman et al.⁶³ In that work, the authors concluded that the cobalt ion is essentially oxidized to Co(III) and the molecular oxygen is reduced to the superoxide ion, O₂⁻ and estimated the transfer of spin density from cobalt to oxygen to be roughly 90%. Schrauzer & Lee determined the ⁵⁹Co isotropic hyperfine coupling for the H-capped cobaloxime and estimated a reduction of unpaired spin density at the cobalt by a factor of 5–10. Since we observe similar hyperfine coupling for the difluoroboryl cobaloxime, we may follow their line of reasoning. Additional experimental evidence that related cobalt complexes form under presence of molecular oxygen Co(III) superoxide complexes, provides further support of an assignment of our complex as being formally LCo(III)O₂^• superoxide.^{58,59,61,65–67}

We thus conclude that there is almost complete transfer of the cobaloxime’s unpaired electron spin density to the oxygen. The g-tensor anisotropy is then mostly determined by the spin density on the oxygen atoms, and the principal component of the g-tensor with the largest deviation from g_e will be in direction of the inter-oxygen axis. The cobalt hyperfine coupling instead is determined by the 3d orbital of the cobalt ion, and this presents a pronounced difference to the non-oxygenated complex. From our experimental data no direct conclusion is possible regarding the presence of the three different conformers (chair, boat-PPh₃, boat-O₂). A comparison with the results from the DFT calculation let us favor the boat-PPh₃ conformation (see discussion below).

DFT Results

The calculated g-values, ⁵⁹Co A-values, and superfine coupling constants are presented in Table 2. To the best of our knowledge, these are the first published EPR parameter calculations for singly- and doubly-ligated Co(II) cobaloxime complexes. Previous semi-empirical calculations focused on the effect of the cobalt displacement on the energetics of the compound²⁹ and four-coordinate Co(II) complexes without axial ligands were reported.⁶⁸ Recent DFT studies on cobaloxime did not report any magnetic parameters.^69,70 The structure of the cobaloxime complex allows multiple conformations of each cobaloxime-ligand(s) complex. As shown in Figure 5, using the common cyclohexane notation, the conformations can be labeled “chair” and “boat” with the possibility of further specifying the boat as towards or away from the attached ligand. If only one axial ligand molecule was included in the calculation, the expressions “boat towards ligand” or “boat away” are used. The “boat” and “chair” conformations refer to the orientations of the BF₂ caps with respect to the macrocycle plane. Unlike the four-coordinate Co(II) complexes investigated by Zbiri,⁶⁸ our calculated g-values do not change significantly when other hybrid functionals are used. Before discussing in detail the results of the calculations, some critical issues regarding the accuracy and reliability of the calculations are addressed briefly.

Table 2.

Conformations, energies, cobalt out-of-plane distances, and magnetic parameters for the cobaloxime Co(dmgBF₂)₂ obtained by DFT calculations. The calculations of magnetic parameters were performed on the geometry optimized structures (see Experimental Procedures for details). The magnetic dipole and the isotropic Fermi contact hyperfine coupling constants were calculated for all atoms, while for ⁵⁹Co second order spin-orbit hyperfine contributions are also included. The ¹⁴N hyperfine coupling constants refer to the axial ligands, not to the macrocycle (equatorial) nitrogen atoms. Values in parentheses are provided if the two axial nitrogen atoms are magnetically not equivalent.

Complex	Conformation	Co out–of–plane distance [Å]*	Energy of complex formation [kcal/mol]#	g-values	A(59Co) [MHz]	Ligand superhyperfine A(14N) [MHz] or A(31P) [MHz]
Pyrdine: Co (2:1)	Boat	0.15	−25.8	2.1382 2.0980 2.0057	−99 −139 +359	+37 (+37) +38 (+38) +46
	Chair	0.03	+2.34	2.0362 2.0157 1.9972	−152 −5 +11	+26 (+29) +30 (+33) +63
	Exp			2.1910 2.1270 2.0080	105 148 242	36 39 48
Pyridine:Co (1:1)	Chair	0.27	−26.8	2.2074 2.1387 2.0074	−52 −69 +355	+29 +30 +36
	Boat towards	0.32	−25.4	2.2043 2.1266 2.0073	−71 −91 +345	+28 +29 +37
	Boat away	0.18	−24.2	2.1890 2.1303 2.0071	−46 −61 +368	+29 +30 +37
	Exp			2.2380 2.1530 2.0058	10 10 285	33 36 43
PDI: Co (2:1) &	Boat	0.14	−21.4	2.1413 2.1008 2.0054	−85 −126 +369	+37 (+37) +37 (+38) +46
PDI: Co (1:1) &	Boat away	0.18	−25.6	2.1910 2.1323 2.0069	−38 −55 +375	+29 +30 +38
	Boat towards	0.14	−23.6	2.2074 2.1290 2.0071	−66 −88 +348	+28 +29 +37
	Chair	0.28	−23.3	2.2183 2.1549 2.0076	+9 +28 +423	+28 +29 +36
	Exp			2.3473 2.1815 2.0000	85 10 306	30 30 40
Methanol: Co (2:1)	Chair	0.00	−24.5	2.1535 2.1153 2.0052	−27 −61 +423	n/a
	Boat	0.08	−23.0	2.1626 2.1212 2.0057	−11 −41 +435	n/a
	Exp			2.2840 2.1820 2.0080	53 20 338	n/a
Methanol: Co (1:1)	Chair	0.17	−22.1	2.2215 2.1564 2.0066	+59 +39 +456	n/a
	Boat towards	0.27	−21.8	2.2338 2.1564 2.0070	+34 +14 +427	n/a
	Boat away	0.34	−14.8	2.2728 2.2116 2.0084	−19 −38 +335	n/a
H2O: Co (2:1)	Chair	0.00	−25.0	2.1529 2.1159 2.0053	−29 −64 +424	n/a
	Boat	0.06	−23.8	2.1507 2.1158 2.0054	−40 −72 +418	n/a
	Exp			2.2750 2.1785 2.0065	15 15 329	n/a
H2O: Co (1:1)	Boat towards	0.23	−22.4	2.2158 2.1527 2.0067	+28 +13 +436	n/a
	Boat away	0.10	−21.0	2.2195 2.1629 2.0068	+94 +69 +486	n/a
	Chair	0.39	−2.2	2.3146 2.1604 2.0093	−27, −59, +311	n/a
Methanol: Co:Pyridine (1:1:1)	Boat-Methanol	0.03	−26.4	2.1452 2.1056 2.0056	−79, −108, +375	+35, +36, +44
	Chair	0.13	−25.0	2.1500 2.1109 2.0056	−101, −66, +385	+34, +35, +43
	Boat-Pyridine	0.21	−24.2	2.1551 2.1076 2.0057	−89, −118, +367	+34, +35, +43
PPh3: Co (2:1)	Chair	0.00	−10.9	2.2070 2.1431 2.0060	+120, +164, +527	+251, +252, +308
PPh3: Co (1:1)	Boat away	0.22	−18.9	2.2213 2.1455 2.0072	+49, +19, +408	+236, +235, +283
	Chair	0.28	−18.0	2.2318 2.1481 2.0073	+38, +6, +396	+241, +240, +290
	Boat towards	0.32	−12.6	2.2467 2.1574 2.0075	+43, +16, +400	+254, +253, +307
	Exp			2.3000 2.1425 1.9995	36, 10, 249	300, 300, 358
PPh3: Co: O2 (1:1:1)§	Chair	0.10	−46.6	2.0462 2.0062 1.9908	−50, −30, −21	−15, −15, −15
	Boat-PPh3	0.13	−45.8	2.0357 2.0005 1.9829	−78, −34, −30	−15, −19, −19
	Boat-O2	0.07	−47.8	2.0454 2.0062 1.9912	−48, −28, −19	−15, −15, −15
	Exp			2.0390 2.0014 1.9879	28, 32, 13	20, 37, 37

^*The cobalt out–of–plane distance is measured from the cobalt atom to the center of a plane formed between the four nitrogen atoms in the cobaloxime structure.

^# Energy of complex formation: The energies of complex formation are estimated from subtracting the energies of the individual geometry optimized substituents (ligands and cobaloxime) from the energy of the geometry optimized complex. The energies include contributions from the COSMO solvent effect.

^& For PDI as axial ligand, the geometry optimizations were done with the complete molecule, while the magnetic parameter calculations were done with a truncated PDI model system.

^§ In this complex the principal axes of the g-tensor and the hyperfine tensors/A-tensors deviate with respect to each other and the molecular axes system. The respective Euler angles are provided in Table S3 in the Supporting Information.

Figure 5.

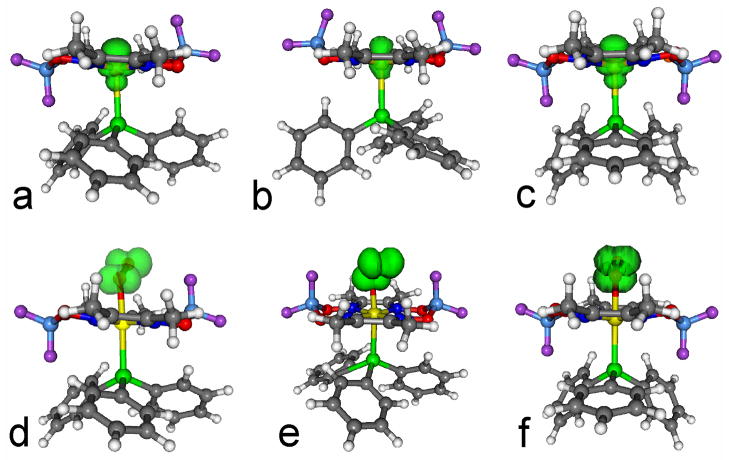
Spin density isosurface plots of cobaloxime Co(dmgBF₂)₂. All isosurfaces are shown at a contour level of 0.005 e/a₀³. From left to right: (a) Doubly-ligated by pyridine (chair), (b) doubly-ligated by pyridine (boat), (c) singly-ligated by pyridine (chair), (d) singly-ligated by pyridine (boat away), (e) singly-ligated by pyridine (boat towards).

One problem of DFT calculations on large open shell transition metal complexes is the high accuracy required to distinguish between conformations which are quite close in energy as compared to the overall energy of the complex. This is partially the result of inherent approximations made in DFT calculations.^71,72 At least part of the discrepancy between actual and calculated energies is due to insufficient inclusion of the interactions with solvent. Increasing the number of solvent molecules in the calculation and thus forming an extended solvent shell around the complex may lead to an improved prediction of conformational energies and also to improved magnetic parameters as compared to pure gas phase calculations.^73–75 However, the explicit inclusion of a large number of solvent molecules is computationally demanding, thus such time consuming calculations were not performed. Instead only the direct ligands to the central cobalt atom were explicitly included and the residual surrounding solvent molecules were implicitly included using the dielectric screening model COSMO.⁴⁴ This neglect is considered to be most problematic for those solvent molecules where significant direct interactions with the cobaloxime are expected. For example, it has been shown that hydrogen bonding is in many cases essential to geometries and electronic structures.^76–78 However, since in our study the experimental spectra of cobaloxime in methanol:pyridine and acetone:pyridine mixtures were almost identical (see Table 1 for the magnetic parameters), possible hydrogen bonding to the cobaloxime by solvent molecules is not considered critical for the electronic structure of the cobalt complex and thus no calculations with solvent molecules ligated to the fluorine atoms were performed.

If conformers exist with comparable energies (same order of magnitude as kT), the complexes in frozen solution studied by EPR spectroscopy may also consist of a mixture of conformers trapped during the freezing process. In addition, our calculations determine the energetic minimum but do not include entropic contributions. Hence, instead of choosing only the lowest energy conformation, we present the magnetic parameters calculated for the various conformations. It is expected that the comparison with the experimentally determined magnetic parameters allows us to more reliably exclude conformers than a discrimination based solely on energy. To validate the quality of the geometry optimization, we repeated selected calculations with different functionals, basis sets, and dielectric constants. Use of a sufficiently large dielectric constant for the COSMO screening model was found to be needed to obtain reasonable structures, i.e. to avoid structures with strong distortion of the macrocycle. Otherwise, all calculations resulted in nearly identical geometries and energetic orderings within the conformations, which suggests that the obtained structures are reliable. Problems with precisely calculating the magnetic parameters for our specific transition metal complexes are discussed below in relation to the available experimental data.

Cobaloxime with axial ligands (except molecular oxygen)

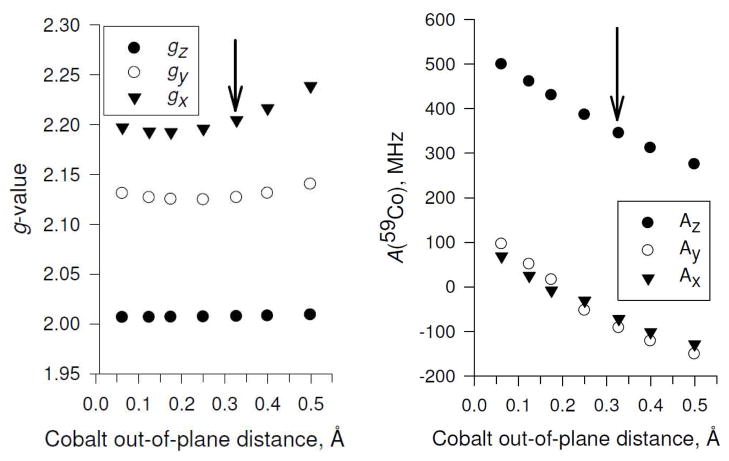
As shown in Table 2, the position of the cobalt with respect to the plane of the cobaloxime macrocycle varies greatly depending on number and nature of the axial ligand(s). Most notably, the di-water and di-methanol complexes result in the cobalt remaining nearly planar while the nitrogen and phosphorus containing ligands pull the cobalt out of plane. Additionally, singly-ligated complexes pull the cobalt out of the plane to a greater degree than their doubly-ligated counterparts and the boat conformations show greater displacements than the chair. To evaluate systematically the effect of this cobalt out-of-plane movement on the electronic g-tensor and the cobalt hyperfine interaction independent of the chemical nature of the ligand, we investigated a model system composed of just the cobaloxime with one pyridine molecule in the “boat towards pyridine” conformation. The energetic minimum for this system has the Co(II) ion located 0.32787 Å below the plane of the macrocycle pulled towards the pyridine. In these calculations, the cobalt atom was moved in and out of the macrocycle nitrogen plane fixed there while the rest of the molecule was allowed to relax. Further details of the calculation are given in the Experimental Procedures section. The effects on the g-values and ⁵⁹Co hyperfine coupling constants A_x, A_y, and A_z are presented in Figure 6 and listed in Table S1. In the case without forced displacement of the Co(II) ion, the principal g-values, ⁵⁹Co A-values, and ¹⁴N A-values resemble those obtained experimentally. The displacement of the cobalt ion leads to a systematic change in both the principal g-values and the ⁵⁹Co A-values while the ¹⁴N A-values (not shown) do not appreciably vary from the non-displaced case. Notably, the ⁵⁹Co A-values exhibit an almost linear relationship with cobalt out-of-plane distance. A_x, A_y, and A_z values all decrease as the cobalt moves further away from the plane. Moving the cobalt into the plane, beyond the energetic minimum position, has a weak influence on the g-values. Despite the correlation shown in the test calculation, the chemical nature of the ligand and the chair/boat conformation seems to obscure this effect on the values of the principal g-values and ⁵⁹Co A-values. Thus it is not possible to directly predict the cobalt position from the g-values or the ⁵⁹Co A-values. For example, consider the singly-ligated water case (Table 2). The two boat conformations differ in the cobalt distance by 0.13 Å, and the ⁵⁹Co A_z-values decrease as expected. The chair conformation has an even larger distortion and a concurrent larger drop in the ⁵⁹Co A_z-value. However, the g-values do not increase for the chair conformation as might have been expected from the model. In general, the ⁵⁹Co A_z-values are most sensitive to the cobalt position while the g-values are a poor indicator of cobalt position. This is in agreement with prior work on d¹ five-coordinate systems that showed only a weak dependence of the g-values on geometry.⁷⁹ In terms of directly predicting the experimental g-tensor, the calculations correctly reproduce the trend of decreasing g-values (g_x, g_y) as the complex goes from singly-ligated by pyridine to doubly-ligated. However, the calculations underestimate the g_x value for all ligands except the PPh₃ oxygen adduct. This is not a problem specific to our study. The systematic underestimation of g-values of transition metal complexes by DFT is common,⁷² nevertheless, they can be used to indicate a trend within the series of calculations.

Figure 6.

Effect of cobalt out-of-plane distance on electronic g-values g_x (▼), g_y (○), g_z (●) and ⁵⁹Co hyperfine coupling constants A_x (▼), A_y (○), A_z (●) for Co(dmgBF₂)₂. The complex contains a single pyridine molecule as the axial ligand in the “boat towards pyridine” conformation. A restricted geometry optimization was performed with the Co(II) ion pulled systematically in and out of the plane of the macrocycle (as compared to the calculation without constraint with a out-of-plane distance of 0.32787 Å) using a torsion constraint (Co-N-N-N, Figure 1). The ¹⁴N A-values of the axial pyridine ligand do not appreciably vary from the case without constraints (data not shown). Details of the DFT calculations are given in the Experimental Procedures section. For both graphs, the arrows mark the unconstrained optimized structure. The numerical values are given in Table S1 (Supporting Information).

Turning to the ⁵⁹Co A-values, qualitative rather than quantitative agreement is present. The three contributions to the (transition metal) hyperfine interaction (Fermi contact, spin-dipolar, and spin-orbit coupling) are known to be difficult to calculate with accuracy.^80,81 In agreement with experiment, the A_z-values of Co(dmgBF₂)₂ in methanol and water are greater than the corresponding values for pyridine.

The ¹⁴N A-values of the equatorial (dimethylglyoxime) nitrogen atoms were also calculated. They are found to be small, below 8 MHz in all (energetically reasonable) cases and in majority of cases well below that (see Table S2). The hyperfine coupling constants of the equatorial nitrogen atoms were not resolved in the EPR spectra. HYSCORE data of Co(dmgBF₂)₂ in methanol (see Figure S6) allows us to estimate these ¹⁴N hyperfine coupling constants as below 4 MHz which is in a good agreement with the principle values obtained by the DFT calculation. The ¹⁴N and ³¹P A-values of the axial ligands which could be determined from the EPR spectra were nicely reproduced by the DFT calculations, see Tables 1 & 2. The general better agreement of superhyperfine interactions than hyperfine interactions of the central metal ion is typical for DFT calculations.⁸²

The binding energies for the six-coordinate complexes (two axial ligands) predicted by the calculations are in general agreement with experiments (pyridine > methanol; PPh₃ > toluene, CH₂Cl₂). In some of these cases, the singly-ligated conformation appears to be more energetically favorable than the doubly-ligated one. As noted previously, some ligands like PPh₃ seem to result in a stabilization of the singly-ligated Co(II) complex.²⁹ Prior authors attributed this observation to a distortion of the cobaloxime structure where the Co(II) is pulled out of the plane towards the ligand and the equatorial glyoxime ligands are folded away from the axial ligand. By comparing binding energies, it is clear that while water and methanol are more stable as doubly-ligated complexes, this is not true for other complexes. The pyridine complex is nearly isoenergetic as a 2:1 and a 1:1 complex while the calculations predict that the PPh₃ and PDI complexes prefer the mono-substituted complex. These results are in good agreement with the experimental results. For PDI and PPh₃ we observed only singly-ligated complexes, while already a moderate excess of pyridine leads to a significant presence of doubly-ligated complexes. However, the optimized structures of complexes singly-ligated by pyridine or PDI are very similar and yield similar magnetic parameters, while the latter is not found experimentally. From calculations it is unclear whether a solvent effect is present (methanol or acetone for pyridine, and toluene or CH₂Cl₂:toluene for PDI and PPh₃). It seems likely, that for cobaloxime singly-ligated by pyridine in the methanol solution, a methanol molecule acts as a second but “weak” ligand.

Computationally, the binding of a single PDI molecule to the cobalt induces out-of-plane displacements almost identical to that of the binding of pyridine. Experimentally, the single PDI molecule binding results in the largest g_x-value. However, in the DFT calculation this large g-tensor anisotropy is not reproduced. In fact, not surprisingly, the calculated magnetic parameters of cobaloxime singly-ligated by one PDI molecule resemble relatively closely those of cobaloxime singly-ligated by pyridine (Table 2). This might be explained by our tentative assumption that the quite non-polar solvents (toluene or CH₂Cl₂:toluene mixture) have an additional effect on the geometry and electronic structure of the cobaloxime complex (see above). For PDI in neat toluene, the second axial ligand may either be absent or hardly coordinating, in contrast to methanol or acetone as solvents. This might be especially prominent since both PDI and PPh₃ are the most bulky ligands studied here. A highly simplified picture would be a kind of “folding” of the macrocycle. However, computationally, optimizing the singly-ligated PDI complex using a low dielectric constant but not explicitly solvent molecules does not appreciably change the geometry or the g-values.

Experimentally, the single PPh₃ ligand results in the second largest g_x component determined, but in a rather small g_y value. While the geometry of the singly-ligated PPh₃ complex after energetic minimization is quite distorted; the calculations still under-estimate g_x but match g_y quite well.

In addition to influencing the location of the cobalt atom, the ligands also seem to influence the stability of the boat/chair conformational preference of the cobaloxime itself. In particular, water and methanol are most stable in the chair conformation shown in Figure 5 while pyridine is most stable in the boat conformation (Table 2). The “chair” structure obtained for two methanol ligand molecules is in good agreement with the crystal structure determined by Bakac et al.²⁵ Our calculated structure has a cobalt-methanol oxygen distance of 2.246 Å and the crystal structure reports a distance of 2.264(4) Å. Within this work the crystal structure of Co(dmgBF₂)₂ with two acetonitrile molecules as ligands was determined (see Supplementary Information). It exhibits a similar distance with 2.25 Å and shows also “chair” conformation. Both the calculated and the two crystal structures have in-plane cobalt atoms. While no di-pyridine crystal structure exists, support for the boat structure is evident both in the energetics and in the g-and A-values.. The calculations also predict that PDI would exhibit the boat conformation. For the PPh₃:Co (1:1) complex, the energetics suggest that the “boat towards” conformers is less likely, but all three conformers have so similar magnetic parameters that we can not distinguish them with reference to the experimental data.

The DFT calculations provide not only the magnitude of the magnetic interactions, but also the orientation of the g-tensor principal axes and those of the A-tensors (⁵⁹Co, ¹⁴N, ³¹P) within the molecular frame. Figure 1 presents the molecular axes system of cobaloxime, with the axes labeled accordingly. For all cases without molecular oxygen bound to the Co(II) ion we observed that the lowest g-value, g_z, is perpendicular to the equatorial plane, i.e. pointing along the d_z2 orbital. The middle g-value, g_y, is always found to be collinear to the boron-boron axis and the highest g-value, g_x, is perpendicular to the two other. The ⁵⁹Co A-tensor principal axes are also to a good approximation collinear to the molecular axes system. The deviation of the electronic g-tensor and ⁵⁹Co A-tensor from the molecular axes system was usually less than 5°. Only the binding of PPh₃ which caused a slight distortion of the macrocycle, resulted in deviations up to 10°. All ligands (¹⁴N, ³¹P) A-tensors were collinear to the molecular axes system with deviations of less than 5°.

Cobaloxime with oxygen and PPh₃ as axial ligands (molecular oxygen adduct)

Finally, DFT calculations on the O₂:Co:PPh₃ complex were done for the three conformers: chair, boat towards PPh₃, and boat towards O₂. All three conformers are rather close in energy (Table 2). Geometry optimizations were performed several times with different starting structures which differed regarding the orientation of the oxygen molecule with respect to the cobaloxime. All calculations resulted in the O-O-Co angle remaining near 120°. For the conformers chair and boat towards PPh₃ the minimum is very shallow (less than 2 kcal/mol as the O₂ is rotated over the macrocycle). In contrast, the boat towards O₂ structure results in structures with unbound oxygen if the initial O-O-Co-N dihedral angle deviates from the one found in the energetic minimum. For all three, the magnetic parameters exhibit no pronounced differences and show reasonable agreement with the experiment, regarding the electronic g-tensor, the ⁵⁹Co A-tensor and the ³¹P A-tensor. However, the g-tensor of the “boat towards PPh₃” conformer shows the best agreement with the experiment and we discuss this boat conformer in the following. The analysis of the other conformers is similar. In the “boat towards PPh₃” conformer, the distance between cobalt and the bound phosphorous atom is 2.57 Å, and hence hardly changed as compared to the corresponding 2.63 Å found in the de-oxygenated complex. The distance between the two oxygen atoms is 1.35 Å. The calculated distance between the two oxygen atoms of unbound molecular oxygen is 1.22 Å, while the calculated distance in O₂⁻ is 1.35 Å (both distances from DFT calculations with 6–31G* basis set). The virtually identical distance between the two oxygen atoms in the oxygen adduct and the O₂⁻ anion is a strong hint that a substantial shift of the electron density from cobalt towards the oxygen has occurred and thus supports the formal description of the oxygen adduct as a LCo(III)O₂⁻ superoxide. The Co-O-O bond angle is 119°, which is in the typical range found for cobalt superoxide complexes.⁵⁸ Also the spin density (shown in Figure 7) exhibits the expected shift from the Co(II) ion to the O₂ molecule. This calculation thus clearly refutes for the cobaloxime the spin-pairing model proposed by Tovrog et al. ^83,84 and supports the view of the oxygen-adduct as a LCo(III)O₂^• superoxide. The principal axes of the g-tensor and the A-tensors (⁵⁹Co and ³¹P) deviate with respect to each other and the molecular axes system (see Table S3 in the Supporting Information). This is typical for O₂:Co:L complexes.^60,62,63,65

Figure 7.

Spin density isosurface plots of cobaloxime Co(dmgBF₂)₂. All isosurfaces are shown at a contour level of 0.005 e/a₀³. Top. The complex PPh₃:Co (1:1) in (a) “chair”, (b) “boat away”, and (c) “boat towards” conformation. Bottom. The complex PPh₃:Co:O₂ (1:1:1) in (d) “chair”, (e) “boat towards O₂”, and (f) “boat towards PPh₃”conformation.

Conclusion

In conclusion, we have presented a comprehensive study of the molecular H₂ catalyst Co(dmgBF₂)₂ by multifrequency EPR spectroscopy at X-band (9 GHz), Q-band (34 GHz), and D-band (130 GHz), combined with DFT calculations. Cobaloxime was investigated in a number of solvents with different polarity, proticity and stochiometric amounts of potential ligands to the cobalt ion. This approach allows a clear distinction between labile and strongly coordinating types of axial ligands to the Co(II) macrocycle, as well as two types of strong Co(II) coordination: singly-ligated LCo(dmgBF₂)₂ and doubly-ligated L₂Co(dmgBF₂)₂. Weakly coordinating ligands like methanol result in larger g-tensor anisotropy than strongly coordinating ligands like pyridine. The presence of two strongly coordinating axial ligands leads to the smallest g-tensor anisotropy. Strongly binding N-donating solvents displace the weaker O-donating solvents as axial ligands to the Co(II) ion in the cobaloxime. Therefore, O-donating solvent environments can more readily facilitate proton binding at the cobalt center to initiate H-H bond formation, rather than forming a tight and rather stable complex with solvent molecules and hindering proton binding. The influence of molecular oxygen and formation of Co(III) superoxide radicals LCo(dmgBF₂)₂O₂^• was also studied. The proportional decrease in both ligand and ⁵⁹Co hyperfine coupling constants for the reversible LCo(dmgBF₂)₂ + O₂ ⇆ LCo(dmgBF₂)₂O₂^• transformation is consistent with a substantial shift of electron spin density to oxygen. Finally, the results obtained experimentally are compared to a comprehensive set of DFT calculations on Co(dmgBF₂)₂ model systems with various axial ligands, and on oxygen adducts in the presence of PPh₃. Comparison with experimental values for the “key” magnetic parameters like g-tensor and ⁵⁹Co A-tensor allows the determination of the identity of the ligands and conformation of the axially ligated Co(dmgBF₂)₂ complexes.

In this study, we chose this BF₂-capped cobaloxime in particular as it stands out among earth-abundant H₂ catalysts as extremely efficient and quite stable under relevant conditions for catalysis. Our observations provide important insight on electro- and photocatalytic efficiencies, and explain for example the results of Fihri et al. on supramolecular cobaloxime photocatalysis, who found a nearly six-fold enhancement in H₂ turnovers in acetone solution as compared to acetonitrile.⁴

Future work will be directed toward understanding the catalytical activity of supramolecular assemblies of cobaloxime as catalyst and photosensitizers, including conventional artificial photosensitizers as well as natural photosentizers (i.e. photosynethetic proteins).⁸⁵ We anticipate that the combination of multifrequency EPR structural analysis and high-level DFT calculations will provide a predictive role in the development of new photocatalysts.