Estimation of the ¹⁸F-FDG Input Function in Mice by Use of Dynamic Small-Animal PET and Minimal Blood Sample Data

Abstract

Derivation of the plasma time–activity curve in murine small-animal PET studies is a challenging task when tracers that are sequestered by the myocardium are used, because plasma time–activity curve estimation usually involves drawing a region of interest within the area of the reconstructed image that corresponds to the left ventricle (LV) of the heart. The small size of the LV relative to the resolution of the small-animal PET system, coupled with spillover effects from adjacent myocardial pixels, makes this method reliable only for the earliest frames of the scan. We sought to develop a method for plasma time–activity curve estimation based on a model of tracer kinetics in blood, muscle, and liver.

Methods

Sixteen C57BL/6 mice were injected with ¹⁸F-FDG, and approximately 15 serial blood samples were taken from the femoral artery via a surgically inserted catheter during 60-min small-animal PET scans. Image data were reconstructed by use of filtered backprojection with CT-based attenuation correction. We constructed a 5-compartment model designed to predict the plasma time–activity curve of ¹⁸F-FDG by use of data from a minimum of 2 blood samples and the dynamic small-animal PET scan. The plasma time–activity curve (TACp) was assumed to have 4 exponential components (TAC_P = A₁e^λ₁t + A₂e^λ₂t + A₃e^λ₃t − (A₁ + A₂ + A₃) e^λ₄t) based on the serial blood samples. Using Bayesian constraints, we fitted 2-compartment submodels of muscle and liver to small-animal PET data for these organs and simultaneously fitted the input (forcing) function to early small-animal PET LV data and 2 blood samples (~10 min and ~1 h).

Results

The area under the estimated plasma time–activity curve had an overall Spearman correlation of 0.99 when compared with the area under the gold standard plasma time–activity curve calculated from multiple blood samples. Calculated organ uptake rates (Patlak K_i) based on the predicted plasma time–activity curve had a correlation of approximately 0.99 for liver, muscle, myocardium, and brain when compared with those based on the gold standard plasma time–activity curve. The model was also able to accurately predict the plasma time–activity curve under experimental conditions that resulted in different rates of clearance of the tracer from blood.

Conclusion

We have developed a robust method for accurately estimating the plasma time–activity curve of ¹⁸F-FDG by use of dynamic small-animal PET data and 2 blood samples.

Pet (1) is ideally suited for the kinetic modeling of radiolabeled compounds because the time–activity curve of a tracer in plasma and selected organs can be realized in a live animal in a single setting. This fact facilitates a population approach (2) to tracer kinetics, in which the statistical distribution of parameters that control in vivo tracer dynamics across a group of subjects can be calculated. It is critical that the concentration of a tracer in plasma is accurately measured to calculate the kinetic properties of the tracer in each organ or tissue. In terms of the system variables written from a “black box” perspective, this process can be expressed as

$$y(t)=h(t)\otimes u(t).$$ Eq. 1

In this equation, h(t) describes the characteristics of the black box, that is, the tissue of interest; the input u(t) and output y(t) represent the concentrations of the tracer in plasma and tissue, respectively; and ⊗ is the convolution operator. h(t) is the unknown quantity to be estimated and is a function of parameters that quantify tissue perfusion rates and subsequent tracer uptake via binding and metabolism.

Although the time–activity curve of a tracer in each organ can be calculated with relative ease from a reconstructed PET image (3), for mice, measurement of the input function (¹⁸F-FDG time–activity curve in plasma) poses a significant challenge (4). In small animals, there exists no large vessel or blood pool within a reconstructed PET image from which to estimate the input function without spillover from adjacent tissue, contrary to the situation in larger mammals. Numerous methods have been developed to circumvent this problem, but so far none have been able to do so with both ease and accuracy. Methods requiring surgical intervention (4) can provide accurate measurements of plasma concentrations but are labor-intensive, whereas computational methods, such as factor analysis (5,6), are hindered by experimental (oscillatory movement of mouse during scanning due to respiration) and resolution issues that reduce accuracy. Serial blood samples can provide accurate information on the ¹⁸F-FDG plasma time–activity curve but usually require surgical insertion of a catheter and tend to result in major blood loss when used in mice.

Here we propose that the input function can be estimated by use of a model based on a standard 4K compartmental model (7), which corresponds to the system equations, h(t), describing ¹⁸F-FDG uptake in liver and muscle. Plasma time–activity curves obtained from serial blood samples from a small population of mice were used to calculate Bayesian constraints (8), which were applied to the 4K model, improving the accuracy of the predicted input function determined from limited blood samples (n = 2). Additionally, the early portion of the plasma time–activity curve was calculated from the PET image of the left ventricle (LV) of the heart and corrected for delay and dispersion (9), partial-volume effects (10–13), and uptake by red blood cells (RBCs) (14). This technique, combined with 2 blood samples and the Bayesian constraints, allowed accurate prediction of the input function from time–activity curves of the tracer in muscle and liver.

MATERIALS AND METHODS

Mouse Imaging Studies

Sixteen C57BL/6 mice (~29 g, nonfasting) were anesthetized (~2% isoflurane) and injected with ¹⁸F-FDG (~18.5 MBq, tail vein bolus). During an approximately 60-min small-animal PET scan, serial blood samples (10 μL each) were taken manually from a femoral catheter (9 ± 4 samples in the first 2 min and 6 ± 2 samples during the remainder of the study) to obtain the blood time–activity curve. Image data were reconstructed by use of filtered backprojection with CT-based attenuation correction. Frame durations for studies m09940 through m11467 were 16 × 0.5 s, 1 × 2 s, 1 × 4 s, 1 × 6 s, 1 × 15 s, 3 × 30 s, 1 × 60 s, 1 × 2 min, 3 × 3 min, and 5 × 15 min; study m10610 had only one 15-min frame; and studies m10296 and m11043 had three 15-min frames. The number and duration of frames for studies m17156 through m11709 varied but were approximately as follows: 1 × 1.5 s, 10 × 0.5 s, 7 × 7 s, 5 × 60 s, 3 × 3 min, and 3 × 15 min. Study m17540 had six 5-min frames and study m17709 had four 650-s frames in place of the 15-min frames. Time–activity curves were obtained for the LV, myocardium, brain, kidneys, bladder, muscle, and liver by use of AMIDE (3). The gold standard input function for each study, with which the image-derived input function was compared for its validation, was constructed by joining the early portion (<1 min) of a partial-volume–, delay–, and dispersion–corrected LV time–activity curve with the serial blood sample measurements (see procedure described later in this section). Blood-to-plasma conversion was performed as described by Wu et al. (14).

¹⁸F-FDG Kinetic Model

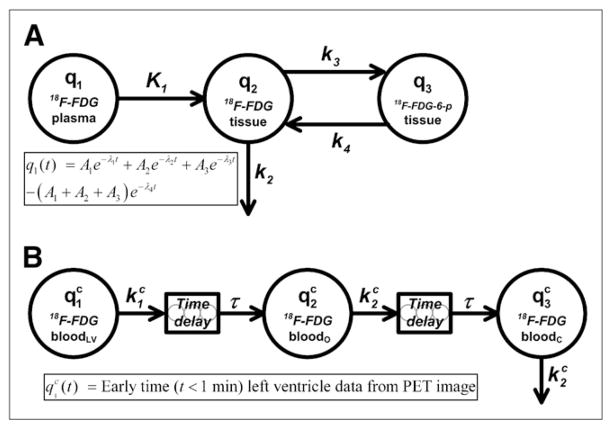
We used the 4K compartmental model (Fig. 1A), with a sum of 4 exponential terms acting as an input (forcing) function in the tissue compartments. Analysis of the serial blood sample data showed that, except for the very early portion, the data were best described by a sum of 3 exponential terms; a single-exponential term and sums of 2-, 3-, and 4-exponential terms were fitted to the data by use of the program DIMSUM (15). A fourth exponential term was added to the input function so that q₁ was forced to be equal to 0 at time 0 (Fig. 1). The system differential equations for the tissue uptake of ¹⁸F-FDG are written as

FIGURE 1.

(A) 4K open-loop model describing ¹⁸F-FDG tissue uptake and metabolism. Left-hand compartment (q₁) represents input (forcing) function described by sum of 4 exponential terms, center compartment (q₂) represents extravascular ¹⁸F-FDG in organ space, and right-hand compartment (q₃) represents phosphorylated ¹⁸F-FDG in organ space. Measurement model (Eq. 5) is defined as total amount of ¹⁸F-FDG and ¹⁸F-FDG-6-phosphate (¹⁸F-FDG-6-p) in organ space. (B) Compartmental model for partial-volume, delay, and dispersion corrections of early portion (t < 60 s) of LV time–activity curve. Left-hand compartment ( $q_1^c$) represents forcing function defined by LV time–activity curve obtained from reconstructed PET image at early times (<1 min), and center ( $q_2^c$) and right-hand ( $q_3^c$) compartments represent arterial concentrations of ¹⁸F-FDG in organ (o) and femoral artery catheter (c) sites, respectively. Two delay components, modeled as string of 5 compartments with fast mass transfer rates, are included to account for time it takes drug to travel from LV to organ and catheter sites. Superscript c indicates that these are model equations used for correction of early-time LV data.

$$\frac{{dq}_2(t)}{dt}=K_1{q}_1(t)+k_4{q}_3(t)-(k_2+k_3)q_2(t)$$ Eq. 2

and

$$\frac{{dq}_3(t)}{dt}=k_3{q}_2(t)-k_4{q}_3(t).$$ Eq. 3

In this equation, q₂ and q₃ are the putative amounts of nonphosphorylated and phosphorylated ¹⁸F-FDG, respectively, in the tissue extravascular space; K₁ and k₂ are the putative rates at which ¹⁸F-FDG crosses the endothelial cells lining the tissue microvasculature; and k₃ and k₄ are the putative rates of phosphorylation and dephosphorylation of ¹⁸F-FDG, respectively, by intracellularly located hexokinase. K₁ through k₄ are written as a function of microparameters k_Q (extravasation rate), V_T (total organ volume), V_E (extra-vascular organ volume), k_P (phosphorylation rate), and R (partition coefficient), as shown in Table 1. The input (forcing) function that dictates the amount of ¹⁸F-FDG in plasma is written as

TABLE 1.

Bayesian Constraints for 4K Model

Parameter*	Units	Mean†	SD†
A1	PET units‡	11.8 × 10−2	9.14 × 10−2
A2	PET units‡	9.27 × 10−3	4.46 × 10−3
A3	PET units‡	2.07 × 10−3	1.31 × 10−3
λ1	min−1	9.21 × 100	4.99 × 100
λ2	min−1	1.78 × 10−1	0.76 × 10−1
λ3	min−1	1.54 × 10−2	0.53 × 10−2
λ4	min−1	41.0 × 100	0.65 × 100
kQ,liver	mL min−1	4.75 × 10−1	0.24 × 10−1
VT,liver	mL	8.85 × 10−1	0.52 × 10−1
VE,liver	mL	3.45 × 10−1	0.45 × 10−1
kP,liver	mL min−1	4.05 × 10−3	2.54 × 10−3
Rliver	Dimensionless	4.74 × 100	1.13 × 100
kQ,muscle	mL min−1	1.32 × 10−1	0.54 × 10−1
VT,muscle	mL	4.89 × 100	0.12 × 100
VE,muscle	mL	3.37 × 10−1	0.32 × 10−1
kP,muscle	mL min−1	5.16 × 10−2	3.24 × 10−2
Rmuscle	Dimensionless	51.8 × 100	53.6 × 100

^*K₁ = k_Q·V_T⁻¹, k₂ = k_Q·V_E⁻¹, k₃ = k_P·V_E⁻¹, k₄ = k_P· (R· V_E)⁻¹.

^†Population mean and SD of parameters calculated by fitting model to all available data (15,16,18,24) from studies m10861, m11043, m11122, m17156, m17464, and m17709.

^‡1 PET unit ≈ 534 MBq·mL⁻¹.

$$q_1(t)=A_1{e}^{-{\lambda }_{1}t}+A_2{e}^{-{\lambda }_{2}t}+A_3{e}^{-{\lambda }_{3}t}-(A_1+A_2+A_3)e^{-{\lambda }_{4}t},$$ Eq. 4

and the measurement model, which corresponds to the image-derived organ time–activity curve, is written as

$$y(t)=f_P\left(\frac{q_1(t)}{R_{PB}}\right)+q_2(t)+q_3(t),$$ Eq. 5

where f_P is fractional blood volume in the organ space and is set to 0.04 and 0.31 mL/g for muscle and liver, respectively (17), and R_PB is the plasma-to-whole blood ¹⁸F-FDG concentration ratio as a function of time. R_PB is written as

$$R_{PB}=0.386e^{-0.191t}+1.165,$$ Eq. 6

where t is given in minutes. R_PB was previously calculated by taking a series of whole-blood samples throughout the course of several studies, centrifuging each sample into plasma and cellular components, and measuring the ¹⁸F-FDG concentration in each fraction as described by Wu et al. (14). Additional parameters are shown in Table 1.

Equations 2 and 3 were written for both muscle and liver with the same input function (Eq. 4) for both submodels, for a total of 5 equations, which were fitted to the time–activity curves derived from the reconstructed small-animal PET image. The model was fitted to all combinations of liver, muscle, kidney, bladder, and myocardium ¹⁸F-FDG time–activity curves. The use of liver and muscle resulted in the most accurate estimation of the input function; that is, the inclusion of additional tissues did not improve accuracy, and the use of any single tissue dramatically reduced accuracy (data not shown). The use of the arterial input function as the sole input to the liver was an approximation that did not affect the predictive capability of the model.

Partial-Volume, Delay, and Dispersion Corrections

A separate compartmental model was constructed to perform partial-volume, delay, and dispersion corrections for the early portion of the LV time–activity curve, considered to be an accurate representation of the blood ¹⁸F-FDG concentration. Figure 1B shows the structure of this compartmental model with time delays (τ). The model equations are written as

$$\frac{{dq}_2^c(t)}{dt}=k_1^c{q}_1^c(t-\tau )-k_2^c{q}_2^c(t)$$ Eq. 7

and

$$\frac{{dq}_3^c(t)}{dt}=k_2^c{q}_2^c(t-\tau )-k_2^c{q}_3^c(t),$$ Eq. 8

where $q_2^c$ and $q_3^c$ represent the plasma ¹⁸F-FDG concentrations in the tissue or organ of interest and at the femoral artery (catheter site), respectively, and account for the tracer dispersion effect. The superscript “c” indicates that these are model equations used for the correction of LV data. The amount of tracer in compartment $q_1^c$ was determined by a forcing function that was equal to the first 60 s of the LV time–activity curve derived from the reconstructed PET image. The LV time–activity curve was calculated by placing a spheric region of interest (ROI) (≈1 mm in diameter) on the PET image in the region that corresponded to the LV, which could be visualized with 0.5-s frames generated during the first 10 s of each study. The organ or tissue of interest ( $q_2^c$) was assumed to be approximately halfway between the LV and the femoral artery catheter; hence, the time delay had the same value for both Eq. 7 and Eq. 8. The ratio $k_2^c/k_1^c$ provided an estimate of the partial-volume correction coefficient. The areas under the curve (AUCs) for all compartments shown in Figure 1B should be equal because they represent different regions of the central blood pool. The ratio $k_2^c/k_1^c$ is approximately equal to the ratio ${\mathit{AUC}}_{q_1^c}/{\mathit{AUC}}_{q_2^c}$ and corrects for the apparent difference between LV and blood sample AUCs caused by partial-volume effects, because

$$\frac{{\mathit{AUC}}_{q_1^c}}{k_2^c/k_1^c·{\mathit{AUC}}_{q_2^c}}\approx 1.$$ Eq. 9

The measurement model is written as

$$y^c(t)=q_3^c(t)$$ Eq. 10

and was fitted to the time–activity curve measured from the whole-blood samples taken from the femoral artery via the surgically inserted catheter. Plasma-to-whole blood ¹⁸F-FDG concentration ratio correction was applied to the blood data after correction for delay, dispersion, and partial-volume effects.

The 7 studies with the most abundant early-time (<1 min) blood sample data were used to calculate average parameter values for the LV correction model (Fig. 1B); these values were subsequently used to correct the LV curves for all 16 studies, thus enabling us to estimate ¹⁸F-FDG concentrations in plasma within tissues of interest, during the first 60 s of each study. For our simulations, $k_1^c$ and $k_2^c$ were measured in minutes⁻¹, and τ was measured in seconds.

Parameter Estimation

The kinetic modeling program SAAM II (18–20) was used to solve the systems of differential equations and estimate parameters by fitting the compartmental models (Fig. 1) to the experimental data. Model parameters were fitted to the data by use of an extended least-squares cost function (18–20) and the relative data weighting scheme (19,21) provided by SAAM II. The weight (w) assigned to each PET-derived liver and muscle data point i was calculated as

$$w_i=\frac{1}{{\sigma }_i^2}=\frac{d_i}{{\mu }_i},$$ Eq. 11

where d_i and μ_i, respectively, were the duration and mean ROI of imaging frame i. LV time–activity curves (t < 60 s) and the 2 late-time blood samples were assigned fractional SDs (0.1 and 0.01, respectively). Bayesian maximum a posteriori parameter estimation (8,19,20) was implemented to improve parameter identification and the accuracy of the predicted input function derived from the 4K model. Bayesian parameter constraints, expressed as mean and SD for each of 17 model parameters, were calculated by fit-ting the compartmental model to small-animal PET and all available blood sample data from 6 randomly chosen mouse studies (Table 1). The Bayesian term is written as

$$B(p_i)=\sum _{i=1}^{17}\left[\frac{{(p_i-{\mathit{Mean}}_{p_i})}^2}{{SD}_{p_i}^2}\right]$$ Eq. 12

and is incorporated into the extended least-squares cost function that is minimized during the parameter estimation process (18,19). For each parameter p_i that is constrained by a priori estimates of Mean_pi and SD_pi, the optimization algorithm will attempt to minimize the extended least-squares cost function while simultaneously minimizing Equation 12 by keeping p_i close to Mean_pi. Each Bayesian term is weighted by ${SD}_{p_i}^{-2}$. The values for Mean_pi and SD_pi used in the present study are shown in Table 1.

Model Validation

The predicted input function was validated by calculating the AUC of the input function and the slope of the Patlak plot (K_i) (22), a measure of the rate of use of ¹⁸F-FDG in tissue, from the predicted plasma time–activity curve and comparing these values with the AUC and K_i values calculated from the gold standard plasma time–activity curve. The predicted input function was calculated by fitting the model (Fig. 1A) to muscle and liver time–activity curves and a plasma curve composed of a concatenation of partial-volume, delay, dispersion, and R_PB corrected early-time LV data points (<60 s) from the reconstructed PET image and R_PB corrected blood sample measurements taken at approximately 10 and 60 min. The gold standard input function was calculated by fitting the model to a concatenation of corrected early-time LV data points and all blood sample measurements taken after 60 s. As a measure of the goodness of fit of the gold standard input function to the blood sample data, the correlation between the fitted model and data collected after 1 min was calculated with GraphPad Prism (23); for all 16 studies, the R value was 0.998 ± 0.002 and the slope was 1.005 ± 0.01; that is, the serial blood sample data were accurately described by the sum of exponential terms shown in Equation 4. After fitting of the model to the data, the predicted and gold standard input functions (IF) used to calculate AUC and K_i values are written as follows:

$$IF(t)=\{\begin{array}{ll}\text{corrected}\text{LV}\text{ROI}\text{data},\hfill & 0<t<60sec\hfill \\ \begin{array}{l}{A}_1{e}^{-{\lambda }_{1}t}+A_2{e}^{-{\lambda }_{2}t}+A_3{e}^{-{\lambda }_{3}t}-(A_1+A_2+A_3)e^{-{\lambda }_{4}t},\end{array}\hfill & t>60sec,\hfill \end{array}$$ Eq. 13

where the A and λ values were calculated during the aforementioned model-fitting process and where sec is seconds. A Patlak graph was constructed for brain, muscle, liver, and myocardium by use of organ time–activity curves for these tissues and the input function defined in Equation 13. The online kinetic modeling program KIS (24) was used to construct the Patlak graphs and calculate the K_i value for each tissue. The small-animal CT and small-animal PET dynamic image files, serial blood sample data, and other experimental information for all studies discussed here can be obtained from the UCLA Mouse Quantitation Project Web site (25,26).

RESULTS

Correction of Small-Animal PET LV Data

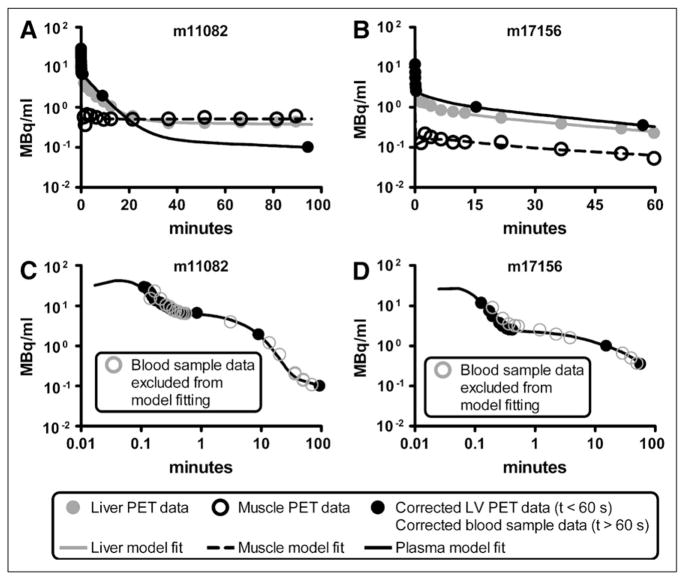
The partial-volume, delay, and dispersion correction model was applied to studies with the most abundant early-time blood samples (studies m17156, m17332, m17385, m17437, m17464, m17540, and m17709 from the Mouse Quantitation Project Web site (25,26)); correction for a selected study is shown in Figure 2. Blood sample data are shown as black circles, and the uncorrected LV blood sample curve, calculated by interpolating small-animal PET LV data, is shown as a gray line. The model output, which was fitted to blood sample data, is shown as a black line. The predicted ¹⁸F-FDG blood time–activity curve within muscle and liver (compartment $q_2^c$ in Fig. 1B) is shown as a dashed black line. Across all 7 model fits, the average (mean ± SD) time delay (τ) between each compartment was 2.39 ± 0.61 s, and the average partial-volume correction factor ( $k_2^c/k_1^c$) was 0.690 ± 0.075, with $k_1^c$ and $k_2^c$ values of 134.9 ± 9.6 min⁻¹ and 92.5 ± 4.6 min⁻¹, respectively. Corrected data were then adjusted for RBC uptake, yielding the concentration of ¹⁸F-FDG in plasma.

FIGURE 2.

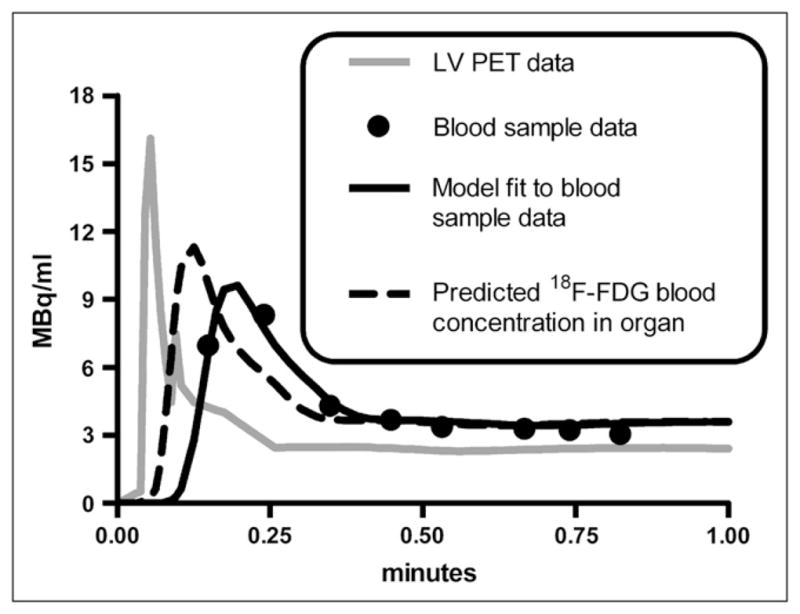
Partial-volume, delay, and dispersion corrections of LV time–activity curve. Results of study m17464 are shown. Gray line represents (interpolated) small-animal PET LV time–activity curve used for forcing function in LV correction model (Fig. 1B). Circles represent ¹⁸F-FDG concentrations measured from serial femoral artery blood samples to which LV correction model was fitted (Eq. 10). Dashed black line represents predicted blood ¹⁸F-FDG concentration in organ of interest (e.g., muscle or liver), which is equal to amount of tracer in compartment $q_2^c$ (Fig. 1B).

Calculation of Bayesian Constraints

The 4K model was fitted to all PET and serial blood sample data from 6 of the 16 ¹⁸F-FDG studies under consideration. Table 1 shows the mean and SD of each estimated model parameter across the 6 studies. The average population co-efficient of variation for all parameters across the 6 studies was calculated to be 50% ± 34%. Bayesian constraints (data not shown) were calculated from 3 studies (m10861, m11122, and m17709) and from a single study (m17709) for subsequent evaluation of the effect of “training set” size on the accuracy of the predicted input function.

Predicted ¹⁸F-FDG Input Function

Figures 3A and 3B show all data used to fit the 4K model and the fitting results for studies m11082 and m17156. Liver and muscle time–activity curves obtained from the reconstructed PET image are shown as solid gray and open black circles, respectively, and the measured plasma time–activity curves are shown as solid black circles. Model fits for ¹⁸F-FDG in plasma, liver, and muscle are shown as black, gray, and dashed lines. As previously described, corrected LV PET data were used to represent the first minute of plasma data, and the last 2 plasma data points were R_PB (Eq. 6)-adjusted serial blood sample data. Figures 3C and 3D show the fitted input function with all R_PB-adjusted serial blood samples obtained for each study. The solid black circles represent data used to fit the model, and the open gray circles represent serial blood sample data not used during the model-fitting process. Parameter estimates for all 16 model fits are shown in Table 2.

FIGURE 3.

(A and B) 4K ¹⁸F-FDG model fitted to corrected PET time–activity curves and 2 blood samples corrected for RBC uptake for studies m11082 (A) and m17156 (B). Black, gray, and dashed lines represent best-fit model simulations of ¹⁸F-FDG time–activity curves in plasma, liver, and muscle, respectively. Liver and muscle PET time–activity curves are shown as solid gray and open black circles, respectively; plasma data are shown as solid black circles. (C and D) Predicted input function with all plasma data shown for studies m11082 (C) and m17156 (D). Simulated plasma time–activity curve (black line) and measured data points (solid black circles) from Figures 3A and 3B are shown along with remaining serial blood sample data (open gray circles) that were excluded from input function prediction process.

TABLE 2.

Parameter Estimates^* for 4K Model Applied to 16 Mouse Small-Animal PET Studies

Mouse study	Muscle				Liver				Input Function
	K1 × 10−2	k2 × 10−1	k3 × 10−2	k4× 10−3	K1 × 10−1	k2 × 100	k3 × 10−3	k4 × 10−3	A1 ×10−2	A2 × 10−3	A3 × 10−4	λ1× 100	λ2 × 10−1	λ3× 10−2	λ4 ×100
m09940	1.60	2.35	20.9	2.95	5.70	1.10	7.58	1.67	12.1	2.74	6.69	11.2	1.53	2.43	41.0
m10296	3.36	4.70	16.6	31.2	5.38	1.08	11.1	2.41	2.72	4.99	28.5	1.47	1.08	1.92	41.0
m10610	2.55	3.72	31.7	4.50	5.42	1.25	7.74	1.63	2.60	5.01	2.90	1.60	1.28	1.64	41.0
m10861	3.30	4.75	17.3	1.90	5.59	1.19	12.4	2.63	5.32	8.80	5.92	4.30	0.70	0.10	41.0
m10911	3.12	4.58	37.7	3.32	5.30	1.66	22.2	3.58	3.63	14.3	5.33	3.70	1.40	0.21	41.0
m11043	3.88	5.42	25.8	2.28	5.35	1.58	25.8	4.07	31.0	12.1	4.46	10.5	1.45	0.71	41.0
m11082	3.92	5.37	17.4	2.82	5.34	1.48	17.0	2.83	8.14	8.53	2.62	9.05	1.21	0.54	41.0
m11122	3.91	5.64	41.5	3.23	5.35	1.43	15.9	2.87	8.74	6.37	4.30	8.98	1.14	1.23	41.0
m11467	2.87	4.22	22.1	12.6	5.57	1.27	21.1	3.83	7.19	5.88	6.66	5.28	1.34	0.47	41.0
m17156	1.88	2.39	0.78	0.15	5.31	1.44	2.83	0.60	8.50	3.29	31.5	13.7	3.01	2.50	41.0
m17332	1.58	2.18	2.40	0.48	6.16	1.00	10.9	2.50	2.94	1.44	19.6	7.21	3.67	2.34	41.0
m17385	3.81	5.34	21.7	34.7	5.36	1.37	21.3	4.10	12.0	4.59	38.8	6.56	1.81	2.23	41.0
m17437	2.83	4.29	9.29	36.3	5.45	1.32	11.7	2.54	6.40	2.61	29.4	9.33	3.84	1.39	41.0
m17464	1.28	1.76	2.44	0.51	5.44	1.27	5.67	1.19	7.10	7.22	35.0	8.92	2.41	1.50	41.0
m17540	2.03	2.87	3.92	0.83	5.31	1.22	5.07	1.07	2.98	5.34	45.4	1.92	1.57	1.38	41.0
m17709	2.21	3.07	4.80	1.13	5.23	1.63	14.5	2.77	1.63	8.31	32.6	1.11	1.02	1.54	41.0

^*%CVs for each parameter estimate were calculated based on the covariance matrix for each fitted model (not shown); average %CV for all 240 estimated parameters is 20% ± 22%. Units are the same as shown in Table 1.

Validation of Predicted ¹⁸F-FDG Input Function

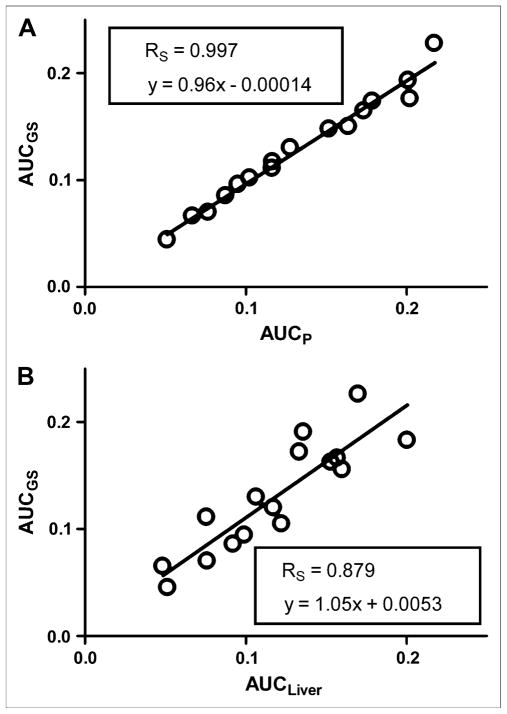
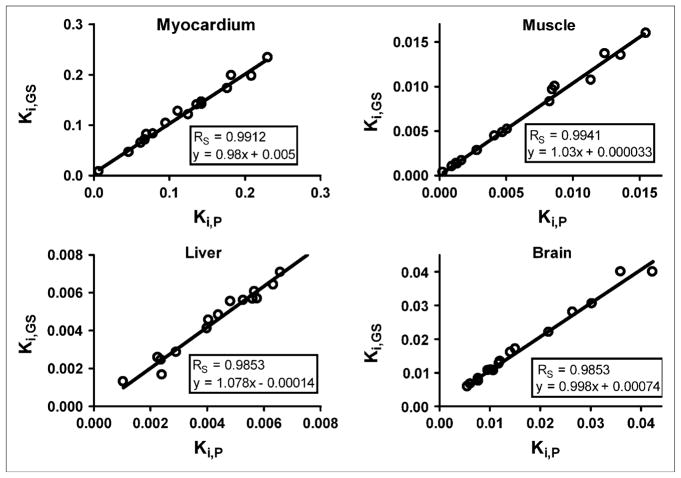
The AUC of the predicted plasma time–activity curve (AUC_P) was compared with the AUC of the gold standard (AUC_GS) input function, which was calculated by fitting the 4K model to all available blood sample data (solid and open circles in Figs. 3C and 3D). A Spearman correlation coefficient (R_S) of 0.997 was calculated with GraphPad Prism (23) for a plot of AUC_GS versus AUC_P for all 16 studies (Fig. 4A). In Figure 4B, AUC_GS is compared with the AUC of the liver time–activity curve (R_S = 0.879). The predicted and gold standard input functions were then used to calculate the Patlak regression slope (K_i), a measure of ¹⁸F-FDG uptake, for selected tissues. An R_S of approximately 0.99 was calculated for myocardium, muscle, brain, and liver (Fig. 5). The average difference between AUC_P and AUC_GS values was 5.7% ± 4.9%; likewise, the difference between K_i values was 6.4% ± 6.6%. Input functions were then reestimated by use of Bayesian constraints calculated from 3 studies and a single study as previously described. The R_S calculated for a plot of AUC_GS versus AUC_P based on both 3 studies and the single study was 0.985.

FIGURE 4.

Comparison of AUC_P and AUC_GS for all 16 studies (A) and predicted area under plasma time–activity curve vs. area under liver time–activity curve (B).

FIGURE 5.

Comparison of predicted (P) and gold standard (GS) Patlak regression coefficients (K_i) for selected tissues.

Analysis of ¹⁸F-FDG Kinetics in Plasma

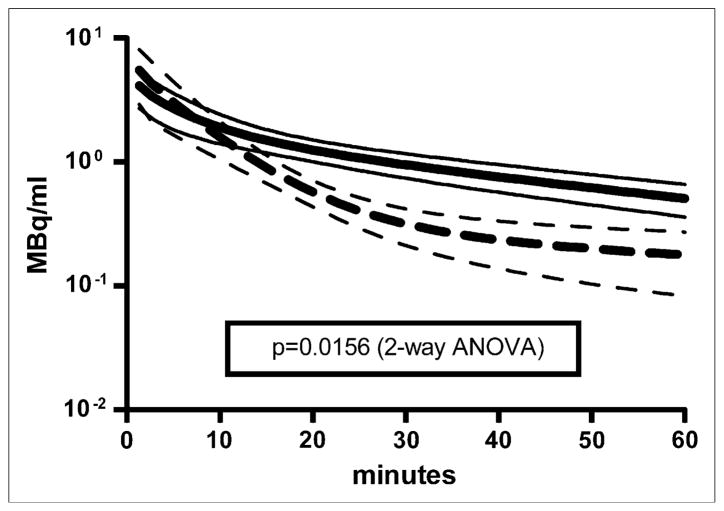
Visual inspection of the 16 plasma time–activity curves revealed distinct kinetic profiles exhibiting fast and slow clearance from blood. Figure 6 shows the average plasma time–activity curves of the studies that fell into each of the 2 groups, with 9 studies exhibiting slower removal of ¹⁸F-FDG from plasma (solid lines) and 7 studies exhibiting faster removal of ¹⁸F-FDG from plasma (dashed lines). Two-way ANOVA (23) for the 2 groups showed that the difference between the lines was statistically significant (P < 0.05). A nonparametric Mann–Whitney t test (23) was performed on the estimated model parameters for the studies in each group (Table 3). There were no statistically significant differences among any of the parameters, with the exception of A₃ and k_3,muscle. The increased rate of ¹⁸F-FDG clearance from plasma, reflected in the approximately 6-fold decrease in the A₃ term of the input function, appeared to be driven by an approximately 3-fold increase in the k_3,muscle term, the putative cell uptake, and phosphorylation rate of ¹⁸F-FDG in muscle (27). The gold standard Patlak K_i values (Fig. 5) exhibited statistically significant increases in the “fast” group for muscle (3.4-fold), myocardium (2-fold), and brain (2-fold); no difference in K_i values was observed for liver.

FIGURE 6.

Plasma time–activity curve simulations for all 16 studies (mean ± SD). ¹⁸F-FDG kinetics in plasma exhibited 2 distinct profiles in these studies and could be described as fast (dashed line) and slow (solid line) removal of ¹⁸F-FDG from plasma. Fast curve was average plasma time–activity curve for studies m09940, m10610, m10911, m11043, m11082, m11122, and m11467; slow curve was average for remaining 9 studies. Two-way ANOVA was performed with GraphPad Prism (23); P value of 0.0156 was calculated, demonstrating statistically significant difference between 2 groups of plasma time–activity curves.

TABLE 3.

Statistical Analysis of Parameter Estimates

Parameter*	Mean†		P‡
	“Fast” group	“Slow” group
A1	1.05 × 10−1	0.55 × 10−1	>0.1
A2	7.85 × 10−3	5.18 × 10−3	>0.1
A3	4.71 × 10−4	2.96 × 10−3	0.0007
λ1	7.19 × 100	6.06 × 100	>0.1
λ2	1.34 × 10−1	2.12 × 10−1	>0.1
λ3	1.03 × 10−2	1.65 × 10−2	>0.1
λ4	41.0 × 100	41.0 × 100	>0.1
K1,muscle	3.12 × 10−2	2.47 × 10−2	>0.1
k2,muscle	4.47 × 10−1	3.48 × 10−1	>0.1
k3,muscle	2.82 × 10−1	8.80 × 10−2	0.0007
k4,muscle	4.53 × 10−3	1.19 × 10−2	>0.1
K1,liver	5.43 × 10−1	5.47 × 10−1	>0.1
k2,liver	1.40 × 100	1.28 × 100	>0.1
k3,liver	1.68 × 10−2	1.06 × 10−2	>0.1
k4,liver	2.93 × 10−3	2.20 × 10−3	>0.1
Ki,muscle	1.10 × 10−2	3.08 × 10−3	0.0012
Ki,myocardium	1.66 × 10−1	8.52 × 10−2	0.0079
Ki,brain	2.44 × 10−2	1.21 × 10−2	0.016
Ki,liver	5.64 × 10−3	3.89 × 10−3	>0.1

^*Units are same as those in Table 1.

^†Population mean of model parameters fitted to all available data for each study. “Fast” group contained studies m09940, m10610, m10911, m11043, m11082, m11122, and m11467, which exhibited relatively fast clearance of ¹⁸F-FDG from plasma; “slow” group contained remaining 9 studies.

^‡Calculated with Mann–Whitney nonparametric t test (23).

DISCUSSION

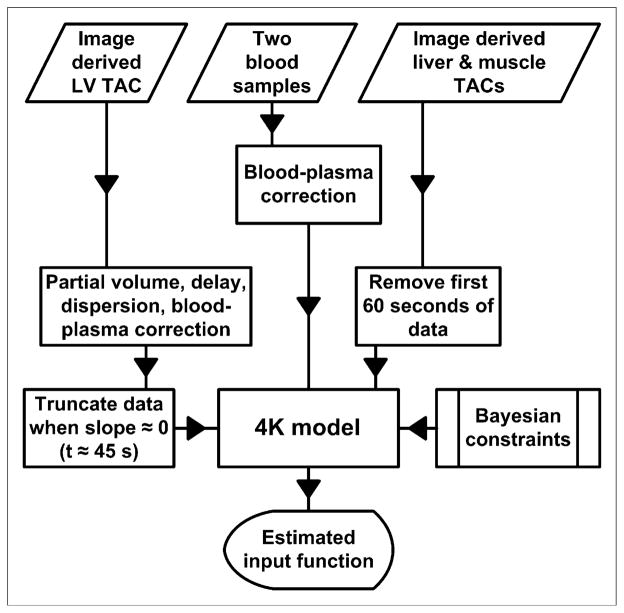
Our method for calculating the input function using limited blood data can be broken down into 3 steps. In step 1, for early-time (t < 60 s) LV data to be used during the model-fitting process, the data must first be corrected for delay, dispersion, partial-volume effects, and uptake by RBCs. The model shown in Figure 1B performs this correction and produces an average partial-volume correction factor of 0.690 ± 0.075, which is close to previously calculated values (10–13). Corrected LV data should closely approximate plasma ¹⁸F-FDG concentrations, as seen in the tissues of interest, during the first minute of the study; indeed, Figures 3C and 3D showed that the corrected LV data matched the early-time serial blood samples quite well. In step 2, the key to successfully estimating the input function lies in the a priori calculation of Bayesian constraints used during the model-fitting process. Here, we fitted the model shown in Figure 1A to all data from 6 (randomly chosen) of the 16 studies under consideration, producing relatively loose Bayesian constraints that rewarded, in terms of a lower cost function value, a fitted model with estimated parameters that were similar in magnitude to the values shown in Table 1. In step 3, after the Bayesian constraints were applied, the model shown in Figure 1A was fitted to liver and muscle time–activity curves in addition to early-time LV data and 2 blood samples, which were taken from the tail vein at approximately 10 and 60 min after the injection of ¹⁸F-FDG. We assumed that partial-volume and spillover effects were negligible in liver and muscle; therefore, no correction was applied to these time–activity curves. Partial-volume effects in these tissues should not alter the predicted input function, because the method depends only on the shapes of the tissue curves. Spillover from other tissue activities could affect the shapes of the curves but is avoidable as long as the muscle and liver ROIs are not drawn near tissues in which tracer kinetics differ greatly. Figures 3C and 3D show that the predicted input function closely matched the serial blood samples. This method is summarized in Figure 7.

FIGURE 7.

Algorithm for estimation of input function. Same Bayesian constraints were applied to animals exhibiting fast clearance and slow clearance of ¹⁸F-FDG from plasma. TAC = time–activity curve.

Analysis of the input function (Fig. 6) and estimated model parameters (Table 3) showed that our method successfully estimated the input function under conditions of both fast and slow clearance of ¹⁸F-FDG from plasma. After comparison of model parameters, the increased rate of clearance of ¹⁸F-FDG from plasma in the “fast” group appeared to be a function of k_3,muscle, which putatively describes cell uptake and phosphorylation of ¹⁸F-FDG in muscle (27), whereas all other model parameters remained essentially unchanged between the 2 groups. A change in the magnitude of k_3,muscle can be associated with changes in insulin levels and cell membrane expression of the glucose receptor, typically associated with the fed or fasting state of the experimental animals. These data suggest that our model is applicable under both conditions.

The input function is commonly used to calculate rates of tissue uptake of ¹⁸F-FDG via the Patlak plot, by taking the slope of the linear portion of

$$\frac{C_T(t)}{C_p(t)}\text{vs}.\frac{{\int }_0^t{C}_P(t)dt}{C_P(t)},$$ Eq. 14

where C_T (t) is the ¹⁸F-FDG concentration in the tissue of interest and C_P(t) is the ¹⁸F-FDG concentration in plasma. Figures 4A and 5 show that the predicted AUC and K_i values calculated from 2 blood samples closely matched the AUC and K_i values calculated from all available blood samples (R_S > 0.985). These data demonstrate the validity of the input function derived from the modeling approach proposed in the present study.

The AUC of the liver time–activity curve is sometimes used as an approximation of the AUC of the plasma time–activity curve; however, our method appears to provide a more accurate estimation of the input function (Fig. 4B). Additionally, even when the AUCs of the liver and input function time–activity curves are similar, the time–activity curves themselves may still be different.

The factor analysis method used by Kim et al. (5) provides a reasonably accurate estimation of the input function when applied to rat data but yields a much less accurate estimation when applied to mouse data (r = 0.93, slope = 1.47).

We initially fitted our model to all data from 6 studies to calculate the Bayesian constraints (step 2) to be used for estimation of the input function. A comparison of predicted input functions determined with Bayesian constraints calculated from 3 studies or even a single study resulted in only a small decrease (from approximately 0.99 to 0.98) in the correlation of the AUC of the predicted input function with the AUC of the gold standard input function shown in Figures 3C and 3D. Thus, the input function may be accurately estimated with Bayesian constraints from serial blood samples from 1–3 animals.

The method outlined here can be applied to any dynamic dataset with limited blood concentration data as long as a priori Bayesian constraints have been calculated for the tracer of interest. Additionally, any model structure can be implemented to account for more complicated tracer kinetics, provided the model parameters are identifiable with regard to available experimental data. For murine ¹⁸F-FDG studies, the Bayesian constraints calculated here can be used because of the robustness of the method; for example, a single set of Bayesian constraints were applied to 16 tracer studies exhibiting 2 significantly different kinetic profiles (Fig. 6) and yielded an accurate estimation of the input function in all studies (Fig. 5). However, this approach should be validated by taking serial blood samples from a subgroup of mice, because it is possible that new Bayesian constraints would have to be calculated if ¹⁸F-FDG kinetics varied considerably from those in the present study.

CONCLUSION

We have developed a compartmental model–based approach to estimating the input function in mice from limited blood sample data and the Bayesian constraints derived in the present study (Table 1). Studies with similar mouse strains and experimental conditions may be able to use these Bayesian constraints to estimate the input function; studies with drastically different mouse strains or experimental conditions can calculate a new set of constraints by obtaining serial blood samples from a subset of mice.