Studying Interactions by Molecular Dynamics Simulations at High Concentration

Abstract

Molecular dynamics simulations have been used to study molecular encounters and recognition. In recent works, simulations using high concentration of interacting molecules have been performed. In this paper, we consider the practical problems for setting up the simulation and to analyse the results of the simulation. The simulation of beta 2-microglobulin association and the simulation of the binding of hydrogen peroxide by glutathione peroxidase are provided as examples.

1. Introduction

Molecular dynamics (MDs) simulation is a powerful tool to study biomolecular processes an atomistic detail [1, 2]. Processes like molecular encounter, that have been traditionally studied by Brownian dynamics simulations [3–5] have also been addressed by MD simulation in the last decade [6–14]. The time required for assembly processes may be exceedingly large, and for this reason implicit solvent or coarse-grained models have been used [9, 15–20]. For an extensive review on coarse grained models, see reference [21]. These models should catch, through relevant energy terms, the essence of the phenomena to be simulated and therefore provide a likely representation of the simulated process.

If the interest is in the encounter of proteins or of a protein and a ligand, much shorter times are required, and if the conformational changes in the molecules are not large, translational and rotational diffusion of the systems (possibly at high concentration, in order to increase sampling) provides a large number of encounters possibly representative of different frequencies and lifetimes. In order to address recognition at the atomic level, we have performed recently all-atom explicit solvent simulations using a high concentration of interacting molecules [10, 12, 13].

The aim of this paper is not to provide an extensive review of methods and results, but rather to consider the practical problems for setting up the simulation and for analysing the results of the simulation.

2. Methods

In setting up simulations aimed at observing molecular encounters, the spacing of the molecules and total simulation time should be considered carefully in order to allow translational and rotational diffusion to take place effectively during the simulation. An excellent review about biomolecular hydrodynamics and diffusion has been given by Bloomfield [22] in an online review, which is unfortunately not available anymore, and by Cantor and Schimmel in their textbook [23]. We resume here the main theoretical results recalling the main equations. The topic is also discussed by Hunter in his treatise on colloid science [24].

2.1. Translational Diffusion

For translational diffusion the Einstein-Smoluchowski equation relates the average quadratic displacement to time

$$\langle {||\mathrm{\Delta }x||}^2\rangle =2d{D}_{t}t,$$ (1)

with a standard deviation equal to $\sqrt{2}\langle {||\Delta x||}^2\rangle$, where D_t is the diffusion coefficient and d is the dimensionality (3 in standard molecular dynamics simulations). The translational diffusion constant D_t depends on the shape of the molecule and must be computed numerically under proper assumptions.

When the molecule may be considered as a sphere the Stokes-Einstein equation relates the diffusion coefficient D_t to the solvent and solute properties:

$$D_t^{\text{sphere}}=\frac{kT}{6\pi r\eta },$$ (2)

where k is the Boltzmann constant, T is the temperature, r is the hydrodynamic radius of the sphere, and η is the medium viscosity. Sometimes proteins do not resemble spheres, but they rather have an elongated shape that can be approximated by a prolate spheroid, that is, an ellipsoid with the two short axes of equal length b and a long axis of length a, with q = b/a. In this case, the above relations are generalized with respect to an equivalent sphere of radius R = (ab²)^1/3 [22–24].

For the translational diffusion coefficient we have

$$D_t^{ps}=D_t^{\text{sphere}}\times \frac{q^{2/3}\log \mathrm{\hspace{0.17em}\hspace{0.17em}}\left(\left(1+\sqrt{\left(1-q^2\right)}\right)/q\right)}{\sqrt{\left(1-q^2\right)}}.$$ (3)

2.2. Reorientation of Molecules

For the simulation to be able to sample reciprocal orientations, the simulation time must be long enough as to allow reorientation of molecules. For rotational diffusion, the Debye relaxation equation holds. For a set of molecules with one axis aligned with the z-axis at time 0:

$$\langle \cos \left(\theta \right)\rangle =\exp \left(-2D_{r}t\right),$$ (4)

where θ is the angle of the same axis with the z-axis at time t. Based on (4) reported in the work by Smith and van Gunsteren [25], the standard deviation is

$$\sqrt{\frac{1}{3}-e^{-4D_{r}t}+\frac{2}{3}{e}^{-6D_{r}t}.}$$ (5)

For the rotational diffusion coefficient of a sphere, an equation similar to the Stokes-Einstein equation, the Stokes-Einstein-Debye relation, holds:

$$D_r^{\text{sphere}}=\frac{kT}{8\pi r^3\eta }.$$ (6)

For elongated molecules, frictional coefficients for rotations about the long and short axis are computed first as

$$\begin{array}{cc}\hfill F_r^{ps}\left(l\right)& =F_R^{\text{sphere}}\hfill \\ \hfill & \hspace{1em}\times \frac{2\left(1-q^2\right)}{3\left(1-q^2{(1-q^2)}^{-1/2}\mathrm{\hspace{0.17em}\hspace{0.17em}}\log \left(\left(1+\sqrt{(1-q^2)}\right)/q\right)\right)},\hfill \\ \hfill F_r^{ps}\left(s\right)& =F_R^{\text{sphere}}\hfill \\ \hfill & \hspace{1em}\times \frac{2\left(1-q^4\right)}{3q^2\left(2-q^2\right){(1-q^2)}^{-1/2}\log \left(\left(1+\sqrt{(1-q^2)}\right)/\left(q-3q^2\right)\right)}.\hfill \end{array}$$ (7)

Then rotational diffusion coefficients are computed based on the frictional coefficients as

$$\begin{array}{cc}\hfill D_r^{ps}\left(l\right)& =D_r^{\text{sphere}}{\left(\frac{F_r^{ps}\left(s\right)}{F_R^{\text{sphere}}}\right)}^{-1},\hfill \\ \hfill D_r^{ps}\left(s\right)& =\frac{D_r^{\text{sphere}}}{2}\left({\left(\frac{F_r^{ps}\left(s\right)}{F_R^{\text{sphere}}}\right)}^{-1}+{\left(\frac{F_r^{ps}\left(l\right)}{F_R^{\text{sphere}}}\right)}^{-1}\right),\hfill \end{array}$$ (8)

and where D_r^ps(l) and D_r^ps(s) are the diffusion constants that enter the Debye relaxation equation for reorientation of vectors along the long and short axes, respectively.

2.3. Temperature and Water Viscosity

For water, the viscosity η has a sharp dependence on temperature which can be described by the following equation reported in [22] (and corrected here):

$$\begin{array}{cc}\hfill {\log }_{10}\eta & =\frac{1301}{998.333+8.1855\left(T-20\right)+0.00585{(T-20)}^2}\hfill \\ \hfill & \hspace{1em}-4.30233\hspace{0.17em}\text{Pa}\hspace{0.17em}\text{s},\hfill \end{array}$$ (9)

in the range 0–20 C and

$${\log }_{10}\frac{\eta }{{\eta }_{20}}=\frac{1.3272\left(20-T\right)-0.001053{(T-20)}^2}{T+105},$$ (10)

in the range 20–100 C, with the temperature T in Celsius degrees. At 20 C, this results in η = 1.0 × 10⁻³ Pa s.

2.4. Choice of the Simulation Time and Molecule Spacing

For a globular protein with hydrodynamic radius of 20 Å (corresponding to a molecular weight of ca. 28 kDa), the rotational diffusion constant D_r at 20 C is 2.0 × 10⁷ s⁻¹  which corresponds to a rotational time constant of 25 ns. The rotational autocorrelation time scales linearly with the mass of the molecule and with the third power of the radius. Note that the rotational time constants considered here are 3 times longer than those considered in NMR experiments, where a different function of θ (〈1/2(3co⁡s²(θ) − 1〉) is used for defining rotational diffusion [26].

The dependence of the diffusion coefficients on the shape is not much pronounced. For long-to-short axis ratios that do not exceed 1.5, the rotational time constant increases by less than 20%. In practice, the size of the system, but not its shape, for typical proteins, determines the choice of the simulation time. From the above considerations, it is seen that simulations in the range of tens to one hundred of nanoseconds should allow complete reorientation of typical proteins studied by molecular dynamics simulations. For convenience, considering an average protein molar volume 0.73 cm³ g⁻¹, the radius (in Å) of a protein of molecular weight M_w Da is

$$r=0.66\ast {M_w}^{1/3}.$$ (11)

The hydrodynamic radius of the protein may be larger due to hydration water by up to ca. 3.0 Å. The rotational time constant (in ns) at 20 C is

$$0.0031\times r^3,$$ (12)

or three times less when the decay of the quantity 〈1/2(3co⁡s²(θ) − 1〉 is considered. During one rotational time constant, under the same solvent conditions, the molecule will experience a root mean square displacement equal to its hydrodynamic diameter.

For practical purposes, therefore, one may first estimate the rotational correlation time constant 1/2D_r and setup the simulation time, to say, at least twice the rotational correlation time. During this time the average displacement of the molecules will be 2.8 times the hydrodynamic radius. The spacing of the molecules (i.e., center-to-center distance) can be chosen therefore equal to four-to-five times the hydrodynamic radius, so that the molecules will get in contact on average after one-to-two rotational correlation times. The spacing will most likely be reduced in order to compromise with the need for a limited-size system.

2.5. Setting up an Ensemble of Randomly Oriented Molecules

Molecules are arranged in a regular way in order to maximize the chances of encounters, and also they are randomly oriented in order to maximize the number of relative orientations sampled. For arrangement on a cubic periodic lattice N × N × N grid, there will, N³ × 26/2 nearest neighbour relative orientations. N should be larger than 2 to ensure that the 26 nearest neighbours are truly different molecules and not just molecules and their periodic images. The spacing of the lattice should be of the order of few molecular radii in such a way that reoriention may take place before encounter, as discussed above.

For protein-protein association, these prescriptions may lead to a very large system size with consequent large number of atoms, which in turn may limit the simulation time. For protein-small molecule association, the above requirements are easily met. It is often reported that molecules may be randomly rotated by choosing a random rotation axis and a random rotation angle. A simple way to do this is to choose a random axis in space and perform a rotation by a random angle about that axis. Although this procedure is reasonable, and a fast algorithm implementing this idea is available [27], the resulting distribution of rotations is not uniform [28]. A truly uniform distribution is obtained by taking random unit quaternions, which can be generated in a simple way by taking four random quantities (w, x, y, and z) between −1 and 1 subject to the condition w² + x² + y² + z² ≤ 1.0, and normalizing them to 1.0. More efficient algorithms are available (see e.g., [28]). The four normalized values are related to the rotation axis v and the rotation angle θ as follows:

$$\left(w,x,y,z\right)=\left(\cos \left(\frac{\theta }{2}\right),v\sin \left(\frac{\theta }{2}\right)\right),$$ (13)

and the corresponding rotation matrix is

$$\begin{array}{cc}\hfill & \mathbf{R}(\mathbf{w},\mathbf{x},\mathbf{y},\mathbf{z})\hfill \\ \hfill & \hspace{1em}=\left(\begin{array}{ccc}1-2(y^2+z^2)& 2xy-2wz& 2xz+2wy\\ 2xy+2wz& 1-2(x^2+z^2)& 2yz-2wx\\ 2xz-2wy& 2yz+2wx& 1-2(x^2+y^2)\end{array}\right).\hfill \end{array}$$ (14)

2.6. Analysis

2.6.1. Translational and Rotational Diffusion Coefficients

Besides traditional analyses that are typically performed on molecular dynamics trajectories (see e.g., those provided with the package GROMACS [29]), it is obvious to check that the molecule's translational and rotational diffusion during the simulation is taking place as expected. For translation, it is sufficient to monitor the center of mass of each molecule as a function of time and apply due corrections for periodic boundary conditions. As long as the particles do not travel an entire periodic box length, the correction for periodic boundary crossing is very easily applied. The average square of the distance from the starting position can be fitted as a linear function of time, the proportionality constant being six times the translational diffusion constant D_t.

For the rotational diffusion constant, each molecule may be superimposed to the starting structure using programs like ProFit [30]. The rotation matrix may then be used to obtain the dot product between any given unit vector before and after rotation, that is, v Rv, which is in turn equal to the cosine of the angle between the two vectors. Averaging overing all possible unit vectors leads to the average cosine value (〈cos⁡(θ)〉), entering the rotational diffusion equation. The average is equal to the trace of the rotation matrix divided by 3, that is, 〈v Rv〉_v = (R_xx + R_yy + R_zz)/3. In turn, the average of the latter quantity over all molecules can be fitted to an exponential whose time decay constant is twice the rotational diffusion constant D_r.

2.6.2. Atomic Contacts

Except for long-range electrostatic effects, molecular interactions result from close atomic contacts. The use of a large number of identical molecules increases the number of both random and specific contacts. The affinity of molecular regions between themselves and with small ligands may be measured by the count of contacts. Contacts are typically defined using a cutoff on the distance between heavy atoms. A typical value, when one considers all heavy atoms, is 4.5 Å (e.g., [31]). A different definition was used by Berrera et al. [32] to take into account the different size of atoms. In this definition, two atoms are in contact when their van der Waals surfaces are closer than 1.0 Å. Only heavy atoms are considered and the radii are 1.4 Å for oxygen, 1.5 Å for nitrogen, 1.9 Å for carbon, and 1.85 Å for sulphur.

We found convenient to map all atoms at nodes of a periodic cubic lattice and then list contacts within the atoms assigned to one node and with the atoms assigned to the 26 neighbouring nodes. The lists of contacts corresponding to different snapshots are grouped together, and the number of occurrences of each atomic contact is counted.

The cumulative counts of atomics contacts, independent of the specific molecules interacting, provide the affinity of a contact. For instance, the same hydrophobic part of different copies of a protein may be contacted by the same hydrophobic part of different copies of a ligand. This will result in a large cumulative number of the same atomic contacts, although due to different interacting molecules. The frequency of atomic contacts (independent of the specific molecular copies involved) is a measure of the affinity, but it does not tell how long a single ligand resides at a given location. In this respect, we can take advantage of the fact that, if the number of interacting molecules is large, the probability of observing the same long-lived contacts for the same molecular copies is very low. In such situation, the count of atomic contacts for specific molecules is proportional to the time the two atoms are close to each other continuously. The analysis of most frequent contacts just requires a sufficient number of snapshots spread over an interval of time sufficient to sample all possible contacts. The analysis of longest-lived contacts requires snapshots to be taken at time intervals which are fractions of the time used for defining a long-lived contact. For instance, if 0.5 ns is considered as a long-residence time than snapshots at 100 ps guarantees that a long-lived contact will count at least five times more than a short-lived contact.

2.7. Simulation of the Association of Beta 2-Microglobulin

Beta 2-microglobulin is a 99-residue protein which is responsible of dialysis-related amyloidosis [33, 34]. Due to its small size and its solubility it has been extensively studied in recent years, and much knowledge has been gained on its structural and dynamical properties in relation with the onset of aggregation [35, 36].

The early steps of protein-protein association have been studied by simulating 27 copies of the protein in explicit solvent [10]. All the details and general context of the simulation are reported in the original paper. Here, we will address only the issue of how the system was set up.

With a molecular weight of 11.7 kDa, the hydrodynamic radius estimated from (11) is 15.0 Å. The simulation was run at 300 K. At this temperature, the viscosity of water is 0.85 · 10⁻³ Pa s. The predicted rotational diffusion time is therefore 8.7 ns, according to the rotational diffusion constant estimated using (6). The chosen length of simulation (5 ns) could only reach ca. half of the rotational diffusion time instead of twice. This choice was dictated by the computational time available at the time and by the large size of the simulated system (ca. half a million atoms). The large number of reciprocal orientations between pairs of molecules should, however, compensate for the short simulation time. Note also that the standard deviation of 〈cos⁡(θ)〉 is fastly increasing towards the limiting value $\sqrt{1/3}$.

During the simulation time, the molecules should travel on average 22.7 Å based on the translational diffusional coefficient estimated using (2). For this reason, the spacing of molecules was chosen 50 Å in such a way that the average van der Waals surface to van der Waals surface distance between closest molecules was slightly less (20 Å) than the average displacement of the molecules. The intermolecular distance was not reduced further in order to avoid close contacts of the randomly oriented molecules which have an elongated shape.

This system illustrates well the kind of considerations and compromises one is to face when dealing with an ensemble of large molecules.

Notwithstanding the nonoptimal simulation parameters, the contact analysis of the trajectory suggested a predominant role of Trp 60 in the early association of beta 2-microglobulin. Following that study, experiments with the W60G mutant showed that indeed the mutation resulted in absence of formation of fibrils by the protein in nonextreme conditions, as a combined result of increased stability and removal of the aromatic chain of Trp 60 prone to intramolecular contacts [37].

2.8. Glutathione Peroxidase-Hydrogen Peroxide Simulations

Glutathione peroxidases were the first seleno-enzymes that were discovered in mammals and up to 8 distinct members have been detected so far [38]. Most of them are selenoproteins (the classical GPx-1 then GPx-2, GPx-3, GPx-4 and, depending on species, GPx-6), while the remaining 2 or 3 variants have a cysteine in the active site. They are included in the heme-free thiol peroxidase class together with peroxiredoxins and catalyze the reduction of H₂O₂ or organic hydroperoxides to water or corresponding alcohols, thus mitigating their toxicity [39]. The catalytic mechanism is still a question of open debate and could be different for selenium versus sulphur-based enzymes. Presently, the commonly accepted kinetic is an “enzyme substitution mechanism”‌, as revealed by ping-pong kinetics rather than classical Michaelis-Menten kinetics [40]. This implies that the catalytic mechanisms do not involve any central complexes of the enzymes with all the substrates bound simultaneously. Instead, the catalytic cycles are composed of sequences of bimolecular reactions between the enzymes and their substrates. In other words, the reaction comprises two independent events. The first one is the oxidation of the catalytic site to a selenenic or sulfenic acid derivative after collision with a hydroperoxide, and the second one is its reduction by a reducing substrate.

Following a previous study [41], the structure of Drosophila melanogaster glutathione peroxidase was surrounded by 198 randomly oriented hydrogen peroxide molecules. For such small molecule the translational and rotational coefficients may be estimated, according to (2) and (6). The hydrodynamic radius of hydrogen peroxide may be estimated in the range of 2.1 Å to 5.1 Å for the absence or presence of hydration, respectively, based on its elongated shape and the average hydrogen to hydrogen distance of 2.4 Å. The van der Waals longest dimension would thus be 4.4 Å, whereas the shortest dimension of the molecule is the radius of the oxygen (1.4 Å). The equivalent volume sphere has a radius of 2.1 Å. The upper limit has been taken 5.1 Å in order to account the possibility of hydration, increasing typically the minimum hydrodynamics radius by 3.0 Å.

The range of estimates for the translational and diffusional coefficients for hydrogen peroxide are thus 12.3 to 5.0 · 10⁻¹⁰ m² s⁻¹ and 21.0 to 1.5 · 10⁹ s⁻¹, respectively at 300 K. These figures mean that reorientation will take place in the ns timescale and that in half nanoseconds a molecule is expected to travel on average 12 Å.

Hydrogen peroxide molecules were arranged on a 6 × 6 × 6 grid with 12 Å spacing in each dimension (Figure 1). Molecules overlapping with glutathione peroxidase were removed from the system. After solvent was added and following relaxation and equilibration, the size of the system was 64.6 × 64.6 × 64.6 ų entailing 27300 atoms (Figure 1). The concentration of hydrogen peroxide was unrealistically high (1.25 M) in order to increase the number of molecular encounters. In practice, however, the consequences of this choice are not so important because water concentration is still dominant and no chemical reactions can take place in simulations. Based on the above figures, the total simulation time was set to 10 ns or larger in order to let all molecules reach the target protein and to possibly probe multiple binding events.

Figure 1.

Simulation setup of glutathione peroxidase surrounded by hydrogen peroxide molecules.

For all simulations, the forcefield used is CHARMM v.27 [42] with the CMAP correction [43] except where mentioned. Forcefield parameters for hydrogen peroxide were taken from the study of De Gioia and Fantucci [44]. The program NAMD [45] was used for all simulations. Solute molecules, including ions and cosolutes, were fixed, and the system was energy-minimized by 300 conjugate gradients steps using periodic boundary conditions and the particle mesh Ewald (PME) method for electrostatic interactions [46]. For all simulations, PME employed a grid of 128 × 128 × 128 points corresponding to a spacing of ca. 0.5 Å. The PME tolerance was set to 10⁻⁶  that, together with the cutoff of 12 Å, resulted in an Ewald coefficient of 0.257952 Å⁻¹. The minimized system was further relaxed, keeping the solute molecules (including ions) fixed, by molecular dynamics simulation. The system was heated to 300 K in 2 ps, and a further 18 ps simulation was run in order to let water molecules reorient, consistent with the average lifetime of a hydrogen bond in water [47]. The system without restraints on solute molecules was energy-minimized by 300 conjugate gradients minimization steps. The system was then heated to 300 K in 2 ps, and a further 1.118 ns simulation was run in order to let the system equilibrate and finally production run could start.

The temperature was kept constant through a simple velocity rescaling procedure, with a relaxation time of 1 ps, while the pressure was controlled through a Berendsen bath [48] using a relaxation time of 100 fs, the default value in the program NAMD. It is well known that a simple rescaling procedure does not provide a correct canonical ensemble and extended-system approaches have been proposed to simulate correct thermodynamic ensembles [49–52]. Recently a stochastic velocity rescaling has been proposed that could provide correct ensemble with limited overhead computation [53].

However, the adopted protocol should not be detrimental for the kind of analysis presented here. For all simulations, the size of the box was fluctuating around its average value within fractions of Å.

3. Results and Discussion

We have used high-concentration molecular dynamics simulations in previous works that addressed different problems [10, 12, 13]. Many analyses have been already reported in those works. As illustrations of the protocols described in the Methods section, we consider two applications:

• (1) the simulation of the association of an amyloidogenic protein (beta 2-microglobulin) [10] which illustrates the setup of the simulation system, detailed in the methods section, and the analysis of rotational and translational diffusion constants reported hereafter;
• (2) the simulation of the encounter of hydrogen peroxide with glutathione peroxidase which illustrates the analysis and the general usefulness of the approach.

3.1. Simulation of the Association of Beta 2-Microglobulin

The analysis of the rotational diffusional constants is provided by Figure 2. The value of 〈cos⁡(θ)〉 is computed as (1/3)tr⁡(R) where R is the matrix that describes the rotation of the molecule with respect to its orientation at the start of the simulation, and tr⁡ denotes the Trace operation, as discussed in Section 2. The average 〈cos⁡(θ)〉 is further averaged over all 27 molecules, thus providing also standard deviation. The plot of 〈〈cos⁡(θ)〉〉 is reported in Figure 2. The time constant (9.6 ns) obtained fitting the decay with an exponential is larger than expected (8.7 ns), but still consistent with the size of the protein.

Figure 2.

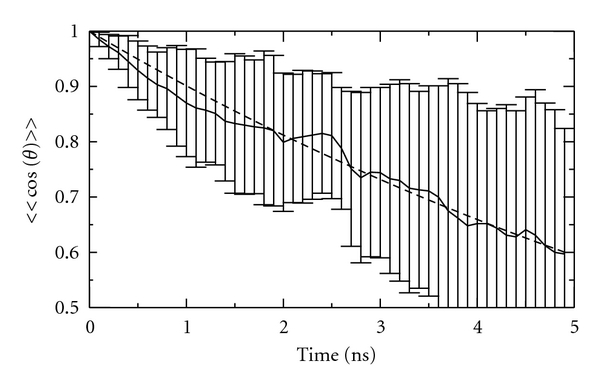
Average of 〈cos⁡(θ)〉 versus time with standard deviations as bars, where 〈cos⁡(θ)〉 is the average cosine of the angle between two vectors rigidly anchored on the diffusing molecule at time 0 and at time t. Averaging is performed over 27 molecules. Data are from the simulation reported in [10].

Analogously, the diffusion coefficient of the molecule is 20.9 Ų ns⁻¹, close to what expected (17.2 Ų ns⁻¹) (Figure 3). Also here the square displacement is averaged over all 27 molecules. Similar results are obtained by considering the average translation and rotation in a small interval of time and fitting the linearized exponential equations of diffusion reported above.

Figure 3.

Average of the square displacement from starting position versus time with standard deviations as bars. Averaging is performed over 27 molecules. Data from the simulation reported in [10].

3.2. Simulation of Glutathione Peroxidase-Hydrogen Peroxide Encounter

For hydrogen peroxide, the translational diffusion constant was 443 Ų ns⁻¹, and orientation was randomized in less than 0.01 ns. Four simulations have been performed in order to acquire some statistics about molecular encounters. Two simulations were performed with different seed number, one for 10 ns and one for 30 ns. One simulation (20 ns long), was performed with the catalytic CYS 36 ionized. In one simulation (10 ns long) the backbone dihedral angle energy correction term CMAP was not applied in order to test the effect of different backbone mobility.

Only few hydrogen peroxide molecules establish long-lived contacts with the peroxidase in each simulation. Ideally, we would like to sample the same long-lived contact many times during each simulation or at least in different simulations. Although in all simulations at least one hydrogen peroxide molecule reaches the catalytic region establishing contacts for more than 500 ps, different long-lived contacts are observed in different simulations. The results reported here are for nonionized CYS 36.

The different results obtained in the two simulations differing only for the seed number point out that a larger number of simulations should be performed for exploring all possible encounter events.

For all simulations, snapshots were taken at 0.1 ns time intervals. The number of contacts between all pairs of atoms was counted. As detailed in the Methods section, this led to a list of the atoms of the protein contacted by hydrogen peroxide molecules together with the number of occurrences of such contacts. With the definition of contact adopted here, on average there are 386 hydrogen peroxide-protein contacts for each snapshot in the longest simulation. The number of different pairs of atoms involved in contacts in the 300 snapshots for the longest simulation is 71830. Of these, only 2000 are involved in contacts lasting more than 0.5 ns.

Most frequently contacted atoms overlap in some cases with the longest-lived contacts. As observed with other small molecules, it is not infrequent that some of the hydrogen peroxide molecules gets trapped in protein cavities and stay for times even longer than 20 ns, as observed in the longest simulation. One such cavity is defined by residues {K45, L46, L49, K130, T147, D148, P149, I152}. Other cavities are defined by other residues throughout the protein.

In all simulations, there were contacts of hydrogen peroxide with residues in the catalytic site lasting at least 0.5 ns. The contacting residues in the catalytic site are {C36, L38, N42, W126, N127, F128, P145}. In general, however, these were not the longest-lived contacts found.

The arrangement of the catalytic site is rather stable for the simulations using the CMAP energy correction, with fluctuations at the backbone of the residues {C36, Q71, W126, N127} on average 0.45 ± 0.15 Å, much lower than the fluctuations displayed by loops. In the same simulations, no conformational transition seems to be required at this region for substrate binding. Also, hydrogen peroxide is able to reach the catalytic site with no aid from other sidechains as can be seen following the trajectories of the molecules before reaching glutathione peroxidase. However, in several cases the hydrogen peroxide reaches the catalytic site by shifting between the C-terminal residues and the helix following C36 or approaching the catalytic site from the side of C36 and W126.

When the CMAP correction energy term is not included in the forcefield, the region entailing C36 moves apart from the other residues and a hydrogen peroxide molecule can enter the cavity entailing residues I32, A33, C36, and F128. In view of the low stability of the catalytic region no other simulations were performed without the CMAP energy corrections.

The distances of atoms W126 HE1, N127 HD2, and Q71 HE2 with the peroxidatic cysteine C36 SG are overall short. As evidenced by other works, these interactions lead to a stabilization of the developing negative charge at the sulphur atom upon deprotonation [41]. During the simulation, an unexpected interaction is conserved between the hydrogen of hydrogen peroxide and the carbonyl oxygen of residue N127. Besides these hydrogen bonds, the sidechain of N127 establishes a hydrogen bond with the thiol group of C65. A representative snapshot of the sidechains involved in this fluctuating network of hydrogen bonds is shown in Figure 4. Residues whose sidechains are shown as sticks are Q71, W126, N127, C36, and C65. Once a hydrogen peroxide molecule exhibiting a long-lived contact has been found, its interactions with the protein may be obtained throughout the simulation (not only at 0.1 ns-spaced snapshots) by using efficient programs like VMD [54]. In Figure 5, the plot of the distances between atoms interacting in the catalytic site is reported.

Figure 4.

Snapshot at time 6.0 ns. Sidechains are shown for residue Q71, W126, N127, C36, and C65. Two contacting hydrogen peroxide molecules are shown as van der Waals spheres.

Figure 5.

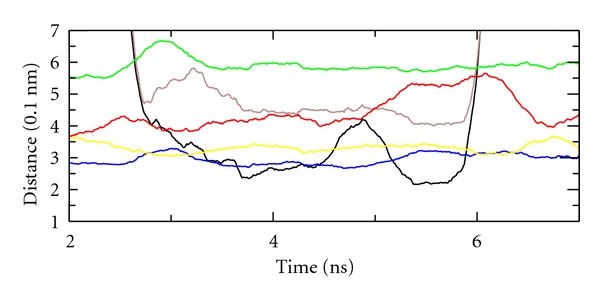
Distance versus time for selected pairs of atoms in the catalytic site: red: W126 HE1-C36 SG; yellow: Q71 HE2-C36 SG; blue: N127 HD2-C36 SG; green: N127 OD1-C36 HG; black: PEO H-N127 O; violet: PEO O-C36 SG.

As said above, the different results obtained in the different simulations point out the need to run more and longer simulations in order to acquire statistics. On the other hand, the results and the other examples cited prove how effective can be high-concentration molecular dynamics simulations.