Longitudinal evaluation of CA-125 velocity and prediction of ovarian cancer

Abstract

Objective

To determine whether CA-125 velocity is a statistically significant predictor of ovarian cancer and develop a classification rule to screen for ovarian cancer.

Methods

In the ovarian component of the PLCO cancer screening trial, 28,038 women aged 55–74 had at least two CA-125 screening tests. Ovarian cancer was diagnosed in 72 (0.26%) women. A multiple logistic regression model was developed to evaluate CA-125 velocity and other related covariates as predictors of ovarian cancer. Predictive accuracy was assessed by the concordance index and measures of discrimination and calibration while the fit of the model was assessed by the Hosmer and Lemeshow's goodness-of-fit χ² test.

Results

CA-125 velocity decreased as the number of CA-125 measurements increased but was unaffected by age at baseline screen and family history of ovarian cancer. The average velocity (19.749 U/ml per month) of the cancer group was more than 500 times the average velocity (0.035 U/ml per month) of the non-cancer group.

Conclusion

Among six covariates used in the model, CA-125 velocity and time intervals between baseline and second to last screening test and between last two screening tests were statistically significant predictors of ovarian cancer. The chance of having ovarian cancer increased as velocity increased, and the chance decreased when the time intervals between baseline and the second to last screening test and between last two screening tests of an individual increased.

Introduction

Cancer antigen CA-125 (CA-125) is a glycoprotein found in greater concentration in ovarian cancer cells than in other cells. CA-125 is useful in monitoring women who are being treated for ovarian cancer and has been suggested as a screening test for ovarian cancer [1–5]. In women without known ovarian cancer a high value may indicate the presence of ovarian cancer. However, because other conditions such as infections of the abdomen or chest, menstruation, pregnancy, endometriosis, benign tumors of the ovaries, and liver disease can also cause a high CA-125 level [6–8], a single high CA-125 measurement is not a highly specific indicator of ovarian cancer. Results from the first randomized trial to evaluate CA-125 and transvaginal ultrasound (TVU) have recently been reported from the Prostate, Lung, Colorectal and Ovarian (PLCO) cancer screening trial [9]. Screening in the ovarian component of the trial using a single CA-125 with the standard clinical test value of 35 U/ml as the reference level was not effective in reducing ovarian cancer mortality, and consequently, CA-125 with 35 U/ml as a reference level is not likely to be widely used as a screening intervention. Since screening test for ovarian cancer in the PLCO trial was a simultaneous test with CA-125 and TVU, the test was positive if either one was positive. Most false-positive results were due to the use of TVU, rather than CA-125 [10]. This suggests that if CA-125 had been used alone, there may have been a better screening result. Thus, questions of theoretical and practical interest are raised: If we want to consider CA-125 alone a screening modality, how can we use its values taken over time efficiently? Could the velocity based on serial CA-125 values over time with some other covariates provide a more accurate prediction of ovarian cancer rather than using a single CA-125 measurement? The answers to both questions are very important to better understand the findings of the PLCO cancer screening trial. As mentioned by Skates et al. [11, 12], only ad hoc rules have been suggested for measuring the information of CA-125 levels taken over time and using it in a screening strategy. They also mentioned that the difficulty in fully using CA-125 changes over time is compounded by the fact that in most ovarian cancer screening settings, CA-125 values are measured only at a long interval, such as annually. Therefore, it is a challenge to develop an efficient method that extracts maximal information from such sparse CA-125 measurements and uses the information to provide a good prediction for the probability of having ovarian cancer at the individual level.

Meier [13] indicated that the slope of CA-125 values detects recurrence in ovarian cancer more accurately than one or two isolated measurements. Skates et al. [11] used the slope of log(CA-125 + 4) following a change-point to detect ovarian cancer. Specially, Skates et al. [11] developed a Bayesian approach to ovarian cancer screening based on calculation of the posterior probability of ovarian cancer given the log-transformed CA-125 levels. Most of the parametric assumptions used in their method are data related, which might not be appropriate for a data set other than their own. Furthermore, their method involves complicated computation and interpretation of data, and the computer program for the method is not publicly available. The purpose of this study is to propose an ovarian cancer prediction method that is based on a multiple logistic regression model whose computer program can be written using any statistical software such as SAS or free software R and apply the method to data from the ovarian component of the intervention arm in the PLCO cancer screening trial. In addition, we used the single CA-125 value at the second to last screen, the velocity calculated from the last two screens, and the predicted probability of having ovarian cancer together to develop a classification rule to screen for ovarian cancer.

Materials and methods

Study design and population

The design of the PLCO cancer screening trial has been described in detail elsewhere [14, 15]. Briefly, the objective of the ovarian component is to determine in healthy women aged 55–74 who had not been diagnosed previously with lung, colorectal, or ovarian cancer at entry whether screening with CA-125 and TVU simultaneously can reduce mortality from ovarian cancer. Enrollment was initiated in 1993 and completed in 2001. The 78,216 female participants are being followed for at least 13 years from enrollment. In this trial, 39,111 women were randomized to the control arm to receive no scheduled PLCO screening exams but rather receive standard care from their primary health care providers, while the other 39,105 women were randomized to the intervention arm to receive six annual CA-125 tests. Annual TVU was performed concurrently with the first four offered CA-125 tests. In other words, CA-125 and TVU tests were done simultaneously. They were not done sequentially such that TVU was applied if the CA-125 test was positive. Ten screening centers participated: the University of Colorado Health Sciences Center; Lombardi Cancer Research Center of Georgetown University; Pacific Health Research Institute, Honolulu; Henry Ford Health System; University of Minnesota School of Public Health/Virginia L. Piper Cancer Institute; Washington University School of Medicine; University of Pittsburgh, Pittsburgh Cancer Institute and Magee-Women's Hospital; Huntsman Cancer Institute at the University of Utah; Marshfield Clinic Research Foundation; and the University of Alabama at Birmingham. Each institution obtained local Institutional Review Board approval to carry out the trial.

The current study analyzed a subgroup of the 39,105 women in the intervention arm. Among these 39,105 women, 11,067 women were excluded from the current analysis for the following reasons: 1,634 women’s information on family history of ovarian cancer was not available; 4,852 women were not offered screening because they had undergone prior oophorectomy; 2,647 women refused to take screening test; 1,934 women had only one CA-125 test because velocity of CA-125 for those women could not be calculated. This study focused on the remaining 28,038 (71.70%) women who had two or more CA-125 screening tests.

A cancer was defined as either an invasive ovarian, peritoneal, or fallopian tube cancer that occurred within 12 months of a woman’s last screen.

Statistical Analysis

The association between cancer and covariates such as CA-125 velocity was evaluated by the following multiple logistic regression model:

$$\text{P}(\text{cancer}\mid \mathbf{X})=exp(\text{B}(\mathbf{X}))/[1+exp(\text{B}(\mathbf{X}))],$$

where the linear predictor B(X) is defined by

$$\text{B}(\mathbf{X})={\beta }_0+{\beta }_{H}H+{\beta }_{A}A+{\beta }_{L}L+{\beta }_{T}T+{\beta }_{C}C+{\beta }_{V}V.$$

Here P(cancer | X) denotes the probability of having ovarian cancer for given covariate X = (H, A, L, T, C, V) and β = (β₀, β_H, β_A, β_L, β_T, β_C, β_V) is the parameter vector to be estimated. H denotes family history of ovarian cancer in a first degree relative reported on the baseline questionnaire, which was entered into the model as a binary variable (H = 1 means family history and H = 0 means no family history); A is a woman's age at baseline, which was entered into the model as a continuous variable in years; L is the difference between the age of a woman at the second to last CA-125 test and the age at baseline, which was also entered into the model as a continuous variable in months; T is the time interval between the last two CA-125 tests, which was entered into the model as a continuous variable in months; C is a woman’s CA-125 value at the second to last test; V is the velocity, which was calculated by dividing the difference in the levels of CA-125 between the last two tests by the time T, which was entered into the model as a continuous variable.

In this study, a p-value of < 0.05 was considered statistically significant. Statistical analyses were conducted using SAS 9.2 software. After estimating the parameter vector β in the model, we (i) determine if CA-125 velocity is statistically significant; (ii) predict the probability of having ovarian cancer for a woman with the given covariate information; and (iii) use the CA-125 value at the second to last test, the velocity from the last two tests, and the predicted probability of having ovarian cancer to develop a clinically useful classification rule for an ovarian cancer screening test .

Assessment of the Multiple Logistic Regression Model

The likelihood ratio, score, and Wald tests were used to test the overall significance of the multiple logistic regression model over the intercept-only model. The statistical significance of individual regression coefficients (i.e., βs) in the model was tested by the Wald χ² statistic. The Hosmer-Lemeshow’s statistic was used to assess the fit of the multiple logistic regression model against actual outcomes [16].

Regarding validation of predicted probabilities, concordance and discordance values, derived from the multiple logistic regression model, were used to measure the association of predicted probabilities and to check the ability of the model to predict outcome. The higher the value of the concordance and the lower the value of discordance, the greater the ability of the model to predict outcome. To assess the overall performance of the multiple logistic regression model, we considered two measures of predictive performance: discrimination and calibration [17–23]. Discrimination was defined as the ability of the model to distinguish high-risk subjects from low-risk subjects and was quantified by the area under the receiver-operating characteristic (ROC) curve [17, 19, 21]. Calibration was defined as whether the predicted probabilities agree with the observed probabilities and was quantified by the calibration slope calculated as [model χ² − (df − 1)] / model χ² [17, 19, 21, 24]. The slopes for well-calibrated models are near 1, whereas models yielding predictions that are too extreme have a slope of < 1[21, 23].

To define a positive test, we used the CA-25 value C at the second to last test, the velocity V based on the last two CA-125 tests, and a cut-off threshold for the predicted probability derived from the multiple logistic regression model. Since ovarian cancer is a low incidence and fatal disease, which usually requires a high specificity for screening because of the consequence of a false-positive outcome, we required a specificity of 98% or higher. Specifically, a positive test was defined if one of the following four conditions was satisfied: (1) C >= 35 U/ml and V > 0; (2) C >= 35 U/ml, V <= 0 and p >= 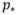; (3) C < 35 U/ml and V >= 2; (4) C < 35 U/ml, 0 < V < 2 and p >= 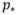, where p is the predicted probability and the cut-off threshold 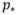= 0.01815. Here the velocity 2 U/ml per month was used to imply that the majority of women with a negative CA-125 test (i.e., C < 35 U/ml) at the second to last screen will probably produce a positive CA-125 test at their last screen because a velocity of 2 U/ml per month is equivalent to 24 U/ml per year. The cut-off threshold 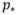= 0.01815 was determined by maximizing the sensitivity under a specificity of 98% or higher.

Results

Characteristics of the 28,038 women and their covariate information are presented in Table 1. The proportion of women with a family history of ovarian cancer in a first degree relative among the groups receiving different numbers of screening tests is relatively constant (p-value = 0.699). There is no statistically significant relationship between family history of ovarian cancer in first-degree relatives (p-value = 0.102), even though the observed proportion 0.083 for the cancer group is nearly double 0.039, the observed proportion for the non-cancer group. This may be a consequence of statistical testing which does not have enough power because of small numbers. Only 6 out of 72 who developed cancer had a family history. There is also no statistically significant difference in average age between women with different numbers of screening tests. It is also interesting to note that average velocity appears to decrease as the number of CA-125 measurements increases. The average velocity (19.749 U/ml per month) of the cancer group is more than 500 times the average velocity (0.035 U/ml per month) of the non-cancer group.

Table 1.

Participant characteristics and covariate information

Covariate	S*=2 (1,545)	S=3 (1,752)	S=4 (3,375)	S=5 (4,964)	S=6 (16,402)	Non-cancer (27,966)	Cancer (72)	All (28,038)
Age at baseline (years)
Mean	63.40	63.27	64.15	63.45	61.44	62.34	63.74	62.35
SD+	5.48	5.34	5.02	5.16	5.24	5.33	5.63	5.33
Family history
Yes (%)	65 (4.21)	65 (3.71)	119 (3.53)	192 (3.87)	655 (3.99)	1090 (3.90)	6 (8.33)	1096 (3.91)
No (%)	1,480 (95.79)	1,687 (96.29)	3,256 (96.47)	4,772 (96.13)	15,747 (96.01)	26,876 (96.10)	66 (91.67)	26,942 (96.09)
Time interval between baseline and second to last test (months)
Mean	7.28	19.84	29.34	40.97	49.40	41.38	21.83	41.33
SD	12.51	11.51	8.06	5.41	1.78	13.37	15.90	13.41
CA-125 value at the second to last test
Mean	13.10	12.77	12.77	12.33	11.96	12.23	17.14	12.24
SD	15.34	8.36	11.74	9.39	11.06	10.99	15.61	11.01
Time interval between last two tests (months)
Mean	15.12	14.97	14.43	18.45	11.84	13.70	12.31	13.70
SD	10.73	8.54	6.61	6.55	2.12	5.72	3.59	5.72
Velocity (U/ml per month)
Mean	0.50	0.33	0.19	0.03	0.02	0.04	19.75	0.09
SD	10.78	4.52	7.23	0.90	0.90	1.27	68.76	3.82

^*S denotes the number of screening tests a woman took.

⁺SD denotes the standard deviation.

Results from the above multiple logistic regression model appear in Table 2. Columns 3, 4, 5, 6 and 7 of Table 2 are parameter estimates, standard errors, Wald χ² statistic, degrees of freedom and p-values, respectively. Among the six covariates used in the model, velocity and time intervals between age at baseline and age at the second to last test and between the last two screening tests are statistically significant, while family history, age at baseline, and CA-125 value at the second to last test are not statistically significant. In particular, the p-value for velocity is very small (p-value < 0.0001). Since the maximum likelihood estimate (0.153) of β_V, the coefficient of the velocity, is positive, one can infer that the probability of having ovarian cancer will increase when the velocity increases. On the other hand, since the maximum likelihood estimate (−0.073) of β_L, the coefficient of the time interval between age at baseline and age at the second to last test, is negative, one can conclude that the probability of having ovarian cancer decreases when an individual's gap between baseline and her second to last CA-125 test is wider. The same conclusion can also be made for β_T. Table 2 also presents an overall evaluation of the multiple logistic regression model and a goodness-of-fit test statistic. Hosmer and Lemeshow’s test yielded a χ² (8) of 13.538 and was not significant (p-value > .05), suggesting that the model fits the data well.

Table 2.

Multiple logistic regression model of relationship between selected independent variables and ovarian cancer in 12 months post test

Predictor	Parameter	Estimate	Std Error	Wald’s χ2	df	P-value
Intercept	β0	−3.012	1.571	3.674	1	0.055
Family history	βH	0.418	0.506	0.681	1	0.409
Age at baseline	βA	−0.003	0.024	0.017	1	0.897
Time interval between entry and second to last test	βL	−0.062	0.007	84.099	1	<.0001
Time interval between last two tests	βT	−0.073	0.033	4.986	1	0.026
Second to last CA-125 test	βC	0.004	0.005	0.682	1	0.409
Velocity	βV	0.153	0.022	49.478	1	<.0001
Test				χ2	df	P-value
Overall model evaluation
Likelihood ratio test				207.736	6	<.0001
Score test				2097.418	6	<.0001
Wald test				168.877	6	<.0001
Goodness-of-fit test
Hosmer & Lemeshow				13.538	8	0.095

Concordance and discordance values used to measure the association of predicted probabilities and the observed responses are calculated below. There are 72 cancers and 27,966 non-cancers, which can form 72 *27,966 = 2,013,552 pairs with different responses, where one is cancer and the other is non-cancer. We used our multiple logistic regression model to calculate the predicted probability of having ovarian cancer for each individual of any pair. A pair is called concordant (discordant) if the predicted probability for the individual with cancer is greater (smaller) than the predicted probability for the individual without cancer. A pair is called a tie if two predicted probabilities are equal. Of those 2,013,552 pairs, 80.6% were concordant, 6.1% were discordant, and 13.3% were ties. The discrimination, a measure of predictive performance, was 87.2%, which is the area under the ROC curve. The other measure of predictive performance, calibration slope, was greater than 97% for all likelihood ratio, score, and Wald χ² tests. For example, the calibration slope was (207.736-5)/207.736 ≈ 98% for the likelihood ratio χ² test.

An attraction of fitting the proposed multiple logistic regression model is the possibility of predicting the probability of having ovarian cancer at the individual level. To illustrate, consider one particular woman from the study population. She had no family history and had three screening tests, with her cancer diagnosed after her last screening test. She was 71 years old when she took her first test. Around eleven months after her second test with a CA-125 value of 50 U/ml she took her last test with a CA-125 value of 355 U/ml. The total time from entry to her last test was around 2 years. Her velocity from her last two tests is 27.727 U/ml per month. That is, her covariate information X = (H, A, L, T, C, V) = (0, 71, 13, 11, 50, 27.727). According to our model with given information X, the predicted probability of having ovarian cancer diagnosed within one year after her last test is 0.404.

Table 3 provides a summary of predicted probability and CA-125 velocity for all 28,038 individuals in our study population. The average velocity for the cancer group is 19.749 U/ml per month or 236.988 U/ml per year, while the average velocity for the non-cancer group is 0.035 U/ml per month or 0.420 U/ml per year. Note that the standard deviation (68.760) of the velocity for the cancer group is much greater than the standard deviation (1.273) of the velocity for the non-cancer group. A similar conclusion can also be made for predicted probabilities between the two groups. Although the maximum predicted probability for the non-cancer group was 1, it might be considered an outlier because this probability was from a woman with covariate information X = (H, A, L, T, C, V) = (0, 68, 11, 13, 45, 139.538). That is, this woman had no family history and was 68 years old when she took her first of three tests. She completed three tests in two years, with 13 months between the last two tests. Her last two CA-125 values were 45 and 1,859, respectively, which produced a velocity of 139.539 U/ml per month. Without any additional information, the huge jump of CA-125 value would lead most people to believe she had ovarian cancer at last test. However, this woman had no report of ovarian cancer. She was diagnosed with breast cancer a little over 18 months following her last CA-125 test.

Table 3.

Summary of predicted probability of ovarian cancer and velocity

Cancer	Number	Variable	Mean	SD	Minimum	Maximum
Yes	72	Predicted probability	0.105	0.262	0.001	1.000
		Velocity	19.749	68.760	−1.250	413.750
No	27,966	Predicted Probability	0.002	0.010	0.000	1.000
		Velocity	0.035	1.273	−74.167	139.538

With the given covariate information X = (H, A, L, T, C, V), one should be able to use our model to calculate the predicted probability of having cancer. With a specificity of 98% or higher, using our definition of a positive test will yield a cut-off threshold of 0.01815 for the predicted probability, which yields a sensitivity of 62.5% and a positive predictive value (PPV) of 9.1%. Although 9.1% looks small, the increase from approximately 2% to 9.1% is more than fourfold [12]. Details are given by Table 4. Among 72 cases, 14 are stage I; 5 are stage II; 43 are stage III; 9 are stage IV, and stage information is not available for one. Our classification rule identified 6 stage I cancers, while using a single CA-125 value of 35 U/ml only identified 4 stage I cancers. This is a potentially significant advantage over using a single CA-125 value to screen for early stage cancer.

Table 4.

The Observed and the predicted frequencies (cut-off threshold = 0.01815)

Observed	Predicted cancer	Predicted Non-cancer	% Correct
Cancer	45	27	62.5
Non-cancer	449	27,517	98.4
Overall % correct			98.3

Discussion

The approach based on the slope of a biomarker such as prostate-specific antigen from two consecutive tests is used to study prostate cancer [25, 26]. In this paper a method for calculating the probability of having ovarian cancer based on serial CA-125 measurements using a specific multiple logistic regression model was proposed and illustrated in the context of screening for ovarian cancer. A clinically useful classification rule for an ovarian cancer screening test was also proposed by using the CA-125 value at the second to last test, the velocity from the last two tests, and the predicted probability of having ovarian cancer derived from the model together. Although our method is also based on the slope calculated from the last two CA-125 measurements, it does not share the weakness mentioned by Skates et al. [11] because the time interval T between the last two tests and the time interval L between the baseline and the second to last test are used in our model and both covariates are statistically significant. Our model can differentiate the same velocity over a short period and the same velocity over a much longer period because the duration T between the last two tests is a statistically significant covariate in our model. Meanwhile, another example specific to CA-125 mentioned by Skates et al. [11] is that a doubling from 3 U/ml to 6 U/ml provides little indication of the presence of ovarian cancer, whereas a doubling from 30 U/ml to 60 U/ml in the same period is a much stronger indication. Our method can also differentiate these two situations because the duration T between last two tests is also used in our model and the velocity of the second situation is (60-30)/T = 30/T U/ml per month, which is 10 times (6-3)/T = 3/T U/ml per month, the velocity of the first situation.We believe that our method can be easily applied in practice because it is simple and a computer program to implement the method is written using common statistical software SAS 9.2.

Determination of the cut-off threshold of predicted probability is very important for physicians who choose to use the CA-125 test to make a recommendation after they have the predicted probability based on our model. That is, they need to know how to define a positive test. In the original version of this paper, we used 10 times the average age-adjusted incidence rate [27] of 45.06 per 100,000 person-years for women aged 65–74 from 2000–2005 as a cut-off threshold of the predicted probability and obtained a specificity of 91.6%, a sensitivity of 66.7%, and a PPV of 2.01%. Clearly, a decision regarding acceptable levels of sensitivity and specificity involves weighting the consequence of leaving cases undetected (false-negative) and classifying healthy women as abnormal (false-positive). Since ovarian cancer is a low incidence disease, a high specificity is required for potential screening. We set a specificity of at least 98% and used the CA-125 value C at the second to last test, the velocity V from the last two tests and a cut-off threshold of 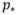= 0.01815 together to define a positive. This approach improved specificity and PPV dramatically. Finally, it is worth mentioning that our multiple logistic model does not involve any distributional assumption for the CA-125 value, velocity and other covariates. The model used only six covariates: family history of ovarian cancer in a first degree relative reported on the baseline questionnaire, age at baseline, the difference between the age of a woman at her second to last CA-125 test and the age at baseline, the interval between the last two CA-125 tests, and the velocity calculated from the last two screening tests. We included these six covariates because this model provided a better fit than the model including the velocity alone, and these covariates are believed to be the most important. The value of including more covariates requires further investigation.

Highlights.

• A new logistic regression model was developed to evaluate CA-125 velocity and other related covariates as predictors of ovarian cancer.

• CA-125 velocity and time interval between baseline and last screening test were significant predictors of ovarian cancer.

• Average velocity (19.749 U/ml/month) of cancer group was more than 500 times average velocity (0.035 U/ml/month) of non-cancer group.