Abstract
Features of the diffusion-time dependence of the diffusion-weighted magnetic resonance imaging (MRI) signal provide a new contrast that could be altered by numerous biological processes and pathologies in tissue at microscopic length scales. An anomalous diffusion model, based on the theory of Brownian motion in fractal and disordered media, is used to characterize the temporal scaling (TS) characteristics of diffusion-related quantities, such as moments of the displacement and zero-displacement probabilities, in excised rat hippocampus specimens. To reduce the effect of noise in magnitude-valued MRI data, a novel numerical procedure was employed to yield accurate estimation of these quantities even when the signal falls below the noise floor. The power-law dependencies characterize the TS behavior in all regions of the rat hippocampus, providing unique information about its microscopic architecture. The relationship between the TS characteristics and diffusion anisotropy is investigated by examining the anisotropy of TS, and conversely, the TS of anisotropy. The findings suggest the robustness of the technique as well as the reproducibility of estimates. TS characteristics of the diffusion-weighted signals could be used as a new and useful marker of tissue microstructure.
Keywords: diffusion time, q-space, scaling, power law, fractal, anomalous diffusion, anisotropy, Rician, noise floor, SHORE
1. Introduction
Understanding developmental and pathological changes in biological tissues relies on performing a detailed examination of the underlying microstructural alterations. The MR measurement of translational self-diffusion of the ubiquitous water molecule provides an indirect method to study local microscopic structure. The sensitivity of diffusion-weighted MRI (DWI) to the microscopic environment has made it an indispensable tool for the examination of neural tissue, proven by its sensitivity to an ever increasing number of pathologies affecting the brain and spinal cord (de Carvalho Rangel et al., 2011).
Although each conventional diffusion-weighted MR image does not possess resolution at the cellular level, a collection of such images nonetheless enables one to quantify attributes of the underlying microscopic architecture. For example, by acquiring a series of diffusion-weighted signals with different diffusion sensitization obtained by varying the wavenumber, q, and subsequently transforming the data, one can directly quantify the dispersion profiles associated with diffusion of water molecules (Cory and Garroway, 1990) using a method called q-space MR. Another important independent quantity one can adjust is time during which diffusion is observed, which determines the distances probed by the molecules (Latour et al., 1994; Pfeuffer et al., 1998; Sen, 2004).
Diffusion acquisitions obtained by independently varying the wavenumber and diffusion time, were used, in conjunction with a diffusion model of Brownian motion taking place in disordered media and fractals, to characterize the temporal and spatial dependence of diffusion propagators in red blood cells, normal human brain tissue, and a specimen of glioblastoma tumor (Özarslan et al., 2006b). Moreover, variations in the parameters quantifying the temporal scaling (TS) behavior were shown to exist, suggesting this method’s potential to generate new contrast.
As in many different areas of science (Mandelbrot, 1982), fractal concepts have been used to model neural tissue from cellular (Smith et al., 1989; Caserta et al., 1990) to voxel and organ levels (Kiselev et al., 2003); such an approach is justified due to the extremely complicated architecture of the neural tissue. Indeed, neural tissue exhibits a great deal of self-similarity across different length scales (Lichtman and Denk, 2011). When the distances that could be probed by DWI are concerned, the influence of macromolecules, cytoskeleton, cell membranes, and myelin needs to be considered. The temporal dependence of the variance of distances (i.e., mean-squared displacements) probed by randomly moving molecules in fractal environments is known to deviate from its normal linear behavior due to the presence of restrictions exhibited at many different length scales. Hence, Brownian motion taking place in fractal media is referred to as anomalous diffusion. Anomalous diffusion has been observed in many different environments (Gefen et al., 1983) including biological tissues and in very different contexts (Langlands and Henry, 2010). The proposal of using the MR technique, as an exquisite probe of molecular diffusion, to measure anomalous diffusion within disordered media has been made since the 1980s in theoretical studies (Banavar et al., 1985; Jug, 1986; Kärger et al., 1988; Widom and Chen, 1995; Zavada et al., 1999). MR measurements have been performed in model systems (Klemm et al., 2002; Müller et al., 1996), sand grains (Stallmach et al., 2002), as well as in lung tissue (Kveder et al., 1988) and duck embryos (Cheng, 1993).
On a very different line of thought, diffusion in biological tissues (carcinomas, fibrous mastopathies, adipose and liver tissue) has been modeled via Lévy alpha-stable distributions (Köpf et al., 1996). The corresponding MR signal attenuation is given in terms of a stretched exponential (Kohlrausch-Williams-Watts, KWW) function (Kohlrausch, 1847). Such processes are characterized by statistical moments that diverge, hence it is not meaningful to quantify the temporal scaling of the variance. This approach has recently been applied to neural tissue (Magin et al., 2008; Hall and Barrick, 2008; Zhou et al., 2010; Santis et al., 2011; Gao et al., 2011). As described in more detail in the Discussion section, the models based on the stretched exponential function differ fundamentally from the fractal-based ones.
In yet another approach, the asymptotic behavior of the q-dependence of the MR signal attenuation curve can be described by a power-law (Köpf et al., 1996), which can be considered a generalization of the Debye-Porod law for MR acquisitions (Sen et al., 1995). The Rigaut-type asymptotic fractal expression (Rigaut, 1984; Rigaut et al., 1998) has been used to capture the power-law decay from the signal attenuation curves (Köpf et al., 1998). More recently, such a dependence was shown to possibly originate from a sample of diffusion tensors drawn from a Wishart distribution (Jian et al., 2007); this finding was used to address the neuronal connectivity problem from multi-directional MR acquisitions.
In this work, we follow the theory of diffusion in disordered media and fractal environments and continue the approach taken by Özarslan et al. (2006b). We use the technique on MRI data sets, and the resulting TS contrast is assessed within excised hippocampi, whose microstructure was previously studied using diffusion tensor imaging (DTI) (Shepherd et al., 2006, 2007). In the next section, we provide a brief overview of the theory of diffusion in disordered media and its MR measurement with minor extensions in the modeling framework of (Özarslan et al., 2006b). MR imaging protocol and a number of computational tools employed to accurately compute the TS parameters are presented in the following section and the associated appendices. The results of the TS characteristics, the contrast based on the TS parameters, and the interplay of diffusion anisotropy with TS behavior are presented in the Results and Discussion sections.
2. Theory
In this paper, we use the method introduced by Özarslan et al. (2006b) with minor extensions. The technique follows the theory of diffusion in fractals and disordered systems, a comprehensive review of which can be found elsewhere, e.g., (Havlin and ben Avraham, 2002). A brief review of the relevant theory is included in this section for completeness.
In disordered media and fractals, the temporal dependence of the diffusional mean-squared displacement (〈r2〉) is known to deviate from linearity (Gefen et al., 1983). For this dependence, a power-law is observed in deterministic fractals (O’Shaughnessy and Procaccia, 1985), which accurately describes the temporal scaling (TS) behavior of diffusion in more realizable environments for a considerable range of length and time scales. For example, Saxton (2007) has shown that, in biological media, the presence of a hierarchy of binding sites leads to a wide anomalous diffusion regime.
Generally speaking, this power-law can be expressed through the relationship
| (1) |
where t is the diffusion time, and dw is the fractal dimension of the diffusion process, which can be considered to be a “statistical fractal.” This point follows from the self-similarity of the random walks; a discrete step taken at one time-point can be envisioned to be the sum of net displacements taken during smaller time intervals. The above scaling relationship provides a means to categorize different diffusion processes. For “normal” (e.g., Gaussian) diffusion, dw is exactly 2, which leads to the linear dependence of 〈r2〉 on diffusion-time mentioned earlier. When the mean-squared displacements increase more rapidly, i.e., dw < 2, the process is considered to be in the superdiffusive regime. The opposite case of dw > 2 is encountered in a subdiffusive process.
Besides the mean-squared displacement, another quantity whose scaling relationship is of interest is the return to the origin probability (RTOP), which is the likelihood of molecules to undergo zero net displacement during the diffusion time. The relevant relationship is given by
| (2) |
where ds is referred to as the spectral or fracton dimension (Alexander and Orbach, 1982), which quantifies the scaling behavior of the density of states for the Laplacian operator. Within the context of random walks on a discrete lattice, it is related to the number of distinct sites visited by the random walker.
Both dw and ds depend on characteristics of the diffusion process taking place within the fractal medium; as such, they are referred to as dynamic exponents. In contrast, the fractal dimension, denoted by df, is a static exponent describing the scaling of the mass of the environment with distance. Remarkably, in deterministic fractals, the two dynamic exponents are related to df through the simple relationship
| (3) |
It should be noted that these quantities have tremendously important implications for transport processes in complex media (Condamin et al., 2007).
A diffusion propagator of the following form possesses all of the scaling relationships described so far (O’Shaughnessy and Procaccia, 1985):
| (4) |
where d is the dimension of the embedding (free) space, which is invariably 3 for our purposes, and Φ is some function whose exact form does not affect the scaling relationships. Comparison of the above expression to the three-dimensional Gaussian propagator reveals that the “normal” values for ds and df are 3 as well.
Note that the above form for the propagator makes a number of assumptions that we shall relax to accommodate more general diffusion processes that are observed in gray-matter. First of all, the above propagator assumes the diffusion process to be isotropic. Second, any even-order moment of the displacements is implied to be related to dw, which is a consequence of the following relationship, which holds for the mth-order radial moment:
| (5) |
For the time being, we shall focus on measuring diffusion along a single direction, taken to be the z-direction, which is determined by the orientation of the diffusion sensitizing gradients. The data are acquired in a space reciprocal to the displacement space, with the wavenumber q = (2π)−1γδG, where γ is the gyromagnetic ratio and δ is the duration of the diffusion gradients whose magnitude is denoted by G. When only one radial line in q-space is sampled, it is meaningful to consider a one-dimensional propagator through a Fourier transform of such one-dimensional q-space data, which is given by
| (6) |
where Δ is the separation of the two gradient pulses and thus represents the diffusion-time, while E(q, Δ) is the MR signal attenuation profile (i.e., the q-space signal values divided by the signal at q = 0) for this diffusion-time. It follows from this expression that, the MR signal can be written in terms of the moments of this one-dimensional propagator through the relationship
| (7) |
where we assumed that the propagator is symmetric, i.e., all odd-order moments vanish. The one-dimensional propagator defined in Eq. 6 is just the projection of the three-dimensional displacement probability onto the axis specified by the gradient orientation. As discussed in detail by Özarslan et al. (2009), in isotropic spaces, the three-dimensional propagator can be obtained from its one-dimensional projection. The moments of the two propagators are also related. For example, the second moment is simply 〈r2〉 = 〈x2 + y2 + z2〉 = 3〈z2〉. Therefore, 〈z2〉 is proportional to Δ2/dw as well. However, in more general cases, one can still expect similar scaling relationships for the projected propagator. In fact, it was shown in Özarslan et al. (2006b) that scaling relationships implied by the following form of the propagator describe the temporal evolution of the diffusion process well:
| (8) |
where is the parameter for the projected propagator corresponding to ds, and Ψ is a well-behaved function of its argument. On the other hand, is defined through the expression
| (9) |
which is analogous to Eq. 3. Note that the “normal” values for and are 1. The value of can be estimated by exploiting the time dependence of the probability for zero net displacement along the z-axis through the relationship
| (10) |
In this work, we go one step further and relax the requirement that 〈zm〉 ∝ Δm/dw, which is implied by Eq. 8. Instead, we allow for the possibility that the temporal scaling of the higher order moments are described by different exponents, i.e.,
| (11) |
Clearly, d2 = dw.
We shall quantify the TS descriptors, dm, for m =2,4,6, and 8, along with and ds. For this purpose, we need to relate the q-space signal profiles to the quantities 〈z2〉, 〈z4〉, 〈z6〉, 〈z8〉, P1(0), and RTOP for different values of the diffusion time. As discussed in (Özarslan et al., 2011), these quantities can be linked to the q-space data profile, denoted by E(q), through the expressions
| (12) |
| (13) |
| (14) |
Note that Eq. 14 holds only when the signal is perfectly isotropic.
3. Methods
3.1. MR Image Acquisition
To investigate the temporal scaling (TS) behavior of diffusional processes in neural tissue, we acquired a series of diffusion-weighted MR images from four excised rat hippocampi with varying diffusion gradient strengths and diffusion times. Prior to imaging, rats were perfusion-fixed with 4% formaldehyde. The hippocampi were dissected medially from each hemisphere and immersed in fresh fixative for 8–10 days, then washed overnight in phosphate-buffered saline (PBS, with pH < 7.4) prior to imaging. Samples were imaged inside an NMR tube containing PBS. Temperature was maintained throughout the experiments using the temperature control unit of the magnet previously calibrated by methanol spectroscopy. Samples were imaged with a 5 mm birdcage coil inside a 600 MHz narrow-bore spectrometer with a Bruker Avance console. These experiments were performed with the approval of the University of Florida Institutional Animal Care Committee (IACUC).
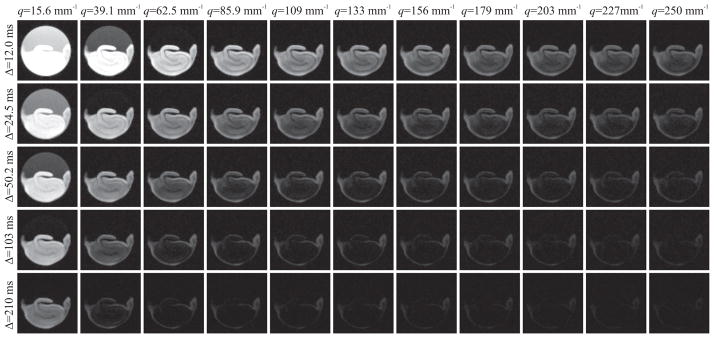
The first sample, which we refer to as “sample A,” was imaged using a pulsed gradient stimulated-echo pulse sequence with the following parameters: TR=1000 ms, TE=12.6 ms, bandwidth=35 kHz, resolution=(78 × 78 × 500) μm3, matrix size=(64 × 64), number of slices=4, diffusion gradient pulse duration (δ)=2 ms. Images were acquired with 32 different diffusion gradient strengths increasing from 91.75 to 2935 mT/m in steps of 91.75 mT/m, yielding a resolution of 4 μm in the displacement domain. The gradients were applied along the slice direction. This q-space acquisition scheme was repeated for 5 values of diffusion pulse separation (Δ) between 12 and 210 ms evenly spaced on a logarithmic scale. The number of averages was increased from 6 to 14 for increasing diffusion time values to produce images with comparable quality at different diffusion times. The experiments were performed at 17 °C. Figure 1 shows DWI data for all diffusion-time points (top to bottom) and every third gradient strength (left to right).
Figure 1.
Diffusion weighted MR images of an excised rat hippocampus (sample A) with varying q-values and diffusion times. All five diffusion time points were included, whereas every third q-value, starting from the second, is included.
In addition to the q-space acquisition described, the same specimen underwent a series of four diffusion tensor imaging (DTI) scans. The diffusion times were 12.0, 24.5, 103, and 210 ms for these DTI acquisitions, respectively. Each data set consisted of a total of 27 scans, 6 of which were at low diffusion-weightings, while the remaining 21 were collected with different gradient orientations at the b-value of 1280 s/mm2. The 6 gradient directions for the lower diffusion weighting were determined by the vertices of an icosahedron residing on one of the hemispheres. Similarly, the 21 gradient directions for the greater diffusion-weighting were computed from the first order tessellation of the icosahedron. The number of averages was varied between 8 and 20 as the diffusion time was prolonged. All other parameters were identical to those for the q-space acquisitions described above.
To assess the reproducibility of the TS features at physiologically more relevant conditions, the remaining three specimens, referred to as samples “B1,” “B2,” and “B3,” were imaged at 37 ± 0.2 °C using a similar protocol. The gradient encoding scheme was identical to that for sample A. However, 8 diffusion time values were used ranging from 12 to 147 ms evenly spaced on a logarithmic scale. The number of experiments was varied between 4 and 8 to reduce the effects of noise at longer diffusion times. To prevent the bias that can be introduced by processes that may occur during the course of the experiment, the ordering of experiments with different Δ values was random.
3.2. Computation of the TS exponents
The estimation of the TS exponents described in the Theory section proves to be a challenging task when there is significant noise in the data, which is expected to be the case in conventional image acquisitions. This fact can be appreciated from an examination of Figure 1 which illustrates the quick disappearance of the signal particularly at longer diffusion times for Sample A. The problem is more severe for Samples B1–3 because of the faster diffusion rate at the higher temperature.
Of particular concern is the estimation of and ds exponents that rely on an accurate estimation of integrals over the entire q-axis (see Eqs. 13 and 14). When magnitude valued data are used, computation of these integrals is problematic because they would diverge due to the finite value of the “noise floor”—the expected value of pure noise. Moreover, since the noise variance in magnitude data is signal-dependent (Koay and Basser, 2006), the influence of noise is different at different diffusion times. Consequently, any bias introduced by noise is expected to shift the estimates of the TS parameters. To overcome these issues, we devised a multi-step procedure that unifies some recent developments in the identification of noise (Koay et al., 2009b) and handling of noisy magnitude signals (Koay et al., 2009a) as well as the representation of q-space signals (Özarslan et al., 2008a).
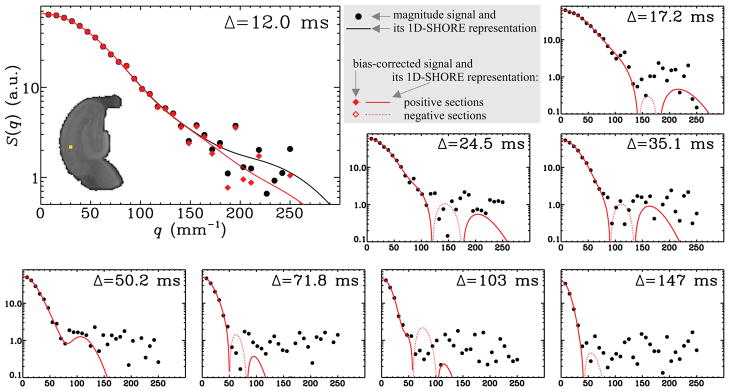
Our goal is to produce voxel-by-voxel estimates of the TS parameters from the five-dimensional (three spatial, one temporal, and one q-space dimensions) data sets. Figure 2 shows the results of our numerical scheme for an arbitrary voxel of the data set obtained from the B1 sample.
Figure 2.
Results of the scheme used to remove the noise-induced bias on the estimates is illustrated for a randomly selected voxel, which is shown by the yellow dot on the hippocampus image belonging to sample B1. The large plot shows the original magnitude-valued data points (black filled circles), its 1D-SHORE representation (black curve), the bias-corrected signal (red solid diamonds), and its 1D-SHORE representation (red curve) for the shortest diffusion time. Also provided are the magnitude-valued data points and the 1D-SHORE representation of the bias-corrected signal for other diffusion times. Note that the latter can assume negative values, which cannot be shown using logarithmic plots. Therefore, the absolute value of the negative sections of the resulting curves is plotted via red dotted curves.
Our strategy involves the following steps:
For each of the time points, the images from one slice, resulting in a three-dimensional array (with two spatial and one q-space), are fed into our PIESNO (probabilistic identification and estimation of noise) framework developed in (Koay et al., 2009b), which automatically identifies the noise-only regions in an image sequence, and provides an accurate estimate for the standard deviation of the underlying Gaussian noise. Note that noise characteristics do not vary from slice to slice. Although all slices could be fed into the algorithm, one slice was sufficient to provide accurate estimates.
For each voxel of the image, we estimate the signal profile using an extension of the 1D-SHORE (one-dimensional simple harmonic oscillator based reconstruction and estimation) method to include regularization as described in detail in Appendix A. The 1D-SHORE framework represents the E(q) profile in an orthogonal basis of Hermite functions, and was shown to provide very accurate interpolations and reasonable extrapolations of the signal. The estimation of the parameter, u, determining the stiffness of the spring, thus the breadth of the basis functions, was accomplished using a scheme similar to that in (Özarslan et al., 2011). More details can be found in Appendix A. N, which determines the number of basis functions to be used, was set to 10. This step produces a meaningful “mean value” for the noisy magnitude signal. This estimate is shown via the continuous black line in the large plot in Figure 2, which is estimated from the original discrete magnitude valued samples depicted by the black dots.
The estimates for the mean values obtained from the previous step were fed into the scheme developed to “break the noise floor” (Koay et al., 2009a), which produces discrete signal values without any bias introduced by the Rician character of the magnitude valued data. The results are depicted by red diamonds in the large panel of Figure 2. As shown by Koay et al. (2009a) the noise in these transformed data is Gaussian, hence the transformed signal can assume negative values, e.g., when the underlying noise-free signal intensity is smaller than the additive Gaussian noise.
The 1D-SHORE estimation (step 2) is repeated for the Gaussian signals, which results in a continuous representation of the signal values without bias due to the magnitude noise, which has been inappropriately called Rician noise. The resulting continuous representation is shown by red lines in Figure 2.
The 1D-SHORE coefficients were used in the estimation of even-order moments of displacement distribution and zero-displacement probabilities. The necessary analytical relationships linking the 1D-SHORE coefficients to these quantities are provided in Appendix B.
The above computations were repeated for all diffusion times and voxels of the image within the hippocampus. The end result includes four-dimensional (three spatial and one temporal) arrays of 〈z2〉, 〈z4〉, 〈z6〉, 〈z8〉, P1(0), and RTOP.
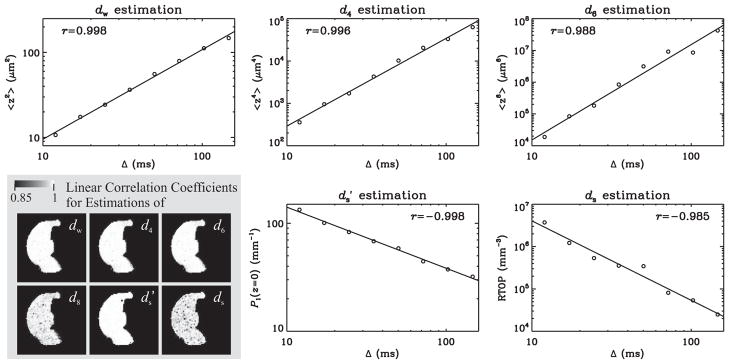
The power-laws in Eqs. 2, 10, and 11 imply a linear dependence of the logarithm of each of the above quantities on the logarithm of the diffusion time. Therefore, a linear regression routine was used to estimate the relevant TS parameters by fitting a line to these data. IDL’s robust linear fitting routine “LADFIT” was used to remove any inaccuracy due to outliers, which could result from unjustifiable values for the quantities. Such robust fitting was observed to be necessary almost exclusively for the RTOP values, which were used in the estimation of ds. Figure 3 illustrates the linear fits for the same voxel used in Figure 2 to illustrate the signal transformational framework.
Figure 3.
Plots illustrate the fits employed to estimate various TS exponents for the same voxel used in Figure 2. The temporal dependence of the second, fourth, and sixth order moments yields the parameters dw, d4, and d6, respectively. The parameter is obtained from the scaling behavior of the return to the xy-plane probability. Similarly, ds is computed from the time-dependence of the return-to-origin probability (RTOP), which is estimated under the assumption that diffusion is isotropic. The images overlaid on the gray background are the absolute value of the linear correlation coefficients for the B1 specimen indicating the robustness of the hypothesized power-law dependence throughout the rat hippocampus.
It is instructive to discuss Figure 2 to understand the effects of the signal transformational framework presented in steps 2–4. The original magnitude valued signal values (black dots) and the final 1D-SHORE representation of the transformed Gaussian-distributed data points (red lines) are shown for all eight values of the diffusion time. Since the latter can assume negative values, it was necessary to plot the absolute value of these curves. However, we used dotted lines to depict the negative sections of the curves as was done previously to illustrate the negative signal values predicted for double pulsed field gradient (double-PFG) experiments (Özarslan and Basser, 2007; Özarslan, 2009). In this figure, the result of step 2, which involves the 1D-SHORE of the signal before transformation is shown in the large plot corresponding to the shortest diffusion time. It should be noted that the computational approach taken does a superb job of estimating the signal at smaller q-values, which is necessary for the accurate estimation of the moments. Moreover, at larger q-values, i.e., when the signal is relatively small, the signal transformational framework yields a curve that decays much faster than what the original data points would imply. In most cases, the scheme introduces an oscillatory tail with zero-crossings, which, unlike in the case of the double-PFG acquisitions mentioned above, are likely to be spurious. However, since this oscillation is around the zero-value, evaluation of integrals over the horizontal axis yields significant cancelations, which are expected to improve the estimates of the quantities P1(0), and RTOP.
The linear fitting employed in the last step of the above procedure further prevents the influence of any unexpected value on the final estimate of the relevant TS parameter.
4. Results
Adequacy of the model
Figure 3 illustrates the linear correlation coefficients for the sample B1, which are found to be very close to 1 for all parameters; this is an exciting finding that demonstrates the adequacy of the power-law dependencies hypothesized in the Theory section for all regions of the rat hippocampus. The biggest deviation for the absolute value of the correlation coefficient from its ideal value of 1 is observed for the ds estimation; however, this is likely to be the consequence of the q2 factor in the integrand of Eq. 2, which makes the evaluation of this integral very challenging when the range of q-values with significant signal is limited.
Contrast in the TS parameters
The images of the TS parameters are shown in Figure 4A. Some contrast within the rat hippocampus is clearly evident in these images. To enable comparisons, we show the apparent diffusion coefficient (ADC) maps for each of the five diffusion times computed from the low-q part of the attenuation curves in panel B, and the results obtained from the DTI-acquisition (with Δ = 24.5 ms) for the same specimen are depicted in panel C. There appear to be three tissue types in the TS maps: (i) Three white-matter structures of fimbria, alveus, and dorsal hippocampal commissure (labeled on the fractional anisotropy map). These regions are known to have highly coherent, traditional white matter histology. On DTI maps (Basser and Pierpaoli, 1996), these areas are characterized by their high anisotropy and low mean diffusivity values (Shepherd et al., 2006). (ii) The granule cell and pyramidal cell layers (labeled on the map). These regions are composed of densely packed neuronal cell bodies and apical and basal dendrites. The DTI results reveal that these regions have intermediate anisotropy and high diffusivity. (iii) All other hippocampal regions composed of a more homogeneous mixture of neurons, glia and neuropil, which have intermediate diffusivity and anisotropy. In these ‘molecular’ areas of the hippocampus, dw values are tightly clustered around 2.0 indicating normal diffusion. The d4, d6, and d8 maps yield qualitatively similar contrast to that provided by the dw index. The contrast in the and ds images also seems similar, though inverted, to that in the dw map. Interestingly, the contrast between the granule and pyramidal cell layers (ii) and remaining gray-matter regions (iii) disappears in the and df maps, whereas some contrast with the fimbria region prevails.
Figure 4.
A. Images of the exponents characterizing the temporal scaling of the diffusion process. B. The apparent diffusion coefficient (ADC) maps for all five diffusion times computed from the low-q regime of the data sets. C. Traditional DTI-derived mean diffusivity (MD), fractional anisotropy (FA), and direction encoded color (DEC) maps computed for the same slice. White-matter structures of dorsal hippocampal commissure (DHC), alveus, and fimbria are identifiable on the FA map, whereas the regions of granule cell layer and pyramidal neurons are shown on the map. Finally, the label, SLM, on the ADC map stands for stratum lacunosum-moleculare.
The contrasts provided in the TS-parameter maps are different from those provided by the ADC maps in Figure 4B and the DTI-derived parameter maps in Figure 4C. The ADC map for the shortest diffusion time appears similar to the dw map. However, even in this map differences can be observed, most notably, in the stratum lacunosum-moleculare region of the hippocampus. Note how the ADC maps evolve as the diffusion time is increased in Figure 4B. A comparison of the pyramidal neurons and SLM regions reveals how differently these two regions behave as the diffusion time is varied. Specifically, the SLM region remains hyperintense throughout, but the region with pyramidal neurons start hyperintense at short diffusion time and end up hypointense at the long diffusion time suggesting a higher rate at which ADC is decaying. Our model enables the quantification of this difference by characterizing the rate of temporal change, which cannot be captured by looking at the diffusivity values at a particular diffusion time as in individual ADC or MD maps. The direction encoded color map (Pajevic and Pierpaoli, 1999) reveals that the orientational preference of diffusion varies significantly throughout different regions of the hippocampus. Although we have one-dimensional sampling of the q-space, the contrast obtained from the TS parameters appears to be independent of this orientational dependence of the anatomy. The relationship between the TS parameters and anisotropy will be discussed in more detail below.
Reproducibility of the TS parameters
Figure 5 shows maps of the three most important TS-parameters for the B1, B2, and B3 datasets (from top to bottom). It is clear that the contrast in these maps (and others, which are not shown) is very similar to that obtained for specimen A. The only difference seems to be in the fimbria region of the and df, which may be attributed to partial volume effects and dissection injury. Perhaps more important is the consistency of the generated maps across the three samples in this figure. This consistency demonstrates the reproducibility of the TS parameters as well as the robustness of the estimation methods. Therefore, these results indicate that the method can be used for population studies.
Figure 5.
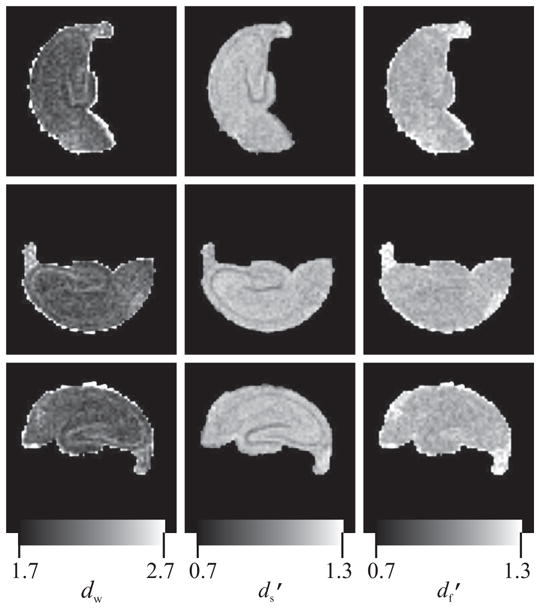
Maps of the walk dimension (dw, left column), projected spectral dimension ( , middle column), and projected fractal dimension ( , right column) for three different excised rat hippocampi scanned at 37°C. Different rows correspond to different specimens (B1 through B3). The similarity of the images for different samples suggests the reproducibility of the temporal scaling parameters under identical experimental conditions.
Anisotropy of TS
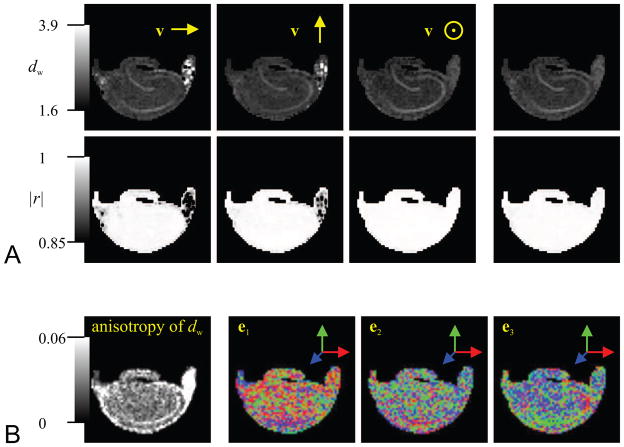
It should be noted that the estimation of the TS exponent dw requires the computation of the second order moment of the displacements, which can be obtained from the data at low q-values (see Eq. 12). In fact, the mean-squared displacement is simply equal to 2DΔ, where D is the apparent diffusion coefficient. When the environment is anisotropic, the diffusion coefficient D exhibits orientational dependence, which can be expressed in terms of the diffusion tensor, D, to be D(v) = vTDv, where v is a unit vector. Therefore, a series of DTI acquisitions with different diffusion times can be used to characterize both the orientational and temporal dependence of the diffusion process. We first investigated whether dw estimates were anisotropic. The top row of Figure 6 illustrates the dw maps for three different orientations of v along with that obtained from the trace of the diffusion tensor. The corresponding maps of the correlation coefficients are included in the second row of panel A. Some sensitivity of the dw estimates on the orientation is evident. Most notably, the contrast between the region with pyramidal neurons and the surrounding tissue disappears when the local preference of diffusion (as suggested by the direction encoded color map in Figure 4C) coincides with v even though there is no anisotropy or orientation contrast between these regions. The most significant contrast is evident when v points through the plane, i.e., when it is consistently perpendicular to the orientational preference of diffusion.
Figure 6.
A. The first three images of the top row show the dw-valued maps computed from the scaling of mean-squared displacement (MSD) values along the right-left, up-down, and through the slice directions, respectively. The last image is computed similarly from the average mean-squared displacement value as suggested by the trace of the diffusion tensor. The second row illustrates the corresponding linear correlation coefficient maps. B. The first image shows the variance of the dw values computed from the MSD values along 130 directions as a measure of anisotropy in the dw estimates. The following three images are the DEC maps illustrating the orientation of the three eigenvectors computed from a tensor fit to these 130 dw values.
Note the poorer performance of the fit in white-matter structures for directions perpendicular to the orientation of the fibers. This is thought to be due to the limited ability of DTI with the current acquisition parameters to describe diffusion in such highly restricted environments. More specifically, the signal attenuation at the employed b-value was insignificant when the gradient orientation was perpendicular to the fibers. However, the correlation coefficients across the remaining regions demonstrate the adequacy of the hypothesized power-law to characterize the TS of diffusion independent of the gradient orientation.
We repeated the above scheme to estimate an array of 130 dw values corresponding to different v directions isotropically distributed over the surface of a sphere. To this end, the mean-squared displacement (MSD) values were obtained along different directions by employing the relationship MSD(v) = 2D(v)Δ along with D(v) = vTDv. This scheme effectively uses the diffusion tensor computed from the DTI acquisitions, which involve only 27 measurements, to obtain a reasonable interpolation of the diffusivity, hence MSD, profiles. The leftmost image of Figure 6B shows the variance of the dw estimates from these 130 estimates. Some anisotropy in the dw estimates is visible in this map, particularly in the white-matter regions of the hippocampus as well as in the pyramidal neurons. The 130-element array of orientation dependent estimates, dw, was used to compute a dw tensor defined through the expression dw(v) = vTdwv. This expression was turned into a matrix equation, and the solution, including the unique components of dw were estimated by computing the pseudoinverse of the design matrix. The dw tensor was subsequently diagonalized. From left to right, the remaining three images of Figure 6B show the direction encoded color (DEC) maps associated with the eigenvectors corresponding to the largest, middle, and smallest eigenvalues. The most visible pattern is obtained within the region containing the pyramidal cells in the last image, which corresponds to the direction along which the dw value is smallest; this observation may suggest that the “special” direction associated with the diffusion process is given by the eigenvector corresponding to the smallest eigenvalue similar to the case of diffusion taking place in the proximity of macroscopic walls (Özarslan et al., 2008b). In fact, the DEC information within the regions containing pyramidal neurons in the last image of Figure 6B appears to be consistent with the DTI-derived DEC map obtained from the principal eigenvector of the diffusion tensor.
TS of anisotropy
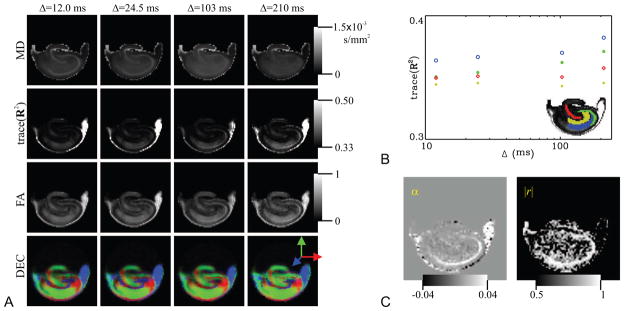
The next question we ask is the obverse of the one asked above: How does the anisotropy information vary with diffusion time? To understand this, we use the same data set that includes a series of four DTI acquisitions with different diffusion times. Unlike above however, we process the DTI data sets separately for each diffusion time. The results are shown in Figure 7. In panel A of this figure, we illustrate the DTI-derived maps of mean diffusivity (MD), fractional anisotropy (FA), and DEC. The FA index is essentially a map of the variance of the eigenvalues onto the [0, 1] interval, where this map is chosen somewhat arbitrarily to generate reasonable contrast within the tissue. As shown by Özarslan et al. (2005), trace(R2), where R is the normalized diffusion tensor obtained by dividing the diffusion tensor by its trace, can be considered a quantity without a particular scaling. We plot the temporal dependence of this quantity for several regions of the hippocampus in panel B where symbols with different colors represent the trace(R2) values for different regions shown on the hippocampus image with matching colors. Anisotropy values seem to increase with increasing diffusion times. Somewhat naively, a scaling relationship of trace(R2) ∝ Δα was fitted to the data on a voxel-by-voxel basis. The resulting map of α values and the corresponding linear correlation coefficient map is shown in Figure 7. The region with pyramidal neurons stands out once again with its elevated α values. In fact, this region appears to be the only region where the TS of diffusion anisotropy, as characterized by trace(R2) values, consistently obeys the hypothesized power-law scaling relationship. No significant change was observed in the temporal dependence of the DEC maps.
Figure 7.
A. DTI-derived mean diffusivity (MD), trace(R2), fractional anisotropy (FA), and direction encoded color (DEC) maps for different diffusion times. Note that trace(R2), where R is the diffusion tensor divided by its trace, is a measure of anisotropy like the commonly used relative anisotropy (RA) and FA parameters but without any particular dimensional scaling Özarslan et al. (2005). B. The variation of trace(R2) with diffusion time in different regions-of-interest specified on the rat hippocampus. C. Under the assumption that trace(R2) obeys the power-law, trace(R2) ∝ tα, a voxel-by-voxel fit reveals the α map on the left. The goodness-of-fit as illustrated by a map of the absolute value of the linear correlation coefficients (|r|) on the right suggests that the power-law assumption is valid only in a limited region of the rat hippocampus.
5. Discussion
Determinants of TS
In this article, we demonstrated how the temporal scaling behavior of certain quantities associated with the underlying diffusion process can be modeled using power laws. The superb agreement between the model and the real MRI data obtained from specimens of excised rat hippocampi suggests the adequacy of such models. However, the determinants of the observed scaling exponents are yet to be understood. It is tempting to interpret the observed contrast within the framework of diffusion in disordered media and fractals—the main source of inspiration for employing power-laws. In fact, anomalous diffusion has been observed within tissues in different contexts using methods other than MR (Sanabria et al., 2007). Subdiffusive behavior within the pyramidal and granule cell layers is attributed to the complex tissue architecture within those regions. In these layers of the rat hippocampus, water diffusion may be restricted on at least 2 length scales: (i) the large neuronal cell bodies (and potentially large nuclei) and (ii) the extremely complicated dendrites and synaptic boutons on the individual neuron’s soma, proximal dendrites and axon. The theory of diffusion on comb-like structures states that when diffusion along the backbone of a comb-like structure is measured, the trapping of particles along channels perpendicular to the backbone leads to anomalous diffusion in the subdiffusion regime. The complicated and intricate neuropil contacting neurons in the rat hippocampal cell layers could trap water molecules in narrow channels resulting in the observed anomalous diffusion.
However, one should be cautious that there may be other factors that may influence the TS-contrast. For example, there is evidence that susceptibility variations within the medium may lead to a deviation of the TS behavior of the apparent MSD values from linearity (Zupanc̆ic̆, 1988), which is expected to be pronounced when the acquisition is performed at high fields like in this study. We note that more recent experimental results by Palombo et al. (2011) have suggested the robustness of the parameter 2/dw on susceptibility differences. Another factor that should be considered is the T1 relaxation and compartmentalization. In the acquisition of the data sets, we employed a stimulated echo pulse sequence, which made it possible to have the same echo time for all diffusion times. However, T1 relaxation is not eliminated between the second and third 90° radiofrequency pulses. In the presence of multiple compartments with different T1 relaxation rates within each voxel, acquisitions with different diffusion times weight these compartments differently. Surface relaxation can play a similar role because the likelihood of an interaction between the confining surfaces and diffusing molecules is influenced by the diffusion time (Grebenkov, 2010). These effects could lead to variations in the TS behavior stemming from sources other than the direct effect of diffusion. As far as diffusion is concerned, some bias in the estimates could be introduced by the pulse duration, which is ignored in the above analysis. Although this effect was mitigated to some extent by employing short (2 ms) gradient pulses, the pulse duration is expected to be important when similar studies are performed on clinical scanners. Despite all these complications, it is interesting to note that the power-law behavior is prevalent throughout the hippocampus, and that the estimated values appear to be approximately uniform in most regions of the sample. Moreover, in a previous study (Özarslan et al., 2006b), we observed similar power-law dependencies in very different specimens of erythrocyte ghosts and glioblastoma multiforme tumor suggesting the applicability of the model to very different environments. Thus, although the exact source of the changes in the TS parameters requires further investigation, the method can be employed to characterize the resulting apparent TS characteristics.
High order moments and the collapse of the propagator
As described in the Theory section, we extended the method introduced in (Özarslan et al., 2006b) by fitting power-laws to higher order moments of the diffusion propagator. The hypothesized dependence seems to prevail for these higher order moments. Moreover, a comparison of the maps generated from the temporal dependence of these moments indicates that it is not possible to characterize the temporal scaling of all moments via a single exponent dw, which is implied by the functional form of the propagator given in Eq. 8. Instead, Eq. 11 seems to be observed with different (usually increasing) dm values suggesting a multifractal nature of the structure (Stanley and Meakin, 1988). This finding suggests that the scaling behavior of the propagator may be more complicated than that in Eq. 8.
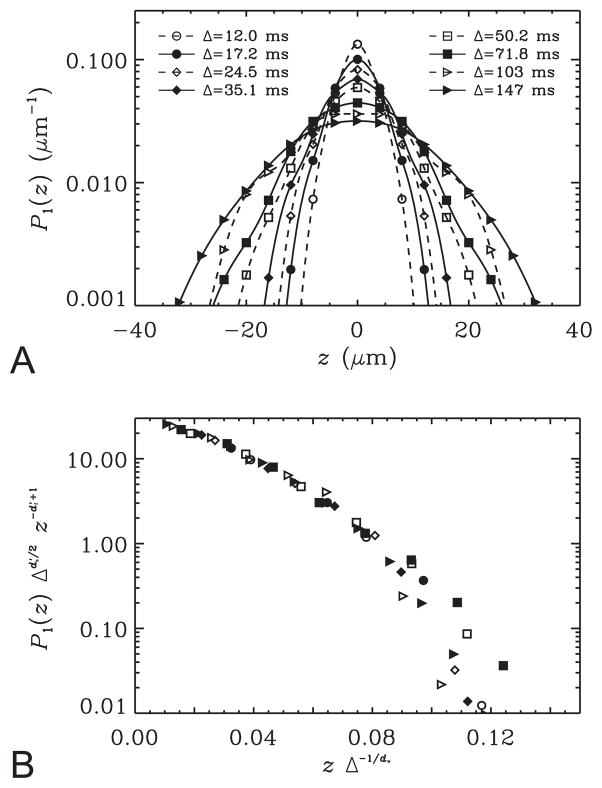
Another test for the form of the propagator in Eq. 8 involves computing the Fourier transform of the q-space signals for each diffusion time point. This transformation is computed readily from the 1D-SHORE coefficients thanks to the remarkable property of the basis functions that each of these functions is essentially the Fourier transform of itself (see Eqs. 18–19). The resulting propagators for the voxel used in Figures 2 and 3 are shown in Figure 8A. As expected, the propagators are broadened as the diffusion time is increased. The form of the propagator in Eq. 8 implies that all points on these curves would fall onto a single curve if the quantity is plotted against the quantity zΔ−1/dw; the shape of this curve is given simply by the shape of the Ψ function. The results are shown in Figure 8B. There is an excellent agreement for the smaller values of the abscissa. The deviations on the right hand side of this plot are likely due to the temporal scaling behavior of moments of order higher than 2, which are not accommodated by Eq. 8.
Figure 8.
A. The data from the voxel used in Figure 2 is Fourier transformed into the displacement domain using the 1D-SHORE framework. The curves indicate the resulting one-dimensional propagators. B. The data points sampled in panel A are re-plotted making use of some derived scaling relationships. The functional form of the propagator hypothesized in Eq. 8 would require all data points corresponding to different diffusion times to lie on a single curve.
Effect of breaking the noise floor
This study demonstrated the use of a technique developed to reduce the undesired effects of employing magnitude valued signals (Koay et al., 2009a). Note that the purpose of this technique is not to reduce the noise itself. Rather, it was designed to transform the Rician distributed signal into a Gaussian distributed signal so that any bias introduced by taking the magnitude of the complex-valued data is removed. An examination of the results with and without this technique revealed that the power law dependencies prevail in both cases. However, the correction obtained by breaking the noise floor seems to influence the estimates for all TS parameters. The most significant change is observed for the ds and indices as data at low signal (i.e., large q) values are most important for these parameters though some changes are observed in the estimates of the TS of the moments as well. The bias removal algorithm appears to be pushing the estimates toward their “normal” values in most voxels thus reducing the occurrences of TS parameters in the superdiffusive regime.
Two-dimensional diffusion encoding
The methods employed in this study involve five-dimensional acquisitions. In addition to the three spatial dimensions of each physical image, two more dimensions are sampled by varying the wavenumber (q) and the diffusion time (Δ) independently, thus yielding a two-dimensional data set for each voxel. Such acquisitions are necessary to compute all of the parameters we discussed above. In the current study, we attempted to collect the data sets that represent a nearly ideal case with wide ranges of Δ and q values. However, the prospect for significantly shortening the acquisitions is apparent. As can be noted from Figures 1 and 2, a substantial portion of the data sets are well within the noise region and could be excluded. Also note that fewer q and Δ values could be sampled. In any case, reasonably large q-values are necessary for the estimation of , ds, , and df as they rely on integrals taken over the entire q-axis. On the contrary, however, the estimation of dw requires data at low q-values only. Clearly, this condition can be realized in most MRI scanners, including clinical ones. In fact, 4 DTI acquisitions with different diffusion times were sufficient to quantify not only dw but also its anisotropy. If the contrast in the dw maps is indeed not that different from the contrast in other TS images, as suggested by the findings in excised rat hippocampi, acquisitions at low q-values will be sufficient to extract all of the desired TS information, thus making the technique practical for clinical applications.
Further, it should be noted that the characterization of TS can be cast as a two-dimensional reconstruction problem as can be best appreciated from Figure 8. Since the propagators corresponding to each diffusion time and their temporal evolution are relatively featureless, significant “compression” of the two-dimensional diffusion sampling is expected to be feasible. Therefore, recently developed sparse reconstruction methods such as compressed sensing (Donoho, 2006; Candés et al., 2006) could be used to efficiently reconstruct all propagators from very few acquisitions.
Comparison with other recent approaches to anomalous diffusion
The observation of anomalous diffusion in biological and medical applications of MR has attracted a great deal of interest in recent years (Özarslan et al., 2006b; Magin et al., 2008; Hall and Barrick, 2008; Zhou et al., 2010; Santis et al., 2011; Gao et al., 2011). The present study is based on the work introduced in (Özarslan et al., 2006b), and applies it to imaging data with a few extensions such as the temporal dependence of higher order moments and the relationship between diffusion anisotropy and TS. (Özarslan et al., 2006b) differs from some of the other articles (Hall and Barrick, 2008; Santis et al., 2011) mentioned above in a fundamental way sometimes overlooked in some articles. Specifically, these studies assume the q-dependence of the MR signal attenuation to be characterized by a stretched exponential function (Kohlrausch, 1847), i.e., E(q) = exp(−(bD)μ/2) with μ < 2—the same assumption employed by Köpf et al. (1996) and Bennett et al. (2003). Since b ∝ q2, the exponent is proportional to qμ. However, it is known that such a dependence emerges in the characteristic function of a Lévy alpha-stable distribution, which is a heavy-tailed distribution, i.e., its variance diverges for μ ≠ 2 (Metzler and Klafter, 2000). Although such a process can be regarded as “anomalous,” the divergence of the second moment prohibits the characterization of its temporal dependence, which we deem as the central criterion for anomalous diffusion (see Eq. 1). In sharp contrast, our method allows for all moments to be finite (see Eq. 7). In this sense, our technique is consistent with conventional methods like the cumulant expansion (Liu et al., 2003) or biexponential function fitting (Mulkern et al., 1999) though the temporal dependence implied by our model is different. From a practical point of view, the approach based on stretched exponentials can be used with one-dimensional diffusion encoding (e.g., by varying the q-values only). In fact, the stretched exponential method mentioned above intrinsically assumes that the dependence of the signal on q2 is identical to that for Δ since b ∝ q2Δ. However, in our spectroscopic (Özarslan et al., 2006b) as well as image acquisitions, we consistently observed that such identical dependence does not exist for real tissue. In a sense, this difference in dependencies is what we exploit to create new forms of MRI contrast. Consequently, our approach demands acquisitions with different Δ as well as q values.
We would like to note that the study by Magin et al. (2008), wherein the authors employ fractional differential operators to relate anomalous diffusion to the MR signal intensity, does not assume the dependence of the signal on q2 and Δ to be the same. Instead, the Bloch-Torrey equation (Torrey, 1956) is generalized by fractionalizing either the spatial or the temporal derivative. The latter approach, which was also taken by Damion and Packer (1997), yields solutions that are consistent with Eq. 1 and to some extent with our technique. However, in real applications of the method, the authors choose to fractionalize the spatial derivatives and fit the solutions to data acquired by varying the q-values only (Zhou et al., 2010; Gao et al., 2011). Since the related solutions are stretched exponential functions of q, they correspond to processes with infinite variance.
6. Conclusion
In conclusion, we exploited the diffusion-time dependence of several q-space MR derived parameters to generate new forms of contrast in neural tissue. Our approach employed the technique introduced by Özarslan et al. (2006b) with several significant extensions. This technique hypothesizes that parameters obey scaling relations characterized by power-laws as is the case of fractals and disordered media, which were shown to be obeyed in all regions of the excised rat hippocampus. It is necessary to encode diffusion by sampling different diffusion times in addition to different q-values. The correction of noise-induced bias was a challenging task and important for handling such data sets. This difficulty was overcome by integrating three recently introduced techniques Özarslan et al. (2008a); Koay et al. (2009b,a) into a multi-step procedure. The generated contrast appears to be novel, i.e., different from the contrast obtained in other traditional quantities such as ADC images, and other DTI-derived maps. Hence, we argue that such contrast may provide unique information about the microstructure of the neural tissue, which could be sensitive to alterations due to numerous pathologies, development, and aging. TS contrast was observed to be reproducible in different specimens and under different conditions, which suggests the possibility of employing the method in population studies. Several DTI acquisitions at different diffusion times revealed some anisotropy of the TS parameters in white-matter and in the region comprising the pyramidal neurons. Diffusion in these regions was found to be in the subdiffusion regime while the anisotropy in the latter region appeared to obey a power-law. In summary, the findings of this study indicate that characterizing the temporal scaling of the diffusion-related parameters via power laws could produce, novel and reproducible contrast that could complement existing MRI markers in assessing the structure of neural tissue, thus increasing the sensitivity and specificity of the available methods. It is too soon to propose these fractal parameters as possible quantitative imaging biomarkers for subtle changes in disease, degeneration, aging, etc., in neural tissue, but it would be worthwhile to begin performing systematic studies in different populations of subjects to test their robustness and sensitivity. Moreover, an examination of the existing findings, eg., in muscle tissue (Kim et al., 2005), suggests that it would be worthwhile to begin testing these parameters in complex tissues other than neural tissue to understand their TS properties.
HIGHLIGHTS.
Diffusion-time dependence of the diffusion MR signal leads to a novel contrast in neural tissue.
Anomalous diffusion was observed via q-space MR experiments on excised rat hippocampi.
We model the temporal scaling (TS) of the signal using fractal and disordered media concepts.
We devised a computational framework to remove any bias due to Rician nature of the signal.
The interplay between TS and diffusion anisotropy was investigated.
Acknowledgments
Support for this work included funding from: (i) the Intramural Research Program of the Eunice Kennedy Shriver National Institute of Child Health and Human Development (NICHD), National Institutes of Health (NIH). (ii) NIH grant number 1R01EB012874. (iii) Department of Defense in the Center for Neuroscience and Regenerative Medicine (CNRM) and the Henry M. Jackson Foundation (HJF). (iv) National Science Foundation (NSF) via the National High Magnetic Field Laboratory (NHMFL). We thank Liz Salak for editing the manuscript and Alexandru V. Avram for helpful discussions.
Appendix A: Signal transformational framework with regularized 1D-SHORE for breaking the noise floor
In this appendix, we outline the necessary steps needed to construct a signal transformational framework (Koay et al., 2009a) of a regularized smoothing spline based upon 1D-SHORE technique (Özarslan et al., 2008a; Özarslan et al., 2011).
Review of 1D-SHORE
In the 1D-SHORE technique, the diffusion-weighted MRI signal, S(q), can be expressed in the 1D-SHORE basis as
| (15) |
The basis functions are given by
| (16) |
where the characteristic length, denoted by u, is a parameter that determines the spread of the basis functions, which can be estimated from the data, and Hn is the Hermite polynomial of order n. Note that for the application in this paper, magnitude valued data are used. Therefore, the purely imaginary odd-ordered terms can be excluded. In this case, the i−n factor is simplified to (−1)n/2. Henceforth, we shall consider only the cases with even n.
The basis functions φn(q, u) are related to the well-known solution to the simple harmonic oscillator problem in quantum mechanics and they satisfy the equation
| (17) |
This eigenvalue equation has the remarkable property that its Fourier transform is of the same form up to some overall factor. Therefore, the propagator can be reconstructed directly from the an coefficients in the same basis, i.e.,
| (18) |
where
| (19) |
In this article, we exploit the ability of the 1D-SHORE basis to represent diffusion-weighted signal profiles to estimate the scaling laws accurately. It should be noted that the fitting described above is performed merely as a computational tool to obtain analytical and continuous representations of the S(q) decay curves and the associated propagators. Since the fitting is performed independently for each diffusion time, no assumption is employed for the TS behavior at this stage, and no biophysical meaning is ascribed to the estimated an coefficients. The cumulant expansion method (Liu et al., 2003) is an alternative that also represents the propagator in terms of Hermite polynomials. However, this scheme employs a Taylor series expansion of the characteristic function (the signal) in terms of the cumulants, resulting in a limited radius of convergence. Reconstructing the propagator from its cumulants is known to be quite problematic (Blinnikov and Moessner, 1998); this fact was recently discussed within the context of diffusion MR (Ghosh et al., 2010).
In the remainder of this Appendix, we incorporate the 1D-SHORE technique into our recently developed framework (Koay et al., 2009a) to correct the noise-induced bias in magnitude valued data.
Regularization
In the presence of noise, it is well known that the higher the number of basis functions used in a simple non-regularized least squares fit, the higher the likelihood that the fit will capture spurious oscillatory trends in the data. To avoid overfitting the data, the estimation needs to be regularized. A general strategy for solving regularized least squares problems has been well described elsewhere, e.g., see (Wahba, 1990; Ruppert et al., 2003).
The regularized 1D-SHORE estimation problem can be solved by finding a model of S(q), denoted by , such that F(q, u) minimizes the following objective function:
| (20) |
where F(m) refers to the mth order derivative of F with respect to q, yi = S(qi) is the ith measurement at the q-value of qi, and λ is the penalty parameter (or the smoothing parameter). In practice, one usually takes m to be 2 so that smoothness is favored over rapid oscillations (or larger curvature). Equation 20 can be expressed concisely in matrix form as follows:
| (21) |
where the superscript T denotes matrix or vector transposition, y is the vector of signal values yi, X is the design matrix with components Xij = φj(qi, u), and a is the vector of the 1D-SHORE coefficients, an. Finally, the (j, k)-component of the matrix R is given by
| (22) |
For the specific case when m = 2, it can be shown that
| (23) |
Note that if any of the argument of the factorials in the denominator is negative, the corresponding term will vanish. Consequently, R is a quintdiagonal symmetric matrix. The second order derivative of the basis functions can be obtained readily from Eq. 17. The derivation of Eq. 23 further entails evaluating integrals involving the product of three Hermite polynomials and an exponential function, which can be found in Equation 7.375.2 of (Gradshteyn and Ryzhik, 2000).
The smoothed observation vector, ŷλ, is given by
| (24) |
where Sλ = X(XTX + λR)−1XT is known as a smoother matrix. Similar to our earlier work in (Koay et al., 2009a), we will use a generalized cross validation (GCV) function to select the optimal λ. The GCV function is defined by:
| (25) |
where RSS(λ) = ||y − ŷλ||2. For a computationally efficient method for finding the optimal λ based on the GCV function, please refer to Appendix C of (Koay et al., 2009a).
Throughout this Appendix, the parameter u has been assumed to have a certain value. However, u can also be thought of as a parameter to be optimized during the regularization. To find the optimal u value, we first compute an initial estimate, u0, based upon the decay rate of the E(q) profile near q = 0. Specifically, the expression is fitted to the first few data points with lowest q-values. This u0 estimate is used to define our search interval, which is given by [0.7u0, 1.2u0]. Finally, within this interval, the u value that minimizes the GCV is deemed optimum.
Signal transformational framework with regularized 1D-SHORE for breaking the noise floor
The basic aim of our recent signal transformational framework for breaking the noise floor (Koay et al., 2009a) is simply to transform noisy signals that follow certain Gaussian-derived distributions (e.g., Rician distribution, non-Central Chi distribution, etc.) to ensure that the transformed signals are Gaussian distributed. This framework consists of three essential steps. First, data are smoothed with any spline model to obtain the average values of the noisy magnitude signals. Second, the “average value” of a noisy magnitude signal is mapped to the “average value” of the corresponding underlying signal intensity using a fixed point formula of the underlying signal intensity or the signal-to-noise ratio (Koay et al., 2009a; Koay and Basser, 2006). Here, we treat the estimations of the underlying signal intensity and of the Gaussian noise standard deviation (SD) separately. Note that we use our Probabilistic Identification and Estimation of Noise (PIESNO) technique (Koay et al., 2009b) to estimate the Gaussian noise standard deviation. Third, the corresponding noisy Gaussian signal of each of the noisy magnitude signals is found through a composition of the inverse cumulative probability density function of a Gaussian random variable and the cumulative probability density function of a non-Central Chi or other specific Gaussian-derived random variable. Please refer to (Koay et al., 2009a) for more in-depth discussion of this framework.
In summary, the essence of the proposed work is to use the regularized 1D-SHORE technique in the first stage of the signal transformation framework and use it again to fit the transformed noisy signals. The end result is a sequence of 1D-SHORE coefficients corresponding to the signal profile after the removal of bias due to noise. These coefficients are subsequently used to estimate the biophysical parameters of interest.
Appendix B: Estimation of the moments and zero-displacement probability
Once the 1D-SHORE coefficients are computed using the scheme outlined in Appendix A, these coefficients can be used to estimate many different features of the diffusion process conveniently and accurately. To this end, analytical relationships between the 1D-SHORE basis functions and the desired quantities are necessary. In this work, the TS behavior of even-order moments of the diffusion propagator are characterized. These moments are given in terms of the 1D-SHORE coefficients as
| (26) |
The probability of zero-displacements along the gradient direction (z) is used to compute the scaling exponent . This return to the xy-plane probability can be computed using the relationship
| (27) |
Finally, as demonstrated by Özarslan et al. (2009), for an isotropic medium, having data along a single radial line in q-space is sufficient to reconstruct the entire three-dimensional propagator. Therefore, a true return to origin probability (RTOP) can be computed from one-dimensional data. It is straightforward to show that the RTOP can be computed directly from the 1D-SHORE coefficients through the expression
| (28) |
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander S, Orbach R. Density of states on fractals: “fractons”. J Phys Lett-Paris. 1982;43(17):L-625–L-631. [Google Scholar]
- Banavar JR, Lipsicas M, Willemsen JF. Determination of the random-walk dimension of fractals by means of NMR. Phys Rev B. 1985;32 (9):6066. doi: 10.1103/physrevb.32.6066. [DOI] [PubMed] [Google Scholar]
- Basser PJ, Pierpaoli C. Microstructural and physiological features of tissues elucidated by quantitative diffusion tensor MRI. J Magn Reson B. 1996;111 (3):209–219. doi: 10.1006/jmrb.1996.0086. [DOI] [PubMed] [Google Scholar]
- Bennett KM, Schmainda KM, Bennett(Tong) R, Rowe DB, Lu H, Hyde JS. Characterization of continuously distributed cortical water diffusion rates with a stretched-exponential model. Magn Reson Med. 2003;50 (4):727–734. doi: 10.1002/mrm.10581. [DOI] [PubMed] [Google Scholar]
- Blinnikov S, Moessner R. Expansions for nearly gaussian distributions. Astron Astrophys Suppl Ser. 1998;130:193–205. [Google Scholar]
- Candés EJ, Romberg JK, Tao T. Stable signal recovery from incomplete and inaccurate measurements. Commun Pur Appl Math. 2006;59:1207–1223. [Google Scholar]
- Caserta F, Stanley HE, Eldred W, Daccord G, Hausman R, Nittmann J. Physical mechanisms underlying neurite outgrowth: A quantitative analysis of neuronal shape. Phys Rev Lett. 1990;64 (1):95–98. doi: 10.1103/PhysRevLett.64.95. [DOI] [PubMed] [Google Scholar]
- Cheng KH. Quantitation of non-Einstein diffusion behavior of water in biological tissues by proton MR diffusion imaging: synthetic image calculations. Magn Reson Imaging. 1993;11 (4):569–583. doi: 10.1016/0730-725x(93)90476-t. [DOI] [PubMed] [Google Scholar]
- Condamin S, Bénichou O, Tejedor V, Voituriez R, Klafter J. First-passage times in complex scale-invariant media. Nature. 2007;450(7166):77–80. doi: 10.1038/nature06201. URL http://dx.doi.org/10.1038/nature06201. [DOI] [PubMed]
- Cory DG, Garroway AN. Measurement of translational displacement probabilities by NMR: An indicator of compartmentation. Magn Reson Med. 1990;14 (3):435–444. doi: 10.1002/mrm.1910140303. [DOI] [PubMed] [Google Scholar]
- Damion RA, Packer KJ. Predictions for pulsed-field-gradient NMR experiments of diffusion in fractal spaces. Proc R Soc Lond A. 1997;453:205–211. [Google Scholar]
- de Carvalho Rangel C, Hygino Cruz LC, Takayassu TC, Gasparetto EL, Domingues RC. Diffusion MR imaging in central nervous system. Magn Reson Imaging Clin N Am. 2011;19(1):23–53. doi: 10.1016/j.mric.2010.10.006. URL http://dx.doi.org/10.1016/j.mric.2010.10.006. [DOI] [PubMed]
- Donoho DL. Compressed sensing. IEEE T Inform Theory. 2006;52:1289–1306. [Google Scholar]
- Gao Q, Srinivasan G, Magin RL, Zhou XJ. Anomalous diffusion measured by a twice-refocused spin echo pulse sequence: analysis using fractional order calculus. J Magn Reson Imaging. 2011;33(5):1177–1183. doi: 10.1002/jmri.22522. URL http://dx.doi.org/10.1002/jmri.22522. [DOI] [PMC free article] [PubMed]
- Gefen Y, Aharony A, Alexander S. Anomalous diffusion on percolating clusters. Phys Rev Lett. 1983;50 (1):77–80. [Google Scholar]
- Ghosh A, Özarslan E, Deriche R. Challenges in reconstructing the propagator via a cumulant expansion of the one-dimensional q-space MR signal. Proc Intl Soc Mag Reson Med. 2010;18 [Google Scholar]
- Gradshteyn IS, Ryzhik IM. Table of Integrals, Series, and Products. 6. Academic Press; London: 2000. [Google Scholar]
- Grebenkov DS. Subdiffusion in a bounded domain with a partially absorbing-reflecting boundary. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;81 (2 Pt 1):021128. doi: 10.1103/PhysRevE.81.021128. [DOI] [PubMed] [Google Scholar]
- Hall MG, Barrick TR. From diffusion-weighted MRI to anomalous diffusion imaging. Magn Reson Med. 2008;59(3):447–455. doi: 10.1002/mrm.21453. URL http://dx.doi.org/10.1002/mrm.21453. [DOI] [PubMed]
- Havlin S, ben Avraham D. Diffusion in disordered media. Adv Phys. 2002;51 (1):187–292. [Google Scholar]
- Jian B, Vemuri BC, Özarslan E, Carney PR, Mareci TH. A novel tensor distribution model for the diffusion-weighted MR signal. NeuroImage. 2007;37(1):164–176. doi: 10.1016/j.neuroimage.2007.03.074. URL http://dx.doi.org/10.1016/j.neuroimage.2007.03.074. [DOI] [PMC free article] [PubMed]
- Jug G. Theory of NMR field-gradient spectroscopy for anomalous diffusion in fractal networks. Chem Phys Lett. 1986;131 (1,2):94–97. [Google Scholar]
- Kärger J, Pfeifer H, Heink W. Principles and applications of self-diffusion measurements by nuclear magnetic resonance. In: Waugh JS, editor. Advances in Magnetic Resonance. Academic Press; London: 1988. pp. 1–89. [Google Scholar]
- Kim S, Chi-Fishman G, Barnett AS, Pierpaoli C. Dependence on diffusion time of apparent diffusion tensor of ex vivo calf tongue and heart. Magn Reson Med. 2005;54(6):1387–1396. doi: 10.1002/mrm.20676. URL http://dx.doi.org/10.1002/mrm.20676. [DOI] [PubMed]
- Kiselev VG, Hahn KR, Auer DP. Is the brain cortex a fractal? Neuroimage. 2003;20 (3):1765–1774. doi: 10.1016/s1053-8119(03)00380-x. [DOI] [PubMed] [Google Scholar]
- Klemm A, Metzler R, Kimmich R. Diffusion on random-site percolation clusters: theory and NMR microscopy experiments with model objects. Phys Rev E. 2002;65 (2):021112. doi: 10.1103/PhysRevE.65.021112. [DOI] [PubMed] [Google Scholar]
- Koay CG, Basser PJ. Analytically exact correction scheme for signal extraction from noisy magnitude MR signals. J Magn Reson. 2006;179(2):317–322. doi: 10.1016/j.jmr.2006.01.016. URL http://dx.doi.org/10.1016/j.jmr.2006.01.016. [DOI] [PubMed]
- Koay CG, Özarslan E, Basser PJ. A signal transformational framework for breaking the noise floor and its applications in MRI. J Magn Reson. 2009a;197(2):108–119. doi: 10.1016/j.jmr.2008.11.015. URL http://dx.doi.org/10.1016/j.jmr.2008.11.015. [DOI] [PMC free article] [PubMed]
- Koay CG, Özarslan E, Pierpaoli C. Probabilistic identification and estimation of noise (PIESNO): a self-consistent approach and its applications in MRI. J Magn Reson. 2009b;199(1):94–103. doi: 10.1016/j.jmr.2009.03.005. URL http://dx.doi.org/10.1016/j.jmr.2009.03.005. [DOI] [PMC free article] [PubMed]
- Kohlrausch R. Über das Dellmann’sche Elektrometer. Ann Phys. 1847;72:393–405. [Google Scholar]
- Köpf M, Corinth C, Haferkamp O, Nonnenmacher TF. Anomalous diffusion of water in biological tissues. Biophys J. 1996;70:2950–2958. doi: 10.1016/S0006-3495(96)79865-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Köpf M, Metzler R, Haferkamp O, Nonnenmacher TF. NMR studies of anomalous diffusion in biological tissues: Experimental observation of Lévy stable processes. In: Losa GA, Merlini D, Nonnenmacher TF, Weibel ER, editors. Fractals in Biology and Medicine. Vol. 2. Birkhäuser; Basel: 1998. pp. 354–364. [Google Scholar]
- Kveder M, Lahajnar G, Blinc R, Zupanc̆ic̆ I. Non-Brownian water self-diffusion in lung tissue. Magn Reson Med. 1988;6 (2):194–198. doi: 10.1002/mrm.1910060207. [DOI] [PubMed] [Google Scholar]
- Langlands TAM, Henry BI. Fractional chemotaxis diffusion equations. Phys Rev E Stat Nonlin Soft Matter Phys. 2010;81 (5 Pt 1):051102. doi: 10.1103/PhysRevE.81.051102. [DOI] [PubMed] [Google Scholar]
- Latour LL, Svoboda K, Mitra PP, Sotak CH. Time-dependent diffusion of water in a biological model system. Proc Natl Acad Sci. 1994;91:1229–1233. doi: 10.1073/pnas.91.4.1229. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lichtman JW, Denk W. The big and the small: challenges of imaging the brain’s circuits. Science. 2011 Nov;334(6056):618–623. doi: 10.1126/science.1209168. URL http://dx.doi.org/10.1126/science.1209168. [DOI] [PubMed]
- Liu CL, Bammer R, Moseley ME. Generalized diffusion tensor imaging (GDTI): A method for characterizing and imaging diffusion anisotropy caused by non-Gaussian diffusion. Isr J Chem. 2003;43 (1–2):145–154. [Google Scholar]
- Magin RL, Abdullah O, Baleanu D, Zhou XJ. Anomalous diffusion expressed through fractional order differential operators in the Bloch-Torrey equation. J Magn Reson. 2008;190(2):255–270. doi: 10.1016/j.jmr.2007.11.007. URL http://dx.doi.org/10.1016/j.jmr.2007.11.007. [DOI] [PubMed]
- Mandelbrot BB. The Fractal Geometry of Nature. Freeman; San Francisco: 1982. [Google Scholar]
- Metzler R, Klafter J. The random walk’s guide to anomalous diffusion: a fractional dynamics approach. Phys Rep. 2000;339:1–77. [Google Scholar]
- Mulkern RV, Gudbjartsson H, Westin CF, Zengingönül HP, Gartner W, Guttmann CR, Robertson RL, Kyriakos W, Schwartz R, Holtzman D, Jolesz FA, Maier SE. Multi-component apparent diffusion coefficients in human brain. NMR Biomed. 1999;12 (1):51–62. doi: 10.1002/(sici)1099-1492(199902)12:1<51::aid-nbm546>3.0.co;2-e. [DOI] [PubMed] [Google Scholar]
- Müller HP, Kimmich R, Weis J. NMR flow velocity mapping in random percolation model objects: Evidence for a power-law dependence of the volume-averaged velocity on the probe-volume radius. Phys Rev E. 1996;54 (5):5278–5285. doi: 10.1103/physreve.54.5278. [DOI] [PubMed] [Google Scholar]
- O’Shaughnessy B, Procaccia I. Analytical solutions for diffusion on fractal objects. Phys Rev Lett. 1985;54:455–458. doi: 10.1103/PhysRevLett.54.455. [DOI] [PubMed] [Google Scholar]
- Özarslan E. Compartment shape anisotropy (CSA) revealed by double pulsed field gradient MR. J Magn Reson. 2009;199(1):56–67. doi: 10.1016/j.jmr.2009.04.002. URL http://dx.doi.org/10.1016/j.jmr.2009.04.002. [DOI] [PMC free article] [PubMed]
- Özarslan E, Basser PJ. MR diffusion - “diffraction” phenomenon in multi-pulse-field-gradient experiments. J Magn Reson. 2007;188(2):285–294. doi: 10.1016/j.jmr.2007.08.002. URL http://dx.doi.org/10.1016/j.jmr.2007.08.002. [DOI] [PMC free article] [PubMed]
- Özarslan E, Basser PJ, Shepherd TM, Thelwall PE, Vemuri BC, Blackband SJ. Characterization of anomalous diffusion from MR signal may be a new probe to tissue microstructure. Conf Proc IEEE Eng Med Biol Soc. 2006a;1:2256–2259. doi: 10.1109/IEMBS.2006.259651. URL http://dx.doi.org/10.1109/IEMBS.2006.259651. [DOI] [PubMed]
- Özarslan E, Basser PJ, Shepherd TM, Thelwall PE, Vemuri BC, Blackband SJ. Observation of anomalous diffusion in excised tissue by characterizing the diffusion-time dependence of the MR signal. J Magn Reson. 2006b;183(2):315–323. doi: 10.1016/j.jmr.2006.08.009. URL http://dx.doi.org/10.1016/j.jmr.2006.08.009. [DOI] [PubMed]
- Özarslan E, Basser PJ, Vemuri BC, Shepherd TM, Thelwall PE, Blackband SJ. Observation of anomalous diffusion in excised tissue using the diffusion time dependence of the MR signal. 47th Experimental Nuclear Magnetic Resonance Conference; 2006c. [DOI] [PubMed] [Google Scholar]
- Özarslan E, Koay CG, Basser PJ. Simple harmonic oscillator based estimation and reconstruction for one-dimensional q-space MR. Proc Intl Soc Mag Reson Med. 2008a;16:35. [Google Scholar]
- Özarslan E, Koay CG, Basser PJ. Remarks on q-space MR propagator in partially restricted, axially-symmetric, and isotropic environments. Magn Reson Imaging. 2009;27(6):834–844. doi: 10.1016/j.mri.2009.01.005. URL http://dx.doi.org/10.1016/j.mri.2009.01.005. [DOI] [PubMed]
- Özarslan E, Nevo U, Basser PJ. Anisotropy induced by macroscopic boundaries: Surface-normal mapping using diffusion-weighted imaging. Biophys J. 2008b;94(7):2809–2818. doi: 10.1529/biophysj.107.124081. URL http://dx.doi.org/10.1529/biophysj.107.124081. [DOI] [PMC free article] [PubMed]
- Özarslan E, Shemesh N, Koay CG, Cohen Y, Basser PJ. Nuclear magnetic resonance characterization of general compartment size distributions. New J Phys. 2011;13:015010. doi: 10.1088/1367-2630/13/1/015010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Özarslan E, Vemuri BC, Mareci TH. Generalized scalar measures for diffusion MRI using trace, variance, and entropy. Magn Reson Med. 2005;53(4):866–876. doi: 10.1002/mrm.20411. URL http://dx.doi.org/10.1002/mrm.20411. [DOI] [PubMed]
- Pajevic S, Pierpaoli C. Color schemes to represent the orientation of anisotropic tissues from diffusion tensor data: application to white matter fiber tract mapping in the human brain. Magn Reson Med. 1999;42 (3):526–540. [PubMed] [Google Scholar]
- Palombo M, Gabrielli A, Santis SD, Cametti C, Ruocco G, Capuani S. Spatio-temporal anomalous diffusion in heterogeneous media by nuclear magnetic resonance. J Chem Phys. 2011;135(3):034504. doi: 10.1063/1.3610367. URL http://dx.doi.org/10.1063/1.3610367. [DOI] [PubMed]
- Pfeuffer J, Flögel U, Dreher W, Leibfritz D. Restricted diffusion and exchange of intracellular water: theoretical modelling and diffusion time dependence of 1H NMR measurements on perfused glial cells. NMR Biomed. 1998;11 (1):19–31. doi: 10.1002/(sici)1099-1492(199802)11:1<19::aid-nbm499>3.0.co;2-o. [DOI] [PubMed] [Google Scholar]
- Rigaut JP. An empirical formulation relating boundary lengths to resolution in specimens showing ‘non-ideally fractal’ dimensions. J Microsc. 1984;133:41–54. [Google Scholar]
- Rigaut JP, Schöevaërt-Brossault D, Downs AM, Landini G. Asymptotic fractals. In: Losa GA, Merlini D, Nonnenmacher TF, Weibel ER, editors. Fractals in Biology and Medicine. Vol. 2. Birkhäuser; Basel: 1998. [Google Scholar]
- Ruppert D, Wand MP, Carroll RJ. Semiparametric Regression. Cambridge University Press; 2003. [Google Scholar]
- Sanabria H, Kubota Y, Waxham MN. Multiple diffusion mechanisms due to nanostructuring in crowded environments. Biophys J. 2007;92:1–322. doi: 10.1529/biophysj.106.090498. URL http://dx.doi.org/10.1529/biophysj.106.090498. [DOI] [PMC free article] [PubMed]
- Santis SD, Gabrielli A, Bozzali M, Maraviglia B, Macaluso E, Capuani S. Anisotropic anomalous diffusion assessed in the human brain by scalar invariant indices. Magn Reson Med. 2011;65(4):1043–1052. doi: 10.1002/mrm.22689. URL http://dx.doi.org/10.1002/mrm.22689. [DOI] [PubMed]
- Saxton MJ. A biological interpretation of transient anomalous subdiffusion. I. Qualitative model. Biophys J. 2007;92(4):1178–1191. doi: 10.1529/biophysj.106.092619. URL http://dx.doi.org/10.1529/biophysj.106.092619. [DOI] [PMC free article] [PubMed]
- Sen PN. Time-dependent diffusion coefficient as a probe of geometry. Concept Magn Reson A. 2004;23A (1):1–21. [Google Scholar]
- Sen PN, Hürlimann MD, de Swiet TM. Debye-Porod law of diffraction for diffusion in porous media. Phys Rev B. 1995;51 (1):601–604. doi: 10.1103/physrevb.51.601. [DOI] [PubMed] [Google Scholar]
- Shepherd TM, Özarslan E, King MA, Mareci TH, Blackband SJ. Structural insights from high-resolution diffusion tensor imaging and tractography of the isolated rat hippocampus. NeuroImage. 2006;32(4):1499–1509. doi: 10.1016/j.neuroimage.2006.04.210. URL http://dx.doi.org/10.1016/j.neuroimage.2006.04.210. [DOI] [PubMed]
- Shepherd TM, Özarslan E, Yachnis AT, King MA, Blackband SJ. Diffusion tensor microscopy indicates the cytoarchitectural basis for diffusion anisotropy in the human hippocampus. AJNR Am J Neuroradiol. 2007;28 (5):958–964. [PMC free article] [PubMed] [Google Scholar]
- Smith TG, Marks WB, Lange GD, Sheriff WH, Neale EA. A fractal analysis of cell images. J Neurosci Methods. 1989;27 (2):173–180. doi: 10.1016/0165-0270(89)90100-3. [DOI] [PubMed] [Google Scholar]
- Stallmach F, Vogt C, Kärger J, Helbig K, Jacobs F. Fractal geometry of surface areas of sand grains probed by pulsed field gradient NMR. Phys Rev Lett. 2002;88 (10):105505. doi: 10.1103/PhysRevLett.88.105505. [DOI] [PubMed] [Google Scholar]
- Stanley HE, Meakin P. Multifractal phenomena in physics and chemistry. Nature. 1988;335:405–409. [Google Scholar]
- Torrey HC. Bloch equations with diffusion terms. Phys Rev. 1956;104 (3):563–565. [Google Scholar]
- Wahba G. Spline Models for Observational Data. SIAM; Philadelphia: 1990. [Google Scholar]
- Widom A, Chen HJ. Fractal Brownian motion and nuclear spin echoes. J Phys A. 1995;28:1243–1247. [Google Scholar]
- Zavada T, Südland N, Kimmich R, Nonnenmacher TF. Propagator representation of anomalous diffusion: the orientational structure factor formalism in NMR. Phys Rev E. 1999;60 (2):1292–1298. doi: 10.1103/physreve.60.1292. [DOI] [PubMed] [Google Scholar]
- Zhou XJ, Gao Q, Abdullah O, Magin RL. Studies of anomalous diffusion in the human brain using fractional order calculus. Magn Reson Med. 2010;63(3):562–569. doi: 10.1002/mrm.22285. URL http://dx.doi.org/10.1002/mrm.22285. [DOI] [PubMed]
- Zupanc̆ic̆ I. Effect of the background gradients on PGSE NMR diffusion measurements. Solid State Commun. 1988;65 (3):199–200. [Google Scholar]