A novel PET tumor delineation method based on adaptive region-growing and dual-front active contours

Abstract

To more accurately and precisely delineate a tumor in a 3D PET image, we proposed a novel, semi-automatic, two-stage method by utilizing an adaptive region-growing algorithm and a dual-front active contour model. First, a rough region of interest (ROI) is manually drawn by a radiation oncologist that encloses a tumor. The voxel having the highest intensity in the ROI is chosen as a seed point. An adaptive region growing algorithm successively appends to the seed point all neighboring voxels whose $\text{intensities}>=T$ of the mean of the current region. When T varies from 100% to 0%, a sharp volume increase, indicating the transition from the tumor to the background, always occurs at a certain T value. A preliminary tumor boundary is determined just before the sharp volume increase, which is found to be slightly outside of the known tumor in all tested phantoms. A novel dual-front active contour model utilizing region-based information is then applied to refine the preliminary boundary automatically. We tested the two-stage method on six spheres $(0.5–20\mathrm{ml})$ in a cylindrical container under different source to background ratios. Comparisons between the two-stage method and an iterative threshold method demonstrate its higher detection accuracy for small tumors (less than $6\mathrm{ml}$). One patient study was tested and evaluated by two experienced radiation oncologists. The study illustrated that this two-stage method has several advantages. First, it does not require any threshold-volume curves, which are different and must be calibrated for each scanner and image reconstruction method. Second, it does not use any iso-threshold lines as contours. Third, the final result is reproducible and is independent of the manual rough ROIs. Fourth, this method is an adaptive algorithm that can process different images automatically.

INTRODUCTION

${}^{18}\mathrm{F}$-FDG PET shows high sensitivity and specificity in many malignancies and has been widely used in staging, detecting primary or recurrent cancer, and monitoring therapeutic response.^{1, 2, 3, 4, 5} Currently, manual contouring and thresholding are two major methods for tumor delineation in PET. Manual tumor contouring in PET has been shown to lead to large variations in GTV delineation,⁶ mainly due to poor spatial resolutions, partial volume effects, scattered photon generated artifacts, and other limitations of this imaging modality. Furthermore, such manual delineation is subjective, may not be reproducible, and is time consuming to perform. Thresholding based on fixed threshold levels of 40%,⁷ 42%,⁸ or 50%^{3, 9} of the maximum intensity or uptake has been traditionally used to automatically delineate tumors. Soon it was reported that a fixed threshold did not generate optimal results for all tumors.^{10, 11, 12, 13, 14, 15, 16} Thresholding based on variable threshold levels in the range of 15%–50% was proposed, where the optimal threshold for a particular case is determined by either matching the GTV to that contoured in CT or MRI,^{10, 11} or as a function of source-to-background (S/B) ratios,¹² or as a regressive function of mean target intensities.¹³ However, there are two concerns for these approaches. First, CT or MRI does not necessarily image biological tumor volumes as PET. Second, CT or MRI generally does not have as high sensitivity or specificity as PET has.

Recently, an iterative threshold method has been described by Jentzen et al. to estimate the PET tumor volumes without a priori knowledge from anatomic images.¹⁵ First, a set of calibrated threshold-volume curves at varying source-to-background (S/B) ratios was derived based on phantom measurements using spheres of known volumes. Then the S/B ratio of a tumor was measured by estimating the source and background activity concentrations in the PET image. The calibrated threshold-volume curve of the S/B ratio closest to the measured S/B ratio was used for iteratively calculating a new threshold and tumor volume. The final tumor volume was determined when the iteration converged. This method may pick the most appropriate threshold for each particular tumor and obtain a better delineation result than that produced via a single fixed threshold. However, this method must be custom fit for each scanner or image reconstruction method. Furthermore, the algorithm accuracy strongly depends on a correct estimation of the initial S/B ratio, limiting its usefulness for patient’s data. Similarly, Drever and co-authors¹⁶ have also created an automated iterative technique to determine local threshold levels based on the slice-specific contrast between target and background. For both fixed and iterative threshold methods, the optimal threshold level for a specific image depends on tumor sizes, S/B ratios, reconstruction methods, tumor heterogeneities, and/or tumor locations. In addition, it should be pointed out that in most cases the final tumor volume is not only based on a specific and solely threshold level. Accurately and precisely delineating tumors in PET is still a very challenging problem.¹⁷

In this paper, we proposed a novel, two-stage PET tumor delineation method combining an adaptive region-growing algorithm and a dual-front active contour model. This two-stage method guarantees a reproducible result, which is independent of the manual rough ROIs. Experimental results on phantom and patient data studies demonstrate the robustness, accuracy, reproducibility, and its potential usefulness in PET tumor delineation for patients.

MATERIAL AND METHODS

The two-stage PET tumor delineation method includes two steps: Preliminary tumor localization based on a novel adaptive region growing algorithm, and final tumor delineation based on a novel dual-front active contour model.

Adaptive region growing algorithm

Classical seeded region growing algorithm^{18, 19, 20} is a well-known image segmentation technique, which is a region-based segmentation algorithm that attempts to divide images into regions based on predefined seed points, image intensity values, and certain termination (or similarity) criteria. Generally, a region starts as one seed point. Every neighbor point of the current region is examined and appended to the region if it satisfies a predefined similarity criterion. The region successively expands and the process continues until there is no neighbor point remaining that satisfies the similarity criterion. The selection of similarity criterions for region growing techniques relies on intensity thresholds, histogram analysis, gradient information, and/or other specific image information,^{18, 19, 20} which can facilitate the segmentation process. However, this method may encounter difficulties with images in which regions are both noisy and have blurred or indistinct boundaries. In addition, the grown region is highly dependent on the choice of seed points. Therefore, using the classic region-growing method and a fixed similarity criterion during the growing process cannot always produce optimal segmentation in many practical cases.

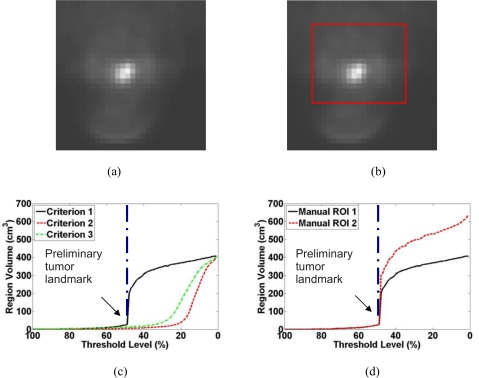
In this study, we proposed a novel and adaptive region growing method for automatically generating the preliminary boundary of a tumor region in PET. First, a rough volumetric ROI is defined by a radiation oncologist and encloses the desired tumor. The voxel having the highest intensity value within the rough ROI is chosen as the seed point for both the adaptive region growing algorithm and the dual-front active contour model. Notice that the seed point determined above does not depend on the size or shape of the rough ROI as long as it encloses the desired tumor. We designed a special similarity criterion $I(x,y,z)⩾T\times \mathit{\text{mean}}\left(R_0\right)$, $I(x,y,z)∊R^3$ [Criterion 1 shown in Fig. 1c], where $I(x,y,z)$ is the intensity of a neighboring voxel, $\mathit{\text{mean}}\left(R_0\right)$ is the mean intensity of the current grown region and it is recalculated whenever a new voxel is appended, T is a threshold level and varies from 100% to 0%. For each T, the region growing terminates when none of the surrounding voxels satisfies the similarity criterion. This criterion is different from those classical similarity criteria, such as $I(x,y,z)⩾T\times I\left(\mathit{\text{seed}}\right)$ [Criterion 2 shown in Fig. 1c], and $I(x,y,z)⩾T\times \mathit{\text{mean}}\left(\mathit{\text{seed}}\right)$ [Criterion 3 shown in Fig. 1c], in which mean(seed) represents the mean of the 26 neighbor voxels of the seed point. Especially, criterion 1 is based on the mean value of the region expending from the seed point, which is constantly undergoing change. However, criterion 2 and 3 are based on fixed mean values which do not change during the whole expanding process. Figure 1c illustrates the difference of the resulting regions by utilizing these three criteria on a same ROI region [shown as the red line in Fig. 1b]. Figure 1a, 1b are the same 2D slice of a real 3D PET image data set. As can be seen in Fig. 1c, for all these three criteria, when T varies from 100% to 0% in a step of 1%, the resulting regions and their volumes monotonically expand from a few voxels surrounding the seed point to the entire rough ROI. However, Fig. 1c also shows that there is a sharp increase in the volume at certain T value, especially when Criterion 1 is used. We presume that when this happens, the higher intensity tumor is growing into the background. The T value and the region just before the sharp volume increase can be identified by detecting the largest change in the volume between two consecutive T values. We designate this T value as the preliminary tumor landmark and the region as the preliminary tumor volume. Notice that the identified T is an adaptive threshold level that may vary for different images. It is, however, independent of the manually drawn rough ROI as demonstrated in Fig. 1d, where two different rough ROIs lead to the same landmark. According to all the tests we did in this paper, we conjecture that the landmark can be reproducibly identified for each image.

Figure 1.

Plot of the grown region volume as a function of the threshold level T for a PET of a patient with a head-and-neck tumor. (a) One slice of the 3D PET. (b) One example of manually drawn rough ROI on this slice. (c) Similarity criterion 1 generates a much sharper volume increase than the other two criteria. (d) Two different rough ROIs enclosing the same tumor lead to the same preliminary tumor landmark at $T=49\%$.

Dual-front active contours

In PET images, the tumor boundary is blurred because of strong partial volume effects. This may contribute to the fact that the preliminary tumor volume is slightly outside of the true tumor volume. Then we need to find a way to refine this preliminary tumor boundary and delineate the true tumor volume.

The dual-front active contour model²¹ is a novel, fast, and flexible dual front implementation of active contours, motivated by minimal path techniques²² and utilizing fast marching algorithms.²³ Its basic purpose is to minimize an energy function

$$E\left(C\right)={\int }_{\Omega }\{\omega +P\left(C\left(s\right)\right)\}ds={\int }_{\Omega }\tilde{P}\left(C\left(s\right)\right)ds$$ (1)

in order to find “a potential weighted global minimum partition curve” within an active region. In Eq. 1, s represents the arc-length parameter on a defined domain, $C\left(s\right)∊{\mathfrak{R}}^n$ represents a curve, $\Vert C^{\prime }\left(s\right)\Vert =1$, $E\left(C\right)$ represents the energy along curve C, P is the potential associated with image features (edges, gradients, or region-based features), ω is a real positive constant that controls the smoothness of the curve, and $\tilde{P}=P+\omega$.

Usually, tumors in PET images are blurred, and most likely they have irregular shapes. In our studies, it is observed that the preliminary boundary obtained from the adaptive region growing is slightly outside of the true boundary, and the true boundary always locates within the narrow region between the preliminary boundary and the seed point. The boundary refinement can therefore be treated as the problem to find the optimal minimal partition curve which minimizes certain energy functional in the above narrow active region. We use the dual-front active contour model to refine the preliminary tumor volume.

In order to solve the energy function 1, a minimal action map $U_{p_0}\left(p\right)$ is defined as the minimal energy integrated along a path between a starting point $p_0$ and a point p,

$$U_{p_0}\left(p\right)=\underset{A_{p_0,p}}{\inf }\left\{{\int }_{\Omega }\tilde{P}\left(C\left(s\right)\right)ds\right\}=\underset{A_{P_0,P}}{\inf }\left\{E\left(C\right)\right\},$$ (2)

where $A_{p_0,p}$ is the set of all paths between $p_0$ and p. $U_{p_0}\left(p\right)$ corresponds to the minimal energy integrated along a path starting from $p_0$ to p.

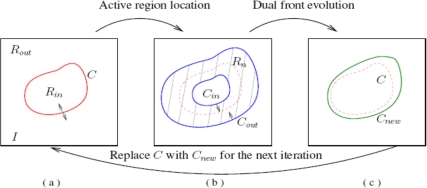
The basic principle of dual-front active contours is shown in Fig. 2. In Fig. 2a, an initial contour C separates image I to two regions $R_{\mathrm{in}}$ and $R_{\mathrm{out}}$. In Fig. 2b, a narrow active region $R_n$ is formed by extending the initial curve C. For example, it may be formed by dilating C with morphological dilation operators. $R_n$ has an inner boundary $C_{\mathrm{in}}$ and an outer boundary $C_{\mathrm{out}}$. As shown in Fig. 2c, the inner and outer boundaries $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ of $R_n$ are set as the initializations of two minimal action maps $U_{C_{\mathrm{in}}}$ and $U_{C_{\mathrm{out}}}$, which are defined by different potentials ${\tilde{P}}_{\mathrm{in}}$ and ${\tilde{P}}_{\mathrm{out}}$, respectively. When the level sets of $U_{C_{\mathrm{in}}}$ and $U_{C_{\mathrm{out}}}$ meet each other, the meeting points form a potential weighted minimal partition curve $C_{\text{new}}$ in active region $R_n$. The evolution of curves $C_{\mathrm{in}}$ and $C_{\mathrm{out}}$ and their meeting locations $p_g$ can be obtained using the “time of arrival” functions which satisfy the following Eikonal equations

$$\Vert \nabla U_{C_{\mathrm{in}}}\Vert ={\tilde{P}}_{\mathrm{in}}\text{with}{U}_{C_{\mathrm{in}}}\left(C_{\mathrm{in}}\right)=0,$$$$\Vert \nabla U_{C_{\mathrm{out}}}\Vert ={\tilde{P}}_{\mathrm{out}}\text{with}{U}_{C_{\mathrm{out}}}\left(C_{\mathrm{out}}\right)=0,$$$$U_{C_{\mathrm{in}}}\left(p_g\right)=U_{C_{\mathrm{out}}}\left(p_g\right)\text{on}{C}_{\text{new}}.$$ (3)

By setting appropriate potentials based on the information from the PET image, the potential weighted minimal partition curve can be close or equal to the intrinsic tumor boundaries. Since the dual front evolution tries to find the global minimal partition curve within an active region instead of the whole image, the degree of this globalness may be changed flexibly by adjusting the size of the active region.

Figure 2.

Iteration process of the dual-front active contour model.

As shown in Eq. 3, the dual-front evolution detects the meeting points of the level sets of two minimal action maps $U_{C_{\mathrm{in}}}$ and $U_{C_{\mathrm{out}}}$. These two minimal action maps may be computed by solving Eikonal equations $\Vert \nabla U_C\Vert =\tilde{P}$. In our algorithm, we use fast sweeping methods²⁴ to solve Eikonal equations, which is suited for computing the solution of Eikonal equations on a rectangular grid. The main idea of fast sweeping methods is to combine nonlinear up-wind differences and Gauss–Seidel iterations with alternating sweeping orders so that the causality along characteristics of all directions is followed in an optimal way. In fast sweeping methods, the characteristics are divided into a finite number of groups according to their directions and each sweep of Gauss–Seidel iterations with a specific order covers a group of characteristics simultaneously. $2n$ Gauss–Seidel iterations with alternating sweeping order are used to compute a first order accurate numerical solution for the distance function in n dimensions. Fast sweeping methods have an optimal complexity of $O\left(N\right)$ for N grid points, are extremely simple to implement in any dimension, and give similar results as fast marching methods. The details of fast sweeping methods may be seen in Ref. 24.

When using fast sweeping methods to implement the dual front evolution, there is no need to solve all Eikonal equations shown in Eq. 3 on the whole active region $R_n$ and then look for the set of $p_g$. The dual front evolution may be implemented by labeling initial curves with different labels and evolving the labeled curves with different potentials simultaneously until each point inside the active region is assigned a label. Dual-front active contours include the dual-front evolution and active region location. Normally morphological dilation is used to locate an active region from an initial curve. Because the low-computational cost of fast sweeping methods is maintained and the calculation of all minimal action maps can be finished simultaneously, the complexity of the dual-front evolution is still $O\left(N\right)$. Furthermore, the complexity of morphological dilation is lower than $O\left(N\right)$, and the boundary tracking process can be finished in finite iterations. So, the total complexity of dual-front active contours is still $O\left(N\right)$, where N is the number of grid points (on average) in an active region $R_n$. More details about the implementation of dual-front active contour models can be found in Ref. 25.

In this study, we first label all points on the preliminary tumor boundary as one front, and the seed point another. Then we use the dual-front active contour model to propagate the two fronts with different speed functions towards each other. The evolution stops at the meeting points forming the final tumor boundary, which is always inside the preliminary tumor volume. Here, we only ran one iteration dual-front active contour evolution because of the following two reasons. First, since the PET image has very blurred boundary, if the segmentation algorithm is applied multiple times to the same data, the active regions will be different for each iteration process and this could potentially lead to different segmentation results for a specific image. Second, how to decide the size of active regions and the difference level between the results from consecutive iterations is also a very challenging problem. As can be seen from the tests on various simulated and phantom data sets, the current settings can achieve satisfied delineation results. Because there is not well defined boundary in PET, we define a region-based speed function: $F(x,y,z)=1∕\tilde{P}=\lambda ∕(I(x,y,z)-\mu \mid +\omega )$, where F is the speed of point $(x,y,z)$ with intensity $I(x,y,z)$, μ is the mean intensity of all points having the same label as $(x,y,z)$, ω is an item which controls the smoothness of evolving curves. The term λ is an item which controls the weight of speed functions of the inner and outer fronts. In this study, we experimentally choose $\omega =10$ and $\lambda =5$ for the inner front evolution, $\omega =10$ and $\lambda =1$ for the outer front evolution.

Phantom experiment

Phantom study is a main part of evaluation in this article. Six spheres in a cylindrical container were used as target volumes (Fig. 3). To mimic clinical head and neck tumor sizes, the volumes of these six spheres are 20, 16, 12, 6, 1, and $0.5\mathrm{ml}$, respectively. To generate various source-to-background ratios, the spheres contained ${}^{11}\mathrm{C}$$(\text{half}\text{life}=20.38\min )$ solution as sources, while the cylindrical container contained ${}^{18}\mathrm{F}$-FDG $(\text{half}\text{life}=109.77\min )$ solution as the background. The phantom was scanned in a Biograph-40 True Point/True View (Siemens Medical Solutions Inc., Knoxville, TN) PET/CT scanner which has a $21.6\mathrm{cm}$ axial FOV and a detector ring of $84.2\mathrm{cm}$ diameter. The PET component of the camera is made of four rings of 48 Lutetium oxy-ortho silicate LSO detector blocks subdivided in an array of $13\times 13$ crystals of $4\mathrm{mm}\times 4\mathrm{mm}\times 20\mathrm{mm}$ thick. All images were acquired in 3D mode (no septa). Spatial resolution for a point source in the transversal direction was reported to be $4.5\mathrm{mm}$ (full width at half maximum) at $10\mathrm{mm}$ from the center of the field of view, and the axial resolution is $5.7\mathrm{mm}$. The sensitivity is $8.1\mathrm{cps}∕\mathrm{KBq}$$(300\mathrm{cps}∕\mu \mathrm{Ci})$ according to NU-2001 analysis. Scatter fraction is less than 35% and the peak noise equivalent count rate (NECR) for a uniform cylinder ($\text{diameter}=20\mathrm{cm}$, $\text{length}=70\mathrm{cm}$) is $161\mathrm{kcps}$ at an activity concentration of $31\mathrm{kBq}∕\mathrm{ml}$.²⁶

Figure 3.

Six spheres in a cylindrical container were used as target volume for the phantom study.

The initial ${}^{11}\mathrm{C}$ activity concentration is $3.627\mu \mathrm{Ci}∕\mathrm{ml}$ in the six spherical phantoms (sources) and the initial ${}^{18}\mathrm{F}$-FDG activity concentration is $0.224\mu \mathrm{Ci}∕\mathrm{ml}$ in the cylindrical phantom (background). The phantom was scanned continuously for $120\min$ in list mode. For each $2\min$ scanning duration, an image was reconstructed using the iterative Ordered Subset Expectation Maximization algorithm (OSEM) with Gaussian filters with a full width at half maximum (FWHM) of $5\mathrm{mm}$, which is our typical clinical reconstruction method. All 60 reconstructed images have the same voxel size of $4.0728\times 4.0728\times 2.027{\mathrm{mm}}^3$. The S/B ratio of each image was calculated using its time (middle time of the $2\min$ period), the initial activity concentrations, and half lives of ${}^{11}\mathrm{C}$ and ${}^{18}\mathrm{F}$. Because of the faster decay rate of ${}^{11}\mathrm{C}$ compared with ${}^{18}\mathrm{F}$-FDG, the 60 $2\min$ images had a range of source-to-background (S/B) ratios from about 16 to 0.5. We studied four groups of three images that have S/B ratios within $\pm 0.3$ of 15, 10, 5, and 2, respectively. The parameters in the dual-front active contour model were experimentally chosen by optimizing the results for spheres in the images with S/B ratio 10. The same set of parameters was then applied to delineate the six spheres one by one in each of the 12 images. The results were compared with the true sphere volumes.

For comparison, we implemented the iterative threshold method as proposed by Jentzen et al.¹⁵ Since we have four groups of three images that have S/B ratios within $\pm 0.3$ of 15, 10, 5, and 2, respectively, we first generated the calibrated threshold-volume curves at S/B ratios of 15, 10, 5, and 2 based on one image in each group, then applied the two-stage method and the iterative threshold method to the remaining eight images, which have S/B ratios within $\pm 0.3$ of the S/B ratios of each calibrated threshold-volume curve. Finally, we compared the segmentation results of these two methods.

Segmentation evaluation

In this study, we performed phantom experiments to quantitatively analyze the accuracy of our two-stage segmentation method, and explored the dependence of delineated volumes on S/B ratios, tumor sizes, reconstruction methods, and smoothing filters. The segmentation results were evaluated with three metrics: Volume detection errors $\left({\mathit{DE}}_v\right)$, diameter detection errors $\left({\mathit{DE}}_d\right)$, and volume overlap metric $\left(\mathit{OM}\right)$ of Dice similarity coefficient.²⁷${\mathit{DE}}_v$ and ${\mathit{DE}}_d$ are defined as,

$${\mathit{DE}}_v=\frac{A_{\mathrm{Det}}-A_{\text{True}}}{A_{\text{True}}}\times 100\%,$$$${\mathit{DE}}_d=\frac{D_{\mathrm{Det}}-D_{\text{True}}}{D_{\text{True}}}\times 100\%,$$ (4)

where $A_{\mathrm{Det}}$ is the detected volume of the true volume $A_{\text{True}}$, $D_{\mathrm{Det}}$ is the detected diameter of the true sphere diameter $D_{\text{True}}$. ${\mathit{DE}}_v$ and ${\mathit{DE}}_d$ consider only the volume or diameter difference without any information on the spatial relationship between the detected and true volumes. Differently, $\mathit{OM}$ is defined as

$$\mathit{OM}=2\cdot \frac{A_{\mathrm{Det}}\cap A_{\text{True}}}{A_{\mathrm{Det}}+A_{\text{True}}}\times 100\%,$$ (5)

which measures the spatial overlap between the detected volume $A_{\mathrm{Det}}$ and the true volume $A_{\text{True}}$. $\mathit{OM}$ approaches 1.0 when two volumes are identical and 0 when they share no overlapping voxels. In the following experiments, we use these metrics to evaluate the segmentation results quantitatively.

RESULTS

In this section, we validated the two-stage method on the phantoms. Also we compared it with the iterative threshold method. All the experimental results shown in this section were obtained from 3D volume processing directly.

Segmentation results on an example phantom

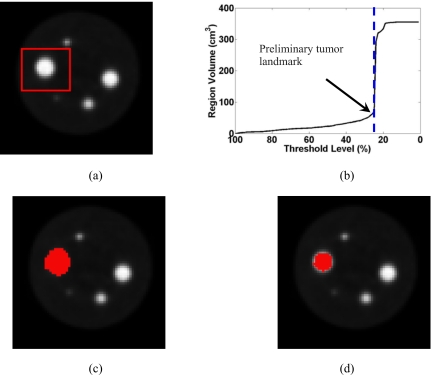
In Fig. 4, we show the segmentation result on one phantom PET image. The actual tumor volume is $20\mathrm{ml}$. The scan duration is $2\min$ and the S/B ratio is 15. The segmentation is reasonably accurate with $\mathit{OM}$ of 96.95%, ${\mathit{DE}}_v$ of $-6.2\%$, and ${\mathit{DE}}_d$ of $-2.0\%$ between the detected volume and the true volume.

Figure 4.

The segmentation result on a phantom PET image. (a) One slice of the original 3D PET image, (b) plot of the grown region volume as a function of the threshold level T, (c) the preliminary tumor volume defined at a threshold level of 25%, just before the sharp volume increase, (d) the result after running the dual-front active contour model.

Segmentation results as a function of S/B ratios

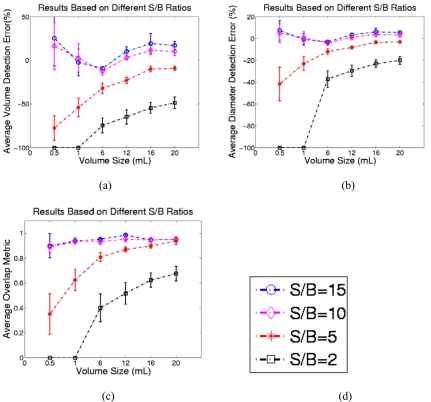
To illustrate the accuracy of the two-stage method as a function of S/B ratios, we tested it on those 12 phantom PET images with S/B ratios of 15, 10, 5, and 2 (see Sec. 2C). For each image, we applied the two-stage method to detect the six spheres one by one. Figure 5 shows the average volume and diameter detection errors and the average volume overlap between our results and the true sphere sizes. As expected, the segmentation is more accurate for higher S/B ratios or larger spheres. On images with S/B ratio of 10, for which the two-stage method was optimized, the best segmentation results were obtained with average $\mathit{OM}$ about 0.94, average ${\mathit{DE}}_v$ of 11.0%, and average ${\mathit{DE}}_d$ of 2.7%. On images with S/B ratio 2, the two-stage method generates the worst segmentation results with average $\mathit{OM}$ about 0.26, average ${\mathit{DE}}_v$ of $-79.0\%$, and average ${\mathit{DE}}_d$ of $-58.6\%$ for tumors larger than $10\mathrm{ml}$. The two-stage method failed to segment the two smallest spheres (0.5 and $1\mathrm{ml}$) on images with the lowest S/B ratio of 2 because the detected seed point (maximum point in the ROI) was outside the tumor region. Also, the detection results do not show significant differences between the two largest tumors (16 and $20\mathrm{ml}$) on images with S/B ratios greater than 5.

Figure 5.

(a) The comparison of the volume detection errors. (b) The comparison of the diameter detection errors. (c) The comparison of the overlap metric values between the delineation results on phantom PET images and the true tumor volumes under different S/B ratios 15, 10, 5, and 2. (d) The labels of different S/B ratios.

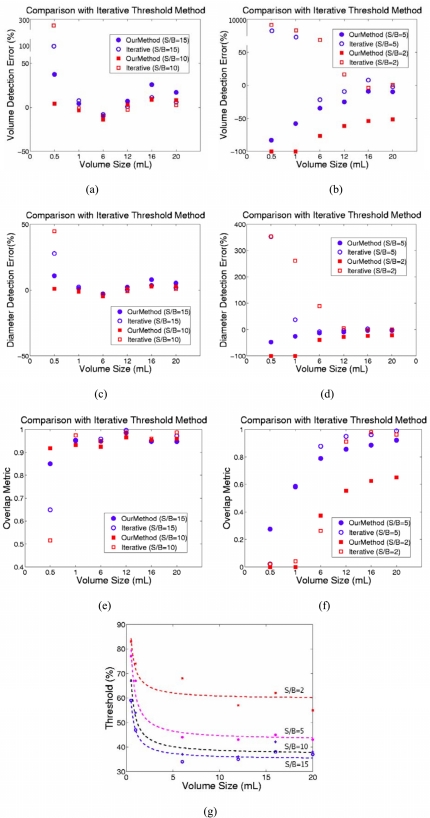
Comparison with iterative threshold method

As discussed in Sec. 1, an iterative threshold method has been proposed¹⁵ to improve the accuracy of results when compared with the fixed threshold method. For comparison, we tested our method and the iterative threshold method on those 8 PET images described in Sec. 2C. For each method and each S/B ratio, we calculated the average ${\mathit{DE}}_v$, ${\mathit{DE}}_d$, and $\mathit{OM}$ of the results on two PET images. Figures 6a, 6c, 6e show the comparison between our two-stage method and iterative threshold method on images with S/B ratios 15 and 10. Figures 6b, 6d, 6f show the comparison between the two-stage method and the iterative threshold method on images with S/B ratios 5 and 2. Figure 6g shows the calibrated S/B-threshold-volume curves related to different S/B ratios 15, 10, 5, 2. As can be seen in Fig. 6, on images with different S/B ratios, the iterative threshold method can obtain slightly better results than our method for phantom targets larger than $6\mathrm{ml}$. However, for smaller tumors with volume sizes less than $1\mathrm{ml}$, the iterative threshold method obtained much worse results than that from the two-stage method. The reason is that on images with such low S/B ratio, small tumors do not have higher intensity values than the background, therefore, the iterative threshold method will detect all the points having highest intensity in the whole ROI region as the tumor volume.

Figure 6.

(a) and (b). The comparison of the volume detection errors, (c) and (d). The comparison of the diameter detection errors, (e) and (f). The comparison of the overlap metric values, between the delineation results from the two-stage method and the iterative threshold method on images with different S/B ratios 15, 10, 5, 2. (g) The calibrated S/B-threshold-volume curves related to different S/B ratios 15, 10, 5, 2.

Independence of initial rough ROIs

As described in Secs. 2A, 2B, the two-stage method is independent of the size and shape of the initial ROIs. In order to verify this property and to evaluate the reproducibility of the two-stage method, the method was applied ten times on two different phantom images, but with a different randomly selected initial ROI each time. These segmentations, when compared to each other and their ground truth using the $\mathit{OM}$, ${\mathit{DE}}_v$, and ${\mathit{DE}}_d$ measurements, always give identical results. This test verified that the final segmentation results are independent of the initial rough ROIs.

Segmentation results on a patient tumor

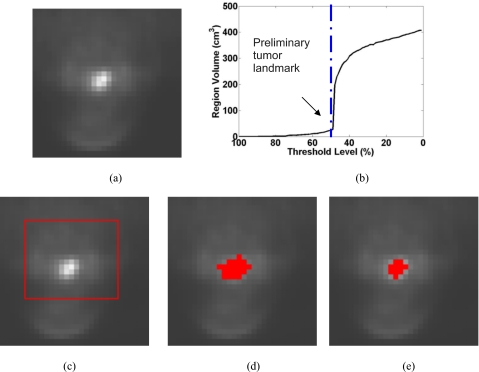
We also tested the described tumor segmentation method on a head-and-neck patient. Figure 7 shows the result on one clinical PET image of a patient with newly diagnosed cancer in the supraglottic region. The image size is $128\times 128\times 109$ with a pixel spacing $5.5\mathrm{mm}\times 5.5\mathrm{mm}$, and slice thickness $3.375\mathrm{mm}$. The tumor does not have spherical shape. The final result is deemed reasonably accurate through visual appraisal by two experienced head-and-neck radiation oncologists. Since our method is based on solving Eikonal equations and finding the minimal partition curve in a narrow active region, the final tumor volume is independent of the shape of the preliminary tumor volume, which is quite different from morphological erosion operators. More importantly, the result is reproducible and does not depend on the initial ROI selection.

Figure 7.

The segmentation result on a clinical PET head-and-neck tumor image. (a) One slice of the original 3D PET image, (b) plot of the grown region volume (in voxel) as a function of the threshold level T, (c) the manual drawn ROI, (d) the initial tumor volume defined at a threshold level of 49%, just before the sharp volume increase, (e) the final result after running the dual-front active contour model.

DISCUSSION

In this study, we proposed and evaluated with phantoms and clinical data, a semiautomatic two-stage PET tumor delineation method based on the adaptive region-growing algorithm and the dual-front active contour model. The entire process of the proposed method is adaptive to each image and independent of the manually drawn rough ROIs. Two steps of the two-stage method can provide refined results. In the first step, our method can provide appropriate threshold levels from the adaptive region-growing algorithm for different images, and generate the preliminary tumor volumes which are slightly outside of the true tumor sizes. The second step can refine the preliminary results and yield more accurate results. The purpose of the first step is to guarantee a consistent preliminary result when having different initial ROIs. Furthermore, since the preliminary volume is only slightly bigger than the actual tumor, it gives a better initialization for the dual-front evolution so that more accurate results are generated than directly using the initial subjectively drawn ROI as an input to the dual-front active contour model. As can be seen in Fig. 1d, the preliminary tumor volume is independent of the size and shape of the rough ROIs, thus it is reproducible. In the second step, with a set of predefined parameters for the dual-front active contour model, the result is also reproducible. As such, this strategy guarantees the reproducibility of the whole process.

As introduced in Sec. 1, when using threshold methods for tumor delineation, the estimated tumor volume depends on the threshold level chosen. The result is very sensitive to the threshold level, particularly for small tumors. In this article, the higher accuracy of the two-stage method on testing small tumors is demonstrated through the comparison with the iterative threshold method on images with four different S/B ratios 15, 10, 5, and 2. As revealed in Fig. 6, for small tumors with volume sizes less then $1\mathrm{ml}$, the iterative threshold method obtained much worse results than that from the two-stage method. Although on images with high S/B ratios 10 and 15, the iterative threshold method can obtain slightly better results than our method for tumors with volume size larger than $6\mathrm{ml}$, the detection accuracy of the iterative method is strongly dependent on the accuracy of the calibrated S/B-threshold-volume curves and the accuracy of the estimated S/B ratio of the detected image. However, for images with lower S/B ratios, it is difficult to estimate accurately the S/B ratios only with the image information. Furthermore, it is also very difficult to estimate the S/B ratios on complex patient data. Compared with this, the two-stage method has distinct advantages on detecting small tumors and is independent of the scanner properties. Also, the two-stage method has the advantages of reproducibility and convenience when compared to the iterative threshold methods. The two-stage method may obtain different threshold levels automatically from the adaptive region-growing algorithm in the first stage for different processed images. In the second stage, with a set of predefined parameters for the dual-front active contour model, the result is also reproducible. In addition, we provided a very convenience way for radiation oncologists to manually draw a rough ROI that encloses the desired selected tumor. The oncologist only need to mark the location of the up-left point and the right-bottom point of the desired ROI on the processed 3D image, then the ROI will be drawn automatically. The experimental results show that the two-stage method is successful in segmenting the simulation and phantom data sets, and is able to differentiate tumors from other structures or background.

In Fig. 5, we showed the effect of different S/B ratios on the segmentation results. In summary, the detection errors are higher for smaller spheres in images with lower S/B ratios. For the detection of tumors with the same size, the higher the S/B ratio is, the more accurate the result is. One of the main reasons is that the speed functions of the dual-front active contour model are only based on the image information. When the S/B ratio is low, the images are very noisy, and the detection accuracy will be affected. Furthermore, when the S/B ratio is 2, the two-stage method cannot detect the tumors with volume sizes less than $1\mathrm{ml}$. We think the main reason is still because the PET images reconstructed under such low S/B ratios are very noisy. Therefore, after choosing an initial ROI region, the seed point (maximum point in the ROI) was outside the actual tumor region. Currently, for all the tests in this study, we did not use any preprocessing de-noising techniques. One of the on-going researches is to apply image de-noising methods to improve the image quality and to increase the accuracy of the two-stage method. Furthermore, in the current study, when a contour passes through a voxel, the whole voxel is considered as the detected tumor volume. This is also a possible reason that for smaller spheres, the detection errors and standard deviations are higher.

Figure 5 shows a trend that the algorithm performance is better for bigger tumors. It is also observed that when S/B ratios are 15 or 10, the detection results for the two largest tumors (16 and $20\mathrm{ml}$) do not show significant differences. It seemed that when S/B ratios are higher than a certain level, the average overlap metric and detection errors for tumors larger than a certain size would be a constant.

Generally, there are several possible reasons for the segmentation errors. First, the partial volume effect plays a big role in small tumors causing a systematic shift in the SUV, which cause the segmentation errors. Second, for some images, the image intensity contrast between the tumor and its background is very low. Third, since the image resolution is poor in PET, the inherent digitization error is large. Furthermore, for the two smallest spheres, they occupy only 2–3 voxels in images. So even if there is only 1 or 2 voxel difference between the detected volume and the true volume, the overlap metric value will be very low. Fourth, we used the same parameter in the dual-front evolution, which might not be the optimal parameter for all the tested images. Further research needs to explore the effect of each factor on the results, and also focus on finding more optimal parameters.

The segmentation parameters used in the two-stage segmentation, especially in the potential definition of the dual-front active contour model, are empirically derived to produce optimal segmentation results. In fact, items ω and λ are the parameters for adjusting potentials and controlling the smoothness of the final obtained boundary. The best or most appropriate values for these parameters have to be chosen for different classes of images. In this study, we have tuned the parameters based on the tests on images which were reconstructed by OSEM methods with $5\mathrm{mm}$ Gaussian filter, and have S/B ratio 10 experimentally. And then we used the same parameters for all images. Figure 5 showed that by choosing these parameters, the two-stage method underestimated tumors on images with lower S/B ratios 5 and 2. The reason is related to the choice of speed functions of dual-front active contour model. Because the images have different S/B ratios and are reconstructed by different methods, it is impossible to get optimized results on all images by using only one set of parameters. We will work on separately tuning these parameters for different groups of images and proposing more appropriate speed functions not only based on image information but also on other imaging properties such as SUV values, activity concentrations, and point spread functions.

CONCLUSIONS

With the hope to develop an adaptive, reproducible, and accurate tumor delineation method in PET, a two-stage method was proposed in this article. It results from the integration of the adaptive region-growing algorithm and the dual-front active contour model. The two-stage method was tested and evaluated on various phantom and clinical images. Furthermore, for all the tests, we used the same potential (speed) function. A cylindrical container with six sphere phantoms of varying volumes $(0.5–20\mathrm{ml})$ was constructed and scanned. The performance of the two-stage method was evaluated, and the effects of different S/B ratios and tumor sizes on the result accuracy were analyzed. The comparison between the two-stage method and the iterative threshold method was also provided and illustrates the advantages of the two-stage method. Experimental results show that this two-stage method can provide accurate, smoothed segmentation results of medical images. We will further test this novel technique on patients with head-and-neck cancer. We expect to utilize this technique to facilitate target definition in radiation therapy planning.