Abstract
The plasma membrane electrical activities of neurons that secrete gonadotropin-releasing hormone (GnRH) have been studied extensively. A couple of mathematical models have been developed previously to explain different aspects of these activities. The goal of this article is to develop a single model that accounts for the previously modeled experimental results and some more recent results that have not been accounted for. The latter includes two types of membrane potential bursting mechanisms and their associated cytosolic calcium oscillations. One bursting mechanism has not been reported in experiments and is thus regarded as a model prediction. Although the model is mainly based on data collected in immortalized GnRH cell lines, it is capable of explaining some properties of GnRH neurons observed in several other preparations including mature GnRH neurons in hypothalamic slices. We present a spatial model that incorporates a detailed description of calcium dynamics in a three-dimensional cell body with the ion channels evenly distributed on the cell surface. A phenomenological reduction of the spatial model into a simplified form is also presented. The simplified model will facilitate the study of the roles of plasma membrane electrical activities in the pulsatile release of GnRH.
Introduction
The regulation of reproductive function is controlled by a pulsatile signal of gonadotropin-releasing hormone (GnRH). In rhesus monkey, GnRH pulses with a period of ∼1 h are both necessary and sufficient for sexual maturation and fertility (1). GnRH is synthesized and secreted by a few hundred GnRH neurons that collectively produce the pulsatile rhythm with a species-specific period ranging from 30 min to ∼1 h. This is achieved with few synaptic connections between GnRH neurons (2). Observations of the calcium oscillations in placode-derived GnRH neurons suggest that their plasma membrane electrical activities are not synchronized most of the time except for a brief period of a few minutes once per hour in rhesus monkey (3) and once per 20 min in mice (4). A recently proposed mechanism for GnRH pulsatility, autocrine regulation, was revealed in cultured hypothalamic tissue (5), placode-derived GnRH neurons (6), and immortalized embryonic GnRH neurons (7,6) and mathematically modeled in the literature (8,9). This study is aimed at developing a mathematical model of reduced complexity that describes the plasma membrane (PM) electrical activities and calcium handling of a GnRH neuron, with an emphasis on second messenger signaling and Ca2+ oscillations. This will facilitate the integration of this model to models of other parts of the GnRH neuron that we believe are directly responsible for the generation of the GnRH rhythm.
Two pioneering physiological models of the electrical activities of GnRH neurons have been developed (10,11). The first was aimed at modeling the ionic basis of action potentials (APs), whereas the second was focused mainly on the responses of an isolated GnRH neuron to a variety of pharmacological stimuli. The two models are not identical and exhibit qualitatively different bifurcation structures. As a result, the second model does not reproduce all the results of the first one for the published set of parameter values. We here construct an integrated and simplified version of the calcium dynamics and electrical activities of GnRH neurons. The new model is capable of consistently reproducing all the experimental results explained previously, as well as some important recent experiments the previous models did not reproduce.
This model contains a reduced number of ionic currents and gating variables. The intracellular calcium compartments number is reduced from four to two, and a more realistic description of Ca2+ dynamics is adopted, including the diffusion of Ca2+ inside both the endoplasmic reticulum (ER) and cytosolic spaces. This gives rise to a system of two partial differential equations (PDEs) describing the cytosolic and ER Ca2+ concentrations ([Ca2+]i and [Ca2+]ER) with time-dependent boundary conditions. The addition of ER Ca2+ release through a realistic model of IP3 receptor (IP3R) channels allows for the occurrence of IP3-dependent [Ca2+]i oscillations, such as those recently observed in mature GnRH neurons (12). The model also predicts another type of bursting that involves the store-operated Ca2+ current (ISOC). We propose a phenomenological simplification of the PDE model into a model described by a system of ordinary differential equations that retain the important features of the PDE model.
Experimental Observations to be Reproduced
A list of experimental observations that the model is aimed at reproducing is presented below (E1–E5):
-
E1.
An unstimulated GnRH neuron often exhibits spontaneous firing of narrow, Na+ current-dominated APs at frequencies between 0.5 and 1 Hz. A depolarizing current injection triggers higher frequency spikes with decreased amplitudes (reduced peaks and elevated baselines), broader width, and higher Ca2+ entry (10,13,14).
-
E2.
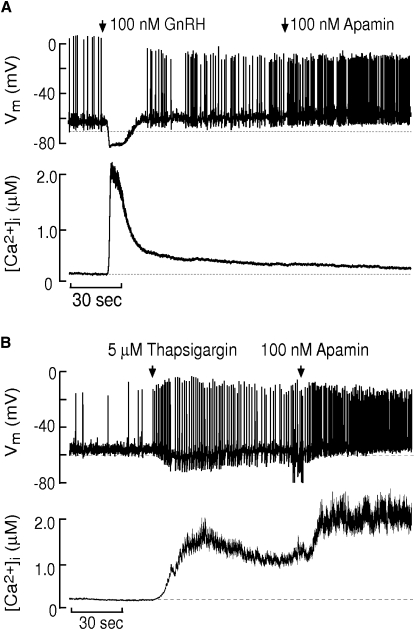
A large dose of GnRH induces a broad pulse of Ca2+ release from the ER (Fig. 1 A). The response is divided into two phases. The first is characterized by a transient hyperpolarization of ∼14 mV that lasts ∼15 s. Apamin and calcium buffers abolish this hyperpolarization, suggesting that the small-conductance and calcium-sensitive K+ channels (SK) are responsible (11,13,15). The second phase is characterized by a [Ca2+]i plateau and increased AP firing frequency relative to prestimulus levels, most likely due to enhanced store-operated Ca2+ entry (SOCE) (11,15).
-
E3.
Thapsigargin (Tg), an inhibitor of the sarco- and ER calcium ATPase (SERCA), causes a slow increase in [Ca2+]i. The AP firing rate transiently increases then decreases before ultimately rising to a level much higher than prestimulus levels (Fig. 1 B). This increase in frequency is best explained by enhanced SOCE (11,15). The deepened after hyperpolarization (AHP) after each spike is due to SK currents since apamin abolishes it, resulting in even higher AP frequency (15). These SK-dependent AHPs clearly indicate that SK channels respond to Ca2+ signals that vary as rapidly as the membrane potential, and not the whole-cell Ca2+ concentration ([Ca2+]).
-
E4.
Activation of adenylyl cyclase by forskolin increases AP firing rate (11,14) and causes cytosolics Ca2+ accumulation of up to a few hundred nM (16,17).
-
E5.
Burst firing patterns with variable burst durations (∼1–20 s) have been reported in GnRH neurons (2,18–20). Spontaneous [Ca2+]i oscillations have also been observed (3,4,12,21). In GT1 neurons, these oscillations are characterized by 1–30 s duration, 3–120 s period, and 100–350 nM amplitude (21). Recently, IP3-dependent [Ca2+]i oscillations have also been reported (12).
Figure 1.
Simultaneous recording of V and whole-cell [Ca2+] of GT1 neurons after the application of (A) GnRH followed by apamin; and (B) Tg followed by apamin. Modified from Van Goor et al. (15). (Original artwork kindly provided by Stanko Stojilkovic. Copyright (1999) National Academy of Sciences, U.S.A.)
Our model is capable of reproducing all the observed experimental results listed above. E1–E4 are reproduced with mechanisms similar to those proposed by LeBeau et al. (11). E5 occurs as a direct consequence of the mechanisms already present in the model. Therefore, modeling results related to E5 should be regarded as model predictions until the underlying mechanisms are confirmed or rejected by experiments.
The Model
Based on the two previous models, we aim to construct an integrated model with more-realistic Ca2+ dynamics and a reduced number of currents and gating variables. The rapid time-variation in apamin-sensitive AHPs suggests that SK channels follow variations of [Ca2+]i near the PM (shell [Ca2+]), but not the bulk [Ca2+] in the whole cell. These fast time-variations of [Ca2+]i occur because Ca2+ only enters the cell across the PM and then slowly diffuses into deeper parts of the cell. LeBeau et al. (11) achieved the separation between the shell and the bulk [Ca2+] by splitting the cytosol and the ER each into two distinct compartments, giving rise to a four-compartment model for intracellular [Ca2+]. This model reproduced fast variations of the shell [Ca2+] during APs. However, owing to the hypothesized diffusive coupling between the shell and the bulk compartments, the contribution of the total amount of Ca2+ entry on the bulk [Ca2+] is not correctly accounted for.
Fig. 2 shows a schematic diagram of this model. We consider a single spherical soma with two compartments only—the cytosol and the ER. Both compartments are assumed to exist at every space point inside the cell, giving rise to a bidomain model (for details, see (22)). At the PM, electrical activity drives Ca2+ ions into the cytosol through Ca2+ channels, whereas Ca2+ ions are extruded by the plasma membrane Ca2+ ATPases (PMCAs) and sodium-calcium exchangers (NCXs). There is no direct path for Ca2+ to enter the ER from the extracellular space. The cytosol and ER are separated by the ER membrane, which contains IP3R channels, SERCAs, and a nonspecific calcium leak. This approach retains a correct account of the amount of Ca2+ entry into the cell and generates a realistic [Ca2+] profile in the whole cell including the shell area. It also eliminates the arbitrariness of introducing two coupling constants between the bulk and shell compartments. Parameters and functions not listed here are defined in detail in the Supporting Material. The Ca2+ dynamics are governed by the PDEs and boundary conditions,
| (1) |
| (2) |
| (3) |
where C and Ce represent the [Ca2+]i and [Ca2+]ER, respectively, and are functions of spatial location and time. The local flux densities jrel and jref, describe Ca2+ release from the ER through the IP3R channel and a passive leak and the uptake into the ER by SERCAs, respectively. The IP3R channels are modeled based on the Li-Rinzel formulation of the De Young-Keizer model (23). The fluxes jin and jout represent Ca2+ entry and extrusion at the PM. jin is determined by three ionic currents: ICaL, ISOC, and INSC, which are described in Supporting Material. Notice that Ca2+ influx and efflux at the PM are treated as the boundary conditions. By assuming spherical symmetry, the PDEs are reduced to a quasi-one-dimensional model with the radius r as the spatial variable. This approach has been adopted previously in a model of PM electrical activities in pituitary gonadotrophs (24).
Figure 2.
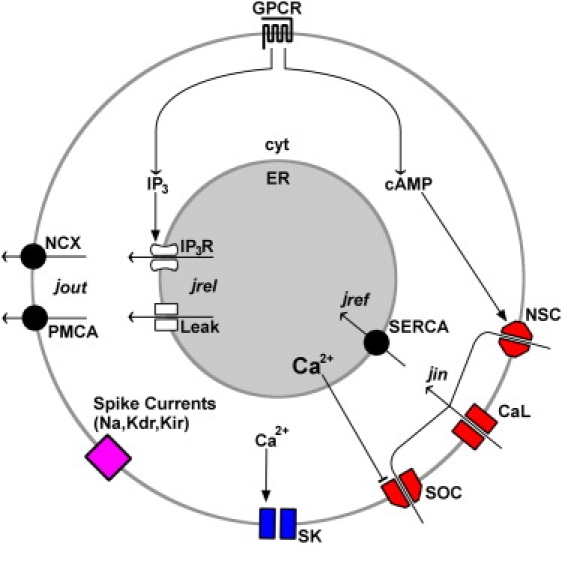
Diagram of the model. G-protein coupled receptors (GPCR) alter intracellular levels of IP3 and cAMP. IP3 activates Ca2+ release from the ER via IP3R channels (IP3R), and cAMP activates nonspecific cation (NSC) channels. Cytosolic Ca2+ activates SK channels, and ER Ca2+ inhibits SOC channels. The direction of the Ca2+fluxes jin, jout, jref, and jrel are indicated with arrows. See The Model section for more details. Na, TTX-sensitive Na+ channel; Kdr, delayed rectifier K+ channel; Kir, inward rectifier K+ channel; and CaL, L-type Ca2+ channel.
Buffering in the cytosol and ER is rapid and is accounted for by scaling the calcium fluxes by fcyt or fER, the fraction of free calcium ions in the cytosol and ER, respectively (both 0.01in this study). D and Do are the Ca2+ diffusion coefficients in the cytosol and a buffer-free medium (15 and 300 μm2 s−1 (25)), and DER is the Ca2+ diffusion coefficient in the ER (1 μm2 s−1). In this model, the shell [Ca2+] is represented by CR = C(r, t)|r=R, and the whole cell [Ca2+]c is represented by the spatial average of C(r, t), . Cav best approximates the [Ca2+]i levels that are observable experimentally by whole-cell calcium imaging.
The membrane electrical activity is governed by
| (4) |
Here, INa is a TTX-sensitive Na+ current, ICaL is an L-type Ca2+ current, IK is a delayed rectifier K+ current, Iir is an inward rectifier K+ current, and ISK represents a small-conductance calcium-activated K+ current. Iapp is zero unless otherwise stated. INSC represents a cAMP-activated, nonspecific cation current that replaces Id in LeBeau et al. (11). The latter includes calcium-dependent inactivation and time-dependent gating, which we found to be unnecessary for reproducing the desired results. The effector of the adenylyl cyclase pathway on membrane excitability is unknown. We here assume that the conductance of INSC is a cAMP-dependent constant and is independent of [Ca2+]i (see Supporting Material for details). ISOC represents a store-operated calcium current that is inhibited by high Ce(R). The molecule responsible for sensing [Ca2+]ER during SOCE is STIM1, and the interaction of STIM1 with pore-forming proteins at the membrane is required for SOCE (for a review, see (26)). For simplicity, we neglect these details of the mechanism for SOCE, and assume that ISOC is activated as the reciprocal of a Hill function of Ce(R) with a Hill coefficient of 4. A direct consequence of a smooth functional dependence of ISOC on Ce(R) is that, at equilibrium, there is always a residual level of ISOC that influences the spiking activity. Such a residual level of ISOC can be reduced by making the sigmoidal Hill function steeper. The currents in Eq. 4 are qualitatively similar to the corresponding currents in previous models, although INa and INSC are expressed in simpler forms. We omitted the M-type K+ channel and T-type Ca2+ channel since, although they have been shown to exist in these neurons, they turned out to be nonessential for the results presented here.
Results
Responses to current injections
The model exhibits spontaneous low frequency spiking (∼0.7 Hz) with AP amplitude of ∼75 mV and duration of ∼9 ms (Fig. 3). With 5 and 15 pA depolarizing current injection, amplitude decreased from 75 mV to 62 and 44 mV, frequency rose to 15 and 22 Hz, and duration rose to 12 and 15 ms, respectively (Fig. 3, A and B). The amount of Ca2+ entry per spike is increased as the spike width increases (data not shown). These results are consistent with the observations described in E1.
Figure 3.
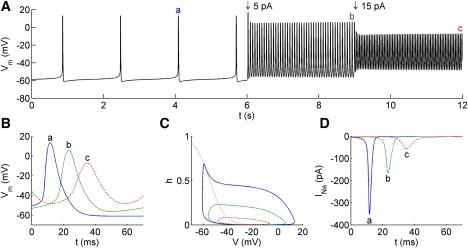
(A) Membrane potential response to current injections. (B) Membrane potential waveforms, (C) inactivation gating variable h, and (D) INa for selected spikes labeled a–c in panel A. Note that in panel C, h is plotted as a function of V, so that h travels clockwise during each spike.
The mechanism underlying the depolarization-induced shift from narrow Na+-dominated to broader Ca2+-dominated spikes is often encountered (see, e.g., (10).). During spikes at elevated baseline potential, Na+ channels do not have time to recover from inactivation. This reduces the relative contribution of the INa in spike generation. To achieve this result, a Hodgkin and Huxley-like model of INa is sufficient. The inactivation variable for INa, h, is plotted in Fig. 3 C as a function of the membrane potential. During the course of an AP, h travels clockwise along the trajectories. In spontaneous APs, h is high during the rising phase, indicating high recovery from inactivation. In the presence of a depolarizing current, less time is spent in a hyperpolarized state and the value of h during the rising phase of the APs is reduced. As a result, there is a two- and fivefold reduction in INa when 5 and 15 pA of current is injected, respectively (Fig. 3 D).
Responses to GnRH
The voltage and calcium responses of GnRH neurons to GnRH stimulation outlined in E2 are reproduced by the model (see Fig. 4). GnRH application is modeled as a global rise in IP3 concentration from 0.01 μM to 1 μM with an exponential time course, as described in the caption of Fig. 4. Such a rise in IP3 causes Ca2+ release from the ER stores everywhere in the cell (Fig. 4 C). The rising phase in [Ca2+]i is due to the fast activation of IP3R channels by IP3 and [Ca2+]i. As [Ca2+]i increases, SK channels are activated resulting in a ∼15 mV hyperpolarization in membrane potential (Fig. 4 A). Falling ER Ca2+ levels gradually activate ISOC (Fig. 4, B and D), and shortly after the initial hyperpolarization, the net current switches from outward to inward. This causes a gradual depolarization of the membrane potential. As [Ca2+]i increases, the inactivation of the IP3R channels catches up, leading to the eventual peak and decline of [Ca2+]i. The net current at the cell surface remains inward and small, maintaining the slow rise in membrane potential. This eventually leads to the resumption of AP firing and the beginning of the second phase of the GnRH response described in E2.
Figure 4.
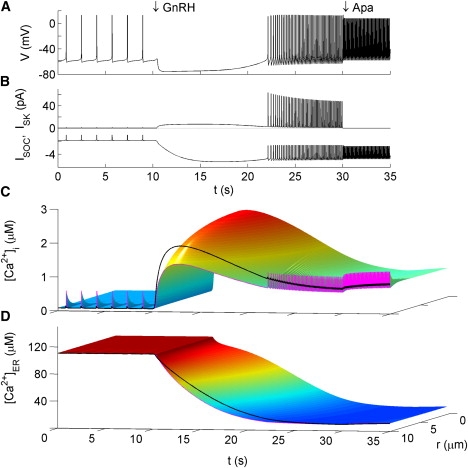
Model response to GnRH and apamin. GnRH is modeled as an exponential increase in IP3 from 0.1 to 1 μM following the expression: x(t) = xfinal − (xfinal − xinitial)exp(– (t – tonset)/τx), where x represents IP3 in this case, with τx = 5 s. Apamin (Apa) is modeled by setting gSK to zero at t = 30 s. (A) Membrane potential. (B) Ca2+-sensitive currents ISK (upper trace) and ISOC (lower trace). (C and D) Spatio-temporal profiles of [Ca2+]i and [Ca2+]ER, respectively. The spatial average of [Ca2+] (Cav) and the [Ca2+]i at the membrane CR are overlaid as thick black and thin magenta curves, respectively. In panels C and D, r = 0 is the cell center and r = 10 is the cell surface. Hot and cold colors represent, respectively, high and low concentrations on the color surfaces.
At elevated IP3 levels, the IP3R channels remain open, preventing the ER from refilling. As a consequence, Ca2+ gets extruded from the cell by PMCAs and the NCXs. Resumption of AP firing provides a source of Ca2+ entry, yielding a [Ca2+]i plateau level that is higher than prestimulus levels. At this point ISK activation has dropped from its peak level. Since [Ca2+]ER stays at a depleted level, ISOC remains high. This results in an increased net inward current, which causes the increased AP firing rate. Since the Ca2+ plateau is higher than prestimulus levels, ISK contributes to keeping the firing rate in check. Application of apamin during this phase yields a further increase in firing rate and drives [Ca2+]i to a level slightly above the GnRH-induced [Ca2+]i plateau (Fig. 4 C).
Voltage-gated calcium entry during each AP results in brief rises in [Ca2+]i near the membrane up to an amplitude of ∼0.5 μM. The [Ca2+]i profile at the membrane (thin magenta curve in Fig. 4 C) closely follows the AP profile, whereas the change in Cav is slower and with smaller amplitude (thick black curve). This is because the Ca2+ ions that enter the cell during an AP are strongly absorbed by buffers and the ER store everywhere inside the cell. As a result, these [Ca2+]i transients are strongly localized near the membrane. Note that CR is larger than Cav during each AP, whereas CR is smaller than Cav between APs due to the action of PMCAs and NCXs on the cell surface. Such compartmentalized [Ca2+]i signals are generated naturally in the spatio-temporal model.
In cells pretreated with apamin, the application of GnRH causes a cessation of firing but no hyperpolarization (11,15). This feature was explained by invoking Ca2+-dependent inhibition of Id in LeBeau et al. (11), but other possible explanations exist. One explanation is an incomplete block of SK channels by apamin. This can be achieved in our model by decreasing gSK to 5% of its original value (data not shown). Another possibility is that there exists a population of Ca2+- or GnRH-activated potassium channels that are insensitive to apamin. Examples of such channels shown to be present in GnRH neurons include BK channels (27), GIRK channels (14), and M-type potassium channels (28). As our goal is to obtain a model of reduced complexity, we do not consider such mechanisms here.
Responses to thapsigargin
When the effect of Tg is modeled, simulations show an immediate rise, followed by a transient drop, and ultimately a gradual rise in firing frequency (Fig. 5 A), consistent with observation in Fig. 1 B. These changes can be explained by the sequential activation of ISOC and ISK. Since the threshold for activating ISOC is reached more rapidly than that for activating ISK, the initial transient behavior after Tg application is an increase in firing rate. During the brief period that follows, the increase in ISK is more rapid than the increase in ISOC, causing a decrease in firing rate. Each AP now significantly activates SK channels, yielding the deep AHPs. Then, ISK reaches a plateau as CR reaches a plateau, wheras ISOC continues to increase. This results in the long-term increase in AP firing rate. The occurrence of deep AHPs after each spike despite the relatively smooth rise in Cav (thick black curve, Fig. 5 C) is a clear indication of the rapid, localized effect of voltage-gated calcium influx near the membrane.
Figure 5.
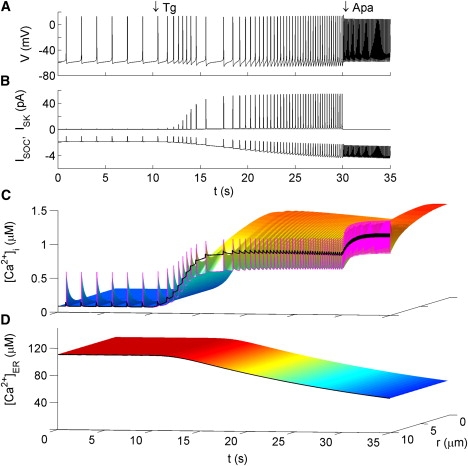
Model response to Tg and apamin. Tg is modeled by exponentially reducing the value of the SERCA pump rate νe from 1.3 μm μM ms−1 to zero with τ = 1.2 s using the expression for x(t) given in the Fig. 4 caption. Apamin is modeled by setting gSK to zero. Figure formatting is the same as in Fig. 4.
Responses to forskolin
Application of forskolin is modeled by an increase in INSC, which causes a rise in firing rate (Fig. 6 A). There exists a notable difference between the present result and that in Le Beau et al. (11). In their model, forskolin causes no observable accumulation of Ca2+ in the cytosol or ER, whereas in our model, there is a forskolin-induced increase in [Ca2+]i and [Ca2+]ER. This result is consistent with the experimentally observed effect of forskolin on [Ca2+]i in GT1 neurons (see E4). Although the increase in [Ca2+]i is modest, there is a significant overload of Ca2+ in the ER due to SERCA activity. Fig. 6 D shows that this effect is most profound in the region just underneath the PM. Such an overload of the ER reduces membrane excitability by reducing ISOC. This becomes obvious when forskolin is removed; a hyperpolarization of ∼5 mV occurs and persists until store Ca2+ leaks back to prestimulus levels, at which time spiking resumes (∼90 s; not shown). Such a hyperpolarization is a direct consequence of having a residual level of ISOC at the unstimulated state. Diffusion acts to spread the incoming Ca2+ into the cell, reducing the [Ca2+]ER at the membrane and thus reduces this effect. Indeed, the hyperpolarization is maximal when DER is set to zero (data not shown). The same behavior occurs when a current injection is terminated. Thus, the model predicts an apamin-insensitive mechanism for long-lasting AHPs in cells that have some ISOC activated spontaneously.
Figure 6.
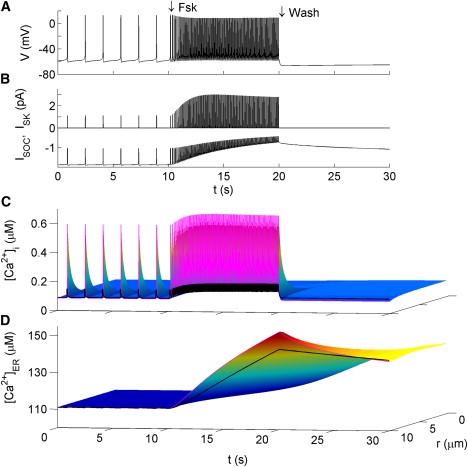
Model response to Forskolin (Fsk). Fsk is modeled by exponentially increasing in cAMP to 1 μM with τ = 1.2 s following the expression for x(t) given in the Fig. 4 caption. Washout of Fsk is modeled by instantaneously returning cAMP to prestimulus levels. Figure formatting is the same as in Fig. 4.
Bursting mechanisms
The model predicts at least two qualitatively distinct types of membrane potential bursting and the associated Ca2+ oscillations. The inclusion of IP3R channel dynamics, with fast activation and slow inactivation by [Ca2+]i, allows for the possibility of IP3-induced [Ca2+]i oscillations. The amplitude, duration, and frequency of such oscillations can be controlled by tuning Ca2+ handling parameters. Due to the presence of SK channels, IP3-induced [Ca2+]i oscillations periodically hyperpolarize the membrane potential, giving rise to a bursting pattern (Fig. 7). The bursting is therefore a periodic disruption of an otherwise continuously spiking state. Application of apamin (modeled by setting gSK to zero) prevents the periodic hyperpolarization, thus abolishing this mode of bursting (data not shown). In that case, the hyperpolarization is replaced by periods of increased firing rate caused by increased ISOC. Note that the firing rate during each burst is significantly higher than prestimulus levels and increases from one burst to the next. This is caused by the gradual depletion of the ER and the associated increase in ISOC. Fig. 7 shows an example of oscillations with ∼8 s bursts, similar to the range of experimentally reported burst durations (see E5).
Figure 7.
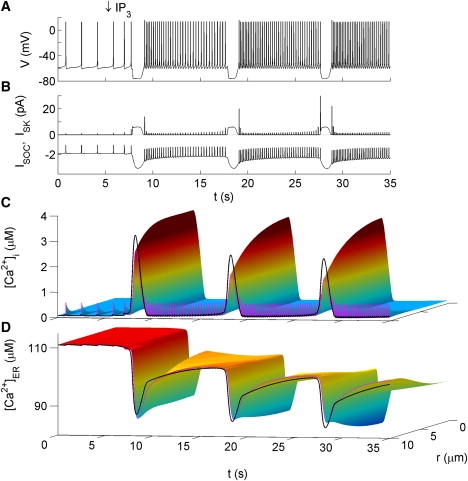
IP3-induced bursting. IP3 application is modeled identically to GnRH application, as described in Fig. 6. The following parameter values differ from those listed in the Supporting Material: τhi = 2 s and P = 0.5 pL ms−1. Figure formatting is the same as in Fig. 4.
A second mode of bursting was also produced that occurs at basal levels of IP3. An example of such bursting is shown in Fig. 8 A. In this case, the duration of each burst is 8 s, and the period is 48 s. The peak firing rate is 11 Hz and drops to 3 Hz near the end of each burst. [Ca2+]ER plays the role of a slow variable, activating and inactivating ISOC. When [Ca2+]ER is high, ISOC is small and the membrane is hyperpolarized. Ca2+ slowly leaks out of the ER, gradually activating ISOC, until it is sufficiently activated to initiate spiking. Ca2+ entry during high frequency spiking refills the ER, causing a reduction in ISOC and the termination of the burst. Such a bursting mechanism has been previously proposed by Chay in models of pancreatic β-cells (for example, (29)). Note that the change in average Ca2+i is modest (∼100 nM) and highly localized to the PM, consistent with the low-amplitude Ca2+ oscillations typically observed in GT1 neurons (21) and placode-derived GnRH neurons (3,4). During each burst, [Ca2+]i is high enough to activate some SK channels (Fig. 8, B and C), contributing to spike frequency adaptation and burst termination. As a result, the application of apamin in the model increased the number of spikes per burst and the burst duration (data not shown). This is consistent with a recent experimental report (20). The store-operated bursting presented here is obtained under the condition that ISOC is nonzero in the unstimulated state. However, we do not think this is essential for this type of bursting. By making the functional dependence of ISOC on [Ca2+]ER extremely steep (approximating a step function), the bursting still occurs (data not shown). Both the electrical and calcium oscillation profiles match the experimental results described in E5.
Figure 8.
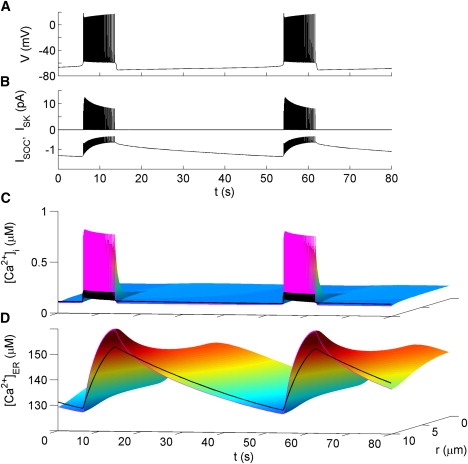
Spontaneous store-operated bursting. The following parameter values differ from those listed in the Supporting Material: ka = 15 mV, gCaL= 1.7 nS, L = 0.004 pL ms−1, νe = 2 μM pL ms−1, and cAMP = 0.5 μM. Figure formatting is the same as in Fig. 4.
The Simplified Model
The spatial description of Ca2+ dynamics is computationally more complicated than previous models. A simpler model that retains these benefits is needed to construct an integrated model of electrical activities, calcium dynamics, and mechanisms for GnRH pulsatility. We present here a simplified model in which [Ca2+]i and [Ca2+]ER are time-dependent only, representing a situation in which the cytosol and ER are well mixed. Under this assumption, the membrane fluxes can be thought of as being distributed everywhere in the cell simultaneously. The model is thus reduced to the following system of ordinary differential equations that describe the whole-cell concentrations of Ca2+ in the cytosol and ER,
| (5) |
| (6) |
where the J values now represent whole-cell fluxes. The fluxes across the PM are rescaled by the factor β to convert from the per-unit area fluxes required by the spatial model's boundary condition (jin and jout) to the whole-cell fluxes desired here.
The simplified model is aimed at a phenomenological reproduction of the [Ca2+] at the cell membrane, CR, while retaining a correct account for the Ca2+entry and its influence on the whole cell [Ca2+], C. We define CR = C + Cm, where Cm represents the contribution of rapidly varying mechanisms of the PM. These include a domain-like approximation of [Ca2+] due to the opening of L-type Ca2+ channels (similar to the approach used in (30)), and Ca2+ removal due to PMCAs and NCXs. The time evolution of Cm is governed by
| (7) |
where Cm, ∞ = ρa2 – KmC. Here, a is the L-Type Ca2+ channel gating variable, and ρ and Km are free parameters (1.46 and 0.123 respectively). Eq. 7 implies that the value of Cm chases that of Cm,∞ exponentially with a time constant τm (17 ms). The parameters have been chosen such that CR rises with a time course that mimics the profile of C(R, t) in the spatial model. When L-type Ca2+channels are closed, the effect of PMCAs and NCXs is to decrease CR compared to the whole cell [Ca2+] (i.e., C). The term −KmC is added to reproduce this effect; it allows Cm to be negative so that CR is smaller than C in this case. Note that the quantity Cm does not have a physical interpretation, serving only to phenomenologically reproduce the temporal profile of [Ca2+] at the membrane.
The simplified model yields all the same results as the full model. As an example, we show in Fig. 9 the responses of the simplified model to GnRH, Tg, and apamin. Note that the profiles of CR and C in the simplified model responses agree with those of the spatial model.
Figure 9.
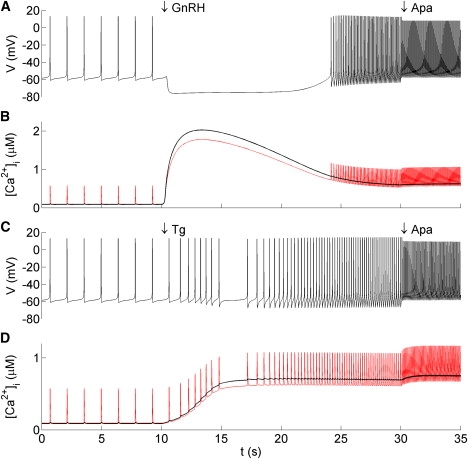
Response of the simplified model to GnRH, Tg, and apamin. (A) Membrane potential and (B) cytosolic Ca2+ response to GnRH and apamin, modeled as in the spatial model (Fig. 5). (C) Membrane potential and (D) cytosolic Ca2+ response to Tg and apamin, modeled as in the spatial model (Fig. 4), except that the SERCA pump rate νe was reduced exponentially from 1.3 to 0.1 μm μM ms−1. In panels B and D, the lower red trace is the [Ca2+]i at the membrane, CR, whereas the thick black trace is the whole cell [Ca2+]i.
Discussion
This article presents an integrated model of the electrical activities and Ca2+ dynamics in GnRH neurons based on two previous models (10,11). We aimed at simplifying the previous models, while adopting a more realistic description of Ca2+ dynamics. The number of ionic currents is reduced by removing the M-type K+ current and the T-type Ca2+ current. In the channels we retained, we reduced the complexity of the descriptions for INa and INSC. Overall, the number of gating variables for the electrical activities are reduced from 9 to 3. We have also added a realistic description of IP3R channels, increasing the number of gating variables by one. This added variable is only necessary for the IP3-induced [Ca2+]i oscillations. A more realistic description of intracellular calcium profiles is accomplished through a spatial description of the calcium dynamics. The computationally more complex spatial model is further reduced to a simplified ODE model. The previous model included five more variables other than the gating variables. This model includes only four additional variables: the membrane potential, whole-cell [Ca2+]i and [Ca2+]ER, and Cm. Thus, the ODE model developed here is significantly simpler than the previous models, and yet retains and extends the ability to explain electrical activities and calcium dynamics in GnRH neurons.
The currents we have omitted may play a role in some aspects of GnRH function that we did not considered here. They may act redundantly to achieve similar roles as are played by some currents we have retained. For instance, the M-type current, which has been shown to be activated by GnRH (28), could help to hyperpolarize the cell during the GnRH response. It would first help the SK current to halt AP firing, then it would limit firing rate once AP firing resumes. The T-type Ca2+ current has been implicated in phasic firing in thalamic neurons. It has been suggested that it may play a similar role in GnRH neurons (31).
Although bursting has been reported in a variety of GnRH neuron preparations (2,18–20,32,33), no specific underlying mechanism has been derived. A few kinds of [Ca2+]i oscillations have also been reported (3,4,12,13,21). As a byproduct of modeling experiments outlined in E1–E4, the model predicts two different mechanisms for bursting and the associated [Ca2+]i oscillations. The first involves IP3-induced oscillatory Ca2+ release from intracellular stores. These oscillations can exhibit both short (Fig. 7) and long periods (23), and reach μM amplitudes. IP3-dependent [Ca2+]i oscillations in adult GnRH neurons have indeed been reported recently (12). The second bursting mechanism involves store-operated Ca2+ entry. Bursting with both long and short periods is possible with this mechanism. The amplitude of [Ca2+]i oscillations associated with this bursting is approximately a few hundred nM, consistent with the amplitude of [Ca2+]i oscillations observed in experiments (3,13,21). This mode of bursting requires voltage-gated calcium entry, as has been reported for both GT1 neurons (21) and placode-derived GnRH neurons (3). There has been no experimental confirmation of such a mechanism in GnRH neurons.
The two modes of bursting presented here have different mechanisms for burst termination. The application of apamin could be used to discriminate between them. The model reveals that in bursting driven by IP3-induced [Ca2+]i oscillations, apamin prevents the burst termination from occurring. In store-operated bursting, however, the application of apamin increased the number of spikes per burst, and prolonged the burst duration. In fact, this has been reported for GnRH neurons in slice preparations (20). Such a phenomenon may not be unique to store-operated bursting, and perhaps could occur in some other forms of electrical bursting that do not rely on SK channels for burst termination. Whether these two mechanisms actually occur in GnRH neurons remains to be determined by experiments. Models of other endocrine cells such the pituitary gonadotrophs (24) and pancreatic β-cells (29) have revealed similar types of IP3-induced and store-operated bursting.
The observed patterns of electrical activity show a high variability in GnRH neurons. These have been broadly classified as quiescence, tonic spiking, and bursting. There are also several reports from long-term recordings of transitions between them. A rich variety of timescales has been exposed in these patterns and transitions between them (2,18,19,32,33). A possible explanation for such a diversity is provided by this model. By varying as parameters the concentrations of cAMP and IP3, we can achieve transitions between all three categories of electrical activities mentioned above (data not shown). The relevance of such second messenger-dependent transitions remains to be fully characterized, and is the subject of ongoing study.
It appears that GnRH pulsatility is accomplished with few close contacts or synapses between GnRH neurons (2). The oscillations of intracellular Ca2+concentrations in placode-derived monkey and mouse GnRH neurons are not synchronized with each other except for a few minutes once every 20–50 min (3,4). These observations suggest that the membrane electrical activities are synchronized periodically by a mechanism independent of synaptic interactions. [Ca2+]i oscillations and hourly synchrony were also observed in the nonneuronal cells in olfactory placode cultures (34). However, the synchronization was reported to be absent without GnRH neurons in such cultures, suggesting a [Ca2+]i oscillation-independent mechanism is responsible for synchronizing these oscillations in both GnRH neurons and nonneuronal cells. We suspect that it is the mechanism that underlies GnRH pulsatility that synchronizes these [Ca2+]i oscillations, and not the other way around.
One mechanism for GnRH pulse generation is reported in cultured GnRH neurons and GT1 cells (7) and enzymatically dispersed hypothalamic tissue cultures (5,35). These works, along with evidence that GnRH neurons express GnRH receptors (36–39), suggest that rhythmogenesis in this system involves autocrine regulation of GnRH secretion by its own release. Mathematical modeling studies demonstrated that this mechanism is viable and robust (8,9). In these studies, the plasma membrane electrical activities were not a direct player for the pulse generation, and thus their roles could not be fully elucidated. Our model could facilitate the investigation of the roles of electrical activities and the associated [Ca2+]i oscillations in the generation of GnRH pulsatility.
Acknowledgments
The authors thank Stanko Stojilkovic for kindly providing the original artwork in Fig. 1.
This work was funded partially by grants from The Natural Sciences and Engineering Research Council of Canada to Y.-X.L. and Eric Cytrynbaum.
Supporting Material
References
- 1.Knobil E. The neuroendocrine control of the menstrual cycle. Recent Prog. Horm. Res. 1980;36:63–88. doi: 10.1016/b978-0-12-571136-4.50008-5. [DOI] [PubMed] [Google Scholar]
- 2.Suter K.J., Wuarin J.P., Smith B.N., Dudek F.E., Moenter S.M. Whole-cell recordings from preoptic/hypothalamic slices reveal burst firing in gonadotropin-releasing hormone neurons identified with green fluorescent protein in transgenic mice. Endocrinology. 2000;141:3731–3736. doi: 10.1210/endo.141.10.7690. [DOI] [PubMed] [Google Scholar]
- 3.Terasawa E., Schanhofer W.K., Keen K.L., Luchansky L. Intracellular Ca2+ oscillations in luteinizing hormone-releasing hormone neurons derived from the embryonic olfactory placode of the rhesus monkey. J. Neurosci. 1999;19:5898–5909. doi: 10.1523/JNEUROSCI.19-14-05898.1999. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Moore J.P., Jr., Shang E., Wray S. In situ GABAergic modulation of synchronous gonadotropin releasing hormone-1 neuronal activity. J. Neurosci. 2002;22:8932–8941. doi: 10.1523/JNEUROSCI.22-20-08932.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Woller M., Nichols E., Herdendorf T., Tutton D. Release of luteinizing hormone-releasing hormone from enzymatically dispersed rat hypothalamic explants is pulsatile. Biol. Reprod. 1998;59:587–590. doi: 10.1095/biolreprod59.3.587. [DOI] [PubMed] [Google Scholar]
- 6.Martinez-Fuentes A.J., Hu L., Krsmanovic L.Z., Catt K.J. Gonadotropin-releasing hormone (GnRH) receptor expression and membrane signaling in early embryonic GnRH neurons: role in pulsatile neurosecretion. Mol. Endocrinol. 2004;18:1808–1817. doi: 10.1210/me.2003-0321. [DOI] [PubMed] [Google Scholar]
- 7.Krsmanovic L.Z., Mores N., Navarro C.E., Arora K.K., Catt K.J. An agonist-induced switch in G protein coupling of the gonadotropin-releasing hormone receptor regulates pulsatile neuropeptide secretion. Proc. Natl. Acad. Sci. USA. 2003;100:2969–2974. doi: 10.1073/pnas.0535708100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Khadra A., Li Y.X. A model for the pulsatile secretion of gonadotropin-releasing hormone from synchronized hypothalamic neurons. Biophys. J. 2006;91:74–83. doi: 10.1529/biophysj.105.080630. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Li Y.X., Khadra A. Robust synchrony and rhythmogenesis in endocrine neurons via autocrine regulations in vitro and in vivo. Bull. Math. Biol. 2008;70:2103–2125. doi: 10.1007/s11538-008-9328-z. [DOI] [PubMed] [Google Scholar]
- 10.Van Goor F., LeBeau A.P., Krsmanovic L.Z., Sherman A., Catt K.J. Amplitude-dependent spike-broadening and enhanced Ca2+ signaling in GnRH-secreting neurons. Biophys. J. 2000;79:1310–1323. doi: 10.1016/S0006-3495(00)76384-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.LeBeau A.P., Van Goor F., Stojilkovic S.S., Sherman A. Modeling of membrane excitability in gonadotropin-releasing hormone-secreting hypothalamic neurons regulated by Ca2+-mobilizing and adenylyl cyclase-coupled receptors. J. Neurosci. 2000;20:9290–9297. doi: 10.1523/JNEUROSCI.20-24-09290.2000. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Jasoni C.L., Todman M.G., Strumia M.M., Herbison A.E. Cell type-specific expression of a genetically encoded calcium indicator reveals intrinsic calcium oscillations in adult gonadotropin-releasing hormone neurons. J. Neurosci. 2007;27:860–867. doi: 10.1523/JNEUROSCI.3579-06.2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Van Goor F., Krsmanovic L.Z., Catt K.J., Stojilkovic S.S. Control of action potential-driven calcium influx in GT1 neurons by the activation status of sodium and calcium channels. Mol. Endocrinol. 1999;13:587–603. doi: 10.1210/mend.13.4.0261. [DOI] [PubMed] [Google Scholar]
- 14.Hu L., Wada K., Mores N., Krsmanovic L.Z., Catt K.J. Essential role of G protein-gated inwardly rectifying potassium channels in gonadotropin-induced regulation of GnRH neuronal firing and pulsatile neurosecretion. J. Biol. Chem. 2006;281:25231–25240. doi: 10.1074/jbc.M603768200. [DOI] [PubMed] [Google Scholar]
- 15.Van Goor F., Krsmanovic L.Z., Catt K.J., Stojilkovic S.S. Coordinate regulation of gonadotropin-releasing hormone neuronal firing patterns by cytosolic calcium and store depletion. Proc. Natl. Acad. Sci. USA. 1999;96:4101–4106. doi: 10.1073/pnas.96.7.4101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Kaneishi K., Sakuma Y., Kobayashi H., Kato M. 3′,5′-cyclic adenosine monophosphate augments intracellular Ca2+ concentration and gonadotropin-releasing hormone (GnRH) release in immortalized GnRH neurons in an Na+ -dependent manner. Endocrinology. 2002;143:4210–4217. doi: 10.1210/en.2002-220508. [DOI] [PubMed] [Google Scholar]
- 17.Yoshida H., Paruthiyil S., Butler P., Weiner R.I. Role of cAMP signaling in the mediation of dopamine-induced stimulation of GnRH secretion via D1 dopamine receptors in GT1–7 cells. Neuroendocrinology. 2004;80:2–10. doi: 10.1159/000080519. [DOI] [PubMed] [Google Scholar]
- 18.Kuehl-Kovarik M.C., Pouliot W.A., Halterman G.L., Handa R.J., Dudek F.E. Episodic bursting activity and response to excitatory amino acids in acutely dissociated gonadotropin-releasing hormone neurons genetically targeted with green fluorescent protein. J. Neurosci. 2002;22:2313–2322. doi: 10.1523/JNEUROSCI.22-06-02313.2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Kuehl-Kovarik M.C., Partin K.M., Handa R.J., Dudek F.E. Spike-dependent depolarizing afterpotentials contribute to endogenous bursting in gonadotropin releasing hormone neurons. Neuroscience. 2005;134:295–300. doi: 10.1016/j.neuroscience.2005.03.047. [DOI] [PubMed] [Google Scholar]
- 20.Liu X., Herbison A.E. Small-conductance calcium-activated potassium channels control excitability and firing dynamics in gonadotropin-releasing hormone (GnRH) neurons. Endocrinology. 2008;149:3598–3604. doi: 10.1210/en.2007-1631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Charles A.C., Hales T.G. Mechanisms of spontaneous calcium oscillations and action potentials in immortalized hypothalamic (GT1–7) neurons. J. Neurophysiol. 1995;73:56–64. doi: 10.1152/jn.1995.73.1.56. [DOI] [PubMed] [Google Scholar]
- 22.Li Y.X. Tango waves in a bidomain model of fertilization calcium waves. Physica D. 2003;186:27–49. [Google Scholar]
- 23.Li Y.X., Rinzel J. Equations for InsP3 receptor-mediated [Ca2+]i oscillations derived from a detailed kinetic model: a Hodgkin-Huxley like formalism. J. Theor. Biol. 1994;166:461–473. doi: 10.1006/jtbi.1994.1041. [DOI] [PubMed] [Google Scholar]
- 24.Li Y.X., Stojilkovic S.S., Keizer J., Rinzel J. Sensing and refilling calcium stores in an excitable cell. Biophys. J. 1997;72:1080–1091. doi: 10.1016/S0006-3495(97)78758-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Allbritton N.L., Meyer T., Stryer L. Range of messenger action of calcium ion and inositol 1,4,5-trisphosphate. Science. 1992;258:1812–1815. doi: 10.1126/science.1465619. [DOI] [PubMed] [Google Scholar]
- 26.Lewis R.S. The molecular choreography of a store-operated calcium channel. Nature. 2007;446:284–287. doi: 10.1038/nature05637. [DOI] [PubMed] [Google Scholar]
- 27.Spergel D.J., Catt K.J., Rojas E. Immortalized GnRH neurons express large-conductance calcium-activated potassium channels. Neuroendocrinology. 1996;63:101–111. doi: 10.1159/000126946. [DOI] [PubMed] [Google Scholar]
- 28.Xu C., Roepke T.A., Zhang C., Ronnekleiv O.K., Kelly M.J. GnRH activates the M-current in GnRH neurons: an autoregulatory negative feedback mechanism? Endocrinology. 2008;149:2459–2466. doi: 10.1210/en.2007-1178. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Chay T.R. Modeling slowly bursting neurons via calcium store and voltage-independent calcium current. Neural Comput. 1996;8:951–978. doi: 10.1162/neco.1996.8.5.951. [DOI] [PubMed] [Google Scholar]
- 30.Van Goor F., Li Y.-X., Stojilkovic S.S. Paradoxical role of large-conductance calcium-activated K+ (BK) channels in controlling action potential-driven Ca2+ entry in anterior pituitary cells. J. Neurosci. 2001;21:5902–5915. doi: 10.1523/JNEUROSCI.21-16-05902.2001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Kelly M.J., Wagner E.J. GnRH neurons and episodic bursting activity. Trends Endocrinol. Metab. 2002;13:409–410. doi: 10.1016/s1043-2760(02)00698-7. [DOI] [PubMed] [Google Scholar]
- 32.Nunemaker C.S., DeFazio R.A., Geusz M.E., Herzog E.D., Pitts G.R. Long-term recordings of networks of immortalized GnRH neurons reveal episodic patterns of electrical activity. J. Neurophysiol. 2001;86:86–93. doi: 10.1152/jn.2001.86.1.86. [DOI] [PubMed] [Google Scholar]
- 33.Nunemaker C.S., Straume M., DeFazio R.A., Moenter S.M. Gonadotropin-releasing hormone neurons generate interacting rhythms in multiple time domains. Endocrinology. 2003;144:823–831. doi: 10.1210/en.2002-220585. [DOI] [PubMed] [Google Scholar]
- 34.Terasawa E., Richter T.A., Keen K.L. A role for non-neuronal cells in synchronization of intracellular calcium oscillations in primate LHRH neurons. Prog. Brain Res. 2002;141:283–291. doi: 10.1016/S0079-6123(02)41099-0. [DOI] [PubMed] [Google Scholar]
- 35.Woller M.J., Meyer S., Ada-Nguema A., Waechter-Brulla D. Dissecting autocrine effects on pulsatile release of gonadotropin-releasing hormone in cultured rat hypothalamic tissue. Exp. Biol. Med. (Maywood) 2004;229:56–64. doi: 10.1177/153537020422900107. [DOI] [PubMed] [Google Scholar]
- 36.Krsmanovic L.Z., Stojilkovic S.S., Mertz L.M., Tomic M., Catt K.J. Expression of gonadotropin-releasing hormone receptors and autocrine regulation of neuropeptide release in immortalized hypothalamic neurons. Proc. Natl. Acad. Sci. USA. 1993;90:3908–3912. doi: 10.1073/pnas.90.9.3908. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Krsmanovic L.Z., Martinez-Fuentes A.J., Arora K.K., Mores N., Navarro C.E. Autocrine regulation of gonadotropin-releasing hormone secretion in cultured hypothalamic neurons. Endocrinology. 1999;140:1423–1431. doi: 10.1210/endo.140.3.6588. [DOI] [PubMed] [Google Scholar]
- 38.Xu C., Xu X.Z., Nunemaker C.S., Moenter S.M. Dose-dependent switch in response of gonadotropin-releasing hormone (GnRH) neurons to GnRH mediated through the type I GnRH receptor. Endocrinology. 2004;145:728–735. doi: 10.1210/en.2003-0562. [DOI] [PubMed] [Google Scholar]
- 39.Todman M.G., Han S.K., Herbison A.E. Profiling neurotransmitter receptor expression in mouse gonadotropin-releasing hormone neurons using green fluorescent protein-promoter transgenics and microarrays. Neuroscience. 2005;132:703–712. doi: 10.1016/j.neuroscience.2005.01.035. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.