Abstract
Electron density maps of membrane proteins or large macromolecular complexes are frequently only determined at medium resolution between 4 Å and 10 Å, either by cryo-electron microscopy (cryoEM) or X-ray crystallography. In these density maps the general arrangement of secondary structure elements is revealed while their directionality and connectivity remain elusive. We demonstrate that the topology of proteins with up to 250 amino acids can be determined from such density maps when combined with a computational protein folding protocol. Furthermore, we accurately reconstruct atomic detail in loop regions and amino acid side chains not visible in the experimental data. The EM-Fold algorithm assembles the secondary structure elements de novo before atomic detail is added using Rosetta. In a benchmark of 27 proteins the protocol consistently and reproducibly achieves models with RMSD values smaller than 3 Å.
Introduction
In the field of protein structure determination cryoEM has been established as a viable approach for studying the structure and dynamics of macromolecular structure of large protein complexes at near native conditions. CryoEM is invaluable in cases where alternative approaches such as X-ray crystallography and NMR fail. In recent years, cryoEM density maps have reached high enough resolutions to provide sufficient detail to trace the protein backbone (Liu et al., 2010a; Ludtke et al., 2008; Zhang et al., 2011; Zhou, 2008). More routinely resolutions better than 10 Å are reached that reveal the location of α-helices (Cong et al., 2010; Liu et al., 2010b; Ludtke et al., 2008; Ludtke et al., 2004; Min et al., 2006; Saban et al., 2006; Serysheva et al., 2008; Villa et al., 2009). Additionally, β-strands become visible at resolutions around 6 Å. However, connectivity and directionality of these secondary structure elements and their alignment with the primary protein sequence remains ambiguous in these medium resolution density maps (5–10 Å resolution), i.e. it remains unknown which part of the protein’s primary sequence forms which α-helix or which β-strand and where the N- and C-termini of the helices and strands reside. Computational methods are needed to help resolve this ambiguity. Several algorithms that help identify secondary structure elements in a density map have been published. α-helices and β-strand regions can be identified automatically by methods using segmentation and feature extraction (Baker et al., 2007; Dal Palu et al., 2006; Jiang et al., 2001; Kong et al., 2004). Furthermore, even high quality medium resolution cryoEM maps typically lack information at atomic detail such as the conformation of loops and side chains. We explore the potential of computational methods to aid in the interpretation of maps by reconstructing structural information that is not readily visible at the respective resolution.
In the past, numerous experimental techniques have been successfully combined with computational methods. A combination of computational algorithms with sparse structural information from NMR spectroscopy (Bowers et al., 2000; Meiler and Baker, 2003b, 2005; Rohl and Baker, 2002) and EPR spectroscopy (Alexander et al., 2008; Hanson et al., 2008; Hirst et al., 2011) experiments has led to the construction of protein models that are accurate at atomic detail. Final models include atomic detail that is beyond the resolution of the experiment because of judicious use of complementary computational algorithms. A prerequisite for success in this regard is that the experimental data restrains the conformational space sufficiently to allow sampling of protein backbone conformations at a density of about 1–2 Å around the global energy minimum. As a result, some protein models will have root mean square deviations (RMSD) from the correct structure of less than 3.0 Å when normalized to a 100 residue protein (RMSD100) (Carugo and Pongor, 2001). This level of accuracy is sufficient to construct side chain coordinates in the protein core and allows discrimination of incorrect protein models on the basis of inferior energy values (Bradley et al., 2005). Several methods, such as Rosetta, Modeller and EM-IMO, exist that can be applied to the refinement of comparative or hand-traced models guided by cryoEM density maps (DiMaio et al., 2009; Topf et al., 2006; Zhu et al., 2010).
Here we demonstrate de novo protein structure determination to a level with accurate atomic detail using medium resolution density maps to restrain the simulation. Our protocol consists of two steps: 1) determination of protein topology with an improved version of EM-Fold (Lindert et al., 2009) and 2) refinement to atomic detail accuracy using Rosetta (DiMaio et al., 2009). These two methods are highly complementary. EM-Fold differs from Rosetta in that it is tailored towards efficient sampling of the conformational search space at the cost of somewhat lower precision in its scoring functions. Its ability to move entire SSEs as one element makes it well suited for folding into medium resolution density maps. EM-Fold also differs from other cryoEM map based model building algorithms such as SSEhunter (Baker et al., 2007) in that it is a de novo protein folding tool at heart that uses the cryoEM map as a restraint. EM-Fold builds topological models for a protein of interest that agree with the density map and fulfill basic requirements of protein structure. These models contain only secondary structure elements, no coordinates for loop regions and no side chains. It was originally developed to build models of α-helical proteins into medium resolution density maps. Here we present an updated version of the program that can place both types of secondary structure elements (α-helices and β-strands) into the density map. Additional improvements to the algorithm include better handling of incorrect secondary structure prediction as well as a more advanced refinement protocol. EM-Fold models provide a good starting point for the Rosetta electron density refinement that also constructs loops and side chains guided by the cryoEM density map. The performance of the new folding and refinement protocol was tested on a benchmark set of 20 α-helical and 7 β-sheet proteins, 13 of which could be refined to atomic resolution detail. If secondary structure elements are visible in the maps, this protocol could also be applied to low resolution X-ray crystallography maps such as those obtained recently for several important membrane proteins (Ward et al., 2007) and macromolecular assemblies (Sibanda et al., 2010).
Results and Discussion
EM-Fold determines the topology of a protein through placement of predicted secondary structure elements into a cryoEM density map (Lindert et al., 2009). It uses a Monte Carlo Metropolis algorithm with a knowledge-based energy function that builds and refines physically realistic models that agree with the density map. The models are constructed from a pool of predicted secondary structure elements. Model changes applied during the folding simulation include addition and deletion of secondary structure elements together with swaps and rotations of these elements. To achieve higher accuracy in the initial models and aid atomic detail refinement, EM-Fold was extended to allow bending, translation, and dynamic length resizing of secondary structure elements. For the models to accurately reflect such detail, the scoring function was adapted for direct comparison of the models with the density map. Furthermore, the present protocol employs a recently added feature in Rosetta that allows construction of loops and side chains guided by a density map (DiMaio et al., 2009). This is critical as we have found that accurate construction of the protein backbone in loop regions that connect secondary structure elements is crucial for successful atomic-level refinement. Rosetta systematically rebuilds regions of the protein backbone that agree the least with the density map.
Benchmark database of twenty α-helical and seven β-sheet proteins with 150 to 250 residues
A benchmark set of 20 α-helical and 7 β-sheet proteins with 150 – 250 amino acids was chosen to test the algorithm. The benchmark was limited to proteins up to 250 residues as this provided the desired range of successes/failures demonstrating the capabilities and limitations of the method. As algorithms advance and computers become faster the benchmark should be expanded to contain larger proteins. The benchmark set is primarily composed of α-helical proteins since these represent the majority of application cases as α-helices are observed more readily than β-strands at medium resolution. However, the performance was also tested on seven proteins with β-sheets to demonstrate general applicability. Density maps at 7 Å resolution were simulated for the 20 α-helical proteins. Density maps at 5 A resolution were simulated for the seven β-sheet containing proteins. At these resolutions, α-helices and β-strands can be unambiguously identified through visual inspection. Since the maps were simulated at 5 Å (β-sheet containing proteins) and 7 Å (α-helical proteins) resolution respectively, these are considered the resolution limits of the EM-Fold method. Maps at higher resolution will likely perform at least as well with EM-Fold as more features tend to be present in these density maps. For higher resolution maps it might however be advantageous to use methods designed to trace the protein backbone if the resolution of the density map allows (Baker et al., 2011).
Results of EM-Fold assembly step with perfect and realistic secondary structure prediction
A schematic representation of the stages of the benchmark is shown in Figure 1. The algorithm adds, deletes, swaps, flips as well as dynamically grows and shrinks secondary structure elements to account for inaccurate secondary structure prediction. To avoid formation of unlikely secondary structure elements, this new move is accompanied by scoring the agreement of the model’s secondary structure with predicted secondary structure. To assess the impact of inaccurate secondary structure prediction on the algorithm, the benchmark was performed in two stages – using perfect and realistic secondary structure prediction, respectively. Realistic secondary structure prediction is generated as a consensus prediction of the methods used without any manual adjustment. Assuming perfect secondary structure prediction, the true topology is found among the top 20 scoring topologies for all but one of the 27 proteins. The exception is 1WBA for which the correct topology ranks at 287 (see Supplemental Table S1). Correct topology is defined as having placed all SSEs into the density rods that they correspond to natively with their correct orientation with respect to rotation around an axis perpendicular to the main axis of the density rod. Table 1 displays the results of the assembly runs for all 27 proteins with realistic secondary structure prediction where RMSD100 values are calculated over all backbone atoms. In the case of realistic secondary prediction, the true topology is constructed in 23 out of the 27 proteins in the benchmark. For 15 of the 20 α-helical proteins and for 4 of the 7 β-sheet proteins the correct topology also ranks among the top 150 scoring topologies. For 4 additional proteins (1Z3Y, 2FQ4, 2IU1, 2NR7) the correct topology was constructed but it was not identified among the best 150 topologies. These results indicate that it is more difficult to predict the correct topology of β-sheet containing proteins. This maybe because of a higher curvature of β-strands in β-sheets compared to α-helices or the generally higher contact order of β-proteins. A total of 19 out of 27 protein topologies (70%) were identified within the best 150 scoring topologies after the assembly step. While a higher success rate was definitely desirable, 70% success rate is very competitive compared to other de novo folding benchmarks.
Figure 1.
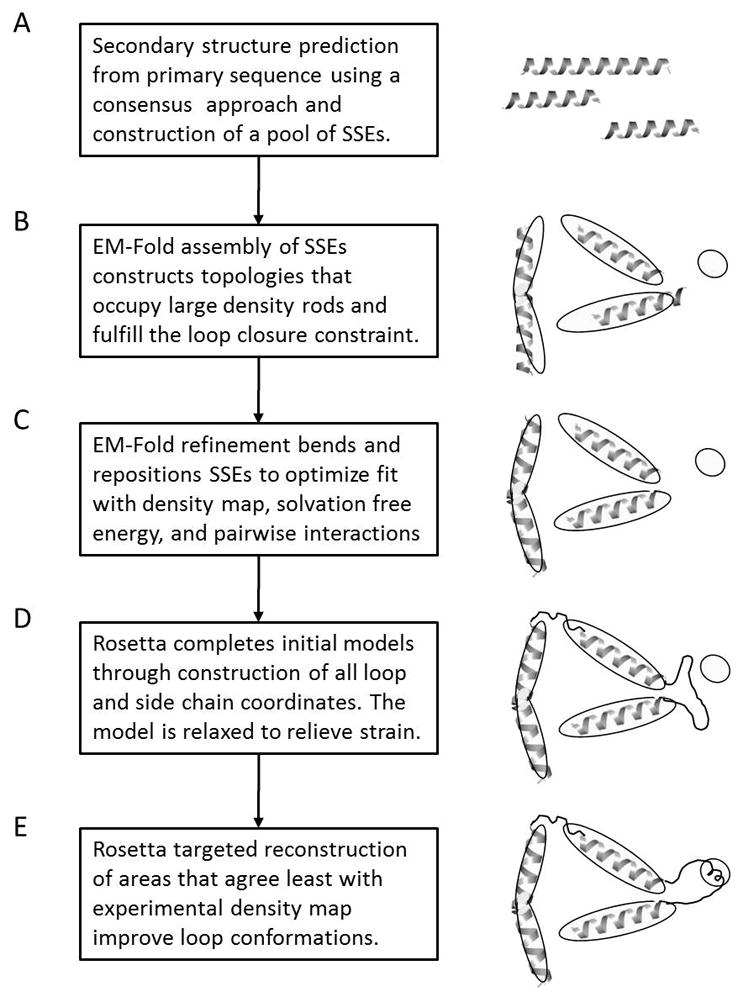
Schematic representation of the folding protocol used in the benchmark. The scheme represents a three density rod density map. (A) Using a consensus of three secondary structure prediction methods likely positions of long stretches of secondary structure in the primary sequence of the protein are identified. These positions are collected in a pool of idealized secondary structure elements. (B) The EM-Fold assembly step builds 50000 models by assembling predicted, idealized secondary structure elements into the identified density rods. The models contain no residues in the loop regions and no side chains. The top scoring 150 topologies are carried over to the next step. (C) The EM-Fold refinement step builds 500 refined models for each of the 150 topologies. The models generated in the assembly step are refined to better fit the density map. In particular bending of idealized secondary structure elements is performed. The top scoring 50 topologies are carried over to the next step. (D) Rosetta (round 1) builds loop models for each of the 50 topologies. Loops are built and the overall structure is relaxed. The top scoring 15 topologies are carried over to the next step. (E) Rosetta (round 2 and 3) identifies regions in the proteins that agree least with the density map and selectively rebuilds these identified regions and relaxes the entire structure. The top scoring 5 topologies after round 2 are carried over into round 3.
Table 1.
Results of benchmark on set of 27 α, α/β and β proteins. See also Tables S1, S2 and S3.
| Rank/RMSD100 [Å] | Rank/RMSD100 [Å] (RMSD100 SSEs [Å]) | ||||||
|---|---|---|---|---|---|---|---|
| protein | size | EM-Fold assembly | EM-Fold refinement | Rosetta 1 | Rosetta 2 | Rosetta 3 | Rotamer recovery |
| α-proteins | |||||||
| 1DVO | 152, 4, 0 | 3/3.73 | 19/2.25 | 1/2.49 (1.30) | 1/2.23 (1.33) | 1/2.07 (1.36) | 0.64 |
| 1GS9 | 165, 4, 0 | 31/3.83 | 15/4.01 | 3/3.76 (3.59) | 5/3.87 (3.69) | 4/3.96 (3.70) | 0.43 |
| 1IAP | 211, 7, 0 | 2/2.57 | 8/2.03 | 1/2.51 (1.31) | 1/2.12 (1.27) | 1/2.43 (1.28) | 0.49 |
| 1ILK | 151, 5, 0 | 73/3.08 | 23/3.17 | 1/2.78 (2.60) | 1/2.75 (2.60) | 1/2.64 (2.53) | 1.00 |
| 1NIG | 152, 4, 0 | 66/5.97 | 22/6.42 | 4/6.04 (4.44) | 3/5.98 (4.47) | 2/5.92 (4.37) | 0.50 |
| 1OXJ | 173, 4, 0 | 71/3.20 | 39/2.62 | 1/5.89 (1.50) | 1/4.34 (1.60) | 1/4.14 (1.68) | 0.54 |
| 1X91 | 153, 5, 0 | 1/3.30 | 1/1.33 | 1/1.37 (0.87) | 1/1.32 (0.92) | 1/1.29 (0.78) | 0.86 |
| 1Z3Y | 238, 7, 0 | 621/− | −/− | −/− | −/− | −/− | - |
| 2A6B | 234, 6, 0 | 131/2.83 | 24/2.55 | 1/3.90 (1.76) | 1/3.12 (1.74) | 1/2.22 (1.80) | 0.60 |
| 2FD5 | 180, 6, 0 | 1/2.88 | 37/2.09 | 1/1.76 (1.17) | 1/1.68 (1.11) | 1/2.19 (1.64) | 0.54 |
| 2FM9 | 215, 9, 0 | 126/3.09 | 1/2.38 | 1/2.63 (2.29) | 1/2.29 (2.11) | 1/2.29 (2.02) | 0.61 |
| 2FQ4 | 192, 7, 0 | 260/− | −/− | −/− | −/− | −/− | - |
| 2G7S | 194, 6, 0 | 1/2.47 | 29/2.52 | 1/2.04 (1.67) | 1/2.00 (1.70) | 1/2.01 (1.74) | 0.58 |
| 2GEN | 197, 7, 0 | 2/2.70 | 18/2.76 | 4/2.67 (2.25) | 1/2.27 (2.05) | 1/2.35 (2.08) | 0.56 |
| 2IGC | 164, 4, 0 | 23/4.51 | 41/6.23 | 1/7.10 (4.19) | 5/6.91 (3.81) | 2/6.93 (3.78) | 0.53 |
| 2IOS | 150, 6, 0 | 60/4.13 | 14/2.68 | 1/3.87 (3.03) | 1/3.48 (3.18) | 1/3.31 (3.04) | 0.49 |
| 2IU1 | 208, 5, 0 | 849/− | −/− | −/− | −/− | −/− | - |
| 2NR7 | 195, 5, 0 | 386/− | −/− | −/− | −/− | −/− | - |
| 2O8P | 227, 9, 0 | 15/2.82 | 18/2.77 | 2/2.35 (2.25) | 2/2.05 (2.01) | 1/2.18 (2.13) | 0.48 |
| 2QK1 | 249, 9, 0 | −/− | −/− | −/− | −/− | −/− | - |
| α-β-proteins | |||||||
| 1BJ7 | 156, 1, 8 | −/− | −/− | −/− | −/− | −/− | - |
| 1CHD | 203, 1, 8 | 24/1.68 | 87/1.65 | 2/15.76 (1.5) | 4/15.44 (1.49) | 4/15.42 (1.5) | 0.53 |
| 1ICX | 155, 1, 7 | 131/2.40 | 47/3.84 | 1/2.51 (2.08) | 1/2.35 (1.89) | 1/2.17 (1.76) | 0.57 |
| 1JL1 | 155, 3, 5 | 32/3.10 | 13/3.56 | 1/3.38 (2.85) | 1/2.84 (2.03) | 2/2.91 (2.30) | 0.71 |
| 1OZ9 | 150, 5, 4 | 1/2.27 | 9/1.67 | 1/1.88 (1.21) | 1/1.89 (1.41) | 1/2.19 (1.85) | 0.55 |
| β-proteins | |||||||
| 1WBA | 175, 0, 10 | −/− | −/− | −/− | −/− | −/− | - |
| 2QVK | 192, 0, 7 | −/− | −/− | −/− | −/− | −/− | - |
| Average RMSD100s | 3.19 | 2.98 | 3.27 (2.20) | 2.97 (2.13) | 2.96 (2.18) | ||
This table summarizes the results of the 27 protein benchmark. The first two columns show the pdb ID of the protein and protein size information. Column 2 lists the number of amino acids, number of α-helices with at least 12 residues and the number of βstrands with at least 5 residues. Realistic secondary structure prediction has been used for the benchmark. Columns 3 and 4 contain the results of the EM-Fold assembly and refinement step, respectively. The rank of the correct topology model within all scored models as well as the RMSD100 of the correct topology model are given. Columns 5 through 7 show the results of the three rounds of Rosetta refinement. Each of these columns lists the rank of the correct topology model within all scored models, the RMSD100 of the correct topology model as well as the RMSD100 of the correct topology model over residues in secondary structure elements (numbers in parentheses). The last column lists the fraction of rotamers in the protein core that were recovered. Recovery is defined as the model having the same rotamers for all side chain angles. Core of the protein is defined as at least 22 neighbors. All RMSD100 values are determined over the backbone atoms N, Cα, C and O. The proteins from the benchmark set that are considered a success after the EM-Fold assembly and refinement steps as well as after the third round of Rosetta refinement are shown in bold. The criteria for the individual success assignments were: correct topology within the top 150 scoring models after the EM-Fold assembly step, correct topology within the top 50 scoring models after the EM-Fold refinement step and correct topology being the top scoring models with an RMSD100 of less than 3Å after the third round of Rosetta refinement.
EM-Fold refinement protocol improves RMSD100s of models
The top 150 scoring models selected after the assembly step were refined in EM-Fold with perturbations including bending in addition to rotations and translations of the individual secondary structure elements as described in (Lindert et al., 2009). The agreement of the model with the density map is scored using a cross correlation coefficient. Table 1 shows the improvement in RMSD100 from the assembly step to the refinement step. RMSD100s are calculated over all backbone atoms. For all but one of the 19 successful proteins, the refinement step generates models that are lower in RMSD100 than the assembly step model. The maximal improvement was 2.4 Å for 1DVO (a model with RMSD100 of 1.32 A was built but didn’t score best) and the average improvement was 1.0 Å. When only considering the best scoring true topology models after refinement, the average improvement in RMSD100 is 0.2 Å, while the best improvement is 2.0 Å (for 1X91). For all but one protein, the correct topologies are among the top 50 scoring topologies after the refinement step. The exception is 1CHD where the best scoring topology ranks 87th after the refinement step. In particular, proteins where the true topology ranks worse than 25 after the assembly step are considerably improved in ranking by refinement. The top scoring model for each of the 50 top scoring topologies after the refinement step is used in the first round of the Rosetta refinement protocol.
Rosetta refinement improves models and reaches atomic detail accuracy for favorable cases
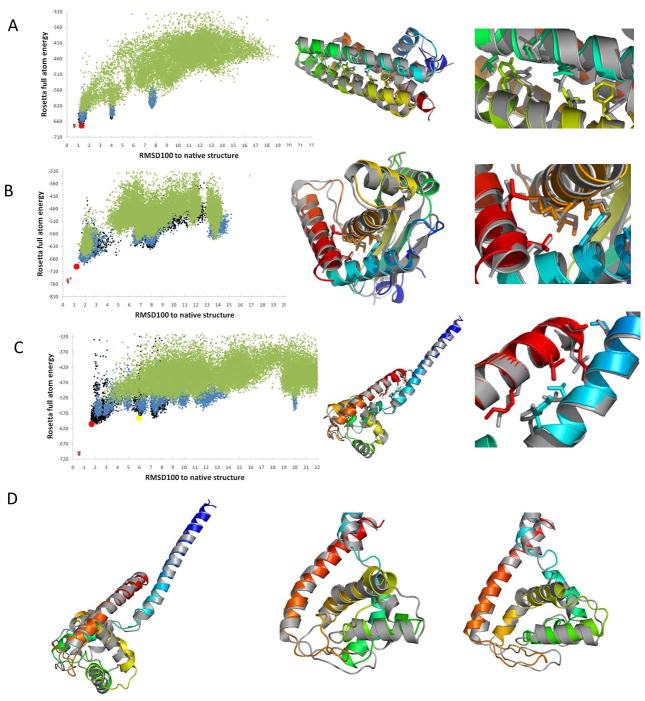
An iterative refinement protocol was applied using Rosetta. The first round built loops and side chains for the 50 top scoring topologies from the EM-Fold refinement step. The resulting models underwent relaxation in the Rosetta force field. Regions that agreed least with the density map in the best scoring 15 topologies were identified using Rosetta’s loops_from_density.linuxgccrelease executable. These regions were rebuilt in a second round of the Rosetta refinement followed by another relaxation of the models. Finally, the regions with the largest discrepancies to the density map in the top five scoring topologies after round 2 were rebuilt in round 3. Table 1 summarizes the results after each of the three rounds of Rosetta refinement. 14 of the 19 final best scoring models correspond to the correct topology. In the remaining cases, the true topology is ranked second in three cases and fourth in the two worst cases (Supplemental Table S2 lists the RMSD100 values of the top scoring models for completeness). Rosetta is thus able to identify the correct topology by score whenever a model with a RMSD100 smaller than 2.8 Å was built. This was the case for 14 of 19 proteins. The RMSD100s of the correct models after completion of the iterative refinement protocol range from 1.3 to 6.9 Å over the full length of the proteins and from 0.8 to 3.8 Å over the secondary structure elements. The average RMSD100 is 3.0 Å over the full length of the protein and 2.2 Å over the SSEs. Indicating correct atomic detail accuracy, thirteen of the proteins have backbone atom RMSD100s of less than 3.0 Å over all residues. Figure 2 shows models for 1X91, 1OZ9 and 1DVO superimposed with the native structure where RMSD100s of 1.1 Å, 1.4 Å and 1.8 Å over all residues were achieved, respectively. Side chain conformations in the protein core are shown for both the model and the native structure. The RMSD100 versus score plots for all three proteins are displayed next to the models. Figure S1 depicts the model evolution over all the rounds of the protocol for two of the proteins – 1X91 and 1OZ9. It can be seen how the quality of the models improve from EM-Fold assembly step to the third round of Rosetta refinement. Figure 3, Figure 4 and Figure S2 display score versus RMSD100 plots and best models for all benchmark proteins. A clear funnel shape is visible for 14 out of 19 benchmark cases, with models having low RMSD100 values scoring better than models with high RMSD100 values. Occasionally models with higher RMSD100 have scores that approach the score of the best scoring models with the correct topology (Figure 2C). An overlay of such a structure with the native model is shown in Figure 2D. All α-helices are placed in the correct density rods with one being placed in the wrong orientation. Most of the native helical interfaces are still present in this model explaining its superior energy.
Figure 2.
Rosetta refinement RMSD100 vs. Rosetta energy plots and superimposition of final models after Rosetta refinement with medium sized native structures. Energy plots for 1X91 (A), 1OZ9 (B) and 1DVO (C) are shown. Models from round 1 (green), round 2 (blue) and round 3 (black) of the Rosetta refinement are plotted. The native structure relaxed in Rosetta’s force field is shown in violet for comparison. RMSD100s are calculated over all backbone atoms. For all three proteins a model funnel is visible in the plot and the models corresponding to the correct topology score best allowing identification of the correct fold by score. Superimposition of the final models (colored in rainbow) of 1X91 (A), 1OZ9 (B) and 1DVO (C) with the original PDB structures (grey) are shown next to the energy funnels. The superimposed models are marked by a red dot in the energy funnels. A close-up view of side chain conformations in interfaces between secondary structure elements is shown. (A) 1X91 has 153 residues. The model shown has a RMSD100 of 1.07 Å over the full length of the protein and 0.63 Å over the helical residues. (B) 1OZ9 has 150 residues. The model shown has a RMSD100 of 1.36 Å over the full length of the protein and 0.99 Å over the residues in secondary structure elements. (C) 1DVO has 152 residues. The model shown has a RMSD100 of 1.83 Å over the full length of the protein and 1.18 Å over the residues in secondary structure elements. (D) Some models score well but exhibit a relatively high RMSD100. One example is the model for 1DVO that is shown here and represented with a yellow dot in (C). Overall the agreement of the model with the native structure is good (picture on the left). Closer evaluation (center picture) reveals that one helix (green) has been placed into the density rod in the wrong orientation. This leads to a high overall RMSD100 (5.94 Å), but preserves many of the contacts between correctly placed secondary structure elements thus ensuring a relatively good score. The picture on the right shows a closeup view of that particular helix in the best scoring model (see red dot in (C)).
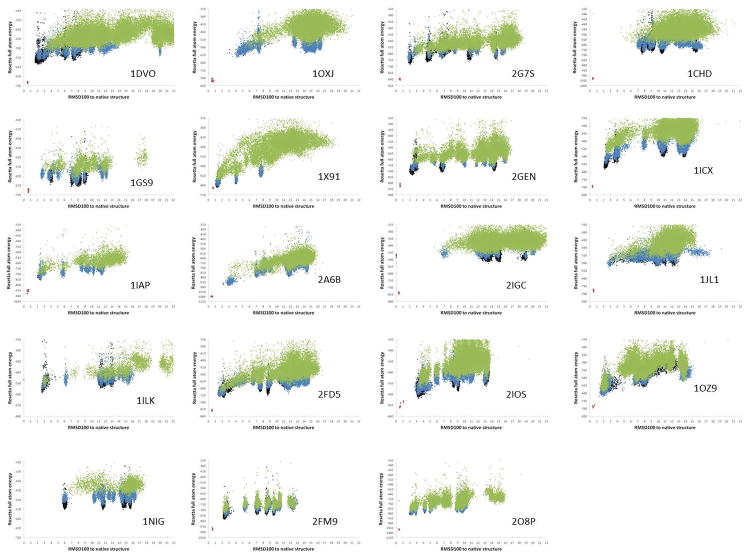
Figure 3.
Gallery of score vs RMSD100 plots for all 19 benchmark proteins. Models from round 1 (green), round 2 (blue) and round 3 (black) of the Rosetta refinement are plotted. The native structure relaxed in Rosetta’s force field is shown in violet for comparison. RMSD100s are calculated over all backbone atoms. The vast majority of the plots exhibit a clear funnel shape, i.e. models with low RMSD100 generally have lower scores than models with high RMSD100 values and vice versa. This feature is desirable in computational protein structure prediction as it makes model identification based on score possible. See also Figure S1.
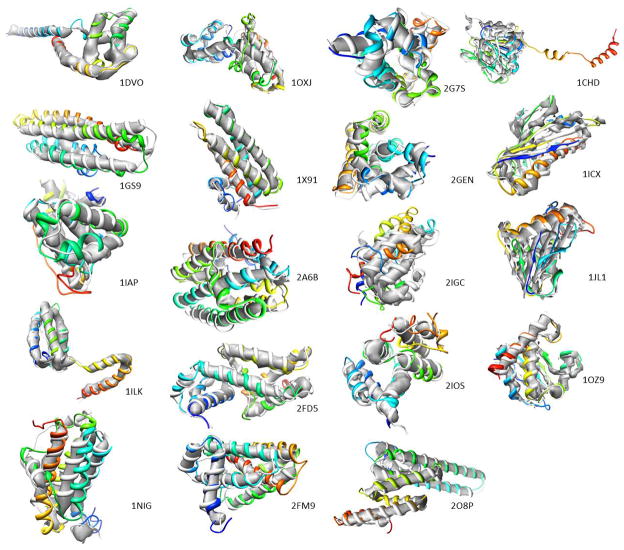
Figure 4.
Gallery of best scoring models after three rounds of Rosetta refinement for all 19 benchmark proteins. Superimposition of the models (rainbow) with the original PDB structures (grey) and the simulated density maps are shown. Density maps were simulated at 5 Å resolution (β-strand containing proteins) and at 7 A resolution (α-helical proteins) respectively. The average RMSD100 of the models shown to the native structure is 2.96 Å, with values ranging from 1.29 Å to 6.93 Å RMSD100. See also Figure S2.
The positive predictive value (PPV or precision) of the method to predict models with RMSD100 below 3.0 Å has been calculated after each of the three rounds of refinement. The positive predictive value in round 1 is 0.34, in round 2 0.51 and in round 3 it is 0.50. This indicates that there is a significant improvement in model quality and our ability to select good models by score when going from round 1 to 2. It also shows that the refinement process converges after round 2 with no further improvement when moving to round 3.
Quality measure can distinguish between successful and unsuccessful cases
Despite the fact that the majority of the Rosetta-refined correct topologies actually score best among all the refined models, there are still few cases when some incorrect topologies score better (see for instance 1GS9, 1NIG, 2IGC or 1JL1). A quality measure that could independently distinguish successful from unsuccessful cases would be desirable for situations when EM-Fold is used to build structures where the correct solution is not known. We developed a measure that is based on the depth of converged ensemble energy minimum (DoCEEM) presented in (Raman et al., 2010). Instead of basing the measure on the mutual RMSD between models it is based on topology assignment. A topology is defined as a placement of specific SSEs into particular density rods noting the individual orientations of SSEs along the density rods main axis (parallel or antiparallel). Given the way the models are assembled and refined with EM-Fold every generated model can be easily classified according to its topology. The DoCEEM is calculated as the energy difference between the median energy of the 10 lowest scoring models with the same topology as the top scoring model after the third round of Rosetta refinement and the median energy of the 10 lowest scoring models with a topology different from the topology of the top scoring model. Graphically speaking the DoCEEM measures how deep the energy funnel is that separates the top scoring model from all other models of different topologies. Ideally, the deeper the funnel the more likely it is that the top scoring model is the correct topology. The DoCEEM values for all the 19 proteins refined with Rosetta are shown in
Table 2. Using a cutoff of 0 Rosetta energy units (REUs), where negative values indicate success, the DoCEEM was able to correctly identify whether the top scoring model was the correct topology for all but one protein (1GS9). These results indeed suggest that deep energy funnels are very likely corresponding to models close to the native structure. This allows the user to employ the DoCEEM as a measure of how likely the algorithm found the true topology as the top scoring topology.
Table 2.
DoCEEM ananlysis of the folding results.
| protein | DoCEEM [REU] | Rank Rosetta 3 |
|---|---|---|
| 1DVO | −10.581 | 1 |
| 1GS9 | 5.087 | 4 |
| 1IAP | 5.192 | 1 |
| 1ILK | −20.213 | 1 |
| 1NIG | 1.843 | 2 |
| 1OXJ | −18.7 | 1 |
| 1X91 | −6.57 | 1 |
| 2A6B | −73.26 | 1 |
| 2FD5 | −24.344 | 1 |
| 2FM9 | −32.335 | 1 |
| 2G7S | −11.522 | 1 |
| 2GEN | −23.86 | 1 |
| 2IGC | 4.405 | 2 |
| 2IOS | −28.615 | 1 |
| 2O8P | −10.12 | 1 |
| 1CHD | 5.764 | 4 |
| 1ICX | −52.623 | 1 |
| 1JL1 | 2.579 | 2 |
| 1OZ9 | −49.456 | 1 |
| 1DVO | −10.581 | 1 |
Depth of converged ensemble energy minimum (DoCEEM) for all 19 proteins used in the benchmark is shown in column 2. DoCEEM values are calculated as the difference between the median energy of the 10 lowest scoring models with the same topology as the top scoring model after the third round of Rosetta refinement and the median energy of the 10 lowest scoring models with a topology different from the topology of the top scoring model. Negative values indicate that the mean energy of the top models of the top scoring topology is lower than the mean energy of the top models of topologies different from the top scoring topology. The table also shows the rank of the correct topology after three rounds of Rosetta refinement. DoCEEM values correlate with the ranking. This is of importance as in a non-benchmark application only DoCEEM values will be available.
Noise in simulated density maps causes slight performance decrease in the loop building steps
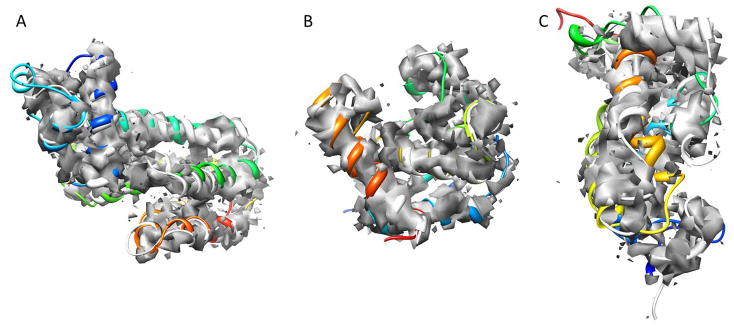
The major difference between the benchmark described so far and a real world application is that the simulated density maps used in the benchmark did not contain noise. This may not have such a profound influence on the EM-Fold assembly and refinement steps as the models only contain residues in SSEs, which are commonly well defined even in experimental maps. Noise may however have a profound impact on the loop building and refinement procedure in Rosetta that relies explicitly on density in loop regions of the proteins. To test the performance of EM-Fold and Rosetta when confronted with noisy maps, noise was added randomly to the simulated maps until a cross correlation of 0.8 between noise-free and noise-containing map was achieved. The procedure was described in (Woetzel et al., 2011) and 0.8 had been established as a realistic value best mimicking experimental density maps. The influence of the actual density map on the assembly step is minimal, so it was not repeated. This way it is also guaranteed that the same starting models are used and the comparison between noise-free and noisy maps is legitimate. All the parameters used were identical to the benchmark with the noise-free simulated density maps. Supplemental Table S3 summarizes the results of the benchmark with the noisy maps in much the same way as Table 1 did for the noise-free maps. The top scoring 150 topologies from the assembly step were refined in EM-Fold using the noisy maps. The results of the refinement step confirm that noise does not have a profound influence on the model quality during this step. The average RMSD100s are virtually identical with 2.98 Å vs. 2.91 Å. The average rank of the top scoring correct topology decreased to 40 (from 24 in the noise-free case). It is more difficult to correctly rank models based on density cross correlation when noise is present. This however does not present a major problem as long as more topologies are carried over to the Rosetta refinement rounds. The top 75 topologies after EM-Fold refinement were chosen for three rounds of Rosetta refinement. As a proof of principle, the proteins 2FD5 and 1CHD were also refined in Rosetta despite their correct topologies having ranks worse than 75. The three rounds of Rosetta refinement ranked all the correct topologies among the top 10 scoring topologies with the majority of the correct topologies scoring best in Rosetta’s force field. Over the course of the three rounds the RMSD100 values improve slightly on average but are about 0.7 Å worse than in the noise-free benchmark. This is not unexpected as the noise has the highest impact on loop regions. The overall quality of the models (10 models have an RMSD100 of less than 3 Å after the third round of Rosetta refinement) is still very good, albeit somewhat lower than in the noise-free benchmark. For illustration purposes Figure 5 shows two examples of successful model building (2G7S and 1OZ9) as well as one protein (1NIG) for which the overall RMSD100 is well beyond the target of 3 Å. It can be concluded that the proposed combination of the new version of EM-Fold with Rosetta can be successfully applied to maps containing noise.
Figure 5.
Three protein models after the third round of Rosetta refinement in the noisy maps benchmark. Superimposition of the final models (colored in rainbow) of 2G7S (A), 1OZ9 (B) and 1NIG (C) with the original PDB structures (grey) as well as the noisy density maps are shown. Density maps were simulated at 5 Å resolution (β-strand containing proteins) and at 7 Å resolution (α-helical proteins) respectively. (A) 2G7S has 194 residues. The model shown has a RMSD100 of 2.23 Å over the full length of the protein and 1.67 Å over the helical residues. (B) 1OZ9 has 150 residues. The model shown has a RMSD100 of 1.76 Å over the full length of the protein and 1.02 Å over the residues in secondary structure elements. (C) 1NIG has 152 residues. The model shown has a RMSD100 of 7.31 Å over the full length of the protein and 4.97 Å over the residues in secondary structure elements.
EM-Fold and Rosetta refinement results in models that display atomic detail beyond that present in the density map
In 14 out of 19 cases Rosetta scores the correct topology as the best topology and results in a model with an RMSD100 below 2.8Å. There is a fifteenth case (2IOS) where Rosetta scores the correct topology as the best topology, but the RMDS100 is somewhat worse. The correct topology is among the top four scoring topologies in all 19 proteins refined with Rosetta. The majority of the RMSD100 vs. score plots show a clear funnel-shape indicating that the Rosetta score correlates with model quality (see Figure 3). The vast majority of the best scoring models is in excellent agreement with the native structure as can be seen in Figure 4 and Figure S2. For 70% of the successful benchmark cases the best scoring model has a RMSD100 below 3.0 Å, indicating that these models are accurate at atomic detail. EM-Fold identifies the correct topology of a protein from a medium resolution density map in 70% of the cases. Refinement with Rosetta yields models that are accurate at atomic detail in 70% of cases where the correct topology was identified. SSEs that have been placed in the same density rod in at least 70% of the top 2000 scoring models after the third round of Rosetta refinement are correctly placed with 97% confidence. Statistics over rotamer recovery reveal that the best scoring models after three rounds of Rosetta refinement recover between 48% and 100% of the native rotamers in the protein core. Average rotamer recovery is 59%. In summary, many of the final refined models have a significant fraction of their native side chain conformations recovered correctly (see Table 1). This recovery is not based on information of side chain conformations in the medium resolution density maps. Rather it is based on Rosetta’s ability to correctly place side chains once the backbone conformation approaches the native structure. Hence the main achievement of the protocol is that we were able to de novo build backbone models of the benchmark proteins guided by the density maps that are of sufficient quality to recover side chain conformations. The main reason for failure of assembly of the correct topology is inaccurate prediction of secondary structure. Primary obstacles for reaching atomic-detail accuracy are a systematic sequence shift in secondary structure elements that results in suboptimal starting models for Rosetta and long loop regions that are difficult to construct at atomic detail.
Applying the protocol to experimental maps yields low RMSD structures for SSE model parts and atomic detail in favorable case
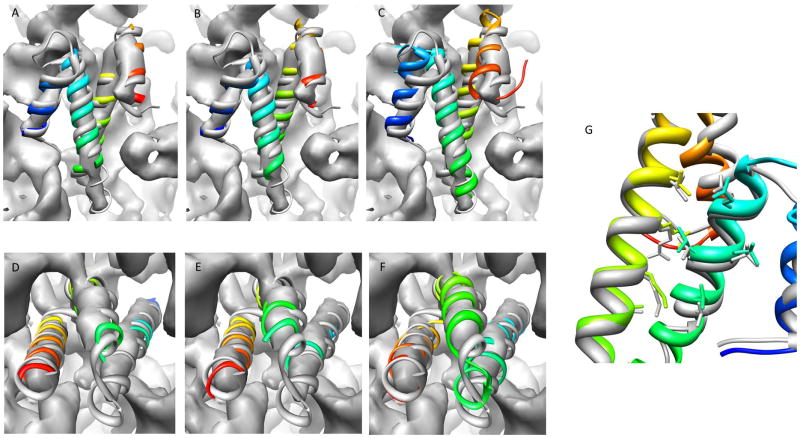
Due to the still limited number of experimental cryoEM density maps at resolutions between 5–7 Å of proteins for which also high resolution crystal structures exist, the benchmark was performed on simulated density maps with added noise. To test performance on experimental density maps five proteins for which experimental maps and high resolution structures are available were selected. Models were built into the bovine metarhodopsin cryoEM density map (EMDB 1079, (Ruprecht et al., 2004), 5.5 Å resolution) and compared to the crystal structure of bovine rhodopsin (PDB ID 1GZM, (Li et al., 2004)). Additionally, model for proteins PrgH and PrgK were built into the subnanometer resolution structure from Salmonella’s needle complex (EMDB 1874, (Schraidt and Marlovits, 2011), subnanometer resolution) and compared to docked crystal structures of these components (PDB ID 2Y9J, (Schraidt and Marlovits, 2011)). Finally, models for the 30s ribosomal proteins S15 and S20 were built into the ribosome cryoEM density map (EMDB 1829, (Bhushan et al., 2011), 5.6 Å resolution) and compared to the crystal structures of these proteins (PDB IDs 2WWLO and 2WWLT, (Seidelt et al., 2009)).
The same EM-Fold folding protocol applied to the benchmark proteins with simulated maps was used for the proteins with experimental density maps. While the ribosome proteins underwent three rounds of Rosetta refinement, only a single round of Rosetta refinement was performed for the other proteins in order to limit the computational resources needed. The results are summarized in Table 3. Additionally, Figure 6 and Figure S3 show the models after EM-Fold assembly step, EM-Fold refinement step and Rosetta loop building and refinement in context with the native structures and the experimental density maps. The correct topology scores within the top 40 topologies for all five proteins after the EM-Fold assembly step. For two of the proteins the ranking of the correct topology improves slightly after EM-Fold refinement. The average RMSD100 of the correct topology models after the initial EM-Fold assembly step is 3.25 Å and improves to 2.86 Å after EM-Fold refinement. These values are in the same range as the RMSD100 values of the benchmark proteins using simulated density maps. Along with the results of the noisy maps benchmark this is confirmation that EM-Fold also works well for experimental density map. The results for the ribosomal proteins S15 and S20 show improvement over all rounds of model building. The final models exhibit RMSD100 values below 3 Å and side chain conformations within the protein core are recovered especially for 2WWLO (see panel G in Figure 6). The good results for these proteins are speculated to be mainly due to their high secondary structure content and the superb quality of the density map. For rhodopsin and salmonella proteins the quality of the models after Rosetta loop building and refinement is lower than the model quality in the benchmarks with simulated density maps. The average RMSD100 over the full length of these proteins is 4.92 Å, while the average RMSD100 over residues in secondary structure elements is 2.79 Å. The average deviation for these proteins is higher mainly because of long, floppy loop regions that are difficult to predict and because of high amount of noise in loop regions in experimental density maps. While the RMSD100 are slightly higher than in the previously discussed benchmarks, even for these challenging cases EM-Fold proves to be a highly valuable tool to determine the correct topology of a protein based on the density map and can predict good models for protein structures even for experimental maps.
Table 3.
Results of benchmark on three experimental density maps.
| Rank/RMSD100 [Å] | Rank/RMSD100 [Å] (RMSD100 SSEs [Å]) | |||
|---|---|---|---|---|
| protein | size | EM-Fold assembly | EM-Fold refinement | Rosetta |
| 1GZM | 349, 8, 0 | 37/2.26 | 35/2.79 | 2/4.60 (2.74) |
| 2Y9JO | 186, 4, 6 | 26/2.81 | 23/2.50 | 2/5.51 (2.71) |
| 2Y9JZ | 170, 4, 6 | 17/3.11 | 48/2.86 | 2/4.64 (2.91) |
| 2WWLO | 88, 4, 0 | 2/3.98 | 33/3.23 | 1/2.96 (2.01) |
| 2WWLT | 85, 3, 0 | 1/4.10 | 8/2.94 | 8/2.84 (2.41) |
This table summarizes the results of the benchmark using experimental density maps from rhodopsin, salmonella and ribosome. The first two columns show the pdb ID of the protein crystal structure and protein size information. Column 2 lists the number of amino acids, number of α-helices with at least 12 residues and the number of β-strands with at least 5 residues. Columns 3 contains the results of the EM-Fold assembly step. Column 4 contains the results of the EM-Fold refinement step. The rank of the correct topology model within all scored models as well as the RMSD100 of the correct topology model are given. Column 5 shows the results of the Rosetta loop building and refinement using using the experimental maps. It lists the rank of the correct topology model within all scored models, the RMSD100 of the correct topology model as well as the RMSD100 of the correct topology model over residues in secondary structure elements (numbers in parentheses). All RMSD100 values are determined over the backbone atoms N, Cα, C and O.
Figure 6.
Results of ribosome benchmark proteins with experimental density maps. Protein models after EM-Fold assembly step (A, D), after EM-Fold refinement step (B, E) and third round of Rosetta loop building and refinement (C, F) are shown for the two benchmark proteins. Superimposition of the models (colored in rainbow) of 2WWLO (A–C) and 2WWLT (D–F) with the original PDB structures (grey) as well as the experimental density maps are shown. Panel G shows atomic detail recovered for 2WWLO after the third round of Rosetta refinement. See also Figure S6.
Conclusion
In summary, the combination of EM-Fold and Rosetta is a powerful tool for de novo folding of proteins into medium resolution density maps. This report demonstrates that computational methods are capable of extending the information available from cryoEM density maps. We further demonstrate that the combination of EM-Fold and Rosetta can build an atomic model from a medium resolution density map and the protein sequence. This will give researchers the opportunity to utilize medium resolution density maps more effectively. This work also demonstrates that medium resolution density maps can contribute valuable information regarding the true atomic resolution structure.
The results show that EM-Fold is the method of choice in cases when a medium resolution density map is determined, SSEs are identifiable as density rods (either manually or using automated software), loop connectivity information is elusive and no backbone trace or template start model are available. For higher resolution maps that contain information on the SSE connectivity backbone tracing techniques such as GORGON may be better suited (Baker et al., 2011). For maps at lower resolution where secondary structure elements are not clearly visible, techniques such as fitting of comparative models should be used (Topf et al., 2005).
It appears that all β-strand proteins are harder to accurately model with EM-Fold. We attribute this observation to a combination of several effects: a) accuracy of secondary structure prediction is reduced for β-strands compared to α-helices, b) it is generally more difficult to de novo fold all β-strand proteins due to the increased number of non-local contacts that have to be sampled (Bonneau et al., 2002), c) all β-strand proteins have a higher number of SSEs per residue leading to a larger number of possible topologies that need to be sampled. d) all β-strand proteins have a larger fraction of residues in loop regions. Because loop regions are less accurately modeled in the EM-Fold protocol, RMSD-values for all β-strand proteins are higher. Table 4 summarizes indicators a through d and relates them to success in the benchmark. While there is no single indicator of success, it seems that particularly the contact order and the fraction of residues in loop regions correlate with success. The average contact order in the benchmark set was about 13 while the average contact order for failures was 16. Similarly the average fraction of residues in loop regions was 0.33 over the benchmark set and 0.42 for the failures. These quantities may give researchers using EM-Fold an indication of what the expected success may be.
Table 4.
Summary of protein statistics and benchmark performance.
| protein | residues | SSPred accuracy | contact order | SSE per residue | fraction loop | success |
|---|---|---|---|---|---|---|
| 1DVO | 152 | 0.74 | 9.28 | 0.03 | 0.26 | atomic resolution |
| 1GS9 | 165 | 0.87 | 11.67 | 0.02 | 0.3 | topology |
| 1IAP | 211 | 0.79 | 14.86 | 0.03 | 0.39 | atomic resolution |
| 1ILK | 151 | 0.81 | 6.08 | 0.03 | 0.26 | atomic resolution |
| 1NIG | 152 | 0.69 | 12.79 | 0.03 | 0.32 | topology |
| 1OXJ | 173 | 0.80 | 8.47 | 0.02 | 0.32 | topology |
| 1X91 | 153 | 0.78 | 11.21 | 0.03 | 0.24 | atomic resolution |
| 1Z3Y | 238 | 0.78 | 12.12 | 0.03 | 0.42 | failure |
| 2A6B | 234 | 0.86 | 24.06 | 0.03 | 0.28 | atomic resolution |
| 2FD5 | 180 | 0.80 | 11.18 | 0.03 | 0.26 | atomic resolution |
| 2FM9 | 215 | 0.82 | 13 | 0.04 | 0.28 | atomic resolution |
| 2FQ4 | 192 | 0.83 | 9.06 | 0.04 | 0.34 | failure |
| 2G7S | 194 | 0.76 | 11.08 | 0.03 | 0.22 | atomic resolution |
| 2GEN | 197 | 0.80 | 10.75 | 0.04 | 0.23 | atomic resolution |
| 2IGC | 164 | 0.69 | 11.29 | 0.02 | 0.31 | topology |
| 2IOS | 150 | 0.80 | 8.52 | 0.04 | 0.34 | topology |
| 2IU1 | 208 | 0.77 | 13.03 | 0.02 | 0.38 | failure |
| 2NR7 | 195 | 0.75 | 13.91 | 0.03 | 0.33 | failure |
| 2O8P | 227 | 0.79 | 8.53 | 0.04 | 0.19 | atomic resolution |
| 2QK1 | 249 | 0.81 | 9.05 | 0.04 | 0.32 | failure |
| 1BJ7 | 156 | 0.79 | 20.86 | 0.06 | 0.36 | failure |
| 1CHD | 203 | 0.73 | 19.04 | 0.04 | 0.43 | topology |
| 1ICX | 155 | 0.77 | 18.63 | 0.05 | 0.36 | atomic resolution |
| 1JL1 | 155 | 0.77 | 11.35 | 0.05 | 0.32 | atomic resolution |
| 1OZ9 | 150 | 0.80 | 7.1 | 0.06 | 0.32 | atomic resolution |
| 1WBA | 175 | 0.80 | 21.541 | 0.06 | 0.54 | failure |
| 2QVK | 192 | 0.72 | 28.262 | 0.04 | 0.69 | failure |
Summary of benchmark protein statistics and the success of the protein in the benchmark. For each of the proteins used in the benchmark the number of residues, the accuracy of the consensus secondary structure prediction, the absolute contact order, the number of secondary structures elements per residue and the fraction of residues that are in loop regions are shown. Additionally it is labeled whether the benchmark protocol managed to predict the protein’s structure to atomic detail, whether atomic detail was not achieved but the protein topology has been predicted correctly or whether EM-Fold failed to predict the structure of this protein.
In summary, substantial progress has been made since the initial EM-Fold release (Lindert et al., 2009). Because of its added features the new version of EM-Fold can refine protein models to atomic-detail accuracy in favorable cases, it is more tolerant to errors in secondary structure prediction, and can assemble proteins that contain β-strands. The consistent ability of predicting protein structure de novo and at atomic detail accuracy based on medium resolution density maps is genuine progress in the field of cryoEM modeling techniques.
Experimental Procedures
Folding protocol
The folding protocol employed in this work is summarized in Figure 1. This basic protocol is based on the initial EM-Fold publication (Lindert et al., 2009). Several improvements have been added to this new version of EM-Fold. These will be discussed in greater detail here. Starting from the primary sequence of the protein, α-helices and β-strands are predicted using jufo (Meiler and Baker, 2003a; Meiler et al., 2001), PsiPred (Jones, 1999) and PROFphd (Rost and Sander, 1993a; Rost and Sander, 1993b; Rost and Sander, 1994). The predictions as well as their consensus are stored in a pool of secondary structure elements (see panel A). The assembly step (panel B) places SSEs from the pool into the density rods. It is assumed that the density for α-helices and β-strands is sufficiently different to exclusively place the correct secondary structure elements into the individual density rods. In addition to the moves described in (Lindert et al., 2009), growing and shrinking of SSEs is performed, helping alleviate some of the problems caused by incorrect secondary structure prediction. In (Lindert et al., 2009) it was shown that the secondary structure prediction algorithms generally under-predict the length of α-helices. In the original implementation of EM-Fold this was addressed by added additional extended copies of α-helices to the pool. Only the predicted SSEs are added to the pool in the new version. Subsequently during the assembly Monte Carlo steps, SSEs are randomly grown or shrunk by up to two residues per step. The resizing is accompanied by a score that evaluates the agreement of secondary structure in the model with the predicted secondary structure. This ensures that SSEs remain in overall agreement with the predicted regions. Growth and shrinkage of SSEs has the potential to compensate for incorrect secondary structure prediction in a more dynamic way than the SSE pool used before. Models built in the assembly step are clustered. The best scoring clusters transition into the refinement step. The refinement step (panel C) applies small translational and rotational perturbations to the SSEs in the model. When SSEs are placed into the density rods they are idealized, i.e. perfectly straight. Some density rods however show at least a slight curvature. A new move that bends SSEs has been added to the refinement step. The center and amount of the bending are determined randomly. With bending in place it is necessary to evaluate the agreement of the model with the density map. In the new implementation this is done using a density cross correlation score. Scores that evaluate solvation free energy and residue-residue pairwise interaction within the protein are used in addition. A small number of top scoring topologies identified in the refinement step will be used for loop building and refinement within Rosetta. Three rounds of Rosetta refinement (panels D and E) build missing coordinates and refine the model further. The first round of Rosetta refinement (panel D) builds missing loop coordinates guided by the density map. The executable used is loopmodel.linuxgccrelease. In the following two rounds (panel E), regions of the models that agree least with the density map are identified (loops_from_density.linuxgccrelease) and rebuilt (loopmodel.linuxgccrelease). Each round includes a relaxation of the overall structure. An increasingly smaller number of topologies enter each of the three rounds of Rosetta refinement. After each round the built models are clustered according to their topology and only the best scoring representative of the top topologies will advance into the next round of refinement. After the third round of Rosetta refinement, the best scoring model is identified as the model for the protein structure.
Benchmark
A benchmark set of 20 α-helical and 7 β-sheet proteins was compiled from the protein data bank. The proteins range in size from 150 to 249 residues. Other selection criteria were secondary structure content of least 60% and the availability of high resolution crystal structures for model comparison. The α-helical proteins contain between 4 and 9 α-helices, while the β-sheet proteins contain between 4 and 10 β-strands. Density maps at 7 and 5 Å resolution were simulated for the α-helical and β-sheet proteins respectively, using PDB2VOL from the SITUS package (Wriggers and Birmanns, 2001). A voxel spacing of 1.5 Å and Gaussian flattening was used. The rational for this was that density maps at these resolutions will exhibit sufficient detail to identify density rods for α-helices and β-strands respectively. Additionally, density maps at 7 and 5 Å resolution which had noise added were simulated using the PDB2DENSITY application of the BCL. Noise was added randomly until a cross correlation between noisy and noise-free maps dropped below 0.8. Jufo, PsiPred and PROFphd were used to predict secondary structure elements for the consensus pool. A three-state model (helix, strand, coil) was used for the pool. α-helices with 12 or more predicted residues and β-strands with at least 5 predicted residues were added to the pool. Shorter secondary elements are omitted from the initial EM-Fold assembly and added in the later Rosetta refinement step. In the assembly step 50,000 models (2,000 rejected Monte Carlo steps) are built for each of the 27 proteins. Building one model takes approximately 60 s on a single 2.4GHz Quad-Core AMD Opteron Processor. Building 50,000 models takes approximately 2–3 hours on a 400 core cluster. The 50,000 models are clustered into topologies according to their placement of particular stretches of sequence into density rods. The topologies are ranked by the overall score and the top scoring models within each of the top scoring 150 topologies advance to the refinement step. If the correct topology is not identified within the top 150 scoring topologies, this protein counts as a failure in the benchmark. Quality of the models is determined by calculating the RMSD100 (Carugo and Pongor, 2001) values over the backbone atoms N, Cα, C and O. For each of the top 150 scoring topologies from the assembly step, 500 refined models are built in the refinement step. Again, building one model takes approximately 60 s on a single 2.4GHz Quad-Core AMD Opteron Processor. Building 75,000 refined models takes approximately 3–4 hours on a 400 core cluster. These models are ranked by their refinement score and the top scoring 50 (75 in the noisy map benchmark) topologies after refinement step are identified. These 50 models serve as input for the first round of Rosetta refinement. Rosetta refinement is performed on the ACCRE computer cluster (2.4GHz Quad-Core AMD Opteron Processors). Timing of Rosetta refinement depends heavily on the size of the protein, the size of the loop regions and the size of the density map. Generally it can be assumed that a single round of refinement for one protein takes about 24 hours on a 400 core cluster. In the first round of refinement Rosetta builds loops models for these 50 topologies guided by the density map. The models are clustered according to topology and the top scoring models from the top 15 clusters enter round 2 of Rosetta refinement. Using the loops_from_density.linuxgccrelease executable, regions within these 15 proteins are identified that agree least with the density map. These regions are subsequently rebuilt using the guidance of the density map. The top scoring 5 topologies after the second round of Rosetta refinement are used as starting models in the third round of refinement. After three rounds of refinement the best scoring model is evaluated.
Software availability
EM-Fold is part of the BCL software library developed in the Meiler laboratory. It is supported for Linux, Windows and Mac environments. EM-Fold is freely available to the scientific community at http://bclcommons.vueinnovations.com/licensing.
Supplementary Material
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
References
- Alexander N, Bortolus M, Al-Mestarihi A, McHaourab H, Meiler J. De novo high-resolution protein structure determination from sparse spin-labeling EPR data. Structure. 2008;16:181–195. doi: 10.1016/j.str.2007.11.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker ML, Abeysinghe SS, Schuh S, Coleman RA, Abrams A, Marsh MP, Hryc CF, Ruths T, Chiu W, Ju T. Modeling protein structure at near atomic resolutions with Gorgon. Journal of Structural Biology. 2011;174:360–373. doi: 10.1016/j.jsb.2011.01.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Baker ML, Ju T, Chiu W. Identification of secondary structure elements in intermediate-resolution density maps. Structure. 2007;15:7–19. doi: 10.1016/j.str.2006.11.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bhushan S, Hoffmann T, Seidelt B, Frauenfeld J, Mielke T, Berninghausen O, Wilson DN, Beckmann R. SecM-stalled ribosomes adopt an altered geometry at the peptidyl transferase center. PLoS Biol. 2011;9:e1000581. doi: 10.1371/journal.pbio.1000581. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bonneau R, Ruczinski I, Tsai J, Baker D. Contact order and ab initio protein structure prediction. Protein Sci. 2002;11:1937–1944. doi: 10.1110/ps.3790102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bowers PM, Strauss CE, Baker D. De novo protein structure determination using sparse NMR data. J Biomol NMR. 2000;18:311–318. doi: 10.1023/a:1026744431105. [DOI] [PubMed] [Google Scholar]
- Bradley P, Misura KM, Baker D. Toward high-resolution de novo structure prediction for small proteins. Science. 2005;309:1868–1871. doi: 10.1126/science.1113801. [DOI] [PubMed] [Google Scholar]
- Carugo O, Pongor S. A normalized root-mean-square distance for comparing protein three-dimensional structures. Protein Sci. 2001;10:1470–1473. doi: 10.1110/ps.690101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cong Y, Baker ML, Jakana J, Woolford D, Miller EJ, Reissmann S, Kumar RN, Redding-Johanson AM, Batth TS, Mukhopadhyay A, et al. 4.0-Å resolution cryo-EM structure of the mammalian chaperonin TRiC/CCT reveals its unique subunit arrangement. Proceedings of the National Academy of Sciences. 2010;107:4967–4972. doi: 10.1073/pnas.0913774107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dal Palu A, He J, Pontelli E, Lu Y. Identification of alpha-helices from low resolution protein density maps. Comput Syst Bioinformatics Conf. 2006:89–98. [PubMed] [Google Scholar]
- DiMaio F, Tyka MD, Baker ML, Chiu W, Baker D. Refinement of protein structures into low-resolution density maps using rosetta. J Mol Biol. 2009;392:181–190. doi: 10.1016/j.jmb.2009.07.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hanson SM, Dawson ES, Francis DJ, Van Eps N, Klug CS, Hubbell WL, Meiler J, Gurevich VV. A model for the solution structure of the rod arrestin tetramer. Structure. 2008;16:924–934. doi: 10.1016/j.str.2008.03.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hirst SJ, Alexander N, McHaourab HS, Meiler J. RosettaEPR: An integrated tool for protein structure determination from sparse EPR data. Journal of Structural Biology. 2011;173:506–514. doi: 10.1016/j.jsb.2010.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang W, Baker ML, Ludtke SJ, Chiu W. Bridging the information gap: Computational tools for intermediate resolution structure interpretation. Journal of Molecular Biology. 2001;308:1033–1044. doi: 10.1006/jmbi.2001.4633. [DOI] [PubMed] [Google Scholar]
- Jones DT. Protein secondary structure prediction based on position-specific scoring matrices. Journal of Molecular Biology. 1999;292:195–202. doi: 10.1006/jmbi.1999.3091. [DOI] [PubMed] [Google Scholar]
- Kong Y, Zhang X, Baker TS, Ma J. A Structural-informatics approach for tracing beta-sheets: building pseudo-C(alpha) traces for beta-strands in intermediate-resolution density maps. J Mol Biol. 2004;339:117–130. doi: 10.1016/j.jmb.2004.03.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li J, Edwards PC, Burghammer M, Villa C, Schertler GF. Structure of bovine rhodopsin in a trigonal crystal form. J Mol Biol. 2004;343:1409–1438. doi: 10.1016/j.jmb.2004.08.090. [DOI] [PubMed] [Google Scholar]
- Lindert S, Staritzbichler R, Wotzel N, Karakas M, Stewart PL, Meiler J. EM-fold: De novo folding of alpha-helical proteins guided by intermediate-resolution electron microscopy density maps. Structure. 2009;17:990–1003. doi: 10.1016/j.str.2009.06.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Jin L, Koh SB, Atanasov I, Schein S, Wu L, Zhou ZH. Atomic structure of human adenovirus by cryo-EM reveals interactions among protein networks. Science. 2010a;329:1038–1043. doi: 10.1126/science.1187433. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu X, Zhang Q, Murata K, Baker ML, Sullivan MB, Fu C, Dougherty MT, Schmid MF, Osburne MS, Chisholm SW, Chiu W. Structural changes in a marine podovirus associated with release of its genome into Prochlorococcus. Nat Struct Mol Biol. 2010b;17:830–836. doi: 10.1038/nsmb.1823. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ludtke SJ, Baker ML, Chen DH, Song JL, Chuang DT, Chiu W. De novo backbone trace of GroEL from single particle electron cryomicroscopy. Structure. 2008;16:441–448. doi: 10.1016/j.str.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Ludtke SJ, Chen DH, Song JL, Chuang DT, Chiu W. Seeing GroEL at 6 Å Resolution by Single Particle Electron Cryomicroscopy. Structure. 2004;12:1129–1136. doi: 10.1016/j.str.2004.05.006. [DOI] [PubMed] [Google Scholar]
- Meiler J, Baker D. Coupled prediction of protein secondary and tertiary structure. Proc Natl Acad Sci U S A. 2003a;100:12105–12110. doi: 10.1073/pnas.1831973100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meiler J, Baker D. Rapid protein fold determination using unassigned NMR data. Proc Natl Acad Sci U S A. 2003b;100:15404–15409. doi: 10.1073/pnas.2434121100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meiler J, Baker D. The fumarate sensor DcuS: progress in rapid protein fold elucidation by combining protein structure prediction methods with NMR spectroscopy. J Magn Reson. 2005;173:310–316. doi: 10.1016/j.jmr.2004.11.031. [DOI] [PubMed] [Google Scholar]
- Meiler J, Muller M, Zeidler A, Schmaschke F. Generation and evaluation of dimension-reduced amino acid parameter representations by artificial neural networks. J Mol Model. 2001;7:360–369. [Google Scholar]
- Min GW, Wang HB, Sun TT, Kong XP. Structural basis for tetraspanin functions as revealed by the cryo-EM structure of uroplakin complexes at 6-A resolution. Journal of Cell Biology. 2006;173:975–983. doi: 10.1083/jcb.200602086. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Raman S, Lange OF, Rossi P, Tyka M, Wang X, Aramini J, Liu G, Ramelot TA, Eletsky A, Szyperski T, et al. NMR structure determination for larger proteins using backbone-only data. Science. 2010;327:1014–1018. doi: 10.1126/science.1183649. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rohl CA, Baker D. De novo determination of protein backbone structure from residual dipolar couplings using Rosetta. J Am Chem Soc. 2002;124:2723–2729. doi: 10.1021/ja016880e. [DOI] [PubMed] [Google Scholar]
- Rost B, Sander C. Improved prediction of protein secondary structure by use of sequence profiles and neural networks. Proceedings of the National Academy of Sciences. 1993a;90:7558–7562. doi: 10.1073/pnas.90.16.7558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rost B, Sander C. Prediction of Protein Secondary Structure at Better than 70% Accuracy. Journal of Molecular Biology. 1993b;232:584–599. doi: 10.1006/jmbi.1993.1413. [DOI] [PubMed] [Google Scholar]
- Rost B, Sander C. Combining evolutionary information and neural networks to predict protein secondary structure. Proteins. 1994;19:55–72. doi: 10.1002/prot.340190108. [DOI] [PubMed] [Google Scholar]
- Ruprecht JJ, Mielke T, Vogel R, Villa C, Schertler GF. Electron crystallography reveals the structure of metarhodopsin I. EMBO J. 2004;23:3609–3620. doi: 10.1038/sj.emboj.7600374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saban SD, Silvestry M, Nemerow GR, Stewart PL. Visualization of alpha-helices in a 6-angstrom resolution cryoelectron microscopy structure of adenovirus allows refinement of capsid protein assignments. J Virol. 2006;80:12049–12059. doi: 10.1128/JVI.01652-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schraidt O, Marlovits TC. Three-dimensional model of Salmonella’s needle complex at subnanometer resolution. Science. 2011;331:1192–1195. doi: 10.1126/science.1199358. [DOI] [PubMed] [Google Scholar]
- Seidelt B, Innis CA, Wilson DN, Gartmann M, Armache JP, Villa E, Trabuco LG, Becker T, Mielke T, Schulten K, et al. Structural Insight into Nascent Polypeptide Chain-Mediated Translational Stalling. Science. 2009;326:1412–1415. doi: 10.1126/science.1177662. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Serysheva II, Ludtke SJ, Baker ML, Cong Y, Topf M, Eramian D, Sali A, Hamilton SL, Chiu W. Subnanometer-resolution electron cryomicroscopy-based domain models for the cytoplasmic region of skeletal muscle RyR channel. Proc Natl Acad Sci U S A. 2008;105:9610–9615. doi: 10.1073/pnas.0803189105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sibanda BL, Chirgadze DY, Blundell TL. Crystal structure of DNA-PKcs reveals a large open-ring cradle comprised of HEAT repeats. Nature. 2010;463:118–121. doi: 10.1038/nature08648. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Topf M, Baker ML, John B, Chiu W, Sali A. Structural characterization of components of protein assemblies by comparative modeling and electron cryo-microscopy. J Struct Biol. 2005;149:191–203. doi: 10.1016/j.jsb.2004.11.004. [DOI] [PubMed] [Google Scholar]
- Topf M, Baker ML, Marti-Renom MA, Chiu W, Sali A. Refinement of protein structures by iterative comparative modeling and CryoEM density fitting. J Mol Biol. 2006;357:1655–1668. doi: 10.1016/j.jmb.2006.01.062. [DOI] [PubMed] [Google Scholar]
- Villa E, Sengupta J, Trabuco LG, LeBarron J, Baxter WT, Shaikh TR, Grassucci RA, Nissen P, Ehrenberg M, Schulten K, Frank J. Ribosome-induced changes in elongation factor Tu conformation control GTP hydrolysis. Proc Natl Acad Sci U S A. 2009;106:1063–1068. doi: 10.1073/pnas.0811370106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ward A, Reyes CL, Yu J, Roth CB, Chang G. Flexibility in the ABC transporter MsbA: Alternating access with a twist. Proc Natl Acad Sci U S A. 2007;104:19005–19010. doi: 10.1073/pnas.0709388104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Woetzel N, Lindert S, Stewart PL, Meiler J. BCL::EM-Fit: Rigid body fitting of atomic structures into density maps using geometric hashing and real space refinement. Journal of Structural Biology. 2011 doi: 10.1016/j.jsb.2011.04.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wriggers W, Birmanns S. Using situs for flexible and rigid-body fitting of multiresolution single-molecule data. J Struct Biol. 2001;133:193–202. doi: 10.1006/jsbi.2000.4350. [DOI] [PubMed] [Google Scholar]
- Zhang R, Hryc CF, Cong Y, Liu X, Jakana J, Gorchakov R, Baker ML, Weaver SC, Chiu W. 4.4 A cryo-EM structure of an enveloped alphavirus Venezuelan equine encephalitis virus. EMBO J. 2011;30:3854–3863. doi: 10.1038/emboj.2011.261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou ZH. Towards atomic resolution structural determination by single-particle cryo-electron microscopy. Curr Opin Struct Biol. 2008;18:218–228. doi: 10.1016/j.sbi.2008.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu J, Cheng L, Fang Q, Zhou ZH, Honig B. Building and refining protein models within cryo-electron microscopy density maps based on homology modeling and multiscale structure refinement. Journal of Molecular Biology. 2010;397:835–851. doi: 10.1016/j.jmb.2010.01.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.