Quantifying Local Stiffness Variations in Radiofrequency Ablations with Dynamic Indentation

Abstract

Elastographic imaging can be used to monitor ablation procedures, however confident and clear determination of the ablation boundary is essential to ensure complete treatment of the pathological target. To investigate the potential for ablation boundary representation on elastographic images, local variations in the viscoelastic properties in radiofrequency ablated regions that were formed in vivo in porcine liver tissue were quantified using dynamic indentation. Spatial stiffness maps were then correlated to stained histology, the gold standard for determination of the ablation periphery or boundary. Regions of interest in eleven radiofrequency ablation samples were indented at 18–24 locations each, including the central zone of complete necrosis and more peripheral transition zones including normal tissue. Storage modulus and rate of stiffening were both greatest in the central ablation zone and decreased with radial distance away from the center. The storage modulus and modulus contrast at the ablation outer transition zone boundary were 3.1 ± 1.0 kPa and 1.6 ± 0.4, respectively, and 36.2 ± 9.1 kPa and 18.3 ± 5.5 at the condensation boundary within the ablation zone. Elastographic imaging modalities were then compared to gross pathology in ex vivo bovine liver tissue. Area estimated from strain, shear wave velocity, and gross pathology images were 470 mm², 560 mm², and 574 mm², respectively, and ablation widths were 19.4 mm, 20.7 mm, and 23.0 mm. This study has provided insights into spatial stiffness distributions within radiofrequency ablations and suggests that low stiffness contrast on the ablation periphery leads to the observed underestimation of ablation extent on elastographic images.

I. Introduction

Methods for imaging the elastic properties of tissue have shown promise in many clinical applications. For example, manual palpation is used by physicians to detect pathological tissue because of known correlations between tissue stiffness and disease state [1]; elastographic imaging can be used in conjunction with traditional B-mode ultrasound imaging to provide more objectivity to this procedure. Strain imaging, one popular elastographic technique, estimates the local displacement and strain distribution in tissue using normalized time-domain cross-correlation on pre- and post-deformation frames of radiofrequency data obtained following a quasi-static deformation [2]. This approach has shown success detecting stiff lesions in the breast, using the ultrasound transducer as a compression device [3]. Newer elastographic imaging modalities utilizing dynamic excitation quantify tissue stiffness by estimating the velocity of shear waves generated within the tissue, which is proportional to the Young's Modulus, an inherent tissue property [4–7].

Elastography is not only used to detect pathologies but also to monitor minimally invasive treatments such as radiofrequency (RF) thermal ablation [4, 8–13]. One common application of RF ablation is hepatic tumor treatment, which provides the patient with a minimally invasive alternative to surgical resection. In RF ablation procedures, an alternating electric current is applied through an electrode inserted into the cancerous target. Ionic agitation produced by the current flow causes localized tissue heating [14]. Technical success of RF ablation is defined when the zone of ablation encompasses the tumor and a surrounding safety margin, so accurate imaging feedback is needed to verify complete treatment. Temperatures exceeding 50°C are considered lethal when maintained for more than 1–2 minutes, with the primary mechanism of cell death being thermal coagulative necrosis [15–16]. At ablative temperatures, cellular proteins are denatured and free water can be vaporized, leading to acute tissue dehydration and an increase in tissue stiffness [17], which can be monitored using a number of elastographic techniques.

Elastographic techniques provide a non-ionizing, real-time approach to monitor ablation procedures, but a discrepancy between RF ablation representation on elastographic images and gross pathology has been observed. Both strain and shear wave velocity imaging have shown that observer boundary delineations tend to underestimate RF ablation area when compared to gross pathology [4, 8–9, 18]. The same discrepancy has also been observed with sonoelastography imaging [19]. One possible explanation may be small differences in the modulus contrast between the ablation boundary and untreated tissue. Understanding ablation representation on elastographic images is imperative, as misinterpretation of the ablation borders may leave untreated viable malignant tissue cells after the ablation procedure, which can lead to tumor recurrence. Currently, no studies have investigated how tissue stiffness correlates with cell viability, the gold standard for the determination of ablation extent.

In this study, we hope to gain an understanding of how spatial stiffness variations in RF ablations correlate to stained histology, the gold standard utilized to determine cell viability and thus ablation extent. This may also help clarify observed discrepancies between gross pathology and elastographic images. Previous work has investigated the mechanical contrast between RF ablations and untreated tissue on a global level. Ablation cores have been dynamically tested to determine a global value of the viscoelastic properties of the ablations [20]. However, studies have not investigated local stiffness variations within RF ablations, which may influence the ablation appearance on elastographic images. In addition, stiffness maps have not been compared to cell viability within ablations, the true measure of the ablation periphery. Dynamic indentation provides the ability to quantify the Young's Modulus in tissue samples from force-displacement curves but has yet to be applied to RF ablations to quantify their viscoelastic properties [21–22]. In this study, we used a dynamic indentation approach to locally quantify the viscoelastic material properties within RF ablated regions and compared these maps to stained gross pathology images to gain a better understanding of the spatial modulus distribution within RF ablations.

II. METHODS

A. Animal Models

RF ablations were created in three female domestic swine. Animals were anesthetized initially with an intramuscular injection of teletamine and zolazepam (Telazol, Fort Lodge Laboratories; Fort Dodge, IA) and xylazine (Rompun, Bayer Corp.; Shawnee Mission, KS). After intubation, anesthesia was maintained with 1–3% inhaled isoflurane. The animals were placed in a supine position, and the liver exposed through a midline incision. Ablation sites were selected in regions of the liver where 1–3 cm of normal tissue would surround the ablation, and sites with large blood vessels were avoided. Ablations were formed using a Cool-tip™ RF ablation system (Valleylab; Boulder, CO) and electrodes 1.5 mm in diameter (17 gauge) with a 3.0 cm active length to create approximately 35 mm × 20 mm ellipsoidal ablations. Power was applied for 10 minutes per ablation using the RF generator's impedance-controlled power pulsing algorithm. After all ablations were formed and a concurrent imaging study completed, the animals were euthanized with an intravenous solution of pentobarbital sodium and phenytoin sodium (Beuthanasia-D; Schering-Plough,Kenilworth, NJ, USA), and the liver was removed en bloc. All protocols and procedures were approved by the University of Wisconsin-Madison Institutional Animal Care and Use Committee.

Matching elastographic imaging planes from in vivo experiments with stained pathology is difficult to attain with confidence. To compare two different elastographic imaging modalities, electrode displacement and electrode vibration elastography, with gross pathology in a controlled setting, an ex vivo ablation was formed in bovine liver tissue using the same radiofrequency ablation system as in the in vivo study. The electrode was inserted approximately 5 cm into the liver, and power was applied for 3 minutes using the radiofrequency generator's impedance-controlled power pulsing algorithm to create ablations similar in size to the in vivo study. Electrode displacement and electrode vibration elastography were performed as previously described [4]. Following data acquisition, fiducial markers were placed into the imaging plane. The ablation zone was then sliced and photographed.

B. Mechanical Testing

The RF ablated regions created in vivo were prepared for dynamic indentation immediately following animal sacrifice. The ablations were sliced down the middle along the long axis, and the face of each half was sliced to ~3 mm thickness. One slice was reserved for indentation, and the opposite side was immersed in a solution containing nitro blue tetrazolium chloride (NBT) to demarcate the zone of complete necrosis. Both faces were photographed, placed in saline, and refrigerated. Before testing, each sample was brought to room temperature, measured for thickness, and placed on the indenter stage on top of a hard felt pad (~1.6 GPa) soaked in saline. All samples were indented within two hours of removal from the saline and within 24 hours of animal sacrifice. A total of nine ablations were mechanically tested, two of which were indented in different regions of interest (ROIs) on opposite sides of the ablation, for a total of eleven samples.

Ablation slices were mechanically tested using an MTS Nanoindenter XP (Agilent, MTS Nano Instruments; Oak Ridge, TN, USA). The indenter is a 2 mm diameter sapphire flat-ended piston that descends from above to contact the surface of the sample. Typically, 18–24 locations with 2 mm spacing in the x and y directions (three rows, 6–8 locations per row) were indented in a raster pattern on each sample at a testing frequency of 1 Hz. Following testing, tissue dye was used to mark the ROI that was indented, and the sample was photographed again.

The mechanical properties at each indentation location were determined using a dynamic indentation technique developed by Herbert et al. [23]. Briefly, the indenter oscillates at 20 Hz and approaches the sample, and the initial contact point is determined by an abrupt change in the phase angle. The indenter then descends 200 μm to reach its full contact point, which corresponds to 10% of the diameter of the piston. After full contact has been established, the indenter piston withdraws vertically and moves laterally off of the sample. The indenter descends to the full contact point in air and determines the reference phase angle, damping, and stiffness of the indenter column for the specified testing frequencies. The indenter then returns to the testing location, moves to full contact, stabilizes, and dynamically indents the sample at each testing frequency. The force amplitude and phase lag are used to compute the complex Young's Modulus (E*) at each frequency, which can be divided into the elastic energy stored (E'; storage modulus) and dissipated (E"; loss modulus) per cycle [24]:

$$E^{\ast }\left(\omega \right)\equiv E^{\prime }\left(\omega \right)+i{E}^{″}\left(\omega \right)$$ (1)

Under the assumption of incompressibility, the complex shear modulus is related to the complex Young's Modulus by

$$E^{\ast }\left(\omega \right)=\frac{1}{3}{G}^{\ast }\left(\omega \right)$$ (2)

The loss factor, or tan δ, is

$$\tan \delta =E^{″}∕E^{\prime }=G^{″}∕G^{\prime }$$ (3)

The complex modulus estimate does not account for the finite thickness of the tissue slice. A correction factor (κ) was developed by Hayes et al. for quasi-static indentation of biological material [25]. For an indenter of radius a indenting a sample of thickness h, as a / h goes to zero, κ goes to one. A complete derivation and table of correction factors for different a / h combinations is presented in [25].

Approximately 1 cm³ of liver free from major inhomogeneities (e.g. blood vessels) was taken from each porcine liver and subjected to dynamic compression testing to provide a global value of the storage modulus in the untreated tissue and used as an estimate of the background stiffness. The sample was tested three times from 1–3% compression at 1 Hz using an Enduratec ELF 3220 system (Bose Corp.; Eden Prairie, MN).

C. Image Analysis

Profiles of the storage modulus within the ablated region of porcine samples were analyzed to investigate local stiffness variations. Photographs of stained and indented samples were registered using the TurboReg plug-in in ImageJ (Wayne Rasband; National Institutes of Health). Raw storage modulus data were interpolated to a grid in MATLAB (The MathWorks, Inc.; Natick, MA) and then linearly interpolated to a resolution of 0.1 mm. The interpolated storage modulus ROIs were manually positioned within the ROI formed by the tissue dye in the indented sample image. Three profiles of the storage modulus were drawn from the outer transition zone boundary to the ablation interior using the MATLAB improfile function and then averaged to provide a representative profile for each sample. Because the storage modulus values inside some ablations were influenced by fiducial marker tracks and not all ROIs reached the ablation center, the profiles were not drawn along the length of the ROI. Rather, each profile was drawn perpendicular between the outer transition zone boundary in the indented, unstained image and the outer edge of the stained “ring” within the white zone of the ablation in the registered, stained image. The ring corresponded to the boundary where water condensed after being driven from the dehydrated ablation core and will be referred to as the condensation boundary [26–28]. The profile distance was normalized for all samples to show average changes between these landmarks. The storage moduli were also normalized to the background modulus determined via ELF testing (E'/ E'_back) to quantify the mechanical contrast as a function of position within the ablation.

Gross pathology, strain, and shear wave velocity images from the ablation generated ex vivo in a bovine liver were also compared. The boundary of the ablation was manually delineated in all three images by a biomedical engineer actively researching shear wave velocity and strain imaging of thermal ablations. The decorrelation halo was used to delineate the strain image, similar to previous studies [11]. For the shear wave velocity image, high velocity contrast was used to differentiate the ablation from the background. On the gross pathology image, the ablation was delineated using color contrast between the ablated and untreated tissue.

III. RESULTS

Dynamic indentation was used to quantify the viscoelastic properties in ROIs overlapping the ablation and the untreated tissue. Raw and interpolated storage modulus and tan δ from a representative sample are presented in Fig. 1. The storage modulus of the untreated tissue was 1.5 – 2.0 kPa and increased monotonically toward the ablation center. The loss factor, or tan δ, showed little correlation with the ablation morphology. Data were upsampled in Fig. 1c and 1d. Because of the poor correlation of tan δ with the ablation features, an extensive analysis of tan δ was not performed. Average values of tan δ in each ROI are presented in Table 1. Dynamic compression testing of one cubic centimeter of untreated tissue in each pig liver estimated the global storage modulus to be 1.91 ± 0.17, 1.66 ± 0.17, and 2.28 ± 0.12 kPa, respectively.

Fig. 1.

Representative dynamic indentation estimates. Raw storage modulus estimates in (a) and tan δ in (b) were collected in a raster pattern over a region of interest of the sample. The storage modulus and tan δ were upsampled to a resolution of 0.1 mm in (c) and (d), respectively.

TABLE I.

Average Tan Delta in the Testing Region of Interest

Sample	1	2	3	4	5	6
Tan δ	0.217 ± 0.042	0.216 ± 0.050	0.208 ± 0.028	0.214 ± 0.039	0.232 ± 0.049	0.219 ± 0.031

Sample	7	8	9	10	11
Tan δ	0.210 ± 0.036	0.200 ± 0.023	0.222 ± 0.032	0.225 ± 0.043	0.231 ± 0.029

Upsampled ROIs were overlaid on the indented pathology slice and the registered, stained pathology images. Figure 2a shows increases in the storage modulus moving from the outer transition zone boundary (white arrow) towards the ablation center. The `flag' colormap in Fig. 2b shows relatively homogenous untreated tissue outside the ablation and an increasing rate of stiffening starting at the outer transition zone boundary. The condensation boundary within the white zone of the ablation is shown in the registered, stained histology image, indicated by the white arrow in Fig. 2c. An example of an indented ROI on the corner of an ablation is presented in Fig. 3. The storage modulus contours in both colormaps closely match the stained and unstained ablation morphology. An example of storage modulus estimates that were influenced by a fiducial marker needle track is presented in Fig. 4. The rate of stiffening follows the expected trend until the needle track is reached, which is highlighted by the white arrow.

Fig. 2.

Representative ablation with storage modulus overlay. The tissue dye in (a) and (b) indicates the region indented, with the red dot representing the first point tested. Stain was used on the opposite face of the ablation in (c) and (d) to reveal cell viability. The arrows in (a) and (c) indicate the outer transition zone boundary and the condensation boundary, respectively. The flag colormap used in (b) and (d) shows the increasing rate of stiffening moving towards the ablation center.

Fig. 3.

Ablation indented on a corner. The upsampled overlays show good correlation with the ablation morphology. The flag colormap in (b) and (d) highlights changes in the rate of stiffening moving toward the ablation center.

Fig. 4.

Ablation with inhomogeneities in the interior. A fiducial needle track is indicated by the white arrow. The estimated storage modulus was influenced by the presence of this track.

Storage modulus profiles further demonstrated the stiffness changes within the ablations. The maximum storage modulus within each ROI was highly variable, as shown in Table 2. Relatively homogenous regions common to all ROIs were selected for profiles, starting at the outer transition zone boundary and ending at the condensation boundary. The storage modulus and modulus contrast are shown for all profiles in Fig. 5. The distance between the outer transition zone boundary and condensation boundary was normalized (4.95 ± 0.95 mm) in Fig. 5b & 5e. Mean storage modulus and modulus contrast (± standard deviation) are shown in Fig. 5c & 5f and were 3.1 ± 1.0 kPa and 1.6 ± 0.4 at the outer transition zone boundary and 36.2 ± 9.1 kPa and 18.3 ± 5.5 at the condensation boundary. The R² of the linear trendline was 0.933 for the entire average profile, and 0.999 halfway through the profile to the condensation boundary.

TABLE II.

Maximum Young's Modulus in the Testing Region of Interest

Layer	1	2	3	4	5	6	7	8	9	10	11
E (kPa)	72	82.3	116.8	59.2	111.4	84.2	83.2	71.1	58.8	58.8	43.7
E/Eback	37.70	49.58	70.36	35.66	67.11	36.93	36.49	31.18	25.79	25.79	19.17

Fig. 5.

Storage modulus and modulus contrast profiles (n = 11). Profiles start at the ablation outer transition zone boundary (OTZB) and end at the condensation boundary (CB). The distance from the outer transition zone boundary to the condensation boundary was normalized in (b) and (e). Average storage modulus and modulus contrast are shown in (c) and (f). The rate of stiffening is approximately linear near the condensation boundary.

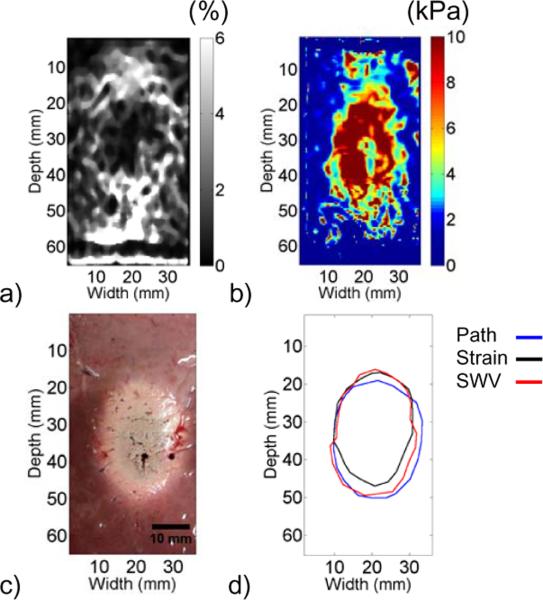
The ablation generated ex vivo revealed differences in boundary delineation among strain, shear wave velocity, and gross pathology images, as shown in Fig. 6. The ablation widths on strain and shear wave velocity images were slightly narrower than on gross pathology. The estimated ablation areas on strain, shear wave velocity, and gross pathology images were 470 mm², 560 mm², and 574 mm², respectively, and the widths of the ablation through the center were 19.4 mm, 20.7 mm, and 23.0 mm, respectively.

Fig. 6.

Elastographic imaging modalities compared with gross pathology in an ex vivo experiment. Electrode displacement elastography and electrode vibration elastography were used to generate (a) strain and (b) shear wave velocity images, respectively. The ablation boundaries were delineated in both images and compared to (c) gross pathology, as shown in (d). Area estimates for strain, shear wave velocity, and gross pathology images were 470 mm², 560 mm², and 574 mm², respectively.

IV. DISCUSSION

We used dynamic indentation to investigate local variations in the viscoelastic properties of RF ablations created in vivo. Our results show that ablation stiffness correlated well with ablation morphology as represented by cell viability staining, the gold standard for determining the ablation periphery. Ablation stiffness and modulus contrast increased from 3.1 kPa and 1.6, respectively, at the outer transition zone boundary to 36.2 kPa and 18.3 at the condensation boundary. The rate of stiffening initially increased nonlinearly and approached a linear trend near the condensation boundary. These data suggest that RF ablation margins are slightly narrower on elastographic images than on gross pathology because of the low mechanical contrast at the periphery. This study has provided a more comprehensive description of the spatial distribution of ablation stiffness than has been previously reported, increasing our understanding of how elastographic images correlate with ablation margins.

Real-time B-mode imaging is widely used to guide the RF needle into the hepatic tumor and provides visualization of the ablation zone [29]; however, during the procedure, B-mode imaging does not accurately depict the ablation boundaries due to the formation of gas bubbles during tissue heating. Studies have shown no consistent echogenic differences between the ablated region and the untreated tissue [30–31]. Contrast-enhanced computed tomography (CT) has been the gold standard for predicting the region of coagulation necrosis [32], but this procedure exposes the patient to ionizing radiation, is less applicable in real-time, and is generally more expensive than ultrasound imaging. Contrast enhanced ultrasound has shown promise in differentiating the ablated and untreated tissue, effectively lowering recurrence rates [32]. Elastographic imaging techniques provide an alternative for monitoring ablation extent that can be used in real-time on the imaging system already being utilized for needle guidance without the need for contrast agents.

Previous work characterized RF ablations by quantifying a global value of the storage modulus and tan δ in ablations formed in canine livers [20] with dynamic compression testing; we quantified viscoelastic properties locally, as shown in Fig. 1. Our storage modulus estimates were approximately 35 kPa near the condensation boundary, comparable to the global estimate of 30 kPa in an ablation formed in canine liver tissue. Tan δ showed poor correlation with ablation boundaries. The average tan δ of each ROI, listed in Table 1, was ~0.22, similar to the global estimate of ~0.3 in [20]. The tan δ of the ablated tissue was slightly higher in that study, possibly a result of ex vivo ablation formation versus the in vivo ablation formation in perfused tissue in the current study, which affects energy deposition within the ablation.

There were limitations to our approach. The storage modulus and tan δ estimated at room temperature may be slightly different than estimates made at physiological temperatures. We also indented a limited number of locations; however, heating and time out of saline solution both lead to desiccation of the samples, which in turn stiffens the tissue. In order to avoid tissue desiccation, we minimized the number of testing points and tested the samples at room temperature. We are confident that the effects of tissue desiccation were minimized because of the consistent estimates obtained among locations in the untreated background, some of which were tested near the beginning and some near the end of the raster scan.

We observed good correlation between the upsampled storage modulus ROIs and pathology images. Clinically, ablations are described as containing an inner “white zone” of frank coagulative necrosis and an outer “red zone,” or “transition zone,” of hyperemia [33]. No cells survive in the white zone, while the transition zone may contain viable cells [34]. We observed high mechanical contrast in the white zone and low mechanical contrast in the red zone, where viable cells are likely present. Ablation stiffness increased starting at the outer transition zone boundary, with the rate of stiffening increasing moving into the white zone of the ablation [33]. The storage moduli within the ablation were quite variable, as shown in Table 2. Heterogeneities such as fiducial needle tracks influenced these estimates, as in Fig. 4. Another source of variability may be the heat sink effect due to blood flow within vessels carrying away the heat energy deposited [35–36]. It was possible to avoid forming ablations near major blood vessels in this study; however, the liver is a vascular structure, and smaller vessels could not be avoided in all cases. Varying levels of perfusion in the vicinity of each ablation undoubtedly affected the stiffness distribution within the ablations. Our interpolation of the indented points assumed that the modulus between raw data points was linear. Finer spacing of indentation locations is needed to confirm this; however, we were limited by the diameter of the indenter piston. Good correlation between the upsampled storage modulus and gross pathology images was observed.

This study provides insights into the spatial modulus distribution within RF ablations, which is likely the cause of area underestimation on elastographic images. Area estimates from sonoelastography images have been compared to gross pathology for both RF and high intensity focused ultrasound (HIFU) ablations. Area estimates from sonoelastography images correlated much better to gross pathology in HIFU ablations [19], likely a result of the differences in energy deposition methods. RF ablations are formed by electrical and thermal conduction, whereas HIFU relies on high intensity insonification to form an ablation. HIFU ablations may have a more uniform stiffness and stiffer periphery than RF ablations because of the differing methods of energy deposition, resulting in better correlation between elastographic imaging and gross pathology.

To spatially quantify changes in ablation stiffness, the condensation boundary inside the white zone was used as an objective end to the storage modulus profile. It was present in all ablations and corresponded to the region where vaporized water condensed after being driven from the ablation center [26–28]. Profiles were not extended to the ablation center, but the most critical region of the ablation to investigate was the region of low modulus contrast, i.e. the ablation boundary. The modulus contrast reached ~18.5 at the condensation boundary, providing ample contrast for elastographic imaging. Profile averages as a function of normalized distance are presented in Fig. 5c & 5f. The rate of stiffening increased initially, but reached a relatively constant rate, which may be a result of decaying conductive heat transfer. The cooling effect within some radius of the electrode may be constant because blood vessel coagulation has stopped blood flow, preventing convective cooling. Outside of this radius, blood perfusion actively removes heat, limiting tissue heating and decreasing tissue stiffness at a nonlinear rate.

Two elastographic imaging modalities were compared against gross pathology to show the area underestimation that has previously been reported. More ablations were not formed because this area underestimation has already been described in several prior studies [4, 8–9, 18–19]. Both the strain and shear wave velocity images show a trend of decreasing stiffness from the center of the ablation moving toward the periphery, similar to the indentation results. In the shear wave velocity image, the velocity within the inclusion was more homogenous than the indentation images suggest. This may be a result of artifacts caused by wave reflections within the ablation when using the electrode vibration technique.

Boundary delineation showed that both strain and shear wave velocity images underestimated the gross pathology area estimate. The ablation width was less than gross pathology for both elastographic imaging modalities, but the margin difference was not equal on both sides of the ablation. This may be a result of slight mis-registration of the gross pathology image with respect to the elastographic images. The larger margins on the gross pathology image likely correspond to the red zone, where the modulus contrast is low. However, it has been observed that the red zone is often not differentiable from the white zone in studies where ablations were formed ex vivo [33]. Clinically, this underestimation is beneficial because a more conservative estimate of ablation extent is prudent to ensure that an appropriate ablative margin is achieved. This study provides evidence that explains area underestimation of RF ablations on elastographic images and insights into the location of the ablated region on elastographic images relative to gross pathology.

Ideally, elastographic images would have been compared to in vivo stained pathology, but matching elastographic planes with stained pathology is difficult during in vivo experiments. Confident matching of imaging planes is more feasible with ex vivo experiments. In addition, the gold standard for determining the extent of the ablated region is cell viability staining, which must be completed immediately after animal sacrifice. It may have been possible to perform ex vivo elastographic imaging following the in vivo experiment, but cell viability staining would have been sacrificed, minimizing the novelty of this work.

We spatially mapped RF ablation stiffness to provide insights into area underestimation on elastographic images. The utility of dynamic indentation was shown in the context of RF ablations, but local estimation of material stiffness has further applications. For example, microwave ablation is a thermal ablation procedure gaining in popularity that does not rely on electrical current [37]. This allows greater energy deposition, increased temperature elevation, and potentially a more uniform ablation zone, which may be associated with a more uniform modulus distribution within the ablation and greater mechanical contrast at the ablation edges. Indentation could be used to clarify these hypotheses. Recent work using supersonic shear imaging has shown that some breast lesions have a heterogeneous modulus distribution [38–39], which may be corroborated via indentation in ex vivo studies. Global estimates of stiffness have provided many insights in elastographic imaging techniques; local mechanical estimation can further increase our understanding of tissue properties and corroborate elastographic imaging approaches.