Protein crowding affects hydration structure and dynamics

Abstract

The effect of protein crowding on the structure and dynamics of water was examined from explicit solvent molecular dynamics simulations of a series of protein G and protein G/villin systems at different protein concentrations. Hydration structure was analyzed in terms of radial distribution functions, three-dimensional hydration sites, and preservation of tetrahedral coordination. Analysis of hydration dynamics focused on self-diffusion rates and dielectric constants as a function of crowding. The results show significant changes in both structure and dynamics of water under highly crowded conditions. The structure of water is altered mostly beyond the first solvation shell. Diffusion rates and dielectric constants are significantly reduced following linear trends as a function of crowding reflecting highly constrained water in crowded environments. The reduced dynamics of diffusion is expected to be strongly related to hydrodynamic properties of crowded cellular environments while the reduced dielectric constant under crowded conditions has implications for the stability of biomolecules in crowded environments. The results from this study suggest a prescription for modeling solvation in simulations of cellular environments.

INTRODUCTION

The cytoplasm contains up to 400 g/L of macromolecules occupying 5 to 40% of the total volume of the cell¹. Macromolecular crowding has been shown to alter biomolecular structure and dynamics compared to dilute environments^2–4. Past studies of crowding have focused largely on volume exclusion by crowder molecules⁴ with the main conclusion that such crowding effects lead to more compact states^3,4. However, when more realistic environments with protein crowders are considered, the effect of crowding tends to destabilize rather than stabilize native states^5–7. Most discussions of crowding so far have focused on the nature of protein-crowder interactions, while relatively little is known about the effect of crowding on the structure and dynamics of water. In highly crowded environments, the fraction of interfacial water is between 30% and 70% of the total water in the cell⁸. Since physical properties of interfacial waters differ from those of bulk water⁹, the overall properties of water are expected to be significantly different in the presence of high concentrations of macromolecular crowders. In particular, highly crowded environments may alter hydration structure due to strong interactions with nearby macromolecules. Furthermore, diffusion rates and the dielectric response may be lowered because of constraints on water mobility. Altered hydration properties as a result of crowding may in turn affect the structure, dynamics, and function of biomolecules. Especially, a reduced dielectric constant would enhance charge-charge interactions, stabilize secondary structure through strengthened hydrogen bonding, and diminish the advantage of sequestering hydrophobic components away from solvent¹⁰. Therefore, the effects of crowding on water properties are a key part in developing a full understanding of the behavior of biomolecules in cellular environments. A good understanding of solvation in cellular environments is also essential for the development of effective mean-field models of cellular environments¹⁰ that allow studies of biomolecular structure and dynamics on cellular scales^11,12.

There is little direct insight into the effect of crowding on hydration to date, but a number of relevant studies have examined water properties near surfaces and under confinement. Water molecules near protein surfaces diffuse more slowly¹³, are more ordered¹⁴, and generally have a lower density over bulk water in confined spaces¹⁵. Moreover, water molecules near hydrophobic surfaces behave significantly different than bulk water because of a lack of hydrogen bond donors and acceptors^15,16 while a slow-down in water dynamics is also observed near hydrophilic surfaces^17–19.

Narrow confinement is expected to further alter the structure of water and significantly perturb the hydrogen-bond network. Indeed, a previous study has reported a reduction of the average coordination number from about 3.6 in the bulk to about 2.2¹⁵. The confinement-imposed constraints on water molecules reduce the possibility for hydrogen-bond exchange and hinder reorientation of water dipoles. This reduces the effective dielectric response and leads to local polarization of interfacial waters that is strong enough to induce an effective long-range attraction between macromolecules^20,21. According to modeling studies water molecules under hydrophobic confinement move about an order of magnitude slower than those in bulk²⁰. An NMR study of water in large confined spaces (300 to 4000 nm) furthermore suggests that even in those environments the molecular mobility of water can be significantly below that of the bulk²². Force microscopy experiments suggest that water confined between two hydrophilic surfaces that are less than about 2 nm apart exhibits an increased viscosity by several orders of magnitude greater compared to bulk solvent^17–19. In addition to a reduction in self-diffusion rates, the dielectric constant is also found to be significantly reduced in confined environments²⁰. Further evidence for a reduced dielectric response in cellular environments comes from a comparison of calculated and experimental solubility. A reduced dielectric constant of 55 for the water in the protein crystal²³, where macromolecular densities are similar to crowded cellular environments, resulted in best agreement between theory and experiment.

In order to obtain a better understanding of water in crowded biological environments, we performed a series of fully-atomistic molecular dynamics (MD) simulations of highly concentrated protein solutions to mimic biological crowding environments. We found that the structure of water remained largely unaffected for low concentrations of crowder proteins but radial distributions of water were affected significantly for highly crowded systems with reduced densities past the first solvation peak. In contrast, diffusion rates and the dielectric constants of water decreased linearly as a function of crowding to about a third of bulk values under most crowded conditions. The observed changes in water properties for highly crowded environments are presumed to have a profound impact on biological macromolecules in cellular environments. Furthermore, our results provide a prescription for developing better mean-field models of crowded cellular environments.

In the remainder of the paper we will describe our results in more detail. The paper is organized as follows: First, the methodology of our simulations is explained, then, results are presented and discussed.

METHODS

To mimic crowded protein environments, two types of systems were set up. For the choice of protein crowders, we considered two simple globular proteins, segment B1 of streptococcal protein G (protein G)²⁴ and chicken villin headpiece sub-domain (villin). Protein G consists of a four-stranded β-sheet against which an α-helix is packed. Villin is a three bundle helix of an F-actin-binding domain located on the far C-terminus of the super villin²⁵. These mini-proteins were selected because their small size allows for long simulation times, because they are known to be well-behaved in computer simulations, stably maintaining their native states, and because they are not known to aggregate to a significant extent with each other. To study crowding effects, we prepared different two systems (Protein G/Protein G and Villin) to cover proteins with different secondary structures (α-helical villin vs. mostly β-sheet) and compare a single protein crowder type vs. system with mixed crowders within the limitations of the computer resources available to us. The first system consisted of eight protein G molecules (56 residues, 864 atoms, PDB entry 1PGB²⁴) (PG1-PG4; cf. Table 1); the second system consisted of four protein G molecules and eight villin headpiece sub-domains (36 residues, 597 atoms, PDB entry 1YRF²⁵) (PGVH1-PGVH5; cf. Table 1). Both systems were solvated in explicit solvent under periodic boundary conditions. Furthermore, to examine the effect of concentration, five different box sizes were considered for each system (cf. Table 1). The protein concentrations ranged from 144 g/L for PG1 to 619 g/L for the mixed protein G/villin system PGVH5 corresponding to protein crowder volume fractions between 10 and 43%. For reference, we also ran a system with a single copy of protein G (PG0) which effectively represents the case of infinite dilution. Equilibrium snapshots of all simulated systems are depicted in Fig. 1. The initial systems were set up by placing the protein G and villin molecules in random orientations at the corners of cubic boxes. More specifically, in the PG1-PG4 systems, protein G was placed with the center of mass at (+/−13 Å, +/−13 Å, +/−13 Å). In the PGVH1-PGVH5 systems the four protein G molecules were placed at (−18 Å, −18 Å −18 Å), (18 Å, 18 Å, −18 Å), (−18 Å, 18 Å, 18 Å), and (18 Å, −18 Å, 18 Å) and the eight villin molecules were placed at (12 Å, 12 Å, 12 Å), (−12 Å, 12 Å, −12 Å), (−12 Å, −12 Å, 12 Å), (12 Å, −12 Å, −12 Å), (22 Å, 0, 0), (−22 Å, 0, 0), (0, −22 Å, 0), and (0, 0, 22 Å). All the systems were then solvated with explicit TIP3P water molecules²⁶ in cubic boxes with different lengths ranging from 54 Å to 83 Å (cf. Table 1). PG1-PG4 were neutralized by 32 sodium ions, placed randomly in the solvent box, PG0 was neutralized with 4 sodium ions. The initial systems were minimized and subsequently heated to 298 K with short simulations at increasing temperature (4 ps at 50 K, 4 ps at 100 K, 4 ps at 200 K, 4 ps at 250K, at 10 ps at 298K). Production simulations were then continued in the NPT ensemble at a temperature of 298 K and a pressure of 1 bar. All simulations were performed using the molecular dynamics simulation package NAMD version 2.7b2²⁷. The CHARMM 27 all-atom force field²⁸ was used in combination with the CMAP correction term²⁹. The SHAKE algorithm³⁰ was used to constrain bond lengths involving hydrogen atoms so that a longer integration time step of 2.0 fs could be used. For temperature and pressure control, a Langevin thermostat and piston were used with a friction coefficient of 5 ps⁻¹ and a collision period of 0.2 ps, respectively. The particle mesh Ewald (PME) method was employed for the calculation of electrostatic interactions³¹. The direct sum and Lennard-Jones interactions were smoothly truncated at a cutoff distance 12 Å using a switching function becoming effective at 10 Å. Each simulation was carried out for 300 ns with coordinates recorded every 0.2 ps. Analysis of the simulations was carried out with the MMTSB Tool set³², CHARMM³³, and custom-written analysis scripts. VMD³⁴ was used to visualize and generate molecular graphics.

Table 1.

Simulation conditions (298K, 1bar)

System	Box* (Å)	NWater	Proteinvol%	Concentration [g/L]		Length [ns]
				Protein-G	Villin**
PG0	60.77	7122	3***	45.8***	–	300
PG1	82.88	16100	10	144.4	–	300
PG2	74.88	11130	14	195.8	–	300
PG3	66.88	7195	20	274.9	–	300
PG4	58.88	4036	30	402.9	–	300
PGVH1	81.88	14815	12	74.9	101.44	300
PGVH2	73.88	9989	17	101.9	138.09	300
PGVH3	65.88	6303	25	143.8	194.75	300
PGVH4	57.88	3456	37	212.0	287.18	300
PGVH5	53.88	2610	43	262.9	356.01	300

^*Length of cubic box;

^**Villin headpiece;

^***Effectively at infinite dilution; PG0: Protein G×1; PG1, PG2, PG3 and PG4: Protein G×8; PGVH1, PGVH2, PGVH3 and PGVH4: Protein G×4 + Villin Headpiece×8

Figure 1.

Simulated systems after 100 ns (cf. Table 1). Protein G is shown in brown and villin headpiece subdomain in green.

RESULTS

The effect of protein crowding on water structure and dynamics was analyzed from molecular dynamics simulations of protein G and protein G/villin solutions at different concentrations. In the following, we will first describe the water structure and then discuss diffusion and dielectric properties as a function of crowding.

Water Structure

To describe the effect of crowding on water structure we first analyzed the water-accessible volume and radial distribution functions of water with respect to the protein crowders. Furthermore, we describe water structure through three-dimensional density distributions and hydrogen-bonding order parameter calculations.

Accessible volume as a function of distance from the closest solute heavy atom was calculated to determine what fraction of water molecules is far enough from any solute to retain bulk properties (cf. Figs 2a, 2b, and S1). The accessible volume is defined as the volume, in which water molecules could exist at a given distance from the closest crowder heavy atom. The accessible volume decreases with distance in the crowded cases compared to the increase in volume of spherical shells in the non-crowded case. Furthermore, for distances over 3 Å, the accessible volume decreases more rapidly with increasing amount of crowding. In the most crowded cases, the accessible volume reduces to zero at 10 Å with 30%vol protein G crowders (PG4) and at 8 Å with 43%vol protein G/villin crowders (PGVH5). To further quantify this point, Table 2 compares the volume within the first two solvation shells vs. bulk volume (> 7 Å from the protein) as a function of crowding. For crowder volume fractions of 30% and more, the bulk volume is reduced to below 10% while most of the accessible volume is found within the first solvation shell (≤4 Å) from the protein. This means that in the most crowded cases there is theoretically almost no room for bulk water and overall hydration properties are therefore expected to be altered significantly.

Figure 2.

Theoretically accessible volume (A,B) and radial distribution functions (C,D) for water molecules as a function of distance from nearest protein crowder heavy atoms in protein G (A,C) and protein G/villin (B,D) systems. The accessible volume was calculated by integrating grid volume elements with 0.5 Å spacing according to nearest distance of a given volume elements to a crowder heavy atom. Accessible volume and radial distribution functions were averaged over 300 ns. Radial distribution functions were normalized by the accessible volumes and standard bulk water number density of 0.033 Å⁻³. Line colors indicate results from different concentrations as follows: PG0: light blue; PGVH1: magenta; PG1/PGVH2: green; PG2/PGVH3: blue; PG3/PGVH4: orange; PG4/PGVH5: red

Table 2.

Accessible volume within first and second solvation shell vs. bulk

System	Protein [vol%]	1st shell (r≤4 Å) [%]	2nd shell (4 Å < r ≤ 7 Å) [%]	Bulk (r >7 Å) [%]
PG1	10	22.4	14.4	63.3
PG2	14	31.7	20.4	47.9
PG3	20	44.0	24.6	31.5
PG4	30	65.6	26.7	7.7
PGVH1	12	28.1	16.3	55.6
PGVH2	17	37.7	19.1	43.3
PGVH3	25	53.4	22.2	24.5
PGVH4	37	76.2	19.6	4.2
PGVH5	43	86.4	13.0	0.6

Radial distribution functions were calculated for the distances between water oxygen atoms and the nearest heavy atoms of any of the protein crowder molecules (cf. Figs. 2c, 2d, and S1). Radial distribution functions d(r) were obtained in a histogram as a function of distance r and then divided by the bulk water density (0.034 Å⁻³) and the theoretically accessible volumes V(r) from Figs. 2a and 2b to give the normalized functions g(r) shown in Figs. 2c and 2d according to Eq. 1:

$$g(r)=\frac{d(r)}{V(r)·0.034{Å}^{-3}}$$ (1)

It can be seen that the first solvation peak remains largely unaffected even under highly crowded conditions. The second solvation peak is also present in all cases but for highly crowded systems with volume fractions of 30% and above the water density is reduced significantly relative to bulk densities with increasing distance from the solute. We also separately analyzed accessible volume and radial distribution functions for different residue types of the closest protein atom (grouped into hydrophobic, polar or charged residues) (cf. Fig. S3) but did not come to significantly different conclusions than for the overall distribution functions. The reduction in bulk density is presumed to be a result of an increasing number of small solvent cavities at highly crowded conditions that are too small to accommodate water molecules. Interestingly this effect is negligible for less than 30%vol but rapidly dominates for crowder fractions of more than 30%vol.

Three-dimensional water densities were calculated to further compare the structure of water between non-crowded and crowded systems (cf. Fig. 3). Most of the high density sites in the first solvation shell appear to be conserved even at highly crowded conditions. However, there are also some regions where the first solvation shell sites are significantly different. One such region is a hydrophobic patch near the surface (marked with a dashed circle in Fig. 3) where hydration in the non-crowded case appears to be more extensive and involve a different water structure than in the crowded case. On the other hand, water sites near polar and charged residues were relatively well conserved. In the second solvation shell, the differences between the non-crowded and crowded case were more pronounced. In particular, many of the ordered sites present in the non-crowded case appear to be missing in the crowded simulation. These results suggest that although the radial distribution of water molecules in the first solvation shell is largely unaffected, crowding may alter specific hydration sites in a crowder-dependent fashion.

Figure 3.

3D water densities around protein G for highly crowded PG4 system (pink) compared to densities from non-crowded PG0 system (blue). The densities were averaged over 300 ns from sampling of water around each of the crowder proteins after superposition to a common reference structure. Density contours are shown at a level of 0.18 Å⁻³. The dashed green circle indicates a prominent solvent-exposed hydrophobic region between residues T25 on the helix and T2 on the sheet, respectively. The left and right figures show front and top view.

Hydrogen-bonding order parameters were calculated to examine the effect of crowding on the tetrahedral coordination of water molecules. As a metric we calculated the following order parameter for water molecule i:

$$q_i=1-\frac{3}{8}\sum _{j=1}^3\sum _{k=j+1}^4{\left(cos{\psi }_{\mathit{ijk}}+\frac{1}{3}\right)}^2$$ (2)

where ψ_ijk is the angle formed between a central oxygen atom i and two of the nearest four oxygen atoms j and k³⁵. This summation is over the six possible O-O-O angles involving the central molecule i and pairs of its four neighbors. For a perfect tetrahedral arrangement such as hexagonal ice, q=1 since the values of cosψ_ijk are equal to −1/3 with ψ_ijk = 109.5°. On the other hand, when the relative arrangement of the central atom is completely uncorrelated with its neighbors, the mean value of q vanishes. This corresponds to the ideal gas limit. The resulting distributions are shown in Figs 4a and 4b. Compared to the non-crowded system, the distributions of the crowded systems were shifted to lower values of q. This indicates that protein crowding disrupts the partial tetrahedral arrangement of water in solution while random orientations (q=0) are slightly increased. This effect appears to be most pronounced for the PGVH5 system where the protein volume fraction is above 40% and is likely due to restricted mobility of water molecules within cavities that disrupt tetrahedral coordination. However, the overall effect is relatively minor even for the most crowded case.

Figure 4.

The distribution of the orientational order parameter q of protein G systems (PG0-PG4) (A) and protein G/villin systems (PGVH1-PGVH5) (B) from the first 100 ns of the trajectories. The fraction of water molecules with q-values between q+dq/2 and q−dq/2 is f(q)dq. The arrows indicate increased crowding. Line colors are the same as in Fig. 2.

Water Dynamics

We will now turn to an analysis of dynamic features, in particular water diffusion and dielectric properties.

Diffusion coefficients were calculated from mean-square displacements (MSD) of water oxygen atoms:

$$\mathit{MSD}(t)={\langle {\mid r(t^{\prime }+t)-r(t^{\prime })\mid }^2\rangle }_{t^{\prime }}$$ (3)

In normal diffusion, the diffusion coefficient is calculated from the MSD according to

$$D=\underset{t\to \infty }{lim}\frac{1}{6t}\mathit{MSD}(t)$$ (4)

where t is time. Finite periodic box size effects were corrected according to

$$D_S=D_{\mathit{PBC}}+\frac{k_{B}T\xi }{6\pi \eta L}$$ (5)

where D_PBC is the uncorrected diffusion coefficient, T is the temperature, L is the box length, η is the shear viscosity of pure water, and the correction factor ξ = 2.83729³⁶. The MSD time evolution indicates a slowdown in diffusion as a function of crowding even for moderate amounts of crowding (cf. Fig. 5a and 5b). Diffusion rates calculated from the long-time slope of MSD vs. time linearly decrease with protein volume fraction (cf. Fig. 6). The results do not seem to depend on the crowder proteins since the results from PG and PGVH systems fall on the same line. This indicates that water diffusion rates may depend on protein crowding in a universal manner. Theoretical extrapolation suggests that diffusion reaches zero for ~55%vol when there would be no more movable water molecules.

Figure 5.

Mean square displacement (MSD) as a function of time for protein G systems (PG0-PG4; A, C) and protein G/villin systems (PGVH1-PGVH5; B, D) calculated from the first 4 ns trajectories for short timescale (0 ns to 0.03 ns) and from the total 300 ns trajectories for long timescale (0.03 ns to 100 ns). Line colors are the same as in Fig. 2.

Figure 6.

Water diffusion constants as a function of crowder protein volume fraction. Blue and red points correspond to PG0-PG4 and PGVH1-PGVH5 systems, respectively. Diffusion constants were calculated from MSD values during 80 to 100 ns (cf. Figs 5A and 5B). The dashed line is a linear fit with D_s = −0.569 f + 0.308 [Ų/ps]/. The green points are theoretical predictions of overall diffusion rates from MD simulations around a single protein and based on the fraction of waters close to a protein surface where diffusion is known to be reduced significantly¹³. Details of how the theoretical predictions were obtained for the crowded system are given in the supplementary material.

In normal diffusion, MSD is strictly a linear function of time. However, previous studies have suggested that anomalous diffusion may occur in crowded environments³⁷. In anomalous diffusion, MSD follows the following law:

$$\mathit{MSD}(t)\sim t^{2/dw}$$ (6)

where d_w is the anomalous diffusion exponent. If d_w=2, normal diffusion is recovered. To judge whether anomalous diffusion occurs, plots of log₁₀[MSD (t)/t] vs. log₁₀t are convenient (cf. Fig. 5c and 5d). Anomalous diffusion is present at short timescales (<10 ns) where log₁₀[MSD (t)/t] varies as a function of log₁₀t. It appears that the degree of anomalous diffusion increases with crowding but at long timescales (>10 ns) diffusion becomes normal in all cases. The presence of anomalous diffusion is likely due to a cage effect in highly crowded environments where water molecules can move freely on short time scales but are more restricted from making long range displacements over longer time scales. In this model, the change from anomalous to normal diffusion essentially depends on the time required for escaping the cage imposed by the crowder molecules.

Dielectric constants ε were calculated for water only in each of the simulations from the box dipole fluctuations. For a finite cubic system with periodic boundary conditions, ε is obtained in general from the following equation:

$$\epsilon -1=4\pi \frac{\langle M^2\rangle -{\langle M\rangle }^2}{3{Vk}_{B}T}$$ (7)

where M is the total box dipole moment, V is the volume of the system, T is the temperature and k_B is Boltzmann’s constant³⁸. Eq. 7 applies directly to a homogeneous system where all molecules contribute to the box dipole moment. To calculate the dielectric constant of only the water component, the dipole moment due to water as well as a cross-term between the water dipole and the dipole of the rest of the system have to be considered³⁹. Furthermore, the volume in Eq. 7 has to be scaled by the fraction occupied by the water molecules instead of the total box volume. This then results in the following modified expression for calculating the dielectric constant of water in the context of the crowder molecules:

$$\epsilon -1=4\pi \frac{\langle M_{\mathit{water}}^2\rangle -{\langle M_{\mathit{water}}\rangle }^2+\left(\langle M_{\mathit{water}}·M_{\mathit{rest}}\rangle -\langle M_{\mathit{water}}\rangle \langle M_{\mathit{rest}}\rangle \right)}{3V(1-f)k_{B}T}$$ (8)

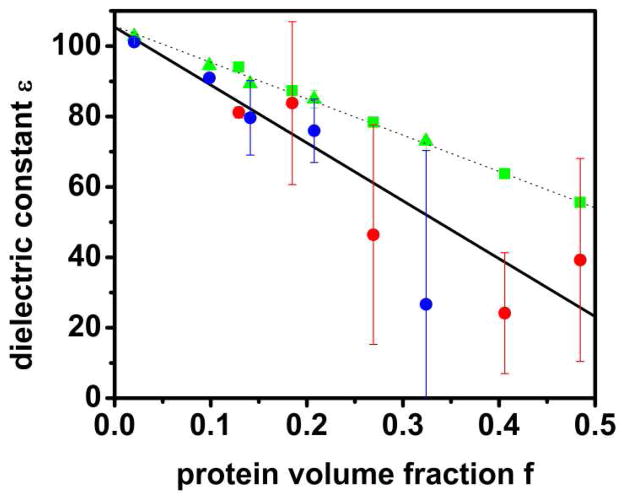
where M_water is the box dipole moment due to all of the water molecules, M_rest is the dipole moment due to the rest of the system (proteins and counterions), and f is the protein volume fraction. The resulting dielectric constants (assuming T=298K) with and without the correlation term are shown in Fig. 7. Without the correlation term, the dielectric constant decreases as a function of the crowder volume fraction to below 60 for a volume fraction of 0.5. As for the diffusion rates, the data from both sets of simulations fall onto the same line (cf. Fig. 7) suggesting that the decrease is universal. Inclusion of the correlation has a negligible effect for the infinite dilution case, consistent with previous studies of a single biomolecule in a box of water³⁹. As the protein crowder fraction increases, the correlation appears to become increasingly important, although, due to sampling limitations, the uncertainty in M_rest is much larger than for M_water (see error bars in Fig. 7). All data points suggest that the water-crowder cross-term further reduces the dielectric constant of water. More specifically, a weighted fit that takes the uncertainties into account suggests that the dielectric constant of water in crowded environments is reduced to below 30 at a volume fraction of 0.5 (cf. Fig. 7).

Figure 7.

Dielectric constants of water only as a function of protein volume fraction for each system from averages over 300 ns. Blue and red circles correspond to values calculated according to Eq. 8 for PG0-PG4 and PGVH1-PGVH5 systems, respectively. Errors estimated by comparing results for 0–150 and 150–300 ns intervals are shown as vertical lines. Green symbols (triangles for PG0-PG4, squares for PGVH1-PGVH5) indicate calculated values according to Eq. 7 without the water-protein/ion correlation term. The data points (including the uncertainties as weights) were fitted to the linear functions ε = −103.4 f + 105.7 (dashed line) and ε = −164.5 f + 105.4 (solid line).

DISCUSSION

Previous simulations of crowded biological environments have relied mostly on coarse-grained models of solutes and crowders and even atomistically detailed models of protein solutes were combined with implicit solvent^12,40. In our study, we have represented both protein crowders and solvent in full atomistic detail to obtain a full picture of hydration in crowded environments. The results from our simulations presented here suggest that macromolecular crowding has a modest effect on water properties for low levels of crowding (<30%vol) but significantly affects hydration structure and dynamics for highly crowded environments (>30%vol). Thus, altered hydration properties are expected to be present in cellular environments where protein volume fractions range between 20 and 40%. For the most crowded environments, water structure beyond the first solvation shell is significantly altered and, even within the first solvation shell, different hydration patterns arise as a result of crowding. Furthermore, diffusion rates are significantly decreased and the dielectric constant is reduced substantially due to constrained water mobility in highly crowded environments,

Reduced diffusion in crowded environments is well known for biomolecular solutes⁴. We show here that self-diffusion of water is also significantly reduced as a result of crowding. It is interesting to compare these results with the previously described reduction of diffusion near biomolecular surfaces in non-crowded environments¹³. In that case, water diffusion rates were found to decrease smoothly from bulk values to about half at the protein surface. Convoluting that profile (cf. Fig. 2 in that work¹³) with radial water density distribution from our simulations in crowded environments (cf. details in supplementary material) yields an estimate of how much diffusion rates would be expected to decrease simply because fewer waters are sufficiently far enough from any protein surface to retain bulk properties. The corresponding data in Fig. 6 shows that the actual decrease in diffusion rates upon crowding is similar but larger than these theoretical estimates. Hence, diffusion is reduced in part simply because a larger fraction of water molecules are near a protein surface. However, there is an additional reduction due to crowding, presumably because of interactions with multiple nearby proteins.

Reduced diffusion translates into increased viscosity according to the Einstein-Stokes equation

$$D_s=\frac{k_{B}T}{3\pi \eta d}$$ (8)

where d is a radius of particle. This means that the experimentally observed increase in viscosity in cellular environments⁴¹ may be partly also due to increased solvent viscosity. Such an increase of viscosity would be directly related to the constraints on water dynamics by the nearby protein crowders that limit their mobility both due to restricted space and protein-water interactions.

The significant decrease in dielectric response of water in highly crowded environments is probably the most important finding from our study. It appears that the decrease is independent of the particular type of crowder protein and follows a linear function. Hence, even at low concentrations of crowders there is already a modest decrease in the dielectric constant while the water dielectric constant appears to be reduced to ε=30–50 for crowder volume fractions between 0.3 and 0.4.

As the reduction in diffusional dynamics upon crowding the decrease in dielectric constant is apparently also due to constrained mobility of the water dipoles that limits their ability to respond to changes in electric fields. To further support this point we calculated the water dipole rotational autocorrelation function (cf. Fig. 8). The data clearly shows an increased correlation as a function of crowding that is consistent with a reduced dielectric response. A reduced dielectric constant in biological environments has been suggested previously from experiments with model hydrophobes²⁰. Furthermore, previous solubility calculations suggest a dielectric constant of ε=55 for modeling the condensed crystalline phase with a protein volume fraction of 0.3²³. According to the fit in Fig. 7 we estimate a dielectric constant of 56 for a protein volume fraction of 0.3 which is surprisingly close to the previous prediction.

Figure 8.

Water dipole autocorrelation function C (t) = 〈d(τ)·d(τ+t)〉_τ for water dipoles d(t) as a function of time t for each system from averages over the last 20 ns for protein G systems (PG0-PG4; A) and protein G/villin systems (PGVH1-PGVH5; B). Line colors are the same as in Fig. 2.

We predict a dielectric constant of water in the range of 30–50 for highly crowded environments. The overall polarization response of a crowded cellular environment is assumed to be further reduced due to the presence of co-solvents⁴² and nearby proteins (with a dielectric constant between 5 and 20⁴³). Such a low effective dielectric constant is expected to profoundly impact the energetics of biomolecules in cellular environments. A reduced dielectric response of the environment would diminish the hydrophobic effect and increase the strength of hydrogen bonds and salt bridges. As a result, we would expect a competing effect of protein tertiary structure destabilization vs. secondary structure stabilization. This effect was illustrated in a previous study of melittin in different dielectric environments¹⁰, where high dielectric environments favored a ‘folded’ conformation with a mini-hydrophobic core while intermediate dielectric constants shifted the equilibrium to a more extended helical conformation where backbone hydrogen bonding was maximized at the cost of exposing hydrophobic side chains to solvent. In particular, the reduced dielectric response of the environment may at least partially explain the recently observed destabilization of proteins in highly concentrated protein solutions⁵ and biological cells⁶.

The present study offers detailed insight into the structure and dynamics of water in concentrated protein solutions that is not available from experiments. However, the computational approach taken here faces certain limitations due to the choice of force fields, small system sizes, and the amount of conformational sampling that could be obtained. One particular issue is the choice of water model, in this case TIP3P, that is necessitated by the CHARMM protein force field used here. TIP3P is known to overestimate dynamic properties. Both, the dielectric constant and self-diffusion rates of water around protein G in dilute solvent, are overestimated compared to the experimental values for pure solvent at T=298K (ε=102 vs. 78⁴⁴. and D_S=0.3 vs. 0.23⁴⁵) but agree with previous studies¹³. However, under the assumption that diffusion rates and dielectric constants are overestimated to a similar extent at different degrees of crowding, the calculated values could be corrected by scaling with a common factor so that the values for dilute solvent match the experimental values.

Limitations in conformational sampling are apparent in the uncertainties of the calculated box dipole moment for the protein/counterion components. Although crowder proteins diffuse significantly on the order of the box size and exchange partners frequently on nanosecond time scales based on visual inspection of the trajectories, it is clear that protein-protein configurations of the most crowded systems are not sampled fully on the sub-μs time scales reported here. However, most of the quantities reported here primarily depend on water relaxation properties and are most certainly converged on the time scales of the simulations presented here as indicated e.g. by the small error bars of the water box dipole moments.

Another caveat concerns the relevance of the model systems studied here for describing real biological environments. Crowded cellular environments contain a more diverse set of proteins, most of them larger than the proteins used here, as well as additional solutes such as nucleic acids and metabolites that are neglected here. It is unclear how a more diverse set of proteins would affect the results presented here, but the small size of the crowder proteins used here may introduce systematic errors. There are likely fewer and larger cavities as crowders become larger at constant crowder volume fraction. As a result, the accessible volume and radial distributions of water far away from a protein surface may decrease less significantly in actual cellular environments as a function of crowding than reported here. Furthermore, if a larger fraction of waters retain more bulk-like properties in the presence of larger crowders, the diffusion rates and dielectric constants may also be reduced to a lesser extent as a function of crowding. It is difficult to fully assess the crowder size effect on hydration properties without carrying out additional simulations with larger crowder molecules, but it appears likely that the effect is small for typical cellular proteins with 200–300 residues.

CONCLUDING REMARKS

In this study, we investigated physical properties of water in the presence of protein crowders at different concentrations. We find that under highly crowded conditions, hydration properties change significantly from bulk solvent. Both, hydration structure and dynamics are altered as a function of crowding. The most dramatic change is a significant decrease in self-diffusion and dielectric response. The reduced diffusion rates are expected to affect hydrodynamic properties in cellular environments while a reduced dielectric response alters the thermodynamics of folded proteins. While the focus of this study has been solely on the structure and dynamics of water, future studies will investigate the effect of altered hydration properties on biomolecular solutes in more detail. The results from this work suggest a prescription for developing mean-field models of solvation in cellular environments, for example by developing implicit descriptions of cellular environments using the reduced dielectric response reported here. It is our hope that such models will facilitate physically realistic studies of biomolecular dynamics on cellular scales.

ABBREVIATIONS

CHARMM

Chemistry at Harvard molecular mechanics

CMAP

cross-correlation map

MD

molecular dynamics

NMR

nuclear magnetic resonance

MMTSB

multi-scale modeling tools in structural biology

MSD

mean-square displacement

NPT

constant number of particles, pressure, and temperature ensemble

PDB

protein data bank

PME

particle-mesh Ewald

TIP3P

transferable interaction potential-3 point