Abstract
The very nature of nuclear medicine, the visual representation of injected radiopharmaceuticals, implies imaging of dynamic processes such as the uptake and wash-out of radiotracers from body organs. For years, nuclear medicine has been touted as the modality of choice for evaluating function in health and disease. This evaluation is greatly enhanced using single photon emission computed tomography (SPECT), which permits three-dimensional (3D) visualization of tracer distributions in the body. However, to fully realize the potential of the technique requires the imaging of in vivo dynamic processes of flow and metabolism. Tissue motion and deformation must also be addressed. Absolute quantification of these dynamic processes in the body has the potential to improve diagnosis. This paper presents a review of advancements toward the realization of the potential of dynamic SPECT imaging and a brief history of the development of the instrumentation. A major portion of the paper is devoted to the review of special data processing methods that have been developed for extracting kinetics from dynamic cardiac SPECT data acquired using rotating detector heads that move as radiopharmaceuticals exchange between biological compartments. Recent developments in multi-resolution spatiotemporal methods enable one to estimate kinetic parameters of compartment models of dynamic processes using data acquired from a single camera head with slow gantry rotation. The estimation of kinetic parameters directly from projection measurements improves bias and variance over the conventional method of first reconstructing 3D dynamic images, generating time–activity curves from selected regions of interest and then estimating the kinetic parameters from the generated time–activity curves. Although the potential applications of SPECT for imaging dynamic processes have not been fully realized in the clinic, it is hoped that this review illuminates the potential of SPECT for dynamic imaging, especially in light of new developments that enable measurement of dynamic processes directly from projection measurements.
Preface
Today our healthcare system is facing challenges in the diagnosis and therapy of cardiovascular disease, cancer and mental disease, which affect all segments of our population. Single photon emission computed tomography (SPECT) continues to be an important tool in the clinical diagnosis of these diseases. It is the number one protocol for clinical evaluation of cardiovascular myocardial ischemia (seriously compromised blood flow) and viability (live tissue with reduced flow).
SPECT is an imaging procedure in which an isotope tagged to a biochemical compound is injected into a patient’s vein. As the isotope decays, it emits photons from the body, and these photons are detected and recorded by a camera that provides a digital image of the distribution of the radiotracer in the body. The SPECT system may consist of one, two (as shown in figure 1) or three detector head(s). The SPECT procedure records images of the distribution of the biochemical compound in the patient’s body from different projections as the detector(s) rotate around the body. The detectors only need to acquire 180° of projection images but may acquire as many as 360° of projections. Newer SPECT systems being built today are constructed in the form of a fixed array of detectors partially or fully encompassing the patient’s body.
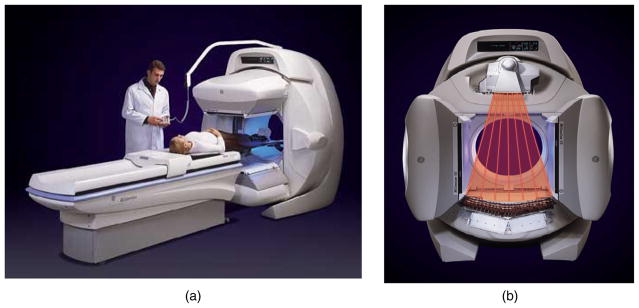
Figure 1.
SPECT/CT camera manufactured by GE Healthcare (Haifa, Israel) (image from GE Healthcare with permission). (a) The system is composed of two large field-of-view gamma ray detectors and (b) an x-ray CT system. Photons that should be counted by the detector but are not (due to scatter or absorption by the tissue) are stated to be attenuated. Photons that travel further through tissue will have a higher likelihood of being attenuated. Information from the CT image is used to correct for the attenuation and to provide information about scatter to obtain a better estimate of the quantitative distribution of the injected radioisotope.
Once the biochemical compound enters the blood stream, it travels to body organs (brain, liver, kidney, heart and the peripheral vascular system) and is absorbed by these organs according to each organ’s affinity for the particular compound. Dynamic SPECT is an imaging procedure that follows the dynamic process of the biochemical compound once it enters the blood—transported by the blood, absorbed in organs and body tissues, and then either trapped within cells or on cell surfaces, or released back into the blood stream or the lymph system. Dynamic SPECT imaging, acquired using detector heads that rotate or remain fixed while radiopharmaceuticals exchange between biological compartments, records the actual movement (speed) of the isotopes through the body.
The premise of this review is that special data processing methods are required to extract dynamic information directly from projection measurements of injected radioactive biochemical compounds from dynamic SPECT data acquired using detector heads that rotate while radiopharmaceuticals exchange between biological compartments. These special data processing methods can also be applied to non-rotating SPECT and position emission tomography (PET) imaging systems.
The extraction of dynamic information and estimation of model parameters directly from projection measurements were first presented in a book chapter (Gullberg et al 1999). The chapter also reviewed work of the conventional approach to reconstructing a sequence of three-dimensional (3D) images, drawing regions of interest (ROIs), generating time–activity curves for these regions, and then estimating kinetic model parameters from these time–activity curves. Much of this work was built upon the developments in dynamic PET imaging. Several references to the PET literature can be found in this first book chapter, as well as in more recent reviews (Lodge et al 2005, Heller et al 2009). Later, a second book chapter (Gullberg et al 2004) reviewed the improvements in the conventional approach resulting from equipment advancements that enabled sufficient timing resolution to obtain wash-in and wash-out rate parameters of compartment models from time–activity curves generated from a sequence of reconstructed ROIs.
This review concentrates on the problem where all kinetic model parameters and time–activity curves are estimated directly from projection measurements and illustrates examples of this approach for imaging applications in dynamic cardiac SPECT. This approach is commonly referred to as 4D or 5D imaging in the literature and presentations at scientific meetings. The terminology of 5D imaging is given to methods of estimating time varying dynamics of the tracer through the organ while the organ, such as the heart, is also moving.
The introduction to this paper evolved out of work presented at an American Society of Nuclear Cardiology meeting (Gullberg et al 2000). The sections following the introduction give the mathematical developments used in dynamic cardiac SPECT, comparing conventional ROI methods, direct methods and semi-direct methods. For readers who do not want to go into the mathematics, the introduction gives a good overview of dynamic cardiac SPECT. The paper assumes a basic understanding of nuclear medicine physics as found in Cherry et al (2003). Other works that give the basics of nuclear medicine physics, SPECT and clinical applications can be found in the chapters of the following two books: (Wagner et al 1995, Henkin et al 2006). Also, chapters 7 and 8 in Phelps et al (1986) give a very good introduction to kinetic modeling and the estimation of model parameters. A glossary is presented that defines several of the terms and acronyms for radiopharmaceuticals that may not be known to the general reader. A list of symbols is also presented to help the reader understand the definition of the different variables used in the equations.
1. Introduction
Dynamic single photon emission computed tomography (SPECT) is a technique that uses tracers to obtain images that reflect fundamental biophysiologic functions of perfusion and metabolism in body organs. This is done by quantifying the temporal changes of radionuclide concentration in tomographic sections through angular sampling of projections (Carson 1986b, Gullberg et al 1999). This technique, in conjunction with mathematical model-based analysis of regional kinetics of the radiotracer, allows for the quantitation of functional parameters, which are estimated by utilizing a time series of dynamic reconstructed images. Physiologic parameter estimation using kinetic analysis is well established in positron emission tomography (PET). However, the methodology has not seen routine clinical application in PET or SPECT. The development and use of kinetic analysis in dynamic SPECT applications have been limited by low sensitivity, poor spatial resolution and poor temporal resolution, which are consequences of the need to mechanically rotate the detector head for most studies. The use of ring detector systems for dynamic brain SPECT applications (figure 2), along with recent advancements in dynamic cardiac SPECT instrumentation (figure 3), has demonstrated SPECT’s effectiveness for extraction of physiologic values of perfusion (Smith et al 1994, 1996) and metabolism (Gullberg et al 1999). This requires measurement of the blood input to the organ of interest and observation over time of the blood input and uptake as well as wash-out from the organ of interest. One then is able to fit physiological compartment models (see section 2.1) that represent the wash-in of the radiopharmaceutical, its metabolism or catabolism, and the wash-out of the tracer and its metabolites from the organ of interest. While this procedure has been used for years with PET to study several in vivo biochemical and physiologic processes in health and disease, it remains a challenge with SPECT, because most data are acquired using slow camera rotations. However, with recent developments in representation of data using a multi-resolution spatiotemporal basis (see section 3), special data processing methods can be used to extract kinetics from dynamic SPECT data acquired using detectors that rotate while radiopharmaceuticals exchange between biological compartments.
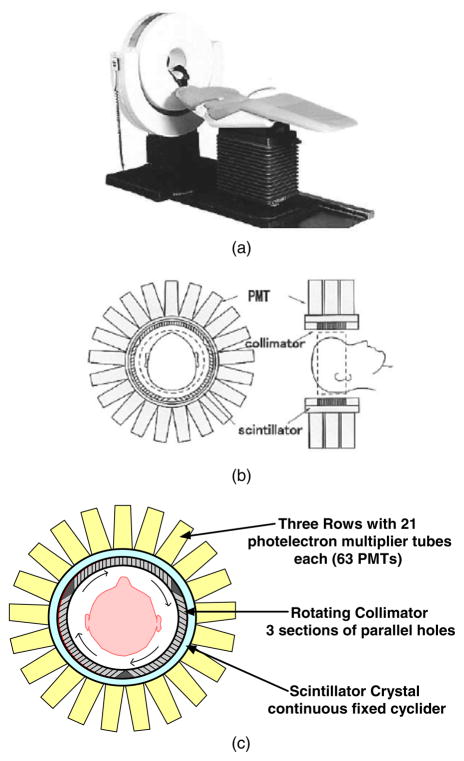
Figure 2.
The CERASPECT dedicated brain system was manufactured by DSI, Inc. (Waltham, MA). (a) Picture of the scanner with patient bed. (b) Drawing illustrating the collimator, scintillator, and PMTs (from figure 1 of Komatani et al (2004), with permission). (c) Diagram of camera detector redrawn to better illustrate the arrangement of the collimator holes in the rotating collimator.
Figure 3.
(a) Triple-headed SPECT system manufactured by Picker (Cleveland, OH). The system consists of an external line source of radioactivity (153Gd) used to obtain a transmission image used for attenuation correction. (b) Dedicated cardiac SPECT system manufactured by GE Healthcare (Discovery NM 530c, GE Healthcare, Haifa, Israel) (image from GE Healthcare with permission). The system consists of a half ring of CZT detectors.
1.1. History
1.1.1. Early development of dynamic SPECT
Dynamic SPECT was used in brain studies as early as 1963 (Kuhl and Edwards 1963) using two discrete detectors and later using a fixed four-headed detector system, each with a linear array of eight discrete scintillation detectors (Kuhl et al 1976). This was followed in 1978 by another fixed four-headed detector system (DCAT) (Stokely et al 1980) capable of rapid acquisition (5 s sampling) of a few transaxial sections for imaging 133Xe in the brain. In 1990, brain imaging was realized with a rotating four-headed gamma camera system (Kimura et al 1990). Also, dedicated brain systems consisting of a ring of scintillation detectors were developed (Rogers et al 1982, 1988, Hirose et al 1982, Moore and Mueller 1986, Genna and Smith 1988, Rowe et al 1993, Ogasawara et al 2000, Komatani et al 2004). These included the SPRINT system (Rogers et al 1982, 1988) developed at the University of Michigan; the Headtome II hybrid emission/CT system (Hirose et al 1982) developed by Shimadzu Corporation, which incorporated scintillation detectors arranged in a circular ring with a set of collimator vanes that swung in front of discrete detectors; a unique Cleon Brain SPECT system originally developed by the Union Carbide Corporation in the 1970s, which consisted of 12 detectors that scanned both radially and tangentially (Stoddart and Stoddart 1979) with a reconstruction method (Moore and Mueller 1986) that was later marketed by Strichman Corporation; ASPECT, a dedicated brain system (Genna and Smith 1988), later manufactured by DSI, Inc. as the CERASPECT (Komatani et al 2004) (figure 2); and the FastSPECT system (Aarsvold et al 1988, Rowe et al 1993) developed at the University of Arizona, which was reported to be able to acquire dynamic tomographic data with a sampling interval of 2 s. A system with multiple rings of scintillation detectors was developed for brain SPECT studies in Japan by Shimadzu (Ogasawara et al 2000). The system consisted of 64 NaI crystals in a 38 cm diameter circle. Early on there were two ring systems proposed for cardiac SPECT imaging—the Shimadzu whole body system (Yonekura et al 1985) and the cardiac FastSPECT system (Rowe et al 1992)—but both systems remained conceptual designs.
In 1990, dynamic SPECT (Stewart et al 1990) was applied to the estimation of the wash-out of 99mTc-teboroxime from the myocardium in canine cardiac studies using a single-slice ring detector (SPRINT). However, it was not until 1991 (Budinger et al 1991) that it was demonstrated that a reliable blood input function could be obtained from 5 s sampling intervals of reconstructed dynamic SPECT data, and that this sampling regime would be sufficient for compartment model-based analysis of the data. Using the triple-headed camera configuration (figure 3(a)) first developed in 1985 (Lim et al 1985), the time–activity curves of a radionuclide were quantified in canine and human experiments. The dynamic data sets were reconstructed and corrected for attenuation using a reconstructed attenuation distribution obtained from a separate transmission scan. During the same period, commercial three-headed SPECT systems were used by two groups to image the wash-out of 99mTc-teboroxime from the heart by obtaining 360° tomographic acquisitions every 1 min (Nakajima et al 1991, Chua et al 1993).
The first results of a compartment model-based analysis of dynamic cardiac SPECT data were obtained using the three-headed PRISM system (figure 3(a)) (Picker, Cleveland, OH) (Smith et al 1994, 1996). Using attenuation-corrected dynamic reconstructed data from canines, it was demonstrated that the estimated wash-in and wash-out of 99mTc-teboroxime correlated with microsphere-derived flow estimates. A similar approach was demonstrated in humans (Chiao et al 1994a). Although the work did not correct for attenuation, it was shown that the wash-in and wash-out estimates of 99mTc-teboroxime for the whole left ventricular myocardium changed significantly in response to coronary vasodilatation.
The original three-headed PRISM SPECT system (figure 3(a)) had the mechanical stability and control hardware to allow acquisition of 360° of data in 5 to 10 s. The major advantage of a system of multiple-gamma camera heads is the improvement in sensitivity afforded by better coverage of the solid angle. However, the arrangement of the detector heads is important for minimizing attenuation of posterior views for cardiac imaging. Another advantage is that multiple heads reduce the angular range of motion necessary to acquire a complete data set. Thus, only 120° of rotation is needed for a three-headed system and 90° is needed for a four-headed system. The disadvantages are that a system of multiple large field-of-view gamma cameras is expensive, and fast rotations (complete tomographic acquisitions of 10 s or less) are not available on all systems.
1.1.2. Dynamic SPECT applications
The main focus of this review is the application of dynamic SPECT to cardiac studies. However, dynamic SPECT has found significant application in pulmonary (Coates 1992, Ercan et al 1993, Sakaji et al 2001), renal (Hansen et al 1994, Akahira et al 1999) and brain studies. Dynamic SPECT imaging has been used to estimate lung regional function using 133Xe (Sakaji et al 2001). It has been used to evaluate renal plasma flow of transplanted kidneys using 99mTc-MAG3 (Akahira et al 1999). A simulation study also showed that dynamic SPECT could be useful for evaluating kidney function using a three-headed SPECT system to image 123I-hippuran (Vanzi et al 2004). A major portion of the application of dynamic SPECT in the study of in vivo physiological function has been directed toward the study of brain disorders.
A body of recent work is directed toward the dedicated ring detector systems for brain imaging and systems with detector arrays partially encompassing the body are currently being introduced into the clinic for cardiac imaging. A ring-type dedicated brain SPECT called the Headtome was successfully used with 99mTc-HMPAO to quantitatively image brain blood flow in patients with a stroke (Toyama et al 1996). Another ring system, the CERASPECT (DSI, Inc. Waltham, MA) (figure 2), was used to study the retention process of 99mTc-ECD in normal and ischemic lesions, and early phase images of the tracer were found to be as useful as 133Xe-rCBF SPECT for detecting mild or moderate ischemic lesions (Komatani et al 2004). A study using 123I-iodoamphetamine (123I-IMP) in patients with meningiomas, which compared lesion-to-normal ratios with angiographic vascularities and histological types, concluded that dynamic SPECT with 123I-IMP was more effective than angiography for evaluating the vascularity of lesions (Nakano et al 1988). Studies using ring SPECT cameras have been employed to image subacute cerebral infarction (Ogasawara et al 2001a), herpes simplex encephalitis (Ogasawara et al 2002b), reperfusion hyperemia after acute cerebral embolism (Ogasawara et al 2002a) and Lhermitte-Duclos disease (Ogasawara et al 2001b).
For several years, dynamic SPECT has been used to evaluate the central benzodiazepine (BZP) receptor binding of 123I-iomazenil (123I-IMZ, a benzodiazepine antagonist) in the diagnosis of central nervous system disorders with abnormalities in BZP receptor binding (Ito et al 1997). These studies with dynamic SPECT and 123I-IMZ have shown defects in the benzodiazepine receptors in brain pathologic diseases such as ischemia, epilepsy, Alzheimer’s disease, Huntington’s disease and schizophrenia (Moriwaki et al 1998), and for prognosis prior to endoreterectony (Tsuchida et al 1999). Recently it was reported that dynamic SPECT was used with 123I-IMZ to study a rare case of slowly progressive neuronal death associated with postischemic hyperperfusion in cortical laminar necrosis (Iihara et al 2009). The condition was experienced after cerebral artery bypass surgery for an intracavernous carotid artery aneurysm. Studies have also shown that dynamic SPECT gives comparable results to those of dynamic PET using 11C-IMZ (Bremner et al 1999). Kinetic model-based methods have been developed for SPECT to quantitatively measure 123I-iomazenil binding to benzodiazepine receptors in the human brain (Dargham et al 1994). The significance of receptor-binding kinetics has generated interest in using a standard input function instead of having to perform arterial sampling to obtain the input function (Seike et al 2004).
It is interesting to note that in Japan, more so than in the USA, noninvasive tests are used for diagnosing brain autoregulatory abnormalities (Rudzinski et al 2007). Dynamic SPECT scans are used to quantify cerebral blood flow (CBF) and cerebral vascular reactivity (CVR) in a single session using a split dose administration of 123I-iodoamphetamine (123I-IMP)—one at rest and one during Diamox challenge (Imaizumi et al 2002). The rest/stress protocol is much like that performed to evaluate myocardial perfusion. First, a rest dynamic cerebral blood flow study is performed after the injection of 123I-IMP. After the completion of the first study, Diamox is administered to stress the cerebral vascular system. A second study is then performed after administration of a second injection of 123I-IMP. A large-scale clinical trial showed that appropriately quantifying dynamic SPECT data by correcting for attenuation, scatter and collimator response gave values for CBF at rest and during Diamox treatment that were reproducible among institutions, and it demonstrated that the modality was useful for diagnosing brain autoregulatory abnormalities and for providing CBF and perfusion reserve from a single scanning session (Iida et al 2006).
1.1.3. Dynamic cardiac SPECT advances
Early work in dynamic cardiac SPECT concentrated on using systems with rotating multiple-gamma camera heads to image tracers with fast kinetics (Chua et al 1993, Smith et al 1994, 1996). However, the focus has changed, since tracers with slower wash-out kinetics, such as 201Tl (Iida and Eberl 1998, Gullberg et al 1999) and 99mTc-sestamibi (Gullberg et al 2007a, Reutter et al 2007a), are more readily available for perfusion studies, and cardiac metabolic agents, such as 123IPPA (Limber et al 1995, Gullberg et al 1999) and 123I-BMIPP (Gullberg et al 2006), are more appealing for myocardial viability studies or for evaluating myocardial fatty acid metabolism in patients with hypertrophic cardiomyopathy (Okizakia et al 2007). In addition, improvements in data processing techniques have allowed processing of kinetics using only a single rotating detector that is commonly used in clinical nuclear medicine. The use of 99mTc-teboroxime (Chua et al 1993, Smith et al 1994, 1996), a rapidly exchanging agent, shows promise in the application of dynamic SPECT for imaging the heart. Also, recent results suggest that implementing a dynamic SPECT protocol can shorten clinical 123I-MIBG imaging studies that are used to assess the severity of heart disease and prognosis in patients with chronic heart failure (CHF) (Takeishi et al 2005, Hu et al 2005).
Although the standard single-gamma camera configuration for SPECT is still commonly encountered in clinic inventories, it has been supplanted at many institutions by dual- or triple-headed detector systems, with dual-headed detector systems being most prevalent. Today, the dual-headed detector SPECT system (figure 1) is the most common imaging system used in nuclear cardiology because it can perform cardiac scans (the most commonly performed procedure) as well as whole body bone scans. The detectors on these dual-headed detector systems are much larger than the original three-headed detector PRISM system (figure 3(a)), but the rotational speed of the modern systems with the most robust gantries is still limited to a single tomographic acquisition every 15 s. As a result, data processing techniques have emphasized the development of methods for processing kinetics directly from projection measurements.
1.1.4. New dedicated cardiac SPECT systems
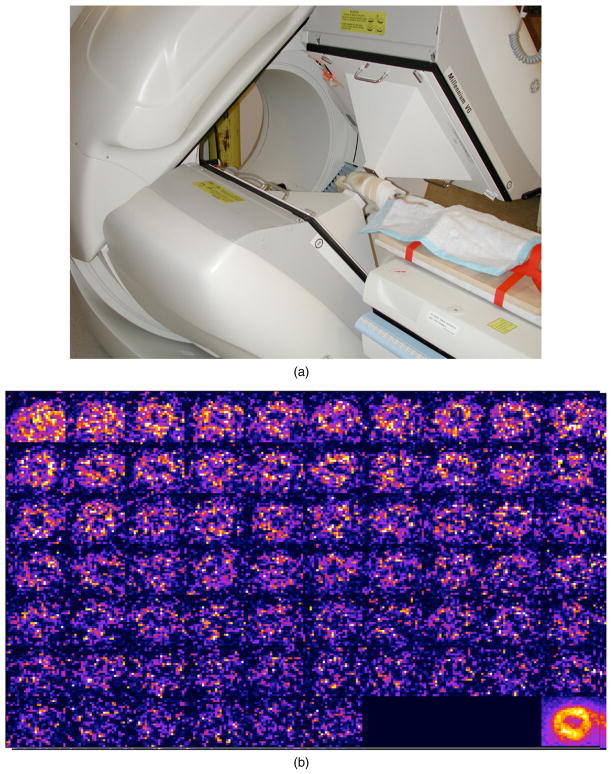
Digirad was the first company to develop and manufacture a dedicated cardiac SPECT scanner (Patton et al 2007). New versions of the system have small multiple-gamma cameras that rotate to obtain sufficient angular sampling along with an x-ray transmission system for obtaining an attenuation map for attenuation correction. The new dedicated cardiac system developed by Spectrum Dynamics (Caesarea, Israel) (Sharir et al 2007, 2008, 2010, Berman 2007, Gambhir et al 2009, Erlandsson et al 2009, Ben-Haim et al 2010, Patton et al 2007) (figure 4) is able to obtain high quality cardiac perfusion images of 2 min stress and 4 min rest acquisition times. Another newly developed dedicated cardiac scanner is the CardiARC (Lubbock, TX) (Berman 2007, Patton et al 2007), which is similar in concept to the original SPRINT design with a fixed ring of detectors and a rotating slit collimator. GE Healthcare (Haifa, Israel) has announced the development of a new dedicated cardiac SPECT system (figure 3(b)) (Volokh et al 2008, Garcia et al 2008, Esteves et al 2008, Buechel et al 2010). Another dedicated cardiac SPECT system called C-SPECT, being built at Rush University Medical Center, Chicago, IL, is being funded by the NIH (Chang et al 2008, Ordonez et al 2008). Ultimately, dedicated cardiac SPECT systems with total acquisition times of 2–3 min may become available. While these more recent non-rotating detector systems are ideal for dynamic cardiac SPECT, rotating three- and two-headed detector systems have been shown to provide adequate temporal resolution (Gullberg et al 2004).
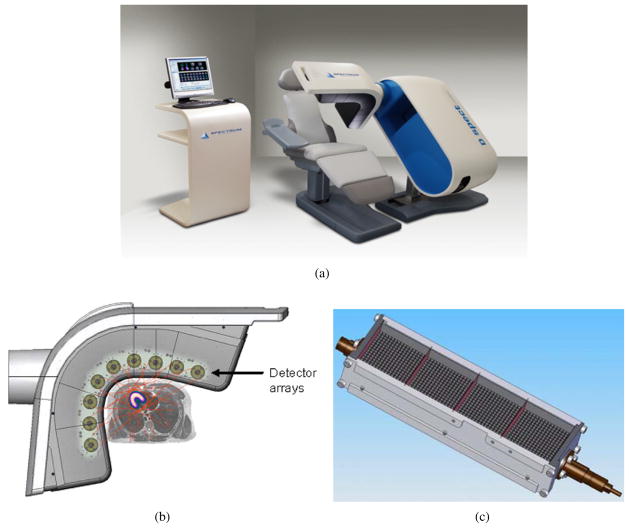
Figure 4.
(a) Dedicated cardiac SPECT camera manufactured by Spectrum Dynamics (Caesarea, Israel) (image from Spectrum Dynamics with permission). (b) The camera consists of nine pixellated cadmium zinc telluride (CZT) detector arrays mounted in a vertical column, each rotating in synchrony and acquiring at multiple angles as the detectors are swept through the imaging field of view (image from figure 1 of Erlandsson et al (2009) with permission). (c) Each detector column consists of an array of 16 × 64 CZT semi-conductor elements (2.46 × 2.46 × 5 mm), collimated by a parallel-hole tungsten collimator with a hole size of 2.46 × 2.46 mm, the same as a detector element (Patton et al 2007). The collimator hole length is shorter than the LEHR collimator with a significant gain in sensitivity. The cadmium zinc telluride provides improved energy resolution and image contrast. The improved geometric sensitivity allows for myocardial perfusion imaging studies of 2 min stress and 4 min rest acquisition times. Reconstruction is performed with a proprietary version of an OSEM-based reconstruction software package developed and implemented by Spectrum Dynamics (image from Spectrum Dynamics with permission).
1.2. Radiopharmaceutical considerations for dynamic cardiac and brain SPECT
This discussion of applications is not a comprehensive review of nuclear medicine imaging approaches to the brain and heart using radiopharmaceutical agents, but is intended to highlight the application of dynamic SPECT along with some comments relative to competitive approaches with PET. A ‘chemical microsphere’ is a term given to a radiotracer that becomes trapped within a cell. Microspheres are small spherical particles with diameters in the micrometer range, typically 15 μm for heart studies so these become trapped in small capillaries. They are used to measure absolute organ blood flow. The microsphere method is based on the principle of conservation of material (Fick principle); that is, the amount accumulating in tissue is equal to flow times concentration of the material available in the blood minus flow times concentration of the venous wash-out. In the microsphere method, there is a no wash-out of the accumulated material. If a single photon tracer is trapped in the tissue, its behavior will approximate the properties of a ‘chemical microsphere’. It has been suggested that 99mTc-sestamibi (99mTc-MIBI) may be useful as a tracer for calculating coronary flow reserve (CFR) using this ‘microsphere’ technique (Sugihara et al 2001). This agent accumulates in the myocardium in proportion to flow but, unlike microspheres, washes out slowly; thus quantitation of flow requires dynamic data acquisition and an appropriate model, unless the wash-out is slow enough that the integral of uptake activity over a short time period can be used in a ‘microsphere’ technique. The agent 99mTc-tetrofosmin has also shown promising initial results for calculating CFR using a single-headed detector SPECT system (Sugihara et al 2001). 123Iodorotenone (Marshall et al 2001) is another potential agent that has an even higher extraction fraction than the commonly used compounds of 99mTc-MIBI or 99mTc-tetrofosmin and may also be a useful tracer for calculating CFR using the microsphere analogy. Further work is required to evaluate the ‘microsphere’ method for calculating CFR and to compare this approach with that of using either dynamic SPECT or dynamic PET imaging of agents that have fast turnover (i.e., rapid exchange, such as H215O).
Dynamic cardiac SPECT imaging could potentially be useful for measuring CFR, but it requires a flow agent with a large range of flow values for which the extraction fraction (arterial concentration minus the venous concentration divided by the arterial concentration) remains linear as a function of flow. It was shown (Chiao et al 1994a) that wash-in and wash-out estimates of 99mTc-teboroxime for the entire left ventricular myocardium change significantly in response to coronary vasodilatation. Quantitative compartmental analysis of 99mTc-teboroxime kinetics provides a sensitive indicator for changes in estimates of wash-in in response to adenosine-induced coronary vasodilatation (Gullberg et al 1999, 2004). It has also been shown that dynamic imaging of 99mTc-teboroxime with compartment modeling provides a better measure of flow with parametric images of better contrast between normal and decreased flow regions than can be obtained from static imaging of 201Tl or, for that matter, static imaging of 99mTc-teboroxime (Gullberg et al 2004). In fact, dynamic SPECT may prove advantageous over static imaging because it may enable better measurement of both perfusion and viability (Gullberg et al 2004).
In addition, dynamic SPECT methods may be useful for evaluating myocardial function using other tracers such as the perfusion agent 99mTc-N-NOET (Calnon et al 1999) and metabolic agents such as the fatty acid 123IPPA (Gullberg et al 1999). The agent 99mTc-N-NOET has features of greater redistribution (the apparent filling in of a myocardial perfusion defect over a period of time due to differential wash-in and wash-out of a tracer between ischemic and normal regions). This agent has good linearity with flow but has not yet been introduced into the clinic (Johnsonet al 1996). 99mTc-N-NOET, like 99mTc-teboroxime, is a neutral compound but unlike 99mTc-teboroxime exhibits slower myocardial clearance. This agent is thus a potentially better alternative for dynamic cardiac SPECT imaging than either 201Tl or 99mTc-teboroxime. In PET, 82Rb, 13NH3 and H215O are the tracers most often used for measuring CFR.
There are also several radiopharmaceuticals used for brain SPECT that may be applicable for dynamic SPECT. For brain tumor imaging the primary modality involves using PET to image 18FDG (Chen and Silverman 2008). 18FDG-PET is also used to diagnose epilepsy. However, SPECT imaging with 99mTc-HMPAO or 99mTc-ECD is also able to identify the ictal (a physiologic state or event such as a seizure) onset zone in the majority of cases (Goffin et al 2008). Interictal (the period of time between seizures as a result of an epilepsy disorder) SPECT imaging is unreliable for determining the seizure onset zone, but interictal 18FDG-PET is routinely used to detect brain areas of hypometabolism. For diagnosing major depression disorders, PET is again an important imaging modality, but 123I-beta-CIT and 123I-ADAM are also used with SPECT to diagnose depression (Meyer 2008). For central motor disorders, both PET and SPECT imaging agents play roles in clinical diagnosis of Parkinson’s disease and other movement disorders (Kung et al 2003, Seibyl 2008). 18F-DOPA-PET is important in the diagnosis of motor disorders. However, 123I-FP-CIT, 123I-beta-CIT, 99mTc-TRODAT and 123I-altropane are also used. These tracers measure different aspects of dopaminergic function and may contribute different and potentially complementary information about the disease process. The focus has been on patients in the early stages of illness. However, these agents might serve as biomarkers of the progression of disease. SPECT has also been used to diagnose dementia (Pimlott et al 2007, Jagust et al 2009, Resnick et al 2010). Specifically, it has been used in the diagnosis of Alzheimer’s disease (Wolfe et al 1995, Jagust et al 1998, 2001). Addiction is an area where there are no SPECT ligand tracers that compete with PET approaches (Volkow et al 2003, 2009) as in the case for dementia studies.
1.3. Data processing techniques
Compartmental modeling of tracer kinetics is utilized to extract kinetic parameters from dynamically measured data of compartment models that describe the pathways and dynamic behavior of tracers in organ tissues (see section 2). Significant work has been accomplished to improve the conventional method of analysis of dynamic cardiac SPECT data in which ROIs are specified in a sequence of reconstructed images and time–activity curves are generated from the data values in these ROIs (Gullberg et al 2004). These time–activity curves are input to a nonlinear estimation program (Huesman et al 1995) that estimates the compartment model kinetic parameters. The ROIs are usually drawn by hand, but semi-automatic programs (Di Bella et al 1997) can improve reproducibility from study to study. Kinetic parameters can also be calculated for every image voxel by fitting a time–activity curve generated from a dynamic reconstructed sequence to a compartment model. The parameter values are then mapped to colors or gray levels and displayed as parametric images (Sitek et al 2002a, Gullberg et al 2004).
This review highlights advancements in the estimation of kinetic parameters from projections as opposed to the conventional method of estimating kinetic parameters from dynamic reconstructed images. This approach can be readily applied to all camera systems, including those with low geometric efficiency and slow camera rotation. The possibility of performing dynamic cardiac SPECT imaging using a single slowly rotating camera head is enticing, since such scanners are both inexpensive and widely deployed. Unfortunately, the angular projections obtained are inconsistent when a rotating camera head is employed to image a distribution of emission sources whose activity varies significantly during the time necessary for the camera head(s) to complete a revolution. Consequently, application of conventional tomographic reconstruction algorithms yields inaccurate reconstructed images that are ‘blurred’. This leads to biases in the estimated kinetic parameters. The inconsistent projection problem may be viewed as one of attempting to interpolate in time and space simultaneously—in sinotimogram space (sinogram of a time-varying distribution corresponding to projection data represented by three coordinates—the angle, the projection bin and the time). Such interpolation is only feasible if a priori knowledge regarding the geometry and time–activity evolution of the image sources is included.
A better approach to analyzing dynamic data (SPECT or PET) than using time–activity curves generated from reconstructed regions is to estimate the time–activity curves or kinetic parameters directly from the projection data of the sinotimogram, using an accurate model of the data acquisition of the spatial and temporal distribution of the radiopharmaceutical within the field-of-view. The simultaneous estimation of blood input function and kinetic model parameters can reduce bias and improve precision by using the interrelationship between blood and tissue imposed by the compartment model to constrain the solution.
1.3.1. Estimating dynamic parameters directly from projection measurements
The modeling of dynamic data is complicated by the combination of camera gantry motion, potential organ motion and the time-varying nature of the radionuclide distribution being imaged, resulting in inconsistent projection data sets wherein the projection from one angle is not consistent with that from another angle because the radionuclide concentration in the field of view changes between the time of acquisition for the different projections. Entire tomographic slices or volumes must be represented by some types of parameterization, and one does not have the option of analyzing a single ROI and ignoring the remainder. The estimation can be formulated as a minimization of a weighted sum of squared differences between the projection data and the model-predicted values. It was shown that biases in estimates from time–activity curves generated by dynamic reconstructions are eliminated by estimating dynamic parameters directly from the projections (Limber et al 1995, Gullberg et al 1999). Results also suggest that direct joint estimation of compartmental or other dynamic model parameters and blood input function from projections produce estimates of kinetic parameters with lower variance and bias than does the estimation of kinetic parameters from time–activity curves generated from dynamic reconstructed ROIs (Reutter et al 2005) (see section 5.1).
There are two main approaches for estimating dynamic parameters directly from projection measurements. One approach (semi-direct—a two step process) is to directly calculate activities for ROIs as a function of time; the results provide time–activity curves from which kinetic compartmental model parameters can be estimated (Carson 1986a, Formiconi 1993). A second approach (direct—a one step process) is to estimate dynamic parameters directly from the projection data, where it is assumed that the ROIs are specified and that expressions between the compartment model parameters and the dynamically acquired projections can be formulated in a chi-square formulation (Limber et al 1995, Zeng et al 1995). There are many variations or refinements that can be used with both methods. One refinement of both methods is the segmentation of organ boundaries or tissue types involving the joint estimation of spatial boundaries and temporal parameters. It was shown that biases of estimates are reduced by simultaneously estimating kinetic model parameters and boundary parameters of ROIs directly from projections and auxiliary boundary information (Chiao et al 1994b, 1994c). These boundaries may be static or dynamic. A method was proposed to estimate kinetic model parameters and boundary parameters for the heart from dynamic gated cardiac SPECT data (Gullberg et al 2007b). This is commonly referred to as 5D tomography.
Semi-direct approach (mathematical examples are presented in section 5)
The estimation of ROI time–activity curves from projections without reconstructing the ROI was first implemented in PET and was fairly easily accomplished using a convolution backprojection algorithm. First, a method to estimate the average activity in a 2D ROI was described (Huesman 1984). Subsequently, these ideas were extended to 3D ROIs (Defrise et al 1990). To compensate for physical factors such as attenuation and detector resolution, iterative algorithms that maximize a likelihood function had to be used (Carson 1986a, Formiconi 1993). An extension of this is to estimate the time–activity curves directly as continuous functions from projections, and then to estimate kinetic model parameters using the estimated time–activity curves (Reutter et al 2000, 2002, 2004a) (see section 5.1).
Some of the first work in SPECT to reconstruct time–activity curves from dynamically acquired projection data was accomplished by the group at the University of British Columbia (Bauschke et al 1999, Farncombe et al 1999, 2000, 2001, Farncombe 2000, Celler et al 2001). That work led to the development of the ‘dSPECT method’, which fits time–activity curves for each voxel directly from projection measurements acquired from single or multiple rotations of the gantry (see section 5.3). Initially, a version of the algorithm reconstructed time–activity curves that were constrained to monotonically rise or monotonically fall (Celler et al 2001). A modification led to the ability to reconstruct time–activity curves that rose to an estimated maximum value and then fell, much as would be expected, by the wash-in and wash-out of a tracer from an organ of interest (Farncombe et al 2001). The method required either prior knowledge or estimating the time frame when the activity peaked in each particular voxel of the object being imaged (Farncombe et al 2001). The main focus of dSPECT was to derive estimates of time–activity curves for studies performed using only a single rotation of a standard SPECT camera. The method has been utilized in clinical applications, including applications for reduction of bladder artifacts in pelvic bone SPECT (Wells et al 2004) and for estimating time–activity curves from gated cardiac SPECT data (Farncombe et al 2003a, 2003b, Feng et al 2006).
Another approach for extracting time–activity curves from dynamic data has been the method of factor analysis of dynamic structures (FADS) (see sections 3.3, 5.2). This method has been applied primarily in nuclear medicine to dynamically acquired planar data and to the dynamic sequence of reconstructions of projection data acquired with fast SPECT acquisition (Sitek et al 1999a, 1999b, 2000, 2002a, 2002b, Su et al 2007). However, it also has potential application for extraction of time–activity curves directly from dynamically acquired projections from slow rotation SPECT camera systems. For example, FADS was applied to extract time–activity curves from projections of the uptake and wash-out of 99mTc-MAG3 from the kidneys (Sitek et al 2001). Factor analysis was also used for extracting the blood input function in rats from dynamic SPECT data acquired with slow camera rotation (Hu et al 2008).
The group at LBNL has put effort into developing computationally efficient methods for estimating the time–activity curves from dynamic SPECT projection data. A direct least-squares estimation of spatiotemporal distributions from dynamically acquired SPECT projection data was developed (Reutter et al 2000, 2002, 2004a). Temporal B-splines (see section 3.1) providing various orders of temporal continuity, as well as various time samplings, were used to model the time–activity curves for blood pool and tissue volumes. An alternative time–activity curve model, based on a small set of orthogonal exponential basis functions and couched in a similar least-squares estimation framework, was also proposed (Maltz and Budinger 2000, Maltz 2000a).
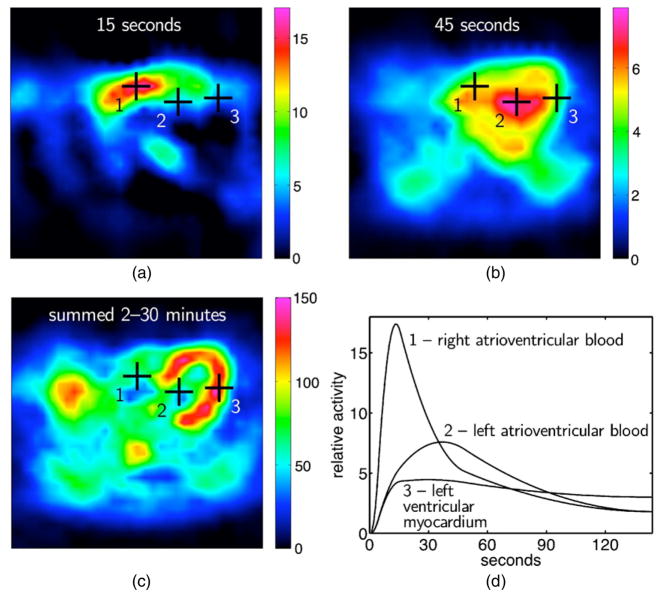
There are several possibilities that could be used for the temporal basis functions in the spatiotemporal representation of reconstructed dynamic data. These could be exponential, spline or factor (discrete temporal function describing a time course of activity concentration for a particular organ or tissue) basis functions. Multi-resolution B-splines and penalized least-squares inversion (see section 5.1) have been used to reconstruct dynamic cardiac SPECT data from rest/stress cardiac patient studies acquired using a clinical SPECT system with slow camera rotation (Gullberg et al 2007a, Reutter et al 2007a). By extending the support of spatial B-splines into the time dimension, estimates of time–activity curves were obtained directly from projections. The use of non-uniform time sampling with piecewise-quadratic splines yielded smooth time–activity curves that captured the relatively fast rise and fall of the tracer in the right (15 s after injection) and left ventricular blood chambers (45 s), as well as uptake and retention of the tracer in the left ventricular myocardium.
The solution to a system of differential equations which express the time varying distribution between compartments involves expressions of exponentials. Therefore, it is very natural to parameterize the kinetics of the radiopharmaceutical distribution in the tissue as a spectrum of exponential terms in time. The spectral-based approach builds on earlier work (Cunningham and Jones 1993) in which it was suggested that, instead of estimating the kinetic parameters of models, one could estimate the coefficients of a predefined spectrum of exponentially decaying factors. It is assumed that the decay constants for the exponentials span some reasonable ranges of physiological values, and those are predefined with sufficient sampling to adequately represent the kinetics of the tracer.
Efforts have been made to calculate these coefficients directly from projections for a few spectral terms, such as for two spectral terms (Hicks et al 1989, Hebber et al 1997) or for several spectral terms (Matthews et al 1997, Maltz 2001, 2002). This approach obviates the need for iterative estimation of the nonlinear parameters (rate constants) of a compartment model, allowing a convenient solution via linear methods (Maltz 2001).
A significant limitation of exponential spectral methods is that the solution obtained may not be unique due to the large amount of parameter redundancy, which is characteristic of sums of decaying exponential terms. Spectral coefficient estimates must therefore be interpreted with caution. Application of dimension-reducing transforms, such as the singular value decomposition (SVD), can decrease the dimension of the spectral estimation problem to approximately 1/20th of its original size while ameliorating the problem of parameter redundancy (Maltz and Budinger 2000).
Unfortunately, because sums of decaying real exponentials are not uniquely parameterized in the presence of noise, solutions in terms of spectral coefficients may not be unique (Lanczos 1956, Reich 1981). A strong dependence may consequently exist between the particular solution obtained and the noise present within the data. The parsimonious exponential spectral analysis (ESA) algorithm ameliorates the inherent problem of non-uniqueness in ESA parameters (Maltz 2002). It has been shown (Maltz 2001) that using an exponential basis with a nonuniform resolution reconstruction grid leads to a tremendous reduction in the dimension of the problem of direct dynamic emission computed tomography reconstruction from inconsistent projections. The solution coefficients, which must be non-negative, can be determined by using either a non-negative least-squares technique (Meikle et al 1996, 1998) or the ML-EM algorithm (Matthews et al 1997). Computationally, it can be performed in succession by first determining spectral components for each projection sample (Meikle et al 1996, 1998). The spectral components for each pixel can then be reconstructed from the spectral components of the projection ray sums. Instead of using an exponential decomposition, one can use some other parametric decomposition (Matthews et al 1997), some other best fit model (Hudson and Walsh 1997, Hutton et al 1997) or some physical factors (FADS method) (Barber 1980, Sitek et al 2002b).
Direct approach (mathematical examples are presented in section 4)
A direct approach involves eliminating the step of estimating time–activity curves by estimating the model parameters directly from the measured projections. This approach must apply the correct model to every voxel or region, which requires modeling the entire object. One voxel or ROI might be an input function, while another voxel or tissue region might be a one-compartment perfusion model, a two-compartment metabolic model or a multi-compartment ligand binding model. An important issue is the segmentation of organs or tissue types, especially the segmentation of the blood ROI, since a direct approach requires the simultaneous estimation of both the input function and the kinetic model parameters (Reutter et al 2005) (see section 4.1). If the tissue or organ moves, such as in the case of cardiac motion, this also needs to be modeled correctly. It is also necessary to model accurately the physics of the imaging detection process, such as scatter, attenuation and collimator response. One can see that this becomes a very large complex nonlinear optimization problem.
A direct approach to estimating dynamic parameters can reduce the bias and variance, but it assumes that the modeling is appropriate for the dynamic process being realized. If the locations of the tissue regions are known, it has been demonstrated that bias is reduced by estimating kinetic parameters of a compartment model directly from projections. This was demonstrated for a 3 × 3 computer-simulated image array (Zeng et al 1995), for a 64 × 64 computer simulation using parallel geometry (Gullberg et al 1999) and for a 48 × 48 × 30 computer simulation using cone-beam geometry (Huesman et al 1998). These studies assumed a one-compartment model with a blood input function (see section 2.2).
The most direct approach is to derive the kinetic model parameters directly from the projection data for each pixel (Kadrmas and Gullberg 2001) (see section 4.3). This could be one or multi compartments. Multiple compartments could be represented by a spectral decomposition (see section 4.4). However, the low signal-to-noise ratio of dynamic SPECT, and the poor condition number of the inverse problem, severely limit the number of regions that may be resolved. To reduce the dimensionality of the problem so that it is not necessary to specify a compartment model for each voxel, methods of presegmentation of particular tissue regions based on anatomical and physiological considerations have been proposed (see section 4.1). For myocardial studies, typical regions might include healthy blood pool, myocardium, myocardial defect, liver and background (Huesman et al 1998, Reutter et al 1998a, 2000) (see section 4.2). The accuracy of the kinetic models depends on an accurate initial segmentation, which might not be easily accomplished. For example, in a clinical study the location of a defect is not known a priori. The most obvious way of ameliorating this problem is to segment the myocardium into several regions such that the smallest physiologically significant defect might be detected. Another approach would be to spatially parameterize the entire myocardium or a small number of regions of the myocardium. However, as the number of regions is increased, the statistical advantages of anatomically or physiologically motivated presegmentation are lost.
Joint estimation of spatial boundaries and dynamic parameters
A refinement in the estimation of dynamic parameters from projections involves simultaneously estimating the geometric regions and the time–activity of the regions directly from the inconsistent projection data. Progress toward the development of practical joint spatial and temporal algorithms has been limited because of the severely ill-conditioned nature of this nonlinear problem. The first joint spatial and temporal algorithm for dynamic emission computed tomography (Chiao et al 1994b, 1994c) enabled the fitting of a single dynamic region (the myocardium) to simulated myocardial data in the presence of noise and background activity. The myocardial activity was described using a first-order single-compartment model, and the geometry of the myocardium was described by a parameterized concentric polygonal model. A local optimization strategy was able to recover the joint parameter set, which consisted of the endocardial and epicardial radii at the vertices of the respective polygons, and compartment model parameters. It was demonstrated that biases in the kinetic parameter estimates were reduced by allowing for estimates of the boundary of the ROI to be included in the estimation process.
Extension of joint spatial and temporal algorithms to multiple regions proves non-trivial because the parameter estimation problem becomes multimodal. Its solution consequently requires a computationally intensive, multi-start optimization algorithm. Such an algorithm was developed at the University of California, Berkeley, and is able to fit more than ten dynamic regions to data acquired with the slow rotation of a single-gamma camera operating at realistic photon count rates (Maltz et al 1998). A set of spatially constrained ellipses is used to model regions within the image where the activity of each region is described using a single-compartment model. It appears that it is the poor condition of the inverse problem rather than a low number of photon counts per resolution element that limits the accuracy of the recovered regional time–activity curves (Maltz 2000b). The ill-conditioning is due, in part, to the well-known problem of parameter redundancy in sums of real exponential functions (Lanczos 1956, Reich 1981). When several sources within the image follow first-order single-compartment tracer kinetic models, the projection measurements are composed of weighted sums of decaying exponential functions convolved with a blood input function. When joint estimation is performed, it is the parameters of these exponentials, along with the geometric model parameters, that are sought. Since vastly different parameterizations of these sums may yield resultant functions that are indistinguishable at realistic noise levels, there can be no certainty that a unique solution exists. This condition may be improved by replacing the exponential functions with orthogonal basis functions that, when convolved with the blood input function, are able to represent all physiologically feasible time–activity curves using a less redundant parameterization (Reich 1981, Maltz et al 1998). The quality of the reconstruction that may be obtained using joint spatial and temporal algorithms applied to single slow rotation data is dependent on the quality of the constrained geometric and kinetic models used to restrict the set of solutions to those that are physiologically feasible.
5D processing of dynamic gated cardiac SPECT data
The estimation of dynamic parameters from projections that model the deformation of the organ as a function of time and the change in the concentration of the tracer as a function of time is referred to as 5D tomography. For the heart, it is assumed that the data are acquired dynamically with cardiac phase information either by list mode acquisition or by binning into gated dynamic frames over the cardiac cycle. The groups at the University of Massachusetts and the University of British Columbia extended the dSPECT method to obtain reconstructions of the time variation of the concentration of the tracer in the heart from dynamically acquired gated cardiac SPECT data (Farncombe et al 2003a, 2003b, Feng et al 2003a, 2006).
The group at the Massachusetts Institute of Technology (Feng et al 2003b, Shi and Karl 2003, 2004, Jin et al 2005, 2006a, 2006b) took a different approach from that used in the dSPECT method by using the level set method (a numerical technique for tracking interfaces and shapes) to delineate boundaries of moving organs, such as the heart, while simultaneously estimating the time variation of the tracer concentration in the organ. 5D tomography has all of the challenges of modeling both rigid and non-rigid body deformation simultaneously with the modeling of a time varying tracer concentration from tomographic projections (Gravier et al 2007, Gullberg et al 2007b). In the future, this will have important applications in diagnostic medicine and in radiotherapy with injected radioisotopes.
1.3.2. Input function
One of the most difficult problems in applying kinetic modeling is estimation of the blood input function (see section 2.3 for a more extensive discussion). The sampling of the blood input at a high temporal resolution is more important than sampling the tissue response with a high temporal resolution. Estimation of the input function from the imaging data is problematic due to partial volume effects, scatter and cardiac and lung motion that tends to contaminate the blood data with data from the myocardium, liver and other surrounding tissues. The input function is especially difficult to measure in pinhole SPECT imaging of small animals using a rotating large field-of-view gamma camera (Hu et al 2005). The blood volume is small, and thus it can be difficult to obtain the blood input function (Laforest et al 2005). Furthermore, limited system resolution can make ROI sampling of the ventricular cavity problematic. In addition, the recirculation time is of the order of seconds (6–8 s in a rat). Therefore, it is difficult to capture the true time–activity curve because the full tomographic acquisition requires 90 s. For this application, it has been shown that factors can be estimated directly from projections but it requires the estimation of greater than a million unknowns (Hu et al 2005). An intriguing approach is to estimate the kinetic model parameters for the myocardium from projections without a priori knowledge of the input function—blind estimation (Di Bella et al 1999). However, this method limits which kinetic parameters can be estimated absolutely.
1.3.3. Multigridding approaches
An advantage of spatiotemporal modeling is the ability to reduce the number of unknown parameters by using multi-resolution or multigridding approaches to represent spatial and temporal distributions of dynamic data. Three possible spatial basis functions involve the use of (1) uniform voxels, (2) splines or (3) point cloud distributions of tetrahedral finite elements. These spatial basis functions can be combined with temporal basis functions using, for example, exponential, spline or factor basis functions or time–activity functions that fit a particular compartment model.
Multigridding approaches using splines
The spatial parameterization can involve a multi-resolution or multigridding approach where inside the organ boundaries the changing tracer kinetics are modeled with high resolution and outside the organ the distribution is modeled with a more coarse resolution (Boutchko et al 2006b, Reutter et al 2006, Sitek et al 2006). B-spline spatial basis functions can be used to model continuous 3D tracer distributions in the heart (Reutter et al 2006, 2007b), and this approach improves signal-to-noise and increases computational efficiency compared to methods based on small cube-shaped voxels. Uniform B-spline basis functions have the property that splines of larger support can be composed from a linear combination of splines of smaller support, thus facilitating creation of a multi-resolution spatial model. B-splines can be evaluated quickly when calculating projection data models or displaying reconstructed images, and there is no image ‘blockiness’ because B-splines yield a spatially continuous representation. A negativity penalty can be incorporated into the estimation of the spline coefficients so that these coefficients that tend to have negative values are constrained to stay near zero, with use of a quadratic penalty that penalizes nonzero contributions to the projection data model (Reutter et al 2007b). Use of the penalty reduces image noise when employing more compact splines to maintain good resolution throughout the body.
Multigridding approaches using point clouds
Another multigridding image representation is the use of point clouds where the points are distributed on an irregular grid that adapts to the information content in the projection data (Sitek et al 2006). The points serve as vertices of a tetrahedral mesh formed using the Delaunay tessellation algorithm (de Berg et al 2008) or some other finite element representation. Inside each tetrahedron, a continuous function is represented by the linear interpolation of the vertex values. An original reconstruction is performed (using the ML-EM algorithm) on a coarse Cartesian grid with the grid points distributed randomly with their density proportional to the second directional derivative of the Cartesian image. The number of points is increased by the user in the regions where high resolution is required. The point cloud is then allowed to deform and increase in density to achieve optimal correspondence with the Cartesian image. The image is reconstructed on the new irregular grid directly from projections. Small deformations of the grid are also allowed during the reconstruction. A reduction in the number of grid points by a factor of 100 was achieved when the heart was reconstructed with high spatial resolution (Boutchko et al 2006a), and other volumes with lower resolution. In the reconstruction of low signal-to-noise ratio dynamic data, the application of the point cloud grid significantly reduced the number of grid points and improved visual perception of single frame images (Boutchko et al 2007). The process can also incorporate the optimization of the grid geometry by optimizing the number of sampling points and their positions. Point clouds constitute a convenient representation of SPECT images, which allows a significant reduction in the number of unknowns (reduces computation time, relaxes memory requirements and improves the stability of the solution) without loss in the image resolution and signal-to-noise ratio.
1.4. Synopsis
Some of the special data processing techniques used for the estimation of dynamic parameters directly from projections is presented in the following sections. The challenge is the accurate estimation of the blood input function. A key to making these techniques robust is the use of multi-resolution (multigridding) approaches to the spatiotemporal modeling of the tracer kinetics. There is significant interest in developing dedicated cardiac SPECT systems for acquisition of dynamics data. These data processing methods will become even more powerful with data acquired with new, dedicated cardiac SPECT cameras, as well as with currently available PET cameras. Finally, the development of hardware and data processing techniques for dynamic SPECT will play a significant role in diagnosing cardiovascular disease and diseases of other organs but will be especially important in preclinical evaluation of diagnostic and therapeutic methodologies in small animals.
2. Principles of tracer kinetic modeling
Tracer kinetic modeling is used in several areas of biological research to follow dynamic processes of blood flow, tissue perfusion, transport, metabolism and receptor binding. The underlying physical principle is conservation of mass wherein the input activity must be balanced by the accumulated activity and the output activity of a tracer within a system. The second principle is that, for a tracer experiment to reflect the true physiology of a biological system, that tracer must not itself perturb the system. These principles are reflected in many early contributions (Fick 1870, Stewart 1897, Hamilton et al 1928 and Kety and Schmidt 1948). Model equations developed from these principles and known physiology are found in Meier and Zierler (1954) and Zierler (1965). In these works, general equations were formulated to estimate flow using tracers for both the injection inflow/outflow detection technique and the injection inflow/residue detection technique (Bassingthwaighte et al 1993). An example of the injection inflow/outflow technique is found in the hanging heart experiment (Marshall et al 2001). Tracer exchange has been modeled down to the scale of actually calculating exchange between blood and extravascular spaces as a function of the length along the capillary (Rose et al 1977).
While physiologic studies in the past used direct sampling of input tracer concentration, tissue concentration and output concentration, it is possible to make all these measurements using external detection methods. Specifically, dynamic SPECT can be used to measure the time sequence of tracer content in tissues of the body from which physiologic parameters can be derived.
2.1. Principle of compartmentalization
The modeling of tracer kinetics relies on the principle of indicator dilution, whereby models are developed that compartmentalize the dilution of a measurable tracer that is introduced into the biological system to be studied in order to follow a physiologic or biochemical process of a particular biochemical substance (Huang and Phelps 1986). An appropriate tracer must be chosen to ensure that it follows the dynamic process of interest, it is measurable and it does not perturb the process being measured. The tracer is required to be of low mass concentration such that it does not affect any saturable process. Upon introduction, the tracer distributes throughout the sample. Measurements of the tracer are taken as a function of time.
The compartmentalization is based on a priori knowledge of structural or configurational information about the process or the organ system. Based on this information, a compartment model is developed that gives a mathematical description of the pathways and dynamic behavior of the tracer in the biological tissue of interest. The model is represented by a number of compartments (volumes where the tracer is uniformly distributed) (Huang and Phelps 1986) linked by arrows indicating transport between the various compartments or network that relates the compartments based on known or assumed physiology. The compartment may be a physical space such as an organ or may represent a metabolic or bound state of the tracer. The amount of tracer leaving a compartment is usually assumed to be proportional to the total amount in the compartment. The constant of proportionality (the rate constant) has the unit of inverse time and denotes the fraction of the tracer that is in one compartment that will leave the compartment per unit time. The kinetics between compartments are described by a system of differential equations. A general formulation and solution for n compartments is presented in Gunn et al (2001).
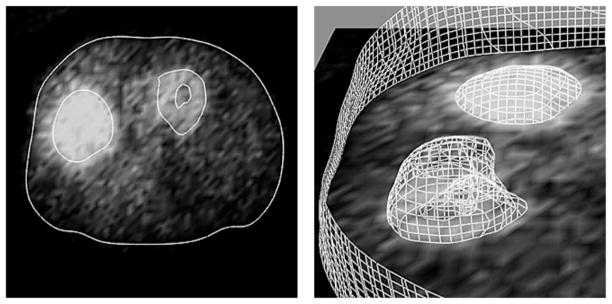
For example, assume that the concentration in the blood B(t) is known. (Throughout we are going to assume that blood and plasma are the same. See section 2.3 for a discussion about the bias incurred when the tracer exchanges between red blood cells and the blood plasma.) The rate equation for the extravascular compartment (intracellular and extracellular space in the extravascular tissue, figure 5) with concentration CEV(t) is
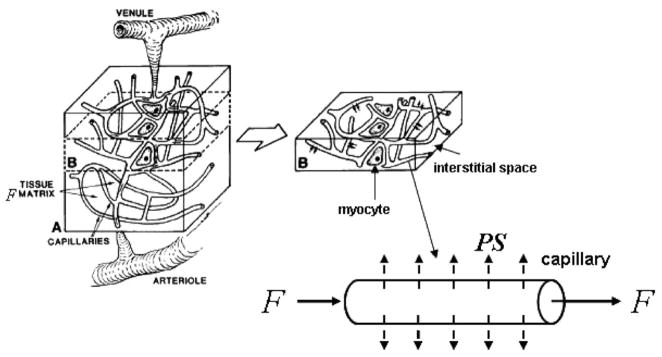
Figure 5.
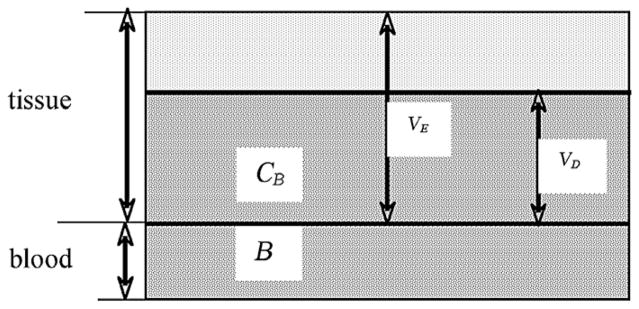
Intravascular blood and extravascular compartments. The intravascular blood compartment is the arteries and capillaries, and the extravascular compartment contains the physical space occupied by myocytes and interstitial space. The blood compartment contains plasma and blood cells. The models presented in this review assume that the tracers exchange between the extravascular spaces and the plasma in the blood in the arteries and capillaries. The models also assume in most cases that the tracers in the blood are in equilibrium between the plasma and the blood cells (see section 2.3).
| (1) |
where VEV is the volume of the extravascular compartment, P1 and P2 (in units of cm min−1) are the permeability coefficients for flux out of and into the capillary, respectively, and S(cm2) is the surface area of the capillary in the sampled voxel. Setting K1 = (P1S)/VEV and k2 = (P2S)/VEV, the rate constants in and out of the extravascular compartment are in units of volume per minute per extravascular volume (VEV). If B(t) is the blood input, the value of K1 includes flow as well as extraction. Throughout this review, we refer to it as flow times extraction. (In the literature, others have used the terminology ‘flow extraction product’.) Substituting K1 and k2 into equation (1), the differential equation describing the exchange between the blood and extravascular compartment can be rewritten as
| (2) |
where the rate of change in and out of the extravascular compartment is proportional to the concentration in the blood and in the extravascular compartment, respectively.
Note that blood is not considered a compartment. For a compartment, the change in concentration as a function of time is specified by a differential equation. In the applications presented in this review, blood is not specified by a differential equation but instead is estimated from the projection data. Also, the flow times extraction K1 is specified using a capital letter instead of a lower case letter. Even though this is commonly found in the literature, some authors will still use a lower case letter. The parameter K1 differs from k2 in that it is a macro parameter (Gunn et al 2001), which is a function of flow (a global system parameter) and the rate of extraction of the tracer from the blood into the extravascular compartment. The parameter K1 is generally more stable with respect to parameter estimation. We will see later that the estimation of k2 involves nonlinear estimation but if known then K1 can be estimated using linear estimation techniques (see section 4.2).
The amount of tracer in a volume of tissue can deviate significantly in value from the chemical concentration in individual spaces if the tracer does not distribute uniformly within all spaces in the tissue. Thus, the ‘apparent distribution volume’ VD (see figure 6) is defined at equilibrium as the volume of space that a tracer would occupy in the tissue extravascular space VEV with the same concentration as in the blood (Huang and Phelps 1986),
Figure 6.
Distribution volume. The distribution volume VD is the volume of the extravascular space that would give the same tracer concentration as that in the blood. The partition coefficient λ is the ratio of the concentration in the blood to that in the extravascular space at equilibrium. The distribution volume is generally given the same value as the partition coefficient, as K1/k2. (The figure is adapted from figure 20-2 of Cherry et al (2003) with permission.)
| (3) |
where
Here, λ is known as the partition coefficient. The partition coefficient analogy comes from the fact that a tracer might have different solubilities in different tissue types.
Strictly speaking, one should define the distribution volume or partition coefficient only in terms of the definition given in equation (3). If we assume equilibrium, we can set equation (2) to zero, which implies that K1B(∞) = k2CEV(∞) or the partition coefficient λ = CEV(∞)/B(∞) = K1/k2 and the distribution volume is VD = (K1/k2)·VEV. Distribution volume is a measure of how much is extracted by extravascular tissue at equilibrium. If a volume of tissue has no net extraction, it is zero; but if all the material is extracted like a microsphere, it is infinity. Thus the distribution volume concept is limited to situations where the wash-out rate is greater than 0. In the literature, the distribution volume may be given the same value as the partition coefficient by dropping the volume VEV from the expression.
2.2. Compartment modeling of cardiac perfusion
It is assumed that B(t) is known, either by fitting the input function to the measured projections or by measuring plasma samples (figure 7). In this case, we have a one-compartment model (figure 8) instead of a two-compartment model, since the kinetics of the blood are estimated using an independent model. Thus, the differential equation in equation (2) completely describes the kinetics of the model. It is assumed that the blood concentration measured in the left ventricular cavity represents the blood concentration of the particular radiopharmaceutical that is available to perfuse into the myocardium.
Figure 7.
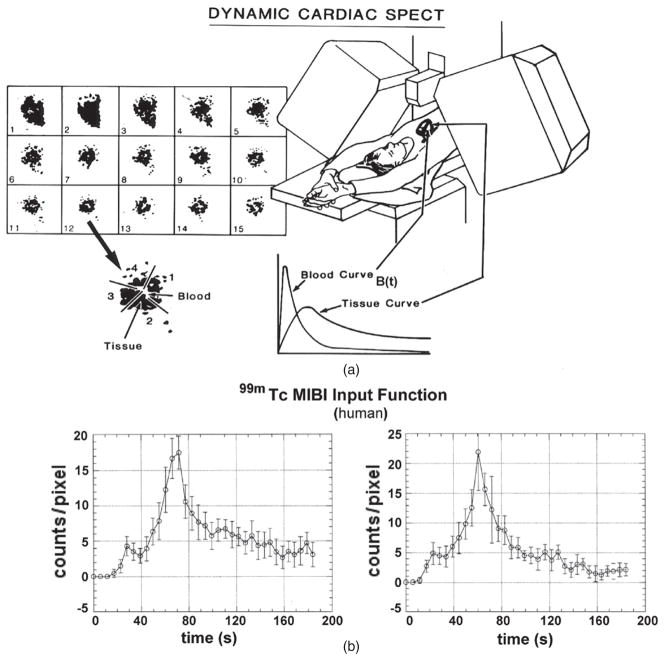
(a) Concept of dynamic cardiac SPECT imaging using a fast-rotating detector system. Here, projections are acquired rapidly in order to reconstruct a dynamic sequence of 3D data acquisitions, each one acquired for 5 s. Regions of interest (ROIs) in the 3D reconstructed images are identified for blood and tissue, and curves for these regions are extracted. These curves are fitted to a one-compartment model. (b) Actual time activity curves generated from a dynamic sequence of 5 s reconstructions (Budinger et al 1991). The plot on the left is for an ROI in the left ventricle and the plot on the right is for an ROI in the atrium.
Figure 8.
One-compartment model. The blood is not a separate compartment because it is assumed to be a known quantity. K1 is the wash-in rate constant (flow times extraction) and k2 is the wash-out rate constant.
The activity concentration in the tissue at the time point t is modeled as
| (4) |
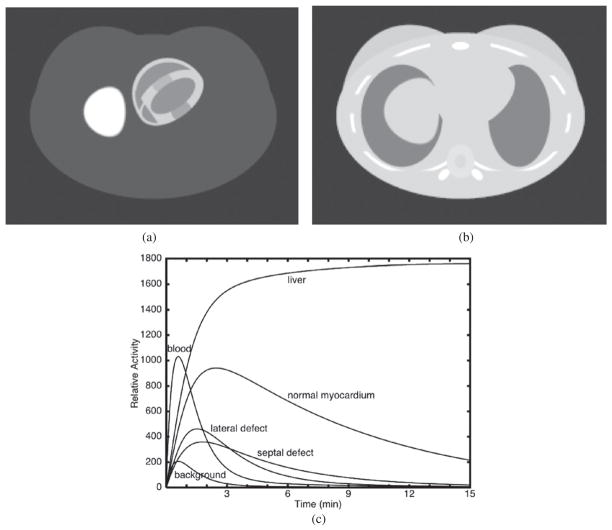
where AT is the model of the myocardial tissue activity concentration (e.g. MBq/cc) in the ROI, fv is the vascular fraction of blood in the tissue, B(t) is the measured activity concentration in the blood at time t, CEV(t) is the activity concentration in the extravascular compartment at time t and (1 − fv ) is the fractional volume of the extravascular space. The blood activity concentration B(t) is measured using an ROI drawn inside the left intraventricular cavity. The fractional blood volume fv accounts for blood in the myocardium capillaries as well as spill-in from the ventricular cavities due to partial volume effects, scatter, and lung and cardiac motion. This can be as high as 35–45% in dynamic SPECT applications. The septum will contain spill-in from both right and left ventricular cavities, whereas the lateral wall of the left ventricle will contain contamination primarily from the left ventricular cavity. The spill-in varies with the tomographic resolution and motion compensation accuracy. There can also be significant contamination from scattered events detected from the liver since myocardial perfusion agents have high liver uptake. Using the RV cavity as a source for an input function does not work well because of the dispersion through the lungs, the time difference from RV to LV, and potential loss of tracer from the blood into the lungs.
The activity concentration CEV(t) from the extravascular compartment is given by the first-order ordinary differential equation in equation (2), which describes the kinetic exchange between the blood and the extravascular space for the compartment model shown in figure 8. If all concentrations are zero at t = 0, the solution to the differential equation in equation (2) is
| (5) |
| (6) |
The transfer function (response to an impulse) for CEV(t) is H1(t) = K1 e−k2t (Gunn et al 2001). The parameters K1 and k2 represent the respective wash-in and wash-out rate constants of the radiopharmaceutical. The units of K1 and k2 are (ml min−1)/(ml of extravascular space), but the units of K1 and k2 will be stated simply as min−1. It is common in the literature to give units for K1 as (ml g−1 min−1). For tissue, a milliliter of tissue has a mass of approximately 1 g, therefore the units of min−1.
The perfusion model presented here has been used to follow the dynamics of the myocardial perfusion agents 201Tl, 99mTc-teboroxime and 99mTc-sestamibi. 201Tl is a potassium analog that accumulates in myocardial cells by active transport associated with the Na+/K+ adenosine triphosphatase pump (Iida et al 2003). It primarily exchanges between the high concentration potassium pool in the cytoplasma of the myocytes and the lower concentration of potassium in the blood pool. 201Tl has a high transcapillary extraction fraction and is rapidly cleared from arterial blood and taken up into myocardial tissue. Its half-life in the human subject can vary with the time dependent blood concentration. 99mTc-labeled sestamibi (Maublant et al 1992, Allman et al 1992, Williams and Taillon 1995, Gioia et al 1996, Maunoury et al 1996, Flamen et al 1995) is more widely used to image perfusion in clinical studies and in some cases is used with 201Tl in rest(201Tl)/stress(99mTc-sestamibi) protocols. Sestamibi has a biological half-life in the myocardium of 6 h. 99mTc-teboroxime (Leppo and Meerdink 1989, Leppo et al 1991, Rumsey et al 1992, Maublant et al 1993, Rosenspire et al 1993) is a boronic acid of technetium dioxime (BATO) complex that is stable, neutral and lipid soluble. Teboroxime has the fastest clearance time (a 10–15 min half-life in the myocardium) (Leppo and Meerdink 1989) of the three tracers and is 90% extracted in the first pass. It is highly linear with flow. However, even though teboroxime is highly extracted on the first pass, there is an indication that extraction from subsequent passes may be affected by the binding of teboroxime to blood cells and plasma proteins (Rosenspire et al 1993), as well as by any changes it might undergo from the chloro to the hydroxide form, which has a lower affinity for the myocardium (Rumsey et al 1992). Dynamic cardiac SPECT studies (Smith et al 1994, 1996, Di Bella et al 2001) indicate that the wash-in rate constant for teboroxime is greater than that for thallium and in one case indicated that the wash-in rate constant for thallium (K1 = 0.44 min−1) was half that for teboroxime (K1 = 0.94 min−1) (Gullberg et al 1999). Thallium distributes as an analog of potassium, thus should follow the membrane polarization/depolarization activity. If this is compromised in ischemic tissues, the wash-in rate constant is expected to decrease. Research indicates that teboroxime has a lower degree of sensitivity to cellular metabolic impairment (Leppo et al 1991, Maublant et al 1993) when compared to sestamibi or 201Tl.
It has been well recognized for years that 201Tl imaging is a sensitive measure of tissue viability. Dynamic imaging of 201Tl may prove to be an even more sensitive measure of tissue viability using volume of distribution measurements [VD = (K1/k2)] instead of static imaging (Gullberg et al 2004). These studies indicated that the distribution volume of teboroxime was an indicator of tissue viability but that the distribution volume of thallium provided an even better contrast of tissue viability. Dynamic SPECT may simultaneously enable measurement of both cardiac tissue perfusion and tissue viability.
The one-compartment model shown in figure 8 assumes the following: (1) the time–activity curve of the blood can be measured independently of the extravascular compartment of the myocardial tissue, (2) all myocardial tissue regions exchange the tracer with blood, (3) the distribution of the tracer is homogeneous throughout the ROI and (4) the tissue ROI contains only regions of blood and extravascular compartments. In dynamic cardiac SPECT, the kinetic parameters are estimated for multiple 3D regions in the left ventricular myocardium.
Due to the low sensitivity of dynamic SPECT and the complexity of the physics of the image detection process, a one-compartment model is usually used to model perfusion in the heart. However, it has been proposed that a two-compartment model is more appropriate for 201Tl kinetics and that it is important to sample plasma (blood void of red cells) to obtain an accurate input function (Eberl 2000). In some earlier work, two- and three-compartment models were used to model cardiac glucose and fatty acid metabolism of 123I-labelled IPPA in cardiac studies (Gullberg et al 1999). However, there is the issue of which is the optimum model for the data presented (Coxson et al 1997). Recent cardiac metabolic studies (Okizakia et al 2007) have demonstrated that fewer compartments may be more optimal even though the kinetics are best represented by more than two compartments.
2.3. Blood and tissue time–activity functions
If the input function is measured from an intraventricular ROI, there are partial volume effects that contaminate the blood with adjacent tissue activity photons and the tissue with blood activity photons. The contamination of the blood data with tissue activity photons is especially evident with high liver uptake where there can be contamination (crosstalk), not only due to partial volume effects but also due to the background from scatter. Cardiac motion will also make it difficult to obtain a pure blood input function (Ross et al 1997a). Models of these effects were used to correct for the spillover of radioactivity both from the myocardium into the LV ROI and from the blood into the myocardial ROI in PET H215O flow studies (Iida et al 1991, 1992, 1995b). The partial volume effect in H215O studies was also measured using data from a C15O (effectively labeled red cells) intravascular study in combination with the transmission data. Another problem is acquisition of the correct data from plasma versus from whole blood. If there is exchange of the tracer with blood cells but the wash-out is relatively slow, then measuring the blood time–activity curve in the ventricular cavity may provide the wrong input function for myocardial tissue unless the fraction trapped in the red cells is known. For 201Tl myocardial perfusion studies, it has been shown that this can bias K1 (Iida et al 2008). In the delineation of the tissue ROI, care is needed to avoid extending the borders beyond the anatomical myocardial volume. This too can increase the partial volume effect (Welch et al 1995b).
Imaging results can be improved by optimizing the shape and sampling intervals of the time activity curves. From linear system theory, it is important to match the spectrum of the input function to the frequency response of the organ (Chen 1984). One also needs to select an acquisition (sampling) interval long enough to maximize statistics but short enough to have the timing resolution necessary to accurately capture the time–activity curves during the first few minutes of rapid change in the tracer distribution. Optimization of time sampling intervals is important for achieving best estimates of kinetic parameters in terms of bias and variance. Measuring the input dynamics rapidly is probably more important than measuring organ dynamics rapidly. In SPECT, hardware limitations hinder achieving short acquisition intervals, which results in trade-offs between bias and variance. A study (Ross et al 1997b) has shown that longer acquisition intervals (10, 20, 40 s) result in the most accurate estimates of kinetic parameters when flow times extraction is high, such as during stress. At rest, with low statistics, a rapid infusion always provides optimal estimates of kinetic parameters. The smallest amount of bias is observed with a 10 s acquisition interval, and the smallest amount of variance is seen with a 20 s acquisition interval. When the count rates are doubled, longer infusions and shorter acquisition intervals provide more accurate estimates of kinetic parameters during a resting state. When flow times extraction is increased during stress, longer acquisition intervals result in better estimates, indicating that good statistics are more important than temporal sampling resolution when estimating fast kinetics.
To alleviate some of the problems of having to measure the input function either from the imaging data or from frequent arterial blood samples, it has been proposed to develop a library of input functions. It has been shown that population-based input functions calibrated with one or two blood samples could be used as the input function in brain blood flow studies using SPECT (Iida et al 1994, Onishi et al 1996). Also, library-based input functions could be used for measuring myocardial blood flow using 201Tl (Eberl 2000). Another approach is to first fit the noisy blood sampled data to a physiological model of the input function, then use the fitted input function to estimate the kinetic model parameters (Feng et al 1993).
Methods of blind estimation eliminate the need to measure an input function. Blind estimation usually limits which kinetic parameters can be estimated absolutely. For the one-compartment model, the flow times extraction K1 and the blood fraction fv are not estimated absolutely (Di Bella et al 1999, Fluckiger et al 2009). This has also been studied for a three-compartment model (Riabkov and DiBella 2004).
Many of the issues discussed in this section have been studied for conventional methods of estimating kinetic parameters from time–activity curves generated from a dynamic sequence of reconstruction images. The focus of this review is the estimation of these kinetic parameters from projection measurements, and the same issues raised here will be important in the estimation of blood input time–activity curves and kinetic model parameters from projections.
2.4. Estimation of kinetic parameters
The goal of parameter estimation in dynamic SPECT is to extract quantitative physiologic information about organ function from dynamically measured data. Parameter estimation is a branch of mathematics and statistics (Zar 1984, Brownlee 1984, Deutsch 1965, Beck and Arnold 1977, Bard 1974) that involves the development of methods that make efficient use of data in the process of estimating parameters of mathematical models. The process of parameter estimation involves the interplay between experimental design, model specification and techniques of data collection (Carson 1986b). The collected data are used in the estimation process to produce parameter estimates of the model. On the basis of a statistical model of the data, the estimation procedure produces improved parameter estimates and statistical measures of their accuracy and precision. Careful statistical analysis and hypothesis testing of the results provide a feedback mechanism whereby the model, the data collection protocol and the parameter estimation process can be evaluated and modified.
The model is a mathematical formulation that uses a set of parameters that reflect local rates of physiologic transport and biochemical reactions. Because of physical complexities of the image detection process, the models used in dynamic cardiac SPECT must necessarily be relatively simple. The process of estimating the model parameters requires maximizing a likelihood function with a statistical model that appropriately represents the statistics in the data. In general, statistical models for the data can be very complex if the data are reconstructed time–activity curves that contain correlations between the curve values in both time and space. The maximization of the likelihood function may involve either nonlinear or linear methods to estimate the parameters (see below).
Careful analysis of the parameter estimates provides useful information about the appropriateness of the entire estimation process (Carson 1986b). Tests for goodness-of-fit can be used to determine whether the model has captured all of the deterministic characteristics of the data (Draper and Smith 1966, Dixon and Massey 1969, Brownlee 1984, Zar 1984). If the noise level is known, one quick and easy test is to determine whether the chi-square of the fit is equal to the number of degrees of freedom (see chapter 12 of Taylor (1982)).
2.4.1. Nonlinear methods
Model parameters are estimated directly from dynamically acquired SPECT projection data or from blood and tissue curves of a particular ROI estimated directly from projections. The process of estimating kinetic parameters of the compartment model is a nonlinear estimation problem (Deutsch 1965, Bard 1974). An iterative algorithm is used to solve the model parameters. If time–activity curves have been estimated, an iterative algorithm, such as that found in the computer software package RFIT (Huesman et al 1995), may be used to fit the model parameters so that the sampled time–activity curves in the tissue ROIs fit the predicted time–response curves of the model. The program estimates the model parameters and the statistical errors.
In the development presented later (see section 5), blood and tissue time–activity curves are estimated directly from the projection measurements. Because this function is known only from measurements of the dynamic reconstructions, it has statistical fluctuations. The kinetic parameters are estimated for each ROI by fitting the measured tissue data to a model of the dynamic emission tomographic reconstructions with a noisy input function (Huesman and Mazoyer 1987).
2.4.2. Linear methods
The Patlak method (Patlak et al 1983, Patlak and Blasberg 1985, Gambhir et al 1989, Kordower 2000, Choi et al 1991, 1993, Maguire et al 1997, Gill et al 2003, Wang et al 2008) is a linear approach to estimating kinetic parameters. The Patlak analysis depends on irreversible trapping of at least a portion of the tracer. It is a simplified linear kinetic modeling technique that was originally developed as a graphic method performed by linear regression of time–activity curves (Patlak and Blasberg 1985). The method does not assume any particular kinetic model and involves only linear estimation techniques. The limiting slope of the Patlak plot is the uptake rate constant of the system (or the steady state response of the system), a very useful quantitative index for characterizing the kinetic properties of tracers. The Patlak method has been applied in the analysis of blood flow (Choi et al 1993), FDG kinetics (Choi et al 1991) and has found application in many disease studies (Gill et al 2003). The linear parameters of the Patlak model have also been estimated directly from projection data (Maguire et al 1997, Wang et al 2008).
The Logan method (Logan 2000) is another linear method that assumes the kinetics have reached an equilibrium. Whereas the Patlak method applies to irreversible systems, the Logan method applies to reversible systems. The method transforms the system of differential equations into a form in which the distribution volume is the slope of a linear equation, which in the case of a one-compartment model is K1/k2. The estimation of linear coefficients is much more straightforward than estimating the nonlinear parameters of kinetic compartment models.
3. Spatiotemporal modeling of dynamic image data
Spatiotemporal basis functions are the basic building blocks for modeling the variation in the reconstructed spatial distribution with time. Time-varying activity concentrations within volumes can be modeled by selecting a set of temporal basis functions that are capable of representing typical time variations and have desired smoothness properties. These may be splines, FADS, curves that fit compartment models, polynomial expansions or several other possible spectral decompositions. Similarly, the spatially nonuniform activity concentration within a particular volume can be modeled by selecting an appropriate set of spatial basis functions defined within the volume. These could be splines, point clouds of tetrahedral elements, blobs, various types of polynomial expansions or indicator functions corresponding to voxels. The number of basis functions and their spatial and temporal extents can be varied so that the spatiotemporal basis can optimally model the spatial and temporal content of the data with the fewest number of basis functions. This provides a multi-resolution structure that is ideal for estimating the parameters from projection data. Given a set of temporal basis functions and a set of spatial basis functions, coefficients for the resulting spatiotemporal basis functions can be estimated directly from the projections (Reutter et al 2000).
Mathematically, the activity distribution A(x, t) in image space is modeled using the following spatiotemporal basis functions,
| (7) |
where Sm(x), m = 1, …, M, are spatial basis functions; Vmn(t), m = 1, …, M; n = 1, …, N, are temporal basis functions and amn are the coefficients of the basis expansion. The temporal basis representation is generalized so that it is indexed with the spatial basis function Sm(x).
Previously, we denoted AT (t) (equation (4)) to specify a particular one-compartment model for myocardial tissue. Here, we provide a general representation of the activity concentration as a function of space x and time t in terms of spatial and temporal basis functions. The following discussion provides examples of different selections of bases and includes examples where the spatial and temporal basis functions are completely independent, being connected only by the coefficient indexed by both types of basis functions, whereas in equation (7) the temporal basis functions are dependent on the index of the spatial basis function.
The goal is to parameterize spatially non-uniform activity within segmented volumes and to include smooth temporal changes within volumes, and so provide 4D and 5D representations of dynamic reconstructions. The approach is to model continuous anatomy throughout continuous time rather than through the use of small image voxels at discrete time segments. This reduces the size of the parameter space and reduces noise. The following exposition contains some examples of temporal and spatial modeling using spatiotemporal basis functions.
The projections of the activity A(x, t) are written as a function of the detector position d at time t (see figure 9),
Figure 9.
The SPECT detector head is assumed to rotate continuously so that the detector coordinate d(t) has a particular angle θ(t) and spatial coordinate ξ(t). The projection measurements pi (tk) are the activity acquired over a time period tk − Δtk to tk for the detector bin di (t).
| (8) |
where A(x, t) is the spatiotemporal distribution of tracer with x ∈ image space χ. The weighting function F [x, d(t)] maps the activity A(x, t) into the projection P (d, t) with detector position d(t) at time t. Therefore, in terms of the spatiotemporal basis functions, the projections are expressed as
| (9) |
where
| (10) |
is the projection of the spatial basis function Sm(x) at the detector sampling position d(t).
The projection data can be recorded as individual events of radioactive emissions of the radioisotope (list mode) or the accumulation of events in a detector bin di (t) over the acquisition time interval Δtk divided by Δtk so that the value at all time points is in terms of activity concentration in units of counts per unit time. The projection at tk in projection bin i is the activity acquired over time Δtk,
| (11) |
| (12) |
where tk, k = 1, …, K is the time at which the projection samples pi (tk), i = 1, …, I, are acquired (figure 9). The number of projection rays per projection angle is denoted by I. The total number of time samples is K. This expression is a general parameterization of both space and time. This can be represented in matrix form as
| (13) |
where p is an IK-element column vector of modeled dynamic projection data values, F is an (I K) × (MN) system matrix containing the elements
| (14) |
a is an MN-element column vector of coefficients, I is the total number of projection measurements acquired by the SPECT detectors and MN is the number of basis functions that span the space and time to be reconstructed.
The forward projection operator F is a linear transformation from the image space with elements a into the projection space with elements p. The matrix F includes effects of the physics of the imaging detection process, which include attenuation (Gullberg et al 1985, 1989, King et al 1995, 1996), geometric response of the collimator (Tsui et al 1988, Zeng et al 1991, 1994, Formiconi et al 1989, Penney et al 1990, McCarthy and Miller 1991, van Elmbt and Walrand 1993, Glick et al 1994) and scatter (Welch et al 1995a, Zeng et al 1999, Bai et al 2000, Laurette et al 2000, Floyd et al 1985, Liang et al 1992, Frey and Tsui 1993, Meikle et al 1994, Beekman et al 1996, 2002, Kadrmas et al 1998). A photon is emitted by a radioactive nucleus traveling in all possible 4π directions. The geometric acceptance of the collimator holes is of the order of 10−5. Also, the photon could be attenuated, meaning that it is not detected at all by the camera, or the photon could be scattered and detected incorrectly on the detector, thus making it unclear as to where the photon originated and blurring the projected image. These effects are modeled by the system matrix, such that the system matrix contains elements fik(mn) that are proportional to the probability that the photon emitted from the support of the basis function Sm(x) during the time t corresponding to the intersection of (tk − Δtk, tk) and the support of Vmn(t) is detected in a projection bin i.
3.1. Spatial and temporal modeling using splines
The use of splines provides an efficient and accurate method of composing continuous functions from discrete samples. Cubic spline functions are probably the most popular. They form smooth functions from fitted data, and cubic spline interpolations do not exhibit oscillatory behavior that is characteristic of high-degree polynomial interpolation.
There are various examples where splines have been used to model dynamic data. Work was done in which five piecewise polynomial spline functions defined over four contiguous time segments were used to fit the blood input function (Chen et al 1991). The segments were determined by varying their endpoints in a prescribed fashion and using the set that yielded the smallest weighted sum of squared errors, averaged over 100 simulated data sets. Others (Nichols et al 1999) first calculated the temporal histogram for all of the data to model the time course of activity in voxels reconstructed from dynamic list-mode PET data. The segmented endpoints for cubic B-splines were defined by selecting a set that yielded approximately equal arc lengths along the resulting time–activity curve.
For the modeling of dynamic cardiac SPECT data, constant, linear, quadratic and cubic B-splines were compared (Reutter et al 2000). A basis of 16 B-splines (see figure 10) spanning 15 time segments that have geometrically increasing lengths were used such that the length of the initial time segment was varied, and the errors in the time–activity curve estimates and the subsequent kinetic model parameter estimates were compared.
Figure 10.
Examples of piecewise (a) constant, (b) linear, (c) quadratic and (d) cubic B-spline basis functions. Sixteen splines were used to span 15 time segments that have geometrically increasing lengths. The 13th spline is shown as a solid curve. The initial time segment length for the splines shown here is 10 s.
In the examples in section 5.1, the temporal spline representation will be independent of the spatial representation, i.e.
| (15) |
Therefore, the model given in equation (7) can be represented as
| (16) |
where the set of temporal basis functions is independent of each of the spatial basis functions and the coupling of the two basis functions is through the coefficients amn.
3.2. Temporal modeling using compartment models
Imposing a compartmental relationship (defined by a first-order differential equation) between blood and tissue activities into the spatiotemporal model will provide more temporal regularization than is provided by splines alone. The general temporal model has two components (blood and extravascular),
| (17) |
where equation (17) is precisely a generalization of AT (t) in equations (4)–(6) in section 2 by coupling the temporal basis to a spatial basis with index m, and where is the blood volume fraction, is the wash-in rate constant, is the wash-out rate constant for the tissue region m and Vn(t) is a temporal basis function for a blood input function . The spatiotemporal representation is
| (7) |
| (18) |
where
| (19) |
In Reutter et al (2005), splines were used to model the blood input function and a physiological compartment model was used to model changes in activity for tissue volumes. In Kadrmas and Gullberg (2001), a compartment model was used as a Bayesian prior to constrain the time–activity curves for each voxel to fit a one-compartment model.
3.3. Temporal modeling using factors of dynamic structures (FADS)
Factor analysis of dynamic structures (FADS) (Barber 1980, Di Paola et al 1982, Buvat et al 1993, Sitek et al 2002a) is a semi-automatic technique used to extract time–activity curves from a series of dynamic images. In applying the method, the goal is to extract time–activity curves that are physiological in that they represent blood activity or an uptake and wash-out of a particular tissue region. The FADS method can separate partially overlapping regions that have different temporal behaviors (Nijran and Barber 1985, Nakamura et al 1989, Houston and Sampson 1997). FADS can also separate different physiological regions and automatically define regions in the image that have the highest concentrations of blood or tissue components. For cardiac studies, the estimation of factors from dynamic SPECT data was originally accomplished using a dynamic sequence of reconstructed images (Sitek et al 1999b, 2000, Hu et al 2008). However, the method has been shown to be effective in estimating factors directly from projection measurements as well (Hu et al 2008, Sitek et al 2001).
Factors are temporal functions that have physiological interpretation (one possibility is a blood input function) so that the elements of the factor curves are non-negative. In the factor model, it is assumed that activity in each tissue region m is a linear combination of factors. The general temporal model has the form
| (20) |
where for each index n there is a factor Fnk (k = 1, …, K) which is a discrete time–activity function, and χk (t) is a characteristic function with χk (t) = 1 for tk − Δtk ≤ t ≤ tk and 0 otherwise. Note that for a given factor Vn(t), this temporal model is the same for all spatial elements m. The total activity as a function of space and time can be written as
| (15) |
| (21) |
where M is the number of spatial basis functions (e.g., may be voxels), N is the number of factors and K is the number of time samples. Usually, the number of factors N is equal to the number of physiologic factors—that is, volumes exhibiting unique kinetics that are actually present in the medical image—but this need not always be the case (Nakajima et al 1991). Note that even though the representation in equation (21) is discrete in time and thus corresponds to a spline representation of zero order, higher order splines can also be used.
3.4. Summary
The material in this section presents the foundation for spatial and temporal representation of the evolution of in vivo physiological processes. An important aspect of the formulation is the flexibility to allow multigridding of both spatial and temporal domains in order to reduce the indeterminacy of the problem of estimating dynamic parameters directly from tomographic projection measurements. The next sections show how direct and semi-direct methods use the basic building blocks of spatiotemporal basis functions to estimate dynamic processes directly from dynamically acquired projection data. The ultimate goal is the eventual quantification of physiological processes (perfusion, metabolic rate, etc) by estimating kinetic parameters of compartment models.
4. Estimation of kinetic model parameters from projections—direct methods
The time–activity curves and kinetic model parameters are estimated directly from dynamic SPECT projection data by modeling the spatial and temporal distributions of the radiopharmaceutical throughout the projected field-of-view for all time. In section 4.2, a compartmental model-based approach is presented for estimating kinetic parameters directly from projections. The organs are assumed segmented (see section 4.1) so that the blood input can be identified and the appropriate models can be formulated for each tissue type.
The segmentation step is not essential but it can reduce dimensionally and the accuracy of the procedure is critical in reducing bias. If the segmented ROI is larger than the desired organ of interest, there could be cross talk from other organs. If the other organ has lower counts, then the time–activity curve for the organ of interest will be too low. If the other organ has higher counts, then the time–activity curve will be too high. The effect on the bias would be the same as that experienced when manually sampling ROIs in the heart (Welch et al 1995b).
4.1. Segmentation
4.1.1. Static segmentation of ungated data using 4D differential boundary detection
The estimation process begins with an image segmented into blood pool, S tissue types of interest and background, as shown in figure 11. In this example, a differential 4D segmentation method was used to automatically create geometric models of the surfaces bounding volumes of time-varying tracer uptake in the myocardium, liver and body from dynamic SPECT images in a late time frame. This method was previously used to automatically segment the time-varying body and lung surfaces in human respiratory-gated PET transmission images (Reutter et al 1997). Bilinear interpolation is used to obtain sub-voxel spatial localization of the zero crossing points. In the output of a second directional derivative operator, the zero-crossing points are linked together to form contours in each spatial plane (Wallin 1991). These contours are linked together to form 3D surfaces. Information about the centroid, bounding box and average image intensity gradient across each contour, as well as each surface, is stored to facilitate identifying the surfaces. The myocardium, liver and body surfaces are identified as being relatively large surfaces associated with relatively high image intensity gradients. Data are analyzed efficiently in 4D over appropriate spatial and temporal scales to extract and to physically model the surfaces bounding volumes of time-varying tracer uptake. This structured analysis imposes spatial and temporal continuity that complement the information which is available from unstructured image voxel intensity alone.
Figure 11.
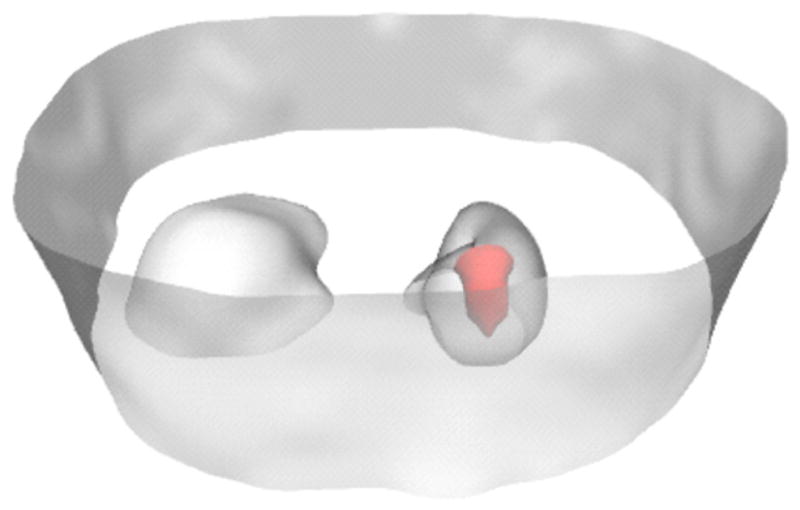
Segmentation of heart, blood pool (red), liver and torso from a dynamic cardiac SPECT study using 99mTc-teboroxime (Reutter et al 1998b). Attenuation-corrected emission results were reconstructed using 20 iterations of the ML-EM algorithm. A 4D second directional derivative operator was applied to the attenuation-corrected dynamic image data set containing ninety 10 s frames to segment the regions of the myocardial tissue, intraventricular blood and background tissue. Shown here is the segmentation at time frame 31 (corresponding to the interval 300–310 s) after injection.
4.1.2. Dynamic segmentation of cardiac-gated data using level sets
The organ boundaries can also be determined using level set methodology (Osher and Sethian 1988, Sethian 1996, Osher and Fedkiw 1999), which is a simple method for computing and analyzing motion of a surface in two or three dimensions. The surface is specified as the zero level set of a smooth function. This approach allows importation of mechanical constraints, and it simultaneously segments organ boundaries and estimates model parameters of changing activity concentration (Shi and Karl 2003, Feng et al 2003b, Shi and Karl 2004).
4.2. Compartmental model-based approach
From the segmentation into anatomical structures of blood, background and myocardial tissue, the activity is modeled by the following spatiotemporal basis functions,
| (22) |
where χB (x) and χG(x) are characteristic functions for the segmented blood pool and background defined on the entire image, i.e. these functions equal 1 if x is an element of the region and zero otherwise. Also, it is assumed that the background tissue follows some constant fraction g of the blood input.
For a one-compartment kinetic model (figure 8, equation (4)), the expression for the uptake in the tissue type m is
| (23) |
where
and is the wash-in parameter, is the fraction of blood in the tissue and is given by
where is the wash-out parameter and B(τ) is the blood input function. In the following, the blood input function is parameterized by the expression
| (24) |
where Vn(t) the temporal basis functions and are coefficients of the expansion for B(t). Therefore
| (25) |
where
| (19) |
and
| (26) |
| (27) |
Substituting this expression for and the expression for B(t) in equation (24) into equation (22) gives
| (28) |
where the spatial basis functions in equation (22) are assumed to be , i.e. the spatial basis functions are taken to be voxels or tissue regions of unit weight.
The projections are written as a function of detector position d at time t (figure 9)
| (8) |
where A(x, t) is the spatiotemporal distribution of the tracer with x ∈ image space χ. From the segmented image, a model of the attenuation distribution is created and the attenuated unit activity projections of the blood pool, tissue and background regions are calculated for each projection ray of each projection angle. That is, the number of events that would be detected from each region, given a unit concentration of activity within the region, is calculated for each projection bin acquired at each projection angle.
Substituting the expression for A(x, t) in equation (28) into equation (8) gives the following expression for the projection,
| (29) |
| (30) |
| (31) |
| (32) |
The sampling of the data can be very irregular in time. Therefore, it is assumed that the time tk specifies some projection angle θ(tk). The model does not imply that the detector needs to be stationary or that the tracer distribution is constant during the time interval Δtk. The projection pi (tk), i = 1, …, I is the activity acquired over a time Δtk for projection bin i,
| (11) |
Substituting P(di (t), t) from equation (29) into equation (11),
Note: from equation (25). Simplifying
| (33) |
where
| (34) |
| (35) |
| (36) |
| (37) |
Note from equation (19). Rearranging the summations and bringing the summation over n outside, the expression for the projection bin i at tk is given as
| (38) |
The constants and are pure geometrical weighting factors for blood, background and tissue type m, respectively. These equations are linear in the unknowns g, and . The nonlinear parameters are contained in . For a list mode acquisition, these weighting factors become more precise as a function of the event arrival time.
In the following equation, (38) is reformulated as a matrix equation. The wash-out parameters are elements of the vector
| (39) |
the multiplicative parameters are elements of the vector
| (40) |
and the parameters of the unknown blood input function are elements of the vector
| (41) |
From the segmented image, the projections of the activity of the blood pool, tissue and background regions along each projection ray for each projection angle are modeled. At a particular time tk (corresponding to a particular projection angle acquired during a particular rotation), the projections of the activity in the blood pool, background and tissue type m along each of the I projection rays are represented by the vectors
| (42) |
The total projection samples are represented by the vector
| (43) |
Thus, a set of I · K equations can be written as
| (44) |
where
| (45) |
| (46) |
| (47) |
This gives
| (48) |
or
| (49) |
where
| (50) |
To determine estimates of the model parameter vectors λ and μ, the background constant factor g and the input parameters β, the weighted sum of squares is minimized,
| (52) |
where p̃ are the measured projection data and the matrix W contains the weighting factors. Typically, W is either the inverse of the covariance matrix for the residual vector p̃ − R(λ, μ, g)β or an identity matrix (for an unweighted least-squares fit).
Previously, efficient estimates of dynamic cardiac SPECT kinetic parameters of a one-compartment cardiac perfusion model were obtained using weighted least-squares estimates of dynamic reconstructions that were obtained from the inversion of the Fisher information matrix (Gullberg et al 1999, Kadrmas et al 1999). Each reconstruction in the dynamic sequence was implemented using matrix inverse reconstruction. The reconstruction was a solution to a weighted least-squares optimization problem (where the weights were equal to the measured projections assuming these to be the variances of a Poisson distribution), which provided a weighted least-squares estimate of the reconstructed values and estimates of the covariances between the reconstructed values. These estimates were used to generate time–activity curves for (1) activity in a blood region inside the left ventricle and a cardiac tissue region, (2) the variance of the two estimates of the sums in the two regions and (3) the covariance between the two ROI estimates. The weighted least-squares estimates and covariances for the reconstructed time–activity curves were fitted to a one-compartment perfusion model to obtain weighted least-squares estimates of the kinetic model parameters (wash-in, wash-out and fractional blood volume). It was shown that the weighted least-squares estimates of the kinetic model parameters gave lower variance than the unweighted least-squares estimates. Typically, the image matrices are large and, therefore, it is difficult to invert the Fisher information matrix to obtain a weighted least-squares estimate of the reconstruction and the covariance matrix. Typically, the sequence of reconstructions is obtained using ML (Lange and Carson 1984) or MAP (Levitan and Herman 1987) iterative algorithms, which properly model the Poisson statistics and the physics of the data acquisition. Work by Barrett et al (1994), Fessler (1996), Wang and Gindi (1997), Qi and Leahy (2000), Stayman and Fessler (2000) and Qi (2003) has developed formulas for estimating the errors in the reconstructions obtained from iterative reconstruction algorithms.
The appealing thing about estimating the kinetic parameters from projections is that the weighting matrix in equation (52) is directly related to the measurement errors, which are often assumed to be independent Poisson random variables with variance equal to the measured data provided the manufacturer has not preprocessed the data.
If the input function is known, then the least-squares problem can be simplified (Huesman et al 1998, Gullberg et al 1999). It has been shown that, if there is no wash-out from the compartment, that is, , the estimation from projections can be reduced to a linear estimation problem (Vanzi et al 2004).
In some cases, the wash-out parameters associated with a one-compartment model may be known then the multiplicative parameters associated with the model can be estimated directly using linear estimation methods. Compartmental modeling imposes constraints on the relationship between blood and tissue time–activity curves. For example, if the tracer or radiopharmaceutical is a physical or a chemical microsphere that is trapped in blood capillaries, within the cell or on a surface membrane protein, then it would be natural to let be zero. With agents such as 123I-iodorotenone and 99mTc-sestamibi, the wash-out is very slow and in the early phase of the study it can be assumed that the wash-out parameter is zero. This is the case when the data acquisition may not be extended long enough to acquire the wash-out phase of the tracer.
4.3. 4D maximum a posteriori reconstruction of dynamic data (one-compartment model for every voxel)
In the previous section, segmentation was performed to obtain like tissue regions for fitting a compartment model from projections. This was done to reduce the dimensionality of the problem. Another approach is to allow each voxel to be a separate tissue region that is constrained to fit a compartment model. Every voxel can be constrained to fit a compartment model given in equation (4). If the voxel is in the intraventricular cavity, for example, then fv in equation (4) will be 1.00. This approach significantly increases the dimensionality of the problem from that of the previous section.
The activity distribution in each voxel m is represented by spatiotemporal basis functions
| (53) |
| (54) |
The projection equations are
| (55) |
where the pi (tk) are the modeled projections, are the fraction of blood in tissue m, are the linear coefficients associated with the blood temporal basis functions Vn(t), are given in equation (36) and are given in equation (37).
As in section 4.2, the solution (a, fv, K1, k2) can be determined by minimizing the weighted sum of squares function,
| (56) |
where p̃i (tk) are the measured projections, Wik are the weighting factors, I is the number of projection rays per angle and K is the number of projection samples over all time. The weighting factors are either unity for an unweighted fit or the reciprocal of the estimated variances of the projections for a weighted fit.
Instead of solving equation (56), consider the application of Bayes’ theorem,
| (57) |
where the probability density function P (A(x, t)) is
| (58) |
and
| (59) |
is the activity at time tk in tissue type m for an assumed one-compartment model, μ̄mk is the mean activity for tissue type m at time tk and is the variance for the activity for tissue type m at time tk. Equation (58) imposed an a priori constraint on the solution.
The likelihood function in equation (57) can be written as
| (60) |
where
| (61) |
Substituting equation (61) into the following expression for the a posteriori probability distribution in equation (57),
| (62) |
and taking the natural logarithm gives
| (63) |
The (âB, f̂v f̂1, k̂2)that maximizes equation (63) can be determined by directly maximizing equation (63) using an optimization algorithm such as the conjugate gradient algorithm, or using an ordered-subset implementation of the expectation-maximization approach to maximizing the a posteriori probability distribution in equation (57) (Kadrmas and Gullberg 2001).
4.4. Spectral approach (multi-compartment model for every voxel)
Suppose the tissue region m satisfies a multi-compartment model instead of a one-compartment model assumed in sections 4.2 and 4.3. One could specify the model for the tissue region by specifying the number of compartments (Gunn et al 2001), or allow it to be a spectrum of exponentially decaying factors (Cunningham and Jones 1993). This is a more general parameterization of the kinetics, independent of any particular compartment model architecture that allows for a series of exponential terms with linear coefficients. The spectral analysis involves the estimation of the coefficients of these pre-selected exponential functions. This approach allows convenient solutions via linear methods.
Suppose that each tissue region has a transfer function Hm(t). For a one-compartment model, . For several compartments, the transfer function would be a sum of several exponentials, Gunn et al (2001). Note that here we do not identify a λr with a tissue region m but instead allow the coefficient to give the appropriate weight to the exponential with a decay constant λr. One could also write this as where the exponential basis functions change from tissue region to tissue region. The coefficients of the basis functions are all greater than or equal to , the decay constants are bounded below by the decay constant λ of the radioisotope, , and R is the maximum number of basis functions allowed in the model. The problem is determining the values of that best fit the measured data given predefined values for . We know from Gunn et al (2001) that . In the case of a one-compartment model, provide a spectral representation of in a particular region or voxel.
In the following formulation, it is assumed that each voxel or tissue region has a transfer function specified by a series of exponentials. The tissue time–activity curve for the voxel m is modeled as a fraction of the arterial blood time–activity function plus a linear combination of single exponential basis functions in time, convolved with the same arterial blood function B(t). The expression for uptake in voxel m is
| (64) |
where γm and λm are vectors and and
| (65) |
Substituting , we obtain
| (66) |
where
| (67) |
The projection equations for activity accumulated over [tk − Δtk, tk ] are expressed as
| (8) |
| (11) |
For the activity in equation (64), the projection is
| (68) |
where is given in equation (36) and
| (69) |
| (70) |
Rearranging terms in equation (68), we have
| (71) |
The total projection samples are represented by the vector
| (72) |
Thus, a set of I · K equations can be written as
| (73) |
where
| (74) |
| (75) |
| (76) |
This gives the following expression
| (77) |
or
| (78) |
where
| (79) |
| (80) |
This is the most general formulation for fitting a multi-compartment model for each voxel to projection measurements.
The parameters λ, μ and β are solved by least-squares minimization. Constraints imposed are and . The spectral components for every pixel in the image are determined directly from the projections by non-negative least squares technique. Computationally, this can be a large problem. It can be broken up by first determining spectral components for each projection sample (Meikle et al 1996, 1998). The spectral components for each pixel can then be reconstructed from the spectral components of the ray sums. Alternatively, a reduced-basis set can be formed and the Moore-Penrose pseudoinverse can be used to find the coefficients of the basis (Maltz 2000a).
4.5. Summary
In Zeng et al (1995), the parameters of a one-compartment model were fitted directly from the projection measurements. It was shown that biases in parameters estimated from the time–activity curves generated from the reconstructions were eliminated by estimating the parameters directly from the projections. The estimation from projections was performed by (1) first estimating the multiplicative factors using a linear estimation technique and (2) then estimating the exponential factors by reducing the nonlinear estimation problem to a linear estimation problem by using linear time-invariant system theory. The estimation was performed on the sum of the counts in a projection.
Later, the problem was formulated as a minimization of a weighted sum of squared differences between the projection data and the model predicted values (Huesman et al 1998). A one-compartment model was assumed for the simulated myocardium tissue, and the blood input function was assumed to be known. Simulated data were used to show that unbiased kinetic parameter estimates for one-compartment models could be obtained directly from parallel-beam and cone-beam SPECT projections with proper segmentation of volumes encompassing the projected field-of-view. These simulations systematically incorporated physical effects, such as attenuation, and led to the development of methods that were used to analyze a dynamic 99mTc-teboroxime patient study (Reutter et al 1998b). For this patient study, the blood input function was estimated directly from the projections, and spatial models for the left ventricular myocardium blood pool, liver and background tissue were determined (as shown in figure 11) by automatically segmenting a dynamic volumetric image sequence reconstructed from the projection data.
Later on, a 4D maximum a posteriori (MAP) approach with a compartmental-model-based temporal prior that constrains each voxel’s behavior in time to conform to a compartmental model was developed for dynamic cardiac SPECT application (Kadrmas and Gullberg 2001). No a priori limitations on kinetic parameters were applied, but the parameter estimates evolved as the algorithm iterated to a solution. The estimated parameters and time–activity curves were used within the reconstruction algorithm to model changes in the activity distribution as the camera rotates, avoiding artifacts that could result from inconsistencies of data between projection views. The ordered-subsets maximum a posteriori (OSMAP) algorithm resulted in images with better myocardial uniformity and definition, yielded time–activity curves with reduced noise variations, and provided wash-in parameter estimates with better accuracy and lower statistical uncertainty than those obtained from conventional ordered-subsets expectation-maximization (OS-EM) processing followed by compartment modeling. The algorithm removed the bias in K1 estimates that can be caused by inconsistent projections from sampling schedules as slow as 60 s per time frame. However, no improvement in wash-out parameter estimates was observed. Incorporation of the compartmental relationship between blood and tissue activities into the spatiotemporal model provides a temporal regularization. Such an approach is desirable for cameras with slow rotation protocols that result in poor temporal sampling and aggravate the problems of data inconsistency. The temporal prior encourages the time behavior of the image values to match a compartmental model. It also provides a means for modeling how the distribution of the tracer changes as the camera rotates during the acquisition, thereby addressing the problem of inconsistent projections. The framework is also well suited for accepting spatially regularizing priors, and such priors could readily be applied to either reconstructed voxel intensities or kinetic parameter estimates, as desired.
The 4D maximum a posteriori approach in section 4.3 assumes the time–activity curve for each voxel is constrained by a one-compartment model. A generalization to multiple compartments is presented in section 4.4, where it is assumed that the kinetics in each voxel can be represented by a spectral decomposition of exponential terms. The solution can be determined by least squares or by maximum a posteriori algorithms. However, the computational effort increases significantly the more general the model.
In summary, the combination of camera gantry motion and the time-varying nature of the radionuclide distribution being imaged results in inconsistent projection data sets. The estimation of kinetic parameters from reconstructed time–activity curves results in biases. Estimating the kinetic parameters directly from projections reduces these biases.
5. Estimation of kinetic model parameters from projections—semi-direct methods
While the estimation of kinetic model parameters directly from projections can potentially provide better variance and bias, it is more computationally demanding. Direct methods involve solving a nonlinear estimation problem (Zeng et al 1995, Huesman et al 1998), and the computational resources required for the straightforward solution of the embedded linear least-squares subproblem grow linearly with the number of SPECT projection measurements. These are nontrivial for typical patient datasets. To make matters worse, the computational requirements for the straightforward solution increase quadratically with the number of linear parameters. A more computationally efficient solution is to use semi-direct methods in which spatiotemporal modeling of the kinetics of the radiopharmaceutical tracer is implemented.
Semi-direct methods reduce the number of parameters and involve the process of solving a linear problem before solving a nonlinear problem to determine the kinetic model parameters. Semi-direct methods first estimate time–activity curves,
| (7) |
from projections
| (9) |
Then, the estimation of compartment model parameters is performed subsequent to direct estimation of time–activity curves.
The following gives various examples of the formation of spatiotemporal basis functions. First, splines are presented. These are used in many scientific applications to fit a continuous smooth function to discrete data. The estimation of spline coefficients is computationally efficient; splines are free form and have finite support. Second, factors which are physiological time–activity curves that are inherent in the data are presented. Then, time–activity curves that rise to a maximum and then decrease monotonically (dSPECT method) are presented.
5.1. Spline spatiotemporal basis functions
For the activity A(x, t) represented using splines as basis functions,
| (16) |
the projection equations can be expressed as
| (81) |
| (82) |
where
| (10) |
Integrating over the time interval Δtk yields
| (11) |
| (12) |
| (83) |
| (84) |
where pi (tk) are the modeled projections, amn are the linear coefficients associated with the time integrals of the projections of the spatiotemporal basis functions, M is the number of spatial basis functions and N is the number of temporal basis functions. The criterion that is minimized by varying the linear coefficients amn associated with the time integrals of the projections of the spatiotemporal basis functions is the weighted sum of squares function,
| (85) |
where p̃i (tk) are the measured projections, Wik are the weighting factors usually taken to be the reciprocal of the measurement errors, I is the number of projection rays per angle and K is the number of projection samples in time.
Equation (84) can be rewritten in the matrix form as
| (13) |
and equation (85) in the form
| (86) |
respectively, where p̃ is an IK element column vector whose [i + (k − 1) I ]th element is pi (tk), F is an I K × MN matrix whose {[i + (k − 1) I ], [m + (n − 1) M]}th element is fik(mn), a is an MN element column vector whose [m + (n − 1) M]th element is amn, p̃ is an IK element column vector whose [i + (k − 1) I ]th element is p̃i (tk) and W is an I K × I K diagonal matrix whose [i + (k − 1) I ]th diagonal element is 1/Wik. The criterion χ2 is minimized by the vector of spatiotemporal basis function coefficients,
| (87) |
The covariance matrix for the coefficients â is
| (88) |
where cov(p̃) is the covariance matrix for the measured projections. Given an estimate of cov(p̃), estimates of the statistical uncertainties of the coefficients â are the square roots of the diagonal elements of the covariance matrix given by Kimura et al (1990). In general, the errors in the coefficients are correlated and the covariance matrix given by Kimura et al (1990) has nonzero elements off the diagonal. If W = cov(p̃)−1,
| (89) |
A preliminary study reported on the biases that result from modeling various orders of temporal continuity and using various time samplings when estimating time–activity curves directly from dynamic cone-beam and parallel-beam SPECT projection data (Reutter et al 2000). Piecewise cubic, quadratic, linear and constant B-splines were used to model the time–activity curves for the blood input, three myocardial volumes of interest, liver and background tissue in simulated data. Segmented volumes encompassing the projected field-of-view were modeled to contain spatially uniform activity concentrations. The effects of spatial segmentation errors were also studied.
5.1.1. Comparison of conventional, semi-direct and direct methods using computer simulations
Computer simulations were performed to compare a semi-direct method using splines with a direct method of estimating kinetic model parameters from projections and with a conventional method of obtaining time–activity curves from a sequence of dynamic reconstructions for a particular ROI. A dynamic version of the MCAT phantom (Tsui et al 1993, Pretorius et al 1999) in figures 12(a) and (b) was created for the simulations. A single 2D slice of the phantom was used for the experiment. The dynamic phantom was constructed by summing each organ of the static phantom using weights derived from the time–activity curves shown in figure 12(c) for each time frame. In this way, a series of 2D phantoms were constructed, one for each time frame of the dynamic acquisition. The time–activity curves shown in figure 12(c) were generated to mimic those seen in patient studies. The myocardium time–activity curve was constructed using blood as the input function while assuming a one-compartment model (figure 8) with wash-in and wash-out rate constants and a blood fraction given in table 1. Each time–activity curve was numerically integrated over the active acquisition time for each time frame. Projection data were formed by projecting each time frame of the 64 × 64 dynamic phantom. A 15 min data acquisition was simulated consisting of 15 revolutions of a single-head SPECT system, acquiring 120 angles per revolution and 64 parallel projection samples per angle. The simulated projections included the effects of attenuation and geometric point response, but neither scatter nor noise. Dynamic sequences of 120 projections (complete revolution) every 60 s were reconstructed using a conjugate gradient algorithm to minimize an unweighted least-squares criterion. Time–activity curves were generated from the reconstructed dynamic sequence (conventional method). These data were submitted to RFIT (Huesman et al 1995) to obtain the unweighted least-squares fit for the kinetic parameters. The regions selected for the fit to the compartment model are shown in figure 12(a). From the known regions of the intraventricular blood, myocardium and background, equations for the projections were formulated using the reconstructed attenuation distribution to obtain expressions for the attenuated projections. Using the system of projection equations for all regions, the kinetic parameters for each region were simultaneously estimated directly from the projections (direct method) (Reutter et al 1998a). Next, B-splines for time–activity curves were estimated directly from projections using the same projection model (Reutter et al 2000), and for these curves kinetic parameters were then estimated using RFIT (Huesman et al 1995) (semi-direct method). In each of the methods, the blood input function was assumed to be known.
Figure 12.
Phantom and time–activity curves used in computer simulations comparing conventional, semi-direct and direct methods of estimation of kinetic parameters. (a) The MCAT emission phantom shown with lateral and septal defects. (b) The attenuator assumed in generating the projection data. (c) Time–activity curves used to generate the dynamic emission data for different organs. The myocardial tissue curves were generated assuming a one-compartment model (figure 8).
Table 1.
Estimates of myocardial uptake and wash-out parameters and volume fraction fv of blood in the tissue obtained using conventional and direct compartmental model parameter estimation from projections, as well as results of fitting compartmental models to directly estimated spline time–activity curves (the semi-direct method). These are compared with the truth used in the simulations (Reutter et al 1998a, 2000).
| Parameter | Truth | Conventional | Direct | Semi-direct | |
|---|---|---|---|---|---|
| Normal myocardium | K1 | 0.700 | 0.665 | 0.700 | 0.700 |
| k2 | 0.150 | 0.149 | 0.150 | 0.150 | |
| fv | 0.150 | 0.160 | 0.150 | 0.151 | |
| Lateral defect | K1 | 0.500 | 0.218 | 0.500 | 0.507 |
| k2 | 0.600 | 0.247 | 0.600 | 0.607 | |
| fv | 0.100 | 0.278 | 0.100 | 0.092 |
Units for K1 and k2 are in min−1; fv is dimensionless.
One can see in table 1 that the direct approach gives the best results, even though they are only slightly better than those of the semi-direct method but significantly better than those of the conventional method. The conventional method did poorly in the defect and did reasonably well in the normal myocardium. The bias is primarily due to artifacts resulting from inconsistent projection data and partial volume effects in the sampled ROI of the reconstructed defect. Noise was purposely not included in the simulations. It was assumed that the measured projections corresponded to the true mean and variance of a Poisson random process. If noise had been added, assuming a Poisson distribution with mean and variance equal to the random variable of the sampled projection, the results of an estimated weighted least-squares reconstruction would have been biased.
5.1.2. Comparison of semi-direct and direct methods using data acquired from a patient study
Data from a patient study were used to compare the estimation of kinetic model parameters using semi-direct and direct methods for the estimation of kinetic model parameters from projection measurements (Reutter et al 1998a, 1998b). Patient data were acquired on a PRISM 3000XP SPECT system at the University of Utah using a fast data acquisition protocol. First, a transmission scan was performed using a 153Gd line source as the transmission source. The patient was stressed using adenosine. A dynamic acquisition obtaining 120 projections over 360° every 10 s was initiated at the same time as the injection of 925 MBq (25 mCi) of 99mTc-teboroxime. The attenuation map was reconstructed using 20 iterations of the transmission ML-EM algorithm (Lange and Carson 1984). The attenuation-corrected emission results were reconstructed using 20 iterations of the ML-EM algorithm. A 4D second directional derivative operator was applied to the attenuation-corrected dynamic image data set containing ninety 10 s frames to segment the regions of the myocardial tissue, intraventricular blood, liver and background tissue. Figure 13 shows the myocardial, liver and body surfaces extracted automatically at time frame 31 (corresponding to the interval 300–310 s).
Figure 13.
Segmentation of a patient study (fast rotation) used in modeling the projection data for estimating the dynamic parameters directly from projections. The image on the left shows the boundaries of the liver (left) and the myocardium (right) resulting from the automatic segmentation of the attenuation-corrected reconstruction at time frame 31 of the sequence of dynamic reconstructions. The image on the right shows anatomical surfaces of the dome of the liver (upper) and myocardium (lower), which were constructed by linking together zero-crossings of the second directional derivative (Reutter et al 1998b).
The spatial activity concentration within these volumes was modeled by indicator functions. From the segmented results, equations for the projections were formulated using the reconstructed attenuation distribution to obtain expressions for the attenuated projections. Using these equations, the kinetic parameters for the patient study were estimated directly from the projections (direct) (Reutter et al 1998a). B-splines of time–activity curves were estimated directly from projections using the same model for the projection measurements (Reutter et al 2000, 2002, 2004a). Compartment model parameters were then estimated using RFIT (Huesman et al 1995) for these fitted time–activity curves (semi-direct). The results are in table 2. Here it is difficult to make a statement as to which is better.
Table 2.
Estimates of myocardial uptake and wash-out parameters and their uncertainties obtained using direct compartmental model parameter estimation from projections, as well as results of fitting compartmental models to directly estimated spline time–activity curves (the semi-direct method) (Reutter et al 1998b).
| Parameter | Direct | Error | Semi-direct | Errora | |
|---|---|---|---|---|---|
| Myocardium | K1 | 0.835 | 0.055 | 0.852 | – |
| k2 | 0.178 | 0.002 | 0.172 | – |
Units are in min−1. The errors for the direct method were estimated as twice the inverse of the Hessian matrix associated with the chi-square criterion in equation (52), where the weights were assumed to be the reciprocal of the measured projections.
The issue of estimating errors using spline curves is complicated because the curves are correlated in time, so this remains an unsolved problem. This example illustrates why direct estimation of kinetic compartment model parameters is much more desirable.
5.1.3. Dynamic SPECT image reconstruction of projections acquired with slow rotation using multi-resolution spatiotemporal B-spline image representation
In the previous example, the data were acquired with a relatively fast camera rotation. This study was performed to see how well time–activity curves could be estimated from projections acquired with a relatively slow camera rotation (Gullberg et al 2007a, Reutter et al 2007a). Projection data were acquired in 1 s time frames with an angular step of 5° per frame on a GE Millennium VH Hawkeye SPECT-CT scanner at UCSF. The acquisition was started immediately at the time of the injection of 740 MBq (20 mCi) of 99mTc-sestamibi. Attenuation and depth-dependent collimator response were modeled, but not scatter. The 4D B-splines were piecewise trilinear in space and piecewise quadratic in time. The splines were organized on a 3D spatial grid that provided uniform sampling of 17.7 mm in each dimension, and on a 1D temporal grid that provided nonuniform sampling intervals of 0–4, 4–15, 15–48 and 48–144 s during the first two gantry rotations. The 4D spatiotemporal distribution was reconstructed via direct matrix inversion to minimize a penalized least-squares criterion. Figure 14 shows results of the blood in the right ventricle at 15 s (figure 14(a)), in the left ventricle at 45 s (figure 14(b)), and the summed image (figure 14(c)) for one transaxial slice. The use of nonuniform time sampling with piecewise-quadratic splines yielded smooth time–activity curves that captured the relatively fast rise and fall of tracer in the right and left intraventricular blood chambers, as well as uptake and retention of tracer in the left ventricular myocardium (figure 14(d)).
Figure 14.
Estimation of time–activity curves from projections acquired with slow camera rotation (patient study, slow rotation). Reconstructed images and time–activity curves for a human dynamic Tc-99m-sestamibi cardiac SPECT study. Kinetics of tracer in blood and myocardium are evident in fully 4D reconstructed dynamic images sampled at (a) 15 s and (b) 45 s; (c) in late summed image and (d) in directly estimated quadratic B-spline time–activity curves. Black crosses in (a)–(c) denote spatial positions at which time–activity curves were obtained (Reutter et al 2007a).
5.1.4. Estimation of kinetic parameters directly from projections provides more efficient estimators
Computer simulations of a human dynamic 99mTc-teboroxime cardiac SPECT study using the MCAT phantom (figure 12) showed that the additional temporal regularization provided by jointly estimating compartmental model and blood input function parameters directly from projections resulted in improved precision of parameter estimates, as well as comparable or improved accuracy (Reutter et al 2005). Four hundred realizations of cone-beam SPECT projection data having Poisson noise were generated. The simulation consisted of a 15 min dynamic cardiac data acquisition by a single-headed SPECT detector system with cone-beam collimator (70 cm focal length) providing 120 angles per revolution and 15 revolutions. The projection data were generated from a mathematical phantom that was composed of 128 contiguous 1.75 mm thick slices and contained M = 6 volumes of interest of uniform activity: the blood pool, three myocardial tissue volumes (normal myocardium, septal defect, lateral defect), liver and background tissue. Attenuation and geometric point response were modeled but scatter was not modeled. The simulated time–activity curves shown in figure 12(c) mimicked the kinetics of 99mTc-teboroxime (Narra et al 1992).
Initially, time–activity curve models for all six volumes were estimated directly from noisy projection data with use of 16 B-spline basis functions spanning 15 time segments having geometrically increasing length. Piecewise quadratic B-splines were used with an initial time segment length of 10 s. For noiseless projections, the modeling error was less than 2%, where the error was defined to be the root mean square (RMS) difference between the simulated curve and the spline model, normalized by the RMS value of the simulated curve (Reutter et al 2000). Compartmental models were then fitted to the curves for the three myocardial tissue volumes and the liver. These semi-direct compartmental model fits were used as starting points for direct joint estimation of refined compartmental models and B-spline time–activity curves for the blood pool and background tissue. The results in table 3 show that using B-splines to model the input function and directly estimating compartmental model parameters and blood input function can improve quantitation of dynamic SPECT by reducing the standard deviation of uptake and wash-out parameters for the septal and lateral defects by 17% to 41%, compared to semi-direct methods that estimate time–activity curves first and then fit compartmental models to the curves. Of course, the accuracy of the model depends upon appropriately modeling the effects of the physics (attenuation, scatter, geometric response) of the imaging detection process and defining the appropriate compartment model for each tissue type. This also has important implications for the estimation of kinetic parameters using dynamic PET.
Table 3.
Comparison of sample means and sample standard deviations of compartmental model parameters estimated semi-directly and directly with joint estimation of the blood input function. The means and standard deviations were estimated from 400 noise realizations. The standard error of the sample mean is approximately 0.05 times the sample standard deviation. Units for the wash-in rate and wash-out rate are min−1; the vascular fraction is dimensionless (Reutter et al 2005).
| Parameter | Truth | Semi-direct (mean ± SD) | Direct joint (mean ± SD) | ||
|---|---|---|---|---|---|
| Normal myocardium |
|
0.7 | 0.7001 ± 0.0061 | 0.6998 ± 0.0056 | |
|
|
0.15 | 0.1500 ± 0.0016 | 0.1499 ± 0.0016 | ||
|
|
0.15 | 0.1501 ± 0.0121 | 0.1511 ± 0.0097 | ||
| Septal defect |
|
0.3 | 0.314 ± 0.077 | 0.312 ± 0.061 | |
|
|
0.3 | 0.311 ± 0.064 | 0.310 ± 0.053 | ||
|
|
0.1 | 0.100 ± 0.119 | 0.097 ± 0.081 | ||
| Lateral defect |
|
0.5 | 0.554 ± 0.222 | 0.514 ± 0.132 | |
|
|
0.6 | 0.639 ± 0.172 | 0.616 ± 0.120 | ||
|
|
0.1 | 0.075 ± 0.162 | 0.100 ± 0.102 | ||
| Liver |
|
0.9 | 0.9001 ± 0.0050 | 0.9001 ± 0.0049 | |
|
|
0.002 | 0.0020 ± 0.0004 | 0.0020 ± 0.0004 | ||
|
|
0.2 | 0.2001 ± 0.0046 | 0.2002 ± 0.0036 |
5.2. Factor basis functions—factor analysis of dynamic structures (FADS)
Factor basis functions are estimated automatically from the data. They correspond to curves which are derived from the data that exhibit a direct physiological interpretation. In the factor model, each image is built from groups of voxels that have similar temporal behavior (Chua et al 1993). These groups may or may not overlap. Identification of these groups (voxels highly correlated in space and time) provides a segmentation of the imaged distribution into organs that have similar physiological behavior. This differs significantly from that of the dSPECT method discussed in the next section where there is no assumed temporal correlation between voxels, but only a spatial correlation imposed by tomography (i.e. each voxel has a separate independent time–activity curve).
One of the limitations of this approach is that the number of factors (number of groups with similar time behaviors) needs to be specified a priori. By limiting the number of these factors (usually not more than four are used), an approximation is used that all voxels are a linear combination of a limited number of temporal basis functions. Increasing the number of factors is difficult and probably not feasible, largely due to effects of non-uniqueness (Sitek et al 2000, 2002b), which are very hard to address. This is especially true when estimating factors from projections where it is difficult to spatially restrict the region that is analyzed because the entire volume is seen on projections and thus the number of factors may have to be limited more than the number used for FADS analysis of reconstructed images.
For the factor model in equation (21), the number of unknowns is equal to N(K + M), which is substantially lower than the NMK unknowns for the complete inverse problem (K is the number of time points (projections), M is the number of spatial basis functions and N is the number of factors or temporal basis functions). For renal studies (Sitek et al 2001), N was chosen to be equal to 2 or 3. Although the number of unknowns is reduced by introducing the factor model, we will see that the objective function becomes nonlinear.
The counts in the projection bin i taken at the time tk, pi (tk) are expressed by the following projection equations,
| (90) |
where
| (10) |
| (11) |
| (12) |
| (91) |
| (92) |
| (93) |
Estimates for a and F can be determined by constructing and minimizing the weighted least-squares objective function,
| (94) |
| (95) |
The value of p̃i (tk) is the experimental value of counts in the ith projection bin collected at the projection taken at time tk. I is the number of bins in each projection and K is the number of projections or the total number of time samples. The value of fik(mk) is an element of the system matrix. The element fik(mk) is proportional to the probability that the photon emitted from the support of the basis function Sm(x) pixel i at time tk is detected in bin i of the projection taken at time tk. N is the number of factors and M is the number of basis functions representing the spatial distribution of the image. The elements Wik are elements of the weighting matrix W.
To ensure the non-negativity of the resulting matrix a and F, non-negativity constraints are imposed by adding the term fneg(a, F) to the objective function,
| (96) |
where
| (97) |
with α being a penalty constant.
In the above formulation, the non-uniqueness of the factor model (Sitek et al 2002b) was not addressed. Even without this, the estimation of factors from projection measurements was proven to be successful in renal studies (Sitek et al 2001). This approach also shows promise for analyzing dynamic cardiac studies in rodents using pinhole collimators mounted on patient SPECT systems with slow rotation (Hu et al 2005, 2008) (see next section).
5.2.1. Direct estimation of factors from projection measurements in small animal studies
One of the greatest difficulties in applying kinetic modeling in small animal studies is measuring the blood input function. The blood volume is small and thus it is difficult to draw blood samples, and the resolution of the ventricular cavity is inadequate for ROI sampling. The following demonstrates that, if factors and factor coefficients are estimated directly from projections, a blood input function can be obtained even with a slowly rotating camera. A dual-headed pinhole SPECT-CT system at LBNL (figure 15(a)) was used for imaging the distribution and kinetics of 123I-MIBG in the myocardium of spontaneously hypertensive rats (SHR) and control Wistar Kyoto (WKY) rats to study the function of the sympathetic nervous system in heart failure (Hu et al 2005, 2008). A dynamic acquisition was performed by injecting 185 MBq (5 mCi) of 123I-MIBG into rats immediately after initiating data acquisition. The detectors rotated, continuously traversing 360° every 90 s for a total acquisition time of 90 min. For the first 90 s rotation of the study, factor analysis estimates of the time–activity curves for the blood pool were obtained directly from the projections. This required the estimation of 1 024 180 unknowns. After the first rotation, the blood input was measured every 90 s from the ROI in the left ventricular blood volume of a contiguous sequence of dynamic tomographic reconstructions. The time resolution was equal to 1 s for the first 90 s and equal to 90 s for the remainder of the 90 min acquisition. By merging the blood input obtained over the first rotation with estimates of blood and tissue curves estimated from the subsequent sequence of dynamic reconstructions, compartmental model parameters were estimated. Figure 15 illustrates the resulting input function for four rats calculated using factor analysis with two factors. For these particular studies, there was no validation with blood samples. This is a semi-direct method in which time–activity curves were first estimated for the blood and the myocardial tissue. Kinetic parameters shown in table 4 were subsequently estimated by fitting the estimated time–activity curves to a one-compartment model.
Figure 15.
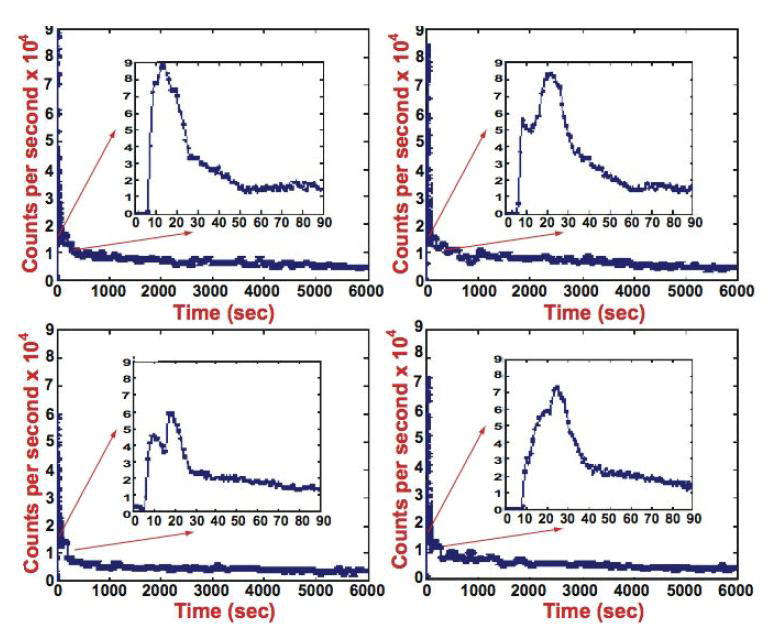
Input functions of factors estimated from projections (rat study, slow rotation). (a) Pinhole collimators (tungsten insert with 1.5 mm aperture, 25 cm focal length with a magnification of approximately 5) mounted on the GE Millennium VG3 Hawkeye SPECT-CT system used in the rat studies. The camera rotated continuously with a pinhole to rotation axis distance of between 5.5 and 5.8 cm. (b) Sequence of dynamic reconstructions and reconstruction of the sum of all of the projections after the first 180 s for one transaxial slice of a rat study. (c) Input functions estimated by factor analysis for four 123I-MIBG studies in rats using two factors. The curves are the convolution of the input injection (5 s) with the circulation function. The double peaks are due to a fast recirculation time of 6–8 s (Hu et al 2008).
Table 4.
Estimates of the kinetic model parameters for a one-compartment model using the input functions in figure 15(c). The data were acquired on 29 November 2005 (Hu et al 2008).
| Animal identifier | Kinetic parameters | Mean | Standard deviation |
|---|---|---|---|
| G1 normal | K1 (s−1) | 7.15 × 10−3 | 6.37 × 10−4 |
| k2 (s−1) | 2.64 × 10−3 | 2.53 × 10−4 | |
| G1 hypertensive | K1 (s−1) | 6.74 × 10−3 | 7.24 × 10−4 |
| k2 (s−1) | 3.44 × 10−3 | 3.92 × 10−4 | |
| G2 normal | K1 (s−1) | 7.41 × 10−3 | 7.21 × 10−4 |
| k2 (s−1) | 2.48 × 10−3 | 2.60 × 10−4 | |
| G2 hypertensive | K1 (s−1) | 5.52 × 10−3 | 5.55 × 10−4 |
| k2 (s−1) | 2.96 × 10−3 | 2.78 × 10−4 |
5.3. dSPECT
The ‘dSPECT method’ fits time–activity curves for each voxel directly from projection measurements. These may only be acquired over a single rotation (Farncombe et al 1999, 2000, 2001, Farncombe 2000, Celler et al 2001). The method does not involve any assumptions about the location of the dynamic regions. However, for the case of bimodal time–activity curves that increase and then decrease, it requires prior knowledge of the time frame in which the activity peaks in each particular image voxel (Farncombe et al 2001). Otherwise, as we explain below, the peak is estimated as part of the optimization problem. This is one approach of constraining the time–activity curves.
For the projections
the dSPECT method is formulated as the solution to the following optimization problem,
| (98) |
subject to
| (99) |
In different applications of the dSPECT method, the constraints have been formulated in other ways. In the expression given in equation (99), the reconstructed (optimum) time–activity curve monotonically increases to a maximum at time tp and then monotonically decreases (Farncombe et al 2001). In some cases, the time–activity curve only decreases or increases monotonically (Celler et al 2001).
5.4. Other methods
Most of the methods implemented for calculating kinetic parameters from dynamic data are based on fitting a compartment model to the change in the tracer concentration in tissue regions over time. Most of these methods demand dynamic data acquisition following the tracer administration and then either a nonlinear or linear least-squares fitting to estimate the kinetic parameters. Other methods have been proposed where a weighted-integration technique is used instead to minimize the data processing time in generating functional maps of cerebral blood flow and distribution volume for 15O water administration studies (Alpert et al 1984, Carson et al 1986). In this technique, the dynamic images are integrated after multiplication by two time-dependent weight functions, and two functional parameters are calculated by means of a table look-up procedure for each image pixel. For example, once the value of k2 is determined, then the value of K1 can be determined from linear equations. This eliminates the need to collect and store dynamic data. The kinetic parameters are calculated from the weighted integrals of the projection data, which are adequate for measuring the time-varying activity changes during the projection sampling, provided that the integrals are calculated with sufficient numerical accuracy.
This technique was extended to calculate up to six independent weighted-integrated sinograms (Iida et al 1995a). Values from the weight-integrated sinograms are inserted into operation equations to generate functional parameter images for H215O and 18FDG. The two-compartment model of 18FDG uses three independent time-weighted integrated images that are inserted into the operation equations. The solution requires integration of the acquired counts over time. The time points for the acquired samples need not be at the same time for each projection, which accommodates the rotation of the camera head. The use of weighted integration to solve kinetic equations is suitable for certain models.
Application of weighted integration has been explored in dynamic SPECT (Tan et al 1994). The advantage of the weighted-integration approach is that it provides a straightforward solution calculated directly from projections that, assuming adequate numerical integration, are independent of the sampling limitations.
6. Discussion and future developments
This review has focused on special data processing techniques of dynamic SPECT highlighting cardiac perfusion imaging. The mathematical methods presented here are applicable to other dynamic imaging applications as well. Research continues in the development of hardware, radiopharmaceuticals and data processing techniques which will enable the realization of the full potential of dynamic SPECT.
6.1. Estimation from projections may produce less bias and variance and has potential even for PET
The estimation of kinetic parameters from projections may produce less bias and less variance than the conventional method of estimating kinetic parameters from time–activity curves generated from reconstructed ROIs. This review presents some examples demonstrating this fact. However, more work is needed to verify these results. Simulations have demonstrated that the simultaneous estimation of the input function and parameters of compartment models for tissue regions reduces variance and bias. A comparison of direct with indirect methods must be done carefully in order to be sure that weighting of the reconstructed data is done reasonably. However, this can be difficult because covariance matrices of reconstructed images or time–activity curves can be difficult to obtain and this requires a solution to an estimation problem with a large number of parameters. Models for dynamic imaging should be constructed so that the parameters are fitted directly to the original acquired data, not as a conventional two- or three-step process that first requires reconstruction followed by time–activity curve generation and then model parameter estimation. This should be accomplished for both consistent and inconsistent tomographic data. The modeling of the time variation in the projection data attempts to remove the inconsistency in the data of the inverse problem. It is also much easier to directly incorporate weighting by the noise in the data in the estimation process. Moreover, it has been demonstrated from simulations that direct estimation of model parameters produces less variance and less bias than the conventional method mentioned above, and also less than the two-step semi-direct methods in which the time–activity curves are estimated directly from projections and then kinetic parameters are estimated from those time–activity curves. This suggests that all kinetic parameters should be estimated directly from dynamic data. It is anticipated that all the completely consistent tomographic data acquired with a stationary SPECT detector system or a PET scanner will produce less bias and less variance than is produced with a rotating SPECT camera.
6.2. Optimum spatiotemporal basis functions
For the models that represent the tracer activity variation directly using the projection data for non-deforming media, the challenge is to determine optimal spatiotemporal basis functions. Splines have been demonstrated to efficiently represent both spatial and temporal variations in the data (Reutter et al 2000, 2002, 2004a, 2007a). There are various orders of splines that can be used depending upon the frequency content of the data. Multigridding (a higher resolution representation used when necessary, and less so otherwise) is required to reduce the number of unknowns so that the system of acquired projection data is not underdetermined. This is especially important when developing models for slow camera rotation. Spherical harmonics could also be used for spatial basis functions. It has also been demonstrated that factors can provide excellent temporal basis functions. However, the solution can require a large number of unknowns, and non-uniqueness is a problem that must be considered (Hu et al 2005, 2008). Still another approach is to use a spectral method for the temporal representation based upon exponential functions as a basis which requires linear estimation of the parameters (Maltz 2000b, 2001, 2002).
6.3. Tomographic reconstruction of tracer kinetics in the heart using a spatiotemporal mechanical model
In organs such as the heart, which deform while the intensity of the signal changes as a result of radiotracer redistribution, both space and time need a parameterization that deforms with the organ. It is necessary to consider these changes as data are taken in order to reduce the bias and variance of model parameters. A generalized model for specifying time changes of tracer activity and mechanics on a deforming differential manifold has been developed (Gullberg et al 2007b). The proposed model is a large optimization problem that seeks to find a number of optimum parameters by focusing on organs, such as the heart, that have rapid simultaneously changing tracer concentrations and organ configurations. The spatial parameterization can be accomplished using smooth functions relative to the Euler frame that can easily be transformed to the differential manifold of the deforming heart. The temporal parameterization can be accomplished using appropriate parameterization of the spatial deformation as a function of time. The temporal basis functions could be splines (Reutter et al 2000), factors of dynamic structures (Sitek et al 2002b) or time–activity curves of a compartment model (Kadrmas and Gullberg 2001). The spatial parameterization can also involve a multi-resolution approach, where inside the organ boundaries the changing tracer kinetics are modeled with high resolution and outside the boundaries the distribution is modeled with a more coarse resolution (Boutchko et al 2006b, Reutter et al 2006, 2007b, Sitek et al 2006). This has been shown to actually reduce the number of parameters of the tomographic problem (Reutter et al 2004a). The accuracy of the model depends upon appropriately modeling the effects of the physics of the imaging detection process (attenuation, scatter, geometric response). The accuracy also depends on the use of appropriate models for the physiology of the tracer kinetics and for the mechanical properties of the heart.
The proposed method involves simultaneous segmentation and estimation of the dynamic parameters. It is assumed that the data are acquired dynamically with cardiac phase information, either by list mode acquisition or by framing into gated dynamic frames over the cardiac cycle. The differential manifold of the heart deforms according to a mechanical model (Sitek et al 2002c, Veress et al 2005, Sitek et al 2005) and incorporates methods (Feng et al 2003b, Shi and Karl 2003, 2004) for determining the boundary of the heart. It also includes a dynamically changing organ boundary and intensity represented by spatiotemporal basis functions within the boundary, defined by a deforming manifold. The organ boundaries are determined using level set methodology, which was devised as a simple method for computing and analyzing motion of a surface in two or three dimensions (Osher and Sethian 1988, Sethian 1996, Osher and Fedkiw 1999). The body within the surface is defined in an Euler reference frame using either Cartesian or curvilinear coordinates. The body within the surface is a differential manifold that is allowed to deform based on a mechanical model. Therefore, the surface is specified as the zero level set of a smooth function, where the spatial parameters are either Cartesian or curvilinear coordinates defined in the deformed space. This approach imposes constraints based upon a mechanical model, and it simultaneously segments the boundary of the organ and estimates model parameters of changing activity.
6.4. Estimation of scatter from dynamic imaging data
Dynamic imaging may help in estimating the physical properties of the imaging detection process, such as scatter, by using the different kinetics of the tracer in different organs to model scatter. Most software-based methods need a transmission image (not an emission image) to simulate scatter (Welch et al 1995a, Zeng et al 1999, Bai et al 2000, Laurette et al 2000, Floyd et al 1985, Liang et al 1992, Frey and Tsui 1993, Meikle et al 1994, Beekman et al 1996, 2002, Kadrmas et al 1998). Methods have been developed to understand the nature of scatter (Reutter et al 2003), to segment scatter from primary photons using principal component analysis (Toennies et al 2003), to identify and remove scatter artifacts (Toennies et al 2004) and to model scatter based upon the temporal information in dynamic SPECT data (Toennies et al 2003, Reutter et al 2004b). Two methods (Reutter et al 2004b) have also been proposed for modeling and estimating scatter jointly with tracer kinetic models. These methods exploit the fact that the scatter distribution from a volume of interest is spatially smooth, and has the same temporal kinetics as unscattered events from the volume. The first method treated scattered events as if they originated from scatter sites distributed in image space. For each volume of interest, the distribution of scatter sites was modeled with a smooth spatial function, and events from this effective scatter source distribution (ESSD) (Frey and Tsui 1997, Kadrmas et al 1998) were forward-projected along with unscattered events from the volume. The second method bypasses modeling an ESSD in image space and simply models the spatial projection of scatter to be a smooth function in projection space. Computer simulations of a dynamic 99mTc-teboroxime cardiac SPECT scan showed that unscattered and scattered events from the blood pool, myocardium and liver have distinct spatiotemporal signatures and that it is feasible to jointly estimate scatter amplitudes and time–activity curves for volumes of interest directly from projection data. This suggested that joint estimation of scatter, blood input function and compartmental model parameters is a well-posed problem and can lead to reduced bias in kinetic parameter estimates.
6.5. Dynamic information in a well-isolated bolus during the input phase
In general, the dynamic temporal/spatial distribution of tracers is complex and varies between different organs of the body. However, at the beginning of a study, soon after administration of the pharmaceutical, the activity is confined to major vessels, including the vena cava, right ventricle, pulmonary artery and vein, left ventricle and aortic arch. This may simplify the modeling of the initial dynamic uptake considerably. For example, the regions of the heart may be treated as compartments during that period, as in the approach described in section 5.3.1 or in Sitek et al (2001) and Hu et al (2008). More complex approaches that model bolus propagation can also be employed in which the bolus is modeled as a delta function propagated over time and confined to these major vessels. This considerably reduces ambiguity caused by insufficient angular sampling in tomographic reconstruction of these studies.
Computer simulations (Herrero et al 1989) have demonstrated that the compartment modeling approach is more sensitive to timing discrepancies—especially discrepancies between the arterial input function and the tissue time–activity curve—than it is to most physical sources of error. Computer simulations have also been employed to investigate the necessary timing resolution and input function shape required to minimize bias and variance of estimated kinetic parameters (Ross et al 1997b).
6.6. Potential for improved temporal sampling resolution with new fast dedicated cardiac SPECT systems
While dedicated brain SPECT cameras have existed for some time, results with new dedicated cardiac SPECT systems are showing improved image quality, higher signal-to-noise ratios and improved energy resolution. The GE dedicated cardiac SPECT camera (Volokh et al 2008, Garcia et al 2008, Esteves et al 2008, Buechel et al 2010) uses a stationary detector that views the myocardium from multiple directions with multiple modular cameras, each collimated with a single pinhole (see figure 3(b)). The GE system has no moving parts but requires reconstruction of pinhole data, whereas the Spectrum Dynamics system (Sharir et al 2007, 2008, Berman 2007, Gambhir et al 2009, Erlandsson et al 2009) (see figure 4) has parallel geometry with individual collimator–detector modules rotating axially. The GE and Spectrum Dynamics designs offer significant advantages in comparison to conventional SPECT systems with parallel-hole collimators that capture the heart on only a small fraction of the available active detector area. These systems have the option to be placed in tandem with volumetric CT (VCT) scanners for attenuation correction and correlated diagnostic information. The GE and Spectrum Dynamics cameras use new CdZnTe (CZT) technology (Barber et al 1993, 1994, James et al 1995, Darambara and Todd-Pokropek 2002, Feichtinger et al 2004, Verger et al 2004, Brzymialkiewicz et al 2005, Luke and Amman 2007). This development has the potential to lessen scatter acceptance and improve contrast. Despite the advances in CZT fabrication technology, a CZT detector is still very expensive and the availability of large-volume and large-area (>2 cm2) CZT detectors continues to be limited.
6.7. Need for developing methods to analyze dynamic data for molecular imaging applications
Small-animal imaging studies associated with molecular imaging are rapidly expanding (Weissleder and Mahmod 2001, Massoud and Gambhir 2003). Dynamic SPECT has been used to evaluate myocardial fatty acid metabolism in rodents with hypertrophic cardiomyopathy (Hirai et al 2001, Hu et al 2005, 2008). For reviews of small animal imaging of single photon tracers, see Weber and Ivanovic (1999), Budinger (2002), Peremans et al (2005) and Beekman and van der Have (2007). The development of models, algorithms and data processing methods will become increasingly important. It has been demonstrated that SPECT imaging of small animals can be performed on commercial clinical imaging systems with specially designed pinhole collimators (Hirai et al 2001, Metzler et al 2005, Zhou et al 2005, Acton et al 2006, Forrer et al 2006, Hu et al 2008). This differs from dedicated small animal SPECT/CT systems (Furenlid et al 2004, Zeniya et al 2006, Vastenhouw and Beekman 2007). Molecular imaging facilitates the study of mechanisms and treatment of human diseases in animal models and permits longitudinal investigations that track physiologic changes over time in the same animal. The evaluation of radiopharmaceuticals in small animals is a major step in the process of the translational development of clinical radiotracers and requires new techniques of data acquisition and new algorithms for processing imaging data.
6.8. Advancements in patient care
The role of SPECT in radionuclide procedures for diagnosis and therapeutic planning continues to grow. Clinically, dynamic SPECT has been used for brain applications with specialized, dedicated brain scanners. However, the application of SPECT to imaging dynamic processes in the heart has not been fully realized. Dynamic SPECT has the potential to improve diagnostic accuracy over conventional SPECT with little, if any, increased cost. Continuing developments of mathematical and clinical tools, coupled with the developments of new agents and cameras, will make dynamic cardiac SPECT imaging clinically viable.
Acknowledgments
We want to thank the reviewers for their very helpful comments and suggestions, which helped make this a much more readable review. We also thank Sean Webb for editing the manuscript. We also want to thank Kathleen Gullberg for her helpful comments and edits. This work was supported by the National Institute of Biomedical Imaging and Bioengineering and the National Heart, Lung, and Blood Institute of the National Institutes of Health under grants R01EB007219 and R01HL50663, and by the Director, Office of Science, Office of Biological and Environmental Research, Medical Sciences Division of the US Department of Energy under contract DE-AC02-05CH11231.
Glossary
- 18F
Fluorine-18 is a radioisotope of fluorine that emits a positron with a half-life of 109 min and is tagged to pharmaceuticals for PET imaging
- 18FDG
2-Fluoro-2-deoxy-d-glucose (FDG) is a glucose analog used for metabolic imaging of brain function, heart metabolism and tumor growth
- 18F-DOPA
Fluorine-18-l-dihydroxyphenylalanine (18F-DOPA) is a PET tracer that is important in the diagnosis of motor disorders
- H215O
Radioactive water is used to measure perfusion of the brain and heart
- 123I
Iodine-123 is a radioisotope of iodine with a predominant gamma emission of 159 keV (half-life of 13.22 h) and is tagged to pharmaceuticals for SPECT imaging
- 123I-ADAM
[123I] [2-((2-((dimethylamino)methyl)phenyl)thio)-5-iodophenylamine (ADAM)] is a very promising imaging ligand for the detection of serotonin transporters (SERT) in human brain because of its high specificity for SERT
- 123I-altropane
2Beta-carbomethoxy-3beta-(4-fluorophenyl)-n-(1-iodoprop-1-en-3-yl) nortropane (IACFT, Altropane) is a cocaine analog with high affinity and selectivity for dopamine transporter (DAT) sites in the striatum. Dopamine transporter density declines in Parkinson’s disease
- 123I-beta-CIT
[123I]beta-CIT is a sensitive marker of dopaminergic degeneration, and the degree of striatal binding reduction in Parkinson’s disease correlates with disease severity
- 123I-BMIPP
123I-β-methyl-p-iodophenyl-pentadecanoic acid (BMIPP) is a modified long-chain fatty acid used for imaging metabolism in the myocardium. A methyl group on the β position of the carbon chain limits the complete oxidation of 123I-BMIPP
- 123I-FP-CIT
123I is labeled to N-o–fluoropropyl-2,f-carbomethoxy-3,B(4-iodophenyl) tropane to produce a radioligand with fast kinetics used for imaging of the dopamine transporter in brain disorders (such as Parkinson’s disease) with SPECT
- 123I-hippuran
I-131-sodium 2-[(2-iodobenzoyl)amino]acetate (hippuran) is a radioactive iodine compound used in diagnostic studies of renal function
- 123I-MIBG
[123I]metaiodobenzyl guanidine ([123I]MIBG) enables the quantification of postganglionic sympathetic cardiac innervation
- 123I-IMP
N-Isopropyl-4-[123I]iodoamphetamine is a lipophilic compound utilized for CBF measurements with SPECT
- 123I-iodorotenone
Novel radiolabeled rotenone analogs (labeled with tritium, carbon-11, fluorine-18 and iodine-123, -125) display efficient myocardial uptake and adequate myocardial retention for clinical evaluation of myocardial blood flow. Rotenone binds to complex I of the mitochondrial electron transport chain
- 123I-Iomazenil
[123I]Iomazenil ([123I]IMZ) is a ligand displaying high affinity for central-type benzodiazepine receptors, with high brain uptake and little nonspecific binding
- 123IPPA
Iodine-123-phenylpentadecanoic acid (123IPPA) is a synthetic long-chain fatty acid used for imaging fatty acid metabolism in the myocardium
- 13N
Nitrogen-13 is a radioisotope of nitrogen that emits a positron with a half-life of just under 10 min and is tagged to pharmaceuticals for PET imaging
- 13NH3
13N-labeled ammonia is used to measure perfusion of organs such as the heart and brain
- 15O
Oxygen-15 is a radioisotope of oxygen that emits a positron with a half-life of 2.25 min and is tagged to pharmaceuticals for PET imaging
- 99mTc
Technetium-99m is a metastable nuclear isomer of technetium-99 that decays to 99Tc, emitting a gamma ray of 140 keV with a half-life of 6 h, and is tagged to pharmaceuticals for SPECT imaging
- 99mTc-ECD
Technetium-99m ethyl cysteinate dimer (99mTc ECD) is used to image regional cerebral blood flow in patients
- 99mTc-HMPAO
Technetium-99m-labeled hexamethylpropyleneamineoxime (99mTc-HMPAO) is a gamma-emitting radionuclide imaging agent useful in the evaluation of regional cerebral blood flow. It has also been used to label leukocytes in the investigation of inflammatory bowel diseases
- 99mTc-MAG3
99mTc-Mercaptoacetyltriglycine (99mTc-MAG3) is a technetium-labeled radiopharmaceutical used in diagnostic studies of renal function
- 99mTc-N-NOET
99mTc-N-Ethoxy-N-ethyl-dithiocarbamato-nitrido is a neutral lipophilic 99mTc-labeled myocardial perfusion agent with a high first-pass extraction fraction
- 99mTc-sestamibi (99mTc-MIBI)
99mTc-hexakis-2-methoxy isobutyl isonitrile (99mTc-MIBI) is a synthetic molecule of the isonitrile family that diffuses through cell membranes and may preferentially accumulate within mitochondria (complex I). 99mTc-sestamibi is used for cardiac and tumor imaging
- 99mTc-teboroxime
99mTc-tris(1,2-bis(dimethoxyphosphino)ethane) is used for myocardial perfusion studies
- 99mTc-tetrofosmin
99mTc-tetrofosmin is a cardiac imaging agent useful in the diagnosis and localization of regions of reversible myocardial ischemia. 2-[bis(2-ethoxyethyl)phosphanyl]ethyl-bis(2-ethoxyethyl)phosphane (tetrofosmin) forms a complex with 99mTc to obtain the imaging agent 99mTc-tetrofosmin
- 99mTc-TRODAT
This is a 99mTc-labeled tropane derivative that binds to a dopamine transporter with high selectivity. Its chemical composition is [2-[[2-[[[3-(4-chlorophenyl)-8-methyl-8-azabicyclo[3,2,1]oct-2-yl]methyl](2-mercaptoethyl)amino]ethyl]amino] ethanethiolato(3-)-N2,N2′,S2,S2′]oxo-[1R-(exo-exo)] (TRODAT-1)
- 201Tl
Thallium-201 (half-life 73 h) is a radioisotope of thallium that decays by electron capture, emitting Hg x-rays (~70–80 keV) and photons of 135 and 167 keV in lesser abundance. Tl-20l is used to image the heart and behaves similarly to potassium in transport across cell membranes
- 133Xe
Xenon-133 is a radioisotope of xenon with a gamma emission of 81 keV and a half-life of 5.2 days. It is used in the study of pulmonary function and blood flow in organs such as the brain
- 133Xe-rCBF
Xenon regional cerebral blood flow (rCBF) is a method that uses the clearance of xenon-133 (133Xe) to quantify rCBF data
- Adenosine
A nucleoside composed of a molecule of adenine attached to a ribose sugar molecule. Adenosine is used as a vascular dilator in nuclear cardiac rest/stress studies. It is used to mimic vascular dilation experienced under cardiac stress
- B-spline
A function that has minimal support with respect to a given degree, smoothness and domain partition
- Blind estimation
The estimation of kinetic model parameters for an organ without knowledge of the input function by assuming that the input function is identical for all tissue regions
- Blood compartment
The blood compartment contains plasma and blood cells. Throughout this review, it has been assumed that this is one compartment with rapid exchange between plasma and blood cells
- Compartment
A compartment is a volume where the tracer is uniformly distributed. The compartment may be a physical space, such as an organ, or may represent a metabolic or bound state of the tracer
- Compartment model
A compartment model is a mathematical description (usually represented by a system of differential equations) of the interrelationships for the rate of exchange of a tracer between various compartments. The amount of tracer leaving a compartment is usually assumed to be proportional to the total amount in the compartment and the rate constant is the fraction of that compartment that leaves per unit time
- Coronary flow reserve
The ratio of coronary flow under maximal drug-induced coronary vasodilation to coronary flow under resting conditions
- Detector
A detector in the context of this review paper is most often a gamma ray detector optimally designed for imaging 140 keV photons. The detector consists of a lead collimator, a NaI(Tl) scintillator, photomultiplier tubes, and electronics for forming a picture of the emitting photons from the patient
- Diamox
Acetazolamide, sold under the trade name Diamox, is a carbonic anhydrase inhibitor that is used, among other things, to vasodilate the cerebral vascular system in order to evaluate brain blood circulation integrity
- Direct method of estimating kinetic model parameters
The kinetic model parameters are estimated directly from the projection data using a model that relates the kinetic compartment model to the projection data
- Distribution volume
See volume of distribution
- Extraction fraction
The extraction fraction is the fraction of a tracer that is extracted as blood flows through a tissue. It is the arterial concentration minus the venous concentration divided by the arterial concentration
- Extravascular compartment
The extravascular compartment contains intracellular and extracellular components (interstitial) that are physically outside vessels
- Factor
See factor basis function
- Factor analysis
See factor analysis of dynamic structures
- Factor analysis of dynamic structures
This is a method of estimation of factors and factor coefficients from a dynamic sequence
- Factor basis function
A factor basis function is a discrete temporal function describing the time course of activity concentration for a particular organ or tissue in the image. This time course has physiological interpretation so elements of the factor curves have to be non-negative
- Factor coefficients
These are coefficients of the linear combination of factors in the factor model. These coefficients have physiological interpretation and must be non-negative
- Factor model
In a factor model of the dynamic data it is assumed that the time course of each volume element (e.g. voxel) is a linear combination of usually not more than three or four factor basis functions
- 5D
Five-dimensional tomography accounts for the dimension of motion in addition to 3D space and time (e.g. lung and heart)
- Flow extraction product (flow times extraction)
Flow extraction product is the wash-in rate constant K1 in the one-compartment perfusion model. It corresponds to the flow times extraction of the tracer from the plasma
- Hyperemia
Hyperemia is the increase in blood flow to body tissues in response to the presence of metabolites and oxygen demand
- Interictal
Interictal is the period of time between epilepsy seizures
- Ischemia
Ischemia is a restriction in blood supply with probable resultant damage or dysfunction of body tissues
- Kinetic model parameters
Kinetic model parameters are the rate constants expressing the rate of exchange between compartments. For linear kinetics, the parameters are the linear coefficients in the system of differential equations that model the kinetics of the physiological process
- Level set method
The level set method is a numerical technique for tracking interfaces and involves numerical computations of curves and surfaces on a fixed Cartesian grid without their having to be parameterized
- Microsphere
A microsphere is a particle with a diameter in the micrometer range (typically 1 μm to 1000 μm (1 mm)). Microspheres can be manufactured from various natural and synthetic materials: glass, polymers and ceramics. In nuclear medicine, microspheres are labeled with various isotopes: 95Nb, 113Sn, 103Ru and 46Sc are common. Microspheres are generally used in animal studies. They are administered intraarterially and are trapped in the small capillaries of the tissue. The tissue of interest is counted later, typically in a well counter, to quantify absolute blood follow to that particular tissue of interest
- Multi-resolution
The spatial parameterization can involve multi-resolution (also referred to as multigridding in this review). This refers to a spatial parameterization where inside an organ boundary of interest the image intensity (tracer concentration) is represented by high-resolution voxels, and outside the organ the distribution is modeled with a coarser resolution
- Partition coefficient
The partition coefficient is the ratio of concentrations of a tracer in the blood to the concentration of the tracer in the tissue
- Positron emission tomography (PET)
This is a nuclear medicine imaging technique that produces a 3D image or picture of functional processes in the body. The imaging system detects pairs of gamma rays emitted at 180° from one another by a positron-emitting radionuclide (tracer), which is introduced into the body on a biologically active molecule
- Rate constant
In biochemical kinetics, a rate constant quantifies the speed of a biochemical reaction. In the present work, the rate constant times the concentration of a tracer in a compartment is equal to the rate of change of the concentration of the tracer from one compartment to another compartment (see compartment model)
- Redistribution
This is the process of a radiopharmaceutical changing its concentration distribution in different regions of an organ over time due to differences in wash-in and wash-out between regions
- Ring detector system versus system of multiple-gamma camera heads
A ring detector refers to a nuclear imaging system where the scintillation detectors are arranged in a ring surrounding the patient. A system of multiple-gamma camera heads refers to a SPECT system with multiple planar gamma cameras surrounding the patient. The cameras are rotated to obtain projection data
- Scintillation detector
A scintillation detector containing material such as NaI(Tl) emits photons when incoming gamma rays interact with the scintillation material. The emitted photons are converted into electronic signals usually by photomultiplier tubes
- Semi-conductor detector
A semi-conductor detector converts gamma rays directly to electronic signal using materials such as CdZnTe
- Semi-direct method of estimation of kinetic model parameters
Here, the time–activity curves for the blood and tissue are first estimated from the projection data. Then the kinetic model parameters are estimated from the estimated time–activity curves for the blood and tissue
- Single photon emission computed tomography (SPECT)
A nuclear medicine imaging technique that produces a 3D image or picture of functional processes in the body. The imaging system differs from PET in that it detects single gamma rays emitted by a radionuclide (tracer), which is introduced into the body on a biologically active molecule
- Sinogram
A sinogram is the distribution of projection data displayed as image intensity values with one Cartesian coordinate corresponding to the projection bin and the other to the angle of the projection
- Sinotimogram
A sinotimogram is a sinogram of a time-varying distribution corresponding to projection data represented by three coordinates—the angle, the projection bin and the time
- Slow versus fast camera rotation
Slow camera rotation refers to a SPECT system with a camera gantry rotation of approximately 5°s−1 versus a fast camera rotation of 24°s−1
- Time–activity curve
A time–activity curve is multiple data points at different times generated from a region of interest from the 3D distribution of the radiotracer
- Tracer
A tracer in the context of this review is a substance containing a radioisotope that is used for tracking the in vivo biochemical and physiological process
- Volume of distribution
The volume of distribution (VD), also known as distribution volume, is a term used to quantify the distribution of a tracer between the blood and the extravascular tissue in the body. It is defined as the volume of the extravascular space that would give the same tracer concentration as that in the blood. It is usually considered the same as the partition coefficient and is calculated from K1/k2
List of variables
- B(t)
activity concentration in the blood (Bq/cc)
- CEV(t)
activity concentration in some extravascular space
- VEV
volume of the extravascular space (compartment)
- P1
permeability coefficient for flux out of the capillary (cm min−1)
- P2
permeability coefficient for flux into the capillary (cm min−1)
- S
surface area of the capillary in the sampled voxel (cm2)
- K1
rate of exchange from blood into the extravascular compartment (units of min−1—volume per minute per extravascular volume VEV)
- k2
rate of exchange from extravascular compartment into blood (units of min−1—volume per minute per extravascular volume VEV)
- VD = λVEV
apparent distribution volume
- λ = CEV(∞)/B(∞)
partition coefficient (ratio of the tracer concentration in the tissue to that in the blood at equilibrium)
- AT = fv B(t) + (1 − fv )CEV(t)
model of the measured myocardial tissue activity concentration at time t in some region of interest (ROI)
- fv
vascular fraction of blood in the tissue
- (1 − fv)
fractional volume of the extravascular space
intermediate function for a one-compartment model, where CEV(t) = K1C(t)
- A(x, t) = Σm,n amnSm(x)Vmn(t)
activity concentration distribution as a function of space and time
- Sm(x)
spatial basis functions m = 1, …, M
- V mn(t)
temporal basis functions n = 1, …, N; m = 1, …, M
- amn
coefficients of the basis functions Sm(t)Vmn(t)
- P(d(t), t) = ∫χF[x, d(t)]A(x, t) dx
projection of the tracer distribution written as a function of the detector position d(t) and time t
- F [x, d(t)]
fraction of activity A(x, t) at spatial position x and time t that projects into the detector bin at position d(t)
- Um(d(t), t) = ∫χF[x, d(t)]Sm(x) dx
projection of the spatial basis function Sm(x) at the detector sampling position d(t)
projection of activity acquired over the time tk − Δtk to tk for the detector bin positions di (t)
- I
number of projection rays per projection angle
- K
number of time samples
- p = Fa
column vector of IK elements of projection data values
- F
system matrix with dimensions (IK) × (MN), where I is the total number of projection measurements, K is the number of time samples, M is the number of spatial basis functions and N is the number of temporal basis functions
elements of the system matrix F
- a
column vector with MN elements of basis coefficients
- Vmn(t) = Vn(t)
the temporal representation is independent of the spatial index m
- A(x, t) = Σm,n amnSm(x)Vn(t)
spatiotemporal representation of the activity where the temporal basis function Vn(t) is independent of the spatial basis function Sm(t)
temporal basis function for where the tissue region m is represented as a one-compartment model assuming
spatiotemporal representation of activity assuming a one-compartment model for each tissue region m
intermediate function for a one-compartment model, where
intermediate function for a one-compartment model, where assuming
temporal basis representation for the factor model where the temporal representation is independent of the spatial index n and for each index n there is a factor Fnk (k = 1, …, K) independent of the index m and χk (t) is a characteristic function with χk (t) = 1 for tk − Δtk ≤ t ≤ tk and 0 otherwise
- A(x, t) = Σm,n,k amnFnk Sm(x) χk (t)
spatiotemporal representation of the activity for the factor model
- χB (x)
characteristic function of the segmented blood input
- χG(x)
characteristic function of the segmented background
- χm(x)
characteristic function of the myocardial tissue region m
- g
ratio of the concentration in the blood to the concentration in the background tissue
blood input function expressed as a function of a set of temporal basis functions Vn(t).
one-compartment model for activity in the tissue-type m
rate of exchange from blood to extravascular compartment for tissue-type m
fraction of vasculature blood in tissue-type m
- θ(t)
projection angle sampled at precisely the time t
- UB(d(t), t) = ∫χχB (x)F[d(t), x] dx
fraction of segmented blood that projects at detector position d(t)
- Um(d(t), t) = ∫χχm(x)F[d(t), x] dx
fraction of segmented tissue-type m that projects at detector position d(t)
- UG(d(t), t) = ∫χχG(x)F[d(t), x] dx
fraction of segmented background that projects at detector position d(t)
fraction of blood activity acquired over a time period Δtk for detector bin at positions di (t)
fraction of background activity acquired over a time period Δtk for detector bin at positions di (t)
fraction of activity from segmented tissue-type m acquired over a time period Δtk for detector bin i at positions di (t)
fraction of activity of the extravascular response to a unit basis input function Vn(t) for tissue-type m acquired over a time period Δtk for detector bin at positions di (t)
References
- Aarsvold JN, Barrett HH, Chen J, Landesman AL, Milster TD, Patton DD, Roney TJ, Rowe RK, Seacat RH, III, Strimbu LM. Modular scintillation cameras: a progress report. Proc SPIE. 1988;914:319–25. [Google Scholar]
- Acton PD, Thomas D, Zhou R. Quantitative imaging of myocardial infarct in rats with high resolution pinhole SPECT. Int J Cardiovasc Imaging. 2006;22:429–34. doi: 10.1007/s10554-005-9046-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akahira H, Shirakawa H, Shimoyama H, Tsushima M, Arima H, Nigawara K, Funyu T, Sato M, Suzuki T. Dynamic SPECT evaluation of renal plasma flow using technetium-99m MAG3 in kidney transplant patients. J Nucl Med Technol. 1999;27:32–7. [PubMed] [Google Scholar]
- Allman KC, Berry J, Sucharski LA, Stafford KA, Petry NA, Wysor W, Schwaiger M. Determination of extent and location of coronary artery disease in patients without prior myocardial infarction by thallium-201 tomography with pharmacologic stress. J Nucl Med. 1992;33:2067–73. [PubMed] [Google Scholar]
- Alpert NM, Eriksson L, Chang JY, Bergstrom M, Litton JE, Correia JA, Bohm C, Ackerman RH, Taveras JM. Strategy for the measurement of regional cerebral blood flow using short-lived tracers and emission tomography. J Cereb Blood Flow Metab. 1984;4:28–34. doi: 10.1038/jcbfm.1984.4. [DOI] [PubMed] [Google Scholar]
- Bai C, Zeng GL, Gullberg GT. A slice-by-slice blurring model and kernel evaluation using the Klein-Nishina formula for 3D scatter compensation in parallel and converging beam SPECT. Phys Med Biol. 2000;45:1275–307. doi: 10.1088/0031-9155/45/5/314. [DOI] [PubMed] [Google Scholar]
- Barber DC. The use of principal components in the quantitative analysis of gamma camera dynamic studies. Phys Med Biol. 1980;25:283–92. doi: 10.1088/0031-9155/25/2/008. [DOI] [PubMed] [Google Scholar]
- Barber HB, Augustine FL, Barrett HH, Dereniak EL, Matherson KL, Meyers TJ, Perry DL, Venzon JE, Woolfenden JM, Young ET. Semiconductor arrays with multiplexer readout for gamma-ray imaging: results for a 48×48 Ge array. Nucl Instrum Methods Phys Res A. 1994;353:361–5. [Google Scholar]
- Barber HB, Barrett HH, Dereniak EL, Hartsough NE, Perry DL, Roberts PCT, Rogulski MM, Woolfenden JM, Young ET. Design for a high-resolution SPECT brain imager using semiconductor detector arrays and multiplexer readout. Phys Medica. 1993;9:135–45. [Google Scholar]
- Bard Y. Nonlinear Parameter Estimation. New York: Academic Press; 1974. [Google Scholar]
- Barrett HH, Wilson DW, Tsui BMW. Noise properties of the EM algorithm: I. Theory. Phys Med Biol. 1994;39:833–46. doi: 10.1088/0031-9155/39/5/004. [DOI] [PubMed] [Google Scholar]
- Bassingthwaighte JB, Raymond GM, Chan JI. In: Nuclear Cardiology: State of the Art and Future Directions. Zaret BL, Beller GA, editors. St Louis, MO: Mosby; 1993. pp. 3–23. [Google Scholar]
- Bauschke HH, Noll D, Celler A, Borwein JM. An EM algorithm for dynamic SPECT. IEEE Trans Med Imaging. 1999;18:252–61. doi: 10.1109/42.764899. [DOI] [PubMed] [Google Scholar]
- Beck JV, Arnold KJ. Parameter Estimation in Engineering and Science. New York: Wiley; 1977. [Google Scholar]
- Beekman F, Van Der Have F. The pinhole: gateway to ultra-high-resolution three-dimensional radionuclide imaging. Eur J Nucl Med Mol Imaging. 2007;34:151–61. doi: 10.1007/s00259-006-0248-6. [DOI] [PubMed] [Google Scholar]
- Beekman FJ, de Jong HWAM, van Geloven S. Efficient fully 3-D iterative SPECT reconstruction with Monte Carlo-based scatter compensation. IEEE Trans Med Imaging. 2002;21:867–77. doi: 10.1109/TMI.2002.803130. [DOI] [PubMed] [Google Scholar]
- Beekman FJ, Kamphuis C, Viergever MA. Improved SPECT quantitation using fully three-dimensional iterative spatially variant scatter response compensation. IEEE Trans Med Imaging. 1996;15:491–9. doi: 10.1109/42.511752. [DOI] [PubMed] [Google Scholar]
- Ben-Heim S, Kacperski K, Hain S, Van Gramberg D, Hutton BF, Erlandsson K, Sharir T, Roth N, Waddington WA, Berman DS, Ell PJ. Simultaneous dual-radionuclide myocardial perfusion imaging with a solid-state dedicated cardiac camera. Eur J Nucl Med Mol Imaging. 2010 doi: 10.1007/s00259-010-1441-1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Berman DS. Advances in instrumentation: dedicated cardiac SPECT cameras Syllabus ASNC2007. 12th Annual Scientific Session of the American Society of Nuclear Cardiology; San Diego, CA. 2007. pp. 60–7. [Google Scholar]
- Boutchko R, Sitek A, Gullberg GT. Three-dimensional reconstruction of dynamic cardiac SPECT data on a point cloud grid (abstract) J Nucl Med. 2006a;47:59. [Google Scholar]
- Boutchko R, Sitek A, Hu J, Reutter BW, Gullberg GT, Botvinick EH. Quantitative processing of cardiac dynamic patient data with slow camera rotation. 2006 IEEE Nuclear Science Symp. and Medical Imaging Conf; San Diego, CA. 2006b. pp. 2933–5. [Google Scholar]
- Boutchko R, Sitek A, Reutter BW, Gullberg GT. Adaptive optimization of point cloud grids for SPECT imaging. J Nucl Med. 2007;48:100P. [Google Scholar]
- Bremner JD, et al. Quantitation of benzodiazepine receptor binding with PET [11C]iomazenil and SPECT [123]iomazenil preliminary results of a direct comparison in healthy human subjects. Psychairty Res. 1999;91:79–91. doi: 10.1016/s0925-4927(99)00015-3. [DOI] [PubMed] [Google Scholar]
- Brownlee KA. Science and Engineering. 2. Malabar, FL: Robert E Kreiger; 1984. Statistical Theory and Methodology. [Google Scholar]
- Brzymialkiewicz CN, Tornai MP, McKinley RL, Bowsher JE. Evaluation of fully 3-D emission mammotomography with a compact cadmium zinc telluride detector. IEEE Trans Med Imaging. 2005;24:868–77. doi: 10.1109/tmi.2005.852501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Budinger TF. Advances in the instruments dedicated to imaging single photon radiopharmaceuticals. 6th Int. Symp. on Technetium in Chemistry and Nuclear Medicine; Bressanone, Italy. 4–7 September 2002; 2002. pp. 617–36. [Google Scholar]
- Budinger TF, Araujo L, Ranger N, Coxson P, Klein G, Huesman RH, Alavi A. Dynamic SPECT feasibility studies (abstract) J Nucl Med. 1991;32:955P. [Google Scholar]
- Buechel RR, et al. Ultrafast nuclear myocardial perfusion imaging on a new gamma camera with semiconductor technique: first clinical validation. Eur J Nucl Med Mol Imaging. 2010;4:773–8. doi: 10.1007/s00259-009-1375-7. [DOI] [PubMed] [Google Scholar]
- Buvat I, Benali H, Frouin F, Bazin J, Di Paola R. Target apex-seeking in factor analysis of medical sequences. Phys Med Biol. 1993;38:123–37. doi: 10.1088/0031-9155/38/1/009. [DOI] [PubMed] [Google Scholar]
- Calnon DA, Ruiz M, Vanzetto G, Watson DD, Beller GA, Glover DK. Myocardial uptake of 99mTc-N-NOET and 201Tl during dobutamine infusion. Comparison with adenosine stress. Circulation. 1999;100:1653–9. doi: 10.1161/01.cir.100.15.1653. [DOI] [PubMed] [Google Scholar]
- Carson RE. A maximum likelihood method for region-of-interest evaluation in emission tomography. J Comput Assist Tomogr. 1986a;10:654–63. doi: 10.1097/00004728-198607000-00021. [DOI] [PubMed] [Google Scholar]
- Carson RE. In: Positron Emission Tomography and Autoradiography: Principles and Applications for the Brain and Heart. Phelps ME, et al., editors. New York: Raven; 1986b. pp. 347–90. [Google Scholar]
- Carson RE, Huang SC, Green MV. Weighted integration method for local cerebral blood flow measurements with positron emission tomography. J Cereb Blood Flow and Metab. 1986;6:245–58. doi: 10.1038/jcbfm.1986.38. [DOI] [PubMed] [Google Scholar]
- Celler AM, Farncombe TH, Bever CA, Noll D, Maeght J, Harrop R, Lyster D. Performance of the dynamic single photon emission computed tomography (dSPECT) method for decreasing or increasing activity changes. Phys Med Biol. 2001;45:3525–43. doi: 10.1088/0031-9155/45/12/302. [DOI] [PubMed] [Google Scholar]
- Chang W, Ordonez C, Liang H, Holcomb M, Li Y, Liu J. C-SPECT/CT-2: design concepts and performance potential. J Nucl Med. 2008;49:124P. doi: 10.1109/TNS.2009.2028138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen C-T. Linear System Theory and Design. New York: Holt, Rinehart and Winston; 1984. [Google Scholar]
- Chen K, Huang SC, Yu DC. The effects of measurement errors in the plasma radioactivity curve on parameter estimation in positron emission tomography. Phys Med Biol. 1991;36:1183–200. doi: 10.1088/0031-9155/36/9/003. [DOI] [PubMed] [Google Scholar]
- Chen W, Silverman DHS. Advances in evaluation of primary brain tumors. Semin Nucl Med. 2008;38:240–50. doi: 10.1053/j.semnuclmed.2008.02.005. [DOI] [PubMed] [Google Scholar]
- Cherry SR, Sorenson JA, Phelps ME. Physics in Nuclear Medicine. 3. Philadelphia, PA: Saunders; 2003. [Google Scholar]
- Chiao P-C, Ficaro EP, Dayanikli F, Rogers WL, Schwaiger M. Compartmental analysis of technetium-99m-teboroxime kinetics employing fast dynamic SPECT at rest and stress. J Nucl Med. 1994a;35:1265–73. [PubMed] [Google Scholar]
- Chiao P-C, Rogers WL, Clinthorne NH, Fessler JA, Hero AO. Model-based estimation for dynamic cardiac studies using ECT. IEEE Trans Med Imaging. 1994b;13:217–26. doi: 10.1109/42.293914. [DOI] [PubMed] [Google Scholar]
- Chiao P-C, Rogers WL, Fessler JA, Hero AO. Model-based estimation with boundary side information or boundary regularization. IEEE Trans on Med Imaging. 1994c;13:227–34. doi: 10.1109/42.293915. [DOI] [PubMed] [Google Scholar]
- Choi Y, Hawkins RA, Huang SC, Gambhir SS, Brunken RC, Phelps MC, Schelbert HR. Parametric images of myocardial metabolic-rate of glucose generated from dynamic cardiac PET and 2-[f-18]fluoro-2-deoxy-d-glucose studies. J Nucl Med. 1991;32:733–8. [PubMed] [Google Scholar]
- Choi Y, Huang SC, Hawkins RA, Kuhle WG, Dahlbom M, Hoh CK, Czernin J, Phelps ME, Schelbert HR. A simplified method for quantification of myocardial blood-flow using nitrogen-13-ammonia and dynamic PET. J Nucl Med. 1993;34:488–97. [PubMed] [Google Scholar]
- Chua T, Kiat H, Germano G, Takemoto K, Fernandez G, Biasio Y, Friedman J, Berman D. Rapid back to back adenosine stress/rest technetium-99m teboroxime myocardial perfusion SPECT using a triple-detector camera. J Nucl Med. 1993;34:1485–93. [PubMed] [Google Scholar]
- Coates C. Isotope lung imaging. Curr Opin Radiol. 1992;4:79–86. [PubMed] [Google Scholar]
- Coxson P, Huesman RH, Borland L. Consequences of using a simplified kinetic model for dynamic PET data. J Nucl Med. 1997;38:660–7. [PubMed] [Google Scholar]
- Cunningham VJ, Jones T. Spectral analysis of dynamic PET studies. J Cereb Blood Flow Metab. 1993;13:15–23. doi: 10.1038/jcbfm.1993.5. [DOI] [PubMed] [Google Scholar]
- Darambara DG, Todd-Pokropek A. Solid state detectors in nuclear medicine. Q J Nucl Med. 2002;46:3–7. [PubMed] [Google Scholar]
- Dargham A, et al. SPECT measurement of benzodiazepine receptors in human brain with iodine-123-iomazenil: kinetic and equilbrium paradigms. J Nucl Med. 1994;35:228–38. [PubMed] [Google Scholar]
- de Berg M, Cheong O, van Kreveld M, Overmars M. Computational Geometry: Algorithms and Applications. New York: Springer; 2008. [Google Scholar]
- Defrise M, Townsend D, Geissbuhler A. Implementation of three-dimensional image reconstruction for multi-ring positron tomographs. Phys Med Biol. 1990;35:1361–72. doi: 10.1088/0031-9155/35/10/002. [DOI] [PubMed] [Google Scholar]
- Deutsch R. Estimation Theory. Englewood Cliffs, NJ: Prentice-Hall; 1965. [Google Scholar]
- Di Bella EV, Clackdoyle R, Gullberg GT. Blind estimation of compartmental model parameters. Phys Med Biol. 1999;44:765–80. doi: 10.1088/0031-9155/44/3/018. [DOI] [PubMed] [Google Scholar]
- Di Bella EV, Ross SG, Kadrmas DJ, Khare HS, Christian PE, McJames S, Gullberg GT. Compartmental modeling of technetium-99m-labeled teboroxime with dynamic single-photon emission computed tomography: comparison with static thallium-201 in a canine model. Invest Radiol. 2001;36:178–85. doi: 10.1097/00004424-200103000-00007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Di Bella EVR, Gullberg GT, Barclay AB, Eisner RL. Automated region selection for analysis of dynamic cardiac SPECT data. IEEE Trans Nucl Sci. 1997;44:1355–61. [Google Scholar]
- Di Paola R, Bazin JP, Aubry F, Auengo A, Cavailloles F, Herry Y, Kahn E. Handling of dynamic sequences in nuclear medicine. IEEE Trans Nucl Sci. 1982;29:1310–21. [Google Scholar]
- Dixon WJ, Massey FJ. Introduction to Statistical Analysis. New York: McGraw-Hill; 1969. [Google Scholar]
- Draper NR, Smith H. Applied Regression Analysis. New York: Wiley; 1966. [Google Scholar]
- Eberl S. Graduate School of Biomedical Engineering. Sydney, Australia: University of New South Wales; 2000. Quantitative physiologocal parameter estimation from dynamic single photon emission computed tomography (SPECT) [Google Scholar]
- Ercan MT, Ulutuncel N, Naldoken S. Evaluation of 99mTc-labelled alpha-d-glucose 1-phosphate aerosols for SPECT ventilation lung imaging. Nucl Med Commun. 1993;14:433–8. [PubMed] [Google Scholar]
- Erlandsson K, Kacperski K, van Gramberg D, Hutton BF. Performance evaluation of D-SPECT: a novel SPECT system for nuclear cardiology. Phys Med Biol. 2009;54:2635–49. doi: 10.1088/0031-9155/54/9/003. [DOI] [PubMed] [Google Scholar]
- Esteves FP, Raggi P, Folks RD, Keidar Z, Askew JW, Rispler S, O’Connor MK, Verdes L, Garcia EV. Novel ultrafast cardiac camera in myocardial perfusion SPECT: initial multicenter comparison with standard dual detector cameras. Proc. Annual Scientific Session of the American Society of Nuclear Cardiology—Late-Breaking Clinical Trials; Boston, MA. 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Farncombe T, Noll D, Maeght J, Harrop R. Dynamic SPECT imaging using a single camera rotation (dSPECT) IEEE Trans Nucl Sci. 1999;46:1055–61. [Google Scholar]
- Farncombe TH. Functional Dynamic SPECT Imaging Using a Single Slow Camera Rotation. Vancouver, BC, Canada: University of British Columbia; 2000. [Google Scholar]
- Farncombe TH, Blinder S, Celler A, Noll D, Maeght J, Harrop R. A dynamic expectation maximization algorithm for single camera rotation dynamic SPECT (dSPECT). 2000 IEEE Nuclear Science and Medical Imaging Conference ; Lyon, France. 2000. pp. 15/31–15/35. [Google Scholar]
- Farncombe TH, Celler AM, Bever CA, Noll D, Maeght J, Harrop R. The incorporation of organ uptake into dynamic SPECT (dSPECT) image reconstruction. IEEE Trans Nucl Sci. 2001;48:3–9. [Google Scholar]
- Farncombe TH, Feng B, King MA, Leppo JA. Investigating acquisition protocols for gated, dynamic myocardial imaging in PET and SPECT. 2003 IEEE Nuclear Science Symp. and Medical Imaging Conf. Record; Portland, Oregon. 19–25 October 2003; 2003a. pp. 3272–5. [Google Scholar]
- Farncombe TH, Feng B, Narayanan MV, Wernick MN, Celler AM, King MA, Leppo JA. Toward 5 dimensional SPECT reconstruction: determining myocardial blood flow and wall motion in a single study. In: Bizais Y, editor. Proc. 2003 International Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine; Saint Malo, France. 29 June–4 July 2003; 2003b. pp. 218–21. [Google Scholar]
- Feichtinger J, Schrottner T, Schwaiger M, Kindl P. Characterisation of selected cadmium–zinc–telluride detectors. Appl Radiat Isot. 2004;61:113–5. doi: 10.1016/j.apradiso.2004.03.030. [DOI] [PubMed] [Google Scholar]
- Feng B, Pretorius PH, Farncombe TH, Dahlberg ST, Narayanan MV, Wernick MN, Celler AM, King MA, Leppo JA. Imaging time-varying Tc-99m teboroxime localization and cardiac function simultaneously by five-dimensional (5D) gated-dynamic SPECT imaging and reconstruction (abstract) J Nucl Cardiol. 2003a;2:S11–S2. [Google Scholar]
- Feng B, Pretorius PH, Farncombe TH, Dahlberg ST, Narayanan MV, Wernick MN, Celler AM, Leppo JA, King MA. Simultaneous assessment of cardiac perfusion and function using 5-dimensional imaging with Tc-99m teboroxime. J Nucl Cardiol. 2006;13:354–61. doi: 10.1016/j.nuclcard.2006.03.004. [DOI] [PubMed] [Google Scholar]
- Feng D, Huang SC, Wang X. Models for computer simulation studies of input functions for tracer kinetic modelling with positron emission tomography. Int J Bio-Med Comput. 1993;32:95–110. doi: 10.1016/0020-7101(93)90049-c. [DOI] [PubMed] [Google Scholar]
- Feng H, Karl WC, Castanon DA. A curve evolution approach to object-based tomographic reconstruction. IEEE Trans Image Process. 2003b;12:44–57. doi: 10.1109/TIP.2002.806253. [DOI] [PubMed] [Google Scholar]
- Fessler J. Mean and variance of implicitly defined biased estimators (such as penalized maximum likelihood): applications to tomography. IEEE Trans Image Process. 1996;5:493–506. doi: 10.1109/83.491322. [DOI] [PubMed] [Google Scholar]
- Fick A. Sitzungsbder Phys-Med Geszu Wurzburg. 1870:36. [Google Scholar]
- Flamen P, Bossuyt A, Franken PR. Technetium-99m-tetrofosmin in dipyridamole-stress myocardial SPECT imaging: intraindividual comparison with technetium-99m-sestamibi. J Nucl Med. 1995;36:2009–15. [PubMed] [Google Scholar]
- Floyd CE, Jaszczak RJ, Coleman RE. Inverse Monte Carlo: a unified reconstruction algorithm for SPECT. IEEE Trans Nucl Sci. 1985;32:779–85. [PubMed] [Google Scholar]
- Fluckiger JU, Schabel MC, DiBella EVR. Model-based blind estimation of kinetic parameters in DCE-MRI. Magn Reson Med. 2009;62:1477–86. doi: 10.1002/mrm.22101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Formiconi AR. Least squares algorithm for region-of-interest evaluation in emission tomography. IEEE Trans Med Imaging. 1993;12:90–100. doi: 10.1109/42.222672. [DOI] [PubMed] [Google Scholar]
- Formiconi AR, Pupi A, Passeri A. Compensation of spatial system response in SPECT with conjugate gradient reconstruction technique. Phys Med Biol. 1989;34:69–84. doi: 10.1088/0031-9155/34/1/007. [DOI] [PubMed] [Google Scholar]
- Forrer F, Valkema R, Bernard B, Schramm NU, Hoppin JW, Rolleman E, Krenning EP, de Jong M. In vivoradionuclide uptake quantification using a multi-pinhole SPECT system to predict renal function in small animals. Eur J Nucl Med Mol Imaging. 2006;33:1214–7. doi: 10.1007/s00259-006-0178-3. [DOI] [PubMed] [Google Scholar]
- Frey EC, Tsui BMW. A practical method for incorporating scatter in a projector-backprojector for accurate scatter compensation in SPECT. IEEE Trans Nucl Sci. 1993;40:1107–16. [Google Scholar]
- Frey EC, Tsui BMW. A new method for modeling the spatially-variant, object-dependent scatter response function in SPECT. IEEE 1996 Nuclear Science Symp. and Medical Imaging Conf. Record; 1997. pp. 1082–6. [Google Scholar]
- Furenlid LR, Wilson DW, Chen YC, Kim H, Pietraski PJ, Crawford MJ, Barrett HH. FastSPECT II: a second-generation high-resolution dynamic SPECT imager. IEEE Trans Nucl Sci. 2004;51:631–5. doi: 10.1109/TNS.2004.830975. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gambhir SS, Berman DS, Ziffer J, Nagler M, Sandler M, Patton J, Hutton B, Sharir T, Ben Haim B, Ben Haim S. A novel high-sensitivity rapid-acquisition singe-photon cardiac imaging camera. J Nucl Med. 2009;50:635–43. doi: 10.2967/jnumed.108.060020. [DOI] [PubMed] [Google Scholar]
- Gambhir SS, Schwaiger M, Huang SC, Krivokapich J, Schelbert HR, Nienaber CA, Phelps ME. Simple noninvasive quantification method for measuring myocardial glucose utilization in humans employing positron emission tomography and fluorine-18 deoxyglucose. J Nucl Med. 1989;30:359–66. [PubMed] [Google Scholar]
- Garcia EV, Tsukerman L, Keidar Z. A new solid state, ultrafast cardiac multi-detector SPECT system (abstract) J Nucl Cardiol. 2008;l:15, S3. [Google Scholar]
- Genna S, Smith AP. The development of ASPECT, an annular single crystal bain camera for high efficency SPECT. IEEE Trans Nucl Sci. 1988;35:654–8. [Google Scholar]
- Gill SS, Patel NK, Hotton GR, O’Sullivan K, McCarter R, Bunnage M, Brooks DJ, Svendsen CN, Heywood P. Direct brain infusion of glial cell line-derived neurotrophic factor in Parkinson disease. Nat Med. 2003;9:589–95. doi: 10.1038/nm850. [DOI] [PubMed] [Google Scholar]
- Gioia G, Milan E, Giubbini R, DePace N, Heo J, Iskandrian AS. Prognostic value of tomographic rest-redistribution thallium 201 imaging in medically treated patients ventricular dysfunction. J Nucl Cardiol. 1996;3:150–6. doi: 10.1016/s1071-3581(96)90007-0. [DOI] [PubMed] [Google Scholar]
- Glick SJ, Penney BC, King MA, Byrne CL. Non iterative compensation for the distance-dependent detector response and photon attenuation in SPECT imaging. IEEE Trans Med Imaging. 1994;13:363–74. doi: 10.1109/42.293929. [DOI] [PubMed] [Google Scholar]
- Goffin K, Dedeurwaerdere S, van Laere K, van Paesschen W. Neuronuclear assessment of patients with epilepsy. Semin Nucl Med. 2008;38:227–39. doi: 10.1053/j.semnuclmed.2008.02.004. [DOI] [PubMed] [Google Scholar]
- Gravier E, Yang Y, Jin M. Tomographic reconstruction of dynamic cardiac image sequences. IEEE Trans Imaging Process. 2007;16:932–42. doi: 10.1109/tip.2006.891328. [DOI] [PubMed] [Google Scholar]
- Gullberg GT, Boutchko R, Sitek A, Reutter BW, Botvinick EH. Dynamic cardiac SPECT with slow camera rotation (abstract). 8th Int. Conf. of Nuclear Cardiology; Prague, Czech Republic. 29 April–2 May 2007.2007a. [Google Scholar]
- Gullberg GT, Budinger TF, Maltz JS. Dynamic cardiac SPECT imaging of photon tracers. American Society of Nuclear Cardiology 5th Invitational Conf; Bar Harbor, Maine. 2000. [Google Scholar]
- Gullberg GT, Hu J, Sitek A, Reutter BW, Huesman RH, Hanrahan SM, VanBrocklin HF, Brennan KM, Qi J, Feng Y. A study of changes in glucose and fatty acid metabolism in the heart as a function of hypertrophy in SHR models using microPET and microSPECT technology. 53rd Annual Meeting of the Society of Nuclear Medicine Conf. Record; San Diego, CA. 2006. p. 72. [Google Scholar]
- Gullberg GT, Huesman RH, DiBella EVR, Reutter BW. In: Clinical Nuclear Cardiology: State of the Art and Future Directions. 3. Zaret BL, Beller GA, editors. Philadelphia, PA: Elsevier/Mosby; 2004. pp. 117–39. [Google Scholar]
- Gullberg GT, Huesman RH, Malko JA, Pelc NJ, Budinger TF. An attenuated projector-backprojector for iterative SPECT reconstruction. Phy Med Biol. 1985;30:799–816. doi: 10.1088/0031-9155/30/8/004. [DOI] [PubMed] [Google Scholar]
- Gullberg GT, Huesman RH, Ross SG, DiBella EVR, Zeng GL, Reutter BW, Christian PE, Foresti SA. In: Nuclear Cardiology: State of the Art and Future Directions. Zaret BL, Beller GA, editors. St. Louis, MO: Mosby; 1999. pp. 137–87. [Google Scholar]
- Gullberg GT, Veress A, Sitek A, Boutchko R, Reutter BW, Huesman RH. Tomographic Reconstruction of Tracer Kinetics in the Heart Using a Spatiotemporal Mechanical Model. Proc. 9th Int. Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine; Lindau, Germany. 9–13 July 2007; 2007b. pp. 425–8. [Google Scholar]
- Gullberg GT, Zeng GL, Tsui BMW, Hagius JT. An iterative reconstruction algorithm for single photon emission computed tomography with cone beam geometry. Int J of Imag Sys & Techn. 1989;1:169–86. [Google Scholar]
- Gunn RN, Gunn SR, Cunningham VJ. Positron emission tomography compartmental models. J Cereb Blood Flow Metab. 2001;21:635–52. doi: 10.1097/00004647-200106000-00002. [DOI] [PubMed] [Google Scholar]
- Hamilton WF, Moore JW, Kinsman JM. Simultaneous determination of the pulmonary and systemic circulation times in man and of a figure related to the cardiac output. Am J Physiol. 1928;84:338–44. [Google Scholar]
- Hansen L, Marzilli LG, Eshima D, Malveaux EJ, Folks R, Taylor AJ. Evaluation of technetium-99m-triamide-mercaptide complexes designed to identify properties favoring renal tubular transport. J Nucl Med. 1994;35:1198–205. [PubMed] [Google Scholar]
- Hebber E, Oldenburg D, Farncombe T, Celler A. Direct estimation of dynamic parameters in SPECT tomography. IEEE Trans on Nucl Sci. 1997;44:2425–30. [Google Scholar]
- Heller GV, Calnon D, Dorbala S. Recent advances in cardiac PET and PET/CT myocardial perfusion imaging. J Nucl Cardiol. 2009;6:962–9. doi: 10.1007/s12350-009-9142-5. [DOI] [PubMed] [Google Scholar]
- Henkin RE, Bova D, Dillehay GL, Karesh SM, Halama JR, Wagner RH, Zimmer AM. Nuclear Medicine. 2. St Louis, MO: Mosby; 2006. [Google Scholar]
- Herrero P, Markham J, Bergmann SR. Quantitation of myocardial blood flow with H215O and positron emission tomography: assessment and error analysis of a mathematical approach. J Comput Assist Tomogr. 1989;13:862–73. doi: 10.1097/00004728-198909000-00021. [DOI] [PubMed] [Google Scholar]
- Hicks K, Ganti G, Mullani N, Gould KL. Automated quantitation of three-dimensional cardiac positron emission tomography for routine clinical use. J Nucl Med. 1989;30:1787–97. [PubMed] [Google Scholar]
- Hirai T, Nohara R, Ogoh S, Chen LG, Kataoka K, Li XH, Fujita M, Matsumori A, Taguchi S, Sasayama S. Serial evaluation of fatty acid metabolism in rats with myocardial infarction by pinhole SPECT. J Nucl Cardiol. 2001;8:472–81. doi: 10.1067/mnc.2001.114519. [DOI] [PubMed] [Google Scholar]
- Hirose Y, Ikeda Y, Higashi Y, Koga K, Hattori H, Kanno I, Miura Y, Miura S, Uemura K. A hybrid emission CT Headtome II. IEEE Trans Nucl Sci. 1982;29:520–5. [Google Scholar]
- Houston AS, Sampson WFD. A quantitative comparison of some FADS methods in renal dynamic studies using simulated and phantom data. Phys Med Biol. 1997;42:199–217. doi: 10.1088/0031-9155/42/1/013. [DOI] [PubMed] [Google Scholar]
- Hu J, Boutchko R, Sitek A, Reutter BW, Huesman RH, Gullberg GT. LBNL Report No LBNL-60008. Berkeley: Lawrence Berkeley National Lab; 2008. Dynamic molecular imaging of cardiac innervation using a dual head pinhole SPECT system. [Google Scholar]
- Hu J, Sitek A, Reutter BW, Huesman RH, Gullberg GT. A new approach of dynamic pinhole SPECT imaging for evaluation of sympathetic nervous system function in animal models of cardiac hypertrophy. Conf. Record of the 2005 IEEE Nuclear Science Symp. and Medical Imaging Conf; Puerto Rico. 2005. pp. 2542–6. [Google Scholar]
- Huang S-C, Phelps ME. In: Positron Emission Tomography and Autoradiography: Principles and Applications for the Brain and Heart. Phelps ME, et al., editors. New York: Raven; 1986. pp. 287–346. [Google Scholar]
- Hudson HM, Walsh C. Density deconvolution using spectral mixture models. Proc. 2nd World Congress of the IASC; Pasadena, CA. 1997. pp. 593–9. [Google Scholar]
- Huesman RH. A new fast algorithm for the evaluation of regions of interest and statistical uncertainty in computed tomography. Phys Med Biol. 1984;29:543–52. doi: 10.1088/0031-9155/29/5/007. [DOI] [PubMed] [Google Scholar]
- Huesman RH, Knittel BL, Mazoyer BM, Coxson PG, Salmeron EM, Klein GJ, Reutter BW, Budinger TF. BNL Report No LBNL-37621. Berkeley: Lawrence Berkeley National Laboratory; 1995. Notes on RFIT: a program for fitting compartment models to region-of-interest dynamic emission tomography data. [Google Scholar]
- Huesman RH, Mazoyer BM. Kinetic data analysis with a noisy input function. Phys Med Biol. 1987;32:973–82. doi: 10.1088/0031-9155/32/12/004. [DOI] [PubMed] [Google Scholar]
- Huesman RH, Reutter BW, Zeng GL, Gullberg GT. Kinetic parameter estimation from SPECT cone-beam projection measurements. Phys Med Biol. 1998;43:973–82. doi: 10.1088/0031-9155/43/4/024. [DOI] [PubMed] [Google Scholar]
- Hutton BF, Hudson HM, Beckman FJ. A clinical perspective of accelerated statistical reconstruction. Eur J Nucl Med. 1997;24:797–808. doi: 10.1007/BF00879671. [DOI] [PubMed] [Google Scholar]
- Iida H, Bloomfield PM, Miura S, Kanno I, Murakami M, Uemure K, Amano M, Tanaka K, Hirose Y, Yamamoto S. Effect of real-time weighted integration system for rapid calculation of functional images in clinical positron emission tomography. IEEE Trans Med Imag. 1995a;14:116–21. doi: 10.1109/42.370407. [DOI] [PubMed] [Google Scholar]
- Iida H, Eberl S. Quantitative assessment of regional myocardial blood flow with thallium-201 and SPECT. J Nucl Cardiol. 1998;5:313–31. doi: 10.1016/s1071-3581(98)90133-7. [DOI] [PubMed] [Google Scholar]
- Iida H, Eberl S, Kim K-M, Tamura Y, Ono Y, Nakazawa M, Sohlberg A, Zeniya T, Hayashi T, Watabe H. Absolute quantitation of myocardial blood flow with 201Tl and dynamic SPECT in canine: optimization and validation of kinetic modelling. Eur J Nucl Med Mol Imaging. 2008;35:896–905. doi: 10.1007/s00259-007-0654-4. [DOI] [PubMed] [Google Scholar]
- Iida H, Hayashida K, Nakazawa M, Katabuchi T. Multicenter evaluation of quantitative SPECT reconstruction package—QSPECT & DTARG. J Nucl Med. 2006;47:121. abstract. [Google Scholar]
- Iida H, Itoh H, Nakazawa M, Hatazawa J, Nishimura H, Onishi Y, Uemura K. Quantitative mapping of regional cerebral blood flow using iodine-123-IMP and SPECT. J Nucl Med. 1994;35:2019–30. [PubMed] [Google Scholar]
- Iida H, Rhodes CG, de Silva R, Araujo LI, Bloomfield PM, Lammertsma AA, Jones T. Use of the left ventricular time-activity curve as a noninvasive input function in dynamic oxygen-15-water positron emission tomography. J Nucl Med. 1992;33:1669–77. [PubMed] [Google Scholar]
- Iida H, Rhodes CG, de Silva R, Yamamoto Y, Araujo LI, Maseri A, Jones T. Myocardial tissue fraction correction for partial volume effects and measure of tissue viability. J Nucl Med. 1991;32:2169–75. [PubMed] [Google Scholar]
- Iida H, Takahashi A, Yoshikazu Tamura Y, Ono Y, Lammertsma AA. Myocardial blood flow: comparison of oxygen-15-water bolus injection, slow infusion and oxygen-15-carbon dioxide slow inhalation. J Nucl Med. 1995b;36:78–35. [PubMed] [Google Scholar]
- Iida I, Hayashi T, Eberl S, Saji H. Quantification in SPECT cardiac imaging. J Nucl Med. 2003;44:40–2. [PubMed] [Google Scholar]
- Iihara K, Okawa M, Hishikawa T, Yamada N, Fukushima K, Iida H, Miyamoto S. Slowly progressive neuronal death associated with postischemic hyperfusion in cortical laminar necrosis after high-flow bypass for a carotid intracavenous aneurysm (abstract) J Neurosurg. 2009;112:1254–8. doi: 10.3171/2009.9.JNS09345. [DOI] [PubMed] [Google Scholar]
- Imaizumi M, et al. Misery perfusion with split-dose I[123]iodoamphetamine single-photon emission computed tomography in patients with carotid occlusive diseases. Stroke. 2002;33:2217–23. doi: 10.1161/01.str.0000027638.19392.7e. [DOI] [PubMed] [Google Scholar]
- Ito K, Momose T, Kotaki H, Kojima Y, Yamamoto K, Katashima M, Sawada Y, Saski Y, Iga T. Pharmacokinetic analysis of benzodiazepine receptor binding of [123]iomazenil in human brain. Phar Res. 1997;8:999–1003. doi: 10.1023/a:1012188909100. [DOI] [PubMed] [Google Scholar]
- Jagust WJ, Haan MN, Reed BR, Eberling JL. Brain perfusion imaging predicts survival in Alzheimer’s disease. Neurology. 1998;51:1009–13. doi: 10.1212/wnl.51.4.1009. [DOI] [PubMed] [Google Scholar]
- Jagust WJ, Landau SM, Shaw LM, Trojanowski JQ, Koeppe RA, Reiman EM, Foster NL, Petersen RC, Weiner MW, Price JC, Mathis CA Alzheimer’s Disease Neuroimaging Initiative. Relationships between biomarkers in aging and dementia. Neurology. 2009;73:1193–9. doi: 10.1212/WNL.0b013e3181bc010c. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jagust WJ, Thisted R, Devous MD, VanHeertum R, Mayberg H, Jobst K, Smith D, Borys N. SPECT perfusion imaging in the diagnosis of Alzheimer’s disease: a clinical-pathological study. Neurology. 2001;56:950–6. doi: 10.1212/wnl.56.7.950. [DOI] [PubMed] [Google Scholar]
- James RB, Schlesinger TE, Lund J, Schieber M. In: Semiconductors for Room Temperature Nuclear Detector Applications Semiconductors and Semimetals. Schlesinger TE, James RB, editors. San Diego: Academic; 1995. pp. 335–81. [Google Scholar]
- Jin M, Yang Y, Wernick MN, King MA. Reconstruction of dynamic gated cardiac SPECT. Conf. Record of the 2005 IEEE Nuclear Science Symp. and Medical Imaging Conf; San Juan, Puerto Rico. 26–29 October 2005; 2005. pp. 2342–45. [Google Scholar]
- Jin M, Yang Y, Wernick MN, King MA. Fully 5D reconstruction of gated dynamic cardiac SPECT images. Conf. Record of the 2006 IEEE Nuclear Science Symp. and Medical Imaging Conf; San Diego, CA. 29 October–1 November; 2006a. pp. 3445–8. [Google Scholar]
- Jin M, Yang Y, Wernick MN, King MA. Motion-compensated dynamic image reconstruction for gated cardiac SPECT. Proc. of IEEE Int. Symp. Biomed Imaging: Macro to Nano; 2006b. pp. 267–70. [Google Scholar]
- Johnson G, III, Allton IL, Nguyen KN, Lauinger JM, Beju D, Pasqualini R, Duatti A, Okada RD. Clearance of technetium 99m N-NOET in normal, ischemic-reperfused, and membrane-disrupted myocardium. J Nucl Cardiol. 1996;3:42–54. doi: 10.1016/s1071-3581(96)90023-9. [DOI] [PubMed] [Google Scholar]
- Kadrmas DJ, Di Bella EVR, Huesman RH, Gullberg GT. Analytical propagation of errors in dynamic SPECT: estimators, degrading factors, bias, and noise. Phys Med Biol. 1999;44:1997–2014. doi: 10.1088/0031-9155/44/8/311. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas DJ, Frey EC, Karimi SS, Tsui BMW. Fast implementations of reconstruction-based scatter compensation in fully 3D SPECT image reconstruction. Phys Med Biol. 1998;43:857–74. doi: 10.1088/0031-9155/43/4/014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadrmas DJ, Gullberg GT. 4D maximum a posteriori reconstruction in dynamic SPECT using a compartmental model-based prior. Phys Med Biol. 2001;46:1553–74. doi: 10.1088/0031-9155/46/5/315. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kety SS, Schmidt CF. The nitrous oxide method for the quantitative determination of cerebral blood flow in man: theory, procedure and normal values. J Clin Invest. 1948;27:476–83. doi: 10.1172/JCI101994. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura K, et al. A new apparatus for brain imaging: four-head rotating gamma camera single-photon emission computed tomograph. J Nucl Med. 1990;31:603–9. [PubMed] [Google Scholar]
- King MA, Tsui BMW, Pan T-S. Attenuation compensation for cardiac single-photon emission computed tomographic imaging: part 1. Impact of attenuation and methods of estimating attenuation maps. J Nucl Cardiol. 1995;2:513–24. doi: 10.1016/s1071-3581(05)80044-3. [DOI] [PubMed] [Google Scholar]
- King MA, Tsui BMW, Pan T-S, Glick SJ, Soares EJ. Attenuation compensation for cardiac single-photon emission computed tomographic imaging: part 2. Attenuation compensation algorithms. J Nucl Cardiol. 1996;3:55–64. doi: 10.1016/s1071-3581(96)90024-0. [DOI] [PubMed] [Google Scholar]
- Komatani A, Sugai Y, Hosoya T. Development of ‘super rapid dynamic SPECT,’ and analysis of retention process of 99mTc-ECD in ischemic lesions: comparative study with 133Xe SPECT. Annals Nucl Med. 2004;18:489–94. doi: 10.1007/BF02984565. [DOI] [PubMed] [Google Scholar]
- Kordower JH. Neurodegeneration prevented by lentiviral vector delivery of GDNF in primate models of Parkinson’s disease. Science. 2000;290:767–73. doi: 10.1126/science.290.5492.767. [DOI] [PubMed] [Google Scholar]
- Kuhl DE, Edwards RQ. Image separation radioisotope scanning. Radiology. 1963;80:653–62. [Google Scholar]
- Kuhl DE, Edwards RQ, Ricci AR, Yacob RJ, Mich TJ, Alavi A. The Mark IV system for radionuclide computed tomography of the brain. Radiology. 1976;121:405–13. doi: 10.1148/121.2.405. [DOI] [PubMed] [Google Scholar]
- Kung HF, Kung MP, Choi SR. Radiopharmaceuticals for single-photon emission computed tomography brain imaging. Semin Nucl Med. 2003;33:2–13. doi: 10.1053/snuc.2003.127296. [DOI] [PubMed] [Google Scholar]
- Laforest R, Sharp TL, Engelbach JA, Fettig NM, Herrero P, Kim J, Lewis JS, Rowland DJ, Tai YC, Welch M. Measurement of input functions in rodents: challenges and solutions. J Nucl Med Biol. 2005;7:679–85. doi: 10.1016/j.nucmedbio.2005.06.012. [DOI] [PubMed] [Google Scholar]
- Lanczos C. Applied Analysis. Englewood Cliffs, NJ: Prentice-Hall; 1956. [Google Scholar]
- Lange K, Carson RE. EM reconstruction algorithms for emission and transmission tomography. J Comput Assist Tomogr. 1984;8:306–16. [PubMed] [Google Scholar]
- Laurette I, Zeng GL, Welch A, Christian PE, Gullberg GT. A three-dimensional ray-driven attenuation, scatter and geometric response correction technique for SPECT in inhomogeneous media. Phys Med Biol. 2000;45:3459–80. doi: 10.1088/0031-9155/45/11/325. [DOI] [PubMed] [Google Scholar]
- Leppo JA, DePuey EG, Johnson LL. A review of cardiac imaging with sestamibi and teboroxime. J Nucl Med. 1991;32:2012–22. [PubMed] [Google Scholar]
- Leppo JA, Meerdink D. Comparison of the myocardial uptake of a technetium-labeled isonitrile analogue and thallium. J Circ Res. 1989;65:632–9. doi: 10.1161/01.res.65.3.632. [DOI] [PubMed] [Google Scholar]
- Levitan E, Herman GT. A maximum a posteriori probability expectation maximization algorithm for image reconstruction in emission tomograpjy. IEEE Trans Med Imaging. 1987;6:185–92. doi: 10.1109/TMI.1987.4307826. [DOI] [PubMed] [Google Scholar]
- Liang Z, Turkington TG, Gilland DR, Jaszczak RJ, Coleman RE. Simultaneous compensation for attenuation, scatter, and detector response for SPECT reconstruction in three dimensions. Phys Med Biol. 1992;37:587–603. doi: 10.1088/0031-9155/37/3/007. [DOI] [PubMed] [Google Scholar]
- Lim Y, et al. Triangular SPECT system for 3D total organ volume imaging: design concept and preliminary results. IEEE Trans Nucl Sci. 1985;32:741–7. [Google Scholar]
- Limber MA, Limber MN, Celler A, Barney JS, Borwein JM. Direct reconstruction of functional parameters for dynamic SPECT. IEEE Trans Nucl Sci. 1995;42:1249–56. [Google Scholar]
- Lodge MA, Braess H, Mahmoud F, Suh J, Englar N, Geyser-Stoops S, Jenkins J, Bacharach SL, Dilsizian V. Developments in nuclear cardiology: transition from single photon emission computed tomography to positron emission tomography-computed tomography. J Invasive Cardiol. 2005;17:491–6. [PubMed] [Google Scholar]
- Logan J. Graphical analysis of PET data applied to reversible and irreversible tracers. Nucl Med Biol. 2000;27:661–70. doi: 10.1016/s0969-8051(00)00137-2. [DOI] [PubMed] [Google Scholar]
- Luke PN, Amman M. Room-temperature replacement for Ge detectors—are we there yet? IEEE Trans Nucl Sci. 2007;54:834–42. [Google Scholar]
- Maguire RP, Calonder C, Leenders KL. An investigation of multiple time graphical analysis applied to projection data: theory and validation. J Comput Assist Tomogr. 1997;21:327–31. doi: 10.1097/00004728-199703000-00033. [DOI] [PubMed] [Google Scholar]
- Maltz JS. Direct recovery of regional tracer kinetics from temporally inconsistent dynamic ECT projections using dimension-reduced time-activity basis. Phys Med Biol. 2000a;45:3413–29. doi: 10.1088/0031-9155/45/11/322. [DOI] [PubMed] [Google Scholar]
- Maltz JS. Region resolvability versus noise level characteristics for joint spatial and kinetic parameter estimation in inconsistent projection dynamic ECT. IEEE Trans Nucl Sci. 2000b;47:1143–8. [Google Scholar]
- Maltz JS. Optimal time-activity basis selection for exponential spectral analysis: application to the solution of large dynamic emission tomographic reconstruction problems. IEEE Trans Nucl Sci. 2001;48:1452–64. [Google Scholar]
- Maltz JS. Parsimonious basis selection in exponential spectral analysis. Phys Med Biol. 2002;47:2341–65. doi: 10.1088/0031-9155/47/13/311. [DOI] [PubMed] [Google Scholar]
- Maltz JS, Budinger TF. Multiresolution constrained least-squares algorithm for direct estimation of time activity curves from dynamic ECT projection data. Proc SPIE. 2000;3979:586–98. [Google Scholar]
- Maltz JS, Polak E, Budinger TF. Multistart optimization algorithm for joint spatial and kinetic parameter estimation from dynamic ECT projection data. IEEE Nuclear Science Symp. and Medical Imaging Conf.; Toronto, Canada. 1998. pp. 1567–73. [Google Scholar]
- Marshall RC, Powers-Risius P, Reutter BW, Taylor SE, VanBrocklin HF, Huesman RH, Budinger TF. Kinetic analysis of 125I-iodorotenone as a deposited myocardial flow tracer: comparison with 99mTc-sestamibi. J Nucl Med. 2001;42:272–81. [PubMed] [Google Scholar]
- Massoud TF, Gambhir SS. Molecular imaging in living subjects; seeing fundamental biological processes in a new light. Genes Dev. 2003;17:545–80. doi: 10.1101/gad.1047403. [DOI] [PubMed] [Google Scholar]
- Matthews J, Bailey D, Price P, Cunningham V. The direct calculation of parametric images from dynamic PET data using maximum-likelihood iterative reconstruction. Phys Med Biol. 1997;42:1155–73. doi: 10.1088/0031-9155/42/6/012. [DOI] [PubMed] [Google Scholar]
- Maublant JC, Marcaggi X, Lusson J-R, Boire J-Y, Cauvin J-C, Jacob P, Veyre A, Cassagnes J. Comparison between thallium-201 and technetium-99m methoxyisobutyl isonitrile defect size in single-photon emission computed tomography at rest, exercise and redistribution in coronary artery disease. Am J Cardiol. 1992;69:183–7. doi: 10.1016/0002-9149(92)91302-k. [DOI] [PubMed] [Google Scholar]
- Maublant JC, Moins N, Gachon P, Renoux M, Zhang Z, Veyre A. Uptake of technetium-99m-teboroxime in cultured myocardial cells: comparison with thallium-201 and technetium-99m-sestamibi. J Nucl Med. 1993;34:255–9. [PubMed] [Google Scholar]
- Maunoury C, Chen CC, Chua KB, Thompson CJ. Quantification of left ventricular function with thallium-201 and technetium-99m-sestamibi myocardial gated SPECT. J Nucl Med. 1996;38:958–61. [PubMed] [Google Scholar]
- McCarthy AW, Miller MM. Maximum likelihood SPECT in clinical computation times using mesh-connected parallel computers. IEEE Trans Med Imaging. 1991;10:426–36. doi: 10.1109/42.97593. [DOI] [PubMed] [Google Scholar]
- Meier P, Zierler KL. On the theory of the indicator-dilution method for measurement of blood flow and volume. J Appl Physiol. 1954;6:731–44. doi: 10.1152/jappl.1954.6.12.731. [DOI] [PubMed] [Google Scholar]
- Meikle SR, Hutton BF, Bailey DL. A transmission-dependent method for scatter correction in SPECT. J Nucl Med. 1994;35:360–67. [PubMed] [Google Scholar]
- Meikle SR, Matthews J, Cunningham VJ, Bailey DL, Livieratos L, Jones T, Price P. Parametric image reconstruction using spectral analysis of PET projection data. Phys Med Biol. 1998;43:651–66. doi: 10.1088/0031-9155/43/3/016. [DOI] [PubMed] [Google Scholar]
- Meikle SR, Matthews JC, Cunningham VJ, Bailey DL, Livieratos L, Jones T, Price P. Spectral analysis of PET projection data. 1996 IEEE Nuclear Science Symp. and Medical Imaging Conf; Anaheim, CA. 1996. pp. 1888–92. [Google Scholar]
- Metzler SD, Jaszczak RJ, Patil NH, Vemulapalli S, Akabani G, Chin BB. Molecular imaging of small animals with a triple-head SPECT system using pinhole collimation. IEEE Trans Med Imaging. 2005;24:853–62. doi: 10.1109/tmi.2005.848357. [DOI] [PubMed] [Google Scholar]
- Meyer JH. Applying neuroimaging ligands to study major depressive disorder. Semin Nucl Med. 2008;38:287–304. doi: 10.1053/j.semnuclmed.2008.02.007. [DOI] [PubMed] [Google Scholar]
- Moore SC, Mueller SP. Inversion of the 3D radon transform for a multidetector, point-focused SPECT brain scanner. Phys Med Biol. 1986;31:207–21. doi: 10.1088/0031-9155/31/3/001. [DOI] [PubMed] [Google Scholar]
- Moriwaki H, Matsumoto M, Hashikawa K, Oku N, Ishida M, Seike Y, Fukuchi K, Hori M, Nishimura T. Iodine-123-iomazenil and iodine-123-lodoamphetamine SPECT in major cerebral artery occlusive disease. J Nucl Med. 1998;39:1348–53. [PubMed] [Google Scholar]
- Nakajima K, Taki J, Bunko H, Matsudaira M, Muramori A, Matsunari I, Hisada K, Ichihara T. Dynamic acquisition with a three-headed SPECT system: application to technetium-99m-SQ30217 myocardial imaging. J Nucl Med. 1991;32:1273–7. [PubMed] [Google Scholar]
- Nakamura M, Suzuki Y, Kobayashi S. A method for recovering physiological components from dynamic radionuclide images using the maximum entropy principle: a numerical investigation. IEEE Trans Biomed Eng. 1989;36:906–16. doi: 10.1109/10.35299. [DOI] [PubMed] [Google Scholar]
- Nakano S, Kinoshita K, Jinnouchi S, Hoshi H, Watanabe K. Dynamic SPECT with iodine-123 IMP in meningiomas. J Nucl Med. 1988;29:1627–32. [PubMed] [Google Scholar]
- Narra RK, Feld RT, Nunn AD. Absorbed radiation dose to humans from technetium-99m-teboroxime. J Nucl Med. 1992;33:88–93. [PubMed] [Google Scholar]
- Nichols TE, Qi J, Leahy RM. Continuous time dynamic PET imaging using list mode data. In: Kuba A, et al., editors. Information Processing in Medical Imaging: Proc. 16th Int. Conf; 1999. pp. 98–111. [Google Scholar]
- Nijran KS, Barber DC. Towards automatic analysis of dynamic radionuclide studies using principal-components factor analysis. Phys Med Biol. 1985;30:1315–25. doi: 10.1088/0031-9155/30/12/005. [DOI] [PubMed] [Google Scholar]
- Ogasawara K, Konno H, Yasuda S, Yukawa H, Ogawa A. Very early and standard Tc-99m ethyl cysteinate dimer SPECT imaging in a patient with reperfusion hyperemia after acute cerebral embolism. Clin Nucl Med. 2002a;27:105–8. doi: 10.1097/00003072-200202000-00006. [DOI] [PubMed] [Google Scholar]
- Ogasawara K, Ogawa A, Ezura M, Konno H, Doi M, Kuroda K, Yoshimoto T. Dynamic and static 99mTc-ECD SPECT imaging of subacute cerebral infarction: comparison with 133Xe SPECT. J Nucl Med. 2001a;42:543–7. [PubMed] [Google Scholar]
- Ogasawara K, Ogawa A, Koshu K, Konno H, Suzuki M, Yoshimoto T. Hypofixation and hyperfixation of 99mTc-hexamethyl propyleneamine oxime in subacute cerebral infarction. J Nucl Med. 2000;41:795–9. [PubMed] [Google Scholar]
- Ogasawara K, Yasuda S, Beppu T, Kobayashi M, Doi M, Kuroda K, Ogawa A. Brain PET and technetium-99m-ECD SPECT imaging in Lhermitte-Duclos disease. Neuroradiology. 2001b;43:993–6. doi: 10.1007/s002340100617. [DOI] [PubMed] [Google Scholar]
- Ogasawara K, Yasuda S, Yukawa H, Yamagata M, Kin M, Ogawa A. Atypical finding of brain Tc-99m-ECD SPECT imaging in herpes simplex encephalitis. Ann Nucl Med. 2002b;5:347–50. doi: 10.1007/BF02988619. [DOI] [PubMed] [Google Scholar]
- Okizakia A, Shuke N, Sato J, Sasaki T, Hasebe N, Kikuchi K, Aburano T. A compartment model analysis for investigation of myocardial fatty acid metabolism in patients with hypertrophic cardiomyopathy. Nucl Med Commun. 2007;28:726–35. doi: 10.1097/MNM.0b013e32828da1c7. [DOI] [PubMed] [Google Scholar]
- Onishi Y, Yonekura Y, Nishizawa S, Tanaka F, Okazawa H, Ishizu K, Fujita T, Konishi J, Mukai T. Noninvasive quantification of iodine-123-Iomazenil SPECT. J Nucl Med. 1996;37:374–8. [PubMed] [Google Scholar]
- Ordonez C, Sheng J, Li Y, Chang W. Simulated imaging studies of C-SPECT/CT. J Nucl Med. 2008;49(Suppl):407P. [Google Scholar]
- Osher S, Fedkiw RP. Level set methods: an overview and some recent results. J Comput Phys. 1999;169:463–502. [Google Scholar]
- Osher S, Sethian J. Fronts propagation with curvature-dependent speed: algorithms based on Hamilton-Jacobi formulations. J Comput Phys. 1988;79:12–49. [Google Scholar]
- Patlak CS, Blasberg RG. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data: generalizations. J Cereb Blood Flow Metab. 1985;5:584–90. doi: 10.1038/jcbfm.1985.87. [DOI] [PubMed] [Google Scholar]
- Patlak CS, Blasberg RG, Fenstermacher JD. Graphical evaluation of blood-to-brain transfer constants from multiple-time uptake data. J Cereb Blood Flow Metab. 1983;3:1–7. doi: 10.1038/jcbfm.1983.1. [DOI] [PubMed] [Google Scholar]
- Patton JA, Slomka PJ, Germano G, Berman DS. Recent technologic advances in nuclear cardiology. J Nucl Cardiol. 2007;14:501–13. doi: 10.1016/j.nuclcard.2007.06.003. [DOI] [PubMed] [Google Scholar]
- Penney BC, King MA, Knesaurek K. A projector, back-projector pair which accounts for the two-dimensional depth and distance dependent blurring in SPECT. IEEE Trans Nucl Sci. 1990;37:681–86. [Google Scholar]
- Peremans K, Cornelissen B, Van Den Bossche B, Audenaert K, Van de Wiele C. A review of small animal imaging planar and pinhole SPECT gamma camera imaging. Vet Radiol Ultrasound. 2005;46:162–70. doi: 10.1111/j.1740-8261.2005.00031.x. [DOI] [PubMed] [Google Scholar]
- Phelps ME, Mazziotta JC, Schelbert HR. Positron Emission Tomography and Autoradiography: Principles and Applications for the Brain and Heart. New York: Raven; 1986. [Google Scholar]
- Pimlott SL, Ebmeier MA. SPECT imaging in dementia. Brit J Radiol. 2007;80:S153–9. doi: 10.1259/bjr/89285735. [DOI] [PubMed] [Google Scholar]
- Pretorius PH, King MA, Tsui BMW, LaCroix KJ, Xia W. A mathematical model of motion of the heart for use in generating source and attenuation maps for simulating emission imaging. Med Phys. 1999;26:2323–32. doi: 10.1118/1.598746. [DOI] [PubMed] [Google Scholar]
- Qi J. A unified noise analysis for iterative image estimation. Phys Med Biol. 2003;48:3505–19. doi: 10.1088/0031-9155/48/21/004. [DOI] [PubMed] [Google Scholar]
- Qi J, Leahy RM. Resolution and noise properties of MAP reconstruction for fully 3D PET. IEEE Trans Med Imaging. 2000;19:493–506. doi: 10.1109/42.870259. [DOI] [PubMed] [Google Scholar]
- Reich JG. In: Kinetic Data Analysis: Design and Analysis of Enzyme and Pharmacokinetic Experiments. Endrenyi L, editor. New York: Plenum; 1981. pp. 39–60. [Google Scholar]
- Resnick SM, Sojkova J, Zhou Y, An Y, Ye W, Holt DP, Dannals RF, Mathis CA, Klunk WE, Ferrucci L, Kraut MA, Wong DF. Longitudinal cognitive decline is associated with fibrillar amyloid-beta measured by [11C] PiB. Neurology. 2010;74:807–15. doi: 10.1212/WNL.0b013e3181d3e3e9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Reutter BW, Gullberg GT, Boutchko R, Balakrishnan K, Botvinick EH, Huesman RH. Fully 4-D dynamic cardiac SPECT image reconstruction using spatiotemporal B-spline voxelization. 2007 IEEE Nuclear Science Symp. and Medical Imaging Conf; Honolulu, HI. 2007a. pp. 4217–21. [Google Scholar]
- Reutter BW, Gullberg GT, Boutchko R, Balakrishnan K, Botvinick EH, Huesman RH. Regularized least-squares SPECT image reconstruction using multiresolution spatial B-splines and a negativity penalty. 9th Int. Meeting on Fully Three-Dimensional Image Reconstruction in Radiology and Nuclear Medicine; Lindau, Germany. 2007b. pp. 305–8. [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Kinetic parameter estimation from attenuated SPECT projection measurements. IEEE Trans Nucl Sci. 1998a;45:3007–13. doi: 10.1088/0031-9155/43/4/024. [DOI] [PubMed] [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Kinetic parameter estimation from dynamic cardiac patient SPECT projection measurements. 1998 IEEE Nuclear Science Symp. and Medical Imaging Conf. Record; Toronto, Ontario, Canada. 8–14 November; 1998b. pp. 1953–8. [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Direct least squares estimation of spatiotemporal distributions from dynamic SPECT projections using a spatial segmentation and temporal B-splines. IEEE Trans Med Imaging. 2000;19:434–50. doi: 10.1109/42.870254. [DOI] [PubMed] [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Effects of temporal modeling on the statistical uncertainty of spatiotemporal distributions estimated directly from dynamic cone-beam SPECT projections. Phys Med Biol. 2002;47:2673–83. doi: 10.1088/0031-9155/47/15/309. [DOI] [PubMed] [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Effects of scatter modeling on time-activity curves estimated directly from dynamic SPECT projections. 2003 IEEE Nuclear Science Symp. and Medical Imaging Conf. Record; Portland, OR. 19–25 October 2003.2003. [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Accuracy and precision of compartmental model parameters obtained from directly estimated dynamic SPECT time-activity curves. IEEE Trans Nucl Sci. 2004a;51:170–6. [Google Scholar]
- Reutter BW, Gullberg GT, Huesman RH. Spatiotemporal scatter models for dynamic SPECT. Conf. Record of the 2004 IEEE Nuclear Science Symp. and Medical Imaging Conf; Rome, Italy. 2004b. pp. 4092–6. [Google Scholar]
- Reutter BW, Gullberg GT, Sitek A, Boutchko R, Botvinick EH, Huesman RH. Modeling spatial smoothness in fully 3D SPECT image reconstruction using multiresolution B-splines. 2006 IEEE Nuclear Science Symp. and Medical Imaging Conf; San Diego, CA. 2006. pp. 1757–61. [Google Scholar]
- Reutter BW, Klein GJ, Huesman RH. Automated 3D segmentation of respiratory-gated PET transmission images. IEEE Trans Nucl Sci. 1997;44:2473–6. [Google Scholar]
- Reutter BW, Oh S, Gullberg GT, Huesman RH. Improved quantitation of dynamic SPECT via fully 4D joint estimation of compartmental models and blood input function directly from projections. Conf. Record of the 2005 IEEE Nuclear Science Symp. and Medical Imaging Conf; Puerto Rico. 2005. pp. 2337–41. [Google Scholar]
- Riabkov DY, DiBella EVR. Blind identification of the kinetic parameters in three-compartment models. Phys Med Biol. 2004;49:639–64. doi: 10.1088/0031-9155/49/5/001. [DOI] [PubMed] [Google Scholar]
- Rogers WL, Clinthorne NH, Shao L, Chiao P, Ding Y, Stamos JA, Koral KF. SPRINT II: a second-generation single photon ring tomograph. IEEE Trans Med Imaging. 1988;MI-7:291–7. doi: 10.1109/42.14511. [DOI] [PubMed] [Google Scholar]
- Rogers WL, Linthorne NH, Stramos JA, Koral KF, Mayans R, Keyes JWJ, Williams JJ, Snapp WP, Knoll GF. SPRINT: a stationary detector single photon ring tomograph for brain imaging. IEEE Trans Med Imaging. 1982;MI-1:63–8. doi: 10.1109/TMI.1982.4307549. [DOI] [PubMed] [Google Scholar]
- Rose CP, Goresky CA, Bach GG. The capillary and sarcolemmal barriers in the heart. Circ Res. 1977;41:515–33. doi: 10.1161/01.res.41.4.515. [DOI] [PubMed] [Google Scholar]
- Rosenspire KC, Rumsey WL, Jurisson S, Hirth W, Narra RK. [99mTc] teboroxime and [99mTc]Cl(DMG)3B2MP: binding characteristics and metabolism of two [99mTc]BATOs in blood and tissues. Nucl Med Biol. 1993;20:395–400. doi: 10.1016/0969-8051(93)90069-7. [DOI] [PubMed] [Google Scholar]
- Ross SG, Gullberg GT, Huesman RH. The effect of heart motion on kinetic parameter estimates for dynamic cardiac SPECT. IEEE Trans Nucl Sci. 1997a;44:1409–16. [Google Scholar]
- Ross SG, Welch A, Gullberg GT, Huesman RH. An investigation into the effect of input function shape and image acquisition interval on estimates of washin for dynamic cardiac SPECT. Phys Med Biol. 1997b;42:2193–213. doi: 10.1088/0031-9155/42/11/014. [DOI] [PubMed] [Google Scholar]
- Rowe RK, Aarsvold JN, Barrett HH, Chen JC, Klein WP, Moore BA, Pang IR, Patton DD, White TA. A stationary hemispherical SPECT imager for three-dimensional brain imaging. J Nucl Med. 1993;34:474–80. [PubMed] [Google Scholar]
- Rowe RK, Aarsvold JN, Barrett HH, Chen J, Hall JN, Landesman AL, Mar LS, Milster TD, Moore BA, Patton DD, Roney TJ. The design and implementation of modular SPECT imaging systems. In: Todd-Pokropek A, Viergever MA, editors. Medical Images: Formation, Handling and Evaluation(NATO-ASI Series F. Vol. 98. Portugal: Springer; 1992. [Google Scholar]
- Rudzinski W, Swiat M, Tomaszewski M, Krejza J. Cerebral hemodynamics and investigation of cerebral blood flow regulation. Nucl Med Rev. 2007;10:29–42. [PubMed] [Google Scholar]
- Rumsey WL, Rosenspire KC, Nunn AD. Myocardial extraction of teboroxime: effects of teboroxime interaction with blood. J Nucl Med. 1992;33:94–101. [PubMed] [Google Scholar]
- Sakaji K, Akiyama M, Umeda H, Nakazawa Y, Takenaka H, Shinozuka A. Lung function assessment using Xe-133 dynamic SPECT in dual-camera system. Japan J Radiol Technol. 2001;57:1138–44. [Google Scholar]
- Seibyl JP. Single-photon emission computed tomography and positron emission tomography evaluations of patients with central motor disorders. Semin Nucl Med. 2008;38:274–86. doi: 10.1053/j.semnuclmed.2008.03.001. [DOI] [PubMed] [Google Scholar]
- Seike Y, Hashikawa K, Oku N, Moriwaki H, Yamamoto H, Fukuchi K, Watanabe Y, Matsumoto M, Hori M, Nishimura T. Evaluation of the use of a standard input function for compartment analysis of [123]imomazenil data: factors influencing the quantitative results. Ann Nucl Med. 2004;18:563–72. doi: 10.1007/BF02984577. [DOI] [PubMed] [Google Scholar]
- Sethian J. Level Set Methods: Evolving Interface in Geometry, Fluid Mechanics, Computer Vision and Material Science. Cambridge, MA: Cambridge University Press; 1996. [Google Scholar]
- Sharir T, Ben-Haim S, Merzon K, Prochorov V, Dickman D, Ben-Haim S, Berman DS. High-speed myocardial perfusion imaging: initial clinical comparison with conventional dual detector Anger camera imaging. J Am Coll Cardiol Imaging. 2008;1:156–63. doi: 10.1016/j.jcmg.2007.12.004. [DOI] [PubMed] [Google Scholar]
- Sharir T, Merzon K, Prochorov V, Dickman D, Nir Y, Ben Haim S, Berman D. D-SPECT: high speed myocardial perfusion imaging: a comparison with dual detector Anger camera (A-SPECT) J Nucl Med. 2007;48:51. doi: 10.1016/j.jcmg.2007.12.004. [DOI] [PubMed] [Google Scholar]
- Sharir T, Slomka PJ, Hayes SW, DiCarti MF, Ziffer JA, Martin WH, Dickman D, Ben-Haim S, Berman DS. Multicenter trial of high-speed versus conventional single-photon emission computed tomography imaging quantitative results of myocardial perfusion and left ventricular function. J Am Coll Cardiol. 2010;55:1965–74. doi: 10.1016/j.jacc.2010.01.028. [DOI] [PubMed] [Google Scholar]
- Shi Y, Karl WC. Tomographic reconstruction of dynamic objects. Proc SPIE. 2003;5016:151–60. [Google Scholar]
- Shi Y, Karl WC. Level set methods for dynamic tomography. 2004 IEEE Int. Symp. on Biomedical Imaging: Macro to Nano; Washington, DC. 15–18 April 2004; 2004. pp. 620–3. [Google Scholar]
- Sitek A, Di Bella EVR, Gullberg GT. Factor analysis of dynamic structures in dynamic SPECT imaging using maximum entropy. IEEE Trans Nucl Sci. 1999a;46:2227–32. [Google Scholar]
- Sitek A, Di Bella EVR, Gullberg GT. In: Lecture Notes in Computer Science. Kuba A, et al., editors. New York: Springer; 1999b. pp. 436–41. [Google Scholar]
- Sitek A, Di Bella EVR, Gullberg GT. Factor analysis with a priori knowledge–application in dynamic cardiac SPECT. Phys Med Biol. 2000;45:2619–38. doi: 10.1088/0031-9155/45/9/314. [DOI] [PubMed] [Google Scholar]
- Sitek A, Di Bella EVR, Gullberg GT, Huesman RH. Removal of liver activity contamination in teboroxime dynamic cardiac SPECT imaging using factor analysis. J Nucl Cardiol. 2002a;9:197–205. doi: 10.1067/mnc.2002.120362. [DOI] [PubMed] [Google Scholar]
- Sitek A, Gullberg GT, Di Bella EVR, Celler A. Reconstruction of dynamic renal tomographic data acquired by slow rotation. J Nucl Med. 2001;42:1704–12. [PubMed] [Google Scholar]
- Sitek A, Gullberg GT, Huesman RH. Correction for ambiguous solutions in factor analysis using a penalized least squares objective. IEEE Trans Med Imaging. 2002b;21:216–25. doi: 10.1109/42.996340. [DOI] [PubMed] [Google Scholar]
- Sitek A, Huesman RH, Gullberg GT. Tomographic reconstruction using an adaptive tetrahedral mesh defined by a point cloud. IEEE Trans Med Imaging. 2006;25:1172–9. doi: 10.1109/tmi.2006.879319. [DOI] [PubMed] [Google Scholar]
- Sitek A, Klein GJ, Gullberg GT, Huesman RH. Deformable model of the heart with fiber structure. IEEE Trans Nucl Sci. 2002c;49:789–93. [Google Scholar]
- Sitek A, Klein GJ, Reutter BW, Huesman RH, Gullberg GT. Measurement of the biomechanics of 3D cardiac function with gated nuclear medicine studies. Conf. Record of the 2005 IEEE Nuclear Science Symp. and Medical Imaging Conf; San Juan, Puerto Rico. 2005. pp. 2346–9. [Google Scholar]
- Smith AM, Gullberg GT, Christian PE. Experimental verification of technetium 99m-labled teboroxime kinetic parameters in the myocardium with dynamic single-photon emission computed tomography: reproducibility, correlation to flow, and susceptibility to extravascular contamination. J Nucl Cardiol. 1996;3:130–42. doi: 10.1016/s1071-3581(96)90005-7. [DOI] [PubMed] [Google Scholar]
- Smith AM, Gullberg GT, Christian PE, Datz L. Kinetic modeling of teboroxime using dynamic SPECT imaging of a canine model. J Nucl Med. 1994;35:484–95. [PubMed] [Google Scholar]
- Stayman JW, Fessler JA. Regularization for uniform spatial resolution properties in penalized-likelihood image reconstruction. IEEE Trans Med Imaging. 2000;19:601–15. doi: 10.1109/42.870666. [DOI] [PubMed] [Google Scholar]
- Stewart J. GN Researches on the circulation time and on the influences which affect it: IV. The output of the heart. Physiology. 1897;22:159–83. doi: 10.1113/jphysiol.1897.sp000684. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stewart RE, Schwaiger M, Hutchins GD, Chiao P-C, Gallagher KP, Nguyen N, Petry NA, Rogers WL. Myocardial clearance kinetics of technetium-99m-SQ30217: a marker of regional myocardial blood flow. J Nucl Med. 1990;31:1183–90. [PubMed] [Google Scholar]
- Stoddart HF, Stoddart HA. A new development in single gamma transaxial tomography Union Carbide focused collimator scanner. IEEE Trans Nucl Sci. 1979;NS-26:2710. [Google Scholar]
- Stokely EM, Sveinsdottir E, Lassen NA, Rommer P. A single photon dynamic computer assisted tomograph (DCAT) for imaging brain function in multiple cross sections. J Comput Assist Tomog. 1980;4:230–40. doi: 10.1097/00004728-198004000-00022. [DOI] [PubMed] [Google Scholar]
- Su Y, Welch MJ, Shoghi KI. The application of maximum likelihood factor analysis (MLFA) with uniqueness constraints on dynamic cardiac microPET data. Phys Med Biol. 2007;52:2313–34. doi: 10.1088/0031-9155/52/8/018. [DOI] [PubMed] [Google Scholar]
- Sugihara H, Yonekura Y, Kataoka K, Fukai D, Kitamura N, Taniguchi Y. Estimation of coronary flow reserve with the use of dynamic planar and SPECT images of Tc-99m tetrofosmin. J Nucl Cardiol. 2001;8:575–9. doi: 10.1067/mnc.2001.115934. [DOI] [PubMed] [Google Scholar]
- Takeishi YY, Arimoto T, Kubota I. Dynamic I-123 MIBG SPECT reflects sympathetic nervous integrity and predicts clinical outcome in patients with chronic heart failure (abstract) J Nucl Cardiol. 2005;12:S6. doi: 10.1007/BF02985105. [DOI] [PubMed] [Google Scholar]
- Tan K, Hutton BF, Feng D. A new approach for parameter estimation in SPECT dynamic using a rotating camera (abstract) Eur J Nucl Med. 1994;21:S29. [Google Scholar]
- Taylor JR. An Introduction to Error Analysis—The Study of Uncertainties in Physical Measurements. Oxford: Oxford University Press; 1982. [Google Scholar]
- Toennies KD, Celler A, Blinder S, Moeller T, Harrop R. Scatter segmentation in dynamic SPECT images using principal component analysis. SPIE Medical Imaging 2003; San Diego, CA. 2003. [Google Scholar]
- Toennies KD, Prang C, Celler A. Local identification and removal of scatter artefacts based on the temporal information in dynamic SPECT images. Cambridge 17th Int. Conf on Pattern Recognition; 2004; Cambridge. 2004. [Google Scholar]
- Toyama H, et al. Evaluation of the clinical usefulness of super dynamic 99mTc-HM-PAO SPECT in ischemic cerebral vascular disease—detection of hypo- and hyperperfusion area (article in Japanese) Kaku Iqaku. 1996;33:521–9. [PubMed] [Google Scholar]
- Tsuchida T, Yonekura Y, Sadato M, Takahashi N, Yamamoto H, Ishii Y. Prediction of improvement of cerebral perfusion with I-123 iomazenil SPECT. Ann Nucl Med. 1999;13:265–8. doi: 10.1007/BF03164903. [DOI] [PubMed] [Google Scholar]
- Tsui BMW, Hu HB, Gilland DR, Gullberg GT. Implementation of simultaneous attenuation and detector response correction in SPECT. IEEE Trans Nucl Sci. 1988;35:778–83. [Google Scholar]
- Tsui BMW, Terry JA, Gullberg GT. Evaluation of cardiac cone-beam single photon emission computed tomography using observer performance experiments and receiver operating characteristic analysis. Invest Radiol. 1993;28:1101–12. doi: 10.1097/00004424-199312000-00004. [DOI] [PubMed] [Google Scholar]
- van Elmbt L, Walrand S. Simultaneous correction of attenuation and distance-dependent resolution in SPECT: an analytical approach. Phys Med Biol. 1993;38:1207–17. [Google Scholar]
- Vanzi E, Formiconi AR, Bindi D, La Cava G, Pupi A. Kinetic parameter estimation from renal measurements with a three-headed SPECT system: a simulation study. IEEE Trans Med Imaging. 2004;23:363–73. doi: 10.1109/TMI.2004.824149. [DOI] [PubMed] [Google Scholar]
- Vastenhouw B, Beekman F. Submillimeter total-body murine imaging with U-SPECT-I. J Nucl Med. 2007;48:487–93. [PubMed] [Google Scholar]
- Veress AI, Gullberg GT, Weiss JA. Measurement of strain in the left ventricle during diastole with cine-MRI and deformable image registration. J Biomech Eng. 2005;127:1195–207. doi: 10.1115/1.2073677. [DOI] [PubMed] [Google Scholar]
- Verger L, Gentet M, Gerfault L, Guillemaud R, Mestais C, Monnet O, Montemont G, Petroz G, Rostaing JP, Rustique J. Performance and perspective of CdZnTe-based gamma camera for medical imaging. IEEE Trans Nucl Sci. 2004;51:3111–7. [Google Scholar]
- Volkow ND, Fowler JS, Wang GJ. Positron emission tomography and single-photon emission computed tomography in substance abuse research. Semin Nucl Med. 2003;33:114–28. doi: 10.1053/snuc.2003.127300. [DOI] [PubMed] [Google Scholar]
- Volkow ND, Fowler JS, Wang GJ, Baler R, Telang F. Imaging dopamine’s role in drug abuse and addiction. Neuropharmacology. 2009;56(Suppl 1):3–8. doi: 10.1016/j.neuropharm.2008.05.022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Volokh L, Lahat C, Beilin L, Hugg J, Blevis I, Jansen FP, Shai E, Hasegawa BH. Initial performance evaluation of an ultra-fast cardiac SPECT camera—a phantom study (abstract) J Nucl Cardiol. 2008;15:S5. [Google Scholar]
- Wagner HN Jr, Szabo Z, Buchanan JW, editors. Principles of Nuclear Medicine. 2. Philadelphia: Saunders; 1995. [Google Scholar]
- Wallin A. Constructing surfaces from CT data. IEEE Comput Graph Appl. 1991;11:28–33. [Google Scholar]
- Wang G, Fu L, Qi J. Maximum a posteriori reconstruction of Patlak parametric image from sinograms in dynamic PET. Phys Med Biol. 2008;53:593–604. doi: 10.1088/0031-9155/53/3/006. [DOI] [PubMed] [Google Scholar]
- Wang W, Gindi G. Noise analysis of MAP-EM algorithms for ECT. Phys Med Biol. 1997;42:2215–32. doi: 10.1088/0031-9155/42/11/015. [DOI] [PubMed] [Google Scholar]
- Weber DA, Ivanovic M. Ultra-high-resolution imaging of small animals: implications for preclinical and research studies. J Nucl Cardiol. 1999;6:332–4. doi: 10.1016/s1071-3581(99)90046-6. [DOI] [PubMed] [Google Scholar]
- Weissleder R, Mahmod U. Molecular imaging. Radiology. 2001;219:316–33. doi: 10.1148/radiology.219.2.r01ma19316. [DOI] [PubMed] [Google Scholar]
- Welch A, Gullberg GT, Christian PE, Datz FL, Morgan HT. A transmission-map-based scatter correction technique for SPECT in inhomogeneous media. Med Phys. 1995a;22:1627–35. doi: 10.1118/1.597422. [DOI] [PubMed] [Google Scholar]
- Welch A, Smith AM, Gullberg GT. An investigation of the effect of finite system resolution and photon noise on the bias and precision of dynamic cardiac SPECT parameters. Med Phys. 1995b;22:1829–36. doi: 10.1118/1.597440. [DOI] [PubMed] [Google Scholar]
- Wells RG, Farncombe T, Chang E, Nicholson RL. Reducing bladder artifacts in clinical pelvic SPECT images. J Nucl Med. 2004;45:1309–14. [PubMed] [Google Scholar]
- Williams KA, Taillon LAJ. Reversible ischemia in severe stress technetium 99m-labeled sestamibi perfusion defects assessed from gated single-photon emission computed tomographic polar map Fourier analysis. Nucl Cardiol. 1995;2:199–206. doi: 10.1016/s1071-3581(05)80056-x. [DOI] [PubMed] [Google Scholar]
- Wolfe N, Reed BR, Eberling JL, Jagust WJ. Temporal lobe perfusion on single photon emission computed tomography predicts the rate of cognitive decline in Alzheimer’s disease. Archives of Neurology. 1995;52:257–62. doi: 10.1001/archneur.1995.00540270049018. [DOI] [PubMed] [Google Scholar]
- Yonekura Y, Senda M, Fujita T, Hirose Y, Tanada S, Tamaki N, Mukai T, Yamamoto K, Torizuka K. System design and performance characteristics of newly developed whole-body multislice single photon emission computed tomograph (abstract) J Nucl Med. 1985;26:11. [Google Scholar]
- Zar JH. Biostatistical Analysis. Englewood Cliffs, NJ: Prentice-Hall; 1984. [Google Scholar]
- Zeng GL, Bai C, Gullberg GT. A projector/backprojector with slice-to-slice blurring for efficient 3D scatter modeling. IEEE Trans Med Imaging. 1999;18:722–32. doi: 10.1109/42.796285. [DOI] [PubMed] [Google Scholar]
- Zeng GL, Gullberg GT, Huesman RH. Using linear time-invariant system theory to estimate kinetic parameters directly from projection measurements. IEEE Trans Nucl Sci. 1995;42:2339–46. [Google Scholar]
- Zeng GL, Gullberg GT, Tsui BMW, Terry JA. Three-dimensional iterative reconstruction algorithms with attenuation and geometric point response correction. IEEE Trans Nucl Sci. 1991;38:693–702. [Google Scholar]
- Zeng GL, Hsieh Y-L, Gullberg GT. A rotating and warping projector-backprojector pair for fan-beam and cone-beam iterative algorithms. IEEE Trans Nucl Sci. 1994;41:2807–11. [Google Scholar]
- Zeniya T, et al. Use of a compact pixellated gamma camera for small animal pinhole SPECT imaging. Ann Nucl Med. 2006;20:409–16. doi: 10.1007/BF03027376. [DOI] [PubMed] [Google Scholar]
- Zhou R, Thomas DH, Qiao H, Bal HS, Choi SR, Alavi A, Ferrari VA, Kung HF, Acton PD. In vivodetection of stem cells grafted in infarcted rat myocardium. J Nucl Med. 2005;46:816–22. [PMC free article] [PubMed] [Google Scholar]
- Zierler KL. Equations for measuring blood flow by external monitoring of radioisotopes. Circ Res. 1965;16:309–21. doi: 10.1161/01.res.16.4.309. [DOI] [PubMed] [Google Scholar]