Evaluating the Viscoelastic Properties of Tissue from Laser Speckle Fluctuations

Abstract

Most pathological conditions such as atherosclerosis, cancer, neurodegenerative, and orthopedic disorders are accompanied with alterations in tissue viscoelasticity. Laser Speckle Rheology (LSR) is a novel optical technology that provides the invaluable potential for mechanical assessment of tissue in situ. In LSR, the specimen is illuminated with coherent light and the time constant of speckle fluctuations, τ, is measured using a high speed camera. Prior work indicates that τ is closely correlated with tissue microstructure and composition. Here, we investigate the relationship between LSR measurements of τ and sample mechanical properties defined by the viscoelastic modulus, G*. Phantoms and tissue samples over a broad range of viscoelastic properties are evaluated using LSR and conventional mechanical testing. Results demonstrate a strong correlation between τ and |G*| for both phantom (r = 0.79, p <0.0001) and tissue (r = 0.88, p<0.0001) specimens, establishing the unique capability of LSR in characterizing tissue viscoelasticity.

It is well recognized that disease progression in most pathological conditions, such as atherosclerosis, cancer, orthopedic disorders and neurodegenerative diseases is accompanied with alterations in the mechanical properties of affected tissues¹,²,³,⁴,⁵. For instance, the leading cause of death, myocardial infarction (MI) is caused by rupture of mechanically compromised vulnerable atherosclerotic plaques⁶,⁷,⁸,⁹. In many neurodegenerative disorders, such as Alzheimers disease, changes in the biomechanical properties of amyloid fibrils are believed to be responsible for the proliferation, growth, and propagation of amyloid plaques¹⁰. Mechanical cues have long been used to detect tumors by sensing tissue stiffness via palpation of the affected site¹¹,¹²,¹³,¹⁴. At the cellular level, altered mechanical properties of the tumor microenvironment have been shown to regulate malignant transformation and cancer cell proliferation independent of biochemical cues²,⁴,¹⁵,¹⁶. Therefore the significant evidence on the role of mechanical factors on disease initiation and progression calls for development of novel technologies for biomechanical evaluation of tissue in situ.

Traditionally, mechanical properties are evaluated using mechanical testing devices such as a rheometer in which the frequency dependent viscoelastic modulus, G*(ω), is measured by applying an oscillatory shear strain and evaluating the corresponding stress in the sample over a limited oscillation frequency range. Defined as the ratio of stress to strain, the viscoelastic modulus, G*(ω) (also termed the complex shear modulus) is given by the expression, G*(ω) = G'(ω) + i G”(ω). The real part of G*(ω), is the elastic or storage modulus, G'(ω), which is a measure of solid-like behavior of the sample and the imaginary part, which is out of phase with the strain is the viscous or loss modulus, G”(ω) and is a measure of viscous energy dissipation by the sample¹⁷.

In order to meet the need for the non-destructive mechanical analysis of tissue in situ, a novel optical approach, Laser Speckle Rheology (LSR) (also termed Laser Speckle Imaging (LSI)) has been demonstrated¹⁸,¹⁹,²⁰,²¹. In LSR, the sample is illuminated with coherent light and time-varying laser speckle patterns are acquired using a high speed CMOS camera. Laser speckle that occurs by the interference of coherent light scattered from the sample, is exquisitely sensitive to the Brownian motion of light scattering particles, in turn influenced by the viscoelastic susceptibility of the surrounding medium. Prior studies have demonstrated that the mechanical properties of homogenous samples (complex fluids) can be probed by the introduction of exogenous light scattering micro-particles into the medium²²,²³,²⁴. In the current study, we demonstrate that these principles can be extended to evaluate the mechanical properties of tissue by measuring laser speckle fluctuations caused by the Brownian motion of endogenous light scattering centers intrinsic within tissue. We have previously shown using LSR techniques that the rate of speckle intensity fluctuations given by the speckle decorrelation time constant, τ, is highly related with tissue microstructure and composition that may in turn govern tissue viscoelastic properties¹⁸,¹⁹,²⁰,²¹.

In this paper, we investigate the relationship between the time constant of laser speckle intensity fluctuations, τ, and the viscoelastic properties of tissue defined by the metric, G*(ω). Using conventional mechanical rheometry as a commercially-available standard, we demonstrate the accuracy and sensitivity of the LSR approach and show that the speckle decorrelation time constant, τ, is highly correlated with the magnitude of frequency dependent viscoelastic modulus, |G*(ω)| over a wide range of viscoelastic moduli.

Results

Laser speckle rheology

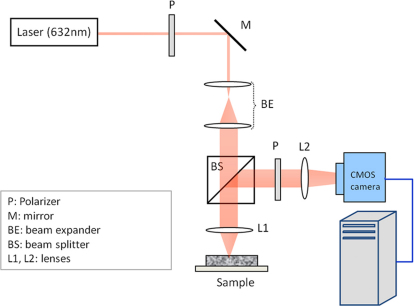
Time-varying laser speckle fluctuations of test samples were measured using an optical set-up described in Fig. 1¹⁸,¹⁹,²⁰,²¹. In this setup, light from a polarized Helium-Neon source (632 nm wavelength, 10 mW) of long coherence length (20 cm) was used to illuminate the sample. The laser beam was focused at the sample site to maximize light penetration depth and the back-scattered intensity, and cross-polarized time series of laser speckle patterns were collected using a high speed CMOS camera equipped with a polarizer to minimize the effect of specular reflection from the sample surface. The high frame rate of the camera allowed measurement of rapid fluctuations occurring over very short time scales in low viscosity samples. The specific details of the optical setup are described in the Methods section. In order to measure the rate of speckle fluctuations, the speckle intensity decorrelation curve, g₂(t), was measured for each sample via cross-correlation analysis of the first speckle frame with the subsequent frames in the time series. To enhance the statistical accuracy in measuring g₂(t), spatial and temporal averaging was performed over the region of interest (ROI) and over multiple g₂(t) curves that evolved in time over the imaging duration. The extent of speckle fluctuations was measured by calculating the speckle decorrelation time constant, τ, computed by fitting a single exponential function to the average g₂(t) curve¹⁸,¹⁹,²⁰,²¹. In the current study, test phantoms and tissue samples of varying mechanical properties were selected and evaluated using LSR and mechanical testing as described below.

Figure 1. LSR Instrumentation, BE: Beam Expander, BS: Beam Splitter, L1, L2: Lenses, M: Mirror, P: Polarizer. Laser beam is polarized, collimated and focused at the sample site.

A time series of cross-polarized, back scattered speckle patterns is captured by the high-speed CMOS camera the intensity decorrelation function of speckle pattern, g₂(t) is measured. Next, a single exponential is fitted to g₂(t) to extract the time constant, τ.

Test phantoms

A set of test phantoms that covered a wide range of mechanical properties (G*(ω): 320 m Pa to 276 K Pa, @ 10 Hz) relevant to tissue were prepared and tested using LSR. For each sample, the speckle decorrelation time constant, τ, was calculated and compared with the magnitude complex modulus, |G*(ω)|, measured using a conventional mechanical rheometer at the oscillation frequency of 10 Hz. The evaluated test phantoms included: low viscosity glycerol mixtures, Dextran and Visipaque (isosmolar Iodixanol) solutions, agarose, gelatin, Poly Ethylene Glycol (PEG) soft gels, and Polydimethylsiloxane (PDMS) samples of various concentrations. Since these samples are optically clear, a small volume fraction (1%) TiO₂ powder was added to serve as exogenous scattering centers.

LSR of the low viscosity liquid test samples (glycerol, dextran and visipaque) was performed within a transparent sealed couvette at a frame rate of 800 fps and compared with mechanical testing. In order to ensure uniform sampling over the entire viscoelastic modulus range, soft agarose, gelatin, and PEG gels, were included in this study, due to their moderate viscoelastic properties, covering the mid-range of |G*(ω)| values from 2 Pa to 976 Pa (at 10 Hz). For these gels, speckle images were acquired at 200 fps.

In order to test the capability of LSR in measuring changes in sample mechanical properties over a wide modulus range, PDMS samples were evaluated throughout curing. LSR evaluation and mechanical testing of PDMS samples were simultaneously conducted at intervals of 30 minutes over 12 hours as the gel cured at room temperature (25°C) from a low viscosity liquid (|G*| ~240 Pa) to an elastic solid (|G*| ~3.8 k Pa). LSR and mechanical testing were similarly performed on fully cured PDMS at 48 hours (|G*| ~ 276 k Pa) and on heat cured PDMS (|G*| ~17.5 k Pa) after 1 hour. Time lapse LSR measurements were conducted by adjusting the frame rate based on speckle fluctuation rate; for instance, a frame rate of 400 frames per second (fps) was used to evaluate rapid speckle fluctuations in the low viscosity PDMS gel at early curing times, and was reduced to 10 fps to comply with slower speckle dynamics of the fully cured PDMS samples. A total of 1600 laser speckle frames were analyzed at each time point corresponding to acquisition times of 4 s–160 s for early curing times and fully cured samples, respectively.

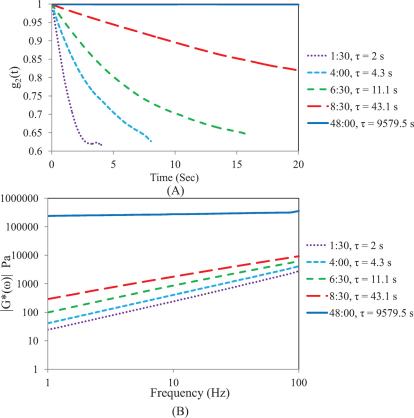
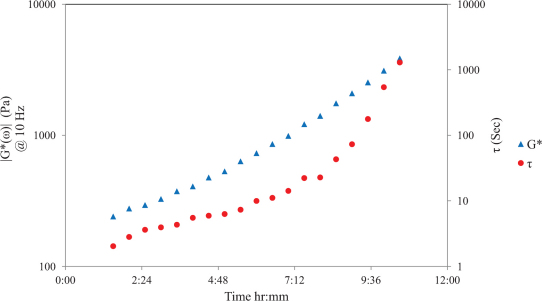
Fig. 2A displays speckle intensity decorrelation curves, g₂(t) with the corresponding τ values for room-curing PDMS substrates (curing agent to resin concentration is 1:10) at 5 different time points during cross-linking process. It is clear that the speckle intensity decorrelation curve, g₂(t), is modulated throughout the curing process due to stiffening of the PDMS sample. At early curing times due to low viscosity of the PDMS sample, a rapid decorrelation of the g₂(t) curve is observed corresponding to a τ value of < 2 s, and at long curing times (> 48 hrs) negligible speckle decorrelation is observed corresponding to a τ > 9000 s for the fully cured PDMS sample. Fig. 2B shows the frequency dependent viscoelastic modulus, G*(ω) for the PDMS samples of Fig. 2A. Similar to LSR results, rheometric measurements of G*(ω) are altered during the curing process over the entire frequency sweep (1–100 Hz): for instance at ω = 10 Hz, for the softer PDMS sample, |G*| ~ 240 Pa at early curing times and increases to 276 kPa for the fully cured stiff PDMS sample at long curing times of 48 hours. These results indicate that LSR values of τ and rheometric measurements |G*(ω)| are similarly remodeled during the thermal curing process. Fig. 3 shows the variation of τ and corresponding |G*(ω)| (at 10 Hz) as a function of time throughout the curing process in the PDMS sample. It is evident that τ increases exponentially with time in a manner consistent with the growth of mechanical moduli. Initially a viscous liquid of moderate modulus with low τ and corresponding low |G*| values, PDMS cures into a highly elastic material of large modulus eliciting slow speckle decorrelation times.

Figure 2.

(A) Speckle decorrelation curves, g₂(t) with the corresponding τ values for 5 room-curing PDMS substrates at durations of 1:30, 4:00, 6:30, 8:30 and 48:00 (hr:mm). It is observed that as the PDMS gel solidifies, speckle pattern dynamics are slowed down and g₂(t) decays slower. (B) Frequency dependent viscoelastic modulus, G*(ω), is plotted for 5 room-curing PDMS substrates at time points 1:30, 4:00, 6:30, 8:30 and 48:00 (hr:mm) for 1–100 Hz. The value of |G*(ω)|, increases during curing and the logarithmic slope of |G*(ω)| reduces.

Figure 3. Time constant, τ, and |G*(ω)| @10 Hz as a function of time for room-curing PDMS substrates (Primary y-axis: complex shear moduli (log scale) versus curing time.

Secondary y-axis: Time constant, τ, (log scale) versus curing time), similar growth trend is observed for τ, and |G*(ω)| during the PDMS curing process.

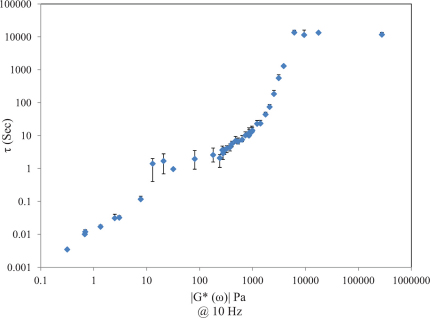
Fig. 4 depicts the scatter diagram of τ versus |G*(ω)| at 10 Hz for all test phantom samples (N = 39). Data is displayed in the log scale to enable better visualization over the wide range of mechanical moduli and τ values. It is evident that a strong correlation exists between τ and |G*| for a wide range of moduli from 320 m Pa (diluted glycerol) to 10 K Pa (room-cured PDMS. Over this range, results of linear regression analysis demonstrates a strong and statistically significant correlation between τ and |G*| (r = 0.79, p < 0.0001). At higher moduli due to the effects of non-ergodicity in stiffer samples, the correlation is diminished and τ plateaus at |G*| > 10 kPa (discussed later).

Figure 4. Scatter diagram of τ versus |G*(ω)| at ω = 10 Hz, each data point depicts the mean ± standard deviation of at least 8 measurements obtained over a 40 mm diameter ROI (solid samples).

A statistically significant and strong correlation is observed for |G*| from 320 mPa to 10 kPa (r = 0.79, p<0.0001).

Tissue samples

In the studies above, the viscoelastic susceptibility of samples over a large modulus range was probed by evaluating speckle decorrelation due to the presence of exogenous light scattering particles (TiO₂) introduced into the sample. In the next set of experiments, LSR was applied to investigate viscoelastic properties of tissue samples over a similar modulus range by exploiting the Brownian displacements of endogenous light scattering particles²⁵, intrinsic within the tissue matrix without the introduction of exogenous agents.

The evaluated tissue samples included: swine aorta, myocardium, cartilage, skeletal muscle, subcutaneous fat, and blood spanning a modulus range of |G*| ~ 60 m Pa (blood) to ~600 K Pa (cartilage) at the arbitrary oscillation frequency of 1 Hz. This oscillation frequency is chosen since for soft tissue samples, results of conventional rheology frequency sweep are limited to below 10 Hz. This is because a smaller top plate of 8 mm dia. tool is used for conducting the mechanical testing for tissue (as described in the methods section) and thus, the high frequency measurements from the rheometer are not reliable. LSR of all tissue samples was conducted at 37°C within a water bath and a total of 6000 frames were captured at 300 fps (20 s duration). In each tissue sample, average τ values were evaluated by scanning the laser spot and measuring g₂(t) curves at 5 spatial locations over a 7 mm dia. ROI to account for tissue heterogeneity. LSR of swine blood specimens was performed using similar parameters as of liquid test samples, i.e. 800 fps, over acquisition duration of 2 s.

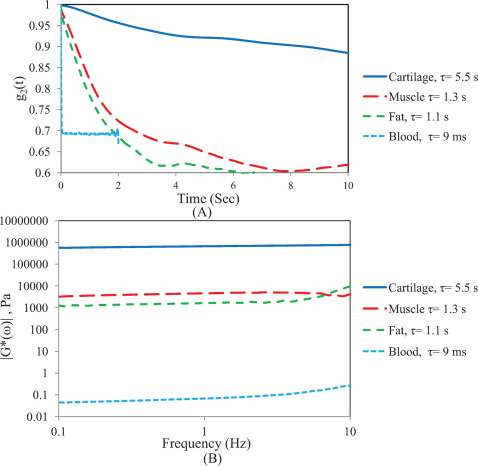
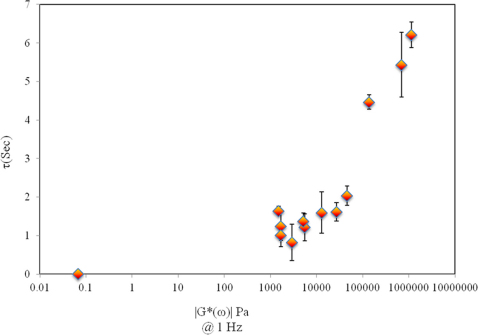
Figures 5 (A and B) show the g₂(t) curves for cartilage, skeletal muscle, subcutaneous fat, and whole blood, with the associated τ value (Fig. 5A) and the corresponding |G*(ω)| values of the same samples measured using the mechanical rheometer in a frequency sweep analysis (0.1–10 Hz) (Fig. 5B). As observed the stiffer cartilage tissue elicits the slowest rate of speckle decorrelation (τ = 5.5 s) corresponding with the highest G* value (662 kPa), whereas for whole blood (|G*| = 60 mPa) due to the rapid Brownian motion of scatterers in the low viscosity medium, a fast decay of g₂(t) (τ = 9 ms) is measured using high frame rates of >800 fps. As expected, g₂(t) curves for skeletal muscle and fat decay with a rate corresponding to the sample stiffness: in other words, g₂(t) for the fat samples decays faster (τ = 1.1, |G*| = 1.6 k Pa) than for muscle (τ = 1.3 s; |G*| = 4.5 k Pa) but both curves decay slower than low viscosity blood samples and more rapidly than stiffer cartilage tissue. Fig. 6 shows the scatter diagram of G* versus τ for all the tissue samples (N = 13). A close correspondence is observed between τ and |G*| (at 1 Hz) and linear regression analysis demonstrates a strong, statistically significant correlation (r = 0.88, p<10⁻⁴) for |G*| from 60 m Pa to 600 K Pa. The saturation region for tissue samples is not as distinct as it is for highly elastic PDMS substrates and it is still possible to differentiate between high modulus tissue samples using LSR (as discussed below).

Figure 5.

(A) Speckle decorrelation curves, g₂(t) along with the corresponding τ values for 4 tissue samples, cartilage, skeletal muscle, fat, and blood. g₂(t), decay is consistent with samples' stiffness. (B) Frequency dependent viscoelastic modulus, |G*(ω)| curves for 4 tissue samples, Cartilage, Skeletal muscle, Fat, and Blood for 1–10 Hz.

Figure 6. Scatter diagram of τ versus |G*(ω)| at ω = 1 Hz, each data point depicts the mean±standard deviation of at least 6 measurements obtained over a ~7 mm diameter ROI (for solid samples).

A larger standard deviation is observed due to tissue heterogeneity in the compared to phantom results of Fig. 4. A statistically significant and strong correlation is observed for |G*| from 60 m Pa to 600 K Pa (r = 0.88, p<0.0001).

Discussion

LSR is a novel technique that can potentially provide an invaluable tool for mechanical evaluation of tissue for a number of applications in clinical medicine, tissue engineering and basic biological research. LSR is based on dynamic light scattering (DLS) principles that relate the mean square displacements (MSD) of scattering particles with the material's viscoelastic susceptibility²²,²⁶,²⁷,²⁸. To probe the mechanical behavior of the medium using DLS in prior studies, exogenous scattering particles have been introduced into the sample and scattered light is collected using an optical fiber. Time-varying intensity fluctuations over a single spot are measured by averaging over several cross-correlation functions that evolve in time to obtain the intensity correlation function, g₂(t)²³,²⁴. Since in DLS g₂(t) is measured over a single speckle spot, data acquisition time is orders of magnitude larger than the typical time scale of fluctuations (acquisition time of several minutes to hours) which is impractical for analysis of tissue in situ²⁹. The use of CMOS camera to acquire laser speckle patterns from the sample enhances the statistical accuracy in measuring g₂(t) by simultaneous ensemble averaging of multiple speckle spots, which significantly reduces data acquisition time¹⁸,¹⁹,²⁰,²¹. This method of speckle acquisition has been applied in LSR to measure the time decay, τ, of g₂(t) functions from laser speckle fluctuations that occur due to light scattering by particles intrinsic within tissue without the need for introduction of exogenous scattering particles. The capability to analyze passive Brownian motion and the resulting MSD of intrinsic biological particles in tissue opens the powerful opportunity for diagnostic mechanical assessment of a number of disease conditions in situ. In prior studies, the relationship of τ with tissue microstructure and composition has been well demonstrated¹⁸,¹⁹,²⁰,²¹. To our knowledge, however, the influence of tissue viscoelastic properties on the modulation of τ has not yet been established and is a necessary step in validating the LSR technology for biomechanical analysis of tissue. Therefore, in the current study, the capability of LSR in characterizing tissue mechanical properties is investigated and the relationship between the rate of laser speckle fluctuations given by τ and the viscoelastic modulus, |G*| measured by a conventional mechanical rheometer, is explored using test phantoms and tissue samples over a wide range of viscoelastic properties. The results of the current study demonstrate a positively correlated relationship between the time scale of laser speckle fluctuations and the modulus |G*(ω)| at an arbitrary frequency over a large range of modulus values in phantom (R = 0.79; p< 0.0001, ω = 10 Hz) and tissue (R = 0.88, p<0.0001, ω = 1 Hz) samples.

Sample mechanics contribute to speckle intensity fluctuations through the MSD of scattering particles, 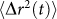. In other words, when the extent of particle displacement is large, 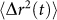grows faster with time and gives rise to a rapid decorrelation and a small τ as observed in low viscosity liquid samples. In contrast, when 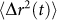is more constraint, such as in fully-cured PDMS sample, speckle decorrelation is much slower and τ is considerably large. For a very simple viscoelastic material, comprised of harmonically bound light scattering spheres in a viscous fluid, a simplified model can be obtained that provides useful insight into the mapping of g₂(t) to G*(ω). In this case, MSD of scattering particles can be written as 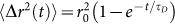, where r₀² is the saturated MSD and τ_D is the diffusion time constant of the confined spheres²⁴,²⁸,³⁰. Therefore, initially particles may diffuse freely but will come to rest at a maximum displacement distance from the start position after some time. Assuming a backscattering illumination and collection geometry, used throughout this study, speckle intensity decorrelation curve, g₂(t), can be described as a function of MSD, optical properties, and experimental setup as follows²²,²⁹:

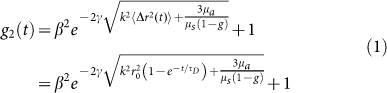where k is the wave number in the scattering medium, and γ is an experimental parameter related to the particle size distribution, illumination and collection geometry (source-detector distance), and polarization state. Also, in eqn. 1, β is a parameter corresponding to the coherence of the collected light, and μ_a, μ_s, and g are the absorption, and scattering coefficients, and anisotropy factor, respectively²⁷,³¹,³². While the first term on the right hand side of eqn. 1 describes the general form of g₂(t), the second term is specific to the simplified model of MSD. For this specific model, G*(ω) is given by²⁴,²⁸,³⁰:

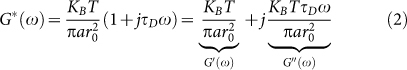where K_B is the Boltzmann constant, a is the average scattering particles radius, and T is the temperature in Kelvin²⁷,³¹,³². From eqns. 1 and 2, it is clear that elastic component of G*(ω) is dominated by r₀², which is more pronounced in the low frequency behavior of G*(ω) and the long time plateau level of g₂(t). On the other hand, the viscous component, is adjusted by diffusion time constant τ_D, which determines the high frequency trend of G*(ω) and modulates the early decay of g₂(t)²⁴,²⁸,³⁰.

Results of Fig. 2A and 2B can be revisited in light of this simplified model described above. In particular, it is observed that for early curing times, when PDMS is primarily viscous (G*(ω) ~ G”(ω)), initial decay trend of g₂(t) is influenced by G”(ω). On the other hand, for fully cured PDMS, which is predominantly elastic (G*(ω) ~ G'(ω)), the plateau level of g₂(t) at long times is adjusted by magnitude of G*(ω). Moreover, the weak frequency dependence of |G*(ω)| for fully-cured, almost purely elastic PDMS is consistent with slowly drifting behavior of g₂(t). This is a consequence of non-ergodic statistics of speckle pattern fluctuations for highly elastic materials, which is caused by restricted thermal motion of scattering particles, trapped in the polymer structure³²,³³. The close correspondence observed between LSR and mechanical testing results is evident from the growth trend of τ and |G*(ω)| during the course of thermal curing (Fig. 3). For soft PDMS samples of moderate viscoelastic modulus, (|G*| < 10 K Pa), τ measured by LSR closely follows small changes in |G*(ω)| measured by conventional rheometry. The sensitivity of LSR to small changes in |G*(ω)| is a result of g₂(t) sensitivity to scattering particle displacements in the order of optical wave length (10⁻⁹ m). In other words, the intensity of the bright spot in the speckle pattern will be modulated if particles in the illumination volume are displaced by a fraction of optical wavelength. During the PDMS curing process, the viscous resin evolves to an elastic solid; therefore, displacements of scattering particles become more and more constrained for the fully cured sample. LSR reflects these small gradual changes in mechanical properties with high sensitivity since it can measure optical phase shifts caused by the extent and scale of particular displacements by measuring changes in speckle intensity.

Similar observations are made for tissue samples. For instance, sharp decay of g₂(t) curve for blood sample in Fig. 5A reveals low viscosity behavior of blood consistent with the conventional rheology measurements (Fig. 5B). Likewise, for g₂(t) curve of cartilage sample, presence of a slowly decaying segment followed by a high plateau at long correlation times indicates the contribution of both elastic and viscous components, G' and G”. This is likely due to hydrophilic and sponge-like nature of the cartilage and its biphasic and inhomogeneous characteristics, which posses coexisting solid-like and fluid-like behaviours³⁴,³⁵. Therefore, cartilage samples of high modulus (|G*|~600 kPa) still exhibit considerable viscous behavior and noticeable speckle decorrelation despite the high plateau level of g₂(t) (Fig. 5A). This is in contrast with the behavior of g₂(t) for elastic fully cured PDMS substrate of Fig. 2A (|G*|>10 kPa), where the initial decay is diminished and only a slow drift is observed. The range of viscoelastic properties, for which τ is related with |G*|, can be defined as LSR dynamic range of measurement. In the current study, for phantom samples, a statistically significant strong correlation is observed between τ and |G*(ω)| over a large moduli range of 320 m Pa to 10 k Pa. However, the correlation is reduced for highly elastic samples (|G*(ω)| > 10 k Pa), giving rise to a saturation region in the scatter diagram (Fig. 4). In this region, the sensitivity of τ evaluation is reduced since the material is almost purely elastic possessing a constant frequency-independent |G*(ω)| and thus a minimally-decaying g₂(t). For tissue samples, however, the saturation region is not distinct and strong correlation is observed over larger moduli range from 60 m Pa to 600 K Pa and considerable speckle decorrelation is retained for stiffest tissue samples, i.e. cartilage (>100 kPa). Nonetheless, the error bars displayed in scatter diagrams of phantom and tissue samples (Fig. 4, and Fig. 6) suggest that variability of measured τ values across the sample are slightly higher in tissue samples due to the heterogeneous nature of tissue. The unique capability of LSR to measure heterogeneous mechanical moduli opens new avenues for high resolution mechanical characterization of tissue heterogeneities which is intractable using conventional mechanical testing methods. The limitations of conventional rheometers are particularly severe for the case of blood and plasma, where straining of the sample leads to deformation of fibrin network, strain hardening, and altered biomechanical properties³⁶. LSR can overcome these fundamental limitations for mechanical evaluations of soft tissue, as it uses only a small sample volume and is able to assess sample mechanics without manipulating the specimen.

In this study, the Pearson's correlation coefficient obtained from linear regression analysis provided a first order approximation of the relationship between τ and |G*| (Fig. 4). However, it is clear from the exponent of the first term in the right hand side of eqn. 1 that the rate of speckle decorrelation, quantified by τ, is a conglomerate of multiple mechanical and optical factors of the sample and the geometric configuration of the experimental setup. Therefore, an estimation of the exact relationship between τ and |G*| is complex for the reasons discussed below.

Firstly, for complex viscoelastic materials such as the phantom and tissue samples measured in the current study, the exact temporal trend of 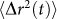curve is governed by the frequency dependent viscoelasticity of the specific material. In these materials, MSD can be modeled as a piecewise power law form 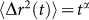, where α is the logarithmic slope of MSD (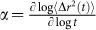)²⁴,²⁸ and varies with time based on sample viscoelasticity, giving rise to multiple relaxation times (time constants)²⁷,³⁷,³⁸. In these cases, g₂(t) can be better defined as a combination of multiple exponential curves, with multiple time constants³⁹. Therefore, depending on the time interval over which a single exponential function is fitted to g₂(t), the time constant τ, reflects an average of particular relaxation times.

Secondly, optical properties of the sample and parameters related to the experimental setup also contribute to g₂(t) curve as seen in eqn. 1. For instance, in multiply scattering tissue samples, the number of scattering events per light path increases with the scattering coefficient and optical phase shifts caused by displacements of multiple particles can potentially cause higher speckle intensity fluctuations. In addition, increased absorption effects may influence the contribution of long paths, causing slower speckle decorrelation at initial times in the g₂(t) curve. For all the phantom samples in this study the contribution of variations in optical properties on τ was minimized by ensuring that the optical properties were maintaining the same across all samples by adding TiO₂ particles at 1% w/v to optically clear materials. For tissue samples, however, sample to sample variations in optical properties may potentially modify g₂(t) and influence relative τ values. In the current study a positive correlation between τ and |G*(ω)| is demonstrated for both phantom and tissue samples. In future studies, in order to accurately extract G*(ω) directly from g₂(t) curves, knowledge of tissue optical properties may be necessary.

Additional experimental factors that may influence τ include the choice of source wavelength which changes the wave number, k, and may alter the absolute decay rate of g₂(t), but not the relative differences of τ between samples. While the absolute level of g₂(t) plateau is strongly influenced by the elastic modulus of the sample, variations in plateau level may also be slightly modulated by experimental parameters such as the coherence parameter β and the presence of ambient noise (eqn. 1). When camera frame rate is smaller than time scales of Brownian motion dynamics, speckle intensity fluctuations are blurred out resulting in lower speckle contrast. Similarly when the pixel to speckle ratio is large speckle intensity is averaged at each pixel and therefore speckle contrast is reduced. These factors will lead to reduction of β and result in a higher plateau level in normalized g₂(t) curve. An observation of this effect in the current study is the relatively higher plateau level of g₂(t) for the blood sample, plotted in Fig. 5A, potentially caused by insufficient camera frame rate, which gives rise to temporal blurring of speckle fluctuations and reduction in contrast.

The demonstrated capability of LSR in providing an accurate and highly sensitive measure of tissue mechanical properties without the need for sample manipulation opens the powerful opportunity to develop novel research and clinical tools for the biomechanical evaluation of a number of pathological conditions in situ. While results of the current study were obtained using a bench-top setup ex vivo, we have recently demonstrated that LSR can be performed in vivo via small diameter endoscopes²¹ potentially opening the exciting opportunity for using endoscopic LSR for multiple clinical applications.

Methods

Test phantom preparation

To test the capability of LSR in evaluating samples of low viscosity, glycerol (60%–100%), dextran and Visipaque (isosmolar Iodixanol) solutions were evaluated in this study using TiO₂ particles (dia. 0.423 µm, Thermo Fisher Scientific, NJ USA) as light scattering particles (1% volume fraction). One milliliter of liquid samples was placed in a sealed transparent plastic couvette for LSR measurements, and ~9 ml was used to fill the double-gap steel couvette of the rheometer for mechanical testing.

Soft gels of mid-range viscoelastic moduli (2–976 Pa) were produced in various concentrations. These include Agarose (0.8%, 1.6%), Gelatine (0.8%, 1.6%, 3.75%), and Poly Ethylene Glycol (5%, 10%, 20%, 30%). PEG gels were made by diluting Poly (ethylene glycol) diacrylate (M_n 575, Sigma-Aldrich Co. LLC., St. Louis MO, USA) with phosphate buffer saline (PBS) in different concentrations (5%, 10%, 20%, and 30%), adding 1% W.V. of photo-activator (DAROCUR 1173, Ciba Specialty Chemical Inc., Basel, Switzerland) and curing for 15 minutes with a UV gun. To render scattering features, TiO₂ of 1% W.V. is evenly distributed within the soft gels prior to curing.

PDMS test substrates were prepared using the Sylgard ® 184 silicone elastomer (Dow Corning, Europe Parc Industriel, Belgium) by mixing the cross-linker and resin in 1:10, 1:20, and 1:30 ratios. Complete cross linking of PDMS was achieved at room temperature (25°C) after 48 hours or by heat curing at 50°C over 1 hour⁴⁰. Since PDMS is optically clear, Titanium Dioxide (TiO₂) microspheres were added (volume fraction ~1%) to the mixture prior to curing to render a back-scattering signal. To properly disseminate the scattering particles across the sample, TiO₂ was first mixed with the cross-linker of lower viscosity prior to sonication and mixing with the resin. PDMS mixtures were poured in 40 mm diameter petri dish plates (sample volume ~4 ml). While one group of PDMS samples (1:10, 1:20, and 1:30 concentrations) were oven cured at 50°C for one hour, a second set of 1:10 PDMS samples were left at room temperature to facilitate time-lapse analysis of evolving mechanical properties during the curing process using LSR and mechanical rheometry.

Tissue preparation

Tissue samples were excised from two swine following sacrifice and prepared for analysis with LSR and mechanical testing. Specifically, tissue samples (N = 13) were obtained from the aorta, myocardium, cartilage, skeletal muscle, and subcutaneous fat using a biopsy punch (diameter = 7 mm), perfused and stored in PBS. Swine blood samples were drawn via the carotid artery and heparinized to prevent clotting. Similar to test liquid samples above, ~1 ml of blood was placed in a sealed transparent plastic couvette for LSR measurements, and ~9 ml was used to perform mechanical testing.

Laser speckle rheology testing

The optical set up in Fig. 1 was used to obtain time-varying laser speckle patterns of test phantoms and tissue samples¹⁸,¹⁹,²⁰,²¹. In this system, light from a polarized Helium-Neon source (632 nm wavelength, 10 mW, 20 cm coherence length) was expanded (1:5), reflected off a mirror and focused to a 50 µm spot at the sample site and cross-polarized time series of laser speckle patterns were collected using a high speed CMOS camera (PixelLINK PL-761F, Ottawa, Canada). A Macro lens was attached to the camera front end to ensure adjustable focus point and pixel to speckle ratio. In order to eliminate specular reflection, a linear polarizer was placed in front of the aperture, limiting the captured light to the cross-polarized component. For liquid test samples, in order to comply with the fast sample dynamics, LSR measurements were conducted at 800 fps, and ROI of 40×40 pixels, capturing a total of 1600 frames, i.e. 2 seconds of speckle acquisition. For soft gels, a frame rate of 200 fps, and an ROI of 112×112 pixels was used. A total of 3000 frames were acquired, corresponding to 15 second acquisition time. For room-curing PDMS substrates, speckle patterns were recorded as the gel was curing at 25°C. The ROI for PDMS substrates was set to 80×80 pixels.

LSR of tissue samples was performed in a water bath maintained at 37°C. For solid tissue samples, camera frame rate was set to 300 fps and ROI was adjusted to include a region of 120×120 pixels. A total of 6000 frames were captured, corresponding to 20 seconds acquisition time. LSR measurement was performed on swine blood sample using similar parameters as of liquid test samples, i.e. 800 fps, ROI of 40×40 pixels, and acquisition time of 2 seconds. Speckle frame series were transmitted to the computer via an IEEE-1394 FireWire interface. The speckle intensity decorrelation curve, g₂(t) was evaluated by cross-correlation analysis of each speckle frame with subsequent frames in the time series, in a pixel by pixel manner, over the entire acquisition time. Spatial and temporal averaging over ROI was performed to obtain adequate ensemble averaging and improve the statistical accuracy of g₂(t) data.

Mechanical testing

The frequency-dependent viscoelastic modulus, G*(ω), was measured for each sample using an AR-G2 rheometer (TA Instruments, New Castle, DE) configured using appropriate loading geometry, control variables, frequency range, and temperature. For liquid test samples, double concentric cuvette and oscillating rod geometry was used to maximize the surface area of measurement by pouring the liquid sample in the gap between two concentric cylinders. Using this geometry and strains of 5% as the control variable, G', G”, and G* were measured over the range of 0.1 to 100 Hz at 25°C. For soft gels, 40 mm steel parallel plate geometry is used. Frequency sweep was performed over the range of 0.1 to 100 Hz at 25°C and 1% strain as the control variables. PDMS mixtures were loaded between the bottom plate and a 40 mm steel parallel top plate. Mechanical testing procedure consisted of a conditioning step followed by a frequency sweep, repeated every 30 minutes for 12 hours in synchrony with LSR measurements described above. Strain was controlled at 0.1%, and G', G”, and G* were measured over a frequency range of 1 to 100 Hz at 25°C. For fully cured PDMS substrates (room cured at 48 hours and heat cured at 1 hour), measurements were performed using the same frequency range and control parameters. For tissue samples, a customized miniature serrated parallel steel plate (8 mm) was utilized to prevent sample slippage and minimize the impact of sample heterogeneity. G', G”, and G* of the swine tissue samples were similarly measured over the range of 0.1 to 100 Hz, at strain of 0.1%. During the measurement process all samples were moistened using phosphate buffer saline (PBS) to minimize dehydration. For swine blood samples, a similar double gap couvette and rod was used and strain percentage was controlled at <5%. All tissue samples were evaluated at 37°C.

Author Contributions

Designed the experiments: ZH SN, Performed the experiments: ZH, Analyzed the data: ZH SN. Wrote the manuscript: ZH SN. Discussed the results and commented on the paper: SN.