Separating the scattering and absorption coefficients using the real and imaginary parts of the refractive index with low coherence interferometry

Abstract

We present an analytical method that yields the real and imaginary parts of the refractive index (RI) from low coherence interferometry measurements, leading to the separation of the scattering and absorption coefficients of turbid samples. The imaginary RI is measured using time-frequency analysis, with the real part obtained by analyzing the non-linear phase induced by a sample. A derivation relating the real part of the RI to the non-linear phase term of the signal is presented along with measurements from scattering and non-scattering samples that exhibit absorption due to hemoglobin.

Substantial efforts have been made to quantitatively measure absorption of biological chromophores in vivo for diagnosis [1–3]. Unfortunately, several drawbacks have been encountered, primarily dealing with the limitation of the number of physical parameters that may be independently measured and determined using analytical models. For example, in spectroscopic optical coherence tomography (SOCT), some promising results for quantifying absorption in vivo have been reported [2–4], but these have been limited owing to the fact that SOCT measures the total attenuation coefficient and the absorption and scattering contributions have not been separated without a priori information. Consequently, in order to assess absorption, models must include additional parameters, such as packing factors and anisotropic coefficients, which results in low confidence intervals, thereby hindering quantification [5]. Rather than using attenuation, some researchers have used phase information as means of obtaining concentrations of chromophores [6]. These methods, however, are often confined to thin, transparent samples and thus are not well suited for in vivo measurements.

In this letter, we analyze the dispersion of turbid samples using low coherence interferometric (LCI) signals, in combination with time-frequency (TF) analysis, to retrieve the real and imaginary parts of the RI independently of scattering contributions and without a priori information. Using a supercontinuum broadband light source, we demonstrate that this method yields wide-band absorption spectral profiles with high spectral resolution, and wavelength-dependent RI profiles. By isolating the contribution due to absorption, the wavelength-dependent scattering coefficient is also obtained.

To understand how the real and imaginary parts of the RI may be obtained, consider a Michelson interferometer with a reference field described as E_r(ω)=S(ω)exp[i(ω/c₀)2z_r], and a sample field returned by m scatterers written as

$$E_s(\omega )=\sum _m\sqrt{I_s^{(m)}(\omega )}·e^{i(\omega /c_0)2z_d}{e}^{i(\omega /c_0)n(\omega )2(z_s^{(m)}-z_d)},$$ (1)

where z_r, z_d, z_s are the distances from the beamsplitter to the reference mirror, dispersive medium, and scatterer, respectively; S(ω) is the spectrum of the source field, c_o is the speed of light in vacuum, and n(ω) is the real part of the RI of the sample [7]. For simplicity, we assume that there is a single scatterer (m = 1), and that the sample can be described by bulk absorption and scattering coefficients μ_a and μ_s, respectively; such that, the sample field intensity may be written as, I_s(ω) =|S(ω)|² exp[−(μ_a+μ_s) 2(z_s−z_d)]. Thus, the interferometric signal, after elimination of dc background terms, is given by,

$$\stackrel{\sim }{I}(\omega )=2\sqrt{I_s(\omega )I_r(\omega )}·e^{i(\omega /c_0)2(z^{\prime }-dn(\omega ))}=2I_r(\omega )e^{-{\mu }_{\mathit{tot}}(\omega )d}·e^{i(\omega /c_0)2(z^{\prime }-dn(\omega ))},$$ (2)

where I_r = |S|², μ_tot = μ_a + μ_s, z′ = z_r − z_d, and d = z_s − z_d. Then, to analyze the information contained in the dispersion of the signal, we consider a Taylor series expansion of n(ω), n(ω) = n(ω₀) +Δn(ω), where n(ω₀) may be evaluated at an arbitrary frequency or wavelength (e.g., at λ = 800nm, n₀ =1.392 for hemoglobin [8]), and Δn incorporates all the terms dependent on ω from the Taylor series expansion. Thus, Eq. 2 may be rewritten as,

$$\stackrel{\sim }{I}(\omega )=2I_r(\omega )e^{-{\mu }_{\mathit{tot}}(\omega )d}·e^{i(\omega /c_0)2(z^{\prime }-dn({\omega }_0))}·e^{-i(\omega /c_0)2d\mathrm{\Delta }n(\omega )}.$$ (3)

As Eq. 3 describes, the measured signal contains three parts: The first part modulates the intensity, which yields spectroscopic information and, if scattering is negligible, the imaginary part of the RI, κ=cμ_a/(2ω), may be directly measured. The second part linearly modulates the phase of the interference signal, which can be processed to yield depth resolved information by simply taking a Fourier transform, as is commonly done in spectral domain OCT. Lastly, the third term describes dispersion due to the sample. This term shows a non-linear modulation of the phase, which can degrade the resolution of the axial information in OCT, but also contains the wavelength-dependent changes in the real part of the RI. Previous efforts to quantify absorption [2–4] and scattering [9], have only used the intensity and the linear phase term and have ignored the information contained in the dispersive term.

Algorithms have been developed for removing dispersion inherent in an optical system or due to a sample, based on removing the phase terms that are non-linear with respect to ω [10]. One such algorithm, presented by Zhu et al. [10], fits the unwrapped phase of the signal to a line of the form φ = (ω/c₀)L−2πm, where m is a positive integer and L is the wavelength-independent, best estimate of the constant 2(z′ − dn₀) in Eq 3. The residual phase, Δφ, which is the difference between the unwrapped phase and φ, is then subtracted from the phase of subsequent acquisitions to obtain dispersion free signals. Therefore, the residual phase is related to the real part of the RI by Δφ =(ω/c₀)2dΔn(ω). Then, by principles of causality, and using Kramers-Kroning (KK) relations, the real part of the RI may be expressed in terms of the imaginary part, which is proportional to the absorption coefficient. Note that Δn and μ_a are quantities linearly-dependent on concentration.

Let us consider the quantification of hemoglobin (Hb) concentration for two cases. In the case where the scattering coefficient is negligible (case A), the real and imaginary parts of the RI may be calculated simultaneously. This case is highly idealized and only serves as a base of comparison for case B, where scattering is not negligible. In case A, μ_tot = μ_a = 2κω/c₀, and the imaginary part of the RI (κ) can be directly obtained using TF analysis, while the real part of the RI can be calculated from Δφ. Both independent measurements may be used to measure the concentration of chromophores. However, in a more biologically relevant case, where μ_s is not negligible and unknown (case B), the measured attenuation, obtained from TF analysis, will overestimate chromophore concentrations. Erroneous estimations may be avoided by introducing other free parameters, but this process yields results with low confidence intervals [5]. On the other hand, for case B,Δφ will give the same results as in the idealized case A, for equal chromophore concentrations, regardless of the influence of scattering. Thus, because the real RI of the absorber is calculated from Δφ, the imaginary part of the RI, which is proportional to the absorption coefficient (μ_a), may be determined independently of scattering using the KK relation. Lastly, by using the determined μ_a and the measured total attenuation coefficient, μ_tot, for case B, the scattering coefficient may also be obtained, simply by subtraction, μ_s = μ_tot − μ_a.

To demonstrate the validity of this approach, LCI signals from scattering and non-scattering Hb phantoms were analyzed. The system used a typical Michelson interferometer geometry, where broadband light from a supercontinuum source (Fianium, Eugene, OR), is focused onto the sample. A series of filters are used to shape the source spectrum, thus delivering a total power of ~1.5mW, with a spectral range from ~450nm to 700nm, onto the sample (see inset of Fig. 2). Scattered light returned from the sample is mixed with a reference field and relayed to a spectrometer for detection. With the center wavelength λ₀=575nm, spectral resolution δλ=0.2nm, and bandwidth Δλ=240nm, we operate in a spectral region where the light experiences high degrees of absorption from Hb, which in turn results in significant changes in the real part of the RI.

Fig. 2.

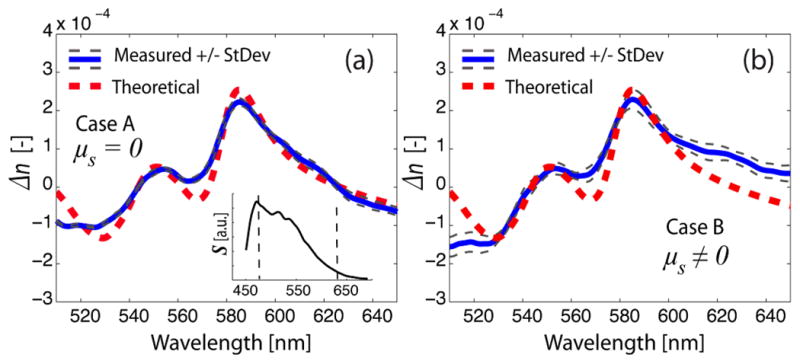
Measured change in the real part of the refractive index of the Hb phantoms without scattering (case A) (a), and with scattering (case B) (b). The theoretical change in the real part of the refractive index of Hb, with a concentration of 40 g/L, is also plotted. The inset illustrates the source’s spectrum, S, with the dotted lines denoting the bandwidth used for estimating concentration using the real part of the RI.

First, the absorption due to the sample is analyzed to obtain the imaginary part of the RI. For case A, fully oxygenated Hb (Sigma-Aldrich, St. Louis, MO), diluted to 40 g/L in water, was used. For case B, 10.75% by volume of the aqueous solution in the phantom was made up of 10%-Intralipid (IL), which possesses a scattering coefficient four orders of magnitude greater than its absorption coefficient. The solutions were then placed between microscope slides with spacers used to set the sample thickness to 400 μm. For comparison, the total Hb absorption from these samples is approximately equivalent to a 100 μm thick sample of whole blood (150 g/L Hb) or a few millimeters of tissue (~2–7 g/L). Depth resolved spectral profiles were acquired from the interferometric data using the dual window method as described in [4]. To obtain concentration values, individual Hb spectra were acquired and normalized by a reference spectrum obtained from the average of 10 acquisitions of a pure water sample. The logarithm of the ratio was taken, yielding, ln(I/I₀) = −μ_ad = −Cdε(ω)/MW, where ε(ω) is the molar extinction coefficient, which is independent of Hb concentration (C), I₀ is the reference water spectrum, and MW is the molecular weight of Hb (MW = 64,500 g/mole). Since ε(ω) is known [11], a linear least squared method was used to estimate C. The average of 10 measurements for case A, gave C = 40.48 +/− 2.30 g/L, in good agreement with the known concentration. For case B, C = 58.13 +/− 4.35 g/L, which, as expected, overestimates the actual Hb concentration due to the contribution to attenuation from scattering, which is not accounted for in this simple model. The measured cumulative absorption for cases A and B, and theoretical absorption from Hb are shown in Fig 1(a). Fig 1(b) shows the measured total attenuation coefficients along with the theoretical absorption coefficient of Hb.

Fig. 1.

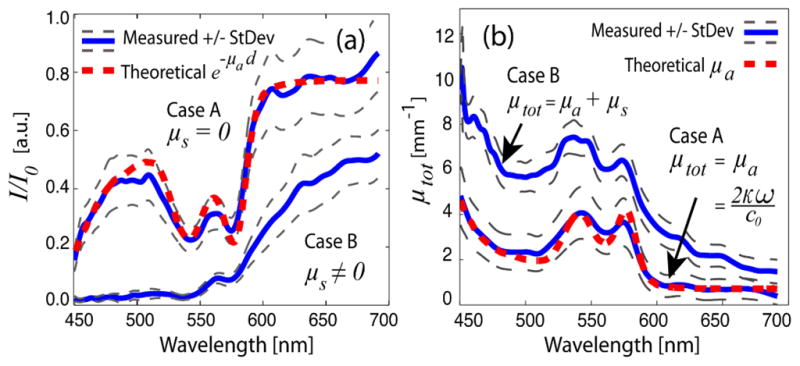
Measured cumulative absorption (a) and total attenuation coefficient (b) of the Hb phantoms without scattering (case A) and with scattering (case B). The theoretical absorption with d = 400μm and C = 40 g/L (a), and absorption coefficient with C = 40 g/L (b), are also plotted.

Next, the non-linear phase term was analyzed to determine the real part of the RI. After dispersion effects inherent in the system and resulting from a water phantom were accounted for, the residual phase, Δφ, from Hb phantoms, was obtained using the method described above. Then, using a subtractive KK relation [8], Δn values, which depend linearly on concentration, were determined; thus allowing assessment of Hb concentrations via a linear least squares fitting method. Here, a limited bandwidth was used to avoid regions of low intensity, due to the source, as seen in the inset of Fig. 2, and due to regions of substantial Hb attenuation at the lower wavelengths, as seen in Fig. 1. Based on analysis of the nonlinear phase, we obtained C = 39.80 +/− 1.00 g/L for case A, and C = 41.09 +/− 1.93 g/L for case B; both are in excellent agreement with the known Hb concentration. The measured and theoretical Δn values are shown in Fig. 2(a) for case A and in Fig. 2(b) for case B. Note that the theoretical and measured real RI profiles are in good agreement for both cases; however, some discrepancies are observed at the edges of the range of analysis for case B, which need further investigation. From these results, the imaginary part of the RI, and hence μ_a, may be determined independently of scattering. Since the calculated concentrations for both cases are approximately equal, the absorption coefficient for case B (not shown) is the same as μ_tot= μ_a for case A in Fig. 1(b).

The scattering coefficient of the scattering sample (case B) can now be determined from the imaginary part of the RI. The obtained μ_a is subtracted from the total attenuation coefficient, μ_tot, to give μ_s (Fig. 3). These results were then compared to a model of the form μ_s = αC_IL λ^−2.4, which has been shown to be an adequate model of 10%-IL scattering for a wavelength range of 400nm–1100nm and concentrations of 4%–17% [12]. Here, the concentration of 10%-IL, C_IL, is defined as the ratio between the volume of 10%-IL and the total aqueous solution. Further, α is a concentration-independent factor, which, in part, accounts for inconsistencies in the manufacturing process and must therefore be experimentally measured for each batch of 10%-IL. To obtain α, a HeNe laser was used in a transmission experiment, where 10%-IL was diluted to different concentrations in 5mm-thick glass cuvettes. The average valueα = 9.62 +/− 2.8 was used to determine a best-fit 10%-IL concentration from the measured μ_s, for case B. This analysis gave C_IL = 10.40 +/− 1.40%, in very good agreement with the actual 10%-IL concentration (10.75%). Note that by using the average α for C_IL =10.75%, we obtain an ideal μ_s = 3.10 +/− 0.9 mm⁻¹ at λ=632.8nm: this value is used as a calibration point to assess the theoretical μ_s illustrated in Fig. 3.

Fig. 3.

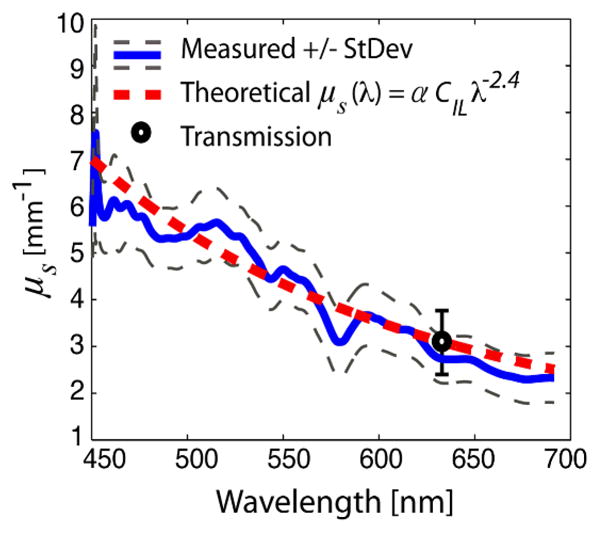
Measured and theoretical scattering coefficient of 10% IL with a 10.75% concentration.

In conclusion, we have derived a relation that yields the real part of the RI from the non-linear phase term of interferometric signals in LCI. Using this relation, in combination with TF analysis, the absorption and scattering coefficients may be separated for samples that both scatter and absorb light, without a priori information. We validated the approach by analyzing the composition of Hb phantoms with and without scattering present. The results show that this method may help overcome the issues that currently prevent depth-resolved interferometric techniques from quantifying absorption in turbid samples. Further, this method may be readily extended to SOCT for imaging, in addition to allowing quantification of chromophores in blood and tissue in vivo.