The Hill Model for Binding Myosin S1 to Regulated Actin is not Equivalent to McKillop & Geeves Model

Abstract

The Hill two-state cooperativity model and McKillop-Geeves (McK-G) three-state model predict very similar binding traces of myosin S1 binding to regulated actin filaments in the presence and absence of calcium and both fit reasonable well the experimental data.¹ Here we compared the Hill model and the McK-G model for binding myosin subfragment-1 (S1) to regulated actin against three sets of experimental data: the titration of regulated actin with S1 and the kinetics of S1 binding of regulated actin with either excess S1 to actin or excess actin to S1. Each data set was collected for large range of specified calcium concentrations. Both models were able to generate reasonable fits to the time course data and to titration data. The McK-G model can fit all three data sets with the same calcium concentration sensitive parameters. Only K_B and K_T show significant calcium dependence and the parameters have a classic pCa curve. A unique set of the Hill model parameters was extremely difficult to estimate from the best fits of multiple sets of data. In summary, the McK-G cooperativity model more uniquely resolves parameters estimated from kinetic and titration data than the Hill model, predicts a sigmoidal dependence of key parameters with calcium concentration and is simpler and more suitable for practical use.

Introduction

Contraction in striated muscle is regulated by calcium and the actin filament-associated proteins tropomyosin (Tm) and troponin (Tn). In relaxed muscle, the absence of Ca²⁺ induces Tn to hold Tm in an azimuthal position that sterically blocks myosin binding sites on F-actin and, therefore, inhibiting muscle contraction and force generation. In contrast, during muscle activation, the presence of Ca²⁺ changes the position of the TmTn complex, moving it azimuthally to a position where it inhibits strong myosin binding to actin, thus favoring actin-myosin interaction and muscle contraction.^{2; 3} When a myosin head strongly binds to an actin filament, it further displaces the TmTn complex, generating a larger angular displacement, which facilitates binding of nearby myosin heads; this is a potential origin of the cooperativity in myosin binding observed during muscle contraction.

Muscle contraction within a sarcomere lattice is generated by cyclic binding and unbinding of myosin heads extending from the thick filament with the actin (thin) filament. Coupling the actomyosin cycle operating in a complex three-dimensional lattice with any model of thin filament regulation is complex and is associated with a large number of uncertainties. Before attempting to model the complete sarcomeric system it is wise to use a simpler system, such as isolated proteins in solution, in order to establish a calcium-dependent kinetic model of myosin binding to regulated actin.^§1

In solution, myosin and its subfragment 1 (S1) bind to unregulated filamentous actin (F-actin in the absence of Tm and Tn) with no measurable cooperativity and no dependence on calcium concentration. The binding kinetics involves at least two binding steps,^{4; 5} an initial weak binding to an actin attached or A-state followed by isomerization to the strongly bound, rigor-like R-state.^§2 In the presence of Tm and Tn, the same two step binding process occurs but the equilibrium binding appears highly cooperative in the absence of Ca²⁺ and is slightly cooperative in the presence of Ca^2+.6 We will consider here three types of myosin binding data where each data set shows different degrees of cooperativity and different sensitivities to the amount of calcium present in solution: two types of kinetic binding reactions under pseudo-first order conditions and a slow titration. We will first examine the case where a small number of myosin heads bind to a large excess of actin sites (pseudo-first order in actin concentration) and then examine the case where a large excess of S1 binds to and saturates actin filaments (pseudo-first order in S1 concentration).

In a previous paper⁷ we considered the best way to perform a robust analysis of a complex regulation model⁸ to a single kinetic data set for excess [actin] to [S1]. Here we will apply this approach to the three types of binding data and compare two fundamental models of thin filament regulation: Hill’s two state model⁹ and McKillop & Geeves three state model.⁸ We will test the ability of each model to define all three data sets, over the full range of calcium concentrations not just at high and low calcium reported before.¹

The cooperative binding isotherm at equilibrium was first interpreted with an one-dimensional Ising model proposed by Hill et al.⁹ (referred to as the Hill model from now on). In this model (see Fig. 1A), a single TmTn complex and seven actin monomers form a unit that can exist in two states: state 1 (inactivated), with weaker binding affinities for myosin, and state 2 (activated), with tighter myosin or S1 affinity. Calcium binding to Tn shifts the population of the two states towards the one with tighter myosin affinity. The binding of myosin is cooperative because seven actin monomers in a unit change state as a group and because of the interactions between two Tm neighboring units. The original model accounted very well for equilibrium binding data,⁹ but the kinetics of the binding reactions was not specified. In a following study model was expanded to account for the steady-state kinetic patterns of ATP hydrolysis at both high and low free Ca²⁺ and for both the excess [S1] and the excess [actin] transient data.¹⁰

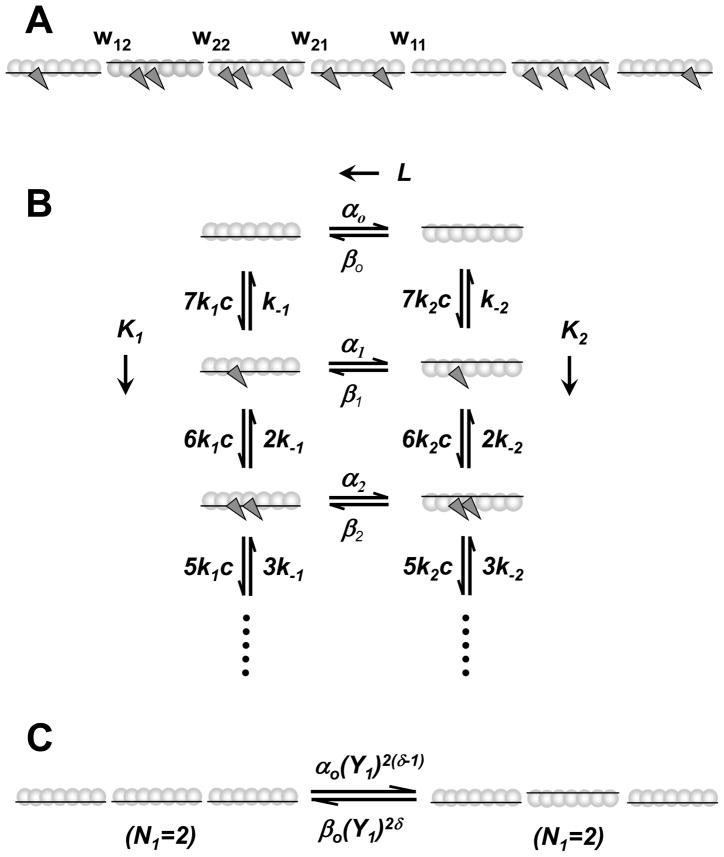
Figure 1.

The Hill two-state model schema. (A) A regulated actin filament is structurally composed as sequential repeat of TmTn complex each interacting with seven actin sites. The TmTn complex is denoted as horizontal line and actin monomers on a single F-actin strand are denoted as circles. Each TmTn complex can be in the inactive state (TmTn line down) and in the active state (TmTn line up). The equilibrium between these states in the absence of S1 in solution is solely defined by the Ca²⁺ concentration. In the presence of S1, the rate of myosin binding to regulated F-actin is regulated by the ratio of the inactive and active states. The binding of S1 (dark gray triangles) is permitted in both inactive and active actin₇·TmTn states but it is severely inhibited in inactive state. The nearest-neighbor interactions between two neighboring TmTn units is defined by the interaction energy, w_ij, between i and j actin₇·TmTn states. (B) The kinetic scheme showing the transitions between for actin₇·TmTn states (columns), defined by intrinsic equilibrium constant, L = α_o/β_o, and the kinetics of myosin binding to either inactivated and activated states, defined by equilibrium constants, K₁ = k₁/k₋₁ and K₂ = k₂/k₋₂ respectively. Here c is the concentration of free S1 in solution, k₁ and k₂ are S1 binding rate constants, and k₋₁ and k₋₂ are rates of unbinding of S1 from F-actin. The transition rate constants of an actin₇·TmTn unit between inactive and active states, α_m and β_m, depends on the number of S1 bound to the unit, m. (C) The cooperativity of TmTn units between inactive and active states depends on the number of the two neighbors that are in State 1, denoted as N₁, the interaction energies Y₁ = Y₁₁Y₁₂, and δ is a fixed constant between 0 and 1. Note that N₁ can have values of 0, 1, or 2. The backward rate constants and other fixed parameters used in all simulations, unless are denoted in the figure legends differently, are taken to be β_o = 300 s⁻¹, Y₂ = 0.208, k₋₁ = 500 s⁻¹ and k₋₂ =0.09 s⁻¹, γ =0.8 and δ =0.5.

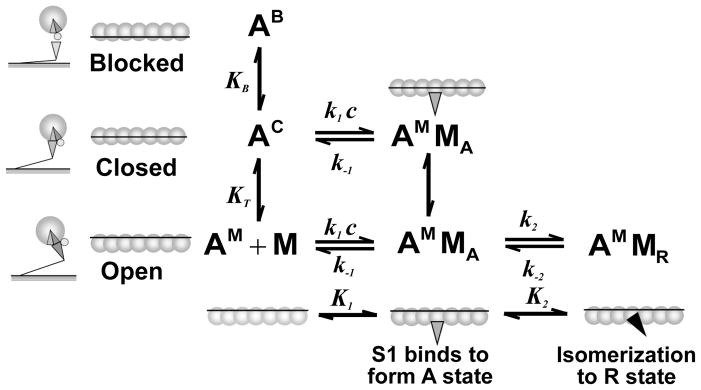
McKillop and Geeves proposed a three-state model⁸ (referred to as the McK-G model) in which several actin monomers (typically 7) and a TmTn complex form a unit which can exist in three states – blocked, closed and open (see Fig. 1B). Subsequently, structural studies using electron microscopy, three-dimensional image reconstruction^{2; 11; 12} and low angle X-ray scattering revealed that addition of calcium (Ca²⁺) causes an 15°–25° azimuthal movement of tropomyosin from the outer to inner domain and that S1 binding causes a further 8°–10° shift. This finding was consistent with the view that the actin filament (F-actin) and the TmTn complex can exist in three distinctive structural states. A common nomenclature for the three states was established as the B or blocked state, the C or calcium induced state, and the M or myosin induced state.¹³ In the B-state, myosin S1 binding to actin is prohibited; in the C-state, S1 can bind with actin, but cannot isomerize further to the strongly bound R-state; in the M state, S1 can bind to F-actin and can be isomerized. The unit distribution between three states is affected by calcium concentration.

Chen, et al.¹ compared the predictions of the Hill and McK-G models by fitting the S1 binding isotherms⁸ and they demonstrated that these two models can equally well fit the experimental data. The Hill model used a Monte Carlo algorithm in order to include nearest neighbor interaction between TmTn units (Fig. 1C) while McK-G model used a probabilistic algorithm (Fig. 2). Although in the original McK-G model the nearest-neighbor interaction between TmTn units was not included, the model predictions fitted the experimental data equally well as the Hill model. This finding led to conclusion that the Hill and the McK-G models could be presumed to be mathematically equivalent.¹ However, it is important to note that the underlying molecular mechanisms of activation and kinetics of S1 binding to actin are substantially different in these two models. In the McK-G model an isolated actin unit needs to pass through an intermediate state between the “off” state to the “on” state which has been identified structurally,^{2; 11; 12} thus, McK-G model requires a two step process for S1 binding. This model more precisely predicts the fall of fluorescence in stop flow and titration experiments because the reduction of the fraction of actin monomers with bound myosin into the isomerized state strictly correlates with reduction of pyrene labeled actin fluorescence. The McK-G model employs a single rate constant for S1 binding to the C-state of actin-TmTn to give the A-state of actin. S1. The actin₇·TmTn complex can shift into the M-State before isomerization of the A-state to the R-state of S1. In contrast, in the Hill model the intermediate state is not necessary, but the model does require two different rate constants for binding of S1 to actin monomers depending whether the Ca²⁺ is bound to troponin or not – in effect the calcium-bound and calcium-free forms of the state have different properties. In addition, the Hill model cannot separate the populations of A- and R-states and therefore the fraction of actin monomers with bound myosin less precisely correlates with reduction of pyrene labeled actin fluorescence. This is of little significance because the A-state occupancy is almost always low.

Figure 2.

Mckillop-Geeves (McK-G) three-state model scheme.⁸ In the McK-G model the structural unit, actin₇·TmTn, is schematically shown as seven open circles representing the actin monomers connected via a line representing the tropomyosin. This unit exists in a dynamic equilibrium between the three states as represented by the different positions of tropomyosin: the blocked state, A^B_, in which no myosin-S1 binding can occur, the closed or calcium induced state, A^C_, in which only weak binding of S1 can occur, and the open or myosin induced state, A^M_, which allows isomerization of the myosin-S1 to the rigor-like state. The ratio of the three states in the absence of myosin-S1 is defined by the equilibrium constants K_B (between the closed and blocked states) and K_T (between the closed and open states). The blocked state is only present in the absence of Ca²⁺ when the Tn complex is tightly bound to the thin filament; in the presence of Ca²⁺, there is little or no occupancy of the blocked state. Weakly bound myosin states are denoted as A-states (A^MM_A) and rigor-like states are denoted as R-states (A^MM_R). The rate of myosin binding is defined by equilibrium constant K₁= k₁c/k₋₁, and the rate of isomeration of S1 into R state is defined by equilibrium constant K₂ = k₂/k₋₂. Backward rate constants used in all simulations are taken to be k_−B = 100 s⁻¹, k_−T = 3000 s⁻¹, k₋₁ = 10 s⁻¹ and k₋₂ =5 s⁻¹. Also the equilibrium constants were fixed over all simulations, unless is denoted differently in the figure legends are: K₁ = 0.22 μM⁻¹ and K₂ = 200.

Overall, both models have sufficient number of chemical states to account for the observed biochemical and structural data. For example, both models were able to generate the lag in the time course of S1 binding observed in stop flow experiments in the absence of calcium when S1 is in excess of regulated actin. Although the good fits achieved using the Hill model suggest that the activation of actin filament does not require the existence of an intermediate state, the McK-G model is more consistent with structural data.^{2; 11; 12} An essential difference between the two models is that Hill model is truly a two-state system and allows the state of the structural units to propagate cooperatively along the filament by including interaction between neighbouring actin₇·TmTn units.

The McK-G model assumes the actin₇·TmTn structural unit as the basic unit that switches among 3-states but has a fudge factor (the apparent cooperative unit size) to account for longer range cooperativity.¹⁴ This “apparent cooperative” unit was only necessary to fit the titration data where the standard unit of 7 was sufficient to fit the data in the absence of calcium but it should be increased to 8–13 for different experimental systems when calcium was present.¹⁴ In the absence of calcium this was rationalised by the strong TnI actin interactions every 7 sites (in the B or blocked state) limiting longer range cooperativity. In the presence of calcium, however, these strong interactions are absent and longer range cooperativity is manifest for the closed to open state transition (Fig. 1B). However, modelling intermediate calcium concentrations become problematic if the cooperativity is a mixture of 7 and larger unit sizes. We resolve this issue by creating a full version of the McK-G model that allows explicit interactions of neighbouring TmTn units, and, therefore, variable cooperativity. This, however, required the modelling of a complete filament.

In this study we evaluate the ability of the Hill and McK-G (probabilistic and stochastic) models to describe a wide range of experiments in both transient and titration binding experiments to evaluate how well the models can fit the data collected at the different experimental conditions. Chen et al.¹ previously compared these models for the high and low calcium conditions and concluded that both models could describe the data well. Here we extend this study to a range of calcium concentrations and demonstrate that these models can predict multiple sets of data with a tight self-consistent set of model parameters. The model parameters are estimated by a Damped Least Square (DSL) method which provides a resolution matrix which quantitatively determines the degree of interdependence between estimated parameters, and therefore quantitative evaluation of the uniqueness of estimated parameters.⁷

Results and Discussion

We examined both the Hill and the McK-G models using data acquired from the two types of transient binding experiment (with either excess [actin] or excess [S1]) and from titrations. In order to minimize the internal errors each data set was collected for an entire pCa range for both excess [actin] and excess [S1] using the same protein preparation on the same day. However, because of the complexities of the experiments and the length of the experimental protocols, the titrations were collected on a different occasion from the kinetic data.

Fitting the Fluorescence Transient and Titrations Data

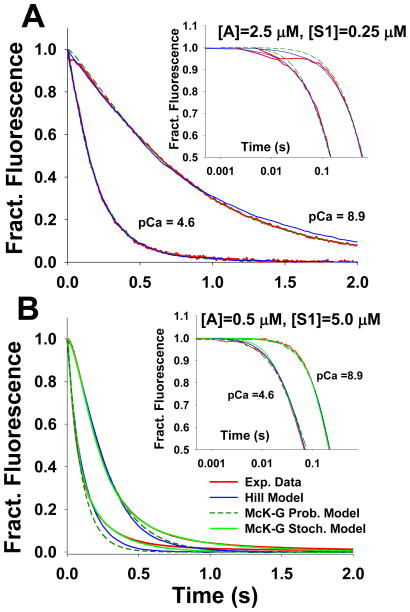
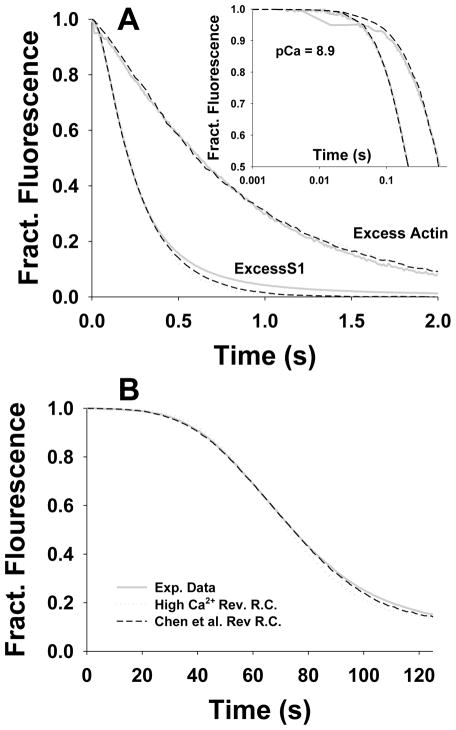
Fig. 3 shows the fluorescence transient data for the excess actin (3A) and excess S1 (3B) measurements at low (pCa 8.9) and high (pCa 4.6) calcium concentrations. The best fits for each model are superimposed on the data. In the case of the excess actin transients, the data can be well described by single exponentials¹⁵ and can be equally well fitted by either model as shown by Chen et al.¹ (Fig. 3A). In the case of the excess S1 transients at high calcium concentrations the transients are similar to those at excess actin except for the appearance of a slow component (Fig. 3B). At low calcium the transient now has a distinct lag at the early times and a similar slow component at longer times. Both models can give an accurate description of the transients for 60–70% of the profile but the fits deviate at longer times where the slow component dominates. This slow component was common to all transients collected at various Ca²⁺ concentrations when [S1] is larger than [actin]. This feature is described in the methods section as “negative cooperativity.” Including the negative cooperativity into the stochastic McK-G model provides excellent fits over the complete data set (Fig. 3B). This cooperativity has no effect on the quality of the fitting to the first 60% of the curves or to the values of estimated parameters. Including negative cooperativity into the Hill model would have a similar effect.

Figure 3.

Model predictions of stopped flow fluorescence transient for S1 binding to regulated pyrene actin at high (pCa 4.6) and low (pCa 8.9) calcium concentrations. The stopped flow transient data (red lines) agreed well with predictions of Hill’s Model (blue line), as well as with the McKillop-Geeves probabilistic and stochastic models (dashed dark green and solid green lines, respectively): A) for excess F-actin (2.5 μM pyrene actin) vs 0.25 μM S1 after mixing; and B) for excess S1 (5 μM) vs 0.5 μM pyrene actin. The slowing of myosin binding at higher level of occupancy of actin by S1s can be only predicted by including negative cooperativity (see methods) into the model, as demonstrated by the fit of McK-G stochastic model (solid green lines).

The McK-G stochastic model and the Hill model include the nearest neighbor Tm-Tm cooperativity. Adding this type of cooperativity provides only a marginally better fit than the McK-G probabilistic model and these minor differences are noticeable only in the early phase of the stopped flow transient with excess S1 (Fig. 3B).

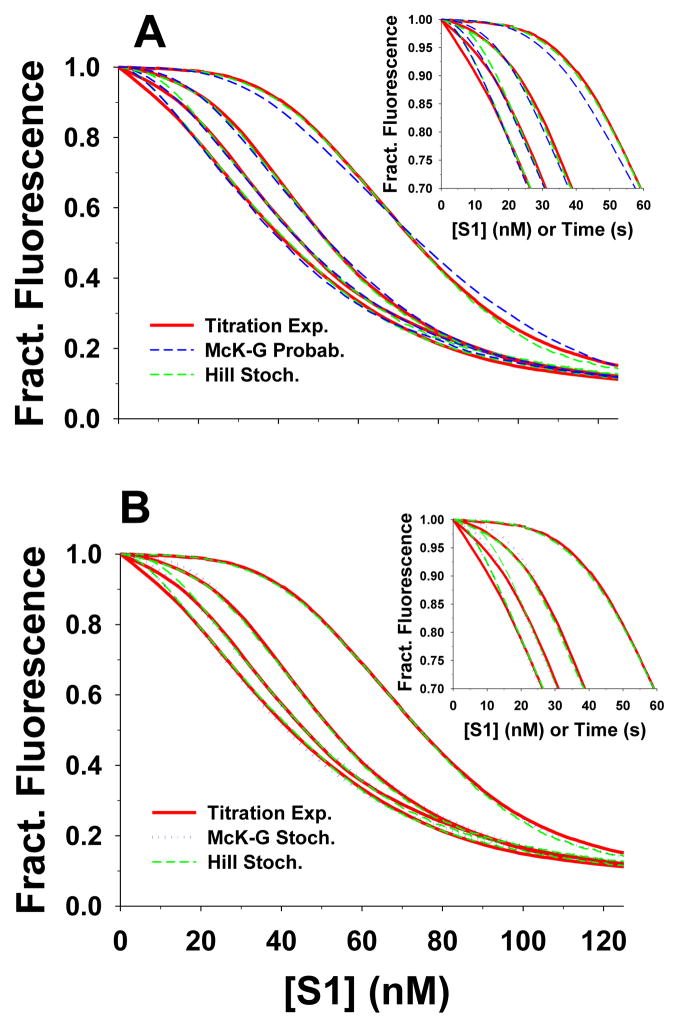
The titration data are technically more difficult to collect than the transient kinetic data. Each titration uses 50 nM pyr-actin and takes up to 5 minutes to complete. These conditions, similar to those developed by Maytum et al.,¹⁴ allow better resolution of the sigmoid shape of the curve and thus more reliable fitted parameters than the original data of McKillop & Geeves.^§3 However, this measurement requires a high degree of stability in the proteins and the fluorimeter. For these reasons we collected data at just four different pCa values. The titration curves and the best fits to the Hill model and the McK-G model are shown in Fig 4. The Hill model predictions for the titrations provided excellent fits to the observed binding isotherms (dashed green line Fig. 4A,B). The McK-G probabilistic model also provided excellent fits to two highest calcium concentrations but the fits progressively deteriorated at the lower two concentrations (dashed blue line in Fig. 4A). The inclusion of cooperativity factors in the McK-G stochastic model, however, provided excellent fits to the titration data for all pCa values (dotted blue line in Fig. 4B). The difference in the estimated parameters by fitting the data by the McK-G probabilistic and the McK-G stochastic model are indistinguishable except for pCa 8.9 and in lesser degree for pCa 6.8. Thus, the inclusion of a TmTn-TmTn cooperativity factor (other than 1.0) was only necessary for pCa 8.9 and 6.8. The full set of fitted parameters is given in Table 1.

Figure 4.

The best fits of titrations of 50 nM pyr-actin-phalloidin with S1 in the presence of TmTn (0.1 μM) using the Hill and McKillop-Geeves models. The titration time courses of four calcium concentrations (pCa 4.6, 5.4, 6.8 and 8.9) are shown as red lines; in all experiments actin concentration was 50 nM and rate S1 injection rate was 1nM/s. The predictions of the Hill model are denoted as green dashed line, whereas the predictions of McK-G (probabilistic and stochastic) model are denoted as blue dotted lines. The backward rate constants of McK-G model are the same as denoted in Fig. 2. A) Predictions of the Hill model and McK-G probabilistic model and B) predictions of the Hill and McK-G stochastic model.

Table 1.

Estimated kinetic rate constants of the McKillop-Geeves stochastic model from the best fits of family of titration experiments at four Ca²⁺ concentrations plotted in Fig. 4.

	Calcium Concentration
pCa	4.6	5.4	6.8	8.9
kB	901.9	714.4	40	30
k−B	100	100	100	100
kT	640	380	236	24.24
k−T	3000	3000	3000	3000
k1	2.5	2.5	2.5	2.5
k−1	10	10	10	10
k2	2000	2000	2000	2000
k−2	5	5	5	5
fTmTm	1.0	1.0	3.0	5.0
fS1	1.0	1.0	1.0	1.2
KB	9.0192	7.1443	0.2000	0.1100
KT	0.2134	0.1269	0.0760	0.0096
K1	0.25	0.25	0.25	0.25
K2	400	400	400	400

k₁ has units of μM⁻¹s⁻¹; K₁ has units of μM⁻¹; equilibrium constants K_B, K_T and K₂, and cooperativity factors f_TmTn and f_S1 are dimensionless; all other rate constants have units of s⁻¹.

Dependence of Parameters on Calcium Concentration

The estimates of the free parameters for the high and low Ca²⁺ stopped flow data (Fig. 3) and the titration data (Fig. 4) does not distinguish between the models as they all generate similar quality fits to the data sets. A more rigorous test is to examine the behavior of the parameters over the full pCa range and to define which of the parameters are sensitive to the calcium concentration. The expectation is that only a subset of the parameters will change with calcium and these should in some way follow the degree of saturation of the thin filament with calcium. We repeated the fitting procedure for a family of stopped flow transients at 8–10 different pCa values between 4.6 and 8.9 for both the excess actin and the excess S1 protocols. Complete sets of experimental data for both excess actin and excess S1 are shown in the supplementary material. To simplify the data fitting approach we initially fixed the values of the reverse rate constant and varied just the forward rate constants. By fixing the reverse rate constants the Hill model is reduced to just four free parameters, L′, Y, K₁ and K₂. For the McK-G model there are two free parameters K_B, K_T and for the stochastic McK-G three (including the Tm-Tm cooperativity factor f_TmTm) since K₁ and K₂ are assumed to be independent of calcium. In addition good fits for excess [S1] to [actin] transients require the negative cooperativity parameter, f_S1, increasing number of McK-G model free parameters to four.

The Hill Model

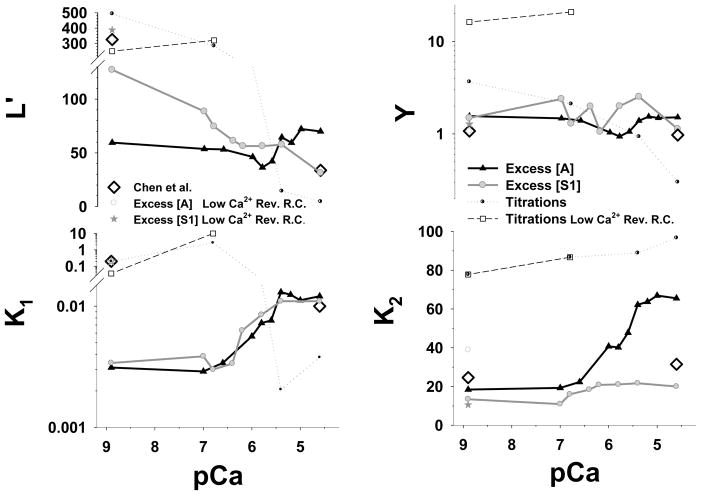
The estimated parameters from the best fits to the Hill model to the stopped flow data (for both excess actin and excess myosin) and titrations over the physiological range of Ca²⁺ concentrations are shown in Fig. 5. The titration parameters are extracted from fits shown in Fig. 4. For the fits to the Hill model we used exclusively the values of the reverse constants, reported by Chen et al.¹ at high Ca²⁺ concentration (Table 2). While good fits to each data set were obtained, the estimated free parameters do not yield a common pattern of the calcium dependence of these parameters. Looking at the plots in detail allows the following observations. Y appears to be almost independent of calcium for all three data sets with a value close to 2 (range 1–3) in each case. In the middle of the pCa range L′ is also almost independent of calcium with a value of approx 55–75 but the values at the two extremes do differ significantly −50, 130 and 500 at pCa 8.9 for excess actin, excess S1 and the titrations respectively; At pCa 4.6 the values were 60, 35 and 10 in the same order.

Figure 5.

Estimated Hill model parameters L′, Y, K₁ and K₂ from the best fits of stopped flow and the titration data are plotted vs. pCa. The parameters L′ and K₁ are plotted on a log scale whereas Y and K₂ are plotted on a linear scale. The black line with filled triangle up symbols is best fit of the excess actin data set, the grey line with grey filled circle symbols is the best fit the excess S1 data, and the black doted line with semi-filled circle symbols is the best fit of the titrations. The reverse constants β₀ =300 s⁻¹, k₋₁ =500 s⁻¹, k₋₂ =0.09 s⁻¹ and Y₂ = 0.208 are kept the same in all simulations. For comparison we also plotted parameters estimated by Chen et al. from different data sets (open black diamonds).¹ Chen used in his fitting scheme different values for the reverse constants k₋₁ and Y₂ at low Ca²⁺ concentration, denoted as “Low Ca²⁺ Rev. R.C.”, having values of 3 s⁻¹ and 0.0703 respectively. The estimated parameters for these reverse constants are denoted grey open circles for the excess actin, as dark grey stars for the excess S1, and as black dashed line with open square symbols for titrations.

Table 2.

Estimated parameters of the Hill model from the best fits of stopped flow data (for both excess [S1] and excess [actin]) and titrations at pCa 8.9. The comparison contrasts the estimated parameters for prescribed reverse constants k₋₁ = 500 s⁻¹ and Y₂ =0.208 reported in Chen at al.¹ at high [Ca²⁺] and used in all our simulations (denoted as “High Ca²⁺ Rev. R.C.”) vs. the reverse constants k₋₁ =0.6 s⁻¹ and Y₂ = 0.0703 reported in¹ at low [Ca²⁺] (denoted as “Low. Ca²⁺ Rev. R.C.”).

	Stopped Flow				Titrations
	Excess Actin		Excess Myosin		High Ca2+ Rev. R.C.	Low Ca2+ Rev. R.C.
	High Ca2+ Rev. R.C.	Low Ca2+ Rev. R.C.	High Ca2+ Rev. R.C.	Low Ca2+ Rev. R.C.
αo	82.3	200	81	200	200	200
βo	300	300	300	300	300	300
Y1	5.576	15.27	7.149	18.2	78.0	52.0
Y2	0.208	0.0703	0.208	0.0703	0.2080	0.0703
k1	2.29	0.6	1.7	0.6	18	0.6
k−1	500	3.0	500	3.0	500	3.0
k2	1.761	3.50	1.207	0.95	7.00	7.00
k−2	0.09	0.09	0.09	0.09	0.09	0.09
γ	0.8	0.8	0.8	0.8	0.8	0.8
δ	0.5	0.5	0.5	0.5	0.5	0.5
K1	0.0046	0.200	0.0034	0.200	0.036	0.200
K2	19.57	38.89	13.42	10.56	77.78	77.78
Y	1.160	1.073	1.487	1.279	16.224	3.656
L′	98	145	127	173	250	493

k₁ and k₂ have units of μM⁻¹s⁻¹; K₁ and K₂, have units of μM⁻¹; equilibrium constants Y and L′, and cooperativity parameters Y₁, Y₂, γ and δ are dimensionless; all other rate constants have units of s⁻¹.

K₁ shows a clear [Ca²⁺] dependence and for the two kinetic data sets the values are similar and vary from 0.003 at low calcium to 0.01 at high calcium. Fitting the K₁-pCa relationship to a classic Hill equation^§4 gave a Hill coefficient of ~ 1.8 for excess [actin] and ~2.5 for excess [S1] with mid point pCas of 5.72 and 6.03 respectively. The titration data gives quite different values and they change in the opposite direction – decreasing as calcium concentration increases. The rate constant K₂ obtained from the best fits of the excess actin data set does show a marked sigmoidal [Ca²⁺] dependence with low calcium values agreeing with the excess S1 data (~20) and high calcium values close to the titration data (of about 70). However, K₂ shows low calcium dependence for both the excess S1 data (in range of 10–20) and the titration (in range of 80–100). Also lower K₂ values are estimated for the excess [S1] (mean of ~15) than for titrations (mean of ~90). A fit to the Hill equation for the K₂ values gives a Hill coefficient of ~1.3 for the excess actin data and ~2.7 for excess [S1] with mid pCa values of 5.79 and 6.62 respectively. The Hill coefficient for the titrations data cannot be extracted because only data for four pCa values were fitted and the K₂- pCa relationship appears linear rather than sigmoidal. The other parameters, L′ and Y, do not show any sigmoidal dependence with pCa or if there is one it is in the opposite direction (Fig. 5A and B).

Looking at the resolution matrix gives some indication of the problems involved in fitting the data (Table 3). For the excess actin data K₂ and Y are well defined in most cases but K₁ and L′ are co-dependent and are not well resolved. For the excess S1 data only K₂ is well resolved but the other 3 parameters are co-dependent and cannot be uniquely defined. The number of parameters in the model is therefore larger than can be uniquely defined by the three sets of experimental data collected over wide range of Ca²⁺ concentrations. We attempted to limit the fitting problem by, for example, fixing the value of Y which appears to be relatively constant and/or the value of L′ but he resultant fit deteriorated significantly. Good fits require all four variable parameters but the magnitudes of these parameters can not be uniquely resolved by the data. The fits, therefore, do not result in a well-defined calcium dependence for each parameter.

Table 3.

Calculated error and diagonal elements of parameter resolution matrix of estimated parameters shown in Figs. 5 and 7.

Excess Actin
McKillop-Geeves Model				Hill Model
pCa	R(Kb)	R(Kt)	Error	R(L′)	R(Y)	R(K1)	R(K2)	Error
4.6	0.0049	0.9968	0.4447	1.0000	0.8184	0.6011	0.9318	0.2322
5.0	0.0031	0.9658	0.5582	1.0000	.6159	0.3906	0.7604	0.5801
5.2	0.0056	0.3854	0.5819	0.9548	.8625	0.6670	0.9291	0.3760
5.4	0.0894	0.5864	0.4400	1.0000	0.9356	0.8627	1.0000	1.0014
5.6	0.0907	0.8840	0.6729	0.9969	0.5422	0.4886	0.7917	1.5592
5.8	0.2653	0.8129	0.3359	0.9997	0.4968	0.4924	0.8326	0.7762
6.0	0.7503	0.7490	0.4978	0.0000	0.5934	0.3819	0.6949	0.3949
6.2	0.9052	0.7373	0.2756	1.0000	0.9527	0.8849	0.9661	2.7942
6.6	0.8902	0.4959	0.2720	0.6032	0.7161	0.2766	0.8911	1.3527
7.0	0.8743	0.3561	0.0474	0.3485	0.7338	0.2203	0.8914	1.2546
8.9	0.9519	0.8291	0.0475	0.9324	0.7957	0.2067	0.8958	1.2907

Excess S1
McKillop-Geeves Model				Hill Model
pCa	R(Kb)	R(Kt)	Error	R(L′)	R(Y)	R(K1)	R(K2)	Error
4.6	0.021047	0.8182861	5.1190	0.2915	0.2717	0.8479	0.9455	7.2000
5.4	0.001423	0.7744983	2.3379	0.4209	0.0950	0.6594	0.9520	5.1166
5.8	0.806671	0.8386622	3.0119	0.3567	0.1476	0.7051	0.9697	5.4858
6.2	0.968426	0.8304166	1.8275	0.2702	0.1937	0.3991	0.8519	8.9833
6.4	0.991323	0.8988176	1.6618	0.9643	0.2093	0.5773	0.8724	5.9099
6.8	0.991698	0.8222741	1.2239	0.4107	0.5288	0.6527	0.9689	4.4163
7.0	0.997855	0.955403	0.83566	0.5278	0.2860	0.8407	0.9958	6.2632
8.9	0.985200	0.626658	1.1933	0.6829	0.1985	0.4401	1.0000	1.6470

The difference in pCa dependence of the Hill model parameters, estimated from the excess actin and the excess S1 data, can be explained, by possible inherent nonlinearities. For reference, in Fig. 5 are shown the Hill model parameters (grey diamond open symbols) reported by Chen et al.¹ These model parameters were obtained from best fits of the data adapted by Chen et al. from McKillop and Geeves, 1993 paper.⁸ Note that McKillop and Geeves data were collected under slightly different conditions from the data used here (4 time higher actin concentration, 1.4 times KCl concentration). To test our methodology we estimated the Hill model parameters from the original McKillop and Geeves data⁸ as used by Chen.¹ The estimated parameters were almost identical to those reported in Chen et al.,¹ confirming that differences in the estimated parameters could be due to specific details in the experimental protocols.

What is the Minimal Number of Free Parameters Required by the Hill Model?

The free parameters obtained by fitting the Hill model to the titration data showed quite different trend with an increase of Ca²⁺ concentration (Fig. 5, black doted line with circle half filled symbols) than the constants obtained from stopped flow experiments (solid black and grey lines). Interestingly, the fits of titration data were excellent for higher Ca²⁺ concentrations (pCa 4.6 and 5.4) as they were for the stopped flow fits. However, they were not so good for lower [Ca²⁺] if the reverse constants are kept constant over all four [Ca²⁺]. By close inspection the number of estimated Hill free parameters reported in Chen et al.¹ was six rather than just four equilibrium constants. In particular Chen et al. estimated four equilibrium constants L′, Y, K₁ and K₂, but used different values for the reverse constants k₋₁ and Y₂, one at low and the other at high Ca²⁺ concentrations. These stets of reverse constants, contrasted in Table 2, provided excellent fits of the titrations by the Hill model at both low and high [Ca²⁺] (Fig. 4B).

We compared the best fits and corresponding free constants of these two different sets reverse constants (i.e. k₋₁ and Y₂) at low [Ca²⁺]. The stopped flow fits (Fig. 6A) with Chen et al.’s reverse constants, k₋₁ and Y₂, used at low [Ca²⁺], show only marginally better fit than those fixed over all [Ca²⁺]. The negligible differences in the fits demonstrated that single set of reverse constants, such as values reported by Chen et al.¹ for high [Ca²⁺] (Fig. 5, solid lines), can provide robust estimation the equilibrium constants over all stopped flow data. However, the fits employing the two sets of k₋₁ and Y₂ (at low [Ca]) predicted significantly different values of the equilibrium constants, except K₂, which was fixed for all fits (see Table 2). The estimated parameters for the rate constants reported by Chen et al. at low calcium¹ are denoted in Fig. 5 as grey open circles for the excess actin and as dark grey stars for the excess S1. These results suggest that almost equivalent data fits can be achieved by different sets of parameters when fitting the stopped flow data.

Figure 6.

The comparative best fits of stopped flow and titration data at low [Ca²⁺] (grey solid lines) by the Hill model for the two sets of reverse constants: (i) High [Ca²⁺] reverse rate constants k_{− 1} =500 s⁻¹, Y₂= 0.208 denoted as dark gray dotted lines and (ii) Chen’s reverse rate constants at low [Ca²⁺] k₋₁ = 3 s⁻¹ and Y₂ =0.0703 denoted as black dashed lines. A) For the excess F-actin (2.5 μM pyrene actin) vs 0.25 μM S1 after mixing and for the excess S1 (5 μM) vs. 0.5 μM pyrene actin both at pCa=8.9. B) For titrations at pCa=8.9.

In contrast, the titrations cannot be fitted well at low calcium with a single set of reverse constants (Fig. 6B), but with Chen et al.’s k₋₁ and Y₂ reported at low [Ca²⁺] (Fig. 4 and Fig. 6B). The parameter values at low Ca²⁺ concentrations (pCa 8.9) for different sets of k₋₁ and Y₂ are contrasted in Table 2 and graphically shown in Fig. 5: the parameters estimated at lower [Ca²⁺] (with Chen et al.’s k₋₁ and Y₂ at low [Ca²⁺]) showed more accurate fits at pCa 8.9 and 6.8 (black dashed line with open square symbols) and they differed significantly from parameters estimated from the best fits which used the same reverse constants over all Ca²⁺ concentrations (black dotted line with semi-filled circle symbols).

Despite the reasonable fits of the titrations by using two sets of reverse constants k₋₁ and Y₂, either of the estimated equilibrium constants were strikingly different than those estimated from the stopped flow data (Fig. 5, Table 2). This result points out that the Hill model may not be the best way to represent multiple sets of data because it requires estimation of large number of free parameters and could result in the estimation of a nonunique set of parameters. Although the Hill model is based on a solid theoretical foundation and the cooperative factors are derived from an energy landscape of TmTn–TmTn interactions, the inability to resolve uniquely the model parameters makes it extremely difficult to relate these fundamental concepts with the observations.

The McK-G Probabilistic Model

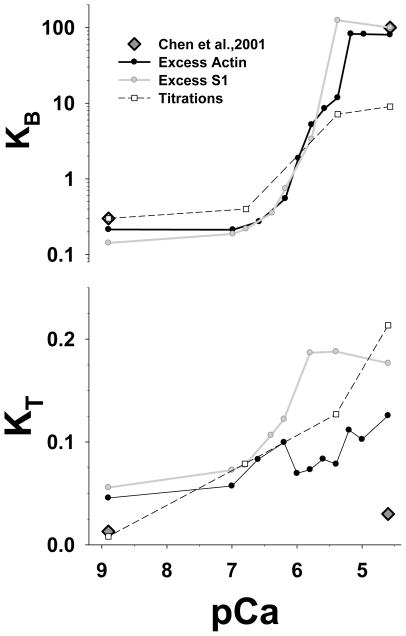
The probabilistic McK-G model provided good fits over all Ca²⁺ concentrations for both stopped flow transients and for titrations fitting only two free parameters (Fig. 7). We showed in our earlier study⁷ that only 2 variable parameters are needed to fit the excess actin data set. Following the same fitting scheme, the estimated K_B shows a similar sigmoidal Ca²⁺ dependence for all 3 data sets over the range pCa 9–6.5 (Fig. 7). Above pCa 6.5 the value of K_B is large and cannot be well resolved, i.e. any value larger or equal 10 fits equally well with minor differences in error. This is because at high [Ca²⁺] only a few of TmTn units (<10%) are in the blocked -state, and the predicted experimental data is insensitive to small changes in the estimated K_B values.

Figure 7.

Estimated McKillop-Geeves (probabilistic) model parameters K_B and K_T from the best fits to the stopped flow and the titration data are plotted vs. pCa. The unit size in all simulations is N=7. The parameter K_B is plotted on a log scale whereas K_T is plotted on a linear scale. The black line is best fit of the excess actin data set, the grey line is the best fit to the excess S1 transient, and the black dashed line with open square symbols is the best fit of the titration data. Dark grey diamonds are the data from Chen et al.¹

A classic Hill analysis shows Hill coefficients of ~2.0 for both the excess actin and the excess S1 data with mid-point pCa values of 5.07. The mid-point pCa values are shifted to higher Ca²⁺ concentrations (than expected) by relatively high values K_B at high [Ca²⁺]. Because the fits are insensitive to K_B if K_B >10, and therefore K_B can take large and somewhat arbitrary value, the mid-point [Ca²⁺] values should be taken with caution, whereas Hill coefficients are more robust, i.e. they are less affected by the relatively large value of K_B at high [Ca²⁺].

The titration data shows similar dependence for the value of K_B. The values of K_B at high [Ca²⁺] are slightly smaller for titrations than from the excess actin and the excess S1. At low [Ca²⁺] the values of K_B for titrations has about the same value as estimated from fits to the standard excess actin and excess S1 data sets (Fig. 7A). The Hill coefficient for titrations is about 1.77, slightly smaller than obtained from stopped flow data sets, and mid-point pCa value is 5.7 i.e. shifted to smaller [Ca²⁺].

The estimated K_T from each of the data sets at pCa 8.9 showed low values of K_T that increase with increasing [Ca²⁺]. The K_T estimated from excess actin and excess S1 data have similar values of about 0.04 low [Ca²⁺] but they differ by factor of 2 at higher [Ca²⁺]. The Hill coefficient of K_T for the excess actin is about 1.45, and slightly larger for the excess S1 of about 1.66. Mid-point pCa values are 6.6 and 6.2 respectively. The estimate of the Hill coefficient is not so reliable for the excess actin case because the sigmoidal shaped K_T -pCa relationship is strongly deteriorated by noisy K_T estimates at higher [Ca²⁺]. The titration data show a similar trend and values as K_T estimated from the stopped flow data, except at low [Ca²⁺] where K_T showed much smaller values, and there is no sigmoidal form of the K_T -pCa relationship.

The McK-G Stochastic Model

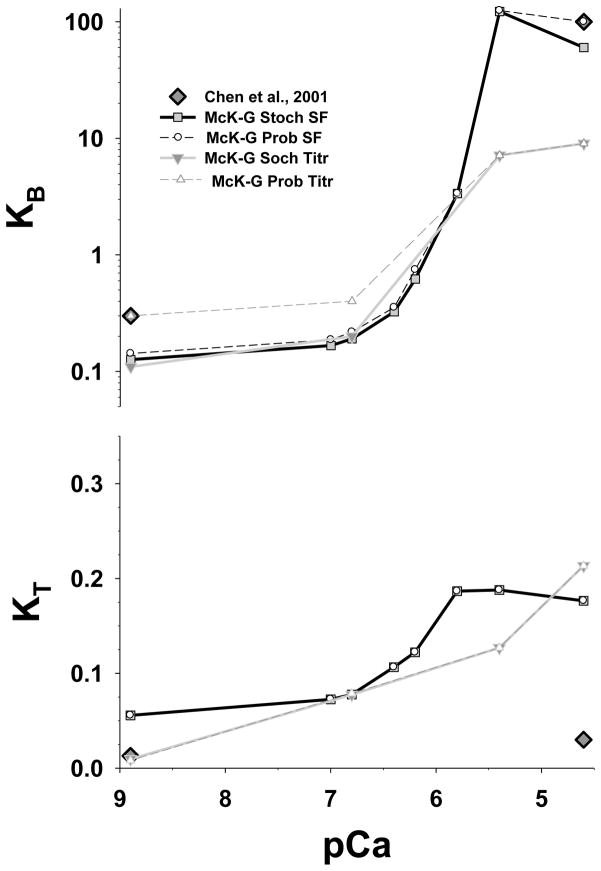
As we showed in Fig. 3, the fits of the excess S1 transients at later times and titrations at low [Ca²⁺] were poor (Fig. 4). We also showed that these fits can be improved by inclusion of cooperativity in McK-G model. The newly developed stochastic McK-G model includes positive cooperativity between TmTn–TmTn units and negative cooperativity of myosin binding. Because the fits to the excess actin data are not affected by either negative or positive cooperativity we only compared predictions of the McK-G probabilistic model with the McK-G stochastic model for excess S1 and for titrations. The estimated parameters are plotted in (Fig. 8), and the parameter values and cooperativity factors are shown in Table 4. TmTn–TmTn cooperativity slightly reduced the estimated value of K_B, and changed K_T very little, while negative cooperativity provided excellent fits at later phase of the transient. The positive cooperativity factor, f_TmTm, is in the range from 1.2 to 2.5 (Table 4), and shows only modest sensitivity to the fits of early part of the transient, suggesting that only weak cooperativity of the neighboring TmTn units is sufficient to make almost perfect fits. The negative cooperativity factor, f_S1, is in the range from 2 to 5.5, has strong effect on later parts of the fit and is essential for obtaining excellent fits to the excess S1 data set. Both K_B- pCa and K_T -pCa show a sigmoidal shape and they have similar absolute values (solid line with filled square symbols in Fig. 8) as predicted by McK-G probabilistic model (dashed line open circle symbols). In order to minimize effect of slowing of myosin binding at longer times, K_B and K_T are estimated from fits of the McK-G probabilistic model to about first 60% of drop in fluorescence. Interestingly, the estimated K_B and K_T from probabilistic and the stochastic McK-G almost coincide confirming that negative cooperativity has no effect on this portion of the fit.

Figure 8.

Estimated McKillop-Geeves parameters K_B and K_T from the best fits of the stochastic cooperative model predictions to stopped flow data for the excess [S1] to [actin] and for titrations as a function of pCa. The unit size in all simulations is N=7. The black line with grey filled square symbols is best fit by McK-G stochastic model of the stopped flow excess S1 data set, the grey line with grey triangle (down) symbols is the best fit the titration data set. For comparison K_B and K_T estimated from the probabilistic McK-G model are show as black dashed line with circle open symbols for the parameters estimated from the stopped flow excess [S1] and from the titration data sets are denoted by dark grey dashed line with triangle up symbols. Dark grey diamonds are the data from Chen et al.¹

Table 4.

Estimated kinetic rate constants of the McKillop-Geeves stochastic model from the best fits of the family of stopped flow transients when [S1] is in excess to [actin].

	Calcium Concentration
pCa	4.6	5.4	5.8	6.2	6.4	6.8	7	8.9
kB	6000	2233.50	336.30	62.00	32.50	19.08	16.70	12.66
k−B	100	100	100	100	100	100	100	100
kT	529.5	563.7	560.1	366.6	319.5	233.1	217.8	167.1
k−T	3000	3000	3000	3000	3000	3000	3000	3000
k1	2.2	2.2	2.2	2.2	2.2	2.2	2.2	2.2
k−1	10	10	10	10	10	10	10	10
k2	1000	1000	1000	1000	1000	1000	1000	1000
k−2	5	5	5	5	5	5	5	5
fTmTm	1.20	1.18	2.00	2.00	2.00	2.50	2.35	2.55
fS1	2.75	2.00	2.00	2.50	3.50	3.80	5.45	5.40
KB	60.000	122.335	3.363	0.620	0.325	0.1908	0.1670	0.1266
KT	0.1765	0.1879	0.1867	0.1222	0.1065	0.0777	0.0726	0.0557
K1	0.22	0.22	0.22	0.22	0.22	0.22	0.22	0.22
K2	200	200	200	200	200	200	200	200

k₁ has units of μM⁻¹s⁻¹; K₁ has units of μM⁻¹; equilibrium constants K_B, K_T and K₂, and cooperativity factors f_TmTn and f_S1 are dimensionless; all other rate constants have units of s⁻¹.

The titration data show almost no change in the fitted values of K_B, except at the two lowest calcium concentrations, nor in the values of K_T which only changed slightly over whole range of calcium concentrations. Positive TmTn-TmTn cooperativity strongly affects fits at these two low calcium concentrations and provides almost perfect fits to the data, suggesting that positive cooperativity is important process at early part of titrations at low [Ca²⁺]. Large cooperativity factor, f_TmTm, > 3, decreases value of K_B at low calcium concentrations (pCa 6.8–8.9). Interestingly, K_B values at the two lowest calcium concentrations coincide with the K_B estimated from fits to the excess S1 data set. This result suggests that TmTn–TmTn cooperatively not only improved overall fits at two lowest calcium concentrations but also brought estimated K_B values close to those estimated from the stopped flow data.

Because of the similarity of the K_B- pCa and K_T-pCa relations obtained from probabilistic vs. stochastic McK-G model fits, the Hill coefficients are also about the same. Only the Hill coefficient for K_B of titrations decreased slightly to 1.82 compared to that estimated from the probabilistic McK-G model (of ~2), and mid point is about the same at pCa of 5.7.

How many Free Parameters are Required by the McK-G model?

The more consistent fits of McK-G model compared to the Hill model are partially due fitting only two parameters, K_B and K_T, unlike the Hill model where for good fits it was necessary to estimate four or even six free parameters. We showed in an earlier study that these 2 free parameters were sufficient to fit the excess actin kinetic data by the McK-G model,⁷ and that increasing of the number of fitted parameters caused poor resolution and inconsistent pCa dependence of these parameters. Our analysis of the resolution matrix suggests that the same is true for each of the three data sets individually. However the best fit of the titration data did require a two fold larger K₂ value than the K₂ used to fit the transient data, and also a slightly larger value of K₁, by about 14%. The increase in K₂ is a likely consequence of lower estimated values of K_T. Because the product of K₁K₂ is directly responsible for fitting the tail of the titration curve, similar fits of the tail can be achieved by decreasing K₂ by factor of two, i.e. taking the same value as used for fits of the transient data sets, and increasing K₁ by factor of two. But, however, the overall fits were not as good as the fits with K₁ and K₂ shown here.

In addition, to achieve excellent fits to the excess S1 data requires negative cooperativity and to a lesser degree positive cooperativity, thus these fits require at least three or strictly speaking four free parameters. Similarly, good fits to the titrations data at low calcium concentrations require positive cooperativity i.e. estimating three free parameters. Therefore fitting the stochastic McK-G model directly to data for a family of stopped flow transients over the physiological range of calcium concentrations could lead to inconsistent estimates of the parameter-pCa relationships similar as shown with the Hill model in Fig. 5. This problem can be overcome though a stepwise approach which can quickly and efficiently obtain estimates of only two free parameters using the probabilistic McK-G model, and then improve the quality of the fits and establish robust relationships between each parameter and pCa (including cooperativity factors) by using the stochastic McK-G model.

Prospective New Directions in Modeling Thin Filament Regulation

In a recent paper¹⁶ we used a different class of regulation model to analyze the same transient data sets as used here. This model treated tropomyosin as a continuous semi-flexible chain in which the cooperativity of the transitions is defined by the persistence length of the chain. In this model the Tm strand binds to a single position on actin (C-position) in a shallow electrostatic well. Thermal fluctuations cause motions away from this position. The binding of TnI or myosin heads confine the Tm to the positions observed by electron microscopy.

This model though starting with different assumptions is as successful as the McK-G model used here in fitting the data. The two can be seen as two extremes of a range of different possible models. The chain model uses the approximation of a uniform continuously flexible chain. The current model assumes the each TmTn can change state alone but influenced by the state of its neighbors. Each of these assumptions has its limitations since structurally Tm is not uniform and the ability of a single Tm to move alone is very unlikely as it would require the braking of two sets of Tm-Tm contacts – and these are the primary contacts keeping Tm on actin. Given the fact that both models fit the data with similar parameters gives us confidence that more physically realistic intermediate models would predict a very similar result. This is illustrated by calculating the average number of actin sites activated by a single R-type myosin binding, (the apparent cooperative unit size in the original formulation of McK-G). In each case a single R-type myosin will activate 7–8 actins in the B to C-sate and ~10 for a C to M state transition. These predictions of apparent unit size are in good agreement with the predicted functional unit size by the flexible chain model.¹⁶

Summary and Conclusions

It is of great interest to establish for the physiological relevant applications the relationship between the Ca²⁺ concentration and the state transition rate constants from data gathered form acto-myosin binding assays in solution. We describe two models, the Hill model and the McKillop-Geeves models that can quantitatively predict the kinetic behavior of multiple experiments in solution. In our previous publication⁷ we thoroughly discussed the difficulties in obtaining robust and unique sets of the rate constants. The most daunting difficulty was to establish a consistent trend, presumably sigmoidal, between the model rate constants and calcium concentration. In this study we estimated the sets of the rate constants vs. calcium concentration from the best fits of Hill and McK-G model predictions to transient and titration data of S1 binding to regulated actin over large range of calcium concentrations.

We found that at high and low Ca²⁺ concentration both models can describe well all three data sets, i.e. transients for the excess actin and for the excess S1 and for titration data. However, the fitted rate constants of the Hill model do not show any consistent trend with an increase of Ca²⁺ concentration, and the fitting error varied over a relatively large range across these concentrations (Fig. 5). Moreover, these relationships were quite different between the one obtained from the titration data and from the stopped flow data or even between the excess actin vs. the excess S1 data sets. Only the Hill model equilibrium constants, K₁ and in part K₂ (for excess actin), show the expected sigmoidal calcium dependence.

The McK-G showed more promising results demonstrating that one parameter, K_B, has a large calcium dependence, this dependence being well described by the classical Hill equation. K_T shows a smaller calcium dependence, although this is not very apparent in the transient data, it is well described by the titrations as originally pointed out by McKillop and Geeves.⁸ The other two equilibrium constants, K₁ and K₂, are essentially calcium independent.⁷ Comparative analysis between the McK-G probabilistic and the McK-G stochastic model showed the McK-G probabilistic model can fit sufficiently well most of the experimental data and can be useful tool in cases when the size of cooperative unit is ~7. The McK-G stochastic model, however, is essential for describing later phase of the excess myosin stopped flow transients (negative cooperativity) and titrations at low [Ca²⁺] in which size of cooperative unit is >7.¹⁴ Overall the predicted sizes of the cooperative units predicted by the McK-G stochastic model are similar to those predicted by the flexible chain model¹⁶ suggesting that the McK-G model and the flexible chain model are two alternate ways of describing the system and both can fit the [Ca²⁺] dependence of the data equally well. The McK-G probabilistic model is very convenient for the estimation of model parameters and it is always recommended for the first estimate of model parameters, however it cannot take into account the cooperativity between neighboring TmTn units. The McK-G stochastic model, similarly to the flexible chain model,¹⁶ accounts very well for the cooperativity but it is inconvenient for a broad search of model parameters. The additional advantage of the stochastic approach is that it would not be affected by “stiffness” of the differential equations used in probabilistic McK-G algorithm and it enables the implementation of cooperativity inside the reaction network. The only drawback of the stochastic approach is that it takes much longer time to perform the simulations the probabilistic approach.

Methods

Model and Mathematical Analysis

In this study we adapted the methods for the Hill and McK-G models from Chen et al.¹ Here we briefly describe the main features of the models and the details are elsewhere.¹ We also developed a new stochastic model based on McKillop–Geeves scheme⁸ that includes cooperativity of neighboring TmTn units.

The Hill Model

In the Hill model, a regulated actin filament in solution is represented by a linear array of units, each of them containing of a TmTn complex and 7 actin monomers (Fig. 1). Each TmTn unit can exist in two states, “off” or the inactive state denominated as State 1 and “on” or the active state denominated as State 2. These states have different Ca²⁺ and S1 affinities. The transition from State 2 to State 1 of an actin₇·TmTn unit with no bound S1 is defined by the intrinsic equilibrium constant L. Binding of S1 to an actin monomer is defined by two equilibrium constants, K₁ and K₂, in corresponding TmTn States 1 and 2. The conformational transitions of an isolated actin₇·TmTn unit and basic kinetics of S1 binding are shown in Fig. 1B. They are defined by S1 binding to actin and its dissociation rate constants denoted as k₁, k₋₁, k₂ and k₋₂, and the transition rate constants of an isolated actin₇·TmTn unit between “on” and “off” states, α_m and β_m (m = 0, 1, 2, …, 7) where m refers to the number of S1 bound to the unit. The equilibrium constants are defined as K₁ = k₁/k₋₁, K₂ = k₂/k₋₂, L = α_o/β_o and α_m/β_m = L(K₁K₂)^m. The transition rate constants, α_m and β_m for isolated Tm–Tn–actin units are for simplicity expressed as α_m = α_o(K₁K₂)^m(γ−1) and β_m = β_o (K₁K₂)^mγ where γ is a parameter with values between 0 and 1. This model is capable of predicting the instantaneous fraction of the total actin monomers bound with S1 and can be compared with light scattering measurements, or the fraction of S1 bound in State 2 that can be compared to the total fluorescence from a pyrene label on each actin monomer. In this paper we exclusively focus on pyrene fluorescence measurements because these give a more reliable data set than light scattering. The fraction of S1 bound in State 2 calculated from a probabilistic formulation of this model cannot describe stop flow data very well and the model fit can be significantly improved by inclusion of nearest-neighbor interaction between TmTn units.¹

The cooperativity between two neighboring TmTn units in states i and j is represented by interaction energies between these states, w_{i, j} (Fig. 1A). The corresponding actin₇·TmTn rate transition constants between “off” and “on” states are defined by the states of the two nearest neighbors and the interaction energies (Fig. 1C), for simplicity defined as Y₁ = Y₁₁ Y₁₂, Y₂ = Y₂₂ Y₁₂, where Y_ij = exp(w_ij/k_BT) and k_BT is the product of the Boltzmann constant and the temperature. The equilibrium constants that account for cooperativity are defined as $Y\equiv Y_{11}{Y}_{22}/Y_{12}^2$ and L′ ≡ LY₁₁/Y₁₂. In a filament, the cooperativity of the system influences rate constants α_m and β_m, and according to¹ these rates modulated by cooperativity can be represented as ᾱ_m = α_m (Y₁Y₂)^N₁(δ−1)(Y₂)^2(1−δ) and β̄_m = β_m(Y₁ Y₂)^N₁δ(Y₂)^−2δ where δ is a constant valued between 0 and 1, and N₁ is the number of the two neighboring units that are in State 1 (see Fig. 1 C).

Because the rate of S1 binding is directly dependent of the current actin₇·TmTn state and the states of its nearest neighbors the instantaneous fraction of S1 bound can only be calculated by a Monte Carlo algorithm in which the state of each actin₇·TmTn unit along actin filament is explicitly registered at the end of each time step. According to this method, the fraction of S1 bound as a function of time is calculated as the ensemble-average of identical and independent small systems, each containing an actin filament (700 actin monomers), TmTn units (100) contained within a small volume. The change of concentration of free S1 in solution is reduced by the amount of myosin bound to actin (in both State 1 and State 2), thus the total amount of S1 is conserved. The kinetic simulation of stop flow experiments starts when S1 is added to the previously equilibrated actin₇·TmTn system at a prescribed Ca²⁺ concentration. This process is simultaneously calculated over all filaments and the average fraction of actin sites with bound S1 at the end of each time step is recorded. A typical simulation included 100 filaments, and this number of filaments was sufficient for stable and converging estimation of the free parameters. Further increase of the number of filaments by a five-fold did not significantly changed calculated fraction of bound S1 over entire time course of the simulation but significantly increased the computational time.

McKillop-Geeves (McK-G) Model

In the McK-G model each myosin head, or S1, binds to an actin unit in two steps. The myosin is initially weakly bound in the attached or A-state then isomerizes to the rigor-like, R-state. TmTn can influence both the initial binding and the isomerization to the R-state. In the actin filament, n actin monomers and a TmTn complex form a unit which can exist in three states as described in the introduction (Fig. 2): the “B” state, in which myosin S1 binding to actin is prohibited; the “C” state, in which S1 can bind with actin, but cannot isomerize to the R-state; and in the “M” state, where no limitation to S1 binding to actin and isomerization is imposed. In this paper the unit size of the TmTn complex is assumed to cover 7 actin monomers – following the structural length of Tm.⁸ The repeat of Tn every 7 actin monomers uniquely define the functional TmTn unit which can rigidly move between the three states (Fig. 2). Because Ca²⁺ binding to actin Tn significantly decreases the affinity of Tn to actin, the distribution between three states is therefore affected by Ca²⁺ concentration. The various combinations of S1-actin states and actin₇·TmTn states define 45 possible states, and the complete system can be described by 45 corresponding chemical kinetics equations, and ten independent rate transition constants k as previously described by Chen et al.^{1; 7} In short, a set of 45 kinetic ordinary differential equations (ODE) are solved numerically by Gear’s backward differentiation formulas (up to order five).¹⁷ The solution is represented by the fraction of TmTn units in a particular state i =1,…, 45 as p_i (t). The subscript “ i ” is defined by the position of a TmTn unit (i.e. in B, C or M states) and a particular combination of actin unoccupied sites, and S1 bound in A- or R-states within seven actin sites of the TmTn unit. Once we determine the vector of the 45 states, p(k,t), where the vector k represents an array of rate transition constants and other relevant model parameters, we calculated the fraction of actin sites in each of the actomyosin states: unoccupied actin, S1 bound in A-state, and in R-state, by simply summing occupancy of actin sites in each TmTn unit over all TmTn units, and normalizing the sum by total number of actin sites. The model predictions were tested against transients of the pyrene fluorescence intensity during kinetic and equilibrium experiments.^{15; 18; 19}

The above set of 45 ODEs can become “stiff”, typically when some transition rates are very fast and others are very slow. For most of the parameter range we were able to find the solution of the set of the ODEs and the predicted values of the model are only minimally affected by the “stiffness” of the ODEs. However, in several extreme cases, when the ODEs were “stiff” we used an alternative method (Monte Carlo simulations) which can effectively solve the set of stiff equations. Besides solving the “stiff” set of ODEs, Monte Carlo simulations also included more realistic way to implement cooperativity between TmTn units.

The Monte Carlo computational algorithm is straightforward and is based on the reaction scheme shown in Fig. 2 in which S1-actin and actin₇·TmTn states are explicitly spatially defined at each actin site along an actin filament. There are two spatial arrangements: (i) a linear arrangement of TmTn units along an actin filament (similar as in Fig. 1C), and (2) of actin-myosin states within each actin₇·TmTn unit. Associated with these two arrangements we have two sequential random number drawings: the first defining the state transitions between actin₇·TmTn states over all TmTn units and then the second defining actin-S1 state transition probabilities over all actin sites. Based on current actin₇·TmTn state the probability to change state in a small time increment, Δt, is defined by the transition probabilities k_i Δt for each possible transition from the original state. These transition probabilities are arranged sequentially starting from 0 toward 1, i.e. as cumulative segments (denoted as ‘bins’). After all transition probabilities are added, the complementary probability to 1 (defined as (1−Σ k_iΔt)) is calculated by defining the probability that the actin₇·TmTn state will not change during time increment Δt. For each TmTn unit, the decision to change state or to remaining in the current state from time t to the time t+Δt is made by a computer generated random number which should fall in one of the predefined bins. Because complementary probability is much larger than any transition probability the most frequent result of each random number drawing is no change of the current state. Repeating the process over all TmTn units completes the first set of the random number drawings and defines the current actin₇·TmTn state at time t+Δt, setting preconditions for the second set of the random number drawings. After updating all actin₇·TmTn states, the same procedure is repeated for the second set the random number drawings for which state transition probabilities are defined for each actin site and its state with respect to S1. Repeating the process over all actin sites completes the second set of the random number drawings and defines all current actin-S1 states at time t+Δt, setting preconditions for the following time step.

Cooperativity Factor in McK-G stochastic model

The Monte Carlo simulation registers the exact spatial position of each actin₇·TmTn unit and its state, and also the spatial occupancy of actin sites with no bound S1 or bound S1 in either A or R states. As such it permits incorporation of cooperativity between neighboring TmTn units similar to that already described in the Hill model. Closest neighbor TmTn cooperativity has an effect on the early time of the binding process and improves the fits to kinetic data by using both the Hill and McK-G models.

The nearest neighbor TmTn cooperativity is defined as follows: (i) when TmTn is in blocked and the nearest neighbors are not, the state transition rate from close to open state, k_B, is increased by ${CF}_B^{+}=1+n_B{f}_{\mathit{TmTm}}/4\text{times}$ where f_TmTm is the assigned overall cooperativity factor, and where n_B is the configuration factor which is increased by one for each neighbor in the closed state and by two for each neighbor in an open state; (ii) when TmTn is in a closed state and one or two neighbors are in an open state the transition rate from closed to open state, k_T is increased by ${CF}_T^{+}=1+n_T{f}_{\mathit{TmTm}}/4\text{times}$ where n_T is assigned to be two or four respectively; (iii) when TmTn is in an open state, the state transition rate from open to closed state, k_−T, is increased ${CF}_{-T}^{+}=1+n_{-T}{f}_{\mathit{TmTm}}/4$ where n_−T is increased by one if one of each neighbor in a closed state, and by two for each neighbor in blocked state. This ad hoc definition of the TmTn–TmTn cooperativtity is taken for simplicity and convenience. A more rigorous approach involving the interaction energy between TmTn unites which is derived from the transition rate theory of Eyring ¹ was not feasible because it requires several more free parameters which cannot be resolved from the stopped flow and titration experiments considered here.

Negative cooperativity in myosin binding

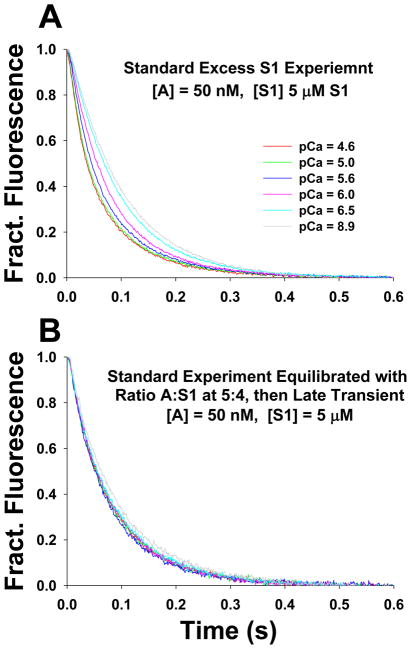
A feature of the kinetic binding transients for excess S1 binding to regulated actin filaments was that the reaction appeared to slow over the last ~20% of the transient. When considering the actin-binding transients these data can be fitted well to single exponential functions with no evidence of the slowing seen for the excess S1 case. We recently reexamined the data for unregulated actin filament and the same phenomena was noted¹⁶, and has been reported previously in the literature.^{4; 20} The solution used by others was to fit 2 exponentials without necessarily defining what the second event is. Possibilities include non-ideality of pseudo first order conditions, non-ideality in the correspondence between the fluorescence signal and the degree of actin occupancy by myosin or the presence of damaged or misassembled protein within the mixture. Having such deviations from ideality in the data it becomes problematic for detailed model fitting, because the relative amplitude of the two phases is an important factor if normalizing between experimental and modeled data. The observation that the deviation from a single exponential process at high calcium was also seen in the unregulated filament is consistent with this being a feature of actin and S1 not a feature of the regulated system. In the appendix to a recent paper¹⁶ we demonstrated that the phenomena could be dealt with by assuming that this was due to a local steric hindrance. This effect was independent of the presence of TmTn on the filament and of the calcium concentration. Here we present additional evidence that this model is reasonable, we examined the transients observed at different degrees of pre loading of the actin with myosin heads for both unregulated and regulated filaments. In particular we observed the transient for regulated actin filaments at 80% preloading with S1 as a function of calcium concentration. Fig. 9A shows the transient for the standard experiment for excess [S1] to [actin] and Fig. 9B shows the standard experiment but actin pre-equilibrated at 5:4 ratio with S1. The rest of the details are in the figure legend. The data show that preloading eliminates all calcium dependence of the transients. This is consistent with the preloaded S1 activating the filament and the negative cooperativity effect is the same in all cases.

Figure 9.

Stopped flow transients of mixing excess of S1 with pyrene actin to quantitatively demonstrate the calcium independent slowing of S1 binding at higher occupancy of actin sites by bound S1. A) The excess S1 stopped flow experiment: 5 μM S1 was quickly mixed with 50 nM pyrene actin in presence of 20 nM TmTn. B) Excess S1 stopped flow experiment repeated with actin preloaded with S1 at 5:4 ratio of A:S1. 50 nM pyrene actin was equilibrated with 40 nM S1 in presence of 20 nM TmTn and then rapidly mixed with 5 μM S1. The same pCa values and color codes were used as in A.

Thus we included in the McK-G stochastic model the negative cooperativity factor which slows S1 binding to actin in later phase of the flow transients when most of actin sites are already occupied by bound S1. The negative cooperativity is based on principle that binding rate of S1 to actin will be hindered when closest neighboring actin sites are occupied by bound S1s. The effective negative cooperativity factor, CF⁻, is assumed to be

$${CF}^{-}=\{\begin{array}{cc}1.2+(n\text{A}.\text{S}1-4)({\text{f}}_{S1}-0.2),& \hfill \text{if}n\text{A}.\text{S}1\ge 4\\ 1.0,& \hfill \text{otherswise}\end{array}$$ (Eq. 1)

here nA.S1 is the number of actin sites with bound S1 in the neighborhood of the unoccupied actin site and f_S1≥1.2 is estimated overall negative cooperativity factor for nA.S1> 4. The counting of closest neighbors up to six, three on each side, the effective S1 binding rate is reduced by CF⁻ (nA.S1) times. Thus the binding probability, that an S1 from solution at concentration c = [S1] binds to actin within time interval of Δt, is p_S1 = k₁cΔt/(CF⁻). The S1 detachment rate is assumed to be unaffected by the negative cooperativity.

This approach differs from our recent paper¹⁶ and includes the negative cooperativity extending beyond the local steric effect of the immediate neighbor. A more comprehensive approach based on local steric effect¹⁶ was ineffective here because slowing become noticeable at much higher level occupancy of actin sites, suggesting that negative cooperativity may be more complex then simple steric effect of the immediate neighbor and may involve other effects and, therefore, may require more comprehensive study of this phenomena. Because the negative cooperativity is only observable for studies in solution at high occupancy of actin sites (>70%) and likely not relevant for myosin binding in fibers, the current formulation is convenient for fitting complete sets of data. This is supported by our fitting procedure that is achieved in two steps: (1) by fitting the data for up to 60% occupancy without taking in account negative cooperativity, and (2) by refitting the complete sets of data with negative cooperativity defined by Eq. 1. The former provided excellent fits, very small error, excellent resolution matrix and consistent sigmoidal dependence of estimated parameters with calcium (see result section below). The latter provided excellent fits by almost exclusively estimating negative cooperativity parameter f_S1 with minor or no change of other parameters obtained in step 1.

Protein preparations

The proteins were all prepared from rabbit fast skeletal muscle. Myosin S1 was prepared by chymotrytic digestion of myosin and column purified to isolate the A1 light chain isoform. Actin prepared from a muscle acetone powder²¹ was labeled to > 90% at Cys 374 with pyrene as described by ²². A TmTn complex was isolated from the same acetone powered used for the actin preparation as described by Ebashi et al.²³ and Greaser & Gergely.²⁴

Stopped-flow and titration experiments

The model predictions are tested against measurements of the pyrene fluorescence intensity during kinetic (stopped-flow) and titration experiments. These have been described in detail in published work.^{15; 18; 19} In outline both experiments fluorescently labeled (regulated) actin filaments in solution are first equilibrated at specific Ca²⁺ concentration and then mixed with myosin-S1. All data were collected at 20°C in a buffer containing 100 mM KCl, 5 mM MgCl₂ 20 mM MOPS pH7.0. The calcium concentration was controlled by the addition of EGTA and calcium saturated EGTA at 2 mM to give the required free calcium concentration.

Titration were performed using a Perkin Elmer LS50B fluorimeter by continuously adding concentrated S1 at 10 μl per min into a stirred cuvette containing 50 nM pyrene labeled actin saturated with Tm and Tn. To work at such low actin concentration, actin is stabilized by preincubation of 10 μM pyrene actin at a ratio of 1:1with phalloidin for at least 2 hours before dilution to 50 nM.

Kinetic binding transient were collect by rapidly mixing a solution of S1 with pyrene labeled actin saturated with TmTn in a Hi-Tech Scientific SF 61DX stopped flow fluorimeter. The concentrations of proteins used for each experiment are listed in the Figure legends and refer to the concentrations after the rapid mixing event (1:1 mixing ratio) that initiates the binding reaction.

Parameter Estimation Methodology

A drop in pyrene fluorescence (excitation at 365 nm emission at 405 nm) is proportional to myosin binding to actin in the R-state. Thus, the calculated instantaneous fractions of actin sites that are not occupied or which are in the A-state (i.e. which are not in the R-state), denoted g(λ,t), can be compared with corresponding experimental data, d^obs(t), at the same instant. Here, the vector λ = (λ₁,···,λ_m) represents the set of m free model parameters that need to be estimated.

We estimated the rate transition constants for each model by minimizing the difference between the predicted history of the fraction of actin sites occupied by bound myosin in the R-state, g(λ,t), and the same fraction deduced from the experimental records of pyrene fluorescence intensity, d^obs(t), for either time for kinetic traces or concentration for equilibrium titrations. For parameter estimation we used the method of damped least square inversion (DSL) because this model has fast convergence, and can quantitatively evaluate the uniqueness of estimated parameters.⁷ The fast convergence of DSL, which requires far fewer iterations than other global searching methods,⁷ is especially convenient for the stochastic approaches in which simulations are lengthy. As such the DSL method provided all the information necessary for quantitative evaluation of the advantages and disadvantages of the Hill model vs. the McK-G probabilistic and stochastic models.