Abstract
Magnetic particle imaging (MPI) uses safe iron oxide nanoparticle tracers to offer fundamentally new capabilities for medical imaging, in applications as vascular imaging and ultra-sensitive cancer therapeutics. MPI is perhaps the first medical imaging platform to intrinsically exploit nanoscale material properties. MPI tracers contain magnetic nanoparticles whose tunable, size-dependent magnetic properties can be optimized by selecting a particular particle size and narrow size-distribution. In this paper we present experimental MPI measurements acquired using a homemade MPI magnetometer: a zero-dimensional MPI imaging system designed to characterize tracer performance by measuring the derivative of the time-varying tracer magnetization, M’(H(t)), at a driving frequency of 25 kHz. We show that MPI performance is optimized by selecting phase-pure magnetite tracers of a particular size and narrow size distribution; in this work, tracers with 20 nm median diameter, log-normal distribution shape parameter, σv, equal to 0.26, and hydrodynamic diameter equal to 30 nm showed the best performance. Furthermore, these optimized MPI tracers show 4 × greater signal intensity (measured at the third harmonic) and 20% better spatial resolution compared with commercial nanoparticles developed for MRI.
INTRODUCTION
MPI is a medical imaging platform designed to image tracers that contain magnetic nanoparticles. MPI exploits the relatively large but thermally unstable magnetic moment that is unique to nanosized ferrimagnetic iron oxide particles. A multitude of names, including SPIO and USPIO, exist for iron oxide nanoparticles but since our particles are phase-pure magnetite we will use MNP, for magnetite nanoparticle. In principle, MPI can detect extremely small quantities of tracer MNPs, on the order of nanograms,1, 2 with resolution comparable to MRI.
At its most fundamental level, MPI is a simple inductive measurement. Tracer MNPs are magnetized by an alternating magnetic field and the resulting change in magnetic flux caused by their changing magnetization, M’(H(t)), generates a signal current in a receiver coil. It follows that the functional form of M’(H(t)), which is predominantly determined by tracer properties, is of fundamental importance in MPI. To date, MPI has been formulated using two distinct theories, each of which defines the image using a convolution with M’(H(t)): the groups at Philips and Lubeck have developed f-space (frequency-space) MPI utilizing a system function,3, 4 while the group at Berkeley has developed x-space (real-space) MPI theory.5
In both f- and x-space MPI the ideal tracer response, M’(H(t)), is a delta function, corresponding to a step-wise equilibrium magnetization, M(H)eq. In real samples M(H)eq is not a step function but is described instead by the Langevin function. Large MNPs, with diameters near the limit where magnetic behavior transitions from superparamagnetism to ferrimagnetism, have been sought for their close approximation of the desired M(H)eq. However, since MPI is not an equilibrium measurement, it is not sufficient merely to produce the largest possible MNPs. Dynamic MNP magnetization must be treated carefully to yield the best-performing tracers. In particular, the size-dependent interplay between M’(H)eq and the magnetic relaxation time, which together determine M’(H(t)), should be considered. Furthermore, it is important to maximize sample monodispersity to ensure that all MNPs in the tracer are magnetized alike at a given field.
We have shown in our previous work that the response of larger sized MNPs can deviate from M’(H)eq in the dynamic MPI environment, resulting in reduced signal compared to predictions that ignore magnetic relaxation. The UC Berkeley group recently measured the deleterious effect of relaxation on the MPI signal using an MPI relaxometer of their construction (operating at ∼4 kHz drive frequency) and tracers prepared in our lab.6 Previously, we had observed that longer magnetic reversal times associated with increased tracer MNP size resulted in a peak in the MPI signal at 250 kHz excitation frequency, as measured by the intensity of the third harmonic of tracer magnetization. Here we observe the same effect at 25 kHz excitation, in direct measurements of M’(H(t)). These results illustrate that magnetic relaxation effectively sets an upper limit on MNP size for a given driving field frequency: tracer MNP magnetic relaxation must be faster than the measurement time window defined by the period of the excitation field. We note that the magnetic relaxation discussed here is relevant for low fields. At fields greater than a certain threshold determined by the magnetocrystalline anisotropy and saturation magnetization, both material properties, the physics of magnetic reversal changes and the reversal time is shortened; for magnetite the low-field limit is below ∼60 mTμ0−1 (peak-peak) according to measurements and ∼68 mTμ0−1 (peak-peak) according to estimates based on theory. For a detailed discussion of the physical aspects of relaxation related to MPI see our recently published work.6, 7
In practice, M’(H(t)) is determined by properties of the magnetic tracer, though certain parameters of the imaging system are also relevant. Especially important are the frequency, f0, and amplitude, H0, of the driving AC field used to magnetize tracers. Generally both f0 and H0 will influence M’(H(t)) for real tracers, but toward what end depends on specific tracer properties. Other properties of the imaging system will also affect the image for an arbitrary tracer, including the gradient strength, G, which determines the theoretically achievable spatial resolution, with a greater G yielding better resolution, the gradient geometry (e.g., field free point versus field free line, or single-sided scanner versus full-surround), and the receive coil sensitivity. Furthermore, in addition to physical hardware, image acquisition and reconstruction algorithms can greatly enhance imaging speed and reduce computational intensity.4, 5
While systems design and image processing play a critical role in producing an image, ultimately the tracer will determine true image quality. It is inevitable that the tracer must be appropriately matched to the specific imaging system and imaging application to produce the best image quality. Tracer size, size-distribution, and tracer-fluid interactions should all be optimized. In the following sections we describe such an optimization and discuss the results of MPI measurements (point spread function and harmonic spectrum) of a series of tracer samples of increasing size, measured using a MPI magnetometer constructed in our laboratory.
MATERIALS AND METHODS
A MPI magnetometer was constructed and used to measure the relevant components of M’(H(t)) in f-space (harmonic spectrum) and x-space (point spread function (PSF)) for a series of MNP tracers synthesized and functionalized in our laboratory to achieve well-defined magnetic core and hydrodynamic diameters in an aqueous medium.8 The MPI magnetometer is a zero-dimensional MPI system that excites tracer magnetization with a harmonic drive field of up to 40 mT μ0−1 (peak-peak) at f0 ∼ 25 kHz and measures the signal induced in a receive coil by M’(H(t)). The MPI magnetometer was designed according to the same principles used in our previous work,7 with the exception that here a broadband receive coil is employed to measure the tracer’s intrinsic PSF and up to 40 harmonics in the induced signal after Fourier transformation.
The MPI magnetometer’s driving field was generated by an arbitrary function generator (model AFG 3022, Tektronix, Beaverton, OR) and amplified by a 200 W, class A RF amplifier (model 2200L, Electronics & Innovation, Rochester, NY). A sinusoidal excitation was used for all experiments. The excitation field was 29 mTμ0−1 (peak-peak), determined from the forward power measured by the RF amplifier’s built-in meter. The received signal was digitized with a PC-based analog-to digital card (model PCIe-6361, National Instruments, Austin, TX) at 2 × 106 samples per second.
Tracer PSFs were obtained by gridding the received signal to the driving field amplitude and normalizing by the velocity of the field-free-point (FFP).5, 6 To reduce inductively coupled signal from the transmit channel the background signal was acquired prior to sample insertion and then subtracted from the sample signal. The signal is averaged 10 times to further reduce noise. Harmonic spectra are determined by the FFT of M’(H(t)).
All non-commercial tracers contained MNPs that were coated with amphiphilic polymers of well-known chain lengths and dispersed in water. MNPs were synthesized in our labs according to procedures detailed in previous work.2, 7, 8, 9, 10 Commercial samples from two different vendors were diluted to concentrations equivalent to non-commercial samples by the addition of water. Tracer concentration (g Fe/L) was measured by ICP atomic emission spectrophotometer (model 955, Thermo Jarrel Ash, Franklin, MA). The average tracer concentration was 2.4 g Fe/L ( + /− 1.3). Magnetic core size (median diameter d0V, and standard deviation, or shape parameter, σV of a volume-weighted, log-normal distribution function) was measured by fitting to M(H)eq at a temperature above the blocking temperature,7, 11 with magnetization measurements acquired by the vibrating sample magnetometer (VSM) (LakeShore, Weterville, OH) and the VSM oven option of a physical property measurement system (PPMS) (Quantum Design, San Diego, CA). Bright field transmission electron microscope (TEM) imaging (model Tecnai G2 F20, FEI, Hillsboro, OR) was also used to measure magnetic core size. TEM measurements were fit to a volume weighted log-normal size distribution for direct comparison with size measurements from magnetic fitting. Hydrodynamic size was measured by dynamic light scattering (DLS) (Zetasizer Nano-S, Malvern Instruments, Westborough, MA). Relaxation times, τ, listed in Table TABLE I. were determined from the complex component of magnetic susceptibility, measured using the PPMS AC measurement system (ACMS) option.12
TABLE I.
Tracer properties.
| d0V [nm] | σV | ||||||
|---|---|---|---|---|---|---|---|
| M(H) | TEM | M(H) | TEM | dH [nm] | Ms [kA/m] | τ (300 K)[μs] | |
| Feridex IV | 7 | 5a | 0.40 | n/a | 150a | 223(± 51) | <1 |
| Resovist | 14 | 5b | 0.47 | 0.37b | 45b | 373(± 30) | 90 |
| UW1 | 20 | 21 | 0.26 | 0.32 | 30 | 360(± 65) | 50 |
TEM and DLS results for Feridex IV from Ref. 14.
TEM and DLS results for Resovist from Ref. 15, which presents extensive characterization of Resovist’s particle size.
MPI samples were prepared by adding 0.2 mL of tracer to a 0.6 mL microcentrifuge tube; the MPI magnetometer was designed so that this sample configuration places the tracer at the center of the receive and transmit coils to ensure measurement repeatability. All samples were measured in triplicate and average values are reported.
DISCUSSION
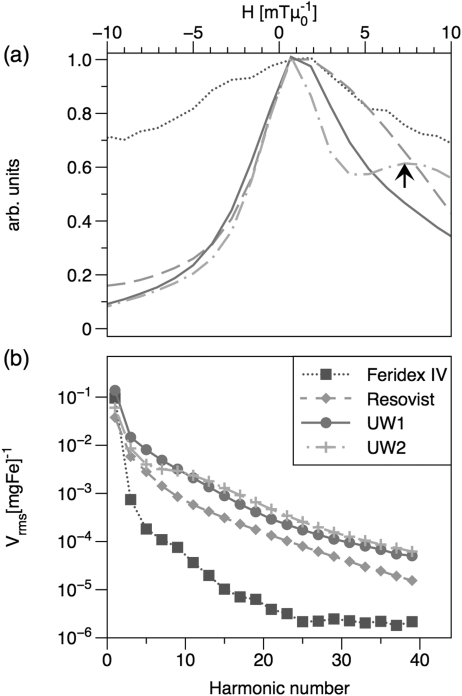
We have demonstrated size-dependence in the MPI response at 25 kHz using a series of tracers of varying size but with narrow size distributions; all of the tracers synthesized in our laboratories contained MNP cores coated with polymer shells and dispersed in aqueous media. TEM images of commercial and synthesized tracers are shown in Fig. 1. MNP cores were confirmed to be phase-pure magnetite by careful electron energy-loss spectroscopy measurements.13 Plots of MPI spatial resolution (Fig. 2) and signal intensity (Figs. 2b and Fig. 3) show that these tracers out-perform the commercial tracers Resovist and Feridex IV for both f-space and x-space MPI formulations, with greater normalized harmonic signal intensity and narrower PSFs, respectively. The best-performing tracer in this study, sample UW1, had d0V = 20 nm measured by magnetic fitting (21 by TEM) and σV = 0.26 (0.32 by TEM). Sample UW1 showed 20% better spatial resolution than Resovist as determined by the full width half-maximum (FWHM) of the PSF and increased harmonics across the full spectrum in Fig. 2b. Sample UW1 also showed greater signal intensity than Resovist as measured by PSF height (Table TABLE II.). PSF height is the amplitude of the induced signal normalized by iron concentration) and 4 × greater signal intensity measured at the third harmonic (Fig. 3a).
Figure 1.
TEM images of (a, b) Feridex, (c, d) Resovist, and (e, f) UW1 showing the disparity in size and distribution between commercial samples and UW samples.
Figure 2.
(Color online) MPI magnetometer measurements taken with an excitation field of 29 mTμ0−1 (peak-peak) at 25 kHz. (a) PSF normalized to 1 for FWHM comparison. The arrow indicates the shoulder in sample UW2’s PSF that is due to relaxation effects; (b) harmonic spectrum normalized by iron concentration.
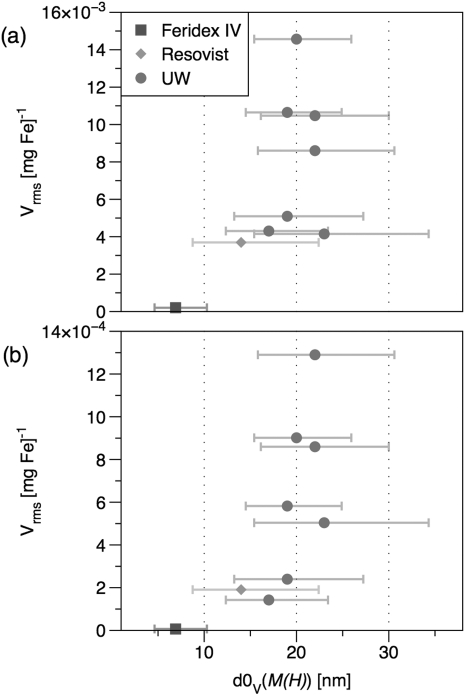
Figure 3.
(Color online) (a) Third and (b) 15th harmonic of normalized signal intensity for commercial and UW MNPs of varying size. Size (d0V) is determined by fitting to M(H) and the horizontal bars show the 68% confidence interval of the log-normal distribution.
TABLE II.
UW MPI measurements at 25 kHz, 29 mTμ0−1 pp.
| Signal intensity | Resolution | ||||
|---|---|---|---|---|---|
| PSF height | Third harmonic | 15th Harmonic | PSF FWHM | w/ 6 Tm−1 grad. | |
| [mVrms(mgFe)−1] | [mVrms(mgFe)−1] | [mVrms(mgFe)−1] | [mTμ] | [mm] | |
| Feridex IV | 5 | 0.2 | 0.01 | >20 | >3 |
| Resovist | 33 | 3.7 | 0.19 | 11 | 1.8 |
| UW1 | 91 | 14.6 | 0.9 | 9 | 1.5 |
In previous measurements of the third harmonic of tracer magnetization, we observed that 15 nm tracer MNPs showed the greatest signal amplitude per unit mass at 250 kHz f0.7 In contrast, for MPI at 25 kHz f0, larger particles are optimal. The effectiveness of larger MNPs here can be attributed to the longer measurement-time window at 25 kHz, which allows larger particles to reverse their magnetization in phase with the driving field. The existence of peak values in Fig. 3 indicate that these experiments occurred in the weak-field regime where Neél and Brownian relaxation dominate, and the relaxation is not shortened by the field to the point where the magnetization remains in phase with the field, as might occur if the field amplitude were larger.
In measurements of the third harmonic of the received signal, signal intensity decreased as the median sample diameter increased beyond 20 nm. This falloff indicates the presence of MNPs in the tracer solution that were “too big” for the measurement conditions and for which significant relaxation delay produced a shoulder at higher fields for a positive scan (increasing field amplitude) in the PSF. An example of such a shoulder, as well as its negative impact on the tracer’s inherent spatial resolution, is clearly visible in the PSF for tracer UW2 in Fig. 2a. Though the PSF-height (not shown) and third-harmonic intensity of tracer sample UW2 are both less than that of UW1, tracer UW2 does show increased higher harmonics in the spectrum shown in Fig. 2b, and the 15th harmonic in Fig. 3b. Results for all samples were similar at the 31st harmonic. Despite the increased high harmonics in tracer UW2, the broad PSF provides evidence of significant relaxation effects that should impede its imaging performance. Though not shown, relaxation shoulders similar to the one seen in tracer UW2 were present in the PSFs of the other samples with median diameter greater than 20 nm. Thus, strong harmonic content alone is not sufficient for good imaging performance; size-dependent relaxation effects can introduce artifacts in the PSF that reduce the tracer’s inherent spatial resolution and signal intensity.
It is worth noting that additional image reconstruction may be applied to improve the imaging quality provided by a tracer like UW2, by effectively removing the shoulder, for example. However, it is our goal to determine how to synthesize the most optimal tracers for a general imaging system, so we have not considered reconstruction in detail. Furthermore, we do not claim that the specific tracer formulations discussed here are the best possible tracers for imaging at 25 kHz; only that our tracers show improvement over available tracers, and tracer UW1 is intrinsically the most suitable of the examples discussed. We present these tracers as examples of a particular synthetic method that produces excellent results, and an evaluation process by which tracer performance can be understood, and therefore improved. Using our synthetic method that produces phase-pure magnetite particles of well-defined core and hydrodynamic size and size distribution, combined with a systematic measurement of their relaxation behavior, we expect to be able to improve tracer performance even further at 25 kHz with additional fine-tuning of core and hydrodynamic size.
MPI performance is enhanced by tuning tracer size to reduce relaxation effects as we have done here. Tuned tracers show improved spatial resolution compared with Resovist at 25 kHz, but we expect, based on these results, better resolution still can be achieved at lower excitation frequencies with appropriately matched tracer sizes and size distributions. Using higher excitation fields6 may also be an alternative approach.
CONCLUSIONS
MPI tracers show size-dependent performance at multiple frequencies. A series of tracers were synthesized and in these experiments at 25 kHz, the tracer with 20 nm median core diameter, σV = 0.26, and 30 nm hydrodyanamic diameter, yielded the best performance: signal intensity 4 × greater and spatial resolution 20% better than the best commercially available tracer (Resovist). In previous work we found that tracers with d0V = 15 nm and σV = 0.22 performed best when the excitation frequency was 250 kHz. We conclude that the existence of a size-dependent peak in MPI performance is due to the effects of relaxation, which become greater as the tracer core size increases. Relaxation is of fundamental importance in MPI and determines the size-limit for tracers used in a given MPI imaging system.
ACKNOWLEDGMENTS
This work was supported partially by grants NIH/NIBIB R21 EB008192 and NIH/NIBIB RO1 EB013689.
References
- Ferguson R. M., Minard K. R., and Krishnan K. M., J. Magn. Magn. Mater. 321, 1548 (2009). 10.1016/j.jmmm.2009.02.083 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan K. M., IEEE Trans. Magn. 46, 1 (2010). 10.1109/TMAG.2010.2046907 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gleich B., and Weizenecker J., Nature 435, 1214 (2005). 10.1038/nature03808 [DOI] [PubMed] [Google Scholar]
- Rahmer J., Weizenecker J., Gleich B., and Borgert J., BMC Med. Imaging. 9, 4 (2009). 10.1186/1471-2342-9-4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Goodwill P., and Conolly S., IEEE Trans. Med Imaging 29, 1851 (2010). 10.1109/TMI.2010.2052284 [DOI] [PubMed] [Google Scholar]
- Goodwill P., Tamrazian A., Croft L., Lu C., Johnson E., Pidaparthi R., Ferguson R., Khandhar A., Krishnan K., and Conolly S., Appl. Phys. Lett. 98, 262502 (2011). 10.1063/1.3604009 [DOI] [Google Scholar]
- Ferguson R. M., Minard K. R., Khandhar A. P., and Krishnan K. M., Med. Phys. 38, 1619 (2011). 10.1118/1.3554646 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Khandhar A. P., Ferguson R. M., Simon J. A., and Krishnan K. M., “Tailored magnetic nanoparticles for optimizing magnetic fluid hyperthermia,” J. Biomed. Mater. Res. Part A (in press). 10.1002/jbm.a.34011 [DOI] [PMC free article] [PubMed]
- Khandhar A., Ferguson R., and Krishnan K. M., J. Appl. Phys. 109, 07B310 (2011). 10.1063/1.3556948 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Krishnan K. M., Pakhomov A. B., Bao Y., Blomqvist P., Chun Y., Gonzales M., Griffin K., Ji X., and Roberts B., J. Mater. Sci. 41, 793 (2006). 10.1007/s10853-006-6564-1 [DOI] [Google Scholar]
- Chantrell R. W., Popplewell J., and Charles S. W., IEEE Trans. Magn. 14, 975 (1978). 10.1109/TMAG.1978.1059918 [DOI] [Google Scholar]
- Gonzales M. and Krishnan K. M., J. Magn. Magn. Mater. 293, 265 (2005). 10.1016/j.jmmm.2005.02.020 [DOI] [Google Scholar]
- Mengast A., Feguson R. M., Khandhar A. P., Grogger W., Hofer F., and Krishnan K. M., “Determination of iron oxide nanoparticle phase by monochromatic electron energy loss spectroscopy”.
- Raynal I., Prigent P., Peyramaure S., Najid A., Rebuzzi C., and Corot C., Invest. Radiol. 39, 56 (2004). 10.1097/01.rli.0000101027.57021.28 [DOI] [PubMed] [Google Scholar]
- Eberbeck D., Wiekhorst F., Wagner S., and Trahms L., Appl. Phys. Lett. 98, 182502 (2011). 10.1063/1.3586776 [DOI] [Google Scholar]