Abstract
As the dominant physiological solvent, water drives the folding of biological macromolecules, influences conformational changes, determines the ionization states of surface groups, actively participates in catalytic events, and provides “wires” for long-range proton transfer. Elucidation of all these roles calls for atomistic simulations. However, currently available methods do not lend themselves to efficient simulation of proton transfer events, or even polarizability and flexibility. Here, we report that an explicit account of valency can provide a unified description for the polarizability, flexibility, and dissociability of water in one intuitive and efficient setting. We call this approach LEWIS, after the chemical theory that inspires the use of valence electron pairs. In this paper, we provide details of the method, the choice of the training set, and predictions for the neat ambient liquid, with emphasis on structure, dynamics, and polarization. LEWIS water provides a good description of bulk properties, and dipolar and quadrupolar responses.
INTRODUCTION
Where computer simulations are concerned, it is important that the model fit the application with respect to both the level of detail and the computational burden. For water, the range of models is broad, from the continuum dielectric1 to high-level quantum mechanics.2 Within this range, empirical atomistic representations occupy an important niche with respect to length scale and efficiency.3, 4 The most basic, “rigid water” construct, with fixed OH bond length, HOH angle, and distribution of partial charges, dates to the pre-computer era5 and still forms the basis of modern mainstream models, such as the TIPnP’s,3, 6, 7, 8 or the SPC’s,9, 10 while flexible variants,11, 12, 13 with variable bond lengths and bond angles, provide improved descriptions of bulk liquid properties.
Recently, more ambitious water models have addressed the polarizability of water.14, 15, 16, 17, 18 Water undergoes substantial internal charge rearrangements in response to neighboring molecules. For example, the molecular dipole moment increases by as much as ∼60% from the gas phase to the liquid.19 These changes are usually modeled by adding oscillating, distributed, or variable charges at some extra computational expense. The last decade has seen promising validation and growing acceptance of polarizable models.20
However, polarizable models remain incapable of breaking bonds. For simulations of reactions, the gold standard is quantum mechanics (QM) where the solution to Schrödinger's equation is numerically approximated for a many-body problem of nuclei and electrons. In principle, ab initio QM methods, can represent both polarization and reactions in arbitrary settings. Liquid water, in neutral,2, 21, 22 protonated23 and deprotonated states,24, 25, 26 and ice27 have been rigorously studied by QM methods, and one study on autoionization28 has managed to bypass computational time limitations by using transition state theory. However, the QM computational burden limits applications to relatively small systems, even with frugal basis sets and the use of density functional theory (DFT).
Empirical approaches, which can simulate far larger systems for far longer times, have generally restricted water reactivity to “protonation.” Several hydronium or excess proton models have been reported.29 In addition, flexible30 or even polarizable31 multi-state empirical valence bond methods can be applied accurately to excess protons in the bulk,31, 32 at interfaces,33 and in biologically relevant media.34 Empirical valence bond (EVB) methods are based on Warshel's general theory of valence states35 where an arbitrary system configuration is expressed as a sum of multiple valence states weighted by energy optimized coefficients. While EVB is applied in the region of interest, other water molecules are typically described by a simple model. EVB states have also been developed for deprotonated systems37 by using a charged ring model for hydroxide.36 However, the excess proton and proton vacancy constructs have yet to be integrated.
Recently, we have unified polarization, flexibility, protonation, and deprotonation in one efficient and self-consistent construct by taking explicit account of valency.38 Our approach is related to that of Stillinger's central force model39 and polarization model90 in the sense that carefully designed pairwise potentials allow full dissociability. However, we obviate extra polarization constructs by taking explicit account of valency. Specifically, we unpack each water molecule into a +6e charged core (i.e., the combination of a +8e oxygen nucleus and a –2e pair of 1s electrons) surrounded by four −2e charged valence electron pairs and two protons bearing +1e charges.38 These LEWIS particles are all independently mobile and represented by point locations that give the electron pairs a pseudo-classical nature. For efficiency, interactions are pairwise only. Quantum effects (i.e., electron delocalization and Pauli exclusion and dispersion) are incorporated implicitly in the deviations of the interactions from Coulombic at relevant distances. The functional forms and parameterization are optimized against a training set that includes: the structures of neutral, protonated and deprotonated monomers, and dimers; monomer proton affinities; the hydrogen bond energy; the rotation7 and stretching40 landscape of the neutral dimer; the proton hopping barrier in the deprotonated dimer;41 and the ambient density of bulk water. Reference data are taken from the literature, with priority given to experimental results. High-level quantum mechanical calculations are considered only when experimental values are not available.
In this paper, we present the analytical forms of the LEWIS potentials, describe the molecular mechanics setup, and report ambient liquid state results with emphasis on liquid structure, dynamics, and polarizability. Because polarization in LEWIS is an incidental benefit of freely mobile protons and valence electron pairs, it does not play a direct role in training the potentials. The response occurs simply via subtle intramolecular rearrangements that involve stretched covalent bonds and an expanded bond angle. Reorganization of electron pairs also contributes, resulting in accurate dipolar and quadrupolar changes. In this respect, LEWIS addresses a longstanding problem of simple flexible and polarizable empirical water models that have difficulties in reproducing the experimentally observed42 and quantum mechanically supported43 changes of the water geometry in the liquid state.11, 14, 44, 45
LEWIS MODEL
Potentials
Upon testing various combinations of different functional forms we arrived at the following set of six pairwise potentials for interactions between our three types of particles, valence pairs (V), hydrogen nuclei (H), and oxygen cores (O):
| (1) |
| (2) |
| (3) |
| (4) |
| (5) |
| (6) |
where r represents the interparticle distance, q represents the particle charge (+6 for O, +1 for H, and −2 for V), and other symbols represent parameters adjusted to provide the best agreement with the physical data in the training set. Note that the leading electrostatic term is softened in the three cases involving valence pairs, and not otherwise. This softening reflects the diffuse and responsive nature of the electron pairs. Additional terms reflect Pauli exclusion (between valence pairs in the VV interaction and between valence pairs and the 1s electrons in the VO interaction) and dispersive attractions (in the OO and OH interactions). Dispersion is finite in the short range and follows an inverse sixth power in the long range.46
The choice of the potential forms is based on a rigorous evaluation of over ∼300 different combinations. Both the mathematical forms and the training set were allowed to coevolve in light of the results of typically several hundred optimization trials for each.
Coulomb softening is found to be well represented by triple-square roots with multiple parameters. The use of a four-parameter variant in the VH potential was crucial to address the rotational barrier of the water dimer. Less-flexible forms typically overestimate this barrier, yielding a “frozen” liquid due to virtually permanent hydrogen bonds.
The explicit dispersion terms were needed primarily to fit the thermodynamic properties and the geometries of the ionic dimers. The shifted polynomial form, with a finite value at zero distance, allowed for large attractions at bonding distances and inverse sixth power decay at long distances.
Exclusion terms are important among explicit valence electron pairs and between valence electron pairs and implicit core electrons. Core-core exclusions, analogous to, e.g., the inverse 12th power polynomial of Lennard-Jonnes, were not helpful.
Potential optimization
The best parameters are obtained using a double-layer optimization program. The outer layer explores potential parameters, seeking those that minimize weighted deviations from structural and thermodynamic data in the training set. These deviations are calculated by the inner layer after exploring the structural parameters of species in the training set to find those that minimize the energies given the current set of potential parameters. Structure optimizations are expedited by making use of all applicable molecular symmetries (including symmetries of electron pairs). Minimum energy configurations are then validated in Monte Carlo47 simulations without the symmetry constraints.
The weights given to elements of the training set in the outer optimization are varied from one run to another in order to facilitate a full exploration of the parameter space. Taking the weight of the H2 molecular bond length as 1, other structural features typically have weights of 4-12 for H2O and H3O+, 2–5 for OH−, and 6–10 for the three water dimers. Proton affinities have relative weights of 2-3 for H2O and OH−, and 0.05–0.1 for H−. The hydrogen bond enthalpy in the neutral dimer generally carries a relative weight of less than 0.5 (see discussion of trade-offs below). Although dimer dissociation and rotation landscapes are sampled at 8–10 equally spaced positions along the reaction coordinate, most weight eventually focuses on a few crucial positions around a prominent energy barrier or wall, with weights comparable to those used for the energy minimum. Short (200 ps – 1ns) NPT simulations at 300 K and 1 atm are run on promising parameter sets to determine liquid water density.
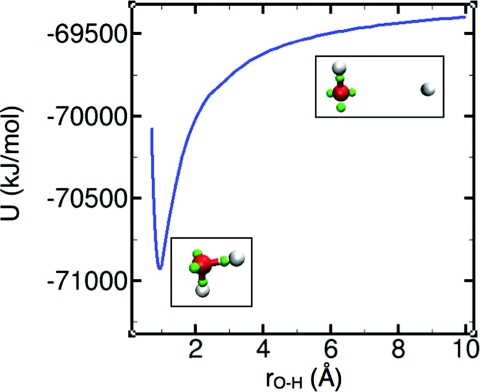
The parameter values for the potentials are listed in Table 1, the degree to which the interactions accommodate the features of monomers and dimers is shown Table 2, the monomer dissociation curve is shown in Fig. 1, and results for small clusters are shown in Table 3. The fits in Table 2 and the predictions in Fig. 1 and Table 3 show that strictly pairwise potentials are capable of approximating a wide range of phenomena.
Table 1.
Model parameters used in Eqs. 1, 2, 3, 4, 5, 6. Distances (ρ's) are in Ångstroms, energies (κ's) are in atomic units, and τ's are unitless.
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| ρVV1 | 0.12820 | ρVV2 | 0.52780 |
| ρVV3 | 0.72342 | κVV | 1.95019 |
| ρVH1 | 0.09122 | ρVH2 | 1.07407 |
| ρVH3 | 0.56994 | ρVH4 | 0.59761 |
| ρVO1 | 0.59188 | ρVO2 | 0.42553 |
| ρVO3 | 0.47725 | ρVO4 | 0.07272 |
| ρOH | 1.08820 | ρOO | 2.94886 |
| κOH | 1.98485 | κOO | 0.22145 |
| τOH | 1.54600 | τOO | 8.05300 |
Table 2.
LEWIS fit to monomer and dimer features. rOH and rHH denote covalent bond lengths, θHOH the HOH bond angle, and PA the proton affinity. All reference values are experimental, except for the O-O distance of the deprotonated dimer, which is taken from a quantum mechanical calculation.
| Molecule | Feature | Unit | Model | Reference |
|---|---|---|---|---|
| H2O | rOH | Å | 0.94 | 0.9581 |
| θHOH | deg | 104.7 | 104.41 | |
| PA | kJ/mol | 617.8 | 691.02 | |
| H3O+ | rOH | Å | 0.96 | 0.9763 |
| θHOH | deg | 109.2 | 111.33 | |
| OH− | rOH | Å | 1.01 | 0.9644 |
| PA | kJ/mol | 1671.2 | 1635.15 | |
| H2 | rHH | Å | 0.66 | 0.7416 |
| H− | PA | kJ/mol | 1667.3 | 1675.37 |
| (H2O)2 | rOO | Å | 2.85 | 2.9768 |
| θdonor | deg | −53.4 | −51.08 | |
| θacceptor | deg | 41.3 | 57.08 | |
| H5O2+ | rOO | Å | 2.38 | 2.409 |
| H3O2− | rOO | Å | 2.38 | 2.4710 |
Figure 1.
Monte Carlo results for the potential energy of a water molecule as one of its protons is moved toward and away from the oxygen. In the insets, oxygen is rendered in red, protons in white, and electron pairs in green. The depth of the minimum relative to the dissociation limit (rO-H →∞) corresponds to the proton affinity of hydroxide.
Table 3.
LEWIS predictions for small neutral water clusters and comparison with QM results. (Refs. 75 and 89) Here n denotes the number of monomers and nhb the number of hydrogen bonds. The formation enthalpy is given by ΔE = (Ecluster – n EH2O), and the energy per hydrogen bond is given by ΔEhb = (ΔE / nhb). For O-O distances (rOO), ranges are given. QM distances are taken from the structures provided by one of the authors (S.X.) of the QM references. The twisted prism hexamer of LEWIS is compared with the straight prism hexamer predicted by QM. The latter has nine hydrogen bonds.
| −ΔE | −ΔEhb | rOO | rOO, QM | −ΔEQM | |||
|---|---|---|---|---|---|---|---|
| Cluster | n | nhb | (kJ/mol) | (kJ/mol) | (Å) | (Å) | (kJ/mol) |
| (H2O)2 | 2 | 1 | 25.27 | 25.27 | 2.85 | 2.91 | 20.85 |
| (H2O)3 | 3 | 3 | 72.71 | 24.24 | 2.74–2.76 | 2.79 | 66.28 |
| (H2O)4 | 4 | 4 | 137.2 | 34.29 | 2.69–2.70 | 2.73 | 115.68 |
| (H2O)5 | 5 | 5 | 188.7 | 37.73 | 2.63–2.67 | 2.71–2.72 | 151.90 |
| (H2O)6,cycle | 6 | 6 | 235.4 | 39.23 | 2.63–2.64 | 2.71 | 187.61 |
| (H2O)6,prism | 6 | 7 | 234.6 | 33.52 | 2.62–2.84 | 2.65–2.95 | 192.01 |
| (H2O)8, D2d | 8 | 12 | 361.3 | 30.11 | 2.70–2.87 | 2.67–2.84 | 305.39 |
| (H2O)8,S4 | 8 | 12 | 361.3 | 30.10 | 2.69–2.91 | 2.66–2.84 | 304.72 |
Molecular dynamics
Newton's equations of motion are solved using a time step of 0.2 fs and electron pair mass of 1 amu. Nuclei are given the masses of their most common isotopes (mO = 16 amu and mH = 1 amu). Temperature is maintained at 300 K using stochastic velocity rescaling48 with a time constant of 0.1 ps. Electrons and nuclei are subject to separate thermostats to avoid spontaneous energy transfers between the two groups. Pressures are maintained at 1 atm using an isotropic Parrinello-Rahman barostat49 that does not distinguish between intra- and intermolecular degrees of freedom. The coupling constant is 20 ps. Stronger coupling can lead to unphysical acceleration of electron pairs. Residual center of mass motion is subtracted every 100 steps. Simulations are run using GROMACS, version 4.5.3,50 where LEWIS interactions are introduced as tabulated potentials. NPT and NVT ensembles are run in single precision leap-frog algorithm51 and NVE in double precision Velocity-Verlet.52 The neighbor list radius is 11 Å and the lists are updated every 25 steps (5 fs). Trajectories were saved every 100 fs.
An 11 ns simulation was run with 500 water monomers in a cubic box with periodic boundaries. The run began with conjugate gradient energy minimization of randomly distributed monomers following a 1 ns NPT simulation and a 10 ns NVT production run. A separate 2 ns NVE run was performed to benchmark energy conservation. Two separate 5 ns NPT simulations of the 500 H2Os box (at 1 atm, and 300 K or 295 K) were run to estimate the heat capacity at constant pressure.
Analyses use GROMACS subroutines as well as homemade scripts. Diffusion constants are calculated from the slopes of mean square displacements using the Einstein relation.53 Dielectric properties are calculated using the conventional dipole fluctuation formula54 where monomers are wrapped at the periodic boundaries. The heat capacity per monomer (at 297.5 K) was obtained by dividing the total energy difference (∆H = H300 K – H295 K) by the temperature difference (∆T = 5 K).
Long-range electrostatics
We compensate for long-range interactions by using a novel version of force shifting, also known as the shifted force gradient, as described earlier.55 This pairwise scheme modifies original potentials such that their first two derivatives go smoothly to zero at the cutoff. For example, for an original interaction potential U in Eq. 1, 2, 3, 4, 5, 6, the long-range compensated potential Uc and its associated compensated force Fc are given by the relations,
| (7) |
| (8) |
where rij denotes the distance between particles i and j, and rc denotes the cutoff distance. LEWIS is parameterized for rc = 9 Å, which outperforms smooth particle mesh Ewald by ∼ 8%-9% in CPU time.55 Note that Fc = −∇Uc and compensated forces are energy-conserving (also see Sec. III).
RESULTS
Structure and dynamics of ambient liquid water
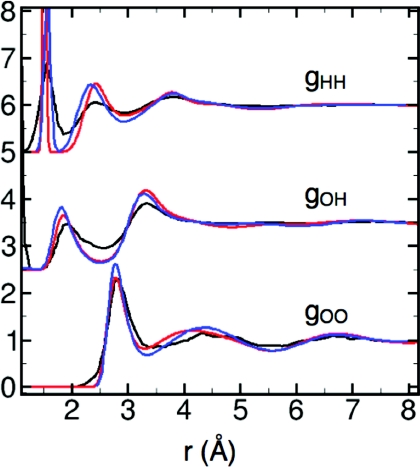
The LEWIS description of the ambient neat liquid is similar to that obtained by Car-Parrinello using the HCTH functional, which was reported to perform well in predicting liquid water properties.56, 57 The radial distribution function, gOO (Fig. 2), correlates well with the most recent model-independent diffraction data58 in terms of first peak position and height, while other features are somewhat shifted and exaggerated as in the Car-Parrinello structure. The peaks of gOH and gHH behave similarly (Fig. 2). Consistent with this excess order, diffusion is somewhat slow, with DH2O = 0.11 Å2 ps−1 compared to the experimental DH2O = 0.23 Å2 ps−1.59 Slow diffusion is common in polarizable models.18 Coordination numbers at Rc = 3.3 Å (nc) and Rc2 = 5.5 Å (nc2) are 3.89 and 22.22, respectively (vs. experimental nc = 4.26 and nc2 = 22.39 (Refs. 11 and 60). At 300 K and 1 atm, the density (ρ) is ∼0.995 g/cm3 and the heat of vaporization (ΔHvap) is 33.24 kJ/mol (vs. experimental ρ = 0.997 g/cm3 (Ref. 61) and ΔHvap = 44.02 kJ/mol (Ref. 62) at T = 298.15 K). Similar deviations in ΔHvap typically occur in quantum mechanical calculations63 and in empirical models that are not optimized for this feature.4 The estimated heat capacity at constant pressure (see Methods) is more than twice the experimental value, as expected given the additional classical degrees of freedom12, 15, 64 inherent in the LEWIS electron pairs.
Figure 2.
Radial distribution functions of ambient water at 300 K: LEWIS (red), Car-Parrinello with the HCTH functional (blue), (Ref. 56) and experimental (black) (Ref. 58).
Polarization and dielectric response
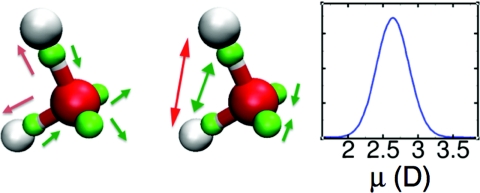
LEWIS predicts a distribution of monomer dipole moments in the neat liquid with an average of 〈μ〉 ∼2.64 D and a width at half maximum of ∼0.54 D (Fig. 3, right panel), consistent with the range of currently accepted experimental estimates65 and with DFT predictions of 2.66 D.22 The LEWIS gas phase dipole moment of μ = 2.01 D is higher than the experimental 1.85 D,66 but less so than in rigid, non-polarizable models such as TIP3P (2.35 D) (Ref. 7) or SPC (2.27 D) (Ref. 9), where the dipoles are optimized between the gas and liquid state values.
Figure 3.
Flexible polarization response of LEWIS water in liquid at 300 K. White, red, and green spheres represent hydrogen, oxygen, and valence pair particles, respectively. Arrows in the left panel indicate direction of changes in distances from the oxygen, and arrows in the middle panel identify the changes in angles. Red arrows refer to protons, and green arrows to electron pairs. The right panel shows the distribution of dipole moments in the liquid.
The traceless quadrupole moment tensor Q is calculated according to
| (9) |
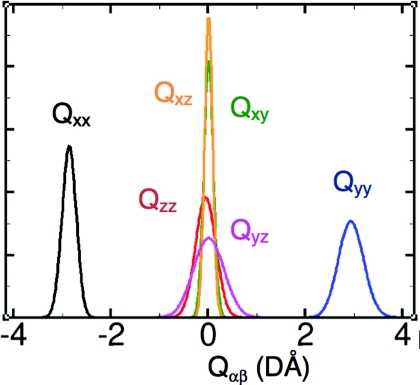
where ri is the position of particle i relative to the center of mass, α and β denote x, y, or z coordinates, δ is the Kronecker delta function, and the sum over i goes through all particles of the molecule (see, e.g., Wu et al.11). Following convention we set the molecule in the yz-plane with the sum of the two OH bond vectors along the z-axis. In the gas-phase LEWIS predicts Qxx = −2.55, Qyy = 2.58, and Qzz = −0.033 DÅ which agree well with the experimental values, −2.50, 2.63, and −0.13 DÅ, respectively.67 In the liquid state, MP2,65 DFT,68 and coupled-cluster calculations69 all predict a 6%–13% increase in the breadth of the tensor. A similar effect is also observed in LEWIS which predicts mean diagonal quadrupole moments in the liquid state of Qxx = −2.86, Qyy = 2.92, and Qzz = −0.060 DÅ and off-diagonal elements close to zero. It is also noteworthy that the six quadrupole elements exhibit different variances with the greatest being in the molecular plane (Fig. 4). To the best of our knowledge, no experimental data are yet available for comparison.
Figure 4.
Distribution of all six elements of the quadrupole tensor at 300 K. Note that normalization imposes an inverse relation between peak heights and widths. For the principal components, e.g., this implies that σQxx < σQzz < σQyy. The greatest variance is observed in the molecular (yz) plane.
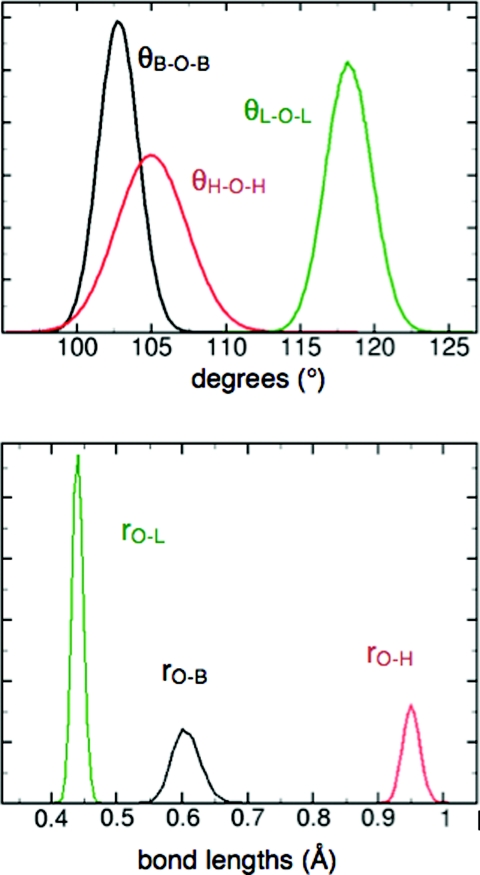
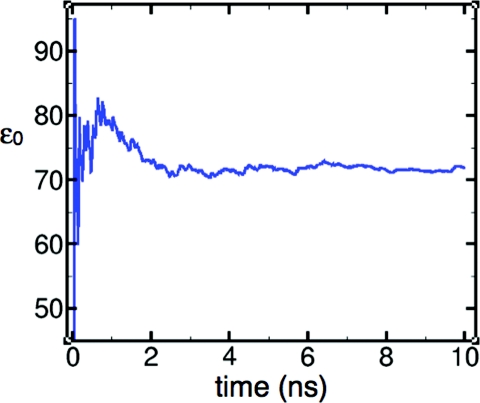
In the liquid state, the distribution of bond angles and bond lengths is broad (Fig. 5), with average values expanded by ∼0.4° and ∼0.01 Å relative to the monomer. This trend is consistent with experimental results,42 but is not captured by most flexible models.14, 15 Geometry-dependent electronic polarization has been suggested as a requirement for capturing this effect correctly.11, 43, 44 Consistent with Wannier function analyses,19 the LEWIS electrons assume a more spherical distribution in the liquid state, in that bonding pairs are drawn somewhat closer the oxygen nucleus while lone pairs drift somewhat further away, and the angular arrangement shifts towards tetrahedrality (Fig. 3). While the average physical displacements are small in magnitude, the impact on the overall polarization is substantial due to the full ionic charges of the particles. The dielectric constant ɛ0 at 300 K converges to ∼71.9 (Fig. 6), and finite and infinite Kirkwood factors to Gk ∼ 2.99 and gk ∼ 2.01, respectively (vs. experimental ɛ0 = 78.49 (Ref. 70 and gk = 2.90 71 at T = 298.15 K).
Figure 5.
Distribution of intramolecular angles and distances in the liquid state. Here, “L” denotes a lone pair and “B” a bonding pair. The molecular angle, H-O-H, has a broader spread than the angles involving electron pairs.
Figure 6.
Time evolution of the dielectric constant ɛ0 of water at 300 K. Reasonable convergence occurs within 10 ns.
Conservation of total energy
One concern about reactive methods is energy conservation.30, 31, 72 While the precision of a non-reactive force field is typically limited by the integrator, most reactive simulations involve calculations that may affect “completeness” such as basis states expansions31 or massive multi-body interactions.73 LEWIS with long-range compensation (see Methods) enjoys the simplicity of smooth pairwise potentials, which yield good energy conservation, even in tabulated forms. Total energy drift in a system of 500 ambient water molecules is within half a kJ/mol ns−1 and may be reduced further by the use of analytical forms. As noted in Methods, we monitor the temperatures of individual particle groups, i.e., TO, TH, and TV, to detect spontaneous energy transfers that may slow dynamics and affect observables. In our experience, constant energy simulations, as well as badly configured NPT and NVT setups, are prone to this effect.
Computational efficiency
While the proliferation of sub-molecular particles is rarely desirable, especially in large-scale systems, the amphiproticity and polarizability provided by LEWIS justifies a reasonable computational cost. In its current sub-optimized implementation (see Methods), single-precision LEWIS is ∼5-fold slower than TIP5P per time-step, as tested on a 2.26 GHz 8 Core MacPro workstation running a cubic box of 500 water molecules subject to periodic boundaries. A similar initial performance was observed for the polarizable (but unreactive) AMOEBA description of water.16 Obviously, there is room for improvement as tabulated potentials can be memory intensive and the inter-nuclear potential forms are simple enough that analytical evaluation may be faster than spline interpolation.74
CONCLUDING REMARKS
In LEWIS, we have developed a chemically intuitive and reasonably simple model that can capture essential features of molecular reactivity, polarizability, and flexibility in a seamless manner. Indeed, it is conceptually difficult to separate polarization from a dissociation or association event. Especially for the hydrides of an electronegative element such as oxygen, strong bond polarization typically signals the beginning of a reaction, while geometric rearrangements typically accommodate the approach of a nucleophile or electrophile. For example, the bond angle of water increases by 5°–7° upon protonation. Such changes should occur continuously in order to capture meaningful transition states and obey energy conservation.
The structures and dynamics that LEWIS predicts for liquid water are comparable to DFT predictions which are orders of magnitude more demanding in computational power. However, like any model, LEWIS has its limitations, some inherent in the underlying approach, and others due to the impossibility of exhaustively exploring its novel space of potential functions and parameters. With regard to the underlying approach, LEWIS makes two key assumptions in the interests of efficiency: a pseudo-classical treatment of the electrons in pairs, and a neglect of multi-body interactions. The former more than doubles the number of degrees of freedom that can be thermally activated, a major consequence of which is a proportional increase in the heat capacity. The pointillist representation of the electron distribution also fails to account for delocalization. A notable case is hydroxide where the lone pair arrangement enforces three-fold symmetry, a poor representation of the proposed donut-shape of the lone pairs.25 The main consequence of eschewing multi-body interactions is difficulty in matching the dihedral angles of the deprotonated dimer41 and hydrogen peroxide.76
Within the LEWIS approach, we encountered a number of trade-offs in the space of potential functions that we were able to explore. For example, the overestimation of water dimer enthalpy (see Table 3), also an issue in common water models such as TIP3P or SPC,6 resulted from a reduced weight given to this feature in the interest of better fits to other properties (see Sec. 2B). Also noteworthy in this category is the behavior of hexameric water clusters. An earlier parameterization of LEWIS, based on a strictly gas phase training set,38 favored cage-like hexamers over ring-like ones, in agreement with high-level QM calculations.75 On the other hand, the LEWIS parameters reported here do the opposite (see Table 3). However, the energy differences involved are fairly small and it is unrealistic to expect chemical accuracy from an empirical model for reactivity, especially in its early stages. It remains that the compromises made in the interests of a highly efficient construct have presented fewer trade-offs than initially expected. This is due to the detailed nature of the potential forms and the training sets that have been employed.
Our follow-up studies with LEWIS will focus on protonic defects in bulk water (i.e., hydrated hydronium and hydrated hydroxide). Our understanding of the solvation of these ions and the relevant proton transfer dynamics has significantly increased over the past decade thanks to both neutron diffraction experiments77 and ab initio simulations.24, 78, 79 However, both diffraction experiments and high-level theory require extremely high ion concentrations. This is unfortunate because, at least in the case of hydroxide, the solvation structure is significantly concentration dependent.79 LEWIS is not so constrained; with its ability to simulate thousands of water molecules on a common desktop platform, overlap between the ion solvation shells can be drastically reduced.
More generally, the approach presented here suggests a new direction for incorporating reactivity in routine molecular mechanics. Current work is extending the model to the hydrides of other elements of the second row of the periodic table with the goal of efficient simulations of organic reactions. We expect that such simulations will suggest reaction pathways that can then be explored by QM if more quantitatively accurate results are needed.
ACKNOWLEDGMENTS
We thank Peter Jordan and Michael Francis Hagan for helpful discussions, Mason Kramer for technical advice, and Vijay Pande for pointing us to Gromacs. This work was supported by the National Institutes of Health (NIH) Grant No. R01EB001035. Additional computational support was provided by the Brandeis HPC.
References
- Cramer C. J. and Truhlar D. G., Chem. Rev. 99(8), 2161 (1999). 10.1021/cr960149m [DOI] [PubMed] [Google Scholar]
- Kuo I. F. W., Mundy C. J., McGrath M. J., Siepmann J. I., VandeVondele J., Sprik M., Hutter J., Chen B., Klein M. L., Mohamed F., Krack M., and Parrinello M., J. Phys. Chem. B 108(34), 12990 (2004). 10.1021/jp047788i [DOI] [Google Scholar]
- Jorgensen W. L. and Tirado-Rives J., Proc. Natl. Acad. Sci. U.S.A. 102(19), 6665 (2005). 10.1073/pnas.0408037102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guillot B., J. Mol. Liq. 101(1–3), 219 (2002). 10.1016/S0167-7322(02)00094-6 [DOI] [Google Scholar]
- Bernal J. D. and Fowler R. H., J. Am. Chem. Soc. 1(8), 515 (1933). 10.1063/1.1749327. [DOI] [Google Scholar]
- Jorgensen W. L., Chandrasekhar J., Madura J. D., Impey R. W., and Klein M. L., J. Chem. Phys. 79(2), 926 (1983). 10.1063/1.445869 [DOI] [Google Scholar]
- Mahoney M. W. and Jorgensen W. L., J. Chem. Phys. 112(20), 8910 (2000). 10.1063/1.481505 [DOI] [Google Scholar]
- Abascal J. L. F., Sanz E., Fernandez R. G., and Vega C., J. Chem. Phys. 122(23), 234511 (2005). 10.1063/1.1931662 [DOI] [PubMed] [Google Scholar]
- Berendsen H. J. C., Postma J. P. M., van Gusteren W. F., and Hermans J., in Intermolecular Forces, edited by Pullman B. (Reidel, Dordrecht, 1981), pp. 331. [Google Scholar]
- Berendsen H. J. C., Grigera J. R., and Straatsma T. P., J. Phys. Chem. 91(24), 6269 (1987). 10.1021/j100308a038 [DOI] [Google Scholar]
- Wu Y. J., Tepper H. L., and Voth G. A., J. Chem. Phys. 124(2), 024503 (2006). 10.1063/1.2136877 [DOI] [PubMed] [Google Scholar]
- Levitt M., Hirshberg M., Sharon R., Laidig K. E., and Daggett V., J. Phys. Chem. B 101(25), 5051 (1997). 10.1021/jp964020s [DOI] [Google Scholar]
- Habershon S., Markland T. E., and Manolopoulos D. E., J. Chem. Phys. 131(2), 024501 (2009). 10.1063/1.3167790 [DOI] [PubMed] [Google Scholar]
- Ponder J. W. and Case D. A., Adv. Protein Chem. 66, 27 (2003). 10.1016/S0065-3233(03)66002-X [DOI] [PubMed] [Google Scholar]
- Ren P. Y. and Ponder J. W., J. Phys. Chem. B 107(24), 5933 (2003). 10.1021/jp027815+ [DOI] [Google Scholar]
- Ren P. Y. and Ponder J. W., J. Phys. Chem. B 108(35), 13427 (2004). 10.1021/jp0484332 [DOI] [Google Scholar]
- Sprik M. and Klein M. L., J. Chem. Phys. 89(12), 7556 (1988); 10.1063/1.455722 [DOI] [Google Scholar]; Cieplak P., Kollman P., and Lybrand T., J. Chem. Phys. 92(11), 6755 (1990). 10.1063/1.458260 [DOI] [Google Scholar]
- Stern H. A., Rittner F., Berne B. J., and Friesner R. A., J. Chem. Phys. 115(5), 2237 (2001). 10.1063/1.1376165 [DOI] [Google Scholar]
- Silvestrelli P. L. and Parrinello M., Phys. Rev. Lett. 82(16), 3308 (1999). 10.1103/PhysRevLett.82.3308 [DOI] [Google Scholar]
- Ponder J. W., Wu C. J., Ren P. Y., Pande V. S., Chodera J. D., Schnieders M. J., Haque I., Mobley D. L., Lambrecht D. S., DiStasio R. A., Head-Gordon M., Clark G. N. I., Johnson M. E., and Head-Gordon T., J. Phys. Chem. B. 114(8), 2549 (2010). 10.1021/jp910674d [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silvestrelli P. L. and Parrinello M., J. Chem. Phys. 111(8), 3572 (1999). 10.1063/1.479638 [DOI] [Google Scholar]
- Laasonen K., Sprik M., Parrinello M., and Car R., J. Chem. Phys. 99(11), 9080 (1993). 10.1063/1.465574 [DOI] [Google Scholar]
- Tuckerman M. E., Marx D., Klein M. L., and Parrinello M., Science 275(5301), 817 (1997); 10.1126/science.275.5301.817 [DOI] [PubMed] [Google Scholar]; Iyengar S. S., Day T. J. F., and Voth G. A., Int. J. Mass Spectrom. 241(2-3), 197 (2005). 10.1016/j.ijms.2004.12.003 [DOI] [Google Scholar]
- Tuckerman M. E., Chandra A., and Marx D., Acc. Chem. Res. 39(2), 151 (2006). 10.1021/ar040207n [DOI] [PubMed] [Google Scholar]
- Tuckerman M. E., Marx D., and Parrinello M., Nature (London) 417(6892), 925 (2002). 10.1038/nature00797 [DOI] [PubMed] [Google Scholar]
- Asthagiri D., Pratt L. R., Kress J. D., and Gomez M. A., Proc. Natl. Acad. Sci. U.S.A. 101(19), 7229 (2004). 10.1073/pnas.0401696101 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yoo S., Zeng X. C., and Xantheas S. S., J. Chem. Phys. 130(22), 2211020 (2009). 10.1063/1.3153871 [DOI] [PubMed] [Google Scholar]
- Geissler P. L., Dellago C., Chandler D., Hutter J., and Parrinello M., Science 291(5511), 2121 (2001). 10.1126/science.1056991 [DOI] [PubMed] [Google Scholar]
- Kozack R. E. and Jordan P. C., J. Chem. Phys. 96(4), 3131 (1992); 10.1063/1.461957 [DOI] [Google Scholar]; Ojamae L., Shavitt I., and Singer S. J., J. Chem. Phys. 109(13), 5547 (1998); 10.1063/1.477173 [DOI] [Google Scholar]; Shevkunov S. V. and Vegiri A., Mol. Phys. 98(3), 149 (2000). 10.1080/00268970009483279 [DOI] [Google Scholar]
- Wu Y., Chen H., Wang F., Paesani F., and Voth G. A., J. Phys. Chem. B 112(23), 7146 (2008). 10.1021/jp8036318 [DOI] [PubMed] [Google Scholar]
- Brancato G. and Tuckerman M. E., J. Chem. Phys. 122(22), 224507 (2005). 10.1063/1.1902924 [DOI] [PubMed] [Google Scholar]
- Schmitt U. W. and Voth G. A., J. Phys. Chem. B 102(29), 5547 (1998). 10.1021/jp9818131 [DOI] [Google Scholar]
- Petersen M. K., Iyengar S. S., Day T. J. F., and Voth G. A., J. Phys. Chem. B 108(39), 14804 (2004). 10.1021/jp046716o [DOI] [Google Scholar]
- Voth G. A., Front. Biosci. 8, S1384 (2003). 10.2741/1213 [DOI] [PubMed] [Google Scholar]
- Warshel A. and Weiss R. M., J. Am. Chem. Soc. 102(20), 6218 (1980). 10.1021/ja00540a008 [DOI] [Google Scholar]
- Ufimtsev I. S., Kalinichev A. G., Martinez T. J., and Kirkpatrick R. J., Chem. Phys. Lett. 442(1–3), 128 (2007). 10.1016/j.cplett.2007.05.042 [DOI] [Google Scholar]
- Ufimtsev I. S., Kalinichev A. G., Martinez T. J., and Kirkpatrick R. J., Phys. Chem. Chem. Phys. 11(41), 9420 (2009); 10.1039/b907859b [DOI] [PubMed] [Google Scholar]; Roberts S. T., Petersen P. B., Ramasesha K., Tokmakoff A., Ufimtsev I. S., and Martinez T. J., Proc. Natl. Acad. Sci. U.S.A. 106(36), 15154 (2009). 10.1073/pnas.0901571106 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kale S., Herzfeld J., Dai S., and Blank M., J. Biol. Phys. 38(1), 49 (2012). 10.1007/s10867-011-9229-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lemberg H. L. and Stillinger F. H., J. Chem. Phys. 62(5), 1677 (1975); 10.1063/1.430718 [DOI] [Google Scholar]; Stillinger F. H. and Rahman A., J. Chem. Phys. 68(2), 666 (1978). 10.1063/1.435738 [DOI] [Google Scholar]
- Burnham C. J. and Xantheas S. S., J. Chem. Phys. 116(4), 1479 (2002). 10.1063/1.1423940 [DOI] [Google Scholar]
- Samson C. C. M. and Klopper W., J. Mol. Struct.: THEOCHEM 586, 201 (2002). 10.1016/S0166-1280(02)00066-0 [DOI] [Google Scholar]
- Ichikawa K., Kameda Y., Yamaguchi T., Wakita H., and Misawa M., Mol. Phys. 73(1), 79 (1991). 10.1080/00268979100101071 [DOI] [Google Scholar]
- Burnham C. J. and Xantheas S. S., J. Chem. Phys. 116(12), 5115 (2002). 10.1063/1.1447904 [DOI] [Google Scholar]
- Jeon J., Lefohn A. E., and Voth G. A., J. Chem. Phys. 118(16), 7504 (2003). 10.1063/1.1560934 [DOI] [Google Scholar]
- Mankoo P. K. and Keyes T., J. Chem. Phys. 129(3), 034504 (2008). 10.1063/1.2948966 [DOI] [PubMed] [Google Scholar]
- Koide A., J. Phys. B 9(18), 3173 (1976). 10.1088/0022-3700/9/18/009 [DOI] [Google Scholar]
- Metropolis N. and Ulam S., J. Am. Stat. Assoc. 44(247), 335 (1949); 10.2307/2280232 [DOI] [PubMed] [Google Scholar]; Metropolis N., Rosenbluth A. W., Rosenbluth M. N., Teller A. H., and Teller E., J. Chem. Phys. 21(6), 1087 (1953). 10.1063/1.1699114 [DOI] [Google Scholar]
- Bussi G., Donadio D., and Parrinello M., J. Chem. Phys. 126(1), 014101 (2007). 10.1063/1.2408420 [DOI] [PubMed] [Google Scholar]
- Parrinello M. and Rahman A., J. Appl. Phys. 52(12), 7182 (1981); 10.1063/1.328693 [DOI] [Google Scholar]; Nose S. and Klein M. L., Mol. Phys. 50(5), 1055 (1983). 10.1080/00268978300102851 [DOI] [Google Scholar]
- van der Spoel D., Lindahl E., Hess B., Groenhof G., Mark A. E., and Berendsen H. J. C., J. Comput. Chem. 26(16), 1701 (2005); 10.1002/jcc.20291 [DOI] [PubMed] [Google Scholar]; Hess B., Kutzner C., van der Spoel D., and Lindahl E., J. Chem. Theory Comput. 4(3), 435 (2008). 10.1021/ct700301q [DOI] [PubMed] [Google Scholar]
- Hockney R. W., Goel S. P., and Eastwood J. W., J. Comput. Phys. 14(2), 148 (1974). 10.1016/0021-9991(74)90010-2 [DOI] [Google Scholar]
- Verlet L., Phys. Rev. 159(1), 98 (1967); 10.1103/PhysRev.159.98 [DOI] [Google Scholar]; Swope W. C., Andersen H. C., Berens P. H., and Wilson K. R., J. Chem. Phys. 76(1), 637 (1982). 10.1063/1.442716 [DOI] [Google Scholar]
- Allen M. P. and Tildesley D. J., Computer Simulation of Liquids (Oxford University Press, New York, 1987). [Google Scholar]
- Neumann M., Mol. Phys. 50(4), 841 (1983). 10.1080/00268978300102721 [DOI] [Google Scholar]
- Kale S. and Herzfeld J, J. Chem. Theory Comput. 7(11), 3620 (2011). 10.1021/ct200392u [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izvekov S. and Voth G. A., J. Chem. Phys. 123(4), 044505 (2005). 10.1063/1.1961443 [DOI] [PubMed] [Google Scholar]
- Boese A. D., Doltsinis N. L., Handy N. C., and Sprik M., J. Chem. Phys. 112(4), 1670 (2000). 10.1063/1.480732 [DOI] [Google Scholar]
- Wikfeldt K. T., Leetmaa M., Ljungberg M. P., Nilsson A., and Pettersson L. G. M., J. Phys. Chem. B 113(18), 6246 (2009). 10.1021/jp9007619 [DOI] [PubMed] [Google Scholar]
- Krynicki K., Green C. D., and Sawyer D. W., Faraday Discuss. 66, 199 (1978). 10.1039/dc9786600199 [DOI] [Google Scholar]
- Soper A. K., Chem. Phys. 258(2–3), 121 (2000). 10.1016/S0301-0104(00)00179-8 [DOI] [Google Scholar]
- Kell G. S., J. Chem. Eng. Data 12(1), 66 (1967). 10.1021/je60032a018 [DOI] [Google Scholar]
- Wagner W. and Pruss A., J. Phys. Chem. Ref. Data 31(2), 387 (2002). 10.1063/1.1461829 [DOI] [Google Scholar]
- Grossman J. C. and Mitas L., Phys. Rev. Lett. 94(5), 056403 (2005). 10.1103/PhysRevLett.94.056403 [DOI] [PubMed] [Google Scholar]
- Eisenberg D. and Kauzmann W., The Structure and Properties of Water (Oxford University Press, New York, 1969). [Google Scholar]
- Tu Y. Q. and Laaksonen A., Chem. Phys. Lett. 329(3–4), 283 (2000). 10.1016/S0009-2614(00)01026-5 [DOI] [Google Scholar]
- Clough S. A., Beers Y., Klein G. P., and Rothman L. S., J. Chem. Phys. 59(5), 2254 (1973). 10.1063/1.1680328 [DOI] [Google Scholar]
- Verhoeven J. and Dymanus A., J. Chem. Phys. 52(6), 3222 (1970). 10.1063/1.1673462 [DOI] [Google Scholar]
- Delle Site L., Alavi A., and Lynden-Bell R. M., Mol. Phys. 96(11), 1683 (1999). 10.1080/00268979909483112 [DOI] [Google Scholar]
- Kongsted J., Osted A., Mikkelsen K. V., and Christiansen O., Chem. Phys. Lett. 364(3-4), 379 (2002). 10.1016/S0009-2614(02)01286-1 [DOI] [Google Scholar]
- Uematsu M. and Franck E. U., J. Phys. Chem. Ref. Data 9(4), 1291 (1980). 10.1063/1.555632 [DOI] [Google Scholar]
- Neumann M., Mol. Phys. 57(1), 97 (1986). 10.1080/00268978600100081 [DOI] [Google Scholar]
- Marx D. and Hutter J., in Modern Methods and Algorithms of Quantum Chemistry, edited by Grotendorst J. (John von Neumann Institute of Computing, Julich, NIC Series, 2000), Vol. 1, pp. 301. [Google Scholar]
- van Duin A. C. T., Dasgupta S., Lorant F., and Goddard W. A., J. Phys. Chem. A. 105(41), 9396 (2001). 10.1021/jp004368u [DOI] [Google Scholar]
- van der Spoel D., Lindahl E., Hess B., van Buuren A. R., Apol E., Meulenhoff P. J., Tieleman D. P., Sijbers A. L. T. M., Feenstra K. A., van Drunen R., and Berendsen H. J. C., Gromacs User Manual version 4.5.3, www.gromacs.org (2010).
- Xantheas S. S., Burnham C. J., and Harrison R. J., J. Chem. Phys. 116(4), 1493 (2002). 10.1063/1.1423941 [DOI] [Google Scholar]
- Oelfke W. C. and Gordy W., J. Chem. Phys. 51(12), 5336 (1969). 10.1063/1.1671954 [DOI] [Google Scholar]
- Botti A., Bruni F., Imberti S., Ricci M. A., and Soper A. K., J. Chem. Phys. 121(16), 7840 (2004); 10.1063/1.1801031 [DOI] [PubMed] [Google Scholar]; Botti A., Bruni F., Imberti S., Ricci M. A., and Soper A. K., J. Chem. Phys. 120(21), 10154 (2004); 10.1063/1.1705572 [DOI] [PubMed] [Google Scholar]; Botti A., Bruni F., Imberti S., Ricci M. A., and Soper A. K., J. Mol. Liq. 117(1–3), 81 (2005). 10.1016/j.molliq.2004.08.013 [DOI] [Google Scholar]
- Marx D., Tuckerman M. E., Hutter J., and Parrinello M., Nature (London) 397(6720), 601 (1999); 10.1038/17579 [DOI] [Google Scholar]; Marx D., Chandra A., and Tuckerman M. E., Chem. Rev. 110(4), 2174 (2010). 10.1021/cr900233f [DOI] [PubMed] [Google Scholar]
- Chen B., Park J. M., Ivanov I., Tabacchi G., Klein M. L., and Parrinello M., J. Am. Chem. Soc. 124(29), 8534 (2002). 10.1021/ja020350g [DOI] [PubMed] [Google Scholar]
- Jensen P., J. Mol. Spectrosc. 133(2), 438 (1989). 10.1016/0022-2852(89)90203-8 [DOI] [Google Scholar]
- Hunter E. P. L. and Lias S. G., J. Phys. Chem. Ref. Data 27(3), 413 (1998). 10.1063/1.556018 [DOI] [Google Scholar]
- Sears T. J., Bunker P. R., Davies P. B., Johnson S. A., and Spirko V., J. Chem. Phys. 83(6), 2676 (1985). 10.1063/1.449270 [DOI] [Google Scholar]
- Owrutsky J. C., Rosenbaum N. H., Tack L. M., and Saykally R. J., J. Chem. Phys. 83(10), 5338 (1985). 10.1063/1.449696 [DOI] [Google Scholar]
- Dewar M. J. S. and Dieter K. M., J. Am. Chem. Soc. 108(25), 8075 (1986). 10.1021/ja00285a033 [DOI] [Google Scholar]
- Lide D. R., CRC Handbook of Chemistry and Physics, 76th ed. (CRC, Boca Raton, FL, 1995). [Google Scholar]
- Bartmess J. E., Scott J. A., and Mciver R. T., J. Am. Chem. Soc. 101(20), 6046 (1979). 10.1021/ja00514a030 [DOI] [Google Scholar]
- Odutola J. A. and Dyke T. R., J. Chem. Phys. 72(9), 5062 (1980). 10.1063/1.439795 [DOI] [Google Scholar]
- Fridgen T. D., McMahon T. B., MacAleese L., Lemaire J., and Maitre P., J. Phys. Chem. A 108(42), 9008 (2004). 10.1021/jp040486w [DOI] [Google Scholar]
- Xantheas S. S. and Apra E., J. Chem. Phys. 120(2), 823 (2004). 10.1063/1.1626624 [DOI] [PubMed] [Google Scholar]
- Stillinger F. H. and David C. W., J. Chem. Phys. 69(4), 1473 (1978). 10.1063/1.436773 [DOI] [Google Scholar]