Skip to main content
PMC home page
Medical Physics logoLink to Medical Physics
. 2012 Feb 29;39(3):1588–1594. doi: 10.1118/1.3685583

The dosimetric impact of inversely optimized arc radiotherapy plan modulation for real-time dynamic MLC tracking delivery

Marianne Falk 1,a), Tobias Larsson 2, Paul Keall 3, Byung Chul Cho 4, Marianne Aznar 5, Stine Korreman 6, Per Poulsen 7, Per Munck af Rosenschöld 8
PMCID: PMC3306442  PMID: 22380391

Abstract

Purpose: Real-time dynamic multileaf collimator (MLC) tracking for management of intrafraction tumor motion can be challenging for highly modulated beams, as the leaves need to travel far to adjust for target motion perpendicular to the leaf travel direction. The plan modulation can be reduced by using a leaf position constraint (LPC) that reduces the difference in the position of adjacent MLC leaves in the plan. The purpose of this study was to investigate the impact of the LPC on the quality of inversely optimized arc radiotherapy plans and the effect of the MLC motion pattern on the dosimetric accuracy of MLC tracking delivery. Specifically, the possibility of predicting the accuracy of MLC tracking delivery based on the plan modulation was investigated.

Methods: Inversely optimized arc radiotherapy plans were created on CT-data of three lung cancer patients. For each case, five plans with a single 358° arc were generated with LPC priorities of 0 (no LPC), 0.25, 0.5, 0.75, and 1 (highest possible LPC), respectively. All the plans had a prescribed dose of 2 Gy × 30, used 6 MV, a maximum dose rate of 600 MU/min and a collimator angle of 45° or 315°. To quantify the plan modulation, an average adjacent leaf distance (ALD) was calculated by averaging the mean adjacent leaf distance for each control point. The linear relationship between the plan quality [i.e., the calculated dose distributions and the number of monitor units (MU)] and the LPC was investigated, and the linear regression coefficient as well as a two tailed confidence level of 95% was used in the evaluation. The effect of the plan modulation on the performance of MLC tracking was tested by delivering the plans to a cylindrical diode array phantom moving with sinusoidal motion in the superior–inferior direction with a peak-to-peak displacement of 2 cm and a cycle time of 6 s. The delivery was adjusted to the target motion using MLC tracking, guided in real-time by an infrared optical system. The dosimetric results were evaluated using gamma index evaluation with static target measurements as reference.

Results: The plan quality parameters did not depend significantly on the LPC (p ≥ 0.066), whereas the ALD depended significantly on the LPC (p < 0.001). The gamma index failure rate depended significantly on the ALD, weighted to the percentage of the beam delivered in each control point of the plan (ALDw) when MLC tracking was used (p < 0.001), but not for delivery without MLC tracking (p ≥ 0.342). The gamma index failure rate with the criteria of 2% and 2 mm was decreased from > 33.9% without MLC tracking to <31.4% (LPC 0) and <2.2% (LPC 1) with MLC tracking.

Conclusions: The results indicate that the dosimetric robustness of MLC tracking delivery of an inversely optimized arc radiotherapy plan can be improved by incorporating leaf position constraints in the objective function without otherwise affecting the plan quality. The dosimetric robustness may be estimated prior to delivery by evaluating the ALDw of the plan.

Keywords: tumor tracking, intra-fraction motion, arc therapy

INTRODUCTION

Dosimetric uncertainty arising from intrafraction motion can have adverse effects on the treatment outcome of radiation therapy.1, 2, 3 Common practice is to treat an extended volume of healthy tissue surrounding a moving clinical target volume to ensure that the tumor is covered with high probability throughout the fraction. Since larger treatment volumes are associated with an increased dose to nearby normal tissues, there has been an increasing interest in developing advanced methods of motion management. As another approach to reduce dose to healthy tissue, inversely optimized arc radiotherapy delivers the treatment in one or several arcs of the gantry, during which the multileaf collimator (MLC) shape, dose rate, and gantry speed are varied. Intensity-modulated arc therapy (IMAT) was introduced by Yu4 in 1995 as a treatment technique using multiple superimposed arcs with varying field shapes, while gantry speed and dose rate remained constant. In 2007, the technique was modified by Otto5 with a novel aperture-based algorithm for treatment planning optimization. In this study, the RapidArc® (RA) solution implemented by Varian Medical Systems6 was used. Complex treatments (e.g., dose painting7) with inversely optimized arc radiotherapy are generally characterized by highly modulated beams and the interplay between the motion of the tumor and the linac motions during treatment has been shown to give errors in the delivered dose.8 Gating9, 10 has been used frequently in the last decade for treatment of breast cancer but has limitations in the treatment time efficiency, since the radiation delivery is interrupted when the tumor motion exceeds the predefined range.11 Other methods and systems for intrafraction tumor motion management in clinical use and/or proposed in the literature include motion adaptation through repositioning the MLC leaves12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22 or the treatment couch,23, 24 the CyberKnife robotic treatment system25, 26 and the gimbaled linac.27 Real-time dynamic MLC tracking has in several studies demonstrated great potential for intrafraction motion management.12, 13, 14, 15, 16, 17, 18, 19 Plans with highly complex MLC patterns could be difficult to deliver accurately with MLC tracking, since the leaves have longer distances to travel when tracking a target moving nonparallel to the MLC trajectory. If the travel distance is too large, the finite speed of the MLC may prevent the leaves from reaching their motion-adapted positions in time for accurate motion management. The purpose of this study was to investigate if the performance of MLC tracking is dependent on the plan modulation of RA plans and if it is possible to predict the accuracy of MLC tracking delivery based on this factor. The plan modulation was varied using a leaf position constraint and the quality of the treatment plans was evaluated to investigate the applicability of the constraint for increasing the compatibility of highly modulated RA plans with MLC tracking delivery.

MATERIALS AND METHODS

Inversely optimized arc radiotherapy plans were created in a research version of EclipseTM (version 8.8) treatment planning system (TPS) using the RA technique for delivery using a Novalis TXTM linear accelerator with a high definition MLC (HD MLC). CT-data of three lung cancer patients were used in this study and the target volumes (Table TABLE I.) were chosen to create treatment plans with varying target size and shape.

TABLE I.

Target volume and size.

Case Volume (cm3) Size (cm)
    SI LR AP
1 108.5 6.8 5.6 5.3
2 18.8 5.4 5.5 3.3
3 29.7 7.5 7.1 5.6
Open in a new tab

The plan modulation was reduced using a leaf position constraint (LPC) that introduced a maximum allowed distance between adjacent leaves (MLD) in the arc optimization. The smallest available MLD was equal to the maximum distance that a leaf can travel between two control points (MLT) (which depends on the distance between the control points, the leaf speed, and the gantry speed). Before the effect on the target coverage and doses to organs at risk had actually been studied, it made sense to also allow for some less stringent constraint on the MLC configuration. This was done considering that if the plan quality was significantly impacted by the side constraint on the MLC in the optimization phase this methodology as a whole would not be attractive, unless the constraint could also be relaxed somewhat. This study investigated if an optimum could be found where the impact on the plan and the leaf positioning accuracy of the MLC tracking are both acceptable. It was estimated that an MLD of 4 times the MLT would leave enough room for an almost free optimization to cover the solution space. The relationship between the MLD and the LPC is given by

MLD=(1.0+(1.0-LPC)·3)·MLT. (1)

An LPC of 1 gives an MLD equal to MLT and an LPC of 0.25 gives an MLD equal to 3.25 × MLT. Equation 1 is only valid for LPC > 0. If LPC = 0, no MLD is applied in the optimization. For each case, five plans with a single 358° arc field were created using LPCs of 0, 0.25, 0.5, 0.75, and 1.

All the plans had a prescribed dose of 2 Gy × 30, used a 6 MV beam and a maximum dose rate of 600 MU/min. The jaws were positioned to have a minimum distance to the field edge of 1 cm to keep them from blocking the field during the tracking delivery. The collimator was rotated by 45° or 315°. The dose volume constraints varied for the three cases to ensure that the clinical objectives (e.g., 45 Gy maximum dose to the spinal canal) were fulfilled but were the same for all plans within the same case. The constraint on the total number of monitor units (MU) was set to 500 MU for all plans. To investigate the impact of the LPC on the plan quality, plans with different LPC priorities within the same case were compared. The plan quality was assessed by evaluating the calculated dose distribution (0.1 cm grid size) from the TPS as well as the number of MU. The dose parameters investigated were the target volume receiving 95% of the prescribed dose, the maximum dose to the target, the maximum dose to the spinal canal, as well as the mean dose to each lung and to the heart. To relate the results to those of the plan with no LPC, the value of each of the investigated parameters was normalized to the value attained for the same parameter in the same case with no LPC (e.g., for all plans, the maximum dose to the target was normalized to the maximum dose to the target for the plan in the same case with no LPC). Linear regression was used in the evaluation and the regression coefficient was calculated. A two tailed confidence level of 95% was chosen, so p-values less than 0.05 were considered significant. Also, the Spearman’s rank correlation coefficient (ρ) was calculated to assess the correlations. Statistical analysis used SPSS version 15.0.

To quantify the effect of the LPC on the plan modulation, the average adjacent leaf distance (ALD) was calculated. The ALD of a plan was derived by calculating the average value of the adjacent leaf distance in each control point and computing the average of this value over all control points in the plan

ALD=1n∑i=1nmi, (2)

where n is the number of control points and mi is the mean adjacent leaf distance for control point i. The impact of mi on the delivered dosimetric accuracy is likely to depend on the dose delivered at control point i. The ALD was, therefore, weighted to the percentage of the beam to be delivered in each control point

ALDw=1n∑i=1nmi·wi, (3)

where wi is the percentage of the beam to be delivered in control point i. The mean adjacent leaf distance for each control point is given by

m=1N·∑jN(|xj-xj-1|+|xj-xj+1|)2, (4)

where xj is the position for leaf j and N is the number of leaves that are included in the calculation in the specific control point. N is calculated for each control point and includes the first and the last open leaf pairs and all leaf pairs in between.

The plans were delivered to the Delta4® dosimetric device (ScandiDos, Sweden) that measures the 3D dose distribution using two orthogonal detector arrays surrounded by a cylindrical PMMA phantom. The detector arrays contain 1069 disk shaped p-Si diodes with volumes of 0.04 mm3. The diodes are separated by 0.5 cm in the central 6 cm × 6 cm area of the detector arrays and by 1 cm in the remaining area (up to 20 cm × 20 cm). The Delta4® was placed on a motion platform (Fig. 1) programmed to form a 1D sinusoidal trajectory to simulate respiratory movements. In this study, a cycle time of 6 s and a peak-to-peak displacement of 2 cm in the superior–inferior direction were used. Real-time position data were received from the ExacTrac® system (Brainlab, Germany) (Refs. 28, 29) that uses two cameras emitting infrared light and passive reflective spheres attached to the phantom surface. The reflected signal was sampled with a frequency of 20 Hz and analyzed for position information. The system also contains two kV x-ray units which could be used to verify the correlation between the internal tumor motion and the external markers.30 However, only the optical part of the system was used in this study. The real-time target position data were sent to the MLC tracking controller (presently a nonclinical research tool) where a tracking algorithm calculated new MLC leaf positions to adjust for the target movements, taking the delay time of the system (260 ms for this study) into account.31 The new leaf positions were then sent to the MLC controller to guide the positioning of the MLC leaves.

Figure 1.

Figure 1

Open in a new tab

The 1D motion platform carrying the Delta4® dosimetric phantom with the ExacTrac® markers attached to its surface.

MLC tracking requires a wider jaw setting than normal delivery and an increase of interleaf leakage is therefore expected. To minimize the leakage through the leaf tips of closed leaf pairs, the tracking system places these under the x-jaws,19 with the exception of a user specified number of leaf pairs (four in this study) closest to the field opening that are kept centered to enable a quick response of the system. The delivery without tracking, on the contrary had the closed leaf pairs adjacent to the field centred, even though the same jaw settings were used. When evaluating the dosimetric results, a measurement with a static target was considered to give the dose distribution that would correspond to optimal motion management. This was, therefore, used as reference in the gamma index evaluation. To avoid the results reflecting discrepancies due to the decrease of interleaf leakage when the MLC tracking system is connected, the static measurement used as reference in the evaluation was made with the MLC tracking system connected for the results with tracking. The reference measurements used for the results without tracking were made with the MLC tracking system disconnected. The gamma index criteria used were the 3% and 3 mm and 2% and 2 mm criteria. The criteria 2% and 2 mm were used as a supplement to the commonly used criteria 3% and 3 mm to thoroughly investigate the dose agreement and to limit the distance to agreement (DTA) to a range smaller than the resolution of the HD MLC (2.5 mm for 32 central leaf-pairs and 5 mm for 28 peripheral leaf-pairs). The dose deviation was evaluated with respect to the isocenter dose and the detector points receiving less than 10% were excluded from the evaluation since these points are likely to pass the evaluation for all cases. The correlation between the gamma index failure rate and the ALDw was evaluated to investigate the impact of the MLC motion complexity on the dosimetric accuracy of MLC tracking delivery.

RESULTS

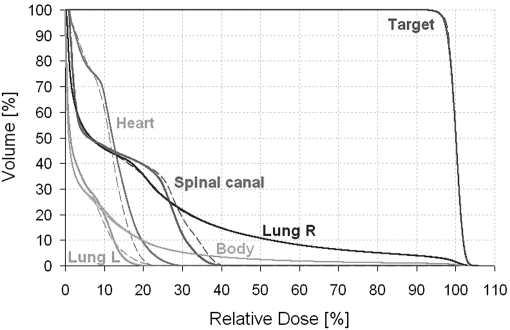
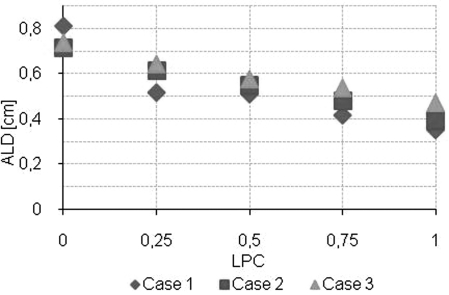
The DVH comparison showed similar coverage of the target for the plans with and without the LPC and the variations for the organs at risk appeared to be random (an example is shown in Fig. 2). There was no significant linear dependence of any of the plan quality parameters on the LPC and the Spearman’s rank correlation coefficients was small (|ρ| ≤ 0.580) (Table TABLE II.). The ALD depended significantly on the LPC and had a Spearman’s rank correlation coefficient of −0.917 (Fig. 3, Table TABLE II.). Note that the LPC does not make the plan approximate a conformal arc, but rather reduces the complexity of the MLC shapes by placing adjacent leaves closer together (Fig. 4). The linear regression coefficient for the plan quality parameters dependence on the LPC was small (≤0.111) and the 95% confidence interval overlapped zero.

Figure 2.

Figure 2

Open in a new tab

Dose volume histograms for case 1 for the plan with no LPC (solid lines) and the plan with maximum LPC (dashed lines).

TABLE II.

The impact of the leaf position constraint (LPC) on the plan quality and the impact of the weighted average adjacent leaf distance (ALDW) on the delivered dosimetric accuracy with and without MLC tracking. The significant correlations are highlighted.

    Linear regression  
Dependent variable Independent variable Coefficient (95% conf interval) p Spearman’s rank correlation (ρ)
Number of MUs LPC 0.092 (−0.021, 0.206) 0.102 0.329
Target V95 LPC −0.002 (−0.005, <0.001) 0.066 −0.580
Target max dose LPC −0.004 (−0.013, 0.005) 0.378 −0.361
Spinal canal max dose LPC 0.111 (−0.122, 0.345) 0.322 0.361
Lung R mean dose LPC 0.036 (−0.021, 0.093) 0.193 0.318
Lung L mean dose LPC 0.008 (−0.049, 0.066) 0.758 −0.011
Heart mean dose LPC 0.026 (−0.139, 0.191) 0.738 −0.055
ALD LPC −0.323 (−0.413,−0.233) <0.001 −0.917
Gamma index failure rate with criteria 3% and 3 mm
With tracking ALDw 48.645 (37.413, 59.876) <0.001 0.949
No tracking ALDw −1.382 (−13.149, 10.384) 0.804 -0.077
Gamma index failure rate with criteria 2% and 2 mm
With tracking ALDw 61.454 (44.348, 78.559) <0.001 0.854
No tracking ALDw 7.769 (−9.245, 24.782) 0.342 0.282
Open in a new tab

Figure 3.

Figure 3

Open in a new tab

ALD as a function of leaf position constraint.

Figure 4.

Figure 4

Open in a new tab

The MLC shape with no LPC (left) and with the maximum LPC (right) in the same control point for case 1.

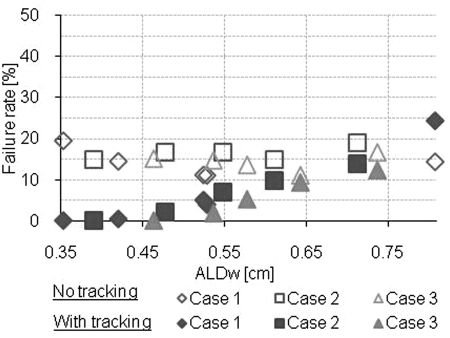
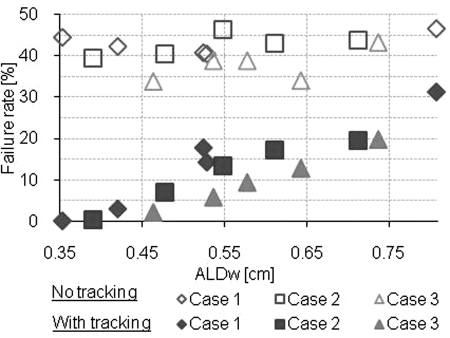
The results of the gamma index evaluation for each plan are shown in Figs. 56. Without any motion compensation, the gamma index failure rate was substantial, >11.1% (3% and 3 mm) and >33.9% (2% and 2 mm) and did not depend significantly on the ALDw (Table TABLE II.). With MLC tracking, the gamma index failure rate depended significantly on the ALDw and the gamma index failure rate was decreased from ≥12.3% (3% and 3 mm) and ≥19.4% (2% and 2 mm) with ALDw > 0.7 cm to ≤ 2.2 (3% and 3 mm) and ≤ 7.1 (2% and 2 mm) with ALDw < 0.5 cm. The Spearman’s rank correlation coefficients for the gamma index failure rate and the ALDw were large when tracking was used (|ρ| ≥ 0.854) and small when MLC tracking was not used (|ρ| ≤ 0.282).

Figure 5.

Figure 5

Open in a new tab

Gamma index failure rate with criteria 3% and 3 mm.

Figure 6.

Figure 6

Open in a new tab

Gamma index failure rate with criteria 2% and 2 mm.

DISCUSSION

The dosimetric results indicated a strong potential of motion management for the cases studied. MLC tracking proved to accurately adjust the treatment to the target movements for the plans with low and intermediate ALDw but for the highly modulated plans, the tracking performance was decreased. This was especially apparent for the plan with no LPC for case 1. The ALDw value for this plan was higher than for the other two cases, which might be due to the larger target volume for this case (109 cm3) compared with the target volumes for the other two cases (19 cm3 and 30 cm3). It should be noted that the targets used in this study were selected to generate complex treatment plans and many RA plans may have a lower ALDw than the cases in this study even without the use of an LPC. The strong correlation between the tracking performance and the ALDw suggests that a good indication of the dosimetric accuracy of MLC tracking delivery can be given by calculating the ALDw of the plan. However, the results vary for the different cases for plans with similar ALDw which implies that other factors may affect the results as well.

The 2% and 2 mm criteria emphasized the motion induced effects for delivery with no motion management while the results with MLC tracking had a similar gamma index failure rate for the two criteria. This suggests that some of the motion induced effects when no motion management was used were hidden with the coarse criteria 3% and 3mm and that a very accurate delivery is possible with MLC tracking for plans with low ALDw.

The Spearman’s rank correlation test indicated that the relationship between the variables could be described as a monotonic function only in the cases where there was also a strong linear dependence. Linear regression showed that the impact of the LPC on the plan quality was not statistically significant, which suggests that it can be used to increase the compatibility of highly modulated plans with MLC tracking delivery. The target V95 and the LPC had a Spearman’s rank correlation coefficient and a two-tailed significance level for the linear regression that might indicate a weak correlation (ρ = −0.580, p = 0.066). However, since the linear regression coefficient was close to zero (−0.002) and the difference between the minimum and maximum value of the target V95 for plans within the same case was found to be less than 1% of the target volume, a possible effect of the LPC is unlikely to be of clinical significance. The observed variations in the treatment plans might be due to the intrinsic stochastic component in the RA optimization that allows variations to avoid traps in local minima.32

In this study, the plan MLD was restricted in the optimization but other options could be investigated in a future study, such as applying a constraint on the average leaf distance or the root mean square of the leaf distance. More details could be included in the optimization, such as the amount of motion observed during pretreatment imaging, as well as the leaf dynamics (velocity and acceleration), to better determine the appropriate plan on an individual basis.

CONCLUSION

The intrafraction motion had adverse effects on the delivered dose distributions of the plans in this study when it was not compensated for. MLC tracking proved to be a suitable tool for motion management for the plans with low and intermediate plan modulations (small and intermediate average adjacent leaf distance) but for the highly modulated RapidArc plans (large average adjacent leaf distance), the tracking performance was decreased. The results indicate that the dosimetric robustness of MLC tracking delivery of a RapidArc plan can be estimated prior to delivery by evaluating the plan modulation complexity. The leaf position constraint was shown to increase the accuracy of MLC tracking delivery of highly modulated RapidArc plans without significantly compromising the plan quality. In cases of exceptionally high modulation, the leaf position constraint was shown to be essential for accurate MLC tracking.

ACKNOWLEDGMENTS

The authors wish to thank Pekka Uusitalo, Janne Nord, and Jarkko Peltola from Varian Medical Systems, Helsinki, Finland, for supplying the treatment planning system used in this study. The authors also thank Stephan Erbel and Cornel Schlossbauer from Brainlab, Feldkirchen, Germany for supporting the ExacTrac® guidance of the MLC tracking delivery. The authors particularly thank Dan Ruan from Stanford Cancer Center, Stanford, CA for development of the MLC tracking code and Herbert Cattell from Varian Medical Systems, Palo Alto, CA for substantial contributions to the DMLC tracking program. Thanks to Thomas Carlslund and Mikael Olsen from Rigshospitalet, Copenhagen, Denmark, for technical support during the installation of the tracking system at Rigshospitalet. Finally thanks to Ivan Vogelius and Gitte Persson from Rigshospitalet, Copenhagen, Denmark for technical assistance and to Julie Baz University of Sydney, Sydney, Australia, for reviewing the manuscript and improving the clarity. Research support from Varian Medical Systems, the Niels Bohr Institute (University of Copenhagen), US NIH/NCI Grant No. CA93626 and from Snedkermester Sophus Jacobsen og hustru Astrid Jacobsens Fond are gratefully acknowledged. The manuscript was reviewed but not commented on by Varian Medical Systems prior to submission.

References

  1. Bortfeld T., Jiang S. B., and Rietzel E., “Effects of motion on the total dose distribution,” Semin. Radiat. Oncol. 14, 41–51 (2004). 10.1053/j.semradonc.2003.10.011 [DOI] [PubMed] [Google Scholar]
  2. Seppenwoolde Y., Shirato H., Kitamura K., Shimizu S., van Herk M., Lebesque J. V., and Miyasaka K., “Precise and real-time measurement of 3D tumor motion in lung due to breathing and heartbeat, measured during radiotherapy,” Int. J. Radiat. Oncol., Biol. Phys. 53, 822–834 (2002). 10.1016/S0360-3016(02)02803-1 [DOI] [PubMed] [Google Scholar]
  3. Schwarz M., Van der Geer J., Van Herk M., Lebesque J. V., Mijnheer B. J., and Damen E. M., “Impact of geometrical uncertainties on 3D CRT and IMRT dose distributions for lung cancer treatment,” Int. J. Radiat. Oncol., Biol. Phys. 65, 1260–1269 (2006). 10.1016/j.ijrobp.2006.03.035 [DOI] [PubMed] [Google Scholar]
  4. Yu C. X., “Intensity-modulated arc therapy with dynamic multileaf collimation: An alternative to tomotherapy,” Phys. Med. Biol. 40, 1435–1449 (1995). 10.1088/0031-9155/40/9/004 [DOI] [PubMed] [Google Scholar]
  5. Otto K., “Volumetric modulated arc therapy: IMRT in a single gantry arc,” Med. Phys. 35, 310–317 (2008). 10.1118/1.2818738 [DOI] [PubMed] [Google Scholar]
  6. Korreman S., Medin J., and Kjaer-Kristoffersen F., “Dosimetric verification of RapidArc treatment delivery,” Acta Oncol. 48, 185–191 (2009). 10.1080/02841860802287116 [DOI] [PubMed] [Google Scholar]
  7. Ling C. C., Humm J., Larson S., Amols H., Fuks Z., Leibel S., and Koutcher J. A., “Towards multidimensional radiotherapy (MD-CRT): Biological imaging and biological conformality,” Int. J. Radiat. Oncol., Biol. Phys. 47, 551–560 (2000). 10.1016/S0360-3016(00)00467-3 [DOI] [PubMed] [Google Scholar]
  8. Court L., Wagar M., Berbeco R., Reisner A., Winey B., Schofield D., Ionascu D., Allen A. M., Popple R., and Lingos T., “Evaluation of the interplay effect when using RapidArc to treat targets moving in the craniocaudal or right-left direction,” Med. Phys. 37, 4–11 (2010). 10.1118/1.3263614 [DOI] [PubMed] [Google Scholar]
  9. Korreman S. S., Pedersen A. N., Josipović M., Aarup L. R., Juhler-Nøttrup T., Specht L., and Nyström H., “Cardiac and pulmonary complication probabilities for breast cancer patients after routine end-inspiration gated radiotherapy,” Radiother Oncol. 80, 257–262 (2006). 10.1016/j.radonc.2006.07.020 [DOI] [PubMed] [Google Scholar]
  10. Ohara K., Okumura T., Akisada M., Inada T., Mori T., Yokota H., and Calaguas M. J., “Irradiation synchronized with respiration gate,” Int. J. Radiat. Oncol., Biol. Phys. 17, 853–857 (1989). 10.1016/0360-3016(89)90078-3 [DOI] [PubMed] [Google Scholar]
  11. Vedam S. S., Keall P. J., Kini V. R., and Mohan R., “Determining parameters for respiration-gated radiotherapy,” Med. Phys. 28, 2139–2146 (2001). 10.1118/1.1406524 [DOI] [PubMed] [Google Scholar]
  12. Keall P. J., Sawant A., Cho B., Ruan D., Wu J., Poulsen P., Petersen J., Newell L. J., Cattell H., and Korreman S., “Electromagnetic-guided dynamic multileaf collimator tracking enables motion management for intensity-modulated arc therapy,” Int. J. Radiat. Oncol., Biol., Phys. 79, 312–320 (2011). 10.1016/j.ijrobp.2010.03.011 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Falk M., af Rosenschöld P. M., Keall P., Cattell H., Cho B. C., Poulsen P., Povzner S., Sawant A., Zimmerman J., and Korreman S., “Real-time dynamic MLC tracking for inversely optimized arc radiotherapy,” Radiother Oncol. 94, 218–223 (2010). 10.1016/j.radonc.2009.12.022 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Poulsen P. R., Cho B., Sawant A., Ruan D., and Keall P. J., “Dynamic MLC tracking of moving targets with a single kV imager for 3D conformal and IMRT treatments,” Acta Oncol. 49, 1092–1100 (2010). 10.3109/0284186X.2010.498438 [DOI] [PubMed] [Google Scholar]
  15. Zimmerman J., Korreman S., Persson G., Cattell H., Svatos M., Sawant A., Venkat R., Carlson D., and Keall P., “DMLC motion tracking of moving targets for intensity modulated arc therapy treatment: A feasibility study,” Acta Oncol. 48, 245–250 (2009). 10.1080/02841860802266722 [DOI] [PubMed] [Google Scholar]
  16. Smith R. L., Sawant A., Santanam L., Venkat R. B., Newell L. J., Cho B. C., Poulsen P., Catell H., Keall P. J., and Parikh P. J., “Integration of real-time internal electromagnetic position monitoring coupled with dynamic multileaf collimator tracking: An intensity-modulated radiation therapy feasibility study,” Int. J. Radiat. Oncol., Biol. Phys. 74, 868–875 (2009). 10.1016/j.ijrobp.2009.01.031 [DOI] [PubMed] [Google Scholar]
  17. Sawant A., Smith R. L., Venkat R. B., Santanam L., Cho B., Poulsen P., Cattell H., Newell L. J., Parikh P., and Keall P. J., “Toward submillimeter accuracy in the management of intrafraction motion: The integration of real-time internal position monitoring and multileaf collimator target tracking,” Int. J. Radiat. Oncol., Biol. Phys. 74, 575–582 (2009). 10.1016/j.ijrobp.2008.12.057 [DOI] [PubMed] [Google Scholar]
  18. Cho B., Poulsen P. R., Sloutsky A., Sawant A., and Keall P. J., “First demonstration of combined kV/MV image-guided real-time dynamic multileaf-collimator target tracking,” Int. J. Radiat. Oncol., Biol. Phys. 74, 859–867 (2009). 10.1016/j.ijrobp.2009.02.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Sawant A., Venkat R., Srivastava V., Carlson D., Povzner S., Cattell H., and Keall P., “Management of three-dimensional intra-fraction motion through real-time DMLC tracking,” Med. Phys. 35, 2050–2061 (2008). 10.1118/1.2905355 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Tacke M., Nill S., Krauss A., and Oelfke U., “Real-time tumor tracking: Automatic compensation of target motion using the Siemens 160 MLC,” Med. Phys. 37(2), 753–761 (2010). 10.1118/1.3284543 [DOI] [PubMed] [Google Scholar]
  21. McMahon R., Papiez L., and Rangaraj D., “Dynamic-MLC leaf control utilizing on-flight intensity calculations: A robust method for real-time IMRT delivery over moving rigid targets,” Med. Phys. 34, 3211–3223 (2007). 10.1118/1.2750964 [DOI] [PubMed] [Google Scholar]
  22. McClelland J. R., Webb S., McQuaid D., Binnie D. M., and Hawkes D. J., “Tracking ‘differential organ motion’ with a ‘breathing’ multileaf collimator: Magnitude of problem assessed using 4D CT data and a motion-compensation strategy,” Phys. Med. Biol. 52, 4805–4826 (2007). 10.1088/0031-9155/52/16/007 [DOI] [PubMed] [Google Scholar]
  23. D’Souza W. D., Malinowski K. T., Van Liew S., D’Souza G., Asbury K., McAvoy T. J., Suntharalingan M., and Regine W. F., “Investigation of motion sickness and inertial stability on a moving couch for intra-fraction motion compensation,” Acta Oncol. 48, 1198–1203 (2009). 10.3109/02841860903188668 [DOI] [PMC free article] [PubMed] [Google Scholar]
  24. Wilbert J., Meyer J., Baier K., Guckenberger M., Herrmann C., Hess R., Janka C., Ma L., Mersebach T., Richter A., Roth M., Schilling K., and Flentje M., “Tumor tracking and motion compensation with an adaptive tumor tracking system (ATTS): System description and prototype testing,” Med. Phys. 35, 3911–3921 (2008). 10.1118/1.2964090 [DOI] [PubMed] [Google Scholar]
  25. Seppenwoolde Y., Berbeco R. I., Nishioka S., Shirato H., and Heijmen B., “Accuracy of tumor motion compensation algorithm from a robotic respiratory tracking system: A simulation study,” Med. Phys. 34, 2774–2784 (2007). 10.1118/1.2739811 [DOI] [PubMed] [Google Scholar]
  26. Voort van Zyp N. C., Prevost J. B., Hoogeman M. S., Praag J., van der Holt B., Levendag P. C., van Klaveren R. J., Pattynama P., and Nuyttens J. J., “Stereotactic radiotherapy with real-time tumor tracking for non-small cell lung cancer: Clinical outcome,” Radiother Oncol. 91, 296–300 (2009). 10.1016/j.radonc.2009.02.011 [DOI] [PubMed] [Google Scholar]
  27. Kamino Y., Takayama K., Kokubo M., Narita Y., Hirai E., Kawawda N., Mizowaki T., Nagata Y., Nishidai T., and Hiraoka M., “Development of a four-dimensional image-guided radiotherapy system with a gimballed X-ray head,” Int. J. Radiat. Oncol., Biol., Phys. 66, 271–278 (2006). 10.1016/j.ijrobp.2006.04.044 [DOI] [PubMed] [Google Scholar]
  28. Willoughby T. R, Forbes A. R., Buchholz D., Langen K. M., Wagner T. H., Zeidan O. A., Kupelian P. A., and Meeks S. L., “Evaluation of an infrared camera and X-ray system using implanted fiducials in patients with lung tumors for gated radiation therapy,” Int. J. Radiat. Oncol. Biol. Phys. 66, 568–575 (2006). 10.1016/j.ijrobp.2006.05.029 [DOI] [PubMed] [Google Scholar]
  29. Jin J. Y., Yin F. F., Tenn S. E., Medin P. M., and Solberg T. D., “Use of the BrainLAB ExacTrac X-Ray 6D system in image-guided radiotherapy,” Med. Dosim. 33, 124–34 (2008). 10.1016/j.meddos.2008.02.005 [DOI] [PubMed] [Google Scholar]
  30. Cho B., Poulsen P. R., and Keall P. J., “Real-time tumor tracking using sequential kV imaging combined with respiratory monitoring: A general framework applicable to commonly used IGRT systems,” Phys. Med. Biol. 55, 3299–3316 (2010). 10.1088/0031-9155/55/12/003 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Ruan D., “Kernel density estimation-based real-time prediction for respiratory motion,” Phys. Med. Biol. 55, 1311–1326 (2010). 10.1088/0031-9155/55/5/004 [DOI] [PubMed] [Google Scholar]
  32. Cozzi L., Dinshaw K. A., Shrivastava S. K., Mahantshetty U., Engineer R., Deshpande D. D., Jamema S. V., Vanetti E., Clivio A., Nicolini G., and Fogliata A., “A treatment planning study comparing volumetric arc modulation with RapidArc and fixed field IMRT for cervix uteri radiotherapy,” Radiother Oncol. 89, 180–191 (2008). 10.1016/j.radonc.2008.06.013 [DOI] [PubMed] [Google Scholar]

Articles from Medical Physics are provided here courtesy of American Association of Physicists in Medicine

RESOURCES