Formulation of a New and Simple Non-Uniform Size-Modified Poisson-Boltzmann Description

Abstract

The nonlinear Poisson-Boltzmann equation (PBE) governing biomolecular electrostatics neglects ion size and ion correlation effects and recent research activity has focused on accounting for these effects to achieve better physical modeling realism. Here attention is focused on the comparatively simpler challenge of addressing ion size effects within a continuum-based solvent modeling framework. Prior works by Borukhov ^{1, 2} have examined the case of uniform ion size in considerable detail. Generalizations to accommodate different species ion sizes have been carried out by Li^{3, 4} and Zhou⁵ using a variational principle, Chu⁶ using a lattice gas model and Tresset⁷ using a generalized Poisson-Fermi distribution. The current work provides an alternative derivation using simple statistical mechanics principles that place the ion size effects and energy distributions on a consistent statistical footing. The resulting expressions differ from the prior non-uniform ion-size developments. However, all treatments reduce to the same form in the cases of uniform ion-size and zero ion size (the PBE). Because of their importance to molecular modeling and salt-dependent behavior, expressions for the salt sensitivities and ionic forces are also derived using the non-uniform ion size description. Emphasis in this article is on formulation and numerically robust evaluation; results are presented for a simple sphere and a previously considered DNA structure for comparison and validation. More extensive application to biomolecular systems is deferred to a subsequent article.

Introduction

In order to reliably model the behavior of biomolecules and predict their dependence upon ambient salt conditions and their interactions with other molecules, an accurate and general treatment of the governing electrostatics is essential. Currently the most widely used characterization of biomolecular electrostatics that accounts for the presence of mobile ions in the solvent, is the Poisson-Boltzmann (PB) description. PB methods adopt an implicit solvent model where the solute is modeled at the atomic level while the solvent is characterized in terms of its macroscopic properties. Among the currently available suite of biomolecular electrostatics modeling methods, PB-based formulations realize a useful compromise between physical modeling fidelity/detail and computational cost. Explicit solvent models offer superior physical realism but require considerably higher computational effort to sample the conformational space by either molecular dynamics or Monte Carlo techniques. Simpler descriptions such as Generalized Borne (GB) ^{8, 9} or particle-based Debye-Hückel models¹⁰, on the other hand, are less expensive, but do not provide the level of detail of the dielectric interface needed for accurate force predictions and binding sites.

PB-based methods have been successfully applied to characterize counterion distributions and ion competition effects^11–13, predict titration curves and pK-shifts, obtain the salt-dependent binding affinities and association rates of biomolecular complexes, analyze the electrostatic fields of biological ion channels ¹⁴, simulate molecular recognition events in nucleic acids and other biopolyelectrolytes and study the effects of salt concentration upon conformational transitions ^15–17. PB-based electrostatics descriptions are also useful in modeling colloidal stability and electrokinetic effects such as electrophoresis and electro-osmosis ^{18, 19} with applications to paper-manufacturing and water purification.

Limitations and cases of failed predictions

Despite such successful applications and widespread use of PB-based electrostatic simulation software, the PB description is subject to important limitations that can become pronounced in some contexts. For example, comparisons against more sophisticated solvent treatments using idealized polyion models^20–22 have shown that while the nonlinear PBE provides good estimates of the ion distributions and electrostatic energies for 1:1 salts at low and moderate salt concentrations, significant discrepancies arise when considering highly charged biopolyelectrolytes immersed in high univalent salt concentration or in multivalent salts. Attraction forces between same-charged molecules in ion channels or close proximity walls ²³ are also poorly predicted using the PBE. Compilations of the biological events that cannot be captured by the PBE, are given in ^{24, 25}.

These discrepancies can be attributed, at least in part, to the omission of ion size and ion-ion correlation effects in the PB framework and recent research has sought to account for these effects ^{1, 6, 26, 27}. Even at modest electrostatic potentials, approximating electrolyte ions as point charges results in ion concentrations that are much higher than when ion size effects are taken into account. In the context of mean-field theories the most common means of accounting for the local excluded volume effects is to insert a charge-free 2–4 Å Stern layer about the molecular surface. Outside this layer is the usual diffuse Gouy-Chapman layer governed by the PBE. Further decomposition of the Stern layer into an inner and outer Helmholtz layer may be made to account for ion adsorption at the surface. However, these models are inadequate when considering multiple salt solutions with different size ions.

Finite Ion Size Modeling

The effect of finite ion size can also be incorporated directly into the expressions for the ion distributions. The incorporation of ion size was carried out by Kralj-Iglič ²⁸ and Borukhov¹ for the case where the ions have comparable size. A generalization to the non-uniform ion size case involving two dissimilar size ion species was developed by Chu using a simple lattice gas representation of the ionic solvent⁶ and incorporated into the Adaptive Poisson-Boltzmann Solver (APBS). An extension to an arbitrary number of disparate size ion species was obtained by Li using variational techniques applied to an ion-size generalization of the mean-field electrostatic free-energy functional ^{3, 4}. Recently computational results using their technique have been produced for spherical geometries ⁵. A similar generalization by means of a first order linearization about the uniform ion case was obtained by Tresset ⁷. The more difficult challenge of addressing ion-ion correlations has also been attempted ²⁷, but development of efficient numerical treatments to implement these terms remains at an early stage.

In the present work we derive a non-uniform ion size description compatible with the mean-field theory using basic statistical mechanics concepts. The effect of ion size is introduced by means of a simple and intuitive constraint condition adduced to the number of system states using a Lagrange multiplier. This constraint replaces an analogous constraint upon the total number of particles imposed in the derivation of the standard PBE. The number of system states is maximized for given conditions (fixed internal energy and volume) and the most probable ion species distributions are found. In addition to deriving the ion distributions and electrostatic free energies, expressions are also obtained for the salt sensitivities of these energies and the ionic pressure at the molecular surface necessary to calculate molecular forces. At low potentials, the linear PBE is recovered and, according to the theory developed below, the influence of ion size effects becomes negligible. For highly charged molecules however, such as nucleic acids and its complexes with proteins, surface potentials become high and ion size plays a prominent role. The well-known previously established forms are recovered in the limits of uniform ion size and vanishing ion size. The resulting size-modified PBE (SMPBE) theory is used to calculate ion distributions about simple spherical geometries containing a central charge for which solutions can be rapidly obtained using a 1D model ²⁹, and compared against the PB solutions and published data.

Formulation

Numerous important properties of a charged low dielectric biomolecule embedded in an ionic solvent can be inferred from the electrostatic potential, ϕ, governed by the Poisson equation

$$\mathrm{\nabla }·(\mathrm{\epsilon }\mathrm{\nabla }\mathrm{\varphi })=-4\mathrm{\pi }({\mathrm{\rho }}^{\mathrm{f}}+{\mathrm{\rho }}^{\text{ion}})$$ (1)

Here ε is the dielectric constant, ρ^f is the charge density associated with the fixed charges comprising the biomolecule and ρ^ion is the charge density associated with the mobile ions in the solvent. Eq.(1) is solved using an appropriate discretization method (e.g., finite differencing or application of a finite volume or finite element method); once the potential solution is known important derivative properties such as the free energy and its dependence upon salt conditions, electrostatic forces, binding properties and pK-shifts can be obtained. The mobile ion distribution responds to the electrostatic field and the challenge posed here is to characterize the mobile charge density, ρ^ion, under the simultaneous consideration of ion size and electrostatic potential. When ion size is neglected, the classical Boltzmann distribution is recovered and (1) reverts to the Poisson-Boltzmann equation. Accounting for finite ion size alters the ionic distributions and imposes physical bounds on the charge densities that can be obtained. The following development aims at deriving expressions for the ion concentrations and associated charge distribution accounting for both ion size and electrostatic potential.

The implicit solvent model accounting for finite ion size is derived in accordance with familiar statistical mechanics procedures ³⁰ where the ion distributions are inferred from a sufficiently large ensemble of system arrangements satisfying a specified thermodynamic state. In what follows a fixed volume of electrolyte with a given energy and electrostatic potential is considered. Local interactions between the ions and solvent molecules are neglected. It is also assumed that the electrostatic potential over the volume is essentially uniform which, in the current context entails considering a sufficiently small volume so that the distance-dependent variation in the electrostatic potential induced by the molecular charges is small. To obtain a statistically meaningful ensemble a large collection of thermodynamically equivalent ion arrangements is taken at different times of the steady state system.

To derive a continuous implicit solvent description begin by considering a configuration in the ensemble where the total number of solvent molecules is n₀ and the number of ions of the i-th species is n_i. The total number of particles is then

$$\mathrm{N}={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}$$ (2)

where p is the number of ion species. In accordance with elementary statistical mechanics³⁰ one is interested in establishing the most likely or probable arrangement of the particles subject to imposed system constraints which, here, will be a volume constraint and an energy constraint. This is tantamount to maximizing the number of combinations

$$\mathrm{Z}=\frac{\mathrm{N}!}{{\displaystyle \prod _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}!}$$ (3)

subject to

$${\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}={\mathrm{V}}_{\text{tot}}\text{ and }{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{E}}_{\mathrm{i}}=\mathrm{E}$$ (4)

where species, i=0, corresponds to the solvent, V_i are the ion and solvent volumes and V_tot is a fixed volume. Now it is assumed further that for any ion the energy is given by the energy to bring the ion from infinity to its actual location, which, if only electrostatic forces are at play, is the potential energy. Thus:

$${\mathrm{E}}_{\mathrm{i}}=-({\mathrm{\mu }}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })$$ (5)

with the implicit understanding that for the neutral solvent ions, z_i=0. Using Stirling's approximation formula:

$$\text{ln }\mathrm{Z}=\text{ln }\mathrm{N}!-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}\text{ln }{\mathrm{n}}_{\mathrm{i}}!}\cong \text{N ln }\mathrm{N}-\mathrm{N}-\left({\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}\text{ln }{\mathrm{n}}_{\mathrm{i}}-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}\right)=\text{N ln }\mathrm{N}-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}\text{ln }{\mathrm{n}}_{\mathrm{i}}$$ (6)

Using standard statistical mechanics procedures the most probable configuration is obtained by appending the constraints (4) using Lagrange multipliers and maximizing the resulting function:

$$(\text{ln Z})-\mathrm{\alpha }{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}-\mathrm{\beta }{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{E}}_{\mathrm{i}}\cong \text{N ln N}-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}\text{ln }{\mathrm{n}}_{\mathrm{i}}-\mathrm{\alpha }{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}-\mathrm{\beta }{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}{\mathrm{E}}_{\mathrm{i}}$$ (7)

Here the signs on the Lagrange multipliers, α and β, are arbitrary, but selected here so that β=1/k_BT. This identity is formally shown below. Maximizing (7) with respect to the n_i results in the most probable distribution:

$$\text{ln N}-\text{ln}{\mathrm{n}}_{\mathrm{i}}-\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}\mathrm{-}\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}}=0$$ (8)

or,

$${\mathrm{n}}_{\mathrm{i}}/\mathrm{N}={\mathrm{e}}^{-\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}-\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}}}$$ (9)

The dependence on V_i is intuitively correct, provided α>0, since one expects to have more of the small particles and fewer of the large particles. Note that for any potential,

$${\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{n}}_{\mathrm{i}}/\mathrm{N}={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{e}}^{-\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}-\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}}}=1$$ (10)

which implicitly yields α as a function of the other terms. The iterative solution for α is discussed later below.

By differentiating (10) with respect to the energy, E, and using the definitions (4) it readily follows that:

$${\mathrm{V}}_{\text{tot}}\frac{\partial \mathrm{\alpha }}{\partial \mathrm{E}}+\mathrm{E}\frac{\partial \mathrm{\beta }}{\partial \mathrm{E}}=0$$ (11)

The entropy of the system is given by:

$$\mathrm{S}={\mathrm{k}}_{\mathrm{B}}\text{ln Z}=-{\mathrm{k}}_{\mathrm{B}}{\displaystyle \sum _{\mathrm{i}}}{\mathrm{n}}_{\mathrm{i}}\text{ ln}({\mathrm{n}}_{\mathrm{i}}/\mathrm{N})={\mathrm{k}}_{\mathrm{B}}{\displaystyle \sum _{\mathrm{i}}{\mathrm{n}}_{\mathrm{i}}(\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}+\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}})}={\mathrm{k}}_{\mathrm{B}}(\mathrm{\alpha }{\mathrm{V}}_{\text{tot}}+\mathrm{\beta }\mathrm{E})$$ (12)

which, together with (11) and the thermodynamic definition of temperature results in:

$${\frac{1}{\mathrm{T}}\equiv \frac{\partial \mathrm{S}}{\partial \mathrm{E}}|}_{\mathrm{V},\mathrm{N}=\text{const}}={\mathrm{k}}_{\mathrm{B}}\mathrm{\beta }$$ (13)

thus confirming the aforementioned identity of the Lagrange multiplier, β.

Using (4) and (9), the concentration in number of ions per unit volume is given by:

$${\mathrm{c}}_{\mathrm{i}}=\frac{{\mathrm{n}}_{\mathrm{i}}}{{\mathrm{V}}_{\text{tot}}}=\frac{\mathrm{N}}{{\mathrm{V}}_{\text{tot}}}\frac{{\mathrm{n}}_{\mathrm{i}}}{\mathrm{N}}=\frac{{\mathrm{e}}^{-\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}+\mathrm{\beta }({\mathrm{\mu }}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })}}{{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{e}}^{-\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}+\mathrm{\beta }({\mathrm{\mu }}_{\mathrm{i}}-{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })}}$$ (14)

from which it is clear that

$${\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{i}}=1$$ (15)

This last result is used to define c₀ in terms of the ion concentrations. Also, from (10) and (14) the average, or most probable ion+solvent volume,

$${\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{e}}^{-\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}-\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}}}=\frac{1}{\mathrm{D}}$$ (16)

where,

$$\mathrm{D}=\frac{\mathrm{N}}{{\mathrm{V}}_{\text{tot}}}={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\mathrm{i}}$$ (17)

At zero potential, the ion bulk concentrations are:

$${\mathrm{c}}_{\text{bi}}={\mathrm{D}}_{\mathrm{b}}{\mathrm{e}}^{-{\mathrm{\alpha }}_0{\mathrm{V}}_{\mathrm{i}}+\mathrm{\beta }{\mathrm{\mu }}_{\mathrm{i}}},{\mathrm{D}}_{\mathrm{b}}={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}$$ (18)

Substituting for the μ_i in (14) results in:

$${\mathrm{c}}_{\mathrm{i}}=\frac{{\mathrm{c}}_{\mathrm{\text{bi}}}{\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{i}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}}{\mathrm{Q}}$$ (19a)

where,

$$\mathrm{h}=\mathrm{\alpha }-{\mathrm{\alpha }}_0\text{ and }\mathrm{Q}\equiv {\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{i}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}=\frac{{\mathrm{D}}_{\mathrm{b}}}{\mathrm{D}}$$ (19b, c)

The last expression can also be written as:

$$\mathrm{Q}\equiv {\mathrm{e}}^{-{\mathrm{V}}_0\mathrm{h}}[1+{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}({\mathrm{e}}^{-({\mathrm{V}}_{\mathrm{i}}-{\mathrm{V}}_0)\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}-1)]$$ (19d)

which eliminates the explicit dependence on c_b0 and has a well defined limit for vanishing solvent size.

The parameter, h, is fundamentally related to the osmotic pressure and is determined from the following nonlinear equation for h readily derived from (9), (10) and (18):

$$\mathrm{F}(\mathrm{h},\mathrm{\varphi })={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}\left({\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{i}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}-1\right)=0$$ (20)

For a given potential, ϕ, the parameter, h, is readily obtained using a simple iterative method such as Newton-Raphson or repeated bisection. The latter option is guaranteed to converge provided an initial pair of points, h₁ and h₂, can be found such that F₁=F(h₁,ϕ)≤0 and F₂=F(h₂,ϕ)≥ 0. The function F_m=F(h_m,ϕ) is then evaluated at the mid-value, h_m=(h₁+h₂)/2. If F_m>0 then one replaces h₂←h_m and F₂←F_m; otherwise h₁←h_m and F₁←F_m. This process is repeated until either F_m=0 or |h₂/h₁−1| is within machine round off.

Relation (20) can also be used to show that for fixed bulk concentrations:

$$\frac{\text{dh}}{\mathrm{d}\mathrm{\varphi }}=-\mathrm{\beta }{\mathrm{\rho }}^{\text{ion}}$$ (21)

where,

$${\mathrm{\rho }}^{\text{ion}}={\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\mathrm{i}}{\text{ez}}_{\mathrm{i}}$$ (22)

In the case of a constant ion size, h can be written explicitly and the resulting expressions for the ion concentration revert to those established previously by Borukhov ¹. This reduction is shown in Appendix A.

Limiting Value for Small Potential

As the potential approaches zero, α→α₀ and so h→0. One can then expand (20) to linear order in h and ϕ and evaluate the results at h=ϕ=0 and thus infer that:

$$\left({\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{V}}_{\mathrm{i}}\right)\mathrm{h}=-\mathrm{\beta }\mathrm{e}\left({\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{z}}_{\mathrm{i}}\right)\mathrm{\varphi }$$ (23)

Now, from charge neutrality and the expressions for c_bi one can show that:

$${\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{z}}_{\mathrm{i}}{\mathrm{n}}_{\mathrm{i}}=0\to {\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{z}}_{\mathrm{i}}=0$$ (24)

meaning that h ∝ Cϕⁿ, where n≥2. It then follows from (19a) that

$${\mathrm{c}}_{\mathrm{i}}=\frac{{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}}{{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}}\approx \frac{{\mathrm{c}}_{\text{bi}}(1-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })}{{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}(1-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })}=\frac{{\mathrm{c}}_{\text{bi}}(1-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })}{1-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}$$ (25)

Thus,

$${\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{z}}_{\mathrm{i}}{\text{ec}}_{\mathrm{i}}=\frac{\mathrm{e}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{z}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}(1-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi })}{1-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{V}}_{\mathrm{i}}{\mathrm{c}}_{\text{bi}}\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}=-\left(\mathrm{\beta }{\mathrm{e}}^2{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{z}}_{\mathrm{i}}^2{\mathrm{c}}_{\text{bi}}\right)\mathrm{\varphi }$$ (26)

which corresponds to the standard linear PBE. Hence, the linear PBE is recovered at small potentials with the term in parentheses on the right hand side of (26) corresponding to the familiar combination, εκ² where ε is the dielectric in the solvent region and κ is the Debye-Hückel parameter. Note that this result differs from the result Eq. (6.1) in ³ where the presence of different sized ions generally changes the effective screening length.

The development above relates the ion species concentrations to the local electrostatic potential, ion size and bulk concentrations. In investigations of biomolecular electrostatics one is generally interested in derived properties such as the system energy and its sensitivities with respect to salt concentration or atomic position, the latter quantity corresponding to the atomic force which is of direct relevance to molecular dynamics, energy minimization and docking applications. In the following development expressions are derived for the three most commonly required properties: the electrostatic free energy, the gradient of this energy with respect to salt concentration and the ionic pressure contribution to the electrostatic force.

Expressions for Energy

The average energy per particle is

$$\mathrm{Ē}={\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{E}}_{\mathrm{i}}\frac{{\mathrm{n}}_{\mathrm{i}}}{\mathrm{N}}$$ (27)

The total energy over the entire space is obtained by converting this result into an energy density and integrating over the volume. Thus, from (14)

$$\mathrm{Ê}={\displaystyle \underset{\mathrm{N}}{\int }}\mathrm{Ē}\text{ dN}={\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{Ē}\left(\frac{\mathrm{N}}{{\mathrm{V}}_{\text{tot}}}\right)\text{ dV}={\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{Ē}\text{D dV}={\displaystyle \underset{\mathrm{V}}{\int }}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{E}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{i}}\text{ dV}$$ (28)

where D is given by (16) and relates (n_i/N)=(c_i/D). Similarly, the total entropy can be obtained from its fundamental definition (see (12)):

$$\mathrm{S}=-{\mathrm{k}}_{\mathrm{B}}{\displaystyle \underset{\mathrm{V}}{\int }}\left\{{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}\left(\frac{{\mathrm{n}}_{\mathrm{i}}}{\mathrm{N}}\right)\text{ln}\left(\frac{{\mathrm{n}}_{\mathrm{i}}}{\mathrm{N}}\right)\right\}\text{D dV}={\mathrm{k}}_{\mathrm{B}}{\displaystyle \underset{\mathrm{V}}{\int }}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\mathrm{i}}(\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}+\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}})\text{ dV}$$ (29)

Consequently, it follows that (using (13) and (15)):

$$\mathrm{Ê}-\text{TS}={\displaystyle \underset{\mathrm{V}}{\int }}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{E}}_{\mathrm{i}}{\mathrm{c}}_{\mathrm{i}}-\frac{1}{\mathrm{\beta }}{\mathrm{c}}_{\mathrm{i}}(\mathrm{\alpha }{\mathrm{V}}_{\mathrm{i}}+\mathrm{\beta }{\mathrm{E}}_{\mathrm{i}})\text{ dV}=-\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}\mathrm{\alpha }{\mathrm{c}}_{\mathrm{i}}{\mathrm{V}}_{\mathrm{i}}\text{dV}=-\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{\alpha }\text{ dV}$$ (30)

It is valid to subtract the contribution at zero potential resulting in:

$${\left[\mathrm{Ê}-\text{TS}\right]}_0^{\mathrm{\varphi }=\mathrm{\varphi }}=-\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}\text{ h dV}$$ (31)

Adding the fixed charge contribution, defined by charge density ρ^f, results in the following expression for the electrostatic free energy:

$$\mathrm{G}=\mathrm{U}-\text{TS}={\displaystyle \underset{\mathrm{V}}{\int }}-\frac{\mathrm{\epsilon }}{8\mathrm{\pi }}|\nabla \mathrm{\varphi }{|}^2+{\mathrm{\rho }}^{\mathrm{f}}\mathrm{\varphi }-\frac{\mathrm{h}}{\mathrm{\beta }}\text{ dV}={\displaystyle \underset{\mathrm{V}}{\int }}\frac{1}{2}\mathrm{\varphi }({\mathrm{\rho }}^{\mathrm{f}}-{\mathrm{\rho }}^{\text{ion}})-\frac{\mathrm{h}}{\mathrm{\beta }}\text{dV}$$ (32)

This latter form is preferred both on the basis of simplicity and a direct equivalence with the energy terms commonly referred to in the nonlinear PBE (e.g., RHS of (24) in ³¹). In particular, the last term in (32) is equal to the negative of the excess osmotic pressure. Thus,

$$\mathrm{\Delta }\mathrm{\Pi }={\displaystyle \underset{\mathrm{V}}{\int }}\frac{\mathrm{h}}{\mathrm{\beta }}\text{ dV}=-{\displaystyle \underset{\mathrm{V}}{\int }}\left({\displaystyle \underset{0}{\overset{\mathrm{\varphi }}{\int }}}{\mathrm{\rho }}^{\text{ion}}\mathrm{d}\mathrm{\varphi }\right)\text{ dV}$$ (33)

where (21) leads to the last equality.

It is straightforward to show that for constant ion size one recovers the same expressions readily derivable from that in ¹. Moreover, from that result the limiting form for zero ion size corresponding to the nonlinear PBE is easily obtained as shown in Appendix A.

Energy Salt Gradient

The change in energy due to a change in salt concentration is referred to as the salt gradient and can be derived for each of the ion species as follows. For a variable, u, let the gradient ∂u/∂c_bk be denoted by u’. Then from (32) and using integration by parts:

$$\frac{\partial \mathrm{G}}{\partial {\mathrm{c}}_{\text{bk}}}=\mathrm{G}\text{'}={\displaystyle \underset{\mathrm{V}}{\int }}-\frac{\mathrm{\epsilon }}{4\mathrm{\pi }}\nabla \mathrm{\varphi }\text{'}·\nabla \mathrm{\varphi }+{\mathrm{\rho }}^{\mathrm{f}}\mathrm{\varphi }\text{'}-\frac{\mathrm{h}\text{'}}{\mathrm{\beta }}\text{ dV}={\mathrm{S}}_{\mathrm{k}}+{\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{\varphi }\text{'}\left(\frac{1}{4\mathrm{\pi }}\nabla ·(\mathrm{\epsilon }\nabla \mathrm{\varphi })+{\mathrm{\rho }}^{\mathrm{f}}+{\mathrm{\rho }}^{\text{ion}}\right)-\mathrm{\varphi }\text{'}{\mathrm{\rho }}^{\text{ion}}-\frac{\mathrm{h}\text{'}}{\mathrm{\beta }}\text{ dV}$$ (34)

where the surface integral taken over the infinitely far sphere,

$${\mathrm{S}}_{\mathrm{k}}=-{\displaystyle \underset{{\mathrm{S}}_{\mathrm{\infty }}}{\oint }}\frac{\mathrm{\epsilon }}{4\mathrm{\pi }}\mathrm{\varphi }\text{'}\frac{\partial \mathrm{\varphi }}{\partial \mathrm{n}}\text{dS}$$ (35)

For solutions that satisfy the ion-size modified PBE, the term in parentheses in (34) is zero so that:

$$\mathrm{G}\text{'}={\mathrm{S}}_{\mathrm{k}}-{\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{\varphi }\text{'}{\mathrm{\rho }}^{\text{ion}}+\frac{\mathrm{h}\text{'}}{\mathrm{\beta }}\text{ dV}$$ (36)

A relationship between h’ and ϕ’ is obtained as follows. First note that it is implicitly assumed that all other ion concentrations are held fixed. It then follows from (15) evaluated at zero potential that to conserve volume the change in solvent concentration:

$$\frac{\partial {\mathrm{c}}_{\mathrm{b}0}}{\partial {\mathrm{c}}_{\text{bk}}}=-\frac{{\mathrm{V}}_{\mathrm{k}}}{{\mathrm{V}}_0}$$

Differentiating (20) with respect to c_bk then leads to

$$\left({\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{k}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{k}}\mathrm{e}\mathrm{\varphi }}-1\right)-\left({\mathrm{e}}^{-{\mathrm{V}}_0\mathrm{h}}-1\right)\frac{{\mathrm{V}}_{\mathrm{k}}}{{\mathrm{V}}_0}-{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi }}({\mathrm{V}}_{\mathrm{i}}\mathrm{h}\text{'}+\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }\text{'}){\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{i}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}=0$$ (37)

or, when combined with (15), (19) and (22),

$$\frac{1}{\mathrm{Q}\mathrm{\beta }}\left[\left({\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{k}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{k}}\mathrm{e}\mathrm{\varphi }}-1\right)-\left({\mathrm{e}}^{-{\mathrm{V}}_0\mathrm{h}}-1\right)\frac{{\mathrm{V}}_{\mathrm{k}}}{{\mathrm{V}}_0}\right]=\frac{\mathrm{h}\text{'}}{\mathrm{\beta }}+\mathrm{\varphi }\text{'}{\mathrm{\rho }}^{\text{ion}}$$ (38)

Inserting this result into (36) results in

$$\frac{\partial \mathrm{G}}{\partial {\mathrm{c}}_{\text{bk}}}={\mathrm{S}}_{\mathrm{k}}-\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}\frac{1}{\mathrm{Q}}\left[\left({\mathrm{e}}^{-{\mathrm{V}}_{\mathrm{k}}\mathrm{h}-\mathrm{\beta }{\mathrm{z}}_{\mathrm{k}}\mathrm{e}\mathrm{\varphi }}-1\right)-\left({\mathrm{e}}^{-{\mathrm{V}}_0\mathrm{h}}-1\right)\frac{{\mathrm{V}}_{\mathrm{k}}}{{\mathrm{V}}_0}\right]\text{ dV}$$ (39)

This expression is well behaved for vanishing solvent size since:

$$-\left({\mathrm{e}}^{-{\mathrm{V}}_0\mathrm{h}}-1\right)\frac{{\mathrm{V}}_{\mathrm{k}}}{{\mathrm{V}}_0}\to {\text{hV}}_{\mathrm{k}},\text{ as }{\mathrm{V}}_0\to 0$$

The surface integral, S_k, generally vanishes for finite salt concentrations. This follows upon noting that at sufficient distance, r, from the molecule of interest where potentials are small the electrostatic field behaves as ϕ=Ae^−κr/r where A is some (finite) amplitude related to the residual charge at an appropriate bounding sphere and κ is the inverse Debye screening length. Inserting this result into (35) then produces a zero result provided ϕ’ is finite. At zero salt, however, no screening occurs in the solvent, A is equal to the net charge, Q_net, and the integral asymptotes to:

$${\mathrm{S}}_{\mathrm{k}}={\mathrm{Q}}_{\text{net}}\mathrm{\epsilon }{\left(\frac{\partial \mathrm{\varphi }}{\partial {\mathrm{c}}_{\text{bk}}}\right)}_{\mathrm{\infty }}={\mathrm{Q}}_{\text{net}}^2\mathrm{\epsilon }\frac{\partial \mathrm{\kappa }}{\partial {\mathrm{c}}_{\text{bk}}}\underset{\mathrm{R}\to \mathrm{\infty }}{\text{lim}}\left\{\underset{\mathrm{\kappa }\to 0}{\mathrm{\text{lim}}}\left(\frac{\partial }{\partial \mathrm{\kappa }}\frac{{\mathrm{e}}^{-\mathrm{\kappa }\mathrm{R}}}{\mathrm{R}}\right)\right\}=-{\mathrm{Q}}_{\text{net}}^2\mathrm{\epsilon }\frac{\partial \mathrm{\kappa }}{\partial {\mathrm{c}}_{\text{bk}}}$$ (40)

Forces

The forces acting on an atomic site in the molecule correspond to the change in energy when the atomic site is perturbed by an infinitesimal amount. This force has two components. The first is simply the electrostatic gradient at the charge site itself. The other force is associated with the surface pressure arising from the perturbations in the dielectric map and ion distribution. The electrostatic forces can be obtained using a procedure similar to the one used to derive the salt sensitivity above. Again, the change of a quantity, u, due to a perturbation of atom, j, along Cartesian direction, k, is denoted by u’. Following Gilson ³² to characterize the forces it is convenient to introduce the parameter, λ, to delineate the region containing the solvent (λ=1) from the rest of the domain (λ=0). Then from (32), the energy:

$$\mathrm{G}=\mathrm{U}-\text{TS}={\displaystyle \underset{\mathrm{V}}{\int }}-\frac{\mathrm{\epsilon }}{8\mathrm{\pi }}|\nabla \mathrm{\varphi }{|}^2+{\mathrm{\rho }}^{\mathrm{f}}\mathrm{\varphi }-\mathrm{\lambda }\frac{\mathrm{h}}{\mathrm{\beta }}\text{ dV}$$ (41)

and the variations,

$$\frac{\partial \mathrm{G}}{\partial {\mathrm{R}}_{\text{jk}}}=\mathrm{G}\text{'}={\displaystyle \underset{\mathrm{V}}{\int }}-\frac{\mathrm{\epsilon }}{4\mathrm{\pi }}\nabla \mathrm{\varphi }\text{'}·\nabla \mathrm{\varphi }-\frac{\mathrm{\epsilon }\text{'}}{8\mathrm{\pi }}|\nabla \mathrm{\varphi }{|}^2+{\mathrm{\rho }}^{\mathrm{f}}\mathrm{\varphi }\text{'}+\mathrm{\varphi }({\mathrm{\rho }}^{\mathrm{f}})\text{'}-\mathrm{\lambda }\frac{\mathrm{h}\text{'}}{\mathrm{\beta }}-\mathrm{\lambda }\text{'}\frac{\mathrm{h}}{\mathrm{\beta }}\text{ dV}$$ (42)

Using the same series of steps used previously to arrive at the expression (36) for the salt sensitivity (integration by parts and use of the ion size-modified PBE) this reduces to:

$$\mathrm{G}\text{'}={\mathrm{S}}_{\text{jk}}+{\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{\varphi }\left({\mathrm{\rho }}^{\mathrm{f}}\right)\text{'}-\frac{\mathrm{\epsilon }\text{'}}{8\mathrm{\pi }}|\nabla \mathrm{\varphi }{|}^2-(\mathrm{\varphi }\text{'}{\mathrm{\rho }}^{\text{ion}}+\mathrm{\lambda }\frac{\mathrm{h}\text{'}}{\mathrm{\beta }}+\mathrm{\lambda }\text{'}\frac{\mathrm{h}}{\mathrm{\beta }})\text{ dV}$$ (43)

The surface integral S_jk is defined analogously to S_k in (35) and can be readily shown to vanish at all salt concentrations (including zero salt). Qualitatively, this is because ϕ’ (the potential perturbation due to a perturbation in an atomic site) vanishes at large distance from the atom whereas previously ϕ’ (there the perturbation in the potential due to a change in the bulk solvent concentration) did not vanish for zero salt concentration.

The first term is in the integrand is simply the change in energy due to moving the charge site with all other parameters, including the molecular geometry unchanged. It is given by (see also Gilson ³²):

$${\mathrm{G}}_1^{\prime }={\displaystyle \underset{\mathrm{V}}{\int }}\mathrm{\varphi }\left({\mathrm{\rho }}^{\mathrm{f}}\right)\text{'}\text{ dV}=-\underset{\mathrm{\delta }{\mathrm{R}}_{\text{jk}}\to 0}{\text{lim}}\frac{\left[\mathrm{\varphi }({\mathbf{R}}_{\mathrm{j}}+{\mathbf{ê}}_{\mathrm{k}}\mathrm{\delta }{\mathrm{R}}_{\text{jk}})-\mathrm{\varphi }({\mathbf{R}}_{\mathrm{j}})\right]}{\mathrm{\delta }{\mathrm{R}}_{\text{jk}}}{\mathrm{q}}_{\mathrm{j}}=-{\mathrm{q}}_{\mathrm{j}}{\left(\nabla \mathrm{\varphi }·{\mathbf{ê}}_{\mathrm{k}}\right)}_{\mathbf{R}={\mathbf{R}}_{\mathrm{j}}}$$ (44)

where q_j is the atomic charge and ê_k is the unit vector in the k-th direction. This result is simply the familiar electrostatic field evaluated at the charge site.

The second term in (43) corresponds to the dielectric pressure and has the exact same form as encountered in the standard PBE. It only contributes where the dielectric is changing – i.e., near the surface. For a dielectric function that varies smoothly across the molecular surface:

$${\mathrm{G}}_2^{\prime }={\displaystyle \underset{\mathrm{V}}{\int }}-\frac{\mathrm{\epsilon }\text{'}}{8\mathrm{\pi }}|\nabla \mathrm{\varphi }{|}^2\text{ dV}=-\frac{1}{8\mathrm{\pi }}{\displaystyle \underset{\mathrm{V}}{\int }}\frac{\partial \mathrm{\epsilon }}{\partial {\mathrm{R}}_{\text{jk}}}|\nabla \mathrm{\varphi }{|}^2\text{ dV}$$ (45)

where the derivative ∂ε/∂R_jk will depend on the details of how the dielectric function is defined. For a sharp jump in dielectric across a surface, elemental considerations show that ε’dV=(ε_in−ε_ex)n∙b_jkdS where n is the outward pointing unit normal vector, b_jk is the surface displacement vector due to a unit change in the atomic site, j, in the k-th direction. For the van der Waals surface, b_jk=ê_k; for the solvent-excluded surface the expression is more complicated (e.g., see Eqs.(45) and (46) in ³³ for simple expressions). With these results one obtains:

$${\mathrm{G}}_2^{\prime }=\frac{1}{8\mathrm{\pi }}{\displaystyle \underset{{\mathrm{S}}_{\mathrm{j}}}{\int }}({\mathrm{\epsilon }}_{\text{ex}}-{\mathrm{\epsilon }}_{\text{in}})\nabla {\mathrm{\varphi }}_{\text{in}}·\nabla {\mathrm{\varphi }}_{\text{ex}}({\mathbf{b}}_{\text{jk}}·\mathbf{n})\text{ dS}$$ (46)

where the integral is taken over the surface, S_j, affected by perturbations in the position of atom. This expression agrees with expressions by Zauhar ³⁴ and Gilson ³² and corresponds to a dielectric pressure integrated over the surface. Note that to obtain the result (46) it is observed that the electrostatic gradients tangential to the surface are continuous whereas in the normal direction one has that ε(∂Φ/∂n) is constant. Then for a small increment across the surface:

$${\displaystyle \underset{-\mathrm{\delta }}{\overset{+\mathrm{\delta }}{\int }}}{\left(\frac{\partial \mathrm{\Phi }}{\partial \mathrm{z}}\right)}^2\frac{\mathrm{d}\mathrm{\epsilon }}{\text{dz}}\text{ dz}={\left({\mathrm{\epsilon }}_1\frac{\partial {\mathrm{\Phi }}_1}{\partial \mathrm{n}}\right)}^2{\displaystyle \underset{{\mathrm{\epsilon }}_1}{\overset{{\mathrm{\epsilon }}_2}{\int }}}\frac{\mathrm{d}\mathrm{\epsilon }}{{\mathrm{\epsilon }}^2}={\left({\mathrm{\epsilon }}_1\frac{\partial {\mathrm{\Phi }}_1}{\partial \mathrm{n}}\right)}^2(\frac{1}{{\mathrm{\epsilon }}_1}-\frac{1}{{\mathrm{\epsilon }}_2})=({\mathrm{\epsilon }}_2-{\mathrm{\epsilon }}_1)\left(\frac{\partial {\mathrm{\Phi }}_1}{\partial \mathrm{n}}\frac{\partial {\mathrm{\Phi }}_2}{\partial \mathrm{n}}\right)$$ (47)

The remaining terms in (43) constitute the ionic pressure. From (21), the first two of these terms cancel resulting in:

$${\mathrm{G}}_3^{\prime }=\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}-\mathrm{\lambda }\text{'}\text{ h dV}$$ (48)

For a sharp change in λ across the molecular surface λ’dV=−n·b_jkdS, so that:

$${\mathrm{G}}_3^{\prime }={\displaystyle \underset{{\mathrm{S}}_{\mathrm{j}}}{\int }}\frac{\mathrm{h}}{\mathrm{\beta }}{\mathbf{b}}_{\text{jk}}·\mathbf{n}\text{ dS}$$ (49)

Combining these terms and assembling contributions for each Cartesian direction results in the following force vector:

$$-\frac{\partial \mathrm{G}}{\partial {\mathbf{R}}_{\mathrm{j}}}={\mathbf{F}}_{\mathrm{j}}={\mathrm{q}}_{\mathrm{j}}{\left(\nabla \mathrm{\varphi }\right)}_{\mathbf{R}={\mathbf{R}}_{\mathrm{j}}}-{\displaystyle \underset{{\mathrm{S}}_{\mathrm{j}}}{\int }}{[\mathbf{B}]}_{\mathrm{j}}({\mathrm{p}}_{\mathrm{d}}+{\mathrm{p}}_{\text{ion}})\mathbf{n}\text{ dS}$$ (50)

where the rows of [B_j] are the vectors b_jk and the dielectric and ionic pressures at the surface,

$${\mathrm{p}}_{\mathrm{d}}=\frac{1}{8\mathrm{\pi }}({\mathrm{\epsilon }}_{\text{ex}}-{\mathrm{\epsilon }}_{\text{in}})(\nabla {\mathrm{\varphi }}_{\text{in}}·\nabla {\mathrm{\varphi }}_{\text{ex}})\text{ and }{\mathrm{p}}_{\text{ion}}=\frac{\mathrm{h}}{\mathrm{\beta }}$$ (51a, b)

With the exception of p^ion all force terms are the same as in the conventional PBE.

Implementation

The incorporation of the non-uniform ion size model into Poisson-Boltzmann solver that computes the electrostatic potential, ϕ, from (1) proceeds as follows. First a subroutine to compute h for a given grid point potential, ϕ, using (20) is developed and incorporated. The parameter h is then used in conjunction with the known bulk solvent properties to calculate the local ion concentrations from (19a) and thus the mobile charge, ρ^ion, from (22). With the right hand side in (1) now fully defined (the fixed charge distribution, ρ^f, is a known input) the local potential can be updated using the iterative procedure of choice in the Poisson-Boltzmann solver. Upon convergence of the potential solution post-processing to compute the electrostatic energies, salt sensitivities and forces can be carried out by evaluating the relevant volume and surface integrals defined in (32), (39) and (50) respectively.

Results

The non-uniform ion-size model is incorporated into a 1D solver described in ²⁹ and used to obtain high resolution solutions for a sphere containing a central charge. Two cases are considered here. The first examines a uniform ion size model whose solution can be obtained using the current model and Borukhov's formulation ¹ (they become identical in the uniform ion case). The second case compares the non-uniform ion size case against results developed by Tresset using a generalized Poisson-Fermi distribution for the ion concentrations. Consideration of true biomolecular systems is reserved for a subsequent publication.

Sphere with Central Charge and Uniform Ion Size

The first case considers a 20Å sphere with a −50e central charge. The temperature is set to 298.15 K and the interior and exterior dielectrics are ε_in=4 and ε_ex=78.5. This configuration is directionally invariant so that the solution depends only on radial distance. It was also examined in ³⁵ using the uniform ion size model ¹ allowing comparison. In the first example a uniform ion size of 1.5Å is assumed and an environment consisting of a mixture of 1:1 and 2:1 salts is considered. Figure 1 shows the variation of the electrostatic free energy with 1:1 salt concentration for various 2:1 salt concentrations. The curves agree closely with those reported in ³⁵ and reproduce the gradual flattening of the curves with increasing 2:1 salt. These results help confirm the proper operation of the software implementation. The same spherical configuration is also considered to compare the bound ion numbers. Now the ion radius is 1.4Å and the 1:1 salt concentration is fixed at 0.1M while the 2:1 salt concentration is varied. The results are depicted in Figure 2 and agree closely with ³⁵.

Figure 1.

Variation of total electrostatic energy with NaCl salt concentration at various MgCl₂ concentrations for sphere with central charge. The ion radius for all species is 1.5 Å.

Figure 2.

Variation of numbers of bound ions with MgCl₂ salt concentration for a mixed salt solution. Here [NaCl] is fixed at 0.1 M and the ion radius of all species is 1.4 Å.

Comparison between Monodisperse and Polydisperse Solutions

The 1D sphere containing a central charge is again considered to examine how the surface potential varies with salt concentration for a mixed salt system with non-uniform ion size. The conditions considered replicate the ones used to produce Fig. 2 of ⁷. The salt consists of a 0.01M 1:1 buffer salt with ion volume, V₁=4πa³/3=150ų to which is added another 1:1 salt of concentration, c₂, and ion volume V₂=800ų. In ⁷ the potential on an infinite plane surface with charge distribution of −0.2C/m² was examined. Here a 100Å radius sphere is used to approximate the infinite plane case and a central charge of −1568.77e is inserted to produce the same areal charge density. For these cases the solvent size, a_solvent=0. The temperature, T=298.15K and the interior and exterior dielectric constants are ε₁=4 and ε₂=78.5 respectively. Figure 3 shows the variation of the surface potential with added salt concentration for the four cases considered in Fig. 2 of⁷: (i) the mixed salt described above; (ii) the same salt mixture, but with V₁=V₂=150ų; (iii) the same as (i), but with V₁=V₂=800ų; (iv) the same as (i), but with V₁=V₂=0. The last case corresponds to the nonlinear PBE. When compared to Fig. 2 of⁷, the curves corresponding to salt properties (ii)–(iv) are in reasonable agreement with the discrepancies being attributable to the use of a spherically symmetric rather than planar geometry and, in cases (ii) and (iii), assigning a zero radius to the solvent (recall that the theory developed here reduces to the uniform ion size model of¹ when the ion and solvent sizes are all identical). For the mixed salt case (i) however, the curve is qualitatively different from ⁷ in that it increases monotonically with salt concentration whereas in ⁷ there is a distinct minimum. The same monotonic behavior is obtained at higher net charge and increased ion size (Fig. 3 of⁷ indicates that the minimum obtained in their model becomes more pronounced with ion size). A possible explanation of this difference between models is that the higher order terms neglected in the linearized treatment of the ion exclusion effect in ⁷ are significant for the case considered here.

Figure 3.

Variation of surface potential with added (1:1) salt concentration for the cases ⁷ of: (i) Mixed salt consisting of a 0.01M (1;1) salt with V=150ų and added salt with V=800ų; (ii) both salts with V=150ų; (iii) both salts with V=800ų; (iv) both salts with V=0ų.

The model can also be used to estimate the ion distributions of counterions with different valences. To this end, the ion concentrations reported in Fig. 5 of ⁷ are reproduced here using the SMPBE and compared to the corresponding distributions obtained with the standard nonlinear PB equation. The parameters are the same as for the previous case except for the following: (i) the net charge is doubled to obtain a surface charge of −0.4C/m²; (ii) the salt mixture contains three electrolytes - 10µM of 3:1 salt, 10mM of 2:1 salt and 0.3M of 1:1 salt; (iii) the counterions have excluded volumes of 1000ų and all coions have excluded volumes of 150ų. Figure 4a shows the ion concentrations for each of the counterions revealing the layered structure consisting of the highest valence ions nearest the surface followed by two lower valence ions further away from the surface. The distributions agree with those shown in Fig. 5 of⁷ with the peaks occurring at virtually the same distances from the surface. The peaks themselves are slightly smaller than those of ⁷, most likely due to the differences in formulation and the solution about a spherical rather than planar geometry. The corresponding distributions obtained with the nonlinear PB solver shown in Figure 4b are completely different and lack the stratification that occurs when ion size is accounted for.

Figure 5.

a. Spatial distributions for +1e, +2e and +3e ions with respective sizes a₊₁=5Å, a₊₂=6Å,and a₊₃=7Å about a 10Å radius sphere containing a net charge of −200e. This case approximates the example used to produce Figure 7a in ⁵.

b. Spatial distributions for +1e, +2e and +3e ions with respective sizes a₊₁=6Å, a₊₂=5Å,and a₊₃=7Å about a 10Å radius sphere containing a net charge of −200e. This case approximates the example used to produce Figure 7b in⁵.

c. Spatial distributions for +1e, +2e and +3e ions with respective sizes a₊₁=4Å, a₊₂=6Å,and a₊₃=7Å about a 10Å radius sphere containing a net charge of −200e. This case approximates the example used to produce Figure 7c in ⁵.

d. Spatial distributions for +1e, +2e and +3e ions with respective sizes a₊₁=4Å, a₊₂=6Å,and a₊₃=8Å about a 10Å radius sphere containing a net charge of −200e. This case approximates the example used to produce Figure 7d in ⁵.

Figure 4.

a. Spatial distributions for ions of different valences about a centrally charged sphere using the same parameters and conditions as for Fig. 5 of ⁷.

b. Ion distributions for the same case considered in Figure 4a, but using the nonlinear PB (zero ion size).

c. Variation of h with potential for the case considered in Figure 4a.

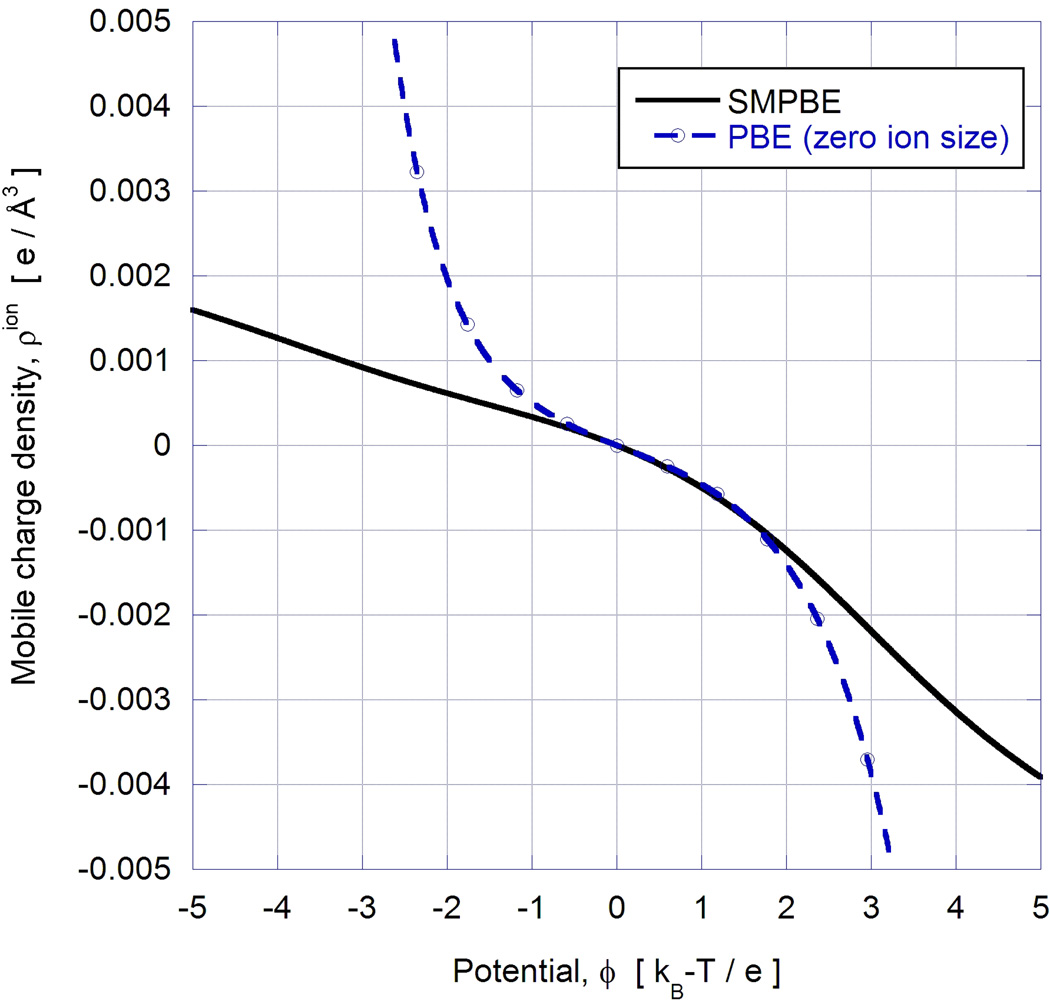
d. Variations of mobile charge density, ρ^ion, with potential for cases considered in Figures 4a (finite ion size) and 4b (zero ion size).

The parameter h as a function of potential for this solvent at finite ion size is shown in Figure 4c and compared against the corresponding curve obtained with the zero ion size PBE approximation by integrating (21). As expected, for small potentials, |ϕ|<<1, both curves are in close agreement and reflect the quadratic behavior expected analytically. At higher potentials while both curves reflect the asymmetric expected from the 2:1 and 3:1 salt components, they deviate from each other with the SMPBE curve assuming smaller values. For large potentials, the h~ϕ curve obtained with the SMPBE asymptotes to a linear relationship. This is expected for all finite ion size models since at high potentials the mobile ion charge density, ρ^ion, asymptotes to a non-zero constant value. The linear dependence between h and ϕ in this potential range then follows from (21). For the zero ion size PBE model, h grows exponentially with ϕ since no constraint on the ion density is imposed. Analogous observations pertain to the curves in Figure 4d relating the mobile ion charge to the potential. At very high values of potential the ion densities obtained with the SMPBE description asymptote to 3e/1000ų (at negative potential) and −1e/150ų (at positive potential) reflecting the full packing of the 3:1 salt counterions and the coions respectively.

Ordering of Ion Layers

In the recent article by Zhou, Wang and Li ⁵ it is proposed that the ordering of the ion concentration peaks near the surface can be estimated by considering the valence to volume ratio, z_i/V_i. Figure 7 of that article considers a solution consisting of only positive ions having valences of +3e, +2e and +1e. The volumes of the ions are varied and the resulting ion distributions due to a 10Å sphere containing a −200e charge calculated. Here the dependence of ion stratification upon valence to volume ratio is investigated using the present analysis approach. Because the problem definition in ⁵ differs somewhat from the ones addressed here (for example, the far-range ion concentrations approach zero rather than bulk values; also the valences and volume properties of the negative ions present in an electrically neutral bulk fluid are not given) direct comparison of the cases is not possible. Nevertheless, reasonable estimates of the solvent conditions can be made to approximate their examples as follows.

The exterior dielectric is set to ε₂=80.1 to match the Bjerrum length of 7Å (T=298K). The ion species are enumerated such that z_i=+i. The bulk solvent conditions are approximated as c_bi=n_i/V where the volume, V, in ⁵ is given as L³−4πR³/3 with the domain side length L=80Å and the sphere radius, R=10Å. The numbers n_i are set to 200/(3z_i). This leads to bulk concentrations of: c_b1=0.2180 M (+1e ions), c_b2=0.1090 M (+2e ions) and c_b3=0.0727 M (+3e ions). The solvent size is fixed at V₀=8ų. All co-ions are assigned a charge of −1e and sized to 8ų. The volumes of the counterions are adjusted to produce varying valence to volume ratios. As in ⁵ the following four cases are considered.

• Case (a): a_i={5, 6, 7} Å. α₊₂ : α₊₃ : α₊₁ = 1.157 : 1.093 : 1

• Case (b): a_i={6, 5, 7} Å. α₊₂ : α₊₃ : α₊₁ = 3.456 : 1.889 : 1

• Case (c): a_i={4, 6, 7} Å. α₊₁ : α₊₂ : α₊₃ = 1.786 : 1.059 : 1

• Case (d): a_i={4, 6, 8} Å. α₊₁ : α₊₂ : α₊₃ = 2.667 : 1.580 : 1

Here the ion volumes are given by V_i=a_i³ and the valence to volume ratios are denoted by α_+i=z_i/V_i.

The computed ion concentrations are shown in Figure 5 and agree qualitatively with those in ⁵ with differences being attributable to the different formulations adopted and necessary approximations between the cases. However, the same conclusions are reached regarding the correspondence between α_+i and the ordering of the ion concentration peaks. Thus for Cases (a) and (b) depicted in Figure 5a–b the ordering of the ion concentration peaks from the surface corresponds to the +2e species followed by the +3e and then +1e species. This is consistent with the ordering (from large to small) of the ratios α_+i listed above. Similarly for Case (d) the peak ordering from +1e to +2e to +3e predicted by the valence to volume ratios is reflected in Figure 5d. For Case (c) the same peak ordering is also maintained although the peak for the +2e species in Figure 5c is smaller than for the +1e species. This is not unexpected since α₊₂ and α₊₁ differ by only 5.9% so that other factors such as the relative bulk concentrations may become more significant in controlling peak amplitude.

The formulation developed here provides a heuristic basis for this relationship between α_+i and the ion peak ordering. From (19a) it follows that:

$$\frac{\mathrm{d}}{\mathrm{d}\mathrm{\varphi }}({\text{Qc}}_{\mathrm{i}})=-{\text{Qc}}_{\mathrm{i}}\left({\mathrm{V}}_{\mathrm{i}}\frac{\text{dh}}{\mathrm{d}\mathrm{\varphi }}+\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\right)=-{\text{Qc}}_{\mathrm{i}}\mathrm{\beta }\left(-{\mathrm{V}}_{\mathrm{i}}{\mathrm{\rho }}^{\text{ion}}+{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\right)$$

where (21) is used to obtain the final right hand term. A peak occurs when this derivative is zero, i.e., when ρ^ion = z_ie/V_i = eα_i. For the negatively charged surface ρ^ion decreases from a positive value at the surface to zero when far away from the surface. If this decrease is monotonic with distance from the surface then it immediately follows that peaks in (Qc_i) will be visited in order of decreasing z_i/V_i as observed in the computation. Note that the ordering of the peaks shown for (Qc_i) does not formally imply the same ordering in c_i. Thus at this point the correlation between α_+i and the ion peak ordering, remains suggestive, but not rigorous.

Nonlinear A/B Junction DNA Structure Associated with Tc3 Transposase Protein

In order to demonstrate application of the non-uniform ion size model to a realistic biomolecular configuration the model has been incorporated into the adaptive Cartesian grid (ACG)-based Poisson-Boltzmann solver described in ³⁶. This solver utilizes an octree data structure to represent the potential solution and provide the variable length scales needed to accommodate large complex structures. Here this solver is used to revisit the deformed and nonlinear DNA structure in association with the Tc3 transposase protein (PDBid: 1tc3 with net charge −37e) previously considered on the basis of the standard PBE in ³⁶ (specifically, Figure 8 of that article). Charges and radii are assigned using the AMBER force field³⁷ and the solute boundary is represented using the solvent excluded molecular surface. The interior and exterior dielectric constants are ε_in=2 and ε_ex=80 respectively and the temperature is 298K. The electrostatic solution for this configuration is calculated using the standard PBE and the SMPBE descriptions. In both cases the same salt mixture employed in the preceding example (10µM of 3:1 salt, 10mM of 2:1 salt and 0.3M of 1:1 salt) are used again here. For SMPBE calculation all counterions and coions are assigned excluded volumes of 1000ų and 150ų respectively; zero ion sizes are used in the PBE calculation. A fine grid spacing of 0.1Å at the surface is used in all calculations to ensure all features and length scales are adequately resolved.

Figure 6 compares the surface potential maps obtained using the PBE and SMPBE. The main difference between the results is a generally more negative potential with the SMPBE model, particularly inside the groove. The minimum surface potentials in units of kcal/mol/e are −2.52 (standard PBE) and −4.70 (SMPBE model). The reason for the more negative potential in the SMPBE is easily explained by noting that finite ion size limits the number of counterions available to neutralize the negative potential. In the PBE no such limit exists allowing higher counterion densities. In Figure 6 the orange-yellow region corresponds to potentials less than −3 kcal/mol/e or −5.07 k_BT/e which, from an expanded view of Figure 4d would yield mobile charge densities of 0.0016 e/1000ų (SMPBE) and 0.40 e/1000ų (PBE) respectively – i.e., an approximately 250-fold difference.

Figure 6.

Surface potential for DNA with three salt mixture. The left view is obtained using the standard PBE whereas the right view is developed using the SMPBE with different ion sizes resulting in a more strongly negative distribution, particularly in the groove region. The view and potential map scale for both surface plots are identical. The salt mixture for this case contains three electrolytes - 10µM of 3:1 salt, 10mM of 2:1 salt and 0.3M of 1:1 salt. For the SMPB calculation all counterions have excluded volumes of 1000ų and all coions have excluded volumes of 150ų.

While these differences in the electrostatic potential maps affect the prediction and possible interpretation of sequence-dependent features and phosphate charge clustering, other properties for this case such as the total electrostatic energy and its salt sensitivities appear to be only weakly affected by ion size effects as indicated in Table 1. The area-averaged ionic and dielectric pressures, p_ion and p_d, for this molecule are also compared showing that smaller values of p_ion are obtained using the SMPBE. However, the ionic pressures obtained with the PBE and SMPBE are both about two orders of magnitude smaller than the dielectric pressures, p_d, and for this case the influence of finite ion size upon surface pressures (and thus forces) is more strongly reflected in the changes to p_d than p_ion. Forming general conclusions on the basis of these limited observations is premature and investigation of biomolecular systems where finite ion size effects may play a more extensive role is presently underway. The results of this investigation will be reported in a follow-on article.

Table 1.

Energies and Salt Sensitivities Obtained with SMBPE and PBE Models.

Property	PBE	SMPBE
Reaction field energy [kcal / mol]	−6936.6	−6925.0
Excess osmotic pressure contributions [kcal / mol]       3:1 Salt       2:1 Salt       1:1 Salt	0.0195 1.856 6.485	0.151 3.438 8.589
Salt sensitivities, ∂G/∂{ln(cb)}×1000 [kcal / mol]       3:1 Salt       2:1 Salt       1:1 Salt	−0.365 −0.138 −5.909	−0.364 −0.470 −5.625
Area-averaged ionic pressure × 1000 [kcal / mol 0/e / Å3]	1.216	0.809
Area-averaged dielectric pressure × 1000 [kcal / mol /e / Å3]	181.1	175.1

Conclusions & Future Activity

Utilizing simple statistical mechanics principles, a non-uniform ion size model has been formulated to provide the ion concentrations and derivative properties such as the electrostatic free energy and its variation with salt concentration and also the ionic pressure. The new model has been applied to simple systems involving a sphere containing a central charge to confirm agreement with existing models for both the uniform and non-uniform ion size cases. Generally good agreement has been established, thus increasing confidence in the overall approach. Results suggest that the effects of ion size are most significant when evaluating electrostatic potentials and ion concentrations at the surface. Volume integrated properties such as total energies and bound ion numbers appear to be only weakly affected by ion size. Simulations carried out using the new ion size model corroborate the correlation between peak ordering in stratified ion distributions and the valence to volume ratio identified in ⁵. The present theory also supports this correlation provided that the mobile charge distribution changes monotonically with distance from the surface.

The model has been incorporated into a 3D SMPBE solver and used to calculate the electrostatic potential solution for a DNA structure. This solver is currently being used to investigate a collection of relevant biomolecules and geometries (e.g., ion channels) where size effects are believed to play a significant role. Means of incorporating ion-ion correlation effects in a similarly simple manner with reliance on ensemble-averaged computational simulations to quantify these effects are also being considered.

Nomenclature

a_i

ion size such that the ion volume, V_i=a_i³

c_i

concentration of i-th species in number of ions per unit volume

c_ib

bulk concentrations (at zero electrostatic potential)

D

sum of concentrations of all species including solvent defined in (17)

D_b

sum of bulk concentrations

ê_k

unit vector in the k-th direction

e

unit electric charge

E_i

potential energy of ion of i-th species defined in (5)

Ē

average energy per particle defined in (27)

Ȇ

total energy per volume developed from (28)

G

Gibbs free energy defined in (32)

G’

derivative of Gibbs free energy with respect to specified parameter

h

difference α−α₀ of Lagrange coefficient from zero potential value

k_B

Boltzmann’s constant

n₀, n_i

number of solvent molecules and ions of i-th species

N

total number of particles

p

number of ion species

p_d, p_ion

dielectric and ionic pressures defined in (51)

q_i

atomic charge of i-th species

Q

ratio D_b/D

Q_net

net charge

R_jk

perturbation of atom j along Cartesian direction k

S

entropy defined in (12)

S_k

surface integral given by Eq. (31)

T

temperature

V_i

volume of ion of i-th species

V_tot

total volume

z_i

valence of i-th species

Z

partition function defined in (3)

α, β

Lagrange coefficients

α₀

value of Lagrange coefficient at zero potential

α_+i

valence to volume ratio, α_+i=z_i/V_i

λ

Gilson parameter used to demarcate the interior and exterior regions

ΔΠ

excess osmotic pressure (33)

μ_i

chemical potential of i-th species

ρ^f, ρ^ion

fixed charge and ion charge density, the latter being defined in (22)

φ

electrostatic potential

Appendix A. Limiting Expressions for Uniform Ion Size and Zero Ion Size

The expressions developed in the main article for non-uniform ion size reduce naturally to previously established results in the limits of uniform ion size and zero ion size (governed by the standard PBE).

Ion Concentration

In the case of constant ion and solvent size, V,

$$\mathrm{D}={\mathrm{D}}_{\mathrm{b}}=1/\mathrm{V};\mathrm{Q}=1\text{ and }{\mathrm{e}}^{\text{Vh}}=\mathrm{V}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}$$ (52)

and the ion concentrations can be expressed:

$${\mathrm{c}}_{\mathrm{i}}=\frac{{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}}{{\text{Vc}}_{\mathrm{b}0}+\mathrm{V}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}}$$ (53)

or, using (15) evaluated at zero potential:

$${\mathrm{c}}_{\mathrm{i}}=\frac{{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}}{1+\mathrm{V}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}({\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}-1)}$$ (54)

Defining:

$$\mathrm{C}=\mathrm{V}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\mathrm{i}}\text{ and }{\mathrm{C}}_{\mathrm{b}}=\mathrm{V}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}$$ (55)

and summing (54) over the ion species shows that

$$\mathrm{V}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}=\left(\frac{1-{\mathrm{C}}_{\mathrm{b}}}{1-\mathrm{C}}\right)\mathrm{C}$$ (56)

which when substituting back into (54) shows that:

$${\mathrm{c}}_{\mathrm{i}}=\left(\frac{1-\mathrm{C}}{1-{\mathrm{C}}_{\mathrm{b}}}\right){\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}$$ (57)

After identifying V=a³ these results agree with the uniform ion size-modified PBE expressions developed by Borukhov ¹. The ion distributions corresponding to the standard PBE are trivially reproduced from (57) since in the limit of vanishing ion size, V→0, C and C_b also vanish per (55).

Total Free Electrostatic Energy

For constant ion size (20) leads to:

$$\mathrm{h}=\frac{1}{\mathrm{V}}\{\text{ln }\left({\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}\right)-\text{ln }\left({\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}\right)\}=\frac{1}{\mathrm{V}}\text{ln }\left(\mathrm{V}{\displaystyle \sum _{\mathrm{i}=0}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}{\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}\right)$$ (58)

which, using (56), leads to:

$$\mathrm{h}=\frac{1}{\mathrm{V}}\text{ln }((1-{\mathrm{C}}_{\mathrm{b}})+\left(\frac{1-{\mathrm{C}}_{\mathrm{b}}}{1-\mathrm{C}}\right)\mathrm{C})=\frac{1}{\mathrm{V}}\text{ln }\left(\frac{1-{\mathrm{C}}_{\mathrm{b}}}{1-\mathrm{C}}\right)$$ (59)

and the excess osmotic pressure,

$$\mathrm{\Delta }\mathrm{\Pi }=\frac{1}{\mathrm{\beta }\mathrm{V}}{\displaystyle \underset{\mathrm{V}}{\int }}\text{ ln }\left(\frac{1-{\mathrm{C}}_{\mathrm{b}}}{1-\mathrm{C}}\right)\text{ dV}$$ (60)

This in fact agrees with the expression readily derivable from the uniform ion size obtained from Borukhov¹.

This result in turn can be used to develop the results for vanishing ion size (i.e., the nonlinear PBE) by expanding the natural logarithmic function. Thus,

$$\underset{\mathrm{V}\to 0}{\text{lim}}\mathrm{\Delta }\mathrm{\Pi }=\underset{\mathrm{V}\to 0}{\text{lim}}\frac{1}{\mathrm{\beta }\mathrm{V}}{\displaystyle \underset{\mathrm{V}}{\int }}(\mathrm{C}-{\mathrm{C}}_{\mathrm{b}})+\mathrm{O}({\mathrm{V}}^2{\mathrm{c}}_{\mathrm{i}})\text{ dV}=\underset{\mathrm{V}\to 0}{\text{lim}}\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}({\mathrm{c}}_{\mathrm{i}}-{\mathrm{c}}_{\mathrm{b}})\text{ dV}$$ (61)

which, using (54), recovers the familiar PBE result:

$$\underset{\mathrm{V}\to 0}{\text{lim}}\mathrm{\Delta }\mathrm{\Pi }=\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\mathrm{\text{bi}}}({\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}-1)\text{ dV}$$ (62)

Energy Salt Gradient

In the case of uniform ion size using (55) and (57) then the expression for the salt gradient (39) becomes

$$\frac{\partial \mathrm{G}}{{\mathrm{c}}_{\text{bk}}}={\mathrm{S}}_{\mathrm{k}}-\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}\left(\frac{1-\mathrm{C}}{1-{\mathrm{C}}_{\mathrm{b}}}\right)\left({\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{k}}\mathrm{e}\mathrm{\varphi }}-1\right)\text{ dV}$$ (63)

Further in the limit of vanishing ion size one recovers the result for the nonlinear PBE:

$$\underset{\mathrm{V}\to 0}{\text{lim}}\frac{\partial \mathrm{G}}{{\mathrm{c}}_{\text{bk}}}={\mathrm{S}}_{\mathrm{k}}-\frac{1}{\mathrm{\beta }}{\displaystyle \underset{\mathrm{V}}{\int }}\left({\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{k}}\mathrm{e}\mathrm{\varphi }}-1\right)\text{ dV}$$ (64)

and reproduces the known relationship between the salt gradient and excess osmotic pressure ³¹

$$\frac{\partial \mathrm{G}}{{\mathrm{c}}_{\text{bk}}}=-\frac{1}{{\mathrm{c}}_{\text{bk}}}{\mathrm{\Pi }}_{\mathrm{k}},{\mathrm{\Pi }}_{\mathrm{k}}={\displaystyle \underset{\mathrm{V}}{\int }}{\mathrm{c}}_{\text{bk}}\left({\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{k}}\mathrm{e}\mathrm{\varphi }}-1\right)\text{ dV }(\mathrm{V}\to 0)$$ (65)

Ionic Pressure

Since p_ion is equal to the integrand of the integral for the excess osmotic pressure (33) the simplifications developed for uniform ion size and the limit of vanishing ion size are immediately available (see (59) and (62))

$${\mathrm{p}}_{\text{ion}}=\frac{1}{\mathrm{\beta }\mathrm{V}}\text{ln}\left(\frac{1-{\mathrm{C}}_{\mathrm{b}}}{1-\mathrm{C}}\right)(\text{uniform ion size})$$ (66a)

$$\underset{\mathrm{V}\to 0}{\text{lim}}{\mathrm{p}}_{\text{ion}}=\frac{1}{\mathrm{\beta }}{\displaystyle \sum _{\mathrm{i}=1}^{\mathrm{p}}}{\mathrm{c}}_{\text{bi}}({\mathrm{e}}^{-\mathrm{\beta }{\mathrm{z}}_{\mathrm{i}}\mathrm{e}\mathrm{\varphi }}-1)(\text{vanishing ion size})$$ (66b)

Vanishing Solvent Size

All of the expressions derived above in the main article are well behaved when the solvent size, V₀, becomes infinitesimally small. While there are terms where the volume V₀ appears as a divisor all such terms are multiplied by the term, exp{−hV₀}−1, whose limiting behavior when divided by V₀ is simply h.