k-neighborhood Decentralization: A Comprehensive Solution to Index the UMLS for Large Scale Knowledge Discovery

Abstract

The Unified Medical Language System (UMLS) is the largest thesaurus in the biomedical informatics domain. Previous works have shown that knowledge constructs comprised of transitively-associated UMLS concepts are effective for discovering potentially novel biomedical hypotheses. However, the extremely large size of the UMLS becomes a major challenge for these applications. To address this problem, we designed a k-neighborhood Decentralization Labeling Scheme (kDLS) for the UMLS, and the corresponding method to effectively evaluate the kDLS indexing results. kDLS provides a comprehensive solution for indexing the UMLS for very efficient large scale knowledge discovery. We demonstrated that it is highly effective to use kDLS paths to prioritize disease-gene relations across the whole genome, with extremely high fold-enrichment values. To our knowledge, this is the first indexing scheme capable of supporting efficient large scale knowledge discovery on the UMLS as a whole. Our expectation is that kDLS will become a vital engine for retrieving information and generating hypotheses from the UMLS for future medical informatics applications.

1. Introduction

The Unified Medical Language System®(UMLS®) [1] is a comprehensive collection of concepts and their relationships in biomedical science. It includes many important sources such as NCI Thesaurus [2], OMIM [3], SNOMED CT [4], etc. By searching the UMLS Metathesaurus®, users can find detailed information on a variety of controlled vocabularies in biomedical science. The UMLS uses semantic relations to mark the available links between two concepts.

Recently, Payne et al. [5, 6, 7] showed that in addition to the available links, the transitive links in the UMLS are valuable sources of knowledge. A transitive link is a consecutive order of links connecting a starting concept to an ending concept via one or more middle concepts in the UMLS. If a transitive link connects two concepts in a meaningful matter, it is regarded as a Conceptual Knowledge Construct (CKC) in [5, 6, 7]. By mining CKCs from a small subset of UMLS, Payne et al. [5, 6, 7] found semantically meaningful results that are confirmed by subject matter experts as hypotheses for Chronic Lymphocytic Leukemia (CLL) research.

However, due to the extremely large size of the UMLS, CKC mining has to be limited within transitive links containing no more than 5 concepts (i.e., no more than 4 consecutive links), and the search is limited to a very small number of data sources in the UMLS [5]. The results, however, are far from complete, as they are obtained from searching a very small portion of the UMLS. Furthermore and because of the extremely bulky size of the UMLS, none of the current methods can produce an efficient indexing scheme for knowledge discovery on the UMLS without setting similar major limits.

To answer the challenge of efficiently indexing the extremely large UMLS to explore the rich knowledge in it, in this paper we propose a k-neighborhood Decentralizing Labeling Scheme (kDLS), a graph labeling scheme tailored for indexing the UMLS under any source configurations ¹ for efficient knowledge discovery. kDLS can efficiently search a large portion (6-neighborhood) of the UMLS with full data source configuration on servers with moderate memory space (≈22GB) and make it possible to search the whole UMLS (unlimited-neighborhood) with full data source configuration on servers with reasonably large memory space (≈209GB), although the latter may not be necessary in most cases. The kDLS running time is decreased by several orders of magnitude, according to the measures reported in Section 3 of this manuscript, as compared with current Breadth-First Search and Depth-First Search methods.

More importantly, kDLS can produce various granularities of information from the UMLS, to efficiently answer reachability, distance, and shortest path queries. In addition to providing efficient solutions to these traditional queries, kDLS is able to construct a set of paths that represents the relationship between two concepts. Furthermore, the number of these representative paths can be estimated without actually constructing them. This nice feature makes the kDLS particularly suitable for large scale knowledge discovery between two sets of biomedical concepts, e.g. between genes and diseases. Our study on large scale knowledge discovery for gene-disease relations demonstrates the efficiency and effectiveness of kDLS.

In summary, kDLS provides a complete solution to index the whole UMLS for large scale knowledge discovery, and we expect that kDLS or its derivations will become key knowledge discovery engines for future biomedical informatics applications.

1.1. UMLS Basic Facts

The UMLS generally consists of three parts: Metathesaurus, Semantic Network, and SPECIALIST Lexicon and Lexical Tools.

The Metathesaurus is the primary part of the UMLS. It is formed by concepts from various sources and the relationships between concepts. The UMLS uses CUIs (Concept Unique Identifiers) to uniquely identify concepts across different data sources. Each CUI is also categorized by at least one semantic type. We have observed 133 semantic types in the UMLS 2011AA.

The Semantic Network is a collection of information related to semantic types which categorize CUIs, and semantic relations which are used to mark the relationship between two CUIs. The semantic network does not actually record the detailed relationships between CUIs and it is very small in size.² It is the Metathesaurus which actually records the detailed relationships between concepts that can be used to build a graph for our study.

The SPECIALIST Lexicon and Lexical Tools facilitate the study of the UMLS concepts with additional syntactic information such as form and spelling.

In this work, we used the UMLS Metathesaurus for indexing and knowledge discovery. To be specific, we used concepts in the Metathesaurus by CUIs as recorded in the source file “MRCONSO.RRF”, and their semantic types as recorded in the source file “MRSTY.RRF”, and we studied relationships between CUIs as recorded in the source file “MRREL.RRF”. To avoid confusion, in this paper we refer to the relation connecting a CUI a to another CUI b in the “MRREL.RRF” file a link from a to b. We call the aggregation of all such links the concept network of the UMLS. Each link is marked by a semantic relation. We have observed 591 semantic relations in the UMLS 2011AA.

The UMLS contains various sources that are available for selection upon its installation.³ The default installation typically includes data sources marked as level 0. The UMLS installation menu also suggests “level 0 + SNOMEDCT” as another installation option. To make our paper complete, we evaluated three typical data source configurations, i.e., UMLS with level 0 data sources, UMLS with level 0 + SNOMEDCT data sources, and UMLS with full data sources, for most of our studies. The data source configuration determines the contents of the three source files: “MRCONSO.RRF”, “MRSTY.RRF”, and “MRREL.RRF”. Some essential details of the UMLS corresponding to different data source configurations are listed in Table 1.

Table 1.

The Basic Fact of UMLS2011AA and the corresponding UMLS graphs.

	# source families	# sources	# CUIs	# links	|V | of UMLS Graph G	|E| of UMLS Graph G	Density (|E|/|V |)
UMLS Level 0	43	63	1,705,032	6,237,554	720,457	5,288,616	7.340640732
UMLS Level0 + SNOMEDCT	44	65	1,913,320	11,821,326	987,293	7,954,122	8.056495893
UMLS Full	85	159	2,404,937	15,333,246	1,339,660	9,441,802	7.047909171

1.2. Basic Definitions

In this section we define a number of terms used in this work. Basic graph theory terms: A graph G = (V, E) consists of a vertex set V and an edge set E. The graph G studied in this work is a directed graph without self-loops (i.e., edges connecting a vertex to itself). e ∈ E, e = (a, b) denotes an edge e connecting vertex a to vertex b. A path P is a vertex sequence such that there is an edge e ∈ E connecting each vertex (other than the ending vertex) to the next vertex in P. A simple path is a path without repeating vertices. The length of a path P is the number of vertices in its vertex sequence minus 1. The distance from vertex a to vertex b in G, denoted as d_G(a, b), is the length of a shortest path connecting a to b. A vertex’s in-degree is the number of edges ending at this vertex. A vertex’s out-degree is the number of edges starting at this vertex. A vertex’s degree is the sum of its in-degree and out-degree.

Definition 1. (UMLS Graph)

A UMLS Graph is a directed graph G = (V, E) built upon the UMLS Metathesaurus in the following way: A CUI in the Metathesaurus corresponds to a vertex v ∈ V if and only if the CUI appears in the concept network. There exists an edge e = (a, b), e ∈ E, if and only if there exists in the concept network at least one link l connecting the CUI corresponding to vertex a, to the CUI corresponding to vertex b (b ≠ a), such that the CUI corresponding to vertex a and the CUI corresponding to vertex b are not categorized in any restricted semantic types, and the semantic relation marking link l is not restricted.

The concept network does not include all CUIs in the Metathesaurus. That is, there are some CUIs without any links to or from other CUIs. For those CUIs not included in the concept network, they do not connect directly or indirectly to any other concepts. Thus we do not include them in the UMLS graph as defined in Definition 1 to simplify our computation.

Although there may exist more than one link connecting a CUI (let it correspond to vertex a) to another CUI (let it correspond to vertex b) in the concept network, at most one edge e = (a, b), e ∈ E, will be built in the UMLS graph to correspond to all these links. Thus, we conclude that the UMLS graph G is free of repeating edges as well as self-loops (i.e., edges connecting a vertex to itself). However, it is necessary to point out that cycles (i.e. a path starting and ending at the same vertex) are widely available in the UMLS graph G, and we properly handled them in this work.

The restriction on semantic types and semantic relations is an option (called semantic restriction in the following) provided in our method. Users can choose to set up the semantic restriction to reduce less-informative paths from the knowledge discovery results for their specific applications. There is no semantic restriction by default. Thus a UMLS graph is determined by both the data source configuration which controls the Metathesaurus, and the optional semantic restriction set up by the users.

The basic characters of the three UMLS graphs with respect to three different data source configurations (no semantic restrictions) are listed in Table 1. The three UMLS graphs will be studied from Section 2 to Section 3.1.

2. Methods

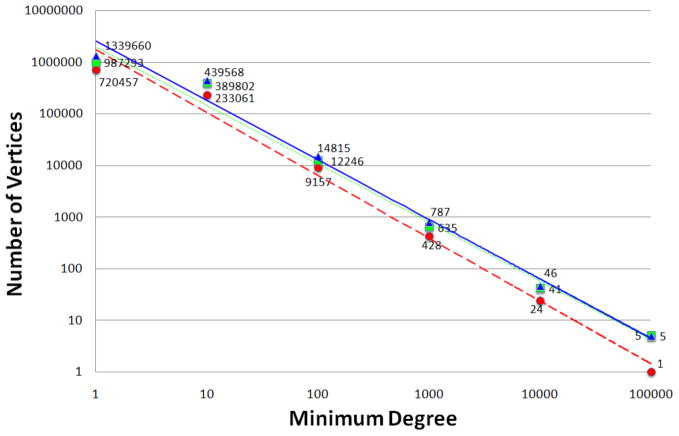
As listed in Table 1, the UMLS graphs with respect to three typical data source configurations are very large and dense. To our knowledge, no available graph database indexing schemes have demonstrated the capacity to handle them for efficiently answering distance and path queries for knowledge discovery. Nevertheless, they are quite different from “random graphs” which are targeted by some available indexing schemes. In contrast, we find that the three UMLS graphs exhibit a clear power-law property on their cumulative vertex degree distributions as shown in Figure 1. From Figure 1 we can see that in any of the three UMLS graphs, there are only hundreds of vertices with a degree 1,000 or larger, and there are less than 10 vertices with a degree larger than 100,000.

Figure 1.

Cumulative vertex degree distributions with power trendlines of of three typical UMLS graphs. The red dashed line and red circles correspond to the UMLS graph of level 0 data source configuration. The green dotted line and green squares correspond to the UMLS graph of level 0 + SNOMEDCT data source configuration. The blue solid line and blue triangles correspond to the UMLS graph of full data source configuration.

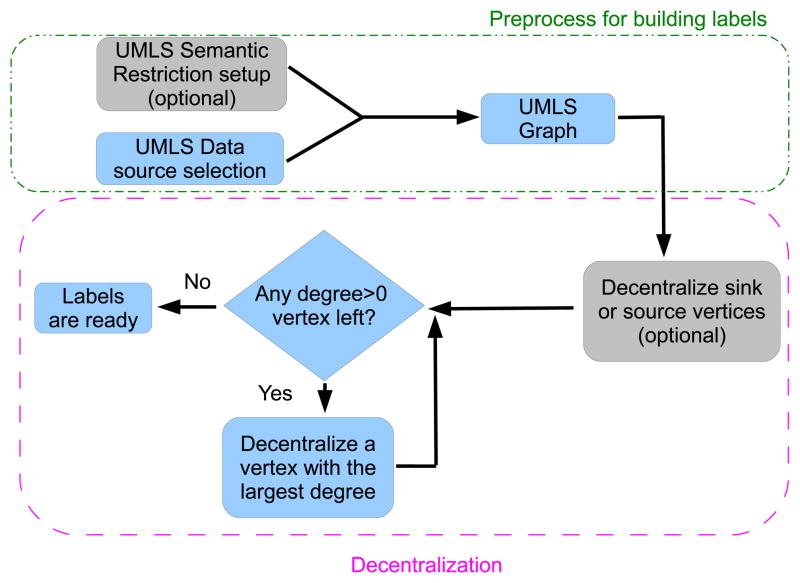
Given the power-law nature of the UMLS graphs, we propose to index them with a flow chart as in Figure 2. The definition for a UMLS graph is introduced in Section 1.2. Its construction follows the definition and is considered as a preprocess step in the index construction. The main part of the index construction is decentralization, whose details are discussed in Sections 2.1 to 2.3.

Figure 2.

The flow chart of index construction.

2.1. The general process of decentralization

Taking the sizes of the three UMLS graphs into consideration, any successful method must be highly scalable. Under this philosophy, we avoid the time-costly approaches to label vertices by constructing densest subgraphs [8, 9, 10, 11], and we also avoid the rigid and costly approach of finding a graph separator for each iteration [12]. Instead, we fully utilize the power-law nature of the UMLS graphs through decentralization. Decentralization is a term used in this work to describe the general process of removing a node and broadcasting its information to others in the UMLS graph.

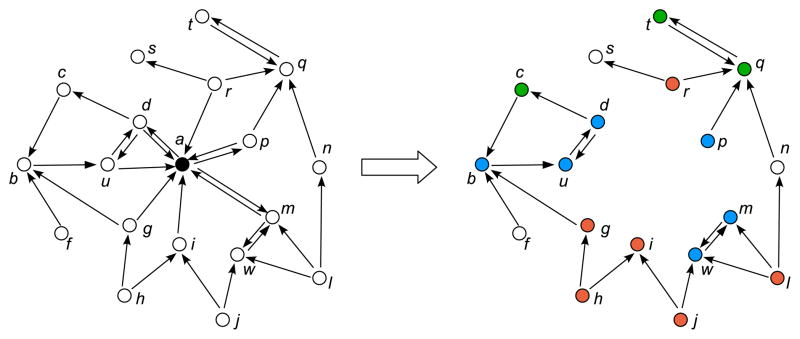
Figure 3 is an example of decentralizing a vertex by kDLS. The information about the removed black vertex will be decentralized to other vertices in the graph. In Figure 3, red vertices will remember how to reach the removed black vertex, and the green vertices will remember how to be reached by the black vertex, and the blue vertices remember both ways. It is easy to see that the decentralization can be implemented by a BFS (Breath-First Search) broadcast procedure.

Figure 3.

Illustration of decentralizing a vertex.

In fact, it is not necessary to broadcast the removal information to every corner of the UMLS graph, if we are primarily interested in concepts that are not too far away. This is further justified by the “small world phenomenon” observations as shown in Figures 4 and 5.

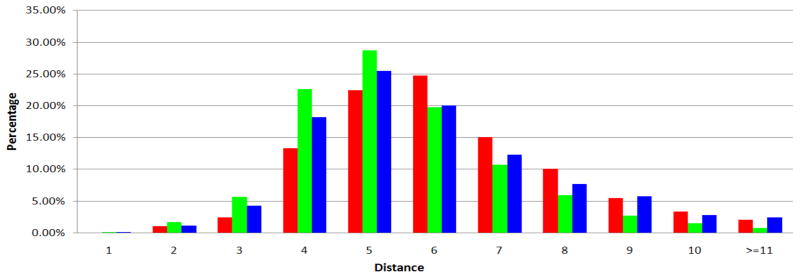
Figure 4.

Percentage of distances among the reachable cases of 10,000 random distance queries. Red columns correspond to the UMLS graph of level 0 data source configuration. Green columns correspond to the UMLS graph of level 0 + SNOMEDCT data source configuration. Blue columns correspond to the UMLS graph of full data source configuration.

Figure 5.

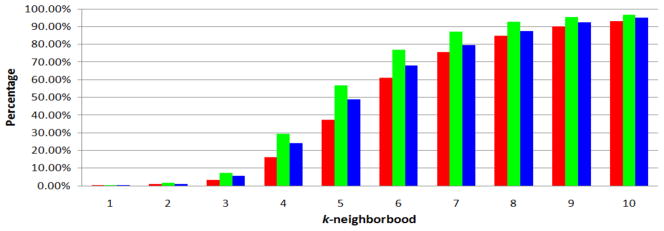
Average percentage of vertices in the k-neighborhood of a vertex among 10,000 random tests. Red columns correspond to the UMLS graph of level 0 data source configuration. Green columns correspond to the UMLS graph of level 0 + SNOMEDCT data source configuration. Blue columns correspond to the UMLS graph of full data source configuration.

Figure 4 shows the percentage of distances among the reachable cases of 10,000 random distance queries on the UMLS graphs. In all three UMLS graphs, we found that in a majority of cases distances are 6 or less, and in most cases, distances are no more than 10.

Further, in Figure 5, we report the average fraction of vertices in the k-neighborhood of a vertex among 10,000 random tests. A vertex a is in the k-neighborhood of another vertex b (or we say a and b are within k hops) if and only if d_G(a, b) ≤ k or d_G(b, a) ≤ k. From this Figure, we can observe that in all three UMLS graphs, the 6-neighborhood of a vertex on average contains a majority of vertices (> 60.0%), and the 10-neighborhood of a vertex on average contains most vertices according to the random tests. (Note that even if we set k to be infinite, a vertex’s k-neighborhood may not cover all vertices.) Thus, users can configure the broadcast range of kDLS by referring to Figure 4 and Figure 5 taking into consideration their needs and, also their computer memory capacities (see Figure 10 in the following).

Figure 10.

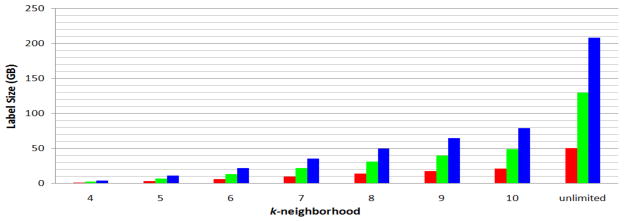
Total label size for different kDLS broadcast ranges. 1 GB=2³⁰ Bytes. Red columns correspond to the UMLS graph of level 0 data source configuration. Green columns correspond to the UMLS graph of level 0 + SNOMEDCT data source configuration. Blue columns correspond to the UMLS graph of full data source configuration.

2.2. Optional handling for sink and source vertices to reduce label sizes

A sink vertex is a vertex in a UMLS graph with a large number of incoming edges but no outgoing edges. In contrast, a source vertex is a vertex in a UMLS graph with a large number of outgoing edges but no incoming edges. We have found in our applications that these sinks or sources are often general or abstract concepts that are less likely to be queried. Thus we provide an option to further reduce label size by decentralizing the sink or source vertices first without broadcasting (consequently, there will be no records for them in any labels). The correctness of answering a query involving no sink or source vertices is clearly unaffected according to the query details described in Section 2.4. In the case that a query involves a source vertex or a sink vertex, a Breadth-First Search limited to k-neighborhood can be used to complete the answer, and it is not difficult to see that the Breadth-First Search will return the same result as “decentralizing the sink and source vertices first with broadcasting” does.

2.3. Compact label formats of kDLS

Designing compact label formats for kDLS is a key technique for obtaining a compact index size. In this section we will introduce the label formats used in this work.

2.3.1. A basic three-tuple compact format

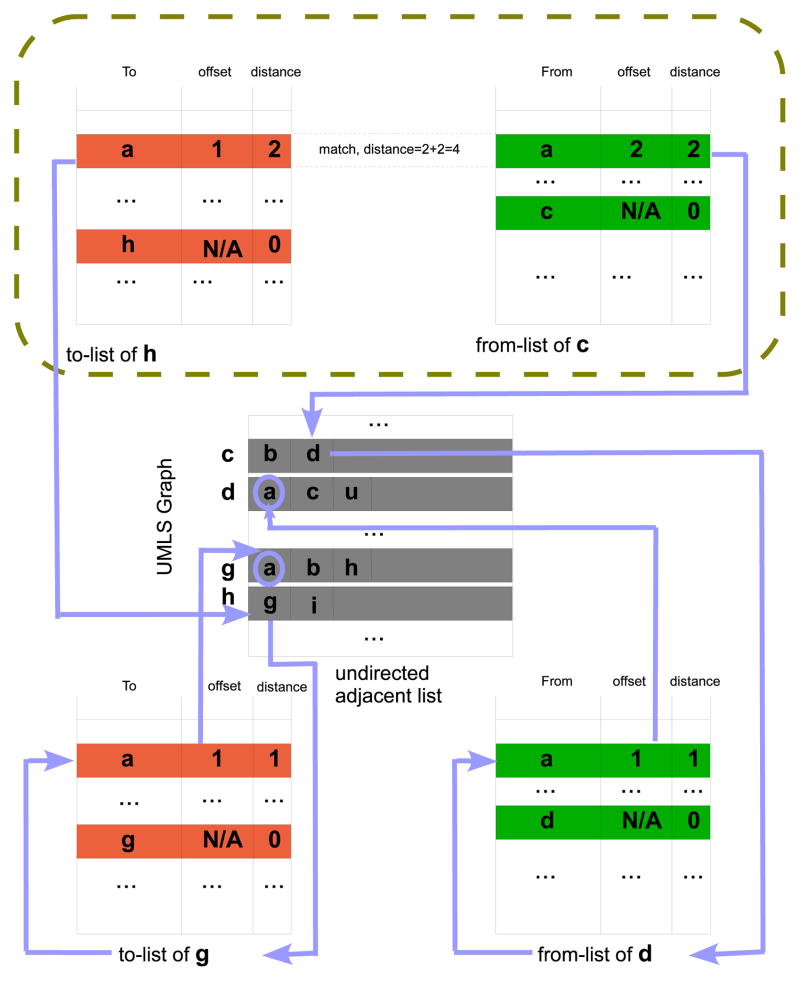
First, we can observe that a three-tuple record is enough to hold the information a vertex receives from decentralizing. For example, in Figure 3, the information c receives from decentralizing the node a, is a from-record containing three tuples “From a; via d; Distance 2”, and the information h receives from decentralizing the vertex a is a to-record “To a; via g; Distance 2”.

The first tuple is a vertex id for which 3 bytes (24 bit) is sufficient to represent (up to 16 million vertices). The last tuple is the distance. According to Figure 4, most of the distances are no more than 10, thus focusing on distances no more than 255 or even 15 (using 1 byte) would be sufficient for most UMLS applications.

It is somewhat tricky to handle the second tuple. Instead of using 3 bytes to record the via-neighbor vertex, we use only 2 bytes to record the port number. A port number is an offset of the neighbor vertex in the vertex adjacent list (in-list or out-list). However, in our study we observed vertices with degree larger than 65, 535 * 2, which implies that either in-list or our-list (or both) exceeds 65, 535, a number that 2-byte is insufficient to represent. This problem can be solved by observing the power-law property of the cumulative vertex degree distributions of the UMLS graphs as shown in Figure 1. There are only a very limited number of vertices with degree larger than 10, 000 even in the UMLS graph of full data source configuration, which implies that the number of vertices with in-list or our-list exceeding 65, 535 is very limited in a UMLS graph. If the power-law property holds for the future UMLS graphs (we conjecture it is highly likely), then we can still expect the number to be small. Thus, we propose to use only 0 – 65, 534 to represent port number, and use 65, 535 as a code of port number overflow. When we encounter a port number larger than or equal to 65, 535 during decentralization, we fill the second tuple with 65, 535, and save the large port number along with other identifiable numbers, in an overflow container so that the large port number can be easily retrieved in a query process. Since there are only a very limited number of vertices with degree larger than 65, 535 in a UMLS graph, we conclude that the overflow container size is very limited even if we use an integer (usually 4-byte) to represent each number in it.

Thus, a vertex only uses 3+2+1=6 bytes (even smaller than the size of an 8-byte long integer) to record the information to or from a decentralized vertex.

2.3.2. Achieving a further compact format by combining from-record with to-record

A vertex may receive a from-record and a to-record from the same neighbor with respect to a decentralizing vertex. To design a compact label format for these cases, we combine both records into one to reduce the label size. For example, in Figure 3, the information w received from decentralizing the node a, is a from-record “From a; via m; Distance 2” and a to-record “To a; via m; Distance 2”. The two records can be combined into one as “From and To a; via m; Distance 2, 2”. This is implementable if we organize an undirected adjacent list of each vertex such that each neighbor corresponds to a single offset regardless of whether the neighbor is linked to the vertex or from the vertex or both. The first tuple still takes 3 bytes, and the second tuple still takes 2 bytes by using the technique discussed in Section 2.3.1. Since 15 hops is enough for most UMLS applications, we still use 1 byte for the last tuple by splitting the upper 4 bits for “From” distance and the lower 4 bits for “To” distance.

Even when a vertex receives a from-record and a to-record from two different neighbors with respect to a decentralizing vertex, we can still achieve a significant label saving by combining the from-record with the to-record. For example, in Figure 3, the information b received from decentralizing the node a, is a from-record “From a; via c; Distance 3” and a to-record “To a; via u; Distance 2”. The two records can be combined into one as “From and To a; via c, u; Distance 3, 2”. The first tuple still takes 3 bytes. The second tuple takes 4 bytes because we need to record two port numbers. We again use 1 byte for the last tuple by splitting the upper 4 bits for “From” distance and the lower 4 bits for “To” distance.

Thus after the decentralization process, we will obtain four label lists plus a port number overflow container. The four label lists are: from-only list, to-only list, from-and-to-via-same-port list, and from-and-to-via-different-port list. Utilizing these labels, kDLS is ready to handle various queries and knowledge discovery applications. The nice properties of kDLS make the large scale knowledge discovery possible, as discussed in Section 2.5.

Finally, when an application involves distances more than 15, we can design a compact label format by differentiating the cases where the from-record and to-record pairs share the same distance, with the cases where they do not. Similarly, we will save a record in a list according to the bytes needed by its distance tuple. This will result in more than four label lists but the number of lists will still be manageable. For the succinctness of the paper, we omit the details as they are simple extensions of the previously-discussed techniques.

2.4. Queries supported by kDLS

The query procedure is similar to 2-hop [9, 10, 11], which compares the labels of two query vertices. However, we are not only interested in the distance and one shortest path, but also all paths that can be found by comparing the kDLS labels of two vertices. The kDLS labels are obtained through the flow chart in Figure 2, whose details are discussed in previous sections.

In the following, a kDLS path between two vertices refers to a path that is identified by comparing the labels (obtained by kDLS) of the two vertices. If sink and source vertices are handled according to Section 2.2, then the kDLS path connecting a sink or source vertex to another vertex refers to the shortest path that can be found by a Breadth-First search limited to k-neighborhood. A kDLS simple path refers to a kDLS path without repeating vertices. The main queries from vertex x to vertex y, as supported by kDLS, are listed as follows.

1. The reachability from x to y.

2. The total number of kDLS paths from x to y.

3. The total number of kDLS simple paths from x to y.

4. The distance from x to y.

5. The total number of shortest kDLS paths from x to y.

6. A shortest path from x to y.

7. All shortest kDLS paths from x to y.

8. All kDLS paths from x to y.

9. All kDLS simple paths from x to y.

Upon receiving a query request from vertex x to vertex y, we reorganize the entries of x on the label lists (as discussed in Section 2.3) into a to-list and the entries of y on the label lists into a from-list. To facilitate query processing, the to-list includes x as a decentralized vertex with distance being 0, and the from-list includes y as a decentralized vertex with distance being 0. Records in the to-list and from-list are in the order of decentralized vertex IDs. Thus, a linear-time comparison between two labels of the two query vertices can answer queries (1)(2)(4)(5). It is easy to see a first match of a decentralized vertex ID is enough to answer (1), while (2) requires a complete comparison between two labels. (4) requires additional computing over (2), and (5) can be done by another sweep of matchings after a complete label comparison. The correctness of kDLS in finding at least one shortest path between two vertices within k hops is guaranteed by Lemma 1.

To answer (3)(6)(7)(8)(9), we need to actually construct paths by recursively locating the next vertex via the offset in the corresponding record, and searching for the next record within the label of the located vertex. This requires more memory accesses and thus takes more computing time compared to answering queries (1)(2)(4)(5).

Among the above 9 types of queries, efficiently answering (2) is the biggest advantage of kDLS over available methods BFS and DFS. That is, to get the total number of kDLS paths, we do not need to actually construct these paths. This feature makes the kDLS more suitable for large scale knowledge discovery for UMLS applications.

Figure 6 gives an illustration for answering queries from x to y.

Figure 6.

An illustration of queries. Query (1) (2) (4) (5) can be performed by coupling two labels as illustrated in the brown-dashed rectangle. Since query (3)(6)(7)(8)(9) involves path constructions, a flow of path construction for path h → g → a → d → c is illustrated outside the brown-dashed rectangle.

2.5. Large scale knowledge discovery

The total number of kDLS paths between two vertices aggregately represent their relationship. These paths are a good summarization of paths between any two vertices, as guaranteed by Lemma 2 and Lemma 3 (please find in the Appendix lemmata and their proofs). The summarization feature implied by Lemma 3 is not guaranteed if we use the densest subgraph construction approach for labeling as in [9, 10, 11].

Thus, instead of using a single shortest path, we use a set of paths as more reliable evidence to describe the relationship. It is easy to observe that other than paths within k hops, comparing the kDLS labels of two vertices may return paths up to 2k hops between the two vertices. Lemma 3 is suitably complemented by the negative result of Lemma 4 (NP-hardness).

As it is a NP-hard problem to construct even a single longest path between any two vertices, it is clearly computationally intractable to construct all paths or all simple paths between any two vertices. Given this limitation, we propose to use the number of kDLS paths (i.e., the paths found by comparing kDLS labels) as well as their lengths, to measure the relationship between two vertices (concepts) in the UMLS graph. Thus, we can prioritize concepts in many applications according to these factors. The extremely fast query speed (particular for calculating the number of kDLS paths, rather than for constructing these paths) makes it possible to perform very large scale knowledge discovery between two sets of concepts. For example, in Section 3.2 we will use kDLS to measure the relationships between 29,333 genes and 8134 diseases.

3. Results

We tested kDLS on cluster nodes equipped with 2.4GHz AMD Opteron processors with a Linux 2.6 kernel, for its general performance and application in large scale knowledge discovery. In our test, each job can maximally access no more than 32GB memory. All programs, including kDLS, BFS, and DFS are implemented in C++ using the Standard Template Library to ensure best performance.

3.1. kDLS Query Performance

To see how efficiently kDLS performs in queries, we compare it with the standard Breath-First Search (BFS), Depth-First Search (DFS) on four aspects from one vertex to another: (1) the time to find the distance, (2) the time to find one shortest path, (3) the time to estimate the number of paths, (4) the time to construct simple paths. We performed these four measurements on 10, 000 randomly generated tests.

Since no other indexing methods have shown the capacity to handle directed graphs with similar sizes and densities as the UMLS graphs, BFS and DFS are the only two methods we compare. As a typical example, we report the results obtained by controlling the kDLS broadcast range within 6-neighborhood. According to Figure 4, Figure 5, and Figure 10, the limit of 6-neighborhood covers a majority of search space on the UMLS graphs while using slightly more than 20GB memory for the full data source configuration, which is a representative usage of the UMLS graph for many applications. Correspondingly, both BFS and DFS have a 6-neighborhood limit on their search depths.

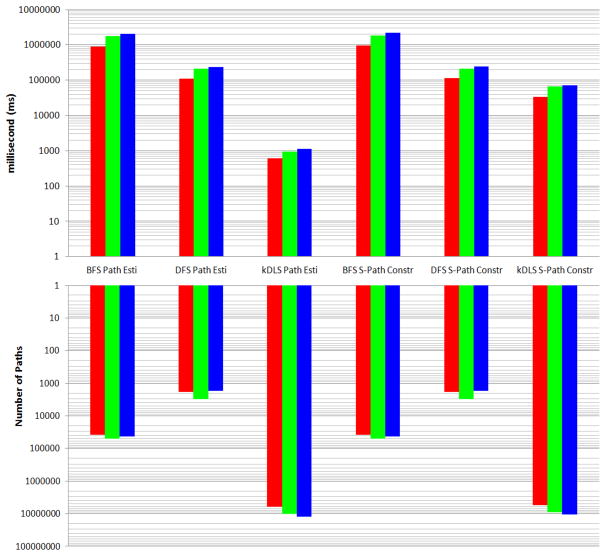
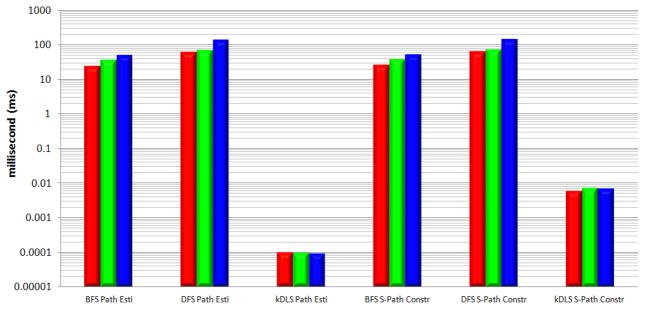
Performances of BFS, DFS and kDLS on 10,000 random tests are shown in Figures 7, 8, and 9. In all the three figures, red columns correspond to the UMLS graph of level 0 data source configuration, and green columns correspond to the UMLS graph of level 0 + SNOMEDCT data source configuration, and blue columns correspond to the UMLS graph of full data source configuration. In the case of BFS or DFS, the number of estimated paths equals the number of constructed simple paths for a given graph.

Figure 7.

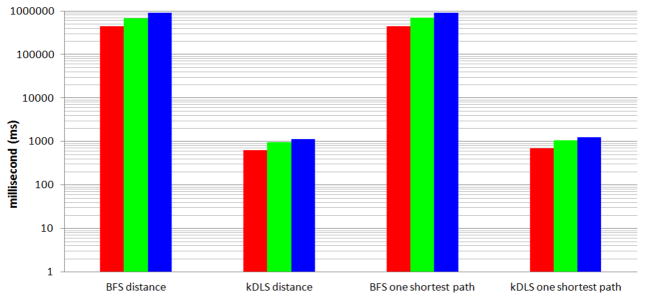
Time to calculate the distance and time to construct one shortest path (total time for 10, 000 random tests).

Figure 8.

Up: time to estimate paths and time to construct simple paths (Total time for 10, 000 random tests). Down: number of estimated paths and number of constructed simple paths (total number for 10, 000 random tests). “S-Path”, “Esti”, and “Constr” stand for “Simple Path”, “Estimation”, and “Construction”, respectively.

Figure 9.

Time per estimated path and time per constructed simple path, derived from Figure 8 by dividing the time by number of paths. “S-Path”, “Esti”, and “Constr” stand for “Simple Path”, “Estimation”, and “Construction”, respectively.

Since the standard DFS algorithm cannot guarantee finding the distance and one shortest path (recalling the visited vertex may block the finding of a shortest path by DFS), it is not available in Figure 7. For the distance and one shortest path queries, kDLS is on average at least 600 times faster than BFS in our tests. From Figures 7, 8, and 9, one can see that kDLS is far superior to BFS and DFS by several orders of magnitude with respect to different measures.

In particular, kDLS can estimate the number of paths from one vertex to another by very quickly comparing their labels without actually finding these paths, while BFS and DFS have to search the graph to obtain an estimation (thus the time saving for the path estimation over the corresponding path construction is very limited in the case of BFS or DFS). This is particularly helpful to build a relationship matrix based on the path estimation. For example, it takes kDLS a few hours to build a 10,000*10,000 relationship matrix using the full data source configuration (measuring the relationship between two vertices, as described in Section 3.2, has the same complexity as estimating the number of paths between two vertices). Utilizing BFS, however, will require months to build the matrix with a significantly smaller number of estimated paths. To measure the efficiency of the path estimation, we calculate the average time for estimating one path as shown in Figure 9, and we are quite surprised to see the speedup of kDLS over BFS or DFS is more than 200, 000 in all our tests. The largest speedup for per path estimation even reaches over 1, 000, 000 when kDLS and DFS are tested on the UMLS graph of full data source configuration.

Although kDLS significantly outperforms BFS and DFS in all the above tests, it does have a small disadvantage. It requires index construction which takes time and storage space. Under the 6-neighborhood limit as for this test, it takes kDLS less than 5 hours to build the index for the UMLS graph of level 0 data source configuration, and around 11 hours for the UMLS graph of level 0 + SNOMEDCT data source configuration, and around 17 hours for the UMLS graph of full data source configuration. The index of a UMLS graph can be saved on the hard disk drive for future use. Before answering queries on a UMLS graph by kDLS, its index needs to be loaded into memory along with the graph. The time to load the index into memory mainly depends on the I/O speed. Loading the index, however, typically takes much less time than constructing them.

We observed that the ratio between the kDLS path number (Figure 8, kDLS Path Esti) and the corresponding kDLS simple path number (Figure 8, kDLS S-Path Constr) is very small (around 1.11 to 1.13) for all three UMLS graphs. This suggests that it is a good approach to use the kDLS path number to estimate the kDLS simple path number when it is needed. This is extremely helpful for large scale knowledge discovery in which we would like to have a quick look on the overall relations, while later focus on the details of the paths that make up some specific relations.

The huge difference between the numbers of simple paths discovered by kDLS and by BFS or DFS, as shown in Figure 8, motivated us to understand what are the fractions of simple paths discovered. Although in general the problem has no practical solution as suggested by Lemma 4, it is still possible to get an exact solution when we restrict the search depth to within very few hops. To understand this, we extended the 10,000 random tests above for the UMLS graph of level 0 data source configuration, with search depth limited to 4-neighborhood for all algorithms, to study the fractions of simple paths discovered by three different methods over the total number of simple paths. It takes a recursive algorithm approximately 2 seconds on average to complete just a one-time all-simple-path search from one vertex to another, and on average the number of simple paths between two query vertices is around 970. With the same restriction, the number of simple paths from one vertex to another discovered by BFS and DFS, are on average around 0.6 and 0.07, respectively. However, the number of simple paths from one vertex to another discovered by kDLS is on average around 38. This suggests that kDLS discovered a good number of simple paths over all simple paths, while BFS and DFS discovered too few simple paths. Given Lemma 2 and Lemma 3, we conclude that kDLS is very efficient in discovering summarized knowledge from the UMLS.

Finally, we would like to understand the scalability of kDLS. To determine this, we calculated the label size for different broadcast limits. Note that we only need size counters for label lists in order to calculate the memory cost in advance, rather than actually create those label lists. Figure 10 displays the results. The total memory requirement for indexing or answering queries given a k-neighborhood restriction (for k ≥ 4) is very close to the corresponding estimated label size in Figure 10, because the overhead for recording a UMLS graph and maintaining the label lists is only a small fraction of the label size. Thus, according to Figure 4, Figure 5, and Figure 10, it takes kDLS only around 22GB memory to explore a majority of search space (6-neighborhood) on the full UMLS data sources for knowledge discovery, and around 80GB memory to explore most of the search space (10-neighborhood), and ultimately, around 209GB to explore the whole search space (unlimited-neighborhood, i.e., k is set to be the number of vertices) for large scale knowledge discovery.

3.2. Application of kDLS on Large Scale Knowledge Discovery

To see how kDLS is applicable to large scale knowledge discovery, we study its application on disease gene prioritization, which has been studied recently by many researchers [13, 14, 15, 16, 17, 18, 19]. We obtained 8, 134 disease concepts from OMIM (Online Mendelian Inheritance in Man) source family in the UMLS by searching concepts whose semantic types include “Disease or Syndrome” or “Neoplastic Process”, and we obtained all gene concepts (29, 333 in total) from HUGO (Human Genome) data source family in the UMLS. Thus, our test can be considered as a comprehensive disease-gene prioritization across the whole genome.

We measure the relationship between a gene concept and a disease concept based on the kDLS paths between them. To make our measurement between a gene concept and a disease concept not affected by known simple facts in the UMLS (indicated by the direct links that connect them), we do not count any paths with length being 1 between them. For any concept not included in the UMLS graph (recall Definition 1 in Section 1.2), we conclude there is no kDLS path connecting it to any other concepts. This is also true if we include these concepts in building the UMLS graph.

Unlike [5, 6] which rely on Subject Matter Experts (SMEs) to evaluate the knowledge discovery results from the UMLS, we can take an objective approach via kDLS. We evaluate our knowledge discovery results by fold-enrichment [16, 17, 18, 20], which measures how well the known gene concepts are ranked with respect to their associated disease concepts. The fold-enrichment in this work follows the definition in [20]. To be consistent with [20], equally ranked genes will get the same low rank (e.g. first two genes in Table 3 with the same R value both ranked 2nd). Typically, if only one disease concept is considered, the fold-enrichment is measured as the maximum α/β such that α% known causative gene concepts are ranked in the top β% gene concepts for this disease concept. We can extend the measurement between a set of gene concepts and a set of disease concepts by considering the two percentiles aggregatively. It is easy to see that if the results are not statistically significant, the fold-enrichment value will be close to 1.

Table 3.

Top thirty ranked gene concepts for Breast Carcinoma (C0678222).

rank	CUI	Gene Concept	R value	percentile	PubMed ID
2 ★	C1537910	MIRLET7A1	1.04687	0.006818%
2 ★	C1537912	MIRLET7A3	1.04687	0.006818%
3 ★	C0079419	TP53	1.04684	0.010227%
4 ★	C0919524	ATM	1.03027	0.013637%
5 ✓	C0376571	BRCA1	1.00283	0.017046%	8807330
6 ★	C1333544	FGFR4	0.966285	0.020455%
7 ✓	C0242957	ERBB2	0.961433	0.023864%	9797688
8 ✓	C0694884	MEN1	0.939749	0.027273%	15168774
9 ✓	C0162832	APC	0.93778	0.030682%	11448917
10 ✓	C0694872	CDH1	0.934644	0.034091%	11597316
11 ★	C1537713	MIR17	0.933832	0.037500%
12 ✓	C1332802	CTLA4	0.914895	0.040910%	16527605
13 ★	C1336686	TSSC4	0.91024	0.044319%
14 ✓	C1537734	MIR29B2	0.899002	0.047728%	19639033
15 ★	C1537859	MIR221	0.898388	0.051137%
16 ✓	C0812241	BRAF	0.896812	0.054546%	12068308
17 ★	C1825998	MIR20A	0.896133	0.057955%
18 ★	C1337001	WNT3	0.893316	0.061364%
19 ★	C1537773	MIR126	0.884353	0.064773%
20 ✓	C0812265	ERBB3	0.88357	0.068183%	1333787
21 ✓	C1332416	BIRC5	0.882932	0.071592%	16873289
22 ★	C0694883	STK11	0.882428	0.075001%
23 ✓	C0812267	ERBB4	0.874504	0.078410%	15735025
24 ★	C1836306	MIR124-1	0.871343	0.081819%
25 ✓	C1333206	DDR1	0.871328	0.085228%	10923103
26 ✓	C1537715	MIR19A	0.869182	0.088637%	21059650
27	C1537699	MIR1-1	0.868504	0.092047%
28 ★	C1335274	PTK6	0.867511	0.095456%
29 ✓	C1835840	MIR29B1	0.86677	0.098865%	21359530
30 ✓	C0694889	RB1	0.860263	0.102274%	11108660

Confirmed disease gene concepts (by available links connecting genes to Breast Carcinoma) are marked by ★. Gene concepts having been studied for Breast Carcinoma in literature are marked by ✓. One paper for each of these gene concepts is listed by its PubMed ID.

Formally, the closeness between a gene concept x and a disease concept y is measured as follows. Let P_(x,y) be the set of kDLS paths from x to y excluding paths with length equal to 1. Let P_(y,x) be the set of kDLS paths from y to x excluding paths with length equal to 1. The relationship between a gene concept and a disease concept is measured by

$$R(x,y)=\sum _{p\in P_{(x,y)}}\frac{1}{{\gamma }^{\mathit{length}(p)-1}}+\sum _{q\in P_{(y,x)}}\frac{1}{{\gamma }^{\mathit{length}(q)-1}},$$

in which each path’s contribution to R(x, y) is determined by its length and γ(R(x, y) is 0 unless P_(x,y) ≠ ∅ or P_(y,x) ≠ ∅). We vary γ from 1 to 50 for our tests.

In order to fully utilize the information in the UMLS for our knowledge discovery, we construct a UMLS graph with the full data source configuration, and with semantic restriction on 14 semantic types and 15 semantic relations to reduce less-informative paths from the results. For example, “Language” is marked as a restricted semantic type because a path will have little or no practical meaning in our application if it connects a gene to a disease via a “Language” concept. Then we apply kDLS with 6-neighborhood to build the index for the UMLS graph.

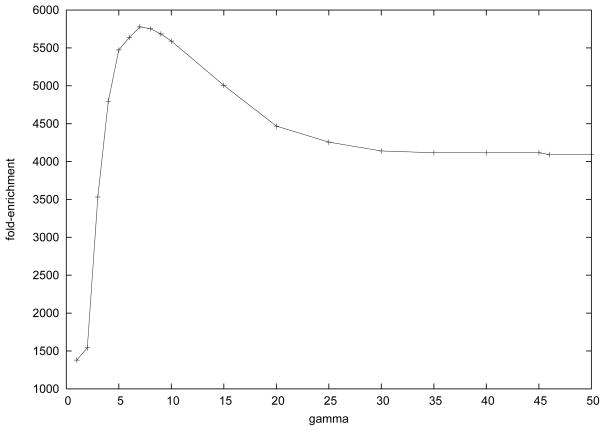
By slightly revising the standard kDLS Query (2) in Section 2.4 to calculate the R value for each disease-gene pair, we build the relationship matrix between 29, 333 gene concepts and 8, 134 disease concepts in only a few hours. We tried γ with quite a few numbers between 1 and 50, and obtained several fold-enrichment values more than 5, 000 when γ is between 5 and 15 as shown in Figure 11. These fold-enrichment values for genome-wide disease gene prioritization are much higher than the highest value (1016.8, as reported in [17]) reported in literature to our knowledge. This demonstrates the very strong statistical significance of our results. More importantly and unlike existing methods [16, 17, 18], our method not only evaluates all relationships between 29,333 gene concepts and 8134 disease concepts, but can also constructs the detailed paths as supporting evidence for any gene-disease pair as needed.

Figure 11.

Fold-enrichment over γ.

It is easy to see that if we set γ = 1, then all paths in P_(x,y) and P_(y,x) contribute equally to the R value regardless of their lengths. In this case we obtained a lowest fold-enrichment among our tests as shown in Figure 11. This clearly suggests that it is unfair to weigh long paths and short paths equally. When γ increases, more weight will be placed on the short paths as opposed to the long paths. It is interesting to observe that the fold-enrichment peaks when γ is around 5–10. The observation suggests that it is a good idea to choose γ between 5 and 10 in weighing path lengths for the tested UMLS graph. In the following study we fix γ to be 7.

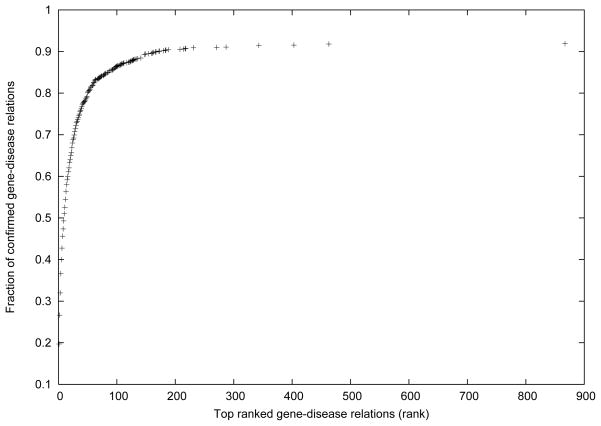
Figure 12 provides an overall look on the percentage of confirmed gene-disease pairs over the top ranked gene-disease pairs. We can observe that the percentage of confirmed gene-disease pairs increases sharply when rank increases from 1 to 100, and more than 80% of confirmed gene-disease pairs are ranked among the top 100. However, the increase rate slows down significantly after rank 200. We suspect this is because some confirmed gene-disease pairs have little or no connection with other concepts. By looking into the original data, we found that 8.13% of the confirmed gene-disease pairs have no kDLS paths with length more than 1 connecting them. Most of them are less studied genes or diseases. For example, “C0795958: GOLABI-ITO-HALL SYNDROME” and “C1418859:PQBP1 gene” is such a pair. These gene-disease pairs provide little to no value in our knowledge discovery at this moment. However, we believe many of them will contribute to knowledge discovery in the future, as the evolution of the UMLS will increasingly add new results that could bring more connections to these less studied genes or diseases.

Figure 12.

Fraction of confirmed gene-disease relations contained in the top-ranked gene-disease relations.

To provide a detailed look at the result, we selected Chronic Lymphocytic Leukemia (CLL), which is the targeted disease concept studied previously in the works of CKCs in [5, 6, 7]. Table 3 lists the 30 top-ranked gene concepts for CLL which covers all the 17 confirmed genes for CLL (i.e., 17 links connecting genes with CLL in the UMLS).

Four gene concepts in Table 3 marked by ★ are confirmed disease gene concepts by direct links in the concept network. For the remaining genes, we searched literature for their relationship with CLL, and found most of the gene concepts having been studied for CLL (marked by ✓ with the PubMed ID of one literature). Some studies are very recent. For example, the relationship between the MIR155 gene and the CLL has been studied in a very recent work [21]. For gene concepts not studied in literature for CLL, our ranking nevertheless suggests that they are very likely to be associated with CLL. This information, together with kDLS simple paths which can be constructed as needed, provides promising research directions for biologists and clinicians.

As another example, we list the top 30 genes for Breast Carcinoma, a well studied disease, to demonstrate the effectiveness of our method. The top 30 genes cover 14 out of 81 confirmed Breast Carcinoma genes. The lowest ranked confirmed Breast Carcinoma gene is CST6 which is ranked 218 (top 0.743190%) out of the 29, 333 genes.

4. Discussion

4.1. The Features of kDLS

Other than the optional handling for sink and source vertices, we determine the decentralizing order according to the largest vertex degree at the moment of decentralization. Under this decentralizing order, the kDLS demonstrates its power for handling the UMLS graph which exhibits a clear power-law property on its cumulative vertex degree distribution. Readers may be interested in how kDLS performs for other graphs.

In fact, kDLS produces optimal results on trees even without the similar power-law nature of the UMLS graph, if given an optimal decentralizing order. For example, if each time we decentralize the centroid of a tree (and recursively for its sub-trees), and set k to be unlimited (i.e., k = n where n is the number of vertices), each vertex will eventually get an O(log²n)-bit label, which is the minimum one can achieve for distance labeling schemes on a tree [22]. However, the optimal decentralizing order on a general graph is still an open question to us, and we believe it will be a promising future research question for computer scientists.

Although the kDLS is a rather simple process, it has several powerful functions as discussed in the previous sections. In addition to these functions, we can find the distance and the corresponding shortest path with respect to the selected broadcast range, as stated in Lemma 1 (See Appendix for lemmata and proofs). An additional feature of kDLS is its unique ability to provide an exact estimate of total label size. For different UMLS graphs and different choices of kDLS broadcast range k, kDLS is able to give an exact estimate of total label size (thus a very close estimation of memory cost) without actually creating those labels. This allows us to understand the memory cost in advance, and circumvents expensive trials ending with “crashing a machine”.

4.2. The Biomedical Results Obtained by kDLS

We have used kDLS to perform large scale knowledge discovery in Section 3.2 without actually constructing paths between any gene concept and any disease concept. However, by actually constructing simple paths between a selected gene-disease pair, we can provide invaluable information regarding their relationships and this information is helpful for experts to decide whether a gene concept rank is legitimate. For example, by constructing the shortest paths from the IDS gene (rank 85 for CLL) to CLL using Query (7), we found 11 shortest kDLS paths from IDS gene to CLL. The following are two sample paths.⁴

• “C1415882:IDS gene”–has_manifestation → “C0019209:HEPATOMEGALY”–clinically_associated_with → “C0015672:Fatigue”–may_be_finding_of_disease → “C0023434:Chronic Lymphocytic Leukemia”

• “C1415882:IDS gene”–has_manifestation → “C0038002:SPLENOMEGALY”–co-occurs_with → “C0024228:Lymphatic Diseases”–may_be_finding_of_disease → “C0023434:Chronic Lymphocytic Leukemia”

These two paths suggest that IDS (a gene associated with Hunters disease) is associated with inflammation and enlargement of the liver (heptomegaly), as well as enlargement of the spleen (splenomegaly) which is a lymphocytic organ. Such information implies that the link to CLL may not be trivial due to the fact that CLL is highly related to inflammation and lymphocyte activation. Thus, we wonder if the IDS gene expression is associated with CLL disease. To test this, we obtained a publicly available CLL gene expression microarray dataset (GSE2466) in the NCBI Gene Expression Omnibus (GEO). This dataset contains gene expression profiles for mononuclear cells in 11 normal subjects and 100 B-cell CLL patients. The IDS express levels indeed show a significant decrease in CLL patients as compared to the normal control (t-test p-value < 10⁻¹¹, mean fold change = 1.63). These observations suggest a new hypothesis on the association between IDS and CLL which has not been previously reported.

In addition, we can find a much larger repertoire of simple paths by using Query (9) in Section 2.4. These paths are a good candidate of Concept Knowledge Constructs between the two query objects. It is certainly true that not all paths are strong evidence of the relations between the two query objects. This is the reason why we use the R value to measure the relationship between a gene concept and a disease concept. However, there are some paths collectively providing some interesting hypotheses, though individually they do not display strong evidence of the relationship between two query objects. For example, the following are three sample paths connecting MIR1-1 gene (rank 27 for Breast Carcinoma) to Breast Carcinoma via drugs.

• “C1537699:MIR1-1 gene”–gene_associated_with_disease → “C0684249:Carcinoma of lung”–mapped_to → “C0024121:Lung Neoplasms”–may_be_treated_by → “C0010583:Cyclophosphamide”–mapped_from → “C0055982:CMF regimen”–regimen_has_accepted_use_for_disease → “C0678222:Breast Carcinoma”

• “C1537699:MIR1-1 gene”–gene_associated_with_disease → “C0878544:Cardiomyopathies”–clinically_associated_with → “C0005779:Blood Coagulation Disorders”–contraindicated_drug → “C0025677:Methotrexate”–mapped_from → “C0055982:CMF regimen”–regimen_has_accepted_use_for_disease → “C0678222:Breast Carcinoma”

• “C1537699:MIR1-1 gene”–gene_associated_with_disease → “C2239176:Liver carcinoma”–clinically_associated_with → “C0027947:Neutropenia”–contraindicated_drug → “C0016360:Fluorouracil”–mapped_from → “C0055982:CMF regimen”–regimen_has_accepted_use_for_disease → “C0678222:Breast Carcinoma”

It has been shown that besides MIR1-1’s well-known relationship with cardiovascular diseases, it is associated with several types of cancers including lung, liver and renal cancers. Such information suggests that it may also be relevant to other cancers such as breast cancer as suggested by our ranking results. For instance, as shown in the three paths above, MIR1-1 gene is connected to breast carcinoma with known relationships to lung and liver cancers. Interestingly, the paths are then led to breast carcinoma via three drugs (Cyclophosphamide, Methotrexate, and Fluorouracil) which are the three components constituting the NCI recommended CMF regimen for breast cancer. These observations along with the high ranking of MIR1-1 gene in the breast carcinoma gene list suggest that the relationship between MIR1-1 and breast cancer could be a new hypothesis to be tested further.

Similarly, we also found paths connecting MIRLET7C gene (rank 26 for CLL) to CLL via drugs by using Query (9).

5. Related Works

Prior to our work, there have been a number of works studying the similarity between two concepts in the UMLS by distance between the two concepts [23, 24, 25, 26, 27]. Using distance (i.e., the length of a shortest path) to measure the similarities between concepts is a good idea if a distance measurement is restricted to a data source, or a few similar data sources. The measurement becomes less controllable if a large number of heterogenous data sources are fused together. Such combinations may build a short path between two concepts that are not considered similar to some applications. Thus, most available works [23, 25, 26, 27] focused on studying similarity between concepts in one or several data sources. Recently, McInnes et al [24] built a general similarity measurement framework that can be extended to include new measures. In contrast to these works, our work studies not only the similarity between two concepts, but the general relationship between two concepts as described by the kDLS paths that connect them through possibly many heterogenous data sources. For example, it is inappropriate to say a disease is very similar to a gene, but it is appropriate to say a disease is very related to a gene. Since our relationship measurement is based on the extracted paths as a whole, rather than a shortest path, our method is robust against occasional noisy paths. This is confirmed by the very high fold-enrichment values. Nevertheless, our work can also be configured to extract relationships in specific data sources (as illustrated in Figure 2) and the extremely fast query time will make it possible to study the relationships between two very large sets of concepts, an ability those available works [23, 24, 25, 26, 27] have not demonstrated. However, we shall point out that at this moment our work can only accept data source configurations before building indices. If the data source or the semantic restriction configuration changes, then we need to rebuild the index. Indexing based on dynamic source types, semantic types, or semantic relations is essentially label-constraint indexing in terms of graph databases, and it is very difficult to handle even for answering reachability queries on moderate-sized graphs with a small number of labels [28]. It could be a long-term future research to make the label-constraint indexing applicable to very large UMLS graphs.

kDLS utilizes the power-law nature of the UMLS graph and decentralizes vertices. The process of decentralizing vertices is analogous to using these vertices as landmarks for index construction. Although using landmarks is not a novel idea, our method is the first to efficiently index the whole UMLS under this general strategy, and provides several flexible options for large scale knowledge discovery. In the following we briefly review related techniques.

In the wireless network research community, using landmarks is one of the basic routing strategies. The well-known Beacon Vector Routing (BVR) [29] is designed under this philosophy, where each node remembers the distances to a small number of beacons for making routing decisions. The BVR, however, cannot guarantee finding shortest routes.

A similar idea of using landmarks is available in the graph database community known as 2-hop [9]. Unlike BVR, 2-hop can guarantee finding the length of a shortest path between any two nodes. However, 2-hop has severe limitations with respect to scalability issues. This is mainly due to its time-costly densest subgraph construction and set cover procedure for labeling. Normally, 2-hop can only handle sparse graphs with less than 10,000 vertices even for answering reachability queries [8]. Several successive works [10, 11, 12] on 2-hop have improved on the scalability issues, but they have not demonstrated the ability to handle graphs with similar sizes and densities as the UMLS graphs for knowledge discovery.

In the graph database community, researchers have been designing algorithms for efficiently indexing graph databases for answering reachability (e.g., [30, 31, 32, 33, 34, 35, 36, 8, 28, 37]), distance (e.g., [9, 10, 11, 12]) and shortest path queries (e.g., [38, 39]). Indexing schemes use additional labels built for a graph database to quickly answer queries. Without indexing, these queries have to be answered by ad-hoc searching, such as Breath-First Search (BFS), Depth-First Search (DFS), and many other heuristics. Generally speaking, a good indexing scheme will be faster than the corresponding ad-hoc searching algorithms in at least one to two orders of magnitude in answering queries.

As the reachability query is a special case of the distance query and the distance query is a special case of the path query, it is not surprising that less work has been done for answering distance and path queries. In addition, since undirected graphs are special cases of directed graphs, it is generally harder to handle distance and path queries on directed graphs.

Given the above background, we can understand why there are only limited works [9, 10, 11, 12, 38, 39] that can index graphs for efficiently answering distance or shortest path queries. Although these works handle small graphs fairly well, they have quite limited power in handling large and dense graphs, especially if the graph is directed. The density of a graph is often measured by the ratio of the edge number to the vertex number.

To our knowledge, the XMK20M [12] is the largest directed graph with both vertex number and edge number reported in works of efficiently indexing graph databases for answering distance or shortest path queries. The XMK20M [12] is a directed graph containing 336, 243 vertices and 397, 713 edges, with a density to be only 397, 713/336, 243 ≈1.18. However, the UMLS graphs in our study contains much more vertices and edges (recall Table 1), with densities larger than 7. These numbers explain why currently there is no work available for effectively indexing the whole UMLS and the queries have to be answered by ad-hoc searching algorithms, such as BFS and DFS, which are too slow for large scale knowledge discovery. Therefore, authors of [5] pose major limits to complete the Conceptual Knowledge Construct (CKC) mining task, such as limiting the concepts to be at most 5 in CKC (i.e., a path of length 4 in the corresponding graph), and searching a very small number of data sources. These limits greatly reduce the search space in order to make the CKC mining possible even though the results are far from complete. It can be conceived that a method that can efficiently index the whole UMLS will significantly help CKC mining tasks.

6. Conclusion

In this paper, we propose kDLS, a decentralizing labeling scheme to index the UMLS graph for answering graph-based queries. kDLS can very efficiently find important information, such as reachability, distance, and a summary of paths, between two concepts on the UMLS using very limited label costs, thus making it possible to process large scale knowledge discovery. kDLS is easy to implement and is very flexible to configure according to different applications and computer hardware settings, and it is highly effective for large scale knowledge discovery on the UMLS, as demonstrated by our application on disease gene prioritization. In addition, our discussion on the optimality of kDLS shows that it has the potential to be further refined by computer scientists in the future. Thus, we expect kDLS or its derivations will be the key knowledge discovery engines for the UMLS for future medical informatics applications.

Table 2.

Top thirty ranked gene concepts for CLL (C0023434).

rank	CUI	Gene Concept	R value	percentile	PubMed ID
1 ★	C1537734	MIR29B2	2.15541	0.003409%
2 ★	C1835840	MIR29B1	2.13243	0.006818%
4 ✓	C1537910	MIRLET7A1	1.83769	0.013637%	19246618
4 ✓	C1537912	MIRLET7A3	1.83769	0.013637%	17989717
5 ★	C0812286	NFKB2	1.7738	0.017046%
6 ★	C1537797	MIR143	1.72205	0.020455%
7 ★	C1537764	MIR106B	1.69907	0.023864%
8 ✓	C1537713	MIR17	1.69729	0.027273%	15284443
9 ✓	C1334913	NUP98	1.68912	0.030682%	10929031
10 ✓	C0694889	RB1	1.68422	0.034091%	8378351
11 ✓	C1537811	MIR155	1.68362	0.0375%	21296997
12 ★	C1537709	MIR15A	1.63211	0.04091%
13 ★	C1537799	MIR145	1.6283	0.044319%
14 ★	C1537712	MIR16-2	1.61734	0.047728%
15 ★	C1333221	DLEU1	1.61367	0.051137%
16 ✓	C0919524	ATM	1.60915	0.054546%	9892178
18 ★	C1537813	MIR181B1	1.60896	0.061364%
18 ★	C1537814	MIR181B2	1.60896	0.061364%
19 ★	C1333223	DLEU2	1.60747	0.064773%
20 ★	C0812238	BCL3	1.59458	0.068183%
21 ★	C1366526	BTG2	1.58792	0.071592%
22 ✓	C1367449	BCL10	1.58539	0.075001%	10583229
23 ✓	C1334894	NPM1	1.58168	0.07841%	18487510
24 ★	C1413172	CCND1	1.56103	0.081819%
25 ✓	C1825998	MIR20A	1.53931	0.085228%	18348159
26	C1537914	MIRLET7C	1.51688	0.088637%
27 ✓	C1412097	ABL1	1.51654	0.092047%	16885384
28 ★	C1537710	MIR15B	1.51344	0.095456%
29 ✓	C1537711	MIR16-1	1.49373	0.098865%	18448218
30 ★	C1366587	MCL1	1.49361	0.102274%

Confirmed disease gene concepts (by available links connecting genes to CLL) are marked by ★. Gene concepts having been studied for CLL in literature are marked by ✓. One paper for each of these gene concepts is listed by its PubMed®ID.

8. Appendix: Lemmata and Proofs

Lemma 1 (Correctness)

kDLS with k-neighborhood broadcast guarantees to find a shortest path between any two vertices within k hops on a UMLS graph.

Proof

Without loss of generally, let x and y be two vertices connected by a shortest path p(x, y), length(p(x, y)) ≤ k. Let z be the first vertex on p(x, y) selected for decentralization. Let p(x, z) and p(z, y) are two sub-paths of p(x, y) where length(p(x, z))+length(p(z, y)) = length(p(x, y)). Let G_z be the graph immediately before the decentralization of z. Since p(x, y) is intact before the decentralization of z, we conclude d_Gz (x, z) = length(p(x, z)) ≤ k and d_Gz (z, y) = length(p(z, y)) ≤ k. z’s information will be broadcasted and recorded in the labels of vertices along a shortest path no longer than p(x, z) from z to x, and along a shortest path no longer than p(z, y) from z to y. Thus, by comparing the labels of x and y, we can construct a shortest path passing z and no longer than p(x, y).

Lemma 2 (Uniqueness)

Let a simple path be a path without repeated vertices. Let P′(x, y) be the collection of all path from vertex x to vertex y obtained by comparing the kDLS labels. By removing non-simple paths in P′(x, y), we can obtain a collection of unique simple paths P″(x, y).

Proof

To prove this lemma, we only need to show that two simple paths in P′(x, y) are unique. Without loss of generally, assume p(x, u, y) and p(x, w, y) are two simple paths, obtained by common vertices u and w, respectively, in comparing the labels of x and y. Without loss of generally again, assume u is decentralized before w. Assume G_w is the graph immediately before decentralizing w. Then their is no path connecting x and y passing u in G_w. Hence p(x, w, y) cannot contain u, and we conclude p(x, u, y) and p(x, w, y) are not equal.

Lemma 3 (Summarization)

Let P (x, y) be the complete collection of paths that connect x to y within k hops in a UMLS graph and are disconnected before decentralizing x and y. Let P′(x, y) be the collection of all path from vertex x to vertex y obtained by comparing the kDLS labels. For any path p(x, y) ∈ P (x, y), there exists a path q ∈ P′(x, y) sharing at least one vertex (other than x and y) with p.

Proof

Assume u is the first vertex on p(x, y) selected for decentralization. By literally following the Proof of Lemma 1, we can find a path q connecting x to y via u by comparing the labels of x and y, and the length of q is no longer than p(x, y).

Lemma 4 (NP-hardness)

There is no polynomial time algorithm for constructing a longest simple path between any two vertices in a directed graph unless P = NP.

Lemma 4 is a common knowledge in the Graph Theory community as it can be proven easily by using a reduction from the Hamiltonian path problem.