Abstract
Morphogens are secreted molecules that specify cell-fate organization in developing tissues. Patterns of gene expression or signalling immediately downstream of many morphogens such as the bone morphogenetic protein (BMP) decapentaplegic (Dpp) are highly reproducible and robust to perturbations. This contrasts starkly with our expectation of a noisy interpretation that would arise out of the experimentally determined low concentration (approximately picomolar) range of Dpp activity, tight receptor binding and very slow kinetic rates. To investigate mechanisms by which the intrinsic noise can be attenuated in Dpp signalling, we focus on a class of secreted proteins that bind to Dpp in the extracellular environment and play an active role in regulating Dpp/receptor interactions. We developed a stochastic model of Dpp signalling in Drosophila melanogaster and used the model to quantify the extent that stochastic fluctuations would lead to errors in spatial patterning and extended the model to investigate how a surface-associated BMP-binding protein (SBP) such as Crossveinless-2 (Cv-2) may buffer out signalling noise. In the presence of SBPs, fluctuations in the level of ligand-bound receptor can be reduced by more than twofold depending on parameter values for the intermediate transition states. Regulation of receptor–ligand interactions by SBPs may also increase the frequency of stochastic fluctuations providing a separation of timescales between high-frequency receptor equilibration and slower morphogen patterning. High-frequency noise generated by SBP regulation is easily attenuated by the intracellular network creating a system that imitates the performance of a simple low-pass filter common in audio and communication applications. Together, these data indicate that one of the benefits of receptor–ligand regulation by secreted non-receptors may be greater reliability of morphogen patterning mechanisms.
Keywords: bone morphogenetic protein, pattern formation, noise, stochastic modelling
1. Introduction
Many developmental patterning processes rely on the interpretation of the local concentration of a morphogen. Morphogens form a spatially non-uniform distribution by long-range transport away from their spatially localized source and kinetic processes that regulate their extracellular availability [1–3]. Secreted morphogens such as the bone morphogenetic proteins (BMPs) transmit extracellular information to the underlying cells by binding to their cognate receptors and initiating a downstream response [4]. It is becoming increasingly clear that interactions between morphogens and receptors are regulated by secreted proteins that are neither obligate co-receptors or inhibitors, but instead provide a context-dependent auxiliary function that can promote or inhibit signalling [5]. In a recent review of extracellular BMP regulation, more than 20 identified secreted regulators have cell autonomous effects on BMP signalling, and many of the regulators have been linked directly with limiting or promoting BMP binding to receptors [6]. Intriguingly, the specific effect on BMP signalling is enigmatic or highly context-dependent, and the secreted regulators often display both promoter and inhibitor properties during different stages of development. Further complicating matters, the molecules are not essential in many developmental contexts leading to a weak phenotype, or high variability in the penetrance of a phenotype [7].
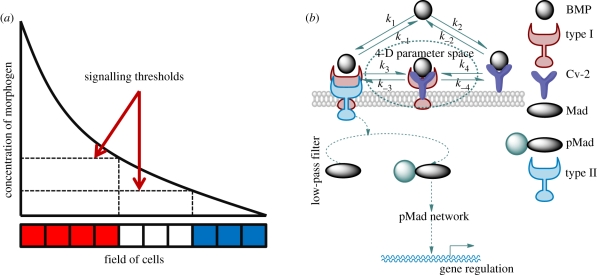
BMP-mediated patterning generally follows a common set of regulatory steps in many organisms: (i) secretion of morphogens from a localized source, (ii) transport of morphogens by diffusion, and (iii) molecular interactions with receptors or other regulatory proteins in the extracellular space [3,8–13] (figure 1a). In developing Drosophila pupal wings, zebrafish embryos and Xenopus embryos, one of the proposed roles for the BMP-binding protein Crossveinless-2 (Cv-2) is that it regulates the accessibility of ligand to type I receptors (a schematic of the proposed mechanism in Drosophila is shown in figure 1b). The mechanism in figure 1b is a characterization of the proposed action for numerous other regulators, including heparan sulphate proteoglycans (HSPGs) such as Dally [14] and Dally-like [15,16], collagen [17] and others such as BAMBI (bone morphogenetic protein and activin membrane-bound inhibitor) [18]. We refer to the molecules that regulate receptor–ligand interaction akin to the schematic in figure 1b as surface-associated BMP-binding proteins (SBPs).
Figure 1.
(a) Classical ‘French Flag’ description of a morphogen-patterning system. (b) Surface-binding protein (SBP) model schematic: BMP signalling is mediated by BMP: type I receptor (BR) forms either by direct interaction between BMP and type I or via an intermediated state with BMP: type I: Cv-2. Upon BR formation, the complex recruits type II receptor, and later initiates the phosphorylation of intracellular Mad protein. Signalling leads to pMad accumulation within the nucleus and gene expressions of BMP targets.
While we focus on the Cv-2 mechanism in figure 1b, there is debate as to whether the receptor has access to the binding sites of the BMP ligand when the ligand is bound to Cv-2 and this may depend on specific context [5,19,20]. The structure of the interface for Cv-2-BMP binding suggests that Cv-2 blocks receptor–ligand binding [20]; however, the dynamics and the stability of BMP-Cv-2 complex [21] support a dynamic-binding interaction that does not preclude a Cv-2 exchange mechanism. Alternative mechanisms include Cv-2 acting as a sink for the BMP inhibitor chordin or acting as a catalyst to enhance kinetic exchange between inhibitors + ligands [5,6,19,21].
According to figure 1b, there are two paths for BMP binding to receptor: direct binding and release from the receptor, and indirect, Cv-2-mediated recruitment and exchange of ligand to type I BMP receptor. Signalling requires further recruitment of type II receptors into a heterotetrameric complex that ultimately contains two type I and two type II receptors. Here, we are primarily concerned with the initial binding event between ligand, receptor and Cv-2, and assume that type II receptors are abundant and binding occurs rapidly once the BR complex is formed [22,23]. While the network in figure 1b is general and may apply to multiple systems, we focus on the regulation of Dpp–receptor binding by Cv-2 in Drosophila, where kinetic data are available and suggest how the properties of this system can be extended to other contexts of developmental signalling.
BMP signalling is likely regulated by a small number of molecules. Insights into the biophysics of signal complex formation can be gained by comparison of the measured kinetic rates for BMP ligand from Biacore experiments and biochemical affinity measurements [6,21,24]. BMP–receptor binding is generally tight with a low dissociation constant (KD = koff/kon) between ≃1 and 50 nM depending on the specific combinations of BMP ligands + receptors [24–26]. Low dissociation constants for BMP–receptor binding in species such as Drosophila, Xenopus, etc. attest that the physiological range of BMPs falls within the range measured in vitro by cell-culture signalling assays [27]. Dpp signalling in the Drosophila S2 cell-line begins to saturate at low extracellular Dpp concentrations that range between 0.1 nM and 1 nM [27], corroborating the measured dissociation constants obtained by Biacore. Levels of ligand much greater than the dissociation constant would saturate the transmembrane receptors leading to ubiquitous high-level signalling [28]. Further evidence in support of low concentrations of BMPs required to regulate cell signalling comes from the demonstration that activin, a related TGF-β superfamily ligand, mediates gene expression [29] in a range of receptor occupancy between 2 to 6 per cent of available binding sites. An upper limit has also been suggested by Lander et al. by mathematical analysis that the maximum level for receptor occupancy is 80 per cent as levels beyond that saturate receptors [3].
The available evidence supports a low concentration range for Dpp activity, which translates into a low total number of individual ligand molecules in many contexts. A simple calculation for 100 pM Dpp in the vicinity of a rectangular cell surface with access to a limited Dpp pool such as the apical surface of columnar epithelial cells with height of 0.5 µm would have a volume that lies between 8 × 10−15 l and 1000 × 10−15 l. The extracellular volume would contain between 1 and 100 Dpp molecules per cell. For a spherical cell, similar calculations suggest that there are between 4 and 51 Dpp molecules per cell. These numbers represent the amount of free or unbound Dpp, and greater numbers will be bound to receptors and other molecules.
Not only is binding tight, but the binding kinetics for Dpp and other BMPs are surprisingly slow, and typical measurements place the BMP binding and reverse rates about 10 times slower than ligand–receptor interactions in other signalling systems [23,24]. The rates of BMP : type I binding (kon = 0.6 × 10−3 nM−1 s−1, koff = 0.4 × 10−3 s−1 [25]) for the forward and reverse steps, respectively, lead to a relatively slow response to Dpp signal and long recovery times for changes in extracellular BMP concentration [30]. In some developmental instances, the slow kinetics suggest that once a ligand binds to its receptor it would remain attached for a long period of time, which—in some cases—exceeds the duration of the development stage.
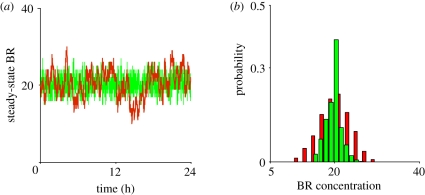
Tight binding, slow kinetics and low concentrations of ligand coalesce into a perfect storm of significant, long-duration stochastic fluctuations in models of BMP-mediated cell signalling and patterning (figure 2a,b). To analyse the signalling system, we developed a series of stochastic and deterministic models for the local control of Cv-2, Dpp and receptor kinetics that vary in the levels of Cv-2, ligand and parameters. We developed a methodology to carry out stochastic simulations for 625 choices of parameter values regulating the exchange of Dpp from Cv-2 to receptors, and for each individual parameter set, we carried out parameter continuation in both the level of Cv-2 and free Dpp ligand. Results of the study suggest that if ligand–receptor interactions are regulated by molecules such as Cv-2, (i) the amplitude of the stochastic fluctuations for the level of BR may be reduced by more than twofold, and (ii) the frequency of fluctuations of BR dramatically increases. When the frequency of fluctuations increases, the slower, intracellular dynamics of pMad effectively averages out the signal over time. We propose that one of the significant, and often overlooked, contributions provided by SBP-mediated regulation of receptor–ligand binding is the suppression of stochastic noise during tissue patterning and development.
Figure 2.
Fluctuation in the level of bound receptor: (a) fluctuations about the steady-state BMP : receptor (BR) owing to stochasticity both in the presence (green line, Cv-2 = 85) and in the absence (red line, Cv-2 = 0) of Cv-2 are shown. Owing to slow-binding kinetics between BMP and its receptor, BR fluctuations exhibit long durations (red) that are shortened when binding between BMP and Cv-2 (green) is included. (b) Probability density functions for BR in the presence (green bars, Cv-2 = 85) and absence of Cv-2 (red bars, Cv-2 = 0).
2. Results
2.1. Stochastic deviations for bone morphogenetic protein–receptor complexes
To quantify the degree and duration of departures from the mean level of bound receptors in the system, we developed a single-cell stochastic model that includes extracellular Dpp, receptors and Cv-2 with rate parameters and connectivity based on the network shown in figure 1b and provided in equations 2.1–2.10.
| 2.1 |
| 2.2 |
| 2.3 |
| 2.4 |
| 2.5 |
| 2.6 |
| 2.7 |
| 2.8 |
| 2.9 |
| 2.10 |
All reactions follow mass action kinetics and the molecular species in equations (2.1)–(2.10) correspond with the following variable names: A = Dpp, B = type I (Drosophila Thickvein (Tkv)), C = Dpp : type I, D = Cv-2, E = Dpp : Cv-2, M = Dpp : Cv-2 : type I. In equations (2.3)–(2.8), the forward reaction rate constants denoted as (ki, i = 1,2,3,4) are second-order (nM−1 s−1) and reverse reaction rate constants (k−i, i = 1,2,3,4) are first-order (s−1). Extracellular influx and decay of BMPs are given in equations (2.1)–(2.2), which are 0th-order (nM s−1) in the forward direction and first-order k−0 (s−1) for decay of Dpp. To focus specifically on noise compensation by regulation of receptors, the extracellular level of Dpp is treated as a parameter A = Ø/k0.
In the absence of Cv-2, significant stochastic fluctuations cause large amplitude and low-frequency departures away from the deterministic mean level of bound receptors for an example choice of the intermediate kinetic parameter (figures 2a and 3a). The remarkably slow frequency of the fluctuations stem from the very slow measured kinetic binding rates between BMP-2 (Dpp-homologue) and BMPR-IA (Tkv homologue), and increases in the kinetic rates lead to less significant departures from the deterministic mean, as expected. High variability about the mean in the absence of Cv-2 is also clearly demonstrated by the probability distribution for the level of BR as shown in figure 2b. Fluctuations in BR routinely depart by more than 20 per cent from the mean for periods of time greater than 30 min as shown by the ‘virtual barcode’ mapping of departures of the stochastic solution from the mean (figure 3a). The duration, amplitude and frequency of departures would be sufficient to alter an individual cell's interpretation of extracellular signals, especially in networks with feedback that are sensitive to the dosage of Dpp such as the Drosophila wing imaginal disc, embryo and germarium. Additionally, the total developmental time for Dpp patterning of the blastoderm embryo is between 30 and 60 min depending on temperature, equivalent to the typical timescale for a departure from the mean in the model (figure 3a). When levels of bound receptors increase (e.g. BMP : type I ≈ 300 molecules), fluctuation amplitude reduces considerably for a given level of extracellular Dpp and the noise depends predominantly on the mean levels of BMP : type I and the first-order dissociation rate in the absence of Cv-2.
Figure 3.
Rationale for stochastic modelling: (a,b) a ‘virtual barcode’ (from 0 to 6 h) and dynamic plot of signalling in the (a) absence and (b) presence of Cv-2. Any deviation that is greater than 20 per cent from the steady-state BR value is marked with a coloured line in the barcode representation. (c) Probability of different deviation (greater than 10%) lengths (DLs) in the absence (Cv-2 = 0) and in the presence of Cv-2 (Cv-2 = 85) for a simulation time of one week. Higher probability for the lower DL (green line) means that Cv-2 may reduce the duration of departures compared with the system without Cv-2. Inset graphs represent the different DL as obtained from 24 h steady-state simulations both in the presence and in the absence of Cv-2. (d–f) Coefficient of variation (Λ = σ/μ) for BR (1 to 30 molecules) formation is shown both in the presence of Cv-2 = 85 molecules (green) and in the absence of Cv-2 (red). For the kinetic rates k±i i = 3,4 used in figure (d–f), refer to table S2 of the electronic supplementary material. (g–i) Λ as a function of BR (BR = 20–22 for ‘g’, ‘h’ and BR = 12–14 for ‘f’) exhibits three quantitative shapes: noise promotion, noise reduction and mixed response. For example, (i), we initially see a gradual increase in noise with small increase in Cv-2 concentration, but it decreases for increasing Cv-2. (a) Red line, Cv-2 = 0; (b) green line, Cv-2 = 85; (c) green line, Cv-2 = 85; red line, Cv-2 = 0; (d,e) red circles with dashed line, Cv-2 = 0; green circles with dashed line, Cv-2 = 85; (g,h) blue circles with dashed line, BR = 20; red circles with dashed line, BR = 22. (i) blue circles with dashed line, BR 12; red circles with dashed line, BR 14.
The measured kinetic rate constants for BMP + Cv-2 binding in the forward and reverse directions are an order of magnitude greater than for BMP + receptor binding (For BMP : Cv-2, kon = 2.3 × 10−3 nM−1 s−1, koff = 3.2 × 10−3 s−1 [21] and For BMP : type I, kon = 0.6 × 10−3 nM−1 s−1, koff = 0.4 × 10−3 s−1 [25]). The dissociation constant for BMP + Cv-2 (KDCv-2 = 1.4 nM) is nearly identical to the dissociation constant for BMP-receptor binding (KDtype I = 0.7 nM); so they are equal competitors at equilibrium [21,25]. Dynamically, Cv-2 can rapidly bind available BMP ligands, but Cv-2 is also much more likely to release ligand than the receptors. Figure 2a,b shows how Cv-2 may impact cell signalling noise relative to a system without Cv-2 for a specific choice of parameters and level of Cv-2. Furthermore, figure 3b,c shows how Cv-2 also increases the frequency of the fluctuations suggesting that, at least for some choices of parameters, Cv-2 can reduce the duration of departures and tend to lower signalling noise.
2.2. Cv-2 noise suppression is parameter-dependent
Quantification of the amplitude and duration of departures of the stochastic simulation provide two measures of Cv-2 action in the local model of Cv-2/receptor regulation. The aforementioned simulation results suggest that Cv-2 has the capability to reduce noise in the level of bound receptors, however, this may depend strongly on the specific choice of parameter values used for the intermediate exchange steps, the level of bound receptor (since Cv-2 functions in morphogen-mediated systems Cv-2 would need to function similarly for many different concentration regimes), and the level of Cv-2.
While the binding and dissociation rates for BMP + Cv-2 and BMP + receptors are largely known [22], the kinetics between Cv-2, Dpp and receptors on the surface are largely unknown. To analyse the parameter dependency, parameter values for the intermediate exchange steps between bound Cv-2 and receptor were selected from a uniform grid of parameter values. The rate at which a non-signalling tripartite complex BMP : type I : Cv-2 forms and decouples are considered to be uniformly spaced (logarithmically) between [10−1 to 101] nM−1 s−1 for second-order processes and between [10−3 to 100] s−1 for first-order processes. This produces a grid with 625 sets of parameter values. For each set of parameters, the levels of both Cv-2 and free BMP are varied, and the dynamic evolution of BR is calculated. The combinatorics of the problem rapidly increase when carrying out a parameter screen with continuation and dynamic stochastic simulations. To increase the computational efficiency of the algorithm, we used a relatively new method to solve the chemical master equation (CME) with a truncated state-space [31,32] (see the electronic supplementary material for a detailed description).
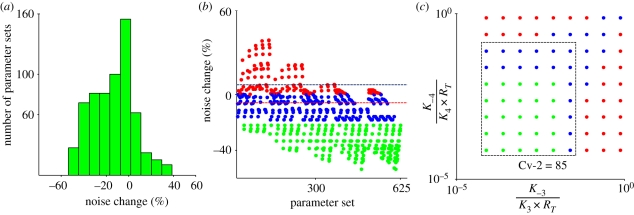
To quantify the degree of noise in the system, the coefficient of variation (Λ = σ/μ) is used that relates the standard deviation (σ) to the mean (μ) level of bound receptors. The parameter screen yields three primary qualitative classifications of BR fluctuation amplitude in the presence of Cv-2: (i) reduced amplitude, (ii) increased amplitude, and (iii) mixed amplitude behaviour (figure 3d–i). We limited the screen to a maximum of 200 Cv-2 molecules for computational tractability. In type i, Cv-2 leads to a reduction in BR noise amplitude for all concentrations and levels of Cv-2 tested in the continuation (figure 3d,g). The value of the coefficient of variation (Λ) decreases for both increases in the level of bound receptor and the level of Cv-2. Furthermore, figure 3g shows an optimal level of Cv-2 for a specific set of parameters. In type ii, increasing the level of Cv-2 in the system increases the value of coefficient of variation (ΛCv2 ≠0 > ΛCv2 = 0) for the range of Cv-2 values considered in the screen (figure 3e,h). There is a slight decrease in Λ for very large increases in the level of Cv-2 (figure 3h), however, ΛCv2 ≠0 is still greater than ΛCv2=0 over the interval Cv-2 ε [0, 200]. Finally, in type iii, Cv-2 can both increase and decrease the level of stochastic noise in the system, depending on the specific level of Cv-2 (figure 3f,i). The qualitative classifications of Cv-2 action and the corresponding rationale are summarized in table 1.
Table 1.
Qualitative classification of Cv-2 on interval Cv-2 ε [0,200].
| condition on coefficient of variation (Λ) | qualitative classification |
|---|---|
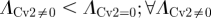 & & 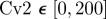
|
noise reduction |
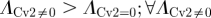 & & 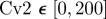
|
noise increase |
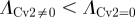 and and 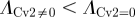 ; & ; & 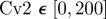
|
mixed |
In the deterministic system analysed in Serpe et al. [5], for some sets of parameters, increasing the level of Cv-2 caused a shift from being supportive of BMP signalling to being inhibitory. We found a similar response in the level of noise behaviour in response to increasing levels of Cv-2. High levels of Cv-2 provide a more effective sink, which would increase the effective kinetic rates for removal of ligand from the receptor and a subsequent decrease in BR noise.
To clarify Cv-2 action further, each parameter set output for a given amount of BR production and Cv-2 value (85 molecules) was classified into categories representing amplitude increase (ΛCv2=85 − ΛCv2=0 > 0, red), moderate amplitude decrease (ΛCv2=85 − ΛCv2=0< 0 && |Percent change| < 20, blue) and significant amplitude decrease (ΛCv2=85 − ΛCv2=0 < 0 &&|Percent change| > 20, green) (figure 4b). Attenuation or amplification of noise in the presence of Cv-2 is quantified by the percent change in the coefficient of variation (Λ = σ/μ) of BR concentration with Cv-2 = 85 relative to the equivalent system Cv-2 = 0. The distribution of behaviour for all parameters is shown as a histogram in figure 4a. To investigate further the parameter dependence of the fluctuations, we tested numerous dimensionless parameter groups and found a strong relationship between the dimensionless forms of the dissociation constants KD = koff/(konRT) and the fluctuation amplitude Λ. Specifically, for high values of K3 and K4, Cv-2 tends to increase the amplitude of the fluctuations, whereas, for smaller KD values, Cv-2 tends to decrease the amplitude of the fluctuations (figure 4c). The low dimensionless dissociation constants both support formation of the intermediate BMP : SBP : receptor complex. This establishes a buffer pool of non-signalling ligand-bound receptors that can absorb or replenish the pool of active signalling receptors rapidly without requiring recruitment of ligand from the extracellular space. High values for dissociation constants limit the role that an SBP has on the level of BMP : receptor complexes and the level of BMP : receptor would be dominated by slow kinetic rates that lead to increased stochastic noise.
Figure 4.
Parameter dependency of Cv-2 noise behaviour: noise change (positive and negative change corresponds to ‘noise increase’ and ‘noise decrease’, respectively) is calculated by considering the absence of Cv-2 as the baseline (% noise change = (ΛCv2=85 − ΛCv2=0)/ΛCv2=0 × 100). Noise change in the presence of Cv-2 is evaluated for Cv-2 = 85 with a target BR level of 20 molecules on the surface. (a) Histogram demonstrates that the majority of solutions result in a reduction in amplitude. (b) Parsing the result into classes based on parameter set index shows that Cv-2 regulation of fluctuation amplitude is highly parameter-dependent and shows increases (red), moderate to no change (blue) and decreases (green) in fluctuation amplitude. (c) Parameter-dependent changes in fluctuation amplitude are captured by the dimensionless form of the dissociation constants, defined as KD = koff/kon × RT.
2.3. Intracellular signalling noise
Modification of the amplitude of departures for BMP-receptor complexes is not the only potential site of noise amplification or suppression, and the analysis is extended to consider noise propagation by a simplified intracellular signalling network. Bound type I receptors recruit type II receptors to form high-order complexes that initiate intracellular phosphorylation of the transcription factor Mad. The intracellular processes operate on different concentration and time-scale regimes than the extracellular molecules, which introduces the possibility that disparate timescales could reduce or amplify signalling noise depending on the specific choice of parameters. In the intracellular region, pMad shuttles between cytoplasm and nucleus, and accumulates within the nucleus [33] as a result of receptor activation. If we assume that intracellular pMad is dominated by two processes: phosphorylation by receptors and dephosphorylation by decay or the action of a phosphatase, the balance equation for intracellular pMad is a linear, first-order differential equation that has the solution PD = PD0 exp(−kdt) where PD is the instantaneous deviation of pMad from the steady-state value (see the electronic supplementary material). The output of the stochastic model is an integer number of bound receptors and a duration of the level of bound receptors between two states of the system. PD0 is the deviation of pMad from steady-state determined at the initial time-point for each interval of BR data. Two outcomes are possible for the intracellular level of pMad: (i) if the intracellular timescale is on the order of, or faster than, the extracellular timescale, the exponential will rapidly reach zero and the level of pMad will track the extracellular fluctuations; or (ii) if the intracellular timescale is slow relative to the timescale of the extracellular processes, the exponential term will buffer out changes in the level of BR owing to a slow response of the intracellular network. Thus, if extracellular fluctuations are frequent, the exponential term could suppress the high-frequency noise and effectively average out the fluctuations over time [34].
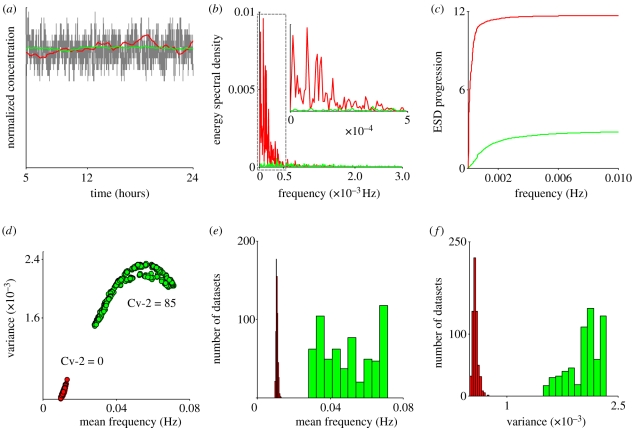
As input to the downstream pMad signalling network, we considered a BR distribution both in the presence and in the absence of Cv-2. In the absence of Cv-2, the fluctuation frequency of BR is relatively low (figure 2b) owing to the slow kinetic rates for binding. This leads to low-frequency departures of intracellular pMad that track the extracellular distribution (red, figure 5a), whereas in the presence of Cv-2, the increase in frequency of fluctuations of BR leads to effective averaging by the intracellular pMad network, even in the presence of no change or an increase in the amplitude of the fluctuations (figure 5a, green). To quantify frequency filtering and develop a metric for parameter screening, the distributions of BR were converted from the time-domain to the frequency domain by taking the Fourier transform of X(t) = |BR(t) − mean (BR)| in the presence and absence of Cv-2 (figure 5b). Terms in the Fourier transform contain the weighting or dominance of each frequency in the total solution and this provides a measure to compare the frequency-dependence of different solutions. If low-frequency terms dominate the dynamics of BR, the Fourier transform will have the greatest magnitude in the region of low-frequency fluctuations (figure 5b), whereas if high-frequency terms dominate, the Fourier transform solution will be biased towards regions of high-frequency noise. Without Cv-2, low-frequency terms dominate (figure 5b). In the presence of Cv-2, there does not appear to be a bias in any frequency range and the Fourier transform depends on contributions from a wide range of frequencies (figure 5b). Moreover, the energy spectral density (ESD) progression plot of figure 5c demonstrates the dominance of low-frequency fluctuations in the absence of Cv-2. The progression of the ESD reaches its maximum at a very low frequency for Cv-2 = 0 and increases more gradually for Cv-2 = 85.
Figure 5.
Noise reduction mechanisms: (a) pMad accumulation within a cell versus BR: BR with Cv-2 (grey line), pMad with Cv-2 (green line) and pMad without Cv-2 (red line). (b,c) Frequency analysis of fluctuations around the steady-state: (b) Fourier transform for BR for Cv-2 = 0, 85 were taken using a sampling frequency of 0.2 Hz. A total of 100 ensemble runs were averaged to get the steady-state BR distribution to avoid any unexpected artefacts in the Fourier response. Inset: Range from 0 to 0.0005 Hz. (c) The energy spectral density (ESD) for the frequency response of BR both with Cv-2 = 0 (red) and Cv-2 = 85 (green) are plotted with same sampling frequency as in (b). For Cv-2 = 0, the energy spectral progression approaches the maximum ESD value at the low-frequency range, indicating a concentrated energy at low-frequency components of the spectrum distribution, whereas for Cv-2 = 85 (green) the ESD shows comparatively weaker contributions by low-frequency components. Cv-2 increases frequency of BR fluctuations (d–f): (d) mean frequency versus standard deviation for each of the 625 parameter sets shows that Cv-2 increases both the mean frequency of fluctuations and the variability of the frequency fluctuations as determined by analysis of the frequency domain from the Fourier transform of dynamic stochastic model output. (e) Histogram of mean frequency and (f) variance of frequency determined by FFT in the presence (green) and absence (red) of Cv-2. (b,c) Red line, Cv-2 = 0; green line, Cv-2 = 85. (e,f) Green bars, Cv-2 = 85; red bars, Cv-2 = 0.
To capture the frequency response for all parameter sets, we determined the mean frequency from the Fourier transform of steady-state BR concentration and the variance around the mean to measure the spread of frequencies. In the absence of Cv-2, the mean frequency and the variability about the mean are both low, suggesting that the Fourier transform of BR is dominated by low-frequency contributions (figure 5d, red). However, in the presence of Cv-2, an increase in variance and mean frequency is evident (figure 5d, green), which demonstrates that the frequency of fluctuations for Cv-2 ≠ 0 is greater than in the case of Cv-2 = 0. It is also clear that a comparatively larger portion (owing to large variance for Cv-2 ≠ 0) of the frequency domain contributes to the solution in the presence of Cv-2 (figure 5d). For all parameter sets tested, the presence of Cv-2 increased the mean frequency of fluctuations (figure 5e,f). Thus, noise in BMP signalling can be suppressed by both a decrease in fluctuation amplitude (figures 2b and 3a) and an increase in the frequency of fluctuations (figure 5).
2.4. Cv-2 reduces spatial pattern variation
Local signalling noise and variability may lead to increased variability in spatial patterning. To quantify how fluctuations in the local models would lead to positional errors in spatial models, we considered a simple reaction–diffusion (RD) model that contains 100 receiving cell in a 500 µm length of tissue. For each cell in the distribution, the local stochastic model was solved using the deterministic concentration of extracellular BMP-ligand as an input (figure 6). Each line in figure 6 corresponds to one realization of the local stochastic models for a fixed extracellular BMP distribution, and therefore, figure 6 also represents the expected pattern of interpretation for a two-dimensional array of cells with a deterministic input. The patterns correspond to the distribution of high signalling cells (black) versus low signalling cells (white) determined by the instantaneous readout of BR occupancy relative to a threshold of 10, 20 or 25 bound receptors per cell. Here, any cells receiving BR more than the predefined threshold condition are considered ‘on’ and cells below the threshold are ‘off’. The presence of Cv-2 significantly reduces the width of region that exhibits high cell-to-cell variability, for both the level of bound receptors, and to a greater extent, the levels of intracellular pMad (figure 6d–f).
Figure 6.
Spatial variation for (a–c) BR and (d–f) pMad: (a–c) Noisy interpretation of BR in the absence (top) and presence (bottom) of Cv-2 for thresholds for 10, 20, 25 molecules per cell. Black points are above threshold, white points are below. (d–f) Plots are obtained as mentioned for figure (a–c) except for pMad with thresholds of 15 000, 25 000, 50 000 molecules per cell.
3. Discussion
BMP-mediated signalling and developmental pattern formation are two pathways that must occur rapidly in the presence of intrinsic and extrinsic variability. Disruptions of signalling and patterning fidelity have significant consequences that could lead to diverse outcomes in a homogeneous signalling environment. The focus of this work is on the extracellular regulation of BMP signalling by SBP molecules such as Cv-2, and one of the salient features of the network is its ability to simultaneously reduce fluctuation amplitude and increase the frequency of fluctuations in the level of bound receptors. The coupled extracellular/intracellular cassette is reminiscent of a simple low-pass filter in audio communication applications that can be built in numerous ways—for example, by placing a resistor in series and capacitor in parallel to a load. The combination of capacitor and resistor attenuates frequencies that exceed a cut off frequency determined by the inverse of the timescale for the resistor/capacitor combination. Low-frequency inputs pass through the filter owing to the reactance of the capacitor that accumulates charge with voltage equal to that of the input signal. The accumulation of charge blocks it from passing through the capacitor and the signal has no option but to pass through the filter as the output signal. At high frequency, low reactance of the capacitor causes it to function like a short-circuit by cancelling out the rapid increases and decreases in voltage. In the absence of an SBP in the cell signalling system, receptor equilibration and extracellular patterning operate on equal timescales, making it difficult to parse noise from signal. With SBP regulation, receptor–ligand fluctuations occur at a much higher frequency, leading to a separation of timescales that can be acted upon by a simple intracellular network. The balance of phosphorylation/dephosphorylation in the cytoplasm establishes the reactance of the signalling system so that it ignores high-frequency fluctuations, responds to low-frequency signals and passes to the nucleus a reliable interpretation of the cell's signalling state.
These two processes, reduction of fluctuation amplitude and increase in the frequency of fluctuations, work in concert and provide a robust mechanism to suppress long duration, high amplitude noise in signalling. We expect these conclusions to hold for other, more complete models of BMP signalling that include type II receptor binding, since (i) reactions that occur between molecules on a surface frequently benefit from increased kinetic rates owing to a reduction of dimensionality, and (ii) the measured binding rates between BMP ligands + type II receptors are relatively weak and fast [25]. The network could be extended to include other features that may impact the noise-filtering function of SBPs. For instance, feedback on SBPs from intracellular signalling may increase the range of reliable morphogen-mediated patterning similar to what was recently shown for systems where feedback enhances ligand clearance [30].
The conclusions of this work could be readily explored experimentally by RNA interference of secreted BMP regulators such as Cv-2 in cell culture or analysis of phenotype variability in wt versus mutant embryos. In fact, a recent study reports that loss of the BMP regulator BAMBI confers increased phenotype variability in Xenopus [18]. Measurement of signalling noise can be investigated in a range of ways, including quantitative immunofluorescence, live imaging and quantification of phenotypic outcome and population variation. The biology of signalling networks mediated by low numbers of molecules can be effectively investigated with local mathematical models as shown here, but the next step in developing a greater understanding of the mechanism of pattern compensation mechanisms requires additional methods for multi-scale spatio-temporal models of patterning to link the local cell-scale models with patterning of an organism.
While mechanisms have evolved to mitigate variability in vivo where reliability is required, taking cells out of the in vivo context to direct signalling in vitro likely eliminates many of the mechanisms that ensure robustness. Exploiting the noise suppression characteristics of BMP-binding proteins like Cv-2 may help reduce heterogeneity and variability in stem cell differentiation from human embryonic stem cells or induced pluripotent stem cells [35]. This study suggests that variability is intrinsic to the system if modulators such as Cv-2 do not play a role directing signal regulation. To test this prediction in vitro, one would need to add inhibitors and binding proteins first to attenuate signalling and add sufficient amounts of ligand to restore signalling. In the model, these experimental conditions reduce stochastic fluctuations in signalling and suggests a mechanism that may decrease heterogeneity and variability in populations of differentiating cells [36,37].
References
- 1.Gurdon J., Bourillot P. Y. 2001. Morphogen gradient interpretation. Nature 413, 797–803 10.1038/35101500 (doi:10.1038/35101500) [DOI] [PubMed] [Google Scholar]
- 2.Ashe H. L., Briscoe J. 2006. The interpretation of morphogen gradients. Development 133, 385. 10.1242/dev.02238 (doi:10.1242/dev.02238) [DOI] [PubMed] [Google Scholar]
- 3.Lander A., Nie Q., Wan F. Y. M. 2002. Do morphogen gradients arise by diffusion? Dev. Cell. 2, 785–796 10.1016/S1534-5807(02)00179-X (doi:10.1016/S1534-5807(02)00179-X) [DOI] [PubMed] [Google Scholar]
- 4.Neumann C., Cohen S. 1997. Problems and paradigms: morphogens and pattern formation. BioEssays 19, 1521–1878 10.1002/bies.950190813 (doi:10.1002/bies.950190813) [DOI] [PubMed] [Google Scholar]
- 5.Serpe M., Umulis D., Ralston A., Chen J., Olson D. J., Avanesov A., Othmer H., O'Connor M. B., Blair S. S. 2008. The BMP-binding protein Crossveinless 2 is a short-range, concentration-dependent, biphasic modulator of BMP signaling in Drosophila. Dev. Cell 14, 940–953 10.1016/j.devcel.2008.03.023 (doi:10.1016/j.devcel.2008.03.023) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Umulis D., O'Connor M. B., Blair S. S. 2009. The extracellular regulation of bone morphogenetic protein signaling. Development 136, 3715–3728 10.1242/dev.031534 (doi:10.1242/dev.031534) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Zhang J. L., Patterson L. J., Qiu L. Y., Graziussi D., Sebald W., Hammerschmidt M. 2010. Binding between Crossveinless-2 and Chordin Von Willebrand factor type C domains promotes BMP signaling by blocking Chordin activity. PLoS ONE 5, e12846. 10.1371/journal.pone.0012846 (doi:10.1371/journal.pone.0012846) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Reeves G. T., Muratov C. B., Schpbach T., Shvartsman S. Y. 2006. Quantitative models of developmental pattern formation. Dev. Cell 11, 289–300 10.1016/j.devcel.2006.08.006 (doi:10.1016/j.devcel.2006.08.006) [DOI] [PubMed] [Google Scholar]
- 9.Coppey M., Berezhkovskii A. M., Kim Y., Boettiger A. N., Shvartsman S. Y. 2007. Modeling the bicoid gradient: diffusion and reversible nuclear trapping of a stable protein. Dev. Biol 312, 623–630 10.1016/j.ydbio.2007.09.058 (doi:10.1016/j.ydbio.2007.09.058) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Coppey M., Boettiger A. N., Berezhkovskii A. M., Shvartsman S. Y. 2008. Nuclear trapping shapes the terminal gradient in the Drosophila embryo. Curr. Biol. 18, 915–919 10.1016/j.cub.2008.05.034 (doi:10.1016/j.cub.2008.05.034) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Umulis D., O'Connor M. B., Othmer H. G. 2008. Robustness of embryonic spatial patterning in Drosophila melanogaster. Curr. Top. Dev. Biol. 81, 65–111 10.1016/S0070-2153(07)81002-7 (doi:10.1016/S0070-2153(07)81002-7) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Umulis D. M., Serpe M., O'Connor M. B., Othmer H. G. 2006. Robust, bistable patterning of the dorsal surface of the Drosophila embryo. Proc. Natl Acad. Sci. USA 103, 11 613–11 618 10.1073/pnas.0510398103 (doi:10.1073/pnas.0510398103) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ben-Zvi D., Shilo B. Z., Fainsod A., Barkai N. 2008. Scaling of the BMP activation gradient in Xenopus embryos. Nature 453, 1205–1211 10.1038/nature07059 (doi:10.1038/nature07059) [DOI] [PubMed] [Google Scholar]
- 14.Kirkpatrick C. A., Knox S. M., Staatz W. D., Fox B., Lercher D. M., Selleck S. B. 2006. The function of a Drosophila glypican does not depend entirely on heparan sulfate modification. Dev. Biol. 300, 570–582 10.1016/j.ydbio.2006.09.011 (doi:10.1016/j.ydbio.2006.09.011) [DOI] [PubMed] [Google Scholar]
- 15.Yan D., Wu Y., Feng Y., Lin S. C., Lin X. 2009. The core protein of glypican Dally-like determines its biphasic activity in wingless morphogen signaling. Dev. Cell. 17, 470–481 10.1016/j.devcel.2009.09.001 (doi:10.1016/j.devcel.2009.09.001) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Khare N., Baumgartner S. 2000. Dally-like protein, a new Drosophila glypican with expression overlapping with wingless. Mech. Dev. 99, 199–202 10.1016/S0925-4773(00)00502-5 (doi:10.1016/S0925-4773(00)00502-5) [DOI] [PubMed] [Google Scholar]
- 17.Wang X., Harris R. E., Bayston L. J., Ashe H. L. 2008. Type IV collagens regulate BMP signalling in Drosophila. Nature. 455, 72–77 10.1038/nature07214 (doi:10.1038/nature07214) [DOI] [PubMed] [Google Scholar]
- 18.Paulsen M., Legewie S., Eils R., Karaulanov E., Niehrs C. 2011. Negative feedback in the bone morphogenetic protein 4 (BMP4) synexpression group governs its dynamic signaling range and canalizes development. Proc. Natl Acad. Sci. USA 108, 10 202–10 207 10.1073/pnas.1100179108 (doi:10.1073/pnas.1100179108) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Ambrosio A. L., Taelman V. F., Lee H. X., Metzinger C. A., Coffinier C., De Robertis E. M. 2008. Crossveinless-2 is a BMP feedback inhibitor that binds Chordin/BMP to regulate Xenopus embryonic patterning. Dev. Cell. 15, 248–260 10.1016/j.devcel.2008.06.013 (doi:10.1016/j.devcel.2008.06.013) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Zhang J., Qiu L., Kotzsch A., Weidauer S., Patterson L., Hammerschmidt M., Sebald W., Mueller T. D. 2008. Crystal structure analysis reveals how the Chordin family member Crossveinless 2 blocks BMP-2 receptor binding. Dev. Cell 44, 739–750 10.1016/j.devcel.2008.02.017 (doi:10.1016/j.devcel.2008.02.017) [DOI] [PubMed] [Google Scholar]
- 21.Rentzsch F., Zhang J., Kramer C., Sebald W., Hammerschmidt M. 2006. Crossveinless 2 is an essential positive feedback regulator of BMP signaling during zebrafish gastrulation. Development 133, 801–811 10.1242/dev.02250 (doi:10.1242/dev.02250) [DOI] [PubMed] [Google Scholar]
- 22.Umulis D. M. 2009. Analysis of dynamic morphogen scale-invariance. J. R. Soc. Interface 6, 1179–1191 10.1098/rsif.2009.0015 (doi:10.1098/rsif.2009.0015) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sebald W., Nickel J., Zhang J. L., Mueller T. D. 2004. Molecular recognition in bone morphogenetic protein (BMP)/receptor interaction. Biol. Chem. 385, 697–710 10.1515/BC.2004.086 (doi:10.1515/BC.2004.086) [DOI] [PubMed] [Google Scholar]
- 24.Saremba S., Nickel J., Seher A., Kotzsch A., Sebald W., Mueller T. D. 2008. Type I receptor binding of bone morphogenetic protein 6 is dependent on N-glycosylation of the ligand. FEBS journal. 275, 172–183 10.1111/j.1742-4658.2007.06187.x (doi:10.1111/j.1742-4658.2007.06187.x) [DOI] [PubMed] [Google Scholar]
- 25.Kirsch T., Nickel J., Sebald W. 2000. BMP-2 antagonists emerge from alterations in the low-affinity binding epitope for receptor BMPR-II. EMBO J. 19, 3314–3324 10.1093/emboj/19.13.3314 (doi:10.1093/emboj/19.13.3314) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Hatta T., Konishi H., Katoh E., Natsume T., Ueno N., Kobayashi Y., Yamazaki T. 2000. Identification of the ligand-binding site of the BMP type IA receptor for BMP-4. Peptide Sci. 55, 399–406 10.1002/1097-0282(2000)55:5%3C399::AID-BIP1014%3E3.0.CO;2-9 (doi:10.1002/1097-0282(2000)55:5<399::AID-BIP1014>3.0.CO;2-9) [DOI] [PubMed] [Google Scholar]
- 27.Shimmi O., O'Connor M. B. 2003. Physical properties of Tld, Sog, Tsg and Dpp protein interactions are predicted to help create a sharp boundary in BMP signals during dorsoventral patterning of the Drosophila embryo. Development 130, 4673–4682 10.1242/dev.00684 (doi:10.1242/dev.00684) [DOI] [PubMed] [Google Scholar]
- 28.Kerszberg M., Wolpert L. 1998. Mechanisms for positional signalling by morphogen transport: a theoretical study. J. Theor. Biol. 191, 103–114 10.1006/jtbi.1997.0575 (doi:10.1006/jtbi.1997.0575) [DOI] [PubMed] [Google Scholar]
- 29.Dyson S., Gurdon J. B. 1998. The interpretation of position in a morphogen gradient as revealed by occupancy of activin receptors. Cell 93, 557–68 10.1016/S0092-8674(00)81185-X (doi:10.1016/S0092-8674(00)81185-X) [DOI] [PubMed] [Google Scholar]
- 30.Lander A. D., Lo W. C., Nie Q., Wan F. Y. M. 2009. The measure of success: constraints, objectives, and tradeoffs in morphogen-mediated patterning. Cold Spring Harbor Perspect. Biol. 1, a002022. 10.1101/cshperspect.a002022 (doi:10.1101/cshperspect.a002022) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Hegland M., Hellander A., Lötstedt P. 2008. Sparse grids and hybrid methods for the chemical master equation. BIT Numer. Math. 48, 265–283 10.1007/s10543-008-0174-z (doi:10.1007/s10543-008-0174-z) [DOI] [Google Scholar]
- 32.Hegland M., Burden C., Santoso L., MacNamara S., Booth H. 2007. A solver for the stochastic master equation applied to gene regulatory networks. J. Comput. Appl. Math. 205, 708–724 10.1016/j.cam.2006.02.053 (doi:10.1016/j.cam.2006.02.053) [DOI] [Google Scholar]
- 33.Schmierer B., Tournier A. L., Bates P. A., Hill C. S. 2008. Mathematical modeling identifies Smad nucleocytoplasmic shuttling as a dynamic signal-interpreting system. Proc. Natl Acad. Sci. USA 105, 6608–6613 10.1073/pnas.0710134105 (doi:10.1073/pnas.0710134105) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Lauffenburger D., Linderman J. 1993. Receptors: models for binding, trafficking, and signaling. New York: Oxford University Press [Google Scholar]
- 35.Fox J. L. 2011. Human iPSC and ESC translation potential debated. Nat. Biotechnol. 29, 375–376 10.1038/nbt0511-375a (doi:10.1038/nbt0511-375a) [DOI] [PubMed] [Google Scholar]
- 36.Kattman S. J., Adler E. D., Keller G. M. 2007. Specification of multipotential cardiovascular progenitor cells during embryonic stem cell differentiation and embryonic development. Trends Cardiovasc. Med. 17, 240–246 10.1016/j.tcm.2007.08.004 (doi:10.1016/j.tcm.2007.08.004) [DOI] [PubMed] [Google Scholar]
- 37.Kattman S. J., Huber T. L., Keller G. M. 2006. Multipotent Flk-1+ cardiovascular progenitor cells give rise to the cardiomyocyte, endothelial, and vascular smooth muscle lineages. Dev. Cell 11, 723–732 10.1016/j.devcel.2006.10.002 (doi:10.1016/j.devcel.2006.10.002) [DOI] [PubMed] [Google Scholar]