Electrical resistivity and thermal conductivity of liquid Fe alloys at high P and T, and heat flux in Earth’s core

Abstract

Earth’s magnetic field is sustained by magnetohydrodynamic convection within the metallic liquid core. In a thermally advecting core, the fraction of heat available to drive the geodynamo is reduced by heat conducted along the core geotherm, which depends sensitively on the thermal conductivity of liquid iron and its alloys with candidate light elements. The thermal conductivity for Earth’s core is very poorly constrained, with current estimates based on a set of scaling relations that were not previously tested at high pressures. We perform first-principles electronic structure computations to determine the thermal conductivity and electrical resistivity for Fe, Fe–Si, and Fe–O liquid alloys. Computed resistivity agrees very well with existing shock compression measurements and shows strong dependence on light element concentration and type. Thermal conductivity at pressure and temperature conditions characteristic of Earth’s core is higher than previous extrapolations. Conductive heat flux near the core–mantle boundary is comparable to estimates of the total heat flux from the core but decreases with depth, so that thermally driven flow would be constrained to greater depths in the absence of an inner core.

The generation of the Earth’s magnetic field is directly coupled to the thermal evolution of the liquid outer core, the cooling of which is modulated by heat flux from the core into the base of the mantle (1–6). In a simple thermally driven core, as, for example, in the absense of a crystallizing inner core and associated latent heat release and chemical buoyancy, heat transported by conduction is not available to drive the geodynamo. Knowledge of its relative contribution to thermal transport in the core is therefore critical to understanding the long term stability of Earth’s magnetic field, which has been present as far back as 3.45 billion years ago (7), when the core was likely too hot for a solid inner core to crystallize (1, 4).

Existing estimates of thermal conductivity (k_el) and electrical resistivity (ρ_el) of Earth’s outer core are based on extrapolations (8, 9) of resistivity measurements in shock-compressed Fe and Fe–Si alloys (10–12) to core temperatures and pressures. These extrapolations assume the direct proportionality of electrical resistivity to temperature, its invariability along and across the Fe liquidus, and adherence to the Wiedemann–Franz law, which relates electrical resisitivity and thermal conductivity for metals through the Lorenz number (13) λ₀ = k_elρ_el/T = 2.44 × 10^-8 WΩ/K². No data are available for Fe alloys of the other candidate light elements that have been proposed to account for the seismically observed density deficit of Earth’s core relative to pure Fe (14). Previous high-pressure studies of the electronic transport properties of Fe at high pressure (15–18) were limited to low temperatures. Clearly, there is a need for direct determination of electrical resistivity and thermal conductivity of ferro-metallic liquids at pressures and temperatures characteristic of Earth’s outer core.

We compute k_el and ρ_el for Fe, Fe₇Si, Fe₃Si, Fe₇O, and Fe₃O liquid alloys (6.7, 14.3 wt% Si; 3.9, 8.7 wt% O) from first principles, using density functional theory and the Mermin functional to determine finite temperature equilibrium charge density and electronic structure (19–21). First-principles molecular dynamics (FPMD) simulations are performed in the canonical ensemble for temperatures of 2,000–8,000 K and volumes corresponding to pressures of 0–360 GPa. Electronic transport properties are subsequently computed for a series of uncorrelated snapshots from the FPMD simulations using the Kubo–Greenwood equation (22, 23) (see Methods), which expresses the electronic Onsager coefficients L_ij directly in terms of the expectation values of the electronic velocity operator (24).

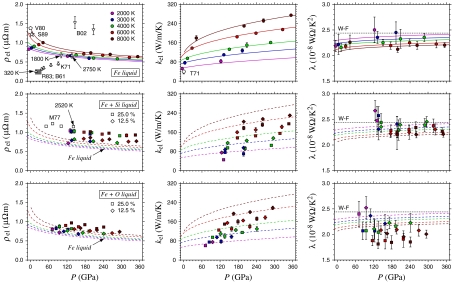
Computed resistivities for pure Fe liquid (Fig. 1) closely agree with the shock compression measurements of Keeler (10) and the lowest pressure point of Bi et al. (11), at pressures where Hugoniot temperatures (25) are comparable to those in our simulations. Similarly, values for Fe₃Si liquid are in agreement with the shock measurements of Matassov (12) for the same composition. Lower pressure shock compression measurements are at progressively lower temperatures; the 18 GPa measument of Keeler (10) is at 320 K, and agrees well with room temperature static measurements in hcp Fe (17, 18), adding confidence to the shock compression resistivity data, and our results. In light of the large scatter in the Bi et al. (11) dataset, and the serious disagreement between the data of Bi et al. (11) and Keeler (10) above 120 GPa, we feel that comparison of our results with the measurements of Keeler (10) is more appropriate. Computed low pressure resistivity for pure Fe liquid is somewhat smaller than experimental values (26, 27), yet computed ambient pressure thermal conductivity does agree closely with experimental estimates for liquid Fe at temperatures above melting (1,810 K) (28).

Fig. 1.

Computed electrical resistivity (ρ_el), thermal conductivity (k_el), and corresponding Lorenz numbers (λ). Solid lines (top row) and dashed lines (middle and bottom rows) show the Bloch–Grüneisen models of Fe liquid; the horizontal dotted line indicates the value of the Lorenz number expected via the Wiedemann–Franz relation (W-F). Hugoniot temperatures (25) for selected shock compression datapoints [K71 (10), M77 (12), B02 (11)] are shown to guide comparisons. Other experimental data (see text): R83 (17), B61 (18), T71 (28), S89 (27), V80 (26).

In drawing comparisons to the shock compression resistivity measurements, we assume that the resistivity of liquid and solid metal phases are similar, which is known to be the case for Fe at low pressure (26, 27). In our comparison of thermal conductivities, we further assume the electronic contribution to heat transport to be much larger than that due to transport by phonons alone. In Fe liquid at ambient pressure, the latter is estimated to be about 3 W/m K (8), much smaller than the experimental total conductivity of 40.3 W/m K (28).

In contrast with previous assumptions for Earth’s core (8, 9), we find that the validity of the Wiedemann–Franz relation depends strongly on temperature and composition. At core temperatures, computed Lorenz numbers for Fe and Fe–Si liquids are in the range of 2.2–2.4 × 10^-8 WΩ/K²; alloying of liquid Fe with O results in a notable decrease in λ, with values as low as 1.8 × 10^-8 WΩ/K² for Fe₃O liquid at high pressure and temperture. This deviation from the Wiedemann–Franz relation suggests that electron scattering in Fe–O liquid alloys is strongly anelastic, resulting in a breakdown of the simple relaxation time picture of electronic migration.

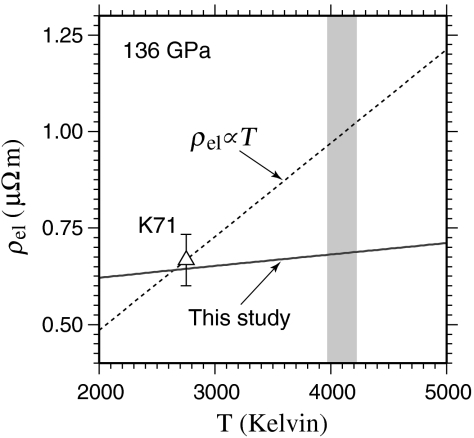
We find electrical resistivity to vary linearly with temperature, consistent with the prediction of the Bloch–Grüneisen equation for systems where electrons are primarily scattered by phonons. However, ρ_el is not directly proportional to T (Fig. 2), as is assumed in the oft-used extrapolations of experimental measurements to core conditions (8, 9). Augmenting the Bloch–Grüneisen formalism (29), we construct model descriptions for k_el and ρ_el as a function of volume and temperature for the different liquid phases considered (Table 1; see Methods). Combining these models with a pressure–volume–temperature equation of state for conductive liquids (30), we derive ρ_el and k_el values along a set of candidate adiabatic thermal profiles for Earth’s core, derived from the range of Fe-melting temperatures (25, 31, 32).

Fig. 2.

Temperature dependence of electrical resistivity for pure Fe liquid at 136 GPa, determined using the model in Table 1 (solid red line), agrees very well with the resistivity measurement of Keeler (10) at the same pressure. Stacey and Anderson (8) used ρ_el ∝ T (dashed line) in their extrapolation of this measurement to temperatures of the core near the core–mantle boundary. The shaded region indicates the T range near the core–mantle boundary from the range of candidate adiabats used (see text).

Table 1.

k_el and ρ_el model parameters for Eq. 5

	Fe	Fe7Si	Fe3Si	Fe7O	Fe3O
ρ0R, μΩm	0.77	0.84	1.26	0.85	1.00
ρ1R, μΩm	0.084	0.13	0.0015	0.090	0.12
λR, WΩ/K2	2.25	2.34	2.40	2.24	2.11
a	0.77	0.41	0.69	0.59	0.83
b	1.29	2.92	4.10	2.02	0.99
c	−0.078	−0.13	−0.016	−0.053	−0.069
d	−0.057	−0.12	−0.057	−0.096	−0.17

In all cases, T_R = 3,000 K and V_R = 7.0 cm³/atom.

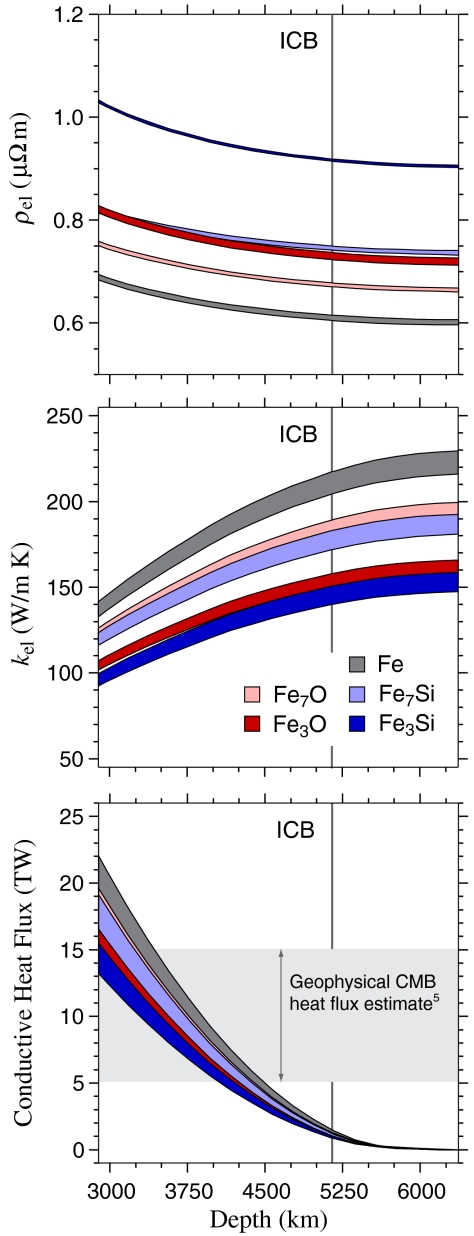
Our k_el values for the outer core are notably higher than previous extrapolations [Fig. 3; 30–60 W/m K (8, 9)], reflecting the incorrect temperature dependence of resistivity assumed in earlier studies (Fig. 2). As a consequence, our predicted conductive heat flux at the top of the core is 14–20 TW, larger than the 5–15 TW of total heat flux across the core–mantle boundary inferred from intraplate volcanism (5). A lower heat flux at the top of the core would require a smaller k_el, which can be obtained through a larger concentration of light elements in this region. Indeed, an anomalous light element fraction at the top of the core has been proposed on dynamical grounds (33) and is supported by seismic observations (34). However, because this concentration of light elements likely results from inner core crystallization and the associated chemical buoyancy, the difficulty posed by a large conductive heat flux remains, especially in the absence of a crystallizing inner core.

Fig. 3.

(Top) Electrical resistivity and (Middle) electronic thermal conductivity for the various compositions considered in this study, evaluated using the models in Table 1 along a range of candidate core adiabats (see text). (Bottom) Corresponding heat flux values computed as 4πr²k_el∇T, where r is the radius, compared to geophysical estimates of core–mantle boundary (CMB) heatflux (5).

Model conductive heat flux decreases rapidly with depth in the core, primarily due to the spherical geometry. Excluding the possible effects of radiogenic heating and latent heat released through inner core crystallization, conservation of energy requires total heat flux to remain constant throughout the core. The fraction of the total heat flux transported via convection would therefore increase with depth, suggesting that thermally driven flow would occur mainly within the deeper portion of the liquid core.

Methods

First-Principles Simulations.

The method used to compute electronic transport properties is similar to that of refs. 22 and 23. Born–Oppenheimer molecular dynamics (FPMD) is performed using the VASP code (35). To test for finite size effects, we consider system sizes of 64, 128, 144, and 192 atoms (see below). The exchange-correlation potential is represented in the generalized gradient approximation (GGA-PBE) (36), with valence electrons represented as planewaves with a cutoff of 300 eV in the projector augmented wave (PAW) formalism (37, 38). The Brillouin zone is sampled at the Γ point only. Simulations are performed in the NVT ensemble for volumes V/V_X = 1.0, 0.7, 0.65, and 0.6, where V_X = 7.121 cm³/mol atom, and temperatures of 2,000, 3,000, 4,000, 6,000 and 8,000 K, and cover at least 20 ps of simulation time. The time dependent mean square displacement is used to check that systems are indeed in the liquid state.

From each FPMD-generated phase trajectory, we extract atomic configuration snapshots every 1,000 fs (i.e., 20 per P–T point) for which we compute the electrical resistivity (ρ_el) and thermal conductivity (k_el). Velocity autocorrelation functions (39) for our simulations all decay within 250 fs, indicating that a 1,000-fs time separation is sufficient for individual snapshots to be uncorrelated. In this way a representative sampling of the liquid structure at each P–T point is obtained.

Electronic transport properties ρ_el and k_el are computed using the Kubo–Greenwood equation, as implemented in the Abinit code (22, 40). The equation, which follows from the electronic current autocorrelation function via Kubo’s linear response formalism, is

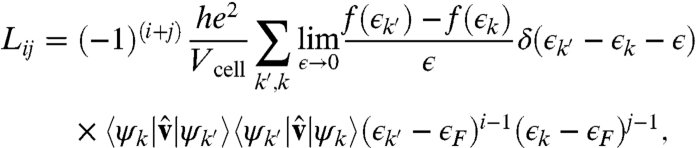[1]

[2]

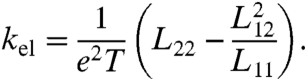[3]

In Eqs. 1–3 ϵ_F is the Fermi energy; ψ_k, ϵ_k, and f(ϵ_k) are the wave function, eigenvalue, and Fermi–Dirac occupation of eigenstate k, respectively; 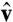is the velocity operator; and V_cell is the simulation cell volume. For a given snapshot, the self-consistent electronic relaxation is performed for electronic temperature equal to the ionic temperature via the Mermin functional (21). ψ_k and ϵ_k are represented by the Kohn–Sham eigenfunctions and eigenvalues for each given snapshot, while 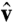is computed from the Hamiltonian gradient, .

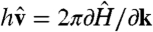Cells of 144 atoms for Fe and 128 atoms for Fe–Si and Fe–O alloys are used in production runs; test simulations with 192 atoms at V/V_X = 0.6 and 1.0 for T = 8,000 K yielded transport coefficients within 1% of the values determined with the smaller systems. To avoid core charge overlap in the linear response calculations at high degrees of compression, we constructed GGA-PAW atomic potentials with small cutoff radii (0.9 Å for Fe and Si, 0.53 Å for O) (36, 41). A planewave basis set cutoff of 400 eV is found to yield converged electronic transport coefficients. Production runs sample the Brillouin zone only at the Γ-point. This choice is appropriate in large simulation cells, where the Brillouin zone edge is effectively folded into its center. Test values computed using a 2 × 2 × 2 Monkhorst–Pack k-point grid (42) at V/V_X = 0.6 and 1.0 for T = 8,000 K vary by no more than 5% from the single k-point results.

It should be noted that the Kubo–Greenwood equation determines the electronic transport properties directly from the self-consistent electronic structure within the Born–Oppenheimer approximation. Ionic and electronic scattering are implicitly included in the computation, but electron–phonon coupling is not described. The approach is therefore well suited to characterizing high temperature electronic transport coefficients, especially in liquid metals.

P-T Model for ρ_el and k_el.

We represent the temperature and volume dependence of electrical resistivity via the Bloch–Grüneisen equation, with volume dependence included through a power law dependence of the prefactor (29)

[4]

where a and b are constants that include volume dependence of the vibrational frequencies. The electronic thermal conductivity is represented self-consistently through the Lorenz number using

[5]

by fitting the computed Lorenz numbers to

[6]

For the Fe liquid alloys we consider, reference volume and temperature are chosen as T_R = 3,000 K and V_R = 7.0 cm³/mol atom. Values for ρ_0R, ρ_1R, λ_R, a, b, c, and d for each of the simulated systems is given in Table 1.