Fast Ultrasound Beam Prediction for Linear and Regular Two-dimensional Arrays

Abstract

Real-time beam predictions are highly desirable for the patient-specific computations required in ultrasound therapy guidance and treatment planning. To address the long-standing issue of the computational burden associated with calculating the acoustic field in large volumes, we use graphics processing unit (GPU) computing to accelerate the computation of monochromatic pressure fields for therapeutic ultrasound arrays. In our strategy, we start with acceleration of field computations for single rectangular pistons, and then we explore fast calculations for arrays of rectangular pistons. For single-piston calculations, we employ the fast near-field method (FNM) to accurately and efficiently estimate the complex near-field wave patterns for rectangular pistons in homogeneous media. The FNM is compared with the Rayleigh-Sommerfeld method (RSM) for the number of abscissas required in the respective numerical integrations to achieve 1%, 0.1%, and 0.01% accuracy in the field calculations. Next, algorithms are described for accelerated computation of beam patterns for two different ultrasound transducer arrays: regular 1-D linear arrays and regular 2-D linear arrays. For the array types considered, the algorithm is split into two parts: 1) the computation of the field from one piston, and 2) the computation of a piston-array beam pattern based on a pre-computed field from one piston. It is shown that the process of calculating an array beam pattern is equivalent to the convolution of the single-piston field with the complex weights associated with an array of pistons.

Our results show that the algorithms for computing monochromatic fields from linear and regularly spaced arrays can benefit greatly from GPU computing hardware, exceeding the performance of an expensive CPU by more than 100 times using an inexpensive GPU board. For a single rectangular piston, the FNM method facilitates volumetric computations with 0.01% accuracy at rates better than 30 ns per field point. Furthermore, we demonstrate array calculation speeds of up to 11.5 × 10⁹ field-points per piston per second (0.087 ns per field point per piston) for a 512-piston linear array. Beam volumes containing 256³ field points are calculated within 1 s for 1-D and 2-D arrays containing 512 and 20² pistons, respectively, thus facilitating future real-time thermal dose predictions.

I. Introduction

The safe application of therapeutic ultrasound requires accurate planning and dosimetry beyond the thermal and mechanical indices currently used for ultrasound imaging. It is well known that thermal damage varies nonlinearly with temperature and time [1], [2]. In ultrasound ablation, the goal is to optimize treatment within a small volume by meeting or exceeding the thermal dose required for irreversible damage [3]. Mild hyperthermia with ultrasound seeks to maintain a volume of tissue at a constant temperature for a period of time, such that the thermal dose is relatively low compared with ablation therapy [4]. In each case, it is critical to accurately predict energy deposition in three dimensions as a function of time. Accurate predictions avoid unintended off-target effects on tissues such as skin and bone, and control algorithms based on temperature feedback gain important information from a priori prediction of the expected temperature distribution [5]. Because thermal dose is critically important in the application of therapeutic ultrasound, be it ablative or hyperthermic in nature, the concept of a thermal dose budget will be a driving force in advancements in treatment planning, monitoring, and prediction.

In this paper, we demonstrate accelerated linear calculations of continuous wave ultrasound fields emitted from arrays of rectangular piston transducers using graphics processing units (GPUs). A growing number of methods and software packages for calculating linear acoustic fields have emerged in the last two decades [6]–[19]; however, these methods have not yet demonstrated the speed required to estimate acoustic power deposition in three dimensions for real-time thermal dose monitoring. The spatial impulse response method originally developed by Oberhettinger [20], later explored by Tupholme and Stepanishen [17]–[19] and implemented in the software packages Field II [11], [12], Ultrasim [7], [9], [10], and the DREAM toolbox [15]–[17], [19], is inherently a wideband method that requires a costly Fourier transform to obtain the time-harmonic response applicable to therapeutic ultrasound. The standard method for calculating continuous wave linear acoustic fields is based on numerically evaluating the Rayleigh-Sommerfeld diffraction integral [8]. Our GPU implementation employs the fast near-field method (FNM) described in [13] and [14], which is a more efficient method that is analytically equivalent to the Rayleigh-Sommerfeld diffraction integral. Furthermore, it is the only method that addresses the singularity issue at the piston surface, thus making it precise in the near-field.

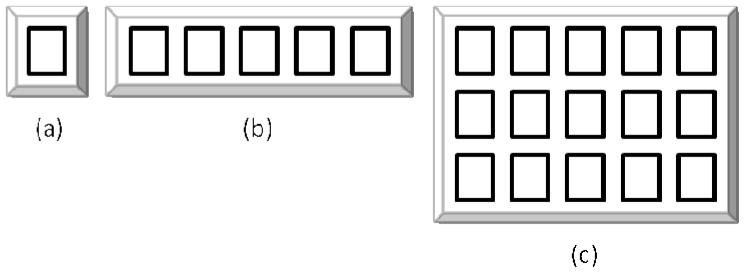
The process of thermal diffusion in most tissues is relatively slow, with thermal diffusion times [21] in the range of 1 to 10 s in many tissue types for distances of 1 mm, approximately the minimum scale of interest for thermal ultrasound. Therefore, a temporal sampling of the heat source function of 1 s or less leads to accurate temperature predictions. The objective of this work is to demonstrate rapid acoustic field predictions using GPUs for single pistons as well as 1-D and 2-D regular linear arrays of rectangular pistons (see Fig. 1). A specific design goal of this work is to calculate the acoustic field for a 256-element array for a volume containing 256³ field points in less than 1 s. Such computations have direct applications to current therapeutic ultrasound techniques.

Fig. 1.

Types of ultrasound piston alignments considered for GPU implementation: (a) single piston, (b) regular linear array of pistons, and (c) regular 2-D array of pistons. GPU implementations of (b) and (c) take advantage of the complex field generated for a single piston. The azimuth and elevation dimensions are defined to be parallel and perpendicular to the array shown in (b), respectively. The same orientations are also respected for (a) and (c).

Background

A. The Rayleigh-Sommerfeld Integral

The classic approach to monochromatic acoustic field prediction for a planar radiator in an infinite rigid baffle involves evaluating the Rayleigh-Sommerfeld diffraction integral [8]

$$p(\mathit{r},t)=j\rho {\mathit{cke}}^{j\omega t}{\int }_{{\mathit{S}}^{\prime }}u({\mathit{r}}^{\prime })\frac{e^{-jk\mid \mathit{r}-{\mathit{r}}^{\prime }\mid }}{2\pi \mid \mathit{r}-{\mathit{r}}^{\prime }\mid }{d\mathit{S}}^{\prime },$$ (1)

where p is acoustic pressure, r is the vector location of the observation point, t is time, j is √−1, ρ and c represent the density and speed of sound of the medium, respectively, k is the acoustic wavenumber, ω is the driving frequency, u is the distribution of the normal velocity on the radiator with surface area S′, r′ is the vector location of the source, and |r − r′| is the distance between the source and the observation coordinates. Attenuation is included by replacing the acoustic wavenumber with k − jα, where α is the attenuation coefficient in Nepers per meter. The Rayleigh integral describes the pressure generated by Green’s functions distributed on a radiating surface. Thus, the field radiated by an aperture is approximated numerically by summing contributions from many individual sources. The Rayleigh-Sommerfeld approach is sufficiently flexible to generate pressure fields from complex aperture geometries and velocity distributions. Unfortunately, this approach converges very slowly in the near field, and it fails altogether at the radiator surface because of the singularity condition at |r − r′| = 0 [13]. Although (1) is only applicable to planar radiators in an infinite rigid baffle, the baffled piston arrangements depicted in Fig. 1 are approximated by this condition.

B. The Fast Near-field Method

The fast near-field method (FNM) is analytically equivalent to (1) for a uniform surface velocity u₀ [13]. The near-field pressure of a uniformly radiating rectangular aperture obtained using the FNM is given by

$$\begin{array}{l}p(x,y,z,t)=j\rho {cu}_0{e}^{j\omega t}\frac{1}{2\pi }(s_1{\int }_{l_1}^{l_2}\frac{e^{-jk\sqrt{z^2+{\sigma }^2+s_1^2}}-e^{-\mathit{jkz}}}{{\sigma }^2+s_1^2}d\sigma \\ +l_1{\int }_{s_1}^{s_2}\frac{e^{-jk\sqrt{z^2+{\sigma }^2+l_1^2}}-e^{-\mathit{jkz}}}{{\sigma }^2+l_1^2}d\sigma \\ -s_2{\int }_{l_1}^{l_2}\frac{e^{-jk\sqrt{z^2+{\sigma }^2+s_2^2}}-e^{-\mathit{jkz}}}{{\sigma }^2+s_2^2}d\sigma \\ -l_2{\int }_{s_1}^{s_2}\frac{e^{-jk\sqrt{z^2+{\sigma }^2+l_2^2}}-e^{-\mathit{jkz}}}{{\sigma }^2+l_2^2}d\sigma ),\end{array}$$ (2)

where s₁ =|x| − a, l₁ = |y| − b, s₂ = |x| + a, l₂ = |y| + b, σ is the 1-D variable of integration, and a and b represent the half-width and the half-height of the rectangular aperture, respectively. As for the Rayleigh-Sommerfeld case, attenuation is included in the FNM by replacing the acoustic wavenumber with k − jα, where α is the attenuation coefficient in Nepers per meter. Important features of the FNM include the analytical reduction of the 2-D Rayleigh-Sommerfeld integral to more efficient 1-D integrals evaluated efficiently using Gauss-Legendre quadrature integration, and the elimination of singularities, particularly in the plane of the aperture. The combination of these features enables the FNM to converge rapidly in the near-field. For a rectangular source 5 wavelengths wide by 7.5 wavelengths high, it has been shown that the FNM reaches accuracy in the near-field close to double-precision epsilon (1.11×10⁻¹⁶) within 85 abscissas [13]. Such accuracy is far beyond what is required for therapeutic ultrasound; however, the fast convergence of the FNM in the near-field makes it appealing for efficient, high- or low-accuracy computations.

C. General Purpose Graphics Processing Unit Computing

Traditionally, a graphics processing unit (GPU) handles parallel operations for computer graphics (e.g., 3-D and 4-D matrix and vector operations such as projections, rotations, and calculations in color-space). A general purpose graphics processing unit (GPGPU) [22] extends this functionality to programs typically executed on a CPU. To accomplish parallelism, a set of records or elements is identified that require similar computation. This set is referred to as a stream, and the similar computation is referred to as the kernel. Therefore, a stream executed on a GPGPU is executed as a single program (i.e., kernel), multiple data (SPMD) operation. For sake of brevity, GPGPUs will be referred to as GPUs throughout.

The class of GPUs considered here was developed by NVIDIA Corporation (Santa Clara, CA). Using the compute Unified Device Architecture (CUDA) programming environment available for NVIDIA GPUs, computations are performed using fine-grained, data-parallel threads organized in a hierarchy. At the top of the hierarchy, threads are organized into a 2-D grid of blocks with up to 65536 blocks in each dimension. Each block consists of a 3-D set of up to 512 threads that all execute the same kernel in parallel. The organization of blocks and threads facilitates parallel execution of a kernel on large arrays where thousands to millions of threads may be generated. A single NVIDIA GPU may consist of up to 960 parallel execution units, each capable of executing a single thread simultaneously at clock rates over 1 GHz. GPU performance is highly dependent on minimizing expensive memory transfers, particularly between CPU host memory and GPU device memory. Shared memory resources available on the GPU (typically 16 kB) reduce latencies associated with kernel execution on large arrays.

Two primary algorithmic features are utilized to accelerate the computation of complex pressure fields from an array of radiators using a GPU. First, the calculation of a pressure field involves evaluating the same function [e.g., (1)] for thousands to millions of field points. Second, in the linear acoustics regime where superposition is assumed, the complex pressure field generated by a transducer array may be generated by pre-computing an extended field from one transducer element, and reusing it using lookup, multiply, and accumulate operations to complete the field computation for the entire array.

II. Methods

A. Hardware and Programming

Source codes were developed in C/C++ and MATLAB (The MathWorks, Natick, MA) for execution on the CPU. C/C++ source codes were developed in Linux and compiled using the gcc compiler for CPU code (using the –O3 –march = core2 compiler flag). MATLAB code was developed using release 2010a. The MATLAB codes were executed on a P8400 Intel Core2 Duo (Intel Corp., Santa Clara, CA) for accuracy measurements, and the C/C++ codes were executed on a single core on the Intel Xenon X5550 (2.67 GHz) processor for timing measurements.

GPU source codes were developed using the nvcc compiler included in the CUDA development package provided by NVIDIA. All reported GPU computation times were performed on a single NVIDIA Tesla C1060 GPU containing 240 streaming processor cores operating at 1.3 GHz. The Tesla C1060 has a peak theoretical single-precision floating-point performance of 933 Gflops, 4 Gb of dedicated GDDR3 memory, and an internal memory bandwidth of 102 GB/s. Less powerful NVIDIA GeFORCE 9600M GT and 9600M GS GPUs were also used in code development and testing. Execution times were measured using microsecond-accurate timing available on the host CPU. CPU host to GPU device memory transfers were not included in timing measurements. The GPUs used in this study were not IEEE 754 compliant for single-precision arithmetic; consequently, errors and times were evaluated for each calculation.

B. Single Rectangular Piston Computations

1) Rayleigh-Sommerfeld Implementation

The Rayleigh-Sommerfeld integral was implemented in MATLAB for the GPU according to (1). The midpoint rule was used to generate weights and abscissas for the integration of (1). In the implementation, a rectangular piston was divided into a regularly spaced grid of smaller pistons with equal numbers in both azimuth and elevation. The area and midpoint of each smaller piston served as the weight and sub-element center for the numerical integration, respectively.

2) Fast Near-field Implementation

The FNM was implemented in MATLAB and for the GPU according to (2). The integrals in (2) were evaluated numerically using Gauss quadrature rules (weights and abscissas) generated in double-precision using two iterations of the algorithm by Davis and Rabinowitz [23]. For single-precision computations, double-precision abscissas and weights are converted to single-precision before being used in the integrals. As detailed in [13], the numerical evaluation of (2) may be improved by splitting the integrals at zero in specific regions. When |x| < a, the 2^nd and 4^th integrals (over s) are split at zero. Likewise, when |y| < b, the 1^st and 3^rd integrals (over l) are split at zero. When |x| = 0 and/or |y| = 0, the respective integrands are symmetric, and the respective integrals are evaluated from zero to the upper limit and the result is doubled. For the remaining regions, |x| ≥ a and |y| ≥ b, the respective integrals are evaluated as shown in (2). Evaluating (2) according to the intervals described above requires a total 6 cases, each requiring a branch condition (e.g. 4 if-else statements and 2 else statements).

3) Accuracy Testing

Reference computations to determine accuracy were performed in double-precision floating-point (IEEE 754 compliant) in MATLAB using FNM with 200 abscissas. Relative errors between the reference and comparison computations were quantified according to

$$E_{\mathit{rel}}(\mathit{r})=\frac{\mid p_{\mathit{ref}}(\mathit{r})-p_{\mathit{comp}}(\mathit{r})\mid }{\mid p_{\mathit{ref}}(\mathit{r})\mid },$$ (3)

where r is the vector location of the field point, E_rel(r) is the relative error, |·| is the magnitude operator, p_ref(r) is the reference pressure, and p_comp(r) is the pressure field for comparison (e.g., obtained from the GPU or MATLAB).

B. Linear Arrays

1) Regular 1-D Linear Arrays

A regular 1-D linear phased array is a set of transducer pistons aligned equidistantly along a line with a constant separation between neighboring pistons as illustrated in Fig. 1(b). The first assumption is that all pistons are geometrically and electrically identical such that the pressure field emitted by the i^th piston, p_i(r, t), is equal to a translated version of a field calculated for a single piston represented by

$$p_i(\mathit{r},t)=p_{SP}(\mathit{r}-{\mathit{q}}_i,t),$$ (4)

where p_sp(r, t) is the pressure field for a single piston and q_i the vector location of the i^th piston relative to the piston p_sp(r, t). Assuming monochromatic excitation, the phase and amplitude required of each piston for focusing and apodization, respectively, is calculated by multiplying the complex pressure field generated by the i^th piston by a complex weight, w_i. By superposition, we can compute the complex pressure at a point in space for a 1D array according to

$$p_{1D}(\mathit{r},t)=\sum _i{w}_i{p}_i(\mathit{r},t),$$ (5)

which upon combining with (4) yields:

$$p_{1D}(\mathit{r},t)=\sum _i{w}_i{p}_{SP}(\mathit{r}-{\mathit{q}}_i,t).$$ (6)

Eq. (6) is a convolution of the single-piston field, p_sp(r, t), with a 1-D filter mask,

$$p_{1D}(\mathit{r},t)=f_{1D}(\mathit{r})\ast p_{SP}(\mathit{r},t),$$ (7)

where * is the convolution operator, and the filter mask is given by

$$f_{1D}(\mathit{r})=\sum _i{w}_i\delta (||\mathit{r}-{\mathit{q}}_i||),$$ (8)

where δ is the Dirac delta function and ||·|| is the Euclidean norm operator.

The complex weights, w_i, are determined according to the field conjugation focusing method originally described by Ibbini and Cain [24]. Because the field from one piston is pre-computed, finding the optimal focusing phase involves a lookup of the complex pressure at the desired focal point (provided that it falls on the regular grid), and using the phase conjugate of this complex pressure as the focusing phase to ensure that all wave fronts are zero phase at the focal point. If the desired focal point does not fall on the regular grid, the optimal focusing phase is determined very rapidly by computing the acoustic field generated by each piston at the focal point using the FNM (i.e., only 1 field point computed for each piston in a 256-piston array).

The pre-computed field for a single-piston is sampled in azimuth such that the distance between pistons is an integer multiple of the spatial sampling. In general, the integer-multiple condition does not limit the distance between pistons or the spatial sampling of the field as it is always possible to find a suitable multiple to sample the field at λ/2 or better, where λ is the acoustic wavelength. Equation (6) is implemented efficiently on this 3-D set by recognizing that the 1-D convolution operation is repeated along each line in azimuth of the precomputed single-piston field. Therefore, each line in azimuth is loaded into fast shared memory prior to applying the weights, w_i, which are stored in constant memory.

2) Regular 2-D Linear Arrays

The regular 2-D linear array consists of M × N pistons with location indices i and j in azimuth and elevation, respectively, as illustrated in Fig. 1(c). Similar to the 1-D case, a 2-D filter mask is described by

$$f_{2D}(\mathit{r})=\sum _i\sum _j{w}_{ij}^{\prime }\delta (||\mathit{r}-{\mathit{q}}_{ij}||),$$ (9)

which, when convolved with the single-piston solution, results in the pressure at vector location r given by

$$p_{2D}(\mathit{r},t)=f_{2D}(\mathit{r})\ast p_{SP}(\mathit{r},t),$$ (10)

where is the complex weight (determined by field conjugation) associated with the piston and is the vector location of the piston.

As in the 1-D case, the pre-computed field for a single piston is sampled such that the distances between pistons in both the azimuth and elevation dimensions are an integer multiple of the respective spatial samplings in each dimension.

3) GPU Implementation Details

We apply certain restrictions to boost the efficiency of the calculation. First, we pre-calculate the single-piston field on a regular 3-D grid such that the grid spacing in the azimuth-elevation plane is regularly sampled at an integer multiple of piston spacing. Second, we assume that the grid is aligned with the piston elements. These restrictions eliminate the need for interpolation. As mentioned previously, the integer-multiple condition does not limit the method because it is always possible to find an integer multiple with which to sample the field at or better.

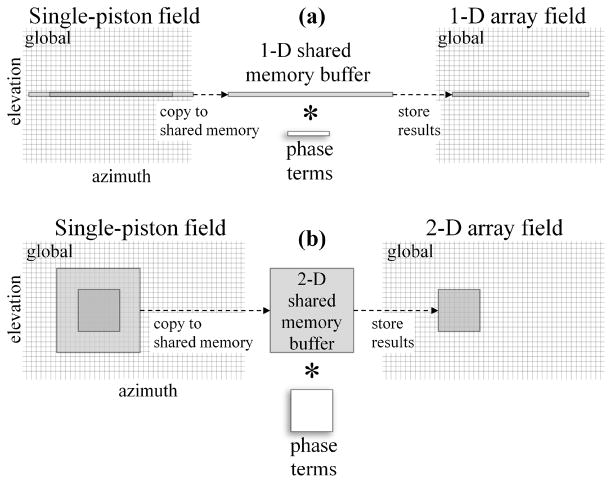
A graphical depiction of the GPU implementations for 1-D and 2-D arrays is shown in Figs. 2(a) and 2(b), respectively. In each case, the field for a single piston is pre-computed and stored in global memory. The initial single-piston field is pre-computed using the FNM on a padded grid of size S_x′ × S_y′ × S_z, where S_x′ = S_x + (M − 1)D_x, S_y′ = S_y + (N − 1)D_y, S_x, S_y and S_z are the final computed field grid dimensions in azimuth, elevation, and depth, respectively; D_x and D_y are the distances between array elements measured in grid samples in azimuth and elevation, respectively; and M and N are the corresponding numbers of pistons in azimuth and elevation, respectively. The single-piston field remains the same as long as the size of the piston, the wave number, and the grid sampling do not change, and the field is invariant to the number of elements in each dimension, their phase terms (e.g., a chosen focal point), and their amplitudes (e.g., apodization).

Fig. 2.

Method for implementing (a) 1-D and (b) 2-D convolutions in the azimuth-elevation plane. In each case, the pre-computed field for a single piston is stored in global memory as illustrated. To reduce the number of accesses to global memory, which is the major bottleneck in the calculation, a block equal to the number of threads used (e.g. 1×8 or 8×8) and padded depending on the array size is copied from global memory to shared memory. The result for this block is then written to global memory. The * indicates the convolution operator.

Next, as depicted in Fig. 2, discrete versions of the previously described masks corresponding to the piston weights are convolved with the single-piston field. To optimize the speed of the computation, we implemented specialized algorithms for the 1-D and 2-D cases described previously. Whereas shared and constant memory access on the GPU is fast, access to global memory is the major limiting factor, and depending on the memory requirements for a given algorithm, different approaches lead to better results.

For the 1-D regular linear array algorithm, a 1-D array in azimuth is transferred from the single-piston field stored in the GPU global memory to much faster GPU shared memory, as illustrated in Fig. 2(a). Due to limited shared memory resources (16 kB on the C1060), just one 1-D array is transferred at a time. Likewise, the complex weights are stored in constant memory, where they are available to all threads. The organization of memory in this fashion reduces global memory access because every field point stored in global memory is accessed only once; thus, no memory read collisions occur, and every field point stored in shared memory is accessed a number times equal to the number of piston elements (M in the 1-D case). Furthermore, both global and shared memory accesses become optimal when care is taken to align the arrays according to the proper boundaries.

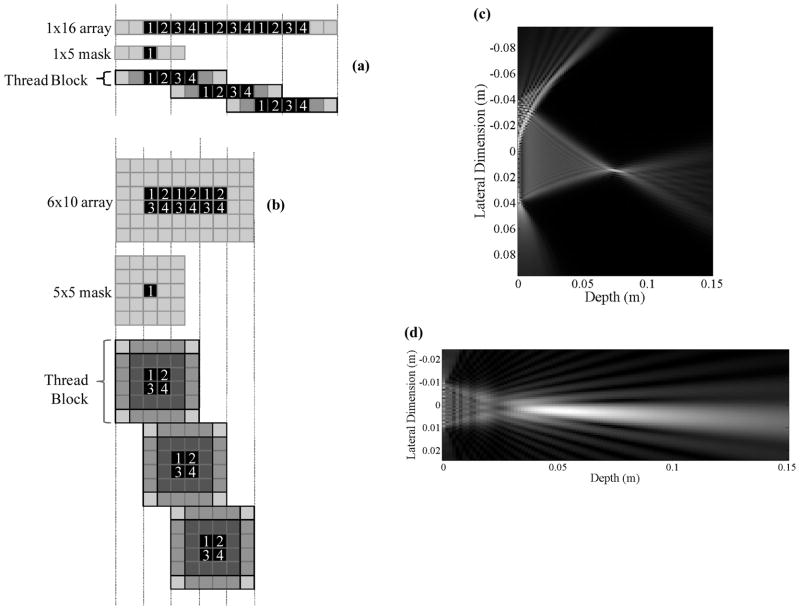
Following the proper memory organization, each iteration of the convolution operation is dispatched across multiple threads as illustrated in Fig. 3(a) for a 1 × 16 array of field points and a 1 × 5 mask of piston weights. In this example, a thread block consists of 4 threads executing concurrently on a 1 × 5 block of shared memory, and 3 thread blocks are depicted to complete the computation. An example beam from a 64-piston array obtained from the 1-D convolution algorithm is shown in Fig. 3(c).

Fig. 3.

GPU shared memory usage and thread organization for (a) 1-D and (b) 2-D convolution, and corresponding example steered beams in (c) and (d) for 1-D and 2-D convolution, respectively. (a) In the 1-D example, a 1 × 5 piston mask is convolved with a 1 × 16 array of field points (aligned in azimuth along the array of pistons) stored in shared memory. The computation is divided into 3 blocks of 4 threads per block (arranged in a 1 × 4 grid), resulting in 20 shared memory accesses per block. Each thread block operates on a 1 × 8 array. (b) In the 2-D example, a 5 × 5 piston mask is convolved with a 6 × 10 array of field points from the azimuth-elevation plane stored in shared memory. The computation is divided into 3 blocks of 4 threads per block (arranged in a 2 × 2 grid), resulting in 100 shared memory accesses per block. In (c), the beam is generated for a 1-D array of 64 pistons with λ/2 spacing in the lateral dimension and 3λ height in elevation. In (d), the beam is generated for a 2-D array of 16 × 16 pistons, with λ/2 spacing in each dimension.

In the general 2-D case, the number of memory accesses becomes much greater, and we follow the concept behind NVIDIA’s matrix multiplication example [25]. Similar to the 1-D case, Fig. 2(b) illustrates the usage of global and shared memory for 2-D convolution. The single-piston field points required to calculate output field points, including padding on the boundaries, are copied to shared memory. Threads operate on blocks of shared memory as illustrated in Fig. 3(b) for a 6 × 10 array of field points and a 5 × 5 mask of piston weights. Here, a thread block consists of 4 threads executing concurrently on a 6 × 6 block of shared memory, and 3 thread blocks are required to complete the computation. The threads are organized in a 2 × 2 grid to maximize reuse of shared memory. An example beam from a 16 × 16 piston array obtained from the 2-D convolution algorithm is shown in Fig. 3(d).

III. Results

A. Single Rectangular Piston

1) Accuracy of the RSM and the FNM

The Rayleigh-Sommerfeld method (RSM) and FNM were implemented in MATLAB and for the GPU to compare accuracy and execution times as a function of the number of field points and the number of abscissas. For a rectangular piston with width a = 5λ and height b = 7.5λ (duplicating in Fig. 2 of McGough [13] and Fig. 13 of Lockwood and Willette [26]), the single-precision GPU result with the FNM is shown in Fig. 4 using 100 Gauss abscissas. By inspection, the GPU result appears to be identical to that in McGough [13] and Lockwood and Willette [26]. To compare accuracy, the MATLAB computation performed in double-precision using the FNM with 200 Gauss abscissas served as the reference for comparison to GPU computations performed in single-precision. Using the results shown in Fig. 4, the normalized relative errors [as defined in (3)] for this specific case using 100 Gauss abscissas are within 2.6 × 10⁻⁶ for the single-precision GPU computations. Fig. 5 extends the computation in Fig. 4 out to 10 far-field transition distances in depth, solidly into the far-field region. Here, the peak normalized relative errors are approximately one order of magnitude greater at 2.5 × 10⁻⁵ for the GPU computations. In the GPU result, the errors are more prominent in the region over the piston, where, in this particular case, |x| < a and |y| = 0 and 6 integrals are evaluated instead of 8.

Fig. 4.

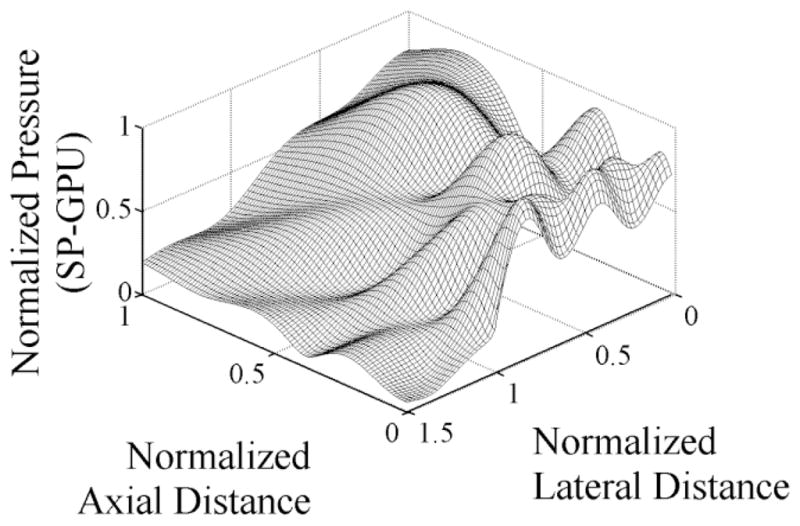
Normalized near-field pressures in the azimuth-depth plane for a single rectangular piston using parameters identical to those used to generate [13, Fig. 2] and [26, Fig. 13], with width a = 5λ and height b = 7.5λ (b/a = 1.5) calculated in single-precision using 100 abscissas on the GPU. The maximum normalized relative error is 2.6 × 10⁻⁶. The horizontal axes are in normalized units of a²/λ in the axial dimension and a/2 in the lateral dimension, and the spatial sampling is λ/16 in each dimension, producing a grid of 61 × 101 points.

Fig. 5.

Normalized far-field pressures (including near-field) in the azimuth-depth plane for a single rectangular piston using parameters identical to those used to generate Fig. 4, except calculated out to 10 normalized units in the depth dimension. Single-precision results using 100 abscissas on the GPU. The maximum normalized relative error is 2.5 × 10⁻⁵. The horizontal axes are in normalized units of a²/λ in the axial dimension and a/2 in the lateral dimension, and the spatial sampling is λ/16 in each dimension, producing a grid of 61 × 1001 points.

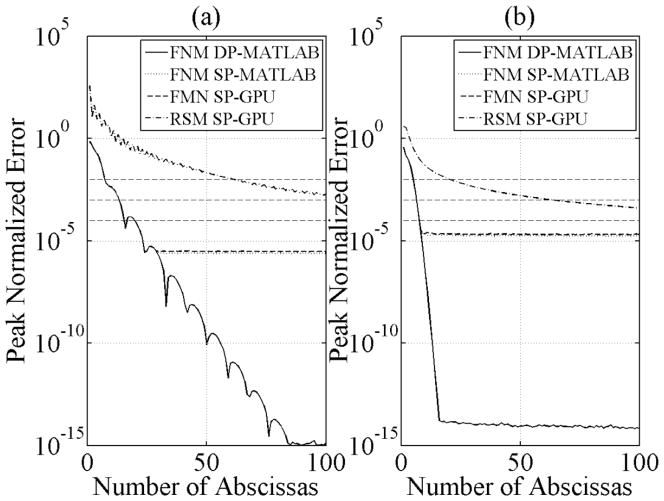
As both the RSN and FNM are numerical approximations, the accuracy of each method was quantified as a function of abscissa count. The peak normalized relative error as a function of abscissa count is summarized in Fig. 6 for four cases: FNM in MATLAB in double-precision (solid), FNM in MATLAB in single-precision (dotted), FNM on GPU in single-precision (dashed), and RSM on GPU in single-precision (dash-dot). Fig. 6(a) shows peak normalized relative error in the near-field out to 1 far-field transition distance (corresponding to the domain in Fig. 4). Likewise, Fig. 6(b) shows peak normalized relative error in the far-field from 1 to 10 far-field transition distances (corresponding to the domain in Fig. 5). In the case of the RSM, field points at the surface of the piston (z = 0) were omitted because of the singularity condition for this method. Several interesting qualitative features are apparent in the results. The double-precision MATLAB result in Fig. 6(a) is in near-exact agreement with McGough [13, Fig. 5]. Except in the case of the RSM-GPU, the single-precision FNM-MATLAB and GPU results track the double-precision FNM-MATLAB results to the numerical limits of the respective computations, above which adding more abscissas does not improve the accuracy. As expected, the far-field results in Fig. 6(b) converge faster (i.e., fewer abscissas are required to achieve the same error limit) than the near-field results in Fig. 6(a), though the errors are slightly higher for the far-field computations. Additionally, the RSM converges much more slowly than the FNM. In Fig. 6(a), the jaggedness in the RSM curve is due to the close proximity of field points to abscissa locations for odd abscissa numbers.

Fig. 6.

Peak normalized relative errors in the azimuth-depth plane for a single rectangular piston using parameters identical to those used to generate Fig. 5, as a function of number of abscissas for (a) the near-field out to 1 far-field transition distance from the piston and (b) for the far-field between 1 and 10 far-field transition distances from the piston. The reference field was calculated in MATLAB in double-precision using 200 abscissas. Results for FNM in double-precision MATLAB (solid), FNM in single-precision MATLAB (dotted), FNM in single-precision GPU (dashed), and RSM in single-precision GPU (dash-dot) are shown. The dashed horizontal lines indicate 1, 0.1, and 0.01% relative error. Note that the single-precision FNM curves track the double-precision FNM curve up the respective numerical accuracy limits of each method. In the near-field, the FNM in single-precision GPU converges to within 1, 0.1, and 0.01% error with 8, 14, and 16 abscissas, respectively, and correspondingly 61², 126², and 396² abscissas for the RSM.

The convergence of the single-precision GPU implementations of the RSM and the FNM was quantified in terms of abscissas required to achieve accuracies within 1%, 0.1%, and 0.01% (denoted by horizontal dashed lines in Fig. 6). It is important to clarify the meaning of abscissas when referring to either RSM or the FNM. Because the RSM is a 2-D algorithm, the number of abscissas listed represent the square root of the true number of abscissas used in the computation (e.g., 100 abscissas correspond to 100² abscissas). For the FNM, the true number of abscissas is a factor of 4, 6, or 8 greater depending on the location of the field point above the piston (e.g., 100 abscissas correspond to 800 abscissas directly over the piston when x ≠ 0 and y ≠ 0). Notwithstanding this factor, the FNM is still a 1-D algorithm, and for sake of clarity, this factor is omitted. In the near-field, the FNM in single-precision GPU computations converges to within 1%, 0.1%, and 0.01% error with 8, 14, and 16 abscissas, respectively, and correspondingly 61², 126², and 396² abscissas for the RSM. In the far-field, the FNM in single-precision GPU computations converges to within 1%, 0.1%, and 0.01% error with 6, 7, and 8 abscissas, respectively, and correspondingly 21², 67², and 200² abscissas for the RSM.

2) Computation Times of the RSM and the FNM

Single-precision computation times for the RSM and the FNM implemented on the C1060 GPU are summarized in Table I for field point numbers ranging from 32³ up to 256³ using the abscissas required to achieve 1%, 0.1%, and 0.01% accuracy in the near-field according to the result in Fig. 6(a). In this benchmark, the field was computed from a rectangular piston, 1λ in azimuth by 1.5λ in elevation with λ/4 spatial sampling in azimuth and elevation and λ/2 sampling in depth. The computation times include a constant attenuation factor of α = 1 neper/m. The speed of the FNM over the RSM increases from approximately 16× faster for 32³ field points at 1% accuracy up to over 661× faster for 256³ at 0.01% accuracy.

Table I.

Comparison of gpu computation times for the rsm and fnm in single-precision for a rectangular piston, 1λ in azimuth by 1.5λ in elevation, as a function of minimum normalized field accuracy and field points.

		RSM			FNM
Min Accuracy		1.0%	0.1%	0.01%	1.0%	0.1%	0.01%
Abscissas Required		612	1262	3962	8*	14*	16*
Field Points	323	16.689 (0.006)	70.60 (0.01)	694.9 (0.1)	1.04 (0.01)	1.72 (0.02)	1.95 (0.01)
	643	127.03 (0.01)	539.55 (0.02)	5 317.0 (0.2)	6.3 (0.5)	9.8 (0.7)	11.0 (0.6)
	1283	1 007.39 (0.04)	4 281.7 (0.1)	42 202.9 (0.6)	38.61 (0.01)	62.92 (0.04)	70.79 (0.06)
	1943	3 391.70 (0.05)	14 416.10 (0.04)	142 091.0 (0.5)	153 (2)	251 (3)	284 (3)
	2563	8 036.87 (0.03)	34 160.9 (0.2)	336 708.0 (0.4)	263 (1)	449 (4)	509 (3)

^*The true number of abscissas for each evaluation of (2) depends on the location of the field point relative to the piston.

All times are in units of milliseconds with standard deviations in parentheses (n=5 for RSM and n=20 for FNM).

As the number of field points outside of the piston increases, the FNM is dominated by 4-integral computations as opposed to 6 and 8 integrals, thus partially explaining the increase in efficiency with increasing numbers of field points. For example, in the 16 Gauss abscissa case, the computation time per field point starts at 59 ns for 32³ points and decreases to 30 ns per field point for 256³ points. For the RSM, the computation time per field point is approximately constant as a function of the number of field points. In the 0.01% accuracy case, the RSM computation times per field point range from 19 to 21 μs. Using the FNM, it is possible to compute 256³ field points for a single rectangular piston in approximately 500 ms.

The FNM and RSM were also implemented in C/C++ for execution on a single core of a fast CPU (Intel Xenon X5550 at 2.67 GHz). The computations were performed in double-precision as the single-precision computation times were longer because of slower execution of single-precision complex exponentials in the standard C/C++ math library. For the same parameters used to generate Table I, the GPU times for the FNM ranged from 114 to 175× faster than the CPU times (times were not tabulated). The computation times of the RSM on the CPU for the parameters in Table I were too long to be measured in a reasonable period of time, taking more than 14 h to calculate only one timing sample for the 0.01% accurate 256³-field point case (see Table II for array computations using the RSM).

Table II.

Comparison of gpu computation times for arrays consisting of 512 and 20² elements and 256³ field points computed using rsm, fnm, the 1-d convolution algorithm, and the 2-d convolution algorithm.

Array Size	RSM	FNM	1-D Convolution	2-D Convolution
512	172 394 s	261 s	0.744 s (0.55 s)	N/A
202	134 683 s	204 s	N/A	0.712 s (0.59 s)

All computation times are in seconds. The RSM and FNM timing is for the 0.01% accuracy case studied in Table I.

Time in parentheses is the time required to pre-compute the single-piston field using the FNM and 0.01% accuracy.

B. Regular Arrays of Rectangular Pistons

1) 1-D Regular Arrays

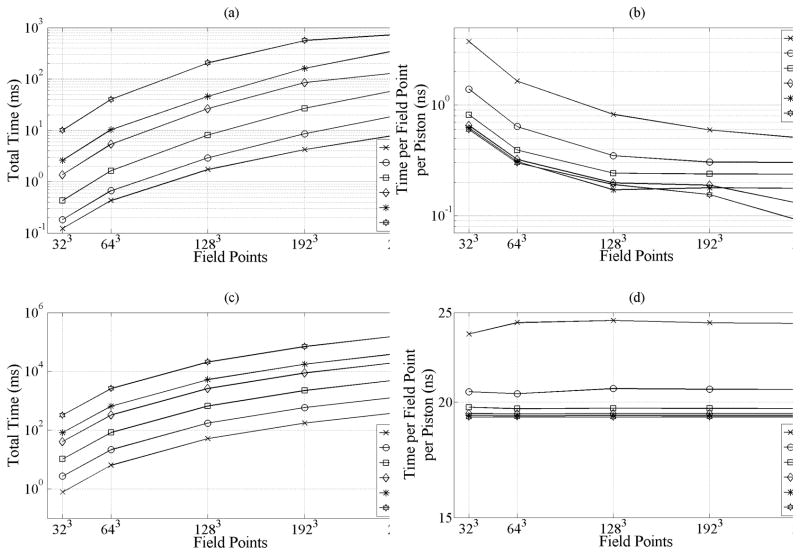
GPU computation times measured for the 1-D convolution algorithm as a function of the number of field points and array pistons are summarized in Fig. 7(a). Notable is the case of a 512-piston array, in which a 256³ point field volume is calculated within 745 ms. Computation times generally increase with increasing numbers of pistons and numbers of field points; however, it is apparent that there is a gain in computation efficiency with increasing numbers of both field points and pistons as is summarized in Fig. 7(b). The most efficient result shown in Fig. 7(b) corresponds to the 512-piston array with 256³ field points, which is calculated within 0.087 ns per field point per piston, in contrast to direct use of the FNM, which requires 30 ns per field point, and the RSM, which requires 21 μs per field point (for 0.01% near-field accuracy). Other notable results for 256³ field points include the 64-piston case, which is 40% more efficient than the 128-element case, and the 16- and 32-piston cases, which have nearly the same efficiency. Corresponding CPU results in Figs. 7(c) and 7(d) illustrate the relative speed improvements obtained from GPU computing for 1-D arrays. The GPU result is 222× faster than the most efficient CPU case of 256³ field points for 512 pistons. The efficiency of CPU computations shown in Fig. 7(d) remains flat as a function of field points.

Fig. 7.

Computation times in milliseconds for (a) GPU and (c) CPU field predictions using 1-D arrays ranging from 1 to 512 pistons and varying numbers of field points. Increasing field points and number of pistons results in increasing computation times. In the case of a 512-piston array, a 256³-point field volume is calculated within 745 ms on the GPU, 165 533 ms on the CPU, thus 222× faster on the GPU. Corresponding computation times in nanoseconds per piston per field point for (b) GPU and (d) CPU. In the case of a 256³-point field volume generated for a 512-piston array, the execution time per field point per piston is within 0.087 ns on the GPU and 19.3 ns on the CPU. The efficiency of GPU computations improves with increasing numbers of field points and pistons, whereas the efficiency of CPU calculations improves primarily with increasing numbers of pistons. All times are averaged over 10 runs; standard deviations are negligible and omitted for clarity.

2) 2-D Regular Arrays

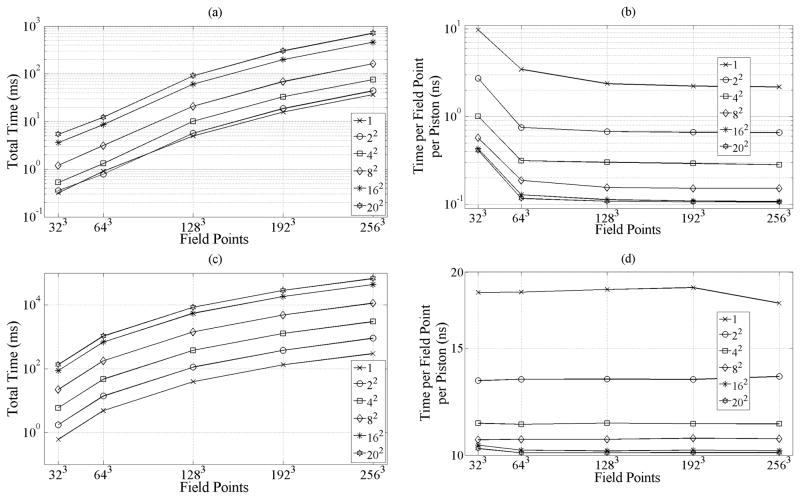
GPU computation times measured for the 2-D convolution algorithm as a function of number of field points and numbers of array pistons are summarized in Fig. 8(a). Notable is the case of a 20² piston array, in which a 256³-point field volume is calculated within 713 ms. Computation times generally increase with an increasing number of pistons and field points; however, it is apparent that there are large gains in computation efficiency with increasing numbers of pistons, as is summarized in Fig. 8(b). The most efficient case shown corresponds to the 20² piston array with 256³ field points, which is calculated within 0.11 ns per field point per piston. Across all array sizes, the computation efficiency is relatively flat for 64³ field points and greater. Corresponding CPU results in Fig. 8(c) and 8(d) illustrate the relative speed improvements obtained from GPU computing for 2-D arrays. The GPU result is 95× faster than the most efficient CPU case of 256³ field points for 20² pistons. As in the 1-D case, the efficiency of CPU computations shown in Fig. 8(d) remains flat as a function of field points.

Fig. 8.

Computation times in milliseconds for (a) GPU and (c) CPU field predictions using 2-D arrays ranging from 1 to 20² pistons and varying numbers of field points. Increasing field points and number of pistons results in increasing computation times. In the case of a 20² piston array, a 256³-point field volume is calculated within 713 ms on the GPU, 67 717 ms on the CPU, thus 95× faster on the GPU. Corresponding computation times in nanoseconds per piston per field point for (b) GPU and (d) CPU. In the case of a 256³-point field volume generated for a 20²-piston array, the execution time per field point per piston is within 0.11 ns on the GPU and 10.1 ns on the CPU. The efficiency of GPU computations improves with increasing numbers of field points and pistons, whereas the efficiency of CPU calculations improves primarily with increasing numbers of pistons. All times are averaged over 10 runs; standard deviations are negligible and omitted for clarity.

3) Full Array Calculations using RSM and FNM

Table II summarizes GPU computation times for 1-D and 2-D arrays using both the RSM and FNM for 256³ field point using parameters identical to the 0.01% accuracy case in Table I. The corresponding 1-D and 2-D convolution times are also tabulated for comparison with the time required to pre-compute the single-piston field shown in parentheses. The times are separated in this case because the single-piston field may be reused repeatedly for array computations in which case there is no pre-computation cost. For the parameters studied, the FNM is 660× faster than the RSM for array calculations. When the pre-computed field for a single-piston is reused, the 1-D and 2-D array algorithms based on convolution are over 5 orders of magnitude faster than the RSM and over 2 orders of magnitude faster than the FNM.

IV. Discussion

The calculation of acoustic fields is a highly parallelizable process that is ideally suited for GPU computation. For single-piston computations, both the RSM and the FNM were implemented on the GPU, and the accuracy was compared to an equivalent MATLAB implementation of FNM in single-precision. The errors in both the MATLAB and GPU computations are larger than the single-precision epsilon value of 5.96×10⁻⁸, which is primarily due to numerical round off, for example, when variables such as wavenumber and field-point locations are converted from double- to single-precision. As expected, the FNM converges much faster than the RSM as a function of abscissas required to achieve minimum accuracy. Improvements in fast, hardware-based GPU functions for calculating complex exponentials and square roots will directly improve accuracy and performance of acoustic field prediction. The choice of large array elements in the accuracy tests demonstrates a critical case for the application of RSM and FNM in the near-field, and it was also necessary for comparison to previously-published results [13], [26]. In therapeutic ultrasound, increased grating lobes and limited steering are often traded in favor of higher total acoustic power for a given number of transmitters, so the elements can easily approach λ or 2λ in each direction (though perhaps not 5λ by 7.5λ as used to obtain results in Figs. 4–6).

The speed of computation realized by GPU computing far surpasses that of CPU computing for the examples explored here. Despite using a relatively current and fast CPU processor, the GPU performed 95–222× faster in the tests presented. In neither case was the code excessively hand-optimized. The CPU times would be improved by utilizing vectorized instructions [27] and multiple processors. Neither the RSM nor the FNM presented here include any far-field approximations, which would lead to speed gains for far-field calculations because of a reduction in the number of square root operations and fewer operation overall. Nonetheless, the FNM performs very well in the far field without additional modification, requiring only 4 to 8 Gauss abscissas to achieve 0.01% accuracy between 1 and 10 far-field transition distances from the piston for the example presented.

The advantages of the FNM approach are further highlighted when the field from a single piston can be reused (assuming that superposition holds) to generate fields from large 1-D and 2-D arrays, while encumbering very little additional computation time to arbitrarily phase or apodize the array. For example, the reference field from a single piston may be pre-calculated with very high degree of accuracy (e.g. using 100 abscissas), in single- or double-precision, and stored in memory. The resulting fields generated for regularly-sampled arrays, being the result of basic multiply-accumulate operations, will not be degraded by function approximations. Observing that this process mirrors the operation of the majority of ultrasound array designs that are based on regularly sampled 1-D and 2-D arrays of (ideally) identical pistons, real-time field prediction for these types of arrays is no longer a limitation. Furthermore, GPUs are inexpensive, compact, integrate well with CPU-based imaging systems, and are suitable for other forms of signal processing commonly found in ultrasound imaging [28].

The simplification of the 1-D and 2-D field computations to a basic process of convolution between a complex array of focusing/apodization terms with the complex field generated for a single piston opens opportunities to further optimize the computation. The most obvious optimization involves the use of the Fast Fourier Transform (FFT) to speed the computation. This optimization was not pursued in this work primarily due to the limited performance gain in the 2-D case since the conventional 2-D convolution is O(MNPQ) operations, where M and N are the padded width and height of the 2-D reference field plane, and P and Q are the width and height of the mask. The FFT-based 2-D convolution is O(MN(log(MN)) operations. The FFT-based convolution may not be faster than the conventional convolution implemented here unless the reference field is very large. Furthermore, additional work is needed to determine if the additional overhead associated with 1-D and 2-D FFTs will yield significant performance advantages.

Another optimization involves the class of separable convolution masks where $w_{ij}^{\prime }$ in (9) may be expressed as the outer product of two 1-D masks. The 2-D separable convolution requires O(MN(P+Q)) operations, thus making it significantly faster than conventional convolution by a factor of PQ/(P+Q) and comparable or faster than FFT-based convolution in many circumstances. Even for masks that are not separable, a low-rank approximation may be obtained using the Singular Value Decomposition (SVD) where the left and right eigenvector pairs corresponding to the most significant singular values serve as 1-D masks in each dimension. Although a very significant performance gain can be obtained from separable masks, more work is needed to determine the accuracy of low rank approximations to complex phases and apodizations typically utilized in therapeutic ultrasound.

The normalized computation times per field point per piston for the 1-D case (0.087 ns) was slightly more efficient than that obtained for the 2-D case (0.11 ns), which is likely due to more efficient use of shared memory in the 1-D case. To keep the algorithms relatively simple, only limited optimizations were pursued. Newer generations of GPU processors will likely feature both level 1 and level 2 caches, which will reduce the burden on the programmer to optimize shared memory usage. Also, all of the algorithms described here are easily distributed across multiple inexpensive GPU boards to obtain faster computation times depending on the application.

V. Conclusion

In summary, we present our initial results using GPUs to accelerate the prediction of large-scale acoustic fields relevant to ultrasound hyperthermia. The FNM was chosen over other methods due to its rapid convergence and accuracy in the near-field up to the surface of the radiator. Algorithms for regularly-sampled 1-D and 2-D piston-arrays were presented and benchmarked to demonstrate the power of GPU-based field prediction for scenarios commonly found in ultrasound therapy. Our goal of generating the complex acoustic field for a volume containing 10 million points within 1 s is easily achieved using the algorithms and hardware presented. The methods developed here may be applied to treatment planning, thermal dose prediction, and real-time control of therapeutic ultrasound.

Biographies

Mario Hlawitschka studied computer sciences and electrical engineering with a focus on signal processing and visualization, and received his B.Sc. and M.Sc. (Diplom-Informatiker) degrees from the University of Kaiserslautern, Germany, in 2004. He received a Ph.D. (Dr. rer. nat.) from the Universität Leipzig, Germany in 2008 for his work on visualization of medical data, and completed postdoctoral research in the Department of Biomedical Engineering and the Department of Computer Sciences at the University of California, Davis.

Dr. Hlawitschka is currently a professor of computer science at the Universität Leipzig.

Robert J. McGough was born in Hinsdale, IL on October 1, 1965. He received the B.E. degree (summa cum laude) in electrical engineering and physics from Vanderbilt University, Nashville, TN, in 1987, the M.S. degree in electrical engineering from the University of Illinois, Urbana-Champaign, in 1990, and the Ph.D. degree in electrical engineering from the University of Michigan, Ann Arbor, in 1995.

He is currently an Associate Professor in the Department of Electrical and Computer Engineering, Michigan State University. His research interests include biomedical ultrasonics, thermal therapy, targeted drug delivery, and medical imaging.

Dr. McGough is a member of IEEE (UFFC and EMB Societies), the Society for Thermal Medicine, the Acoustical Society of America, and the International Society for Therapeutic Ultrasound.

Katherine W. Ferrara (S′82 M′87 SM′99) received the B.S. and M.S. degrees in electrical engineering in 1982 and 1983, respectively, from the California State University, Sacramento, and the Ph.D. degree in electrical engineering and computer science in 1989 from the University of California, Davis. From 1983 to 1988, she worked for Sound Imaging, Inc., Folsom, CA, and for General Electric Medical Systems, Rancho Cordova, CA, in the areas of magnetic resonance and ultrasound imaging.

From 1989 to 1993, she was an associate professor in the Department of Electrical Engineering at California State University, Sacramento. From 1993 to 1995, she was a principal member of the research staff at the Riverside Research Institute, New York, NY. From 1995 to 1999, she was an associate professor at the University of Virginia, Charlottesville, VA. She is currently a professor of Biomedical Engineering, at UC Davis and is a Fellow of the IEEE, the American Association for the Advancement of Science, the Biomedical Engineering Society, the Acoustical Society of America, and the American Institute of Medical and Biological Engineering. She is an author of more than 200 papers in the areas of imaging and drug delivery and is currently focused on the use of advanced imaging techniques to enhance therapeutic efficacy.

Dustin E. Kruse received a B.A. degree in physics from the State University of New York College at Geneseo in 1996, the M.E. degree in electrical engineering from the University of Virginia, Charlottesville, VA, in 1999, and the Ph.D. degree in biomedical engineering in 2004, also from the University of Virginia. His graduate work involved the development and application of high-frequency ultrasound to image blood flow in the microcirculation.

Currently, Dr. Kruse is an assistant research professor in the Department of Biomedical Engineering at the University of California at Davis. His research interests include ultrasound imaging, ultrasound tissue heating, contrast-assisted ultrasound imaging, and radio-frequency electromagnetic tissue heating. He is a member of the Society for Thermal Medicine.