Factors limiting the transmission of HIV mutations conferring drug resistance: fitness costs and genetic bottlenecks

Abstract

Transmission of HIV strains with drug-resistance mutations (DRMs) causes public health problems in resource-rich countries. We use a stochastic model, with data from viral competition experiments, to analyze the effect of fitness costs (FCs) and genetic bottlenecks on limiting transmission of 10 clinically significant DRMs. Transmission of DRMs with low FCs (∼0.2%) is similar to wild-type; transmission chains last ∼8 generations causing clusters of ∼60 infected individuals. Genetic bottlenecks substantially limit transmission of DRMs with moderately high FCs (∼0.6%); chains last ∼1–3 generations with transmission clusters of 2–7. Transmission of DRMs with extremely high FCs (>6%) only occurs from ∼5% of index cases. DRMs can revert to wild-type and remain as minority strains, within treatment-naïve individuals, undetectable by current resistance assays. We calculate, based on assay sensitivity, the length of time each DRM is detectable within individuals. Taken together, our results imply a hidden epidemic of transmitted resistance may exist.

A wide variety of HIV mutations conferring resistance to antiretrovirals have evolved over the past 20 years. The presence of even a minority population of certain variants with drug resistant mutations (DRMs) to HIV can increase an individual’s risk of virologic failure on first-line therapy as much as threefold¹,²,³. Viral competition experiments have shown DRMs reduce the replication rate (i.e., fitness) of HIV; some have a limited effect on reducing fitness, whilst others have a substantial effect⁴,⁵. Reduced fitness limits the transmission of DRMs to some degree, because these mutations can revert to wild-type and wild-type strains can then out-compete the strains with the DRM. Analysis of viral sequences in acutely infected individuals has shown that at each transmission event a genetic bottleneck occurs and most HIV infections are initiated by a single variant⁶,⁷. Due to this founder effect, individuals infected with both wild-type and resistant strains are only likely to transmit one strain. Hence, genetic bottlenecks could also limit transmission of DRMs. Here, we use data from viral competition experiments and a novel stochastic model to evaluate the effect of fitness costs and genetic bottlenecks on limiting transmission of 10 isogenic strains of HIV with DRMs. For comparative purposes, we also model the transmission of the corresponding wild-type strain. Each of the 10 DRMs that we investigate (Y181C, K103N, K70R, L74V, K219Q, M41L, D67N, T215Y, M184V and K65R) is a single point mutation associated with resistance to nucleoside or non-nucleoside reverse transcriptase inhibitors. They range from those with a very high fitness cost to those with a very low fitness cost⁴. Our modeling study is the first to investigate the impact of relative fitness and genetic bottlenecks on limiting transmission of DRMs. The stochastic model we present in this study can be used to assess transmission between Men Who Have Sex With Men (MSM) or heterosexuals; here we parameterize it to reflect transmission in a MSM community in a resource-rich country.

All of the DRMs we investigate are of clinical significance⁸. For example, M184V reduces susceptibility to emtricitabine (FTC) and lamivudine (3TC) by >100-fold and K65R is the primary mutation associated with resistance to tenofovir (TFV)⁹,¹⁰. We measure transmission in terms of the length of transmission chains and the size of the transmission clusters that each strain can generate. For wild-type strains of HIV, we define the length of a transmission chain to be the number of generations of individuals that are directly, or indirectly, infected by the index case; where the index case represents the first generation. We define the size of the a transmission cluster as the index case plus the total number of individuals who are directly, or indirectly, infected by the index case over the duration of the transmission chain. Definitions of transmission chains and transmission clusters for strains with DRMs are not as simple as for wild-type strains. DRMs in untreated individuals can revert to wild-type by back-mutation, then decrease in the plasma relative to the wild-type strain and subsequently not survive a genetic bottleneck. At that point the DRM would no longer be transmitted and its transmission chain will terminate. For each of the 10 strains with DRMs that we investigate, only one nucleotide change is necessary for the resistant strain to revert to wild-type. In the case of a strain with the T215Y mutation, a single nucleotide change results in a unique set of wild-type viruses that fully restore replication capacity and drug susceptibility¹¹,¹². For a strain with a DRM we define the length of a transmission chain to be the number of generations of HIV-infected individuals that receive the DRM directly, or indirectly, from the index case; where the index case represents the first generation. We define the size of a transmission cluster as the index case plus the total number of HIV-infected individuals that receive the DRM directly, or indirectly, from the index case over the duration of the transmission chain.

To begin our analyses we used data from viral competition experiments to estimate the relative fitness costs for each of the 10 isogenic strains with DRMs relative to the fitness of the corresponding wild-type strain; see Methods and Cong et al.⁴ We then designed a stochastic mathematical model that includes the effect of relative fitness costs and genetic bottlenecks on limiting transmission (see Methods). We used this model to calculate the expected lengths of transmission chains and the size of transmission clusters generated by the wild-type strain and each of the 10 isogenic strains with DRMs. To make our calculations we constructed a hierarchial modeling framework. Specifically, we coupled the stochastic model with a previously published within-host model¹³ in order to track the viral dynamics within each infected individual in a transmission chain. For individuals infected with only wild-type strains the within-host model simulated the temporal dynamics of the individuals’ viral load over time until the individual was treated. For individuals initially infected by strains with a DRM, the wild-type strain evolved through back-mutation and the within-host model simulated the competitive dynamics between the wild-type strain and the strain with the DRM. In each infected individual the proportion of the virion population containing the DRM decreased over time; the rate of decrease was a function of the relative fitness cost. Within-host viral dynamics for each of the 10 DRMs were modeled using their estimated relative fitness cost (see Methods).

We modeled the probability that an infected individual in the transmission chain would transmit HIV at any point in time as a stochastic process that was a time-dependent function of their infectivity (we estimated their infectivity by using viral load data simulated by the within-host model) and their sexual behavior. Sexual behavior was modeled independently for each infected individual using stochastic functions to determine their number of sex acts, as well as the timing of these sex acts. Hence the number of transmission events that occurred, and the timing of these events, was determined probabilistically for each individual based on virologic and behavioral factors. At each transmission event we modeled a genetic bottleneck. Whether the founder virus was wild-type or a strain with a DRM was determined probabilistically, but depended upon the composition (at the time of the transmission event) of the virion population in the transmitting individual (which was tracked by the within-host model). For further details of the modeling framework see Methods.

The model was designed to reflect the stochastic development of transmission chains and transmission clusters, which resulted from sexual transmission, in communities of men who have sex with men (MSM) in resource-rich countries. Since treatment is readily available in these countries we assumed individuals would receive first-line and, if necessary, second-line regimens. Effective treatment reduces the viral load in HIV-infected individuals below 50 copies/mL and once viral load falls below 400 copies/mL transmission has been found to be extremely unlikely¹⁴; consequently, in our modeling we assumed the probability that treated individuals with undetectable viral load would transmit HIV would be negligible. Even in resource-rich countries, individuals who become infected with HIV are generally not treated until there has been significant decline in CD4 cells, which does not generally occur for several years. We estimated the time from infection to treatment initiation by using data from the Department of Public Health in San Francisco¹⁵. Based on these estimates we varied time to treatment from 6 to 8 years when modeling the stochastic development of transmission chains. See Methods for details.

We also estimated the value of the Basic Reproduction Number (R₀) for each of the strains with a DRM (see Methods) by tracking transmission chains. For both the wild-type and resistant strains R₀ is defined to be the average number of secondary infections resulting from an index case in a population of entirely susceptible individuals. Individuals who are directly infected by the index case are defined as secondary infections. When we model a transmission chain for a DRM we begin with an index case initially infected with only a resistant strain. During the course of their infection the resistant strain can revert to wild-type. Hence, the index case can transmit both wild-type and resistant strains. When calculating the value of R₀ for a DRM we include in our calculations only individuals who are directly infected with resistant strains by the index case.

Even when a DRM is being transmitted, the presence of the DRM may be undetectable in a treatment-naïve individual. The sooner the strain is genotyped, after transmission occurs, the more likely the DRM will be detected. However, whether or not a DRM is detected will also depend upon its relative fitness cost and the sensitivity of the resistance assay. If reversion occurs, the wild-type strain (due to its greater fitness) will begin to out-compete the strain with the DRM¹⁶,¹⁷. Hence, over time the DRM may eventually become undetectable in a treatment-naïve individual. The lower the relative fitness cost of the DRM and/or the more sensitive the assay (i.e., the lower the detection threshold of the assay), the longer the DRM will remain detectable³,¹⁸. Currently, DRMs are only detected if they are present in at least 20% of the virus population in the plasma of an HIV-infected individual; this is the sensitivity of current resistance assays which are based on sequence analysis¹⁹. A new generation of resistance assays, based on real-time PCR, is gradually being introduced; currently, these assays serve only as research tools²⁰,²¹. These assays are much more sensitive than the current resistance assays as they have much lower detection thresholds²². Therefore, the introduction of these new assays will increase the detection of DRMs²³. Detection thresholds of these new resistance assays differ by strain (from 0.8% to 2%) based on the primers used in the assay, as well as the frequency of naturally occurring polymorphisms in the region of the DRM²². We calculated detection times, in treatment-naïve individuals, for each of the 10 DRMs. To make these calculations we used our estimates of relative fitness costs and the within-host model of viral dynamics¹³ (see Methods). We calculated detection times based on using current resistance assays with detection thresholds of 20%, and also using next generation resistance assays with detection thresholds of 1%.

Results

Relative Fitness Costs of DRMs

Our results show that the 10 DRMs that we investigated show considerable variation in their relative fitness cost; ranges are given in Table 1. We note that we did not estimate the relative fitness cost listed for M184V in Table 1. This is because it had already been estimated by Paredes et al.¹⁶. In our analyses we used it as a calibration factor to calculate the relative fitness costs for the other 9 DRMs (see Methods). Relative fitness costs range from a minimum of 0.11% for K70R (the most fit strain in our analysis) to a maximum of 16% for K65R (the least fit strain in our analysis).

Table 1. The relative fitness cost of M184V was previously calculated ¹⁶, and used as a calibration factor to estimate the relative fitness costs for the other 9 DRMS (see Methods). Ranges reflect heterogeneity in the data. Values (median and interquartile range (IQR)) for R₀’s and detection times were estimated using uncertainty analyses. The maximum detection time was 8 years, because individuals in resource-rich countries are on treatment by then.

DRM	Relative fitness cost (%)	R0 Median (IQR)	Detection Time (years) Assay Sensitivity (20%) Median (IQR)	Assay Sensitivity (1%) Median (IQR)
K70R	0.11–0.23	1.5 (1.5–1.6)	>8	>8
Y181C	0.17–0.35	1.4 (1.3–1.5)	7.8 (6.8–8.0)	>8
K219Q	0.40–0.80	0.74 (0.62–0.84)	3.7 (3.2–4.3)	5.3 (4.6–6.2)
L74V	0.57–1.2	0.51 (0.43–0.61)	2.7 (2.4–3.1)	3.8 (3.3–4.5)
D67N	1.1–2.1	0.27 (0.22–0.32)	1.5 (1.3–1.8)	2.1 (1.9–2.5)
M41L	1.2–2.5	0.21 (0.18–0.25)	1.3 (1.1–1.5)	1.8 (1.5–2.1)
K103N	1.7–3.5	0.14 (0.12–0.18)	0.97 (0.84–1.1)	1.3 (1.1–1.6)
T215Y	3.7–7.3	0.05 (0.04–0.06)	0.47 (0.40–0.56)	0.63 (0.55–0.75)
M184V	4.0–8.016	0.04 (0.04–0.05)	0.43 (0.37–0.52)	0.58 (0.50–0.70)
K65R	8.0–16	0.02 (0.02–0.04)	0.21 (0.17–0.25)	0.28 (0.23–0.33)

Detection Times of DRMs

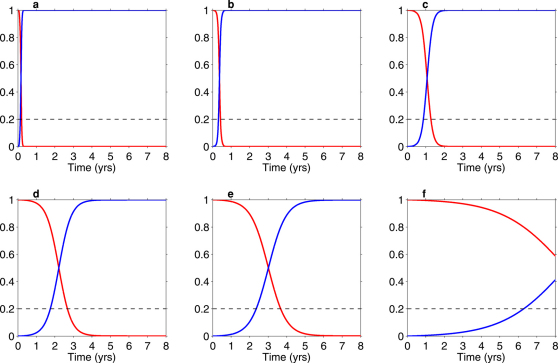
Figure 1 and Figure S1 in the Supplementary Information (SI), show the competitive-reversion dynamics within treatment-naïve HIV-infected individuals. The dynamics of the wild-type strain within an individual are shown by the blue line and the dynamics of the strain with a DRM by the red data. In these simulations the individual is assumed to be initially infected with the strain with the DRM and the wild-type strain emerges due to back-mutation. The between strain competitive dynamics are shown up until the time the individual receives treatment (Figure 1 and Figure S1 in the SI). The maximum time to treatment is assumed to be 8 years, as this is the maximum time to treatment initiation we estimated from data from HIV-infected individuals in MSM communities (see Methods). The horizontal black line in Figure 1 (and Figure S1 in the SI) delimits the 20% threshold at which DRMs can no longer be detected by current resistance assays. In each simulation the wild-type strain out-competes the strain with the DRM because the wild-type strain has the highest viral replication rate (i.e., the strain with the DRM is less fit); see Table 1.

Figure 1. Numerical results from the within-host model showing the fraction of virions that are resistant (red curve) as a function of years since infection in a treatment-naïve individual.

The blue curve indicates the fraction of virions that are wild-type. The 20% threshold for detection of resistance based on current resistance assays, is denoted by the dashed black line. DRMs shown are K65R (a), M184V (b), M41L (c), L74V (d), K219Q (e), K70R (f).

Simulations are shown for K65R (Figure 1a), M184V (Figure 1b), M41L (Figure 1c), L74V (Figure 1d), K219Q (Figure 1e) and K70R (Figure 1f). Simulations for the remaining 4 DRMs (Y181C , T215Y, D67N and K103N) are shown in Figure S1 in the SI, because their dynamics are similar to DRMs shown in Figure 1. Specifically, the dynamics of Y181C are similar to K70R, T215Y to M184V, and both D67N and K103N are similar to M41L. The higher the relative fitness cost of the DRM, the faster it is out-competed by the wild-type strain and the shorter the detection time (Figure 1 and Figure S1 in the SI, and Table 1). Our results show the detection times of transmitted DRMs range from a maximum of ∼8 years for K70R (the most fit strain in our analysis) to a minimum of ∼2 months for K65R (the least fit strain in our analysis). Based on our calculated estimates of relative fitness costs and detection times (based on the 20% detection threshold of the current resistance assays) we categorize the DRMs into 4 fitness categories: (i) DRMs that have very low fitness costs with detection times of ∼8 years after transmission (K70R and Y181C), (ii) DRMs that have moderate fitness costs with detection times of ∼3 to 4 years after transmission (K219Q and L74V), (iii) DRMs that have high fitness costs with detection times of ∼1 to 1.5 years after transmission (D67N, M41L and K103N), and (iv) DRMs that have very high fitness costs with detection times of only ∼2 to 6 months after transmission (T215Y, M184V and K65R) (Figure 1, Figure S1 in the SI, and Table 1; median and interquartile ranges (IQRs) are shown).

Table 1 also shows the detection times of the DRMs if the next generation resistant assays are used, assuming their detection threshold is 1%. Relative fitness costs will be extremely important in determining the effect of increasing assay sensitivity on increasing the detection time (Table 1). Our results show that using the next generation of resistance assays will not significantly increase the detection time of transmitted DRMs with low fitness costs (K70R and Y181C), because they can already be detected for up to ∼8 years when treatment has generally already been initiated. However, the introduction of the new assays will increase the detection time for transmitted DRMs that have moderate fitness costs (K219Q and L74V) by ∼1 year and the detection time for transmitted DRMs with high fitness costs (D67N, M41L and K103N) by ∼6 months. Notably, the introduction of the new assays will have very little effect on increasing the detection time of transmitted DRMs with very high fitness costs (T215Y, M184V and K65R). For example, the detection time after the transmission of K65R will remain very low; it will only increase from the current time of ∼1 month to ∼2.3 months.

Estimates of R₀: wild-type strains & strains with DRMs

The values of R₀ for the strains with DRMs (Table 1) correspond to the four fitness categories we defined based on their relative fitness costs and detection times; median and IQRs for the R₀’s for each of the DRMs are given in Table 1. Our calculations show that DRMs with very low fitness costs (K70R and Y181C) have a R₀ of ∼1.4-1.6, very close to the R₀ of 1.6 for the wild-type strain. Since the R₀’s for K70R and Y181C are greater than one, the transmission of these DRMs could reach self-sustaining levels. However, the R₀ values for the DRMs with a moderate fitness cost (K219Q and L74V) are less than one; they range from 0.5 to 0.7. These results indicate the transmission of K219Q or L74V is unlikely to be self-sustaining, but they would be transmitted to some extent if they evolve under treatment pressure. The values of R₀ for the DRMs with a high fitness cost (D67N, M41L and K103N) are much lower than one, ranging from 0.1 to 0.3. These results indicate that even if high levels of D67N, M41L or K103N evolve under treatment pressure their transmission is likely to be low. DRMs that have very high fitness costs (T215Y, M184V and K65R) have extremely low R₀’s, ranging from 0.02 to 0.05. Since these values are close to zero these DRMs, in general, would only be infrequently transmitted.

Transmission Chains & Clusters: wild-type strains & strains with DRMs

The percentage of simulations where no transmission from the index case occurred is given in Table 2; results are given for both the wild-type strain and the 10 strains with DRMs. For each strain, results are based on 10,000 realizations of the stochastic model; each simulation was run for a maximum of 20 years. In order to predict (for each DRM) the length of a transmission chain that would result from a single mutation, we used the same number of realizations for each of the 10 DRMs. This enabled us to eliminate the confounding effect that would occur due to the differences in the mutation frequency of each DRM in treated individuals. Mutation frequency for each of the 10 DRMs is extremely variable, and depends on both adherence and treatment regimens. For each of the 4 DRMs with the lowest fitness costs, transmission occurred in over 5,300 realizations. For each of the remaining 6 DRMs, with higher fitness costs, transmission occurred in at least 400 realizations. The standard deviations (SDs) of the cluster sizes for these 6 DRMs ranges from 0.24 to 1.1 (see Table S1 in the SI). These SDs are small, all are essentially less than one individual, indicating the sample size of 10,000 realizations is sufficient to describe the distributions.

Table 2. Results from 110,000 simulations of the stochastic transmission chain model; 10,000 simulations were conducted for each DRM and the wild-type strain. Values of the relative fitness costs were used in the within-host model to track viral dynamics within each individual in a transmission chain.

DRM	Simulations where no transmission occurred (%)	Expected Cluster Size (if transmission occurs)	Expected Chain Length (if transmission occurs)	Relative fitness cost used in simulation (%)
Wild-type	18	76.4	7.82	−−
K70R	20	63.0	7.51	0.17
Y181C	23	48.3	7.04	0.26
K219Q	47	6.55	3.05	0.60
L74V	58	3.70	1.97	0.86
D67N	75	2.59	1.37	1.6
M41L	80	2.42	1.28	1.9
K103N	86	2.27	1.18	2.6
T215Y	95	2.09	1.07	5.5
M184V	96	2.06	1.05	6.0
K65R	96	2.05	1.04	12

A transmission chain that lasts for only one generation indicates there is only direct transmission from the index case and no subsequent transmission (i.e., only transmission from the first generation to the second generation). A cluster size of two indicates the index case only infects one individual, since the index case is included when calculating cluster size. Transmission chains terminate due to either stochastic effects or to reaching the cutoff of twenty years. Figure S4 in the SI shows cumulative distribution functions for the proportion of (non-null) transmission chains that terminated in each year for each strain with a DRM, and the wild-type strain. Strains with R₀>1 generally terminated due to reaching the cutoff of 20 years, while strains with R₀<1 generally terminated (due to stochastic effects) before reaching the cutoff of 20 years.

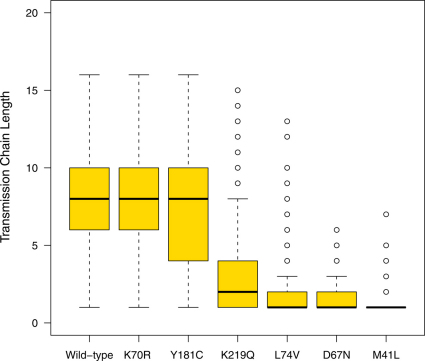
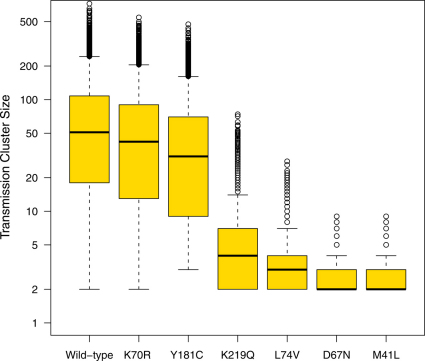
The expected length of transmission chains and the transmission cluster size for each DRM, given there was at least one transmission event from the index case, are presented in Table 2, and shown in Figures 2 and 3 (and S2 and S3 in the SI). Box-plots in Figures 2 and 3 (and Figures S2 and S3 in the SI) show the median and IQRs of the simulations where there was at least one transmission event from the index case. Whiskers on the box-plots indicate the largest and smallest estimates, obtained from the simulations, which are within 1.5 times the IQR. Outliers beyond this are represented with open circles. In Figure 2 (and Figure S2 in the SI) outliers are shown for the chain lengths for the wild-type and 8 of the DRMs (K219Q, L74V, D67N, M41L, K103N, T215Y, M184V and K65R), the remaining 2 DRMs (K70R and Y181C) do not have outliers. Note, transmission cluster size is shown on a logarithmic scale in Figure 3 and S3 in the SI.

Figure 2. Box plots showing distributions of the length of transmission chains for two DRMs with low fitness costs (K70R with a fitness cost of 0.17%; Y181C with a fitness cost of 0.26%), two DRMs with moderate fitness costs (K219Q with a fitness cost of 0.6%; L74V with a fitness cost of 0.86%), two DRMs with high fitness costs (D67N with a fitness cost of 1.6%; M41L with a fitness cost of 1.9%) and the wild-type strain.

Each box plot is based on 10,000 simulations of the stochastic model. Only simulations for which there is at least one transmission of the DRM from the index case are plotted. Medians are denoted by solid black lines while the top and bottom box edges denote the first and third quartile. Whiskers denote the largest and smallest data within 1.5 times the interquartile range.

Figure 3. Box plots showing distributions of the transmission cluster size for two DRMs with low fitness costs (K70R with a fitness cost of 0.17%; Y181C with a fitness cost of 0.26%), two DRMs with moderate fitness costs (K219Q with a fitness cost of 0.6%; L74V with a fitness cost of 0.86%), and two DRMs with high fitness costs (D67N with a fitness cost of 1.6%; M41L with a fitness cost of 1.9%) and the wild-type strain.

Box plots showing distributions of the transmission cluster size for two DRMs with moderate fitness costs. Each box plot is based on 10,000 simulations of the stochastic model. Only simulations for which there is at least one transmission of the DRM from the index case are plotted. Medians are denoted by solid black lines while the top and bottom box edges denote the first and third quartile. Whiskers denote the largest and smallest data within 1.5 times the interquartile range. Note the logarithmic scale.

In our simulations, no transmission occurred from 20% of the index cases infected with wild-type strains (Table 1). Furthermore, when transmission did occur there was very wide variation in the length of transmission chains and their associated transmission clusters that were generated by an index case (Figures 2 and 3). When transmission did occur from an index case infected with wild-type strains, transmission chains could last for ∼8 (mean) generations and generate transmission clusters of ∼76 (mean) infected individuals (Table 2, Figures 2 and 3). In a transmission cluster of this size, ∼2 individuals would be directly infected by the index case and ∼74 would be indirectly infected in the second, third and subsequent generations.

As we found for wild-type strains, no transmission occurred from ∼20% of the index cases infected with strains with DRMs that have very low fitness costs and R₀’s above one (K70R or Y181C) (Table 2). If these DRMs were transmitted there was very wide variation in the length of their transmission chains and the size of the associated transmission clusters (Figures 2 and 3). Transmission of K70R (the most fit of the 10 DRMs) was fairly similar to wild-type, but with slightly smaller transmission clusters of ∼63 (mean) infected individuals (Table 2, Figures 2 and 3). Transmission of Y181C was noticeably lower than wild-type and generated significantly smaller transmission clusters of ∼48 (mean) infected individuals (Table 2, Figures 2 and 3).

Transmission of DRMs with moderate fitness costs and R₀’s just below one (K219Q and L74V) was significantly lower than wild-type strains (Table 2, Figures 2 and 3). Only ∼40-50% of the index cases infected with these DRMs transmitted them (Table 2). Furthermore, when transmission occurred, chains were much shorter (2–3 generations, mean values) and transmission clusters were much smaller (∼4–7 infected individuals, mean values) than for wild-type strains (Table 2, Figures 2 and 3).

Transmission of DRMs with high fitness costs and R₀’s much lower than one (D67N, M41L and K103N) was substantially lower than wild-type strains (Table 2, Figures 2 and 3, Figures S2 and S3 in SI). In this case only 14–25% of index cases transmitted DRMs. When transmission occurred, the index case generally only transmitted the DRM to the next generation and then there was no further transmission; hence transmission chains only lasted for ∼1 generation and transmission clusters were small, ∼2–3 infected individuals (Table 2, Figures 2 and 3, Figures S2 and S3 in SI). However, due to stochastic factors, longer transmission chains and larger transmission clusters sometimes occurred (Figures 2 and 3, Figures S2 and S3 in SI). For example, one index case transmitted M41L for 7 generations and generated a transmission cluster of 9 infected individuals (Figures 2 and 3).

Our results show transmission of DRMs with very high fitness costs and R₀’s close to zero (T215Y, M184V and K65R) are unlikely to be transmitted; only 4%–5% of index cases that were infected with these DRMs transmitted them (Table 2, Figures S2 and S3 in SI). When transmission occurred, as for DRMs with high fitness costs, the transmission chains generally only lasted for ∼1 generation and transmission clusters were small, ∼2 infected individuals (Table 2, Figures S2 and S3 in SI). Due to stochastic factors, these DRMs were occasionally transmitted for 3 generations and generated transmission clusters of 4–5 infected individuals (Figures S2 and S3 in SI).

Temporal Patterns & Network Structure: transmission chains of DRMs

We tracked chronological time during our stochastic simulations in order to visualize the temporal patterns in the development of a transmission chain for both wild-type strains and strains with a DRM. In the majority of cases strains with DRMs that had high (D67N, M41L and K103N) or very high (T215Y, M184V and K65R) fitness costs quickly went extinct (see Table 1). When they were transmitted they showed almost no diversity in the pattern of their transmission chain, as transmission chains were short and cluster sizes were small. However, strains with DRMs with low (K70R and Y181C) fitness costs, moderate (K219Q and L74V) fitness costs and the wild-type strain showed a wide diversity of patterns during the development of their transmission chains and associated transmission clusters.

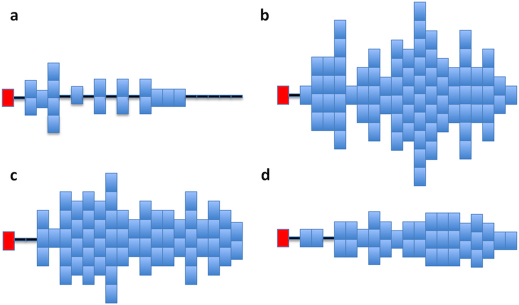
This diversity is illustrated in Figure 4; as an example the DRM K219Q is shown. Each pattern is the result of one stochastic simulation and shows the number of new infections, with K219Q, which occurred each year (over a maximum of 20 years) during the development of one transmission chain. The red block represents the index case and each blue block represents a new infection with K219Q. Horizontal black lines represent the years in which there was either no transmission of either K219Q (or the wild-type strain) or only the wild-type strain was transmitted; transmission of the wild-type strain is not shown. The four transmission chains for K219Q differ in length, the size of the transmission cluster and their transmission pattern (i.e., their development). Chain length varies from a minimum of 9 generations (Figure 4a) to a maximum of 13 generations (Figure 4b), and cluster size varies from a minimum of 18 (Figure 4a) to a maximum of 81 (Figure 4b). In Figure 4A the chain develops fairly slowly and then increases to 2 or 3 infections per year before all transmission of K219Q terminates at ∼15 years. In Figure 4b the chain for K219Q evolves in a complex manner; initially transmission is fairly high, but after a few years it begins to alternate between periods of high and low transmission. In Figure 4c the index case does not transmit K219Q until several years after infection; transmission remains fairly steady for a few years and then increases to form a large cluster. In Figure 4d transmission of K219Q remains low and fairly constant for 20 years.

Figure 4. Figures (a), (b), (c) and (d) show temporal patterns for four transmission chains of K219Q which were generated using the stochastic model.

Each chain is tracked over 20 years beginning with the index case. Red blocks represent index cases and each blue block represents one new infection with a DRM. Years in which no infections occur are denoted by a horizontal black line.

Our stochastic model, as well as tracking the length of a transmission chain, the associated cluster size and the transmission pattern that develops, also tracks network structure. The term network has several definitions in the literature. In previous modeling studies, networks have been specified and then used as inputs to a mathematical model; these networks have been defined based on sexual/social behaviors. Whereas in empirical molecular epidemiological studies, networks are determined from the empirical data that are collected; these networks are defined based on the specific transmission events that have occurred. Consequently, the observed transmission network is a subset of a behavioral network. A novel feature of our model is it generates a transmission network, and not a behavioral network. Each transmission chain generates its own transmission network. The structure of the network shows which HIV-infected individual has transmitted HIV to which susceptible individual over a specified window of time. Hence the network represents a directed tree. Network structure reflects a cross-section of the transmission chain over a specified period of time. Consequently network structure, as in molecular epidemiological studies, depends on the length of the window period. The transmission networks we generate are constrained by the unspecified underlying behavioral networks. Therefore it is possible that the length of transmission chains and the size of transmission clusters that we have calculated represent upper bounds as to that which may be observed from empirical data.

In Figure 5 we show the network structure, based on the number of transmission events that occurred over a time period of 10 years, for each of the 4 transmission chains of K219Q shown in Figure 4. Only the events in which the DRM was transmitted are shown. As can be seen, very different network structures can develop (Figure 5). Similar results were found for the other DRMs with moderate (L74V) and low (K70R and Y181C) fitness costs and the wild-type strain (results not shown).

Figure 5. Network structure (over the last 10 years of a transmission chain) for the four transmission patterns for K219Q shown in Figure 4.

Infections with wild-type strains are not shown. Each of the 4 networks was generated by one index case.

Discussion

Using our novel stochastic model, and empirical data, we have gained important new insights into the transmission of wild-type strains. Notably, we have found a significant proportion of index cases (20%) infected with wild-type strains, although they have sex with uninfected partners, may not transmit HIV. Our results suggest stochastic factors that influence sexual transmission in a MSM community could have fairly substantial effects on limiting transmission of wild-type strains. This occurs because the probability of transmission of HIV during any single sex act is low (0.001–0.003). We have found that if transmission does occur, the length of the resulting transmission chain is likely to be fairly long and the number of infected individuals in a transmission cluster to be fairly high. Notably, our results are in agreement with recent results from a study of wild-type strains in a community of MSM; this study identified 38 transmission clusters with a mean cluster size of 29 and a maximum cluster size of 263²⁴. We have found wild-type strains can be expected to show considerable variation in the length of their transmission chains and the size of their transmission clusters. These results imply that molecular epidemiologic and phylogenetic studies are likely to uncover a wide diversity of transmission patterns and network structures.

We have also gained important new insights into the factors limiting the transmission of DRMs. As with wild-type strains, their transmission is influenced by stochastic factors²⁵. In addition, they are limited by other factors. We have found the effects of reduced fitness and genetic bottlenecks have a relatively minor impact on limiting transmission of very fit DRMs (K70R and Y181C). Transmission of these DRMs, because their fitness costs are low, is almost comparable to wild-type; because they have a high probability of “surviving” multiple genetic bottlenecks. DRMs with low to moderate fitness costs (K70R, Y181C, K219Q and L74V) can be expected to show considerable variation in the length of transmission chains and the size of transmission clusters, as well as a high diversity in transmission patterns and network structures. We have found that the higher the fitness cost of a DRM, the lower the probability that it will “survive” many genetic bottlenecks; hence the shorter the transmission chains and the smaller the associated transmission clusters. Reduced fitness and genetic bottlenecks have a very substantial effect on limiting the transmission of DRMs with high (D67N, M41L and K103N) or very high fitness costs (T215Y, M184V and K65R). Our results are in agreement with the limited empirical data; for example, we have estimated the average cluster size for K103N to be ∼2, and empirical studies have identified clusters of this DRM consisting of only two individuals¹⁹. Notably, we have found DRMs with very high fitness costs, between 6 to 12%, result in very infrequent transmission.

Our modeling shows that the transmission of DRMs with very low fitness costs (K70R and Y181C) has the potential to reach self-sustaining levels in certain communities as the value of their R₀ is greater than one. This is broadly in agreement with recent phylogenetic studies that have established the presence of self-sustaining drug resistant lineages circulating in treatment naïve individuals²⁶. However, if a DRM has a fitness cost greater than 0.4% its R₀ is less than one; consequently transmission of this DRM is not high enough to be self-sustaining. Notably, if a DRM (with an R₀< 1) evolves fairly frequently under the selective pressure of treatment it could be highly prevalent. For example, M184V is rarely observed in treatment-naïve individuals¹⁹ but its prevalence is nearly 50% in treatment-experienced individuals²⁷,²⁸,²⁹. Conversely, if a DRM with an R₀ greater than one only emerges infrequently under the selective pressure of treatment it could have a low prevalence. Due to the interaction between acquired resistance and transmitted resistance in driving prevalence, the prevalence of individual DRMs that are associated with resistance to non-nucleoside reverse transcriptase inhibitors (NNRTIs) has been found to be very variable²⁹: 22% for K70R, 13% for K219Q, 2.7% for L74V, 25% for D67N, 34% for T215Y, 33% for M41L, 51% for M184V, and 1.2% for K65R among NRTI experienced individuals. The prevalence in treatment-experienced individuals for the two DRMs associated with resistance to NNRTIs, that we investigate, ranges from 22% for Y181C to 40% for K103N.

In this study we limited our analysis to investigating the effect of fitness costs and genetic bottlenecks on limiting the transmission of DRMs which result from single nucleotide mutations. We focused on single mutants to first define how well-known fitness effects may influence the dynamics of transmitting resistance. Interestingly, our findings are generally in agreement with the limited in-vivo data on length of transmission chains and size of transmission clusters associated with drug-resistant transmission¹⁹,³⁰,³¹. However, we caution that the overall in-vivo fitness cost of resistance mutations may in some instances be modulated by other mutations, as some results from in-vitro studies have recently suggested⁴. In future work we plan to investigate the effect of complex mutational patterns and fitness modulations on the transmission of DRMs. We will also extend our analyses to include DRMs which confer resistance to protease, integrase, and fusion inhibitors. In addition, we will develop more complex models that include behavioral networks and assess their effect on constraining transmission networks. At that final stage we will compare our predictions for transmission networks with empirical network data obtained from well characterized cohorts of primary HIV infections.

Using the current resistance assays, our results indicate transmitted DRMs with low fitness costs (K70R and Y181C) are very likely to be detected in treatment-naive individuals, because these DRMs can persist for 8 or more years. However, DRMs with moderate fitness costs (K219Q and L74V) may not be detected if treatment-naïve individuals are tested for resistance more than 3.5 years after the transmission event. DRMs with high fitness costs (D67N, M41L and K103N) are unlikely to be detected if resistance testing occurs more than one year after the transmission event. Notably, we have found DRMs with very high fitness costs (T215Y, M184V and K65R) will not be detected unless resistance testing takes place during, or soon after, primary infection.

Our results imply there could be a hidden epidemic of transmitted resistance composed of strains with DRMs that have moderate, high or very high fitness costs. Although these DRMs may be present at very low levels in individuals they are likely to reemerge under treatment pressure and have clinical significance. A recent study has shown that even when DRMs are present at very low levels (0.003% to 2%) within an individual, well below the detection level of current resistance assays, they more than double the risk of virologic failure³. Consequently, a hidden epidemic of transmitted resistance is likely to have significant consequences for public health. Our results have shown that introducing the next generation of resistance assays, with sensitivities as low as 1%, is unlikely to increase the detection of DRMs that have low fitness costs (K70R and Y181C) since these DRMs can already be detected for 8 or more years. However introducing these new assays could substantially increase the detection of DRMs with moderate fitness costs (K219Q and L74V) as their detection time will increase to ∼3–5 years post-seroconversion. Notably, our results indicate the new assays are unlikely to increase detection of DRMs with high (D67N, M41L, and K103N) or very high (T215Y, M184V and K65R) fitness costs because their detection times will only increase by one to two months. Therefore, even after the introduction of the next generation of more sensitive resistance assays, an epidemic of transmitted resistance could remain partially hidden.

Methods

Defining Fitness Costs

Fitness cost of a DRM can be expressed as either an absolute fitness cost or a relative fitness cost. The absolute fitness cost of a DRM is the difference in the replication rate of a wild-type and a resistant strain; this is expressed in terms of virions per unit time. The relative fitness cost of a DRM is the difference in the replication rate between a wild-type and a resistant strain divided by the replication rate of the wild-type strain; this can be expressed either as a percentage or a proportion.

Estimating Fitness Costs

To conduct our modeling analyses we needed to estimate the relative fitness cost for 9 (Y181C, K103N, K70R, L74V, K219Q, M41L, D67N, T215Y and K65R) of the 10 DRMs in our analysis. We note that that the relative fitness cost of M184V is known, it has been estimated previously by Paredes et al.¹⁶. The absolute fitness cost can be converted into the relative fitness cost. Conversely, the relative fitness cost can be converted into the absolute fitness cost. To make this conversion it is necessary to know the replication rate³². We calculated relative fitness costs in two steps. In step one, we used estimates for absolute fitness costs from Cong et al.⁴ and the estimate of the relative fitness cost of M184V from Paredes et al.¹⁶ as a calibration factor to calculate the replication rate of the wild-type strain. In step two, we divided estimates for the absolute fitness costs from Cong et al. by our calculated replication rate of the wild-type strain.

Cong and colleagues estimated absolute fitness costs for each of the 10 DRMs by conducting a series of viral competition experiments. In these experiments each strain with a DRM was compared, in terms of its replication rate, with the corresponding isogenic wild-type strain⁴. During experiments the proportion of virions that were wild-type versus those which contained the DRM were tracked over a series of passages (i.e., over time) in MT4-cell culture; several passages were used to prevent significant depletion of MT4 cells. As shown by their experimental data⁴ the log of the ratio of the number of virions with a DRM to the number of wild-type virions decreases linearly over time. Standard mathematical growth-competition models, as described in Maree et al.³², predict that the relationship is:

where M(t) represents the number of virions with a DRM per microliter of blood at time t, W(t) the number of wild-type virions per microliter of blood at time t, R the replication rate of the wild-type strain and Δ the relative fitness cost (due to the DRM) expressed as a proportion. Note that in equation 1 the product of R and Δ equals the absolute fitness cost.

By dividing the value of the absolute fitness cost for M184V estimated by Cong et al. by the relative fitness cost of M184V estimated by Paredes et al.¹⁶ we calculated the replication rate of the wild-type strain. We assumed this replication rate was approximately constant in all of the competition experiments conducted by Cong and colleagues, because MT4 concentrations were non-limiting.

We then, for each of the DRMs except M184V, estimated their relative fitness cost by dividing the value of their absolute fitness cost (estimated by Cong et al.) by our calculated rate of replication of the wild-type strain. Due to the fact that Paredes et al.¹⁶, by using data from several patients, had calculated a range of estimates for the relative fitness cost of M184V we calculated (for each DRM) a range for their relative fitness cost. Estimates of the relative fitness costs of M184V, measured by Paredes et al¹⁶, ranged from 4% to 8%.

Estimating Detection Times

We used the estimated relative fitness costs for the 10 DRMs and a published within-host model of viral dynamics to calculate the length of time each DRM is likely to remain detectable in the plasma of a treatment-naïve individual (i.e., their detection time)¹³; see SI for a detailed description of the within-host model and parameter values. Using the model, we were able to track the temporal dynamics of the total viral load within an individual. In addition, for individuals infected with a strain with a DRM we were also able to calculate what percentage of their virion population, at any point in time, was composed of strains with a DRM. We simulated the within-host model for a maximum of 8 years because we simulated sexual transmission in MSM in resource-rich countries, and most HIV-infected MSM in these countries are on treatment by that time¹⁵. We calculated detection times based on a detection threshold for resistance of 20% (which is the detection limit for current resistance assays) and we also calculated detection times based on using next generation resistance assays with a detection limit of 1%.

To estimate the detection time for each of the 10 DRMs we conducted an uncertainty analysis. For this analysis we varied the relative fitness cost (over the range shown in Table 1), the viral clearance rate (from 10 to 30 day⁻¹)³³, the set point viral load (from 20 to 60 virions/μL¹⁵,³⁴,³⁵) and the set point for CD4 cells (from 350 to 550 cells/μL²²,³⁴). For further discussion of parameter ranges see SI. The uncertainty analysis was based on Latin Hypercube Sampling³⁶ and we used Monte Carlo Filtering to ensure the burst size of the wild-type strain was always greater than 100 virions per cell.

Modeling the stochastic development of Transmission Chains

Our novel stochastic transmission model is constructed to track the development of one transmission chain and the associated transmission cluster. We begin each transmission chain with an index case in the primary/acute stage of infection and infected with either the wild-type strain or a strain with a DRM that can revert (over time) to wild-type. We model the probability an infected individual transmits HIV (either wild-type or the strain with the DRM) at any point in time (pre-treatment) as a stochastic process that is a function of viral load. Therefore we model sexual transmission as a series of stochastic events. A genetic bottleneck occurs at each transmission event and, due to the founder effect, only the wild-type or the strain with the DRM is transmitted. Whether the founder virus is wild-type or has the DRM is determined probabilistically, but depends upon the composition (at the time of transmission) of the virion population in the transmitting individual. We use the within-host model to track the competitive-reversion dynamics between wild-type and a strain with a DRM within each treatment-naïve individual in the transmission chain¹³. We model the reversion rate of each of the DRMs using our estimates of the relative fitness costs.

The model is parameterized to reflect the current epidemiological and treatment conditions in the MSM community in San Francisco. Current treatment guidelines for HIV recommend treatment should begin when an individual’s CD4 count drops below 350 cells/μL. However, there is considerable variation in as to when HIV-infected individuals actually begin treatment; in resource-rich countries many individuals begin treatment before their CD4 counts fall to 350 cells/μL¹⁵. Therefore, when conducting our stochastic simulations, we modeled variation in time to treatment. Using CD4 data from San Francisco data and published rates of CD4 decline in HIV-infected individuals³⁷,³⁸, we calculated that HIV-infected individuals in San Francisco generally begin treatment 6 to 8 years after infection¹⁵. Consequently, for each individual (in each stochastic simulation), we sampled from a range of 6 to 8 years to determine when they would begin treatment. For each individual, we then used the within-host model to track their viral load over time. When the individual began treatment, we set their viral load to effectively zero.

We conducted 10,000 simulations of transmission chains for each of the 10 DRMs and the wild-type strain; each simulation tracked one transmission chain. Hence we conducted a total of 110,000 simulations. Chains were tracked for a maximum of 20 years. We chose a cutoff of 20 years as this represents the approximate time of introduction of antiretroviral therapy in resource-rich countries, when DRMs first evolved. Chains terminated due to either stochastic effects or to reaching the time point of 20 years. To identify the reason for termination of each of the transmission chains, we calculated cumulative distribution functions for the proportion of (non-null) chains that terminated in each year (See Figure S4 in the SI). We tracked each chain that did not terminate stochastically, beyond the 20 year cutoff to ensure that we correctly identified the terminal transmission event.

Estimating R₀

We used the value of R₀ for wild-type strains of HIV to estimate the values of R₀ for the strains with DRMs (see SI). The R₀ for the wild-type strain was set at 1.6, as this is the value of R₀ that has recently been estimated for wild-type strains of HIV (in the presence of treatment programs) in the community of MSM in San Francisco³⁴. To estimate R₀ for each of the DRM we used the 100,000 simulations of transmission chains. For each simulation, we determined the number of infections with a DRM in the second generation of the chain (i.e., R₀). We conducted an uncertainty analysis on the R₀ for each DRM. The uncertainty analysis was conducted using the same parameter set for the within-host model as employed in the uncertainty analysis of the detection times. We then computed the median value of R₀ and the interquartile range over all simulations.

Author Contributions

All authors contributed to the design of the project, the formulation and analysis of the models, the interpretation of the results, and the writing of the manuscript. J.G.G.-L. contributed the necessary data for the project. B.G.W. conducted the numerical analysis of the within-host and stochastic transmission models.

Supplementary Material

Supplementary Information

Supplementary Information