Regression-assisted deconvolution

Abstract

We present a semi-parametric deconvolution estimator for the density function of a random variable X that is measured with error, a common challenge in many epidemiological studies. Traditional deconvolution estimators rely only on assumptions about the distribution of X and the error in its measurement, and ignore information available in auxiliary variables. Our method assumes the availability of a covariate vector statistically related to X by a mean–variance function regression model, where regression errors are normally distributed and independent of the measurement errors. Simulations suggest that the estimator achieves a much lower integrated squared error than the observed-data kernel density estimator when models are correctly specified and the assumption of normal regression errors is met. We illustrate the method using anthropometric measurements of newborns to estimate the density function of newborn length.

1. Introduction

In this paper, we present a general class of semi-parametric deconvolution estimators for the density function of a random variable that is measured with error, and study one member of this class in detail. Let the random variable X have density function f_x, and suppose that X is observed only as W where

$$W=X+{\sigma }_{u}U$$ (1)

and U is a standardized random error that is independent of X and has density f_u. The density function of W is given by the convolution of f_x and f_u,

$$f_w(w)={\int }_{-\infty }^{\infty }{f}_x(x)\frac{1}{{\sigma }_u}{f}_u((w-x)/{\sigma }_u)\text{d}x.$$

The objective is to estimate f_x from the random sample W₁, …, W_n. It is typically assumed that f_u is known, or can be characterized sufficiently well with additional information such as replicate measurements or validation data.

This problem arises commonly in epidemiological studies, where the variable of interest cannot be measured precisely. For example, deconvolution has been used to estimate usual dietary intake distributions using data from self-report surveys such as 24-h recalls, which are known to inaccurately measure individuals’ nutritional intake [1, 2]. Our research is motivated in part by a study to assess error in anthropometric measurements of newborns. Estimating the density of such measurements is of interest for detecting abnormal fetal growth.

The deconvolution problem has a long history in the statistical literature. A number of nonparametric estimators of f_x have been suggested. Estimators based on Fourier transformation of the kernel density estimator of f_w were proposed by Stefanski and Carroll [3] and have received a great deal of attention. A number of recent contributions to this approach have been presented [4–7, among others]. Other researchers have presented nonparametric maximum likelihood estimators [8], wavelet estimators [9, 10], and spline-based estimators [2]. Chen et al. [11] suggest a semi-parametric estimator of f_x that assumes the existence of a transformation that maps X into a normal random variable. Elmore et al. [12] propose a nonparametric estimator applicable to the deconvolution problem. Their estimator uses covariate information to calibrate error-prone measurements in the population of interest from a reference population in which measurements are error-free. Our approach is closely related to that of Delaigle [13] who presented an estimator of the density of a variable measured with a mixture of Berkson and classical errors.

For the most part, density deconvolution has been studied in a univariate context in the sense that modeling assumptions are made only about the distribution of X and the measurement W given X. For many important cases even the best convergence rates for nonparametric estimation of f_x are slow. For example, when U is known to be normally distributed, nonparametric deconvolution estimators achieve at best a logarithmic rate of convergence [14] in general, although faster rates are possible for super-smooth target densities [10].

These results may discourage researchers from using deconvolution estimators in cases where sample sizes are not large. However, Wand [15] shows that deconvolution can be beneficial with moderate sample sizes.

Although the objective in a deconvolution problem is estimating the univariate density of X, in practice most data sets are multivariate and thus often contain covariates that are correlated with the error-prone variable. The class of estimators we propose assumes the availability of a covariate vector Z, statistically related to X, but independent of the error in measuring X. The idea is to exploit the auxiliary information in Z to obtain improved deconvolution estimators.

Our approach is flexible and relies on procedures familiar to statisticians, namely modeling the conditional mean and variance of X given Z. The particular estimator we study in detail assumes that the residual variation in the regression of X on Z is normal, though it need not be homoscedastic. The utility of this special case derives from two facts: (i) the assumption of normal residuals, after transformation possibly, is often reasonable, and (ii) statisticians are adept at detecting non-normality and thus can often determine when the method is not appropriate. We also make the assumption that measurement errors are normally distributed with mean zero and known, constant variance.

Our research is one of the first to investigate the use of covariate information in density deconvolution problems, and there are many variations to the basic strategy. We describe the approach in general, but we study only one particular version in detail through a simulation study and a real-data example estimating the density of newborn length.

2. The semi-parametric approach

Let X, W, and U be as in equation (1), where U is a N(0,1) random variable and ${\sigma }_u^2$ is known. Supposethat conditional on Z, the mean and variance of X are

$$E(X\mid \mathit{Z})={\mu }_{x\mid z}(\mathit{Z},\beta )\text{and}\text{Var}(X\mid \mathit{Z})={\sigma }_{x\mid z}^2({\mu }_{x\mid z}(\mathit{Z},\beta ),\xi )$$ (2)

respectively. We study in detail the case in which the mean and variance functions are specified parametrically, hence the chosen notation, but in general one or both or these functions could be estimated nonparametrically. Thus apart from the existence of the specified moments, the only restrictive modeling assumption is that the conditional variance of X given Z is a function of the conditional mean. The practical utility of such models in applications is well documented and methods for fitting them are readily available [16].

The additional assumption that the standardized equation errors are independent and identically distributed N(0,1) leads to the regression model

$$X_j={\mu }_{x\mid z}({\mathit{Z}}_j,\beta )+{\sigma }_{x\mid z}({\mu }_{x\mid z}({\mathit{Z}}_j,\beta ),\xi ){\epsilon }_j,j=1,\dots ,n,$$ (3)

where ε₁, …, ε_n, are the iid errors with common standard normal density φ, independent of Z₁, …, Z_n. Under these assumptions the density function of X is

$$f_x(x)={\int }_{-\infty }^{\infty }\frac{1}{{\sigma }_{x\mid z}(t,\xi )}\phi \left(\frac{x-t}{{\sigma }_{x\mid z}(t,\xi )}\right)f_{\mu }(t)\text{d}t,$$ (4)

where f_μ(t) is the density function of μ_x|z(Z, β). We are implicitly assuming that the covariates are random, not fixed, and that ${(X_j,{\mathit{Z}}_j^{\text{T}})}^{\text{T}}$ are independent and identically distributed for j = 1, …, n.

An estimator of f_x(x) is constructed by replacing the unknown components in (4) with consistent estimates derived from the observed data. Under the assumption that the measurement error U is independent of Z, it follows from equations (1) and (2) that

$$\begin{array}{l}E(W\mid \mathit{Z})={\mu }_{w\mid z}(\mathit{Z},\beta )={\mu }_{x\mid z}(\mathit{Z},\beta ),\\ \text{Var}(W\mid \mathit{Z})={\sigma }_{w\mid z}^2({\mu }_{w\mid z}(\mathit{Z},\beta ),\xi )={\sigma }_{x\mid z}^2({\mu }_{x\mid z}(\mathit{Z},\beta ),\xi )+{\sigma }_u^2.\end{array}$$ (5)

The induced regression model for W given Z is

$$W_j={\mu }_{x\mid z}(\mathit{Z},\beta )+{\{{\sigma }_{x\mid z}^2({\mu }_{x\mid z}(\mathit{Z},\beta ),\xi )+{\sigma }_u^2\}}^{1/2}{\epsilon }_j^{\ast },j=1,\dots ,n,$$

where the induced equation errors,

$${\epsilon }_j^{\ast }=\frac{{\sigma }_{x\mid z}({\mu }_{x\mid z}(\mathit{Z},\beta ),\xi ){\epsilon }_j+{\sigma }_u{U}_j}{{\{{\sigma }_{x\mid z}^2({\mu }_{x\mid z}(\mathit{Z},\beta ),\xi )+{\sigma }_u^2\}}^{1/2}}$$

are again iid N(0,1), given Z.

Now consider a random sample of the observed data, ${(W_j,{\mathit{Z}}_j^{\text{T}})}^{\text{T}}$ for j = 1, …, n. Mean and variance function models fit to these data provide the estimates μ̂_x|z(Z, β) and ${\widehat{\sigma }}_{w\mid z}^2({\widehat{\mu }}_{x\mid z}(\mathit{Z},\widehat{\beta }),\widehat{\xi })$, and hence of ${\widehat{\sigma }}_{x\mid z}^2({\widehat{\mu }}_{x\mid z}(\mathit{Z},\widehat{\beta }),\widehat{\xi })$ via equation (5)

$${\widehat{\sigma }}_{x\mid z}^2({\widehat{\mu }}_{x\mid z}(\mathit{Z},\widehat{\beta }),\widehat{\xi })={\widehat{\sigma }}_{w\mid z}^2({\widehat{\mu }}_{x\mid z}(\mathit{Z},\widehat{\beta }),\widehat{\xi })-{\sigma }_u^2.$$ (6)

In principle any reasonable method of consistent estimation could be employed at this stage. The key is that the variance is modeled as a function of the mean.

Model predicted values, μ̂_x|z(Z_j, β̂), j = 1, …, n, are used to estimate f_μ. For example, a kernel density estimator of f_μ is given by

$${\widehat{f}}_{\mu }(t)=\frac{1}{n\lambda }\sum _{j=1}^n\phi \left(\frac{t-{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta })}{\lambda }\right),$$ (7)

where λ is the kernel bandwidth. It follows from well-known results that, provided the model assumptions are valid and that the regression mean function is consistently estimated, the empirical distribution of the predicted values will converge to the distribution of μ_x|z(Z, β). For appropriate bandwidth sequences, therefore, the kernel density estimator will converge to f_μ.

Substituting the variance estimator (6) and the kernel estimator (7) into equation (4) gives

$${\widehat{f}}_x(x)=\frac{1}{n\lambda }\sum _{j=1}^n{\int }_{-\infty }^{\infty }\frac{1}{{\widehat{\sigma }}_{x\mid z}(t,\widehat{\xi })}\phi \left(\frac{x-t}{{\widehat{\sigma }}_{x\mid z}(t,\widehat{\xi })}\right)\phi \left(\frac{t-\widehat{\mu }({\mathit{Z}}_j,\widehat{\beta })}{\lambda }\right)\text{d}t,$$ (8)

which we refer to as a regression-assisted deconvolution estimator of f_x(x).

The regression-assisted deconvolution estimator is appealing for its reliance on regression methods that are familiar to statisticians. Modeling the conditional mean of X given Z is required, but can be done via any method. Modeling the conditional variance of X given Z as a function of the conditional mean is critical. However, variance function modeling is common statistical practice with many methods available [16]. The proposed estimator does not rely on any particular technique for fitting these models. Indeed, models may be fit using any appropriate regression method, including linear, nonlinear, semi-parametric and nonparametric methods. Equally important is the assumption that regression errors are normally distributed. Fortunately, violations of this assumption often can be detected with a variety of techniques, and model transformations can be employed to yield normally distributed regression errors.

An interesting feature of the regression-assisted deconvolution estimator is that in theory, it does not require estimation of the bandwidth parameter λ. There is no variance penalty for letting λ shrink to zero, provided the variance function estimate in (6) is bounded away from zero asymptotically. This is seen by making the change-of-variables with z = {t − μ̂(Z_j, β̂)}/λ in equation (8), obtaining

$${\widehat{f}}_x(x)=\frac{1}{n}\sum _{j=1}^n{\int }_{-\infty }^{\infty }\frac{1}{{\widehat{\sigma }}_{x\mid z}(\lambda z+{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta }),\widehat{\xi })}\phi \left(\frac{x-\lambda z-{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta })}{{\widehat{\sigma }}_{x\mid z}(\lambda z+{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta }),\widehat{\xi })}\right)\phi (z)\text{d}z.$$

Setting λ = 0 and simplifying yields

$${\widehat{f}}_x(x)=\frac{1}{n}\sum _{j=1}^n\frac{1}{{\widehat{\sigma }}_{x\mid z}({\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta }),\widehat{\xi })}\phi \left(\frac{x-{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta })}{{\widehat{\sigma }}_{x\mid z}(\widehat{\mu }({\mathit{Z}}_j,\widehat{\beta }),\widehat{\xi })}\right).$$ (9)

This form of the estimator is appealing because it avoids integration and the need to choose a bandwidth. Note that when the conditional variance of X given Z is constant, i.e. $\text{Var}(X\mid \mathit{Z})={\sigma }_{x\mid z}^2$, equation (8) directly simplifies to

$${\widehat{f}}_x(x)=\frac{1}{n\sqrt{{\widehat{\sigma }}_{x\mid z}^2+{\lambda }^2}}\sum _{j=1}^n\phi \left(\frac{x-{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta })}{\sqrt{{\widehat{\sigma }}_{x\mid z}^2+{\lambda }^2}}\right),$$ (10)

which, upon setting λ = 0 becomes

$${\widehat{f}}_x(x)=\frac{1}{n}\sum _{j=1}^n\frac{1}{{\widehat{\sigma }}_{x\mid z}}\phi \left(\frac{x-{\widehat{\mu }}_{x\mid z}({\mathit{Z}}_j,\widehat{\beta })}{{\widehat{\sigma }}_{x\mid z}}\right).$$ (11)

In both cases, the bandwidth is superfluous whenever Var(X|Z) is estimated well enough to avoid instability caused by values too close to, or less than, zero. For small to moderate sample sizes, when Var(W|Z) is close to ${\sigma }_u^2$, it is possible that Var(X|Z) estimated from (6) will be negative, and using a positive value of λ will be necessary. Empirical evidence from simulations suggests that using a standard bandwidth estimator such as the normal-reference bandwidth [17] is sufficient to provide stability in these cases.

The scope of this paper is limited to exploring the feasibility of regression-assisted deconvolution for the case where mean and variance functions are modeled parametrically (e.g. least squares). We examine its finite-sample performance via simulation and a real-data example. A discussion of the estimator’s asymptotic properties is provided in [18], where it is shown that when the estimated mean and variance function parameters are $\sqrt{n}$-consistent for their true values, the regression-assisted density estimator is also pointwise $\sqrt{n}$-consistent and asymptotically normal.

3. Simulations

The regression-assisted deconvolution estimator relies heavily on the regression model assumptions and normality of the regression errors. We performed a simulation study to determine how the success of the method is influenced by three key factors: (i) correct specification of the mean and variance functions, (ii) precision of model predicted values, and (iii) normality of the regression errors. As this study represents a first look at the feasibility of using covariate information in density deconvolution, we restricted our attention to relatively simple cases. All simulations considered multiple linear regression models, i.e.

$$X_j={\beta }^{\text{T}}{\mathit{Z}}_j+{\sigma }_{x\mid z}({\beta }^{\text{T}}{\mathit{Z}}_j,\xi ){\epsilon }_j,j=1,\dots ,n,$$ (12)

where ε₁, …, ε_n are independent N(0, 1) random variables and are independent of Z₁, …, Z_n. Our first two simulations examined models with constant residual variance, ${\sigma }_{x\mid z}^2({\beta }^{\text{T}}\mathit{Z},\xi )={\sigma }_{x\mid z}^2$, while a third examined a model with residual variance equal to an exponential function of the mean. In each case the observed-data model is

$$W_j={\beta }^{\text{T}}{\mathit{Z}}_j+{\sigma }_{x\mid z}({\beta }^{\text{T}}{\mathit{Z}}_j,\xi ){\epsilon }_j+{\sigma }_u{U}_j,j=1,\dots ,n,$$ (13)

where U_j is a N(0, 1) measurement error that is independent of both Z_j and ε_j.

Simulations investigated how well the regression-assisted deconvolution estimator uncovers features such as bimodality and skewness in the true-data density. Each of our three simulations considered a different density for X: the standard normal density (Simulation 1), a mixture of normals (Simulation 2), and an unnamed density with a minor right skew (Simulation 3). In each case, the density of X was standardized to have mean 0 and variance 1.

Our interest is in small to moderate sample sizes, at least relative to the sample sizes needed for nonparametric deconvolution. Simulated data sets contained n = 100 observations. For each data set, in addition to computing the regression-assisted deconvolution estimator, we computed the naive kernel density estimator which ignores the error in measuring X

$${\widehat{f}}_{\text{naive}}(x)=\frac{1}{n\lambda }\sum _{j=1}^n\phi \left(\frac{x-W_j}{\lambda }\right)$$ (14)

as well as the true-data kernel density estimator

$${\widehat{f}}_{\text{true}}(x)=\frac{1}{n\lambda }\sum _{j=1}^n\phi \left(\frac{x-X_j}{\lambda }\right).$$

For comparison with a traditional nonparametric deconvolution estimator, we computed the deconvoluting kernel density estimate proposed by Stefanski and Carroll [3]. This estimator has the form

$${\widehat{f}}_{\text{sc}}(x)=\frac{1}{2\pi n\lambda }\sum _{j=1}^n{\int }_{-a}^a{\text{e}}^{-\text{i}t(x-W_j)/\lambda +{\sigma }^2{t}^2/2{\lambda }^2}{\mathrm{\Phi }}_Q(t)\text{d}t,$$ (15)

where σ² is the measurement error variance and Φ_Q(t) is the characteristic function of the kernel function Q(x), taken in these simulations to be Q(x) ∝ {sin(x)/x}⁴, so that a = 4. To select bandwidth for this estimator we used the bootstrap procedure described by Delaigle and Gijbels [19].

The regression-assisted deconvolution estimator requires an estimate of the true-data variance, ${\sigma }_{x\mid z}^2({\beta }^{\text{T}}\mathit{Z},\xi )$, found by subtracting ${\sigma }_u^2$ from the variance function estimated with the fitted regression model, as in (6). With the sample size n = 100, this variance function is not estimated well enough to avoid occasional negative values, or values very close to zero, for the true-data variance. To avoid instability caused by such estimates, we used a version of our estimator that included a positive bandwidth parameter λ, and set any negative variance estimates to zero. For Simulations 1 and 2, with constant residual variance, we computed the regression-assisted deconvolution estimator in equation (10). For Simulation 3, we used a version of the estimator motivated by (10)

$${\widehat{f}}_x(x)=\frac{1}{n}\sum _{j=1}^n\frac{1}{\sqrt{{\widehat{\sigma }}_{x\mid z}^2({\widehat{\beta }}^{\text{T}}\mathit{Z},\widehat{\xi })+{\lambda }^2}}\phi \left(\frac{x-{\widehat{\beta }}^{\text{T}}{\mathit{Z}}_j}{\sqrt{{\widehat{\sigma }}_{x\mid z}^2({\widehat{\beta }}^{\text{T}}\mathit{Z},\widehat{\xi })+{\lambda }^2}}\right).$$

The normal-reference bandwidth was used as the constant for all three simulations, λ = 1.06 σ̂_*n^−1/5, where σ̂_* is the sample standard deviation of the data [17]. While these versions of our estimator are not bound by the same asymptotic behavior referred to in Section 2, they should provide a good indication of the method’s potential performance in practical situations.

Several factors were controlled in the study to allow investigation of the regression-assisted deconvolution estimator’s sensitivity to key components of the regression model. Two components controlled the precision of the predicted values. The reliability ratio, κ, describes the ratio of the variance in the true data to the variance in the observed data

$$\kappa =\frac{\text{Var}(X)}{\text{Var}(W)}=\frac{1}{1+{\sigma }_u^2}$$ (16)

and was varied at two levels, 0.7 and 0.9. The theoretical coefficient of determination of the regression of X on Z

$$R^2=\frac{\text{Var}({\beta }^{\text{T}}\mathit{Z})}{\text{Var}(X)}$$ (17)

was varied at five levels, 0.1, 0.3, 0.5, 0.7, and 0.9.

Perhaps most critical to the performance of the regression-assisted deconvolution estimator is the assumption that the density of the model errors, f_ε(ε), is normal. Robustness to this assumption was checked by generating model errors from non-normal distributions. We considered skewed error distributions, namely centered Chi-squared(16) and Chi-squared(4).

Because the assumption of normal errors plays such an important role in the regression-assisted estimator, we investigated the likelihood that departures from normality could be detected in practice. As part of our simulation we included a study of the power of a common test for detecting non-normality of residuals. Our intent was to determine whether it would be possible to detect non-normal regression residuals in those cases where the extent of non-normality adversely affects the performance of the estimator. The regression errors from the fit of the observed-data model in equation (13) have density function defined by the convolution of f_ε(ε) and the $\text{N}(0,{\sigma }_u^2)$ density. Residuals were tested for normality with the D’Agostino–Pearson K² statistic [20], which has higher power than many others for detecting non-normal skewness and kurtosis in data.

An additional factor included in the simulations was determined to have limited effects on the performance of the estimator. Model mis-specification due to over-fitting and under-fitting had no significant effect on the estimator’s performance in those simulations where residual variance was constant (Simulations 1 and 2). For these simulations we report results for the correctly specified model only.

3.1. Simulation 1: estimation when f_x (x) is the standard normal density

This simulation examined the performance of the regression-assisted deconvolution estimator when f_x(x) is the N(0, 1) density. We considered the linear model in (12) where Z_j is a 4 × 1, N(0,I₄) random vector independent of ε_j. For the case where the model assumptions are met, and ε_j is a N(0, 1) random variable, it follows that X₁, …, X_n is a random sample from the normal distribution with mean 0 and variance ${\beta }^{\text{T}}\beta +{\sigma }_{x\mid z}^2$. Adding the constraint

$${\beta }^{\text{T}}\beta +{\sigma }_{x\mid z}^2=1$$ (18)

results in the sample X₁, …, X_n of independent standardized normal random variables. Note from equations (17) and (18) that this implies

$$R^2={\beta }^{\text{T}}\beta =1-{\sigma }_{x\mid z}^2.$$ (19)

Data were generated for each level of R², κ, and f_ε(ε) as follows. Covariate vectors, Z₁, …, Z_n, were generated as independent N(0,I₄) random vectors. Regression errors, ε₁, …, ε_n, were generated from their standardized density and were scaled by ${\sigma }_{x\mid z}^2$. For β satisfying equation (19), a true-data sample was computed from equation (12). Standard normal measurement errors were generated and scaled by ${\sigma }_u^2={\kappa }^{-1}-1$, and added to the true data to form an observed-data sample as in equation (13).

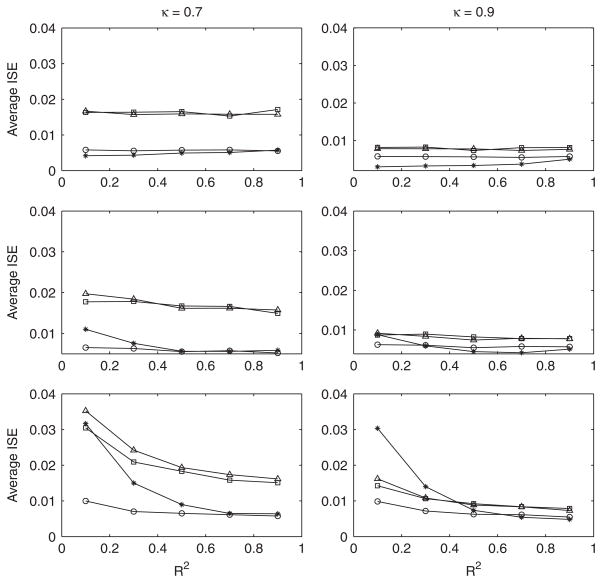
Average integrated squared errors are plotted in Figure 1. In the case of normal regression errors, the regression-assisted deconvolution estimator yields a significantly smaller integrated squared error than both the naive estimator and the Stefanski–Carroll estimator. It is even superior to the true-data estimator for small values of R². This seemingly anomalous finding is explained by the fact that the true-data kernel density estimator does not make use of any assumptions about the distribution of X. Underlying the construction of the regression-assisted estimator is the implicit assumption that the density of X has a component that is normal. The regression-assisted estimator exploits this assumption and thus it is not surprising that it can beat the true-data estimator when the assumption is satisfied.

Figure 1.

Average ISE for Simulation 1. Circle: f̂_true(x); triangle: f̂_naive(x); square: f̂_sc(x); star: f̂_x(x). Top: N(0,1) errors; middle: standardized Chi-squared(16) errors; bottom: standardized Chi-squared(4) errors. Pooled standard error of mean ISE is 0.00024 for N(0,1) errors, 0.00021 for Chi-squared(16) errors and 0.00033 for Chi-squared(4) errors. Sample size for all simulations is n = 100.

That the regression-assisted deconvolution estimator performs well when the assumption of normal model errors is met is not surprising. However, our results suggest that it should be used cautiously when regression errors are determined to be far from normal. Note from equation (12) that in these cases, the density function of X is the convolution of a $\text{N}(0,1-{\sigma }_{x\mid z}^2)$ and a Chi-squared density centered at 0 and scaled to have variance ${\sigma }_{x\mid z}^2$. From equation (19) it is seen that f_x(x) changes with R², its skewness increasing as R² decreases. Indeed, Figure 1 shows that the integrated squared error of the regression-assisted estimator is most strongly influenced by non-normality when R² is small and the distribution of the model errors is highly skewed. However, non-normality in the residuals from the fit of the observed-data model was detected consistently in these cases with the D’Agostino–Pearson K² test. The power of this test is summarized in Table I.

Table I.

Power of the D’Agostino–Pearson K² test in Simulation 1 to detect non-normality in observed-data regression residuals when true model errors are standardized Chi-square(4) and Chi-square(16) random variables.

R2	Chi-square(4)		Chi-square(16)
	κ = 0.7	κ = 0.9	κ = 0.7	κ = 0.9
0.1	0.54	0.87	0.24	0.40
0.3	0.47	0.82	0.18	0.36
0.5	0.36	0.75	0.15	0.33
0.7	0.26	0.63	0.10	0.27
0.9	0.10	0.31	0.06	0.14

3.2. Simulation 2: estimation when f_x (x) is a normal mixture density

The aim of this simulation was to investigate how well the regression-assisted deconvolution estimator uncovers bimodal features in the true-data density. We generated X from a mixture of two normal densities. For clarity, we rewrite the linear model in equation (12) as

$$X_j=-{\beta }_1\alpha +{\beta }_1{Z}_{1,j}+{\beta }_2^{\text{T}}{\mathit{Z}}_{2,j}+{\sigma }_{x\mid z}{\epsilon }_j,j=1,\dots ,n,$$ (20)

where Z_{1, j} is a Bernoulli(α) random variable, Z_{2, j} is a 3 × 1, N(0,I₃) random vector, Z_{1, j}, Z_{2, j}, and ε_j are mutually independent, and the residual variance ${\sigma }_{x\mid z}^2$ is again constant. When model assumptions are met and ε_j is a N(0, 1) random variable, it follows that X₁, …, X_n is a random sample from an {α:(1−α)} mixture of normals having means β₁(1− β) and − β₁α respectively, and common variances ${\beta }_2^{\text{T}}{\beta }_2+{\sigma }_{x\mid z}^2$. Standardizing X required that

$${\beta }_1^2\alpha (1-\alpha )+{\beta }_2^{\text{T}}{\beta }_2+{\sigma }_{x\mid z}^2=1.$$ (21)

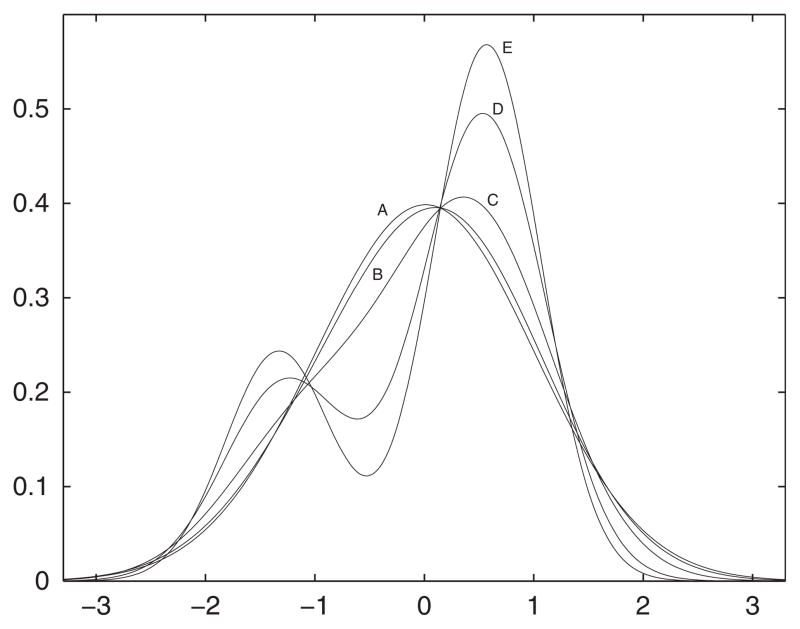
Note from (19) that this induces the constraint that $R^2\ge {\beta }_1^2\alpha (1-\alpha )$. The parameters β₁ and α determine the appearance of distinct modes in f_x(x), and for small values of R², the modes of densities that satisfy this constraint are obscured. In this simulation, we allowed the true-data density to vary with R². We fixed α = 0.7 and chose β₁ close to its maximum value for each R², resulting in the variety of shapes for the true-data density displayed in Figure 2. Although this complicates comparisons of estimators among levels of R², comparisons within levels of R² are straightforward.

Figure 2.

70–30 normal mixture densities with means ±β₁ for different values of R². A: R² = 0.1, β₁ = 0.6; B: R² = 0.3, β₁ = 1.1; C: R² = 0.5, β₁ = 1.5; D: R² = 0.7, β₁ = 1.8; E: R² = 0.9, β₁ = 1.9.

Data for this simulation were generated as follows for each level of R², κ, and f_ε(ε). First, Z_{1, 1} …, Z_{1, n} were generated as independent Bernoulli(0.7) random variables, and Z_2,1, …, Z_{2, n} were generated as independent N(0,I₃) random vectors. Second, model errors, ε₁, …, ε_n, were generated from f_ε(ε) and scaled by ${\sigma }_{x\mid z}^2=1-R^2$. With β₁ determined by the level of R², and β₂ satisfying equation (21), these components were combined according to equation (20) to form the true-data sample. Finally, N(0,1) measurement errors with variances ${\sigma }_u^2={\kappa }^{-1}-1$, were added to the true data to produce the observed-data sample.

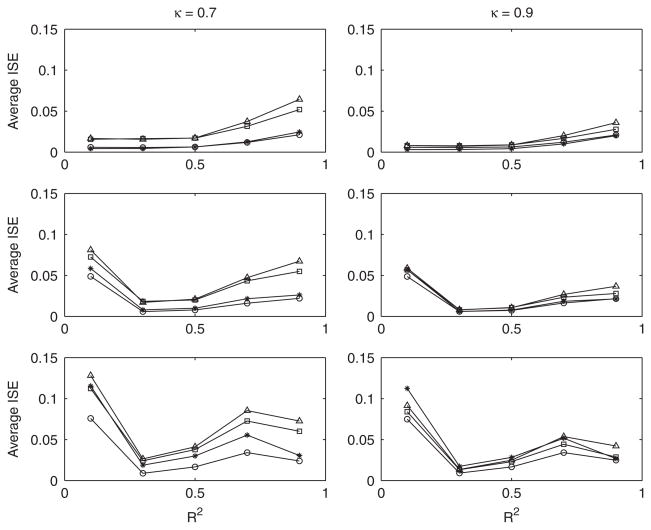
Average integrated squared errors are displayed in Figure 3. When model errors are normally distributed, the regression-assisted deconvolution estimator is superior to the naive and Stefanski–Carroll [3] estimators for all values of R² and κ, and performs at least as well as the true-data estimator. It is less effective when model errors are Chi-squared distributed, particularly when errors are highly skewed and R² is small. We note that as in Simulation 1, f_x(x) becomes increasingly skewed with the density of the regression errors. Our estimator performed significantly worse than the naive estimator when errors were Chi-squared(4) distributed, R² was equal to 0.1, and κ was equal to 0.9. In general, the D’Agostino–Pearson K² statistic was effective in detecting non-normality in the residuals from the regression of W on Z in the situations where the regression-assisted deconvolution estimator performed weakly. The power of this test is summarized in Table II.

Figure 3.

Average ISE for Simulation 2. Circle: f̂_true(x); triangle: f̂_naive(x); square: f̂_sc; star: f̂_x(x). Top: N(0,1) errors; middle: standardized Chi-squared(16) errors; bottom: standardized Chi-squared(4) errors. Pooled standard error of mean ISE is 0.00033 for N(0,1) errors, 0.00047 for Chi-squared(16) errors and 0.00059 for Chi-squared(4) errors. Sample size for all simulations is n = 100.

Table II.

Power of the D’Agostino–Pearson K² test in Simulation 2 to detect non-normality in observed-data regression residuals when true model errors are standardized Chi-square(4) and Chi-square(16) random variables.

R2	Chi-square(4)		Chi-square(16)
	κ = 0.7	κ = 0.9	κ = 0.7	κ = 0.9
0.1	0.64	0.90	0.23	0.43
0.3	0.56	0.87	0.25	0.39
0.5	0.41	0.83	0.16	0.33
0.7	0.26	0.70	0.09	0.25
0.9	0.09	0.33	0.07	0.11

3.3. Simulation 3: estimation of f_x(x) under non-constant residual variance

Our objective in this simulation was to determine how well our estimator performs when regression errors are heteroscedastic. We assumed the conditional mean of X is given by the linear model in (12), and the conditional variance by an exponential function of the mean. Specifically

$${\sigma }_{x\mid z}^2({\beta }^{\text{T}}\mathit{Z},\xi )={\xi }^2{\text{e}}^{-{\beta }^{\text{T}}\mathit{Z}}.$$ (22)

As in Simulation 1, Z_j was taken to be a N(0,I₄) random vector, independent of ε_j. For the case where model assumptions are met and ε_j is a N(0, 1) random variable, the resulting distribution for X is non-standard, and from (4) is seen to be

$$f_x(x)={\int }_{-\infty }^{\infty }{(2\pi \xi )}^{-1}{({\beta }^{\text{T}}\beta )}^{-1/2}exp\left\{\frac{y}{2}-\frac{y^2}{2{\beta }^{\text{T}}\beta }-\frac{{\text{e}}^y{(x-y)}^2}{2{\xi }^2}\right\}\text{d}y.$$ (23)

It is straightforward to show that E(X)= 0 and Var(X)= ξ²e^βTβ/2 + β^Tβ. Equation (17) and the requirement that Var(X)= 1 impose the constraint

$${\xi }^2=(1-{\beta }^{\text{T}}\beta ){\text{e}}^{-{\beta }^{\text{T}}\beta /2}.$$ (24)

There is a slight left skew in the density function which depends on the value of R². For the values considered in our simulation study, the skew is most pronounced for R² = 0.5 and least pronounced for R² = 0.1 or 0.9.

Simulated data sets were generated as follows. Covariates Z₁, …, Z_n were generated as independent N(0,I₄) random vectors. For each level of R2, β was chosen to satisfy (17), and ξ computed using (24). Regression errors were generated from their standardized density f_ε(ε) and scaled by the variance function in (22). A true-data sample was then constructed with (12). Standard normal measurement errors were scaled by ${\sigma }_u^2={\kappa }^{-1}-1$ and added to the true data, resulting in the observed-data sample. Parameters for the mean and variance functions were estimated using iteratively reweighted least squares.

Two incorrectly specified models were also fit to each simulated data set. This was done as follows. For each data set, eight additional covariate vectors were generated, each uncorrelated with the observed response. The observed data were regressed on all 12 covariates. An under-fit model was estimated by selecting the two covariates whose estimated parameters had the largest absolute t-statistics. Similarly, an over-fit model was estimated by selecting the eight covariates whose estimated parameters had the largest absolute t-statistics.

We again used the D’Agostino–Pearson K² test to test for normality of residuals in those cases where regression errors were generated from Chi-squared distributions. Regression errors for this model have non-constant variance that is a function of unknown parameters. Therefore, we standardized residuals using the estimated parameters in the variance function. The test was performed only using residuals from the correctly specified model.

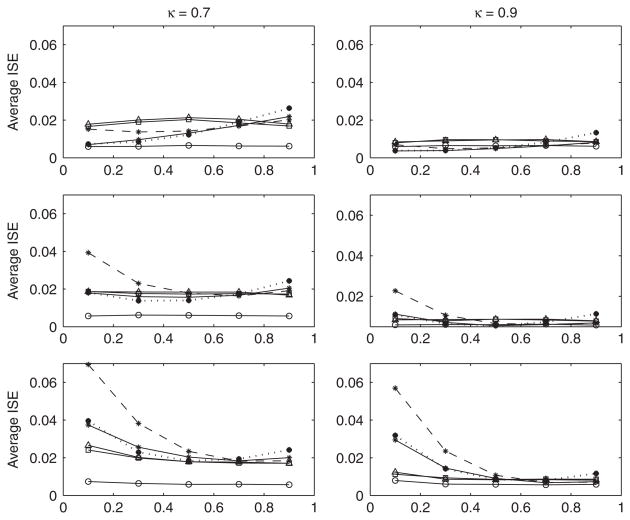
Average integrated squared errors are plotted in Figure 4. We note that due to the non-standard form of f_x(x) in this simulation, e.g. equation (23) for the case of normal errors, we determined this density via a kernel density estimate based on a Monte Carlo sample of size one million. The most striking result here is the obvious effect of model mis-specification, particularly in terms of over-fitting, and for small values of R². A likely explanation is the increased variability caused by over-fitting, which will have a larger impact for this model than one with constant residual variance. Conversely it appears that under-fitting is a greater problem for larger values of R², when the introduced bias becomes more obvious. For the correctly specified model, however, the average ISE is generally smaller than that of the naive estimator when regression errors are normal or even Chi-squared(16) distributed. The effect of the highly skewed Chi-squared(4) errors is substantial even when the model is correctly specified. Here our estimator does as well as the naive estimator only for the largest values of R².

Figure 4.

Average ISE for Simulation 3. Circle: f̂_true(x); triangle: f̂_naive(x); square: f̂_sc; star, solid line: f̂_x(x) with correctly specified model; star, dotted line: f̂_x(x) with under-fit model; star, dashed line: f̂_x(x) with over-fit model. Top: N(0,1) errors; middle: standardized Chi-squared (16) errors; bottom: standardized Chi-squared (4) errors. Pooled standard error of mean ISE is 0.0079 for N(0,1) errors, 0.0074 for Chi-squared(16) errors and 0.0102 for Chi-squared(4) errors. Sample size for all simulations was n = 100.

Unfortunately, as shown in Table III, the power to detect non-normality is small for almost every case considered here. This simulation suggests that our estimator be used cautiously with a more complex mean–variance function model when regression errors may be non-normal.

Table III.

Power of the D’Agostino–Pearson K² test in Simulation 3 to detect non-normality in observed-data regression residuals when true model errors are standardized Chi-square(4) and Chi-square(16) random variables.

R2	Chi-square(4)		Chi-square(16)
	κ = 0.7	κ = 0.9	κ = 0.7	κ = 0.9
0.1	0.61	0.89	0.32	0.48
0.3	0.48	0.85	0.25	0.41
0.5	0.43	0.77	0.26	0.34
0.7	0.38	0.57	0.30	0.25
0.9	0.52	0.40	0.49	0.34

4. Application

We illustrate our deconvolution estimator on data from a study conducted at the Magee Womens Hospital in Pittsburgh, PA to assess error in anthropometric measurements of newborns. Anthropometric measurements are used to identify abnormal fetal growth, which can indicate an elevated risk of cardiovascular disease in adulthood. Measurements are typically taken by clinical staff immediately following delivery, and are known to be subject to error. Clinical measurements of length (cm), weight (g), and head circumference (cm) were obtained on 354 infants within two hours of birth. Measurements were repeated on all newborns by trained research staff within five days of the clinical measurement. Additional covariates including race, sex, and gestational age were recorded for each infant.

We used these data to estimate the density function of newborn length. We took the view that measurements taken by trained research staff were error-free, and used them as validation data. The estimated reliability ratio for the clinical length measurements was 0.66, and measurement errors had an estimated standard deviation of 1.73 cm. Errors also had a slight positive bias of 1.03 cm, which was subtracted from the data before analysis. The hypothesis that measurement errors were normally distributed was not rejected with the D’Agostino–Pearson K² test (p = 0.40).

We fit a multiple linear regression model to the clinical length measurements. The validation data showed that clinical measurements of infant weight were relatively precise, with an estimated reliability ratio of 0.98. We assumed that measurement error in this variable was negligible and included it as a covariate in the regression. Our regression model included terms for weight, sex, and a weight–sex interaction, and resulted in an R² of 0.47. Model MSE was 3.57, which with equation (6) resulted in an estimate of 0.57 for the conditional true-data variance. Residuals showed weak evidence of non-normality with the D’Agostino–Pearson K² test (p = 0.10).

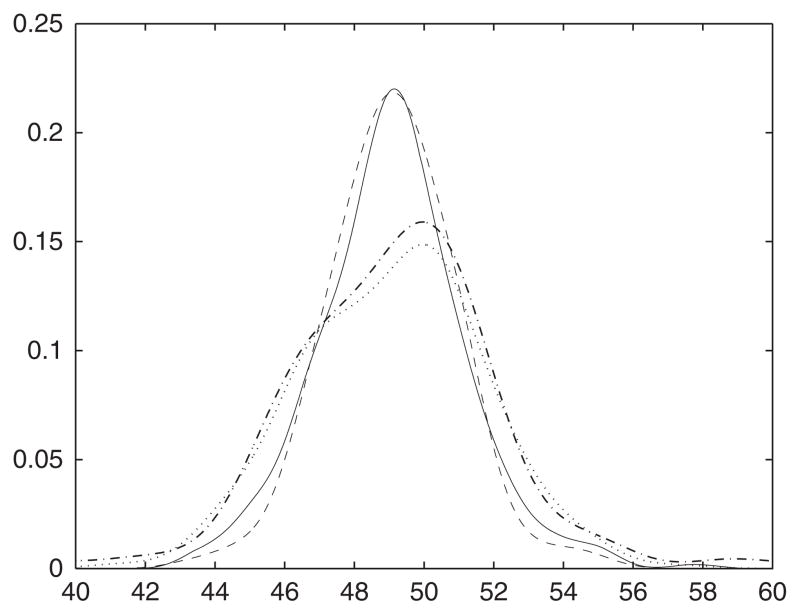
The regression-assisted estimate was computed from equation (11) and is plotted in Figure 5. Also plotted are kernel density estimates computed from both the clinical and research staff measurements, using the normal-reference bandwidth [17], as well as the Stefanski–Carroll [3] estimator in equation (15) with bandwidth chosen as the value that minimized the ISE between f̂_sc(x) and the kernel density estimate from the research measurements.

Figure 5.

Density estimates of newborn lengths. Solid line: kernel density estimate computed from research measurements; dotted line: kernel density estimate computed from clinical measurements; dashed line: regression-assisted estimate; dot–dash: Stefanski–Carroll estimate.

The regression-assisted estimate agrees well with the estimate computed from the research staff measurements. An important difference appears in the tails of the four estimated densities. Tail probabilities are of particular interest in this application for identifying newborns at risk for health complications. Judging from the research data, the regression-assisted estimate underestimates the density in the tails, corresponding to smaller estimated tail probabilities. We note that the estimate computed from the research data indicates that the true length density is not far from normal. Part of the success of our estimator in this example likely comes from this fact. The marginal R² value for our regression model means that our estimator models a large portion of the density as normal, and thus has a relatively easy time approximating that shape.

5. Discussion

Our results indicate that the regression-assisted deconvolution estimator is a potentially powerful tool for density deconvolution. Although departures from assumptions are clearly problematic for more complicated mean–variance function models.

Our initial investigation of regression-assisted deconvolution considered only parametric regression models. For the method to achieve its full potential nonparametric (or semi-parametric) mean and variance function modeling will likely be necessary. Of course then the $\sqrt{n}$ convergence rates obtained with parametric modeling will likely not hold. We conjecture that in general, the regression-assisted estimator will inherit the minimum of the convergence rates of the mean and variance function estimates. The slower rates associated with nonparametric function estimation would come as the trade-off for a more robust estimator. Still, the rates of convergence associated with fully nonparametric mean and variance function estimation are typically faster than those associated with deconvolution [10, 14], and thus the proposed approach offers a substantial improvement over standard deconvolution estimators.