Estimating abundances of retroviral insertion sites from DNA fragment length data

Abstract

Motivation: The relative abundance of retroviral insertions in a host genome is important in understanding the persistence and pathogenesis of both natural retroviral infections and retroviral gene therapy vectors. It could be estimated from a sample of cells if only the host genomic sites of retroviral insertions could be directly counted. When host genomic DNA is randomly broken via sonication and then amplified, amplicons of varying lengths are produced. The number of unique lengths of amplicons of an insertion site tends to increase according to its abundance, providing a basis for estimating relative abundance. However, as abundance increases amplicons of the same length arise by chance leading to a non-linear relation between the number of unique lengths and relative abundance. The difficulty in calibrating this relation is compounded by sample-specific variations in the relative frequencies of clones of each length.

Results: A likelihood function is proposed for the discrete lengths observed in each of a collection of insertion sites and is maximized with a hybrid expectation–maximization algorithm. Patient data illustrate the method and simulations show that relative abundance can be estimated with little bias, but that variation in highly abundant sites can be large. In replicated patient samples, variation exceeds what the model implies—requiring adjustment as in Efron (2004) or using jackknife standard errors. Consequently, it is advantageous to collect replicate samples to strengthen inferences about relative abundance.

Availability: An R package implements the algorithm described here. It is available at http://soniclength.r-forge.r-project.org/

Contact: ccberry@ucsd.edu

Supplementary information: Supplementary data are available at at Bioinformatics online.

1 INTRODUCTION

The new deep sequencing methods allow longitudinal tracking of DNA sequence variation in cell populations. These methods have been applied extensively to studies of activation of host cell genes by integration of retroviral DNA. In human gene therapy, vectors derived from retroviruses have been used to treat a sizeable and growing number of diseases, but there have been several cases of insertional activation of cancer genes, leading to intense interest in the relationship of vector integration sites in the human genome to the size of cell populations harboring that clone (Cavazzana-Calvo et al., 2010; Deichmann et al., 2007; Gabriel et al., 2009; Hacein-Bey-Abina et al., 2008; Wang et al., 2007, 2008, 2010). In infections by human T-cell leukemia viruses, the relationship between integration site position and cell clone size is likely to be important for leukemia, but the full importance remains to be clarified (Gillet et al., 2011; Meekings et al., 2008). Distributions of large numbers of integration sites can be determined using the new deep sequencing methods, but use of this information to estimate abundance is complicated by several types of recovery biases (Gabriel et al., 2009; Wang et al., 2008). In a typical experiment, blood cells are obtained from an HTLV1-infected subject or gene therapy patient, genomic DNA is purified from the heterogeneous populations of cells and then DNA is cleaved, ideally by a relatively random method such as DNA shearing. Short DNA linkers are ligated onto the DNA ends, then host–virus junctions are amplified by polymerase chain reaction (PCR) using one primer that binds the linker and another that binds the viral DNA end. PCR products are then sequenced in bulk, and the resulting reads are aligned to the human genome. Here we present computational tools for relating this type of data to the relative abundance of each cell clone, as marked by integration sites, in the starting cell population.

Suppose that the number of cells in a patient that could harbor a viral insertion is C and the number of sites or locations in the genome of each cell (determined by chromosome, position and strand) is L. Then there are C×L places in which such an insertion might be found. Use M_il to indicate whether there is an insertion in site i in cell l. Let M_il=1 for an insertion and M_il=0 for no insertion there. The abundance of an insertion at one of the L sites is the number of cells hosting an integrated retroviral DNA at that site. That is, M_i+=∑_l=1^C M_il is the abundance of insertions at site i. The relative abundance

is the fraction of the places harboring an insertion whose site is i. The collection of relative abundances is used to characterize a retroviral infection and monitor it for changes. As examples, the number of different insertion sites, the appearance of a highly abundant site, an increase in the number of different sites and measures of the diversity of sites such as the Shannon Information or Gini coefficient all indicate features of the disease or its response to treatment. Previous work has tracked such measures to understand disease progression after infection with human T-cell leukemia virus type 1 (HTLV-1) (Gillet et al., 2011; Meekings et al., 2008), latency in human immunodeficiency virus (HIV) infections (Finzi et al., 1997; Han et al., 2007) and cell dynamics after human gene correction with integrating vectors (Deichmann et al., 2007; Gabriel et al., 2009; Hacein-Bey-Abina et al., 2008, 2010; Wang et al., 2010).

Cleaving the DNA from a sample of cells using restriction enzymes or mu transposons (Brady et al., 2011; Gabriel et al., 2009; Wang et al., 2008) and sequencing the fragments (Hacein-Bey-Abina et al., 2003; Mitchell et al., 2004; Schroder et al., 2002; Wang et al., 2007; Wu et al., 2003) potentially allows characterization of the relative abundance of cell clones marked by distinct integration sites (Gabriel et al., 2009; Schmidt et al., 2003; Wang et al., 2008; 2010), but variation in the genomic distribution of restriction sites or sites favored by mu transposons introduces biases that can be hard to correct.

Breaking DNA by sonication is nearly random (Aird et al., 2011), so that if those fragments could be directly counted, estimates of abundance could be obtained. However, it is necessary to amplify the fragments by PCR before they can be sequenced, and variation in the number of fragments that each parent fragment generates vastly inflates the variance of estimates or abundance (Section 12 in Supplementary Material) based on the read count—the number of fragments whose sequence is mapped to a single site. In data such as Gillet et al. (2011) report, where most insertion sites only contribute one or two parent fragments to the sequencer, simple read counts are useless. However, when multiple cells contain an insertion at the same site, random shearing by sonication usually produces fragments of different lengths. The number of different lengths associated with each integration site tends to increase with its abundance, but the increase is non-linear due to coincidental shearing at the same site in multiple genomes. Gillet et al. (2011) empirically fitted a calibration curve for this non-linear function using three dilutions of genomic DNA from an HTLV-1 infected individual, and used it to estimate the number of parent fragments of each site in their samples.

Below, estimation of the relative abundance of a retroviral insertion site in an infected patient using the collection of fragment lengths for each integration site is considered. We introduce some notation for referring to data on retroviral insertions and mention some measures that may be of interest in studying populations of sites. Then we describe a maximum likelihood estimator based on the distinct lengths of clones recovered. A brief review of procedures for collecting fragment length data for retroviral insertions is given in Section 2, see Gillet et al. (2011) for more details. We devise a statistical approach for estimating the abundances of retroviral insertion sites and an algorithm to implement it. The algorithm is applied to real and simulated data and the accuracy of the approach is assessed and compared with the method of Gillet et al. (2011). Supplementary Material provides extensive notes and more details, including studies of estimators of number of unseen species proposed by Chao (1987) and by Chao and Lee (1992), of the Shannon Information and the Chao-Shen coverage adjusted entropy (Chao and Shen, 2003) and the Gini Coefficient.

2 METHODS

2.1 Recovering fragments, insertion sites and lengths

A detailed description of sample acquisition and sequencing methods is found in Gillet et al. (2011). Eleven HTLV-1-infected subjects were studied on three different dates. Genomic DNA was purified from blood cells, divided into three replicate subsamples, fragmented by sonication, amplified by ligation-mediated PCR, and then sequenced using the Illumina Flow Cell. Sequences were determined for both the HTLV-1/human DNA junction, and the junction between human DNA and the added linker. Mapping these determined the insertion site (i) and the fragment length (j) as the difference of their positions.

For every replicate, the unique sites and lengths were presented as a table of zeros and ones with one row for every site of the genome and one column for each fragment length. Each table cell, w_ij, was set to zero if no fragment of length j was observed for an insertion at site i and one otherwise. The table is very large, but has only a few thousand non-zero rows and only these need to be stored for data analysis.

2.2 Likelihood methods for integration sites

The probability distribution of the observed data, w_ij, depends on where the insertions are in the parent population of C×L places (cells and sites), the sampling of cells and DNA from them and the generation of DNA fragments.

The number of cells hosting a retrovirus integrated in a particular site in a simple independent random sample of cells follows the hypergeometric probability law. The expected count for insertion site i is μρ_i, where μ is the expected number of insertion sites in the sample and ρ_i is the relative abundance of site i. Once the DNA has been fragmented, this count is subdivided according to ϕ_j, the probability that a fragment has length j. The expected number of fragments for insertion site i of length j is μρ_iϕ_j.

When the number of sampled cells is a small fraction of the population total, the multinomial probability law closely approximates the sample counts for the insertion sites. Poisson likelihoods offer a convenient approach to multinomial data ‘yielding identical estimates and asymptotic variances’ (Baker, 1994). This observation would motivate the use of an estimating equation based on the Poisson law whose parameter is the expected number of fragments (μρ_iϕ_j) if the number of fragments could be observed. However, once fragments bearing the insertion are amplified and sequenced, one cannot know whether multiple sequence reads of the same insertion and length represent a single amplified, parent fragment or multiple parent fragments—only the presence or absence of one or more parent fragments among the sequence reads is known. Under Poisson sampling of parent fragments, the probability that a parent fragment is seen among the sequence reads (i.e. w_ij=1) is one minus the Poisson probability that the count of parent fragments is zero, p_ij=1−exp(−μρ_iϕ_j). The probability that it is not seen (i.e. w_ij=0) is 1−p_ij=exp(−μρ_iϕ_j).

From these probabilities, the likelihood for the data , w_ij, for one replicate is given by :

(1)

(Here, we take 0⁰=1.) It is convenient to parameterize the likelihood with θ_i=μρ_i, which is the expected number of parent fragments of site i. The value of μ (and so θ) depends on the particulars of the experimental setup, i.e. setups that allow more DNA parent fragments to be sequenced will lead to larger values. In the end, ρ_i holds greater scientific interest.

The method of maximum likelihood provides a means for estimating the parameters in (1), and their standard errors. There are two potential difficulties in their use in this setting. One is that the maximum of Equation (1) with respect to the free parameters requires the solution of non-linear equations with a large number of parameters. Sometimes this is difficult, but a workable algorithm is presented below. The other potential difficulty is that maximum likelihood methods usually require that the sample size is large relative to the number of parameters, that the model is correctly specified, that the parameter values are not too near the boundary of the parameter space and that certain other technical requisites are met. In the present context, the small number of replicates obtained and the existence of insertion sites whose abundance is low must lead to some caution. Some simulations are described below that test whether the maximum likelihood approach is suitable for data such as might be collected for HTLV-1 infected patients. In addition, jackknife bias corrections, jackknife standard errors and a P-value adjustment due to Efron (2004) are employed to obviate potential shortcomings of the maximum likelihood method in the present context. Also, a method for identifying departures from the assumed homogeneity of the fragment length distribution across sites is illustrated.

2.3 A maximization algorithm

The likelihood in (1) usually has high-dimensional parameters—there will be one non-trivial value of θ_i for every site detected in the sample, and at least one element of ϕ_j for every distinct length observed. The dimensionality of ϕ may be reduced substantially by estimating it as a regression function with a low dimension parameter, and this seems reasonable given the apparent smoothness of ϕ when one examines the actual data. The accuracy of may be improved by such fitting, but it turns out not to be necessary to solve the maximization problem. Under (1) it is straightforward to implement the EM algorithm (Dempster et al., 1977); the so-called complete data (which we denote by Y_ij) are the counts of parent fragments according to the length for each insertion site and are deemed to have Poisson distributions. The expectation of the complete data, conditioning on the incomplete data (w_ij, the indicator variables for the distinct lengths observed at each insertion site), yields the E-step of the EM algorithm. Given values for the parameters, θ_i and ϕ_j, the expectation of the complete data given the incomplete data, w_ij, is

(2)

The maximization step is trivial: for ϕ, sum the expectations over i, optionally smooth the result or fit a regression function, and scale the result to 1.0 for ϕ; for θ sum the expectations over j. The well-known slow convergence of the EM algorithm is evident here, too. However, it is easy to improve upon the EM algorithm by using the complete data to estimate ϕ_j, j=1,…, J, and then updating θ by fixing ϕ and taking a step using the Newton–Raphson method. As shown in Section 3.3 in Supplementary Material, the Fisher Information for θ is a diagonal matrix, and so this update is fast and simple. Repetition of this process usually converges in just a few steps.

2.4 Estimating

The distribution of fragment lengths can be estimated by the relative frequencies of the different lengths in the complete data of Equation (2). However, inspection of raw data (such as in Supplementary Fig. S2) suggests that the underlying probabilities have a fairly smooth dependence on fragment lengths. Estimates based on a suitable, low dimension regression function for the probabilities would have less variation than those based on relative frequencies. It turns out that excessive variation in leads to an upward bias in the estimates of θ that is greater for large values of θ and negligible for θ < 1000 in the present setting (Supplementary Figs S4 and S5). So, it is worth looking at the distribution of fragment lengths with an eye toward fitting it with a smooth curve.

The distribution of fragment lengths depends on several factors. The settings of the machine that performs sonication allow the user to influence the overall number of shear events. If the probability of shearing at a given site was the same at every site, and if the occurrence of a break at one site did not influence the occurrence at another site, then the fragment lengths would follow the geometric distribution. However, even if fragment sizes follow the geometric distribution, very short fragments yield too little sequence to uniquely match the reference genome, and the capabilities of the sequencer and processing done in preparation for sequencing limit recovery of fragments to a range of lengths. As a consequence, only fragments in the range of 25–500 bp can be recovered.

2.5 Extension to multiple replicates

The likelihood [Equation (1)] and the algorithm outlined in Section 2.3 (and detailed in Section 3.4 in Supplementary Material) can be adapted to handle the case in which multiple replicates are obtained for a single sample. In place of ϕ_j, a collection of parameters, ϕ_jr, r=1,…, R is specified with r indexing the replicate and R indicating their number. ϕ_jr gives the probability that an insertion site contributes a fragment of length j in replicate r. Likewise, w_ij is replaced by w_ijr.

2.6 Diagnosing heterogeneity of ϕ between sites

The expected value of w_ij is just the probability that w_ij=1, denoted by p_ij. The cumulative sum of the observed w_ij is y_k=∑_j=1^k w_ij and that for the expected is x_k=∑_j=1^k p_ij. For a sufficiently abundant site, the plot of the pairs (x_k, y_k), k=1,…, J should approximate the line of identity. Departures from the line of identity can identify discrepancies between the actual and presumed distribution of fragment lengths. Section 11 in Supplementary Material describes this approach as well as its limitations in more detail.

2.7 Standard errors for change in relative abundance

The difference in relative abundance is

(3)

where ρ_id1 (ρ_id2) is the relative abundance of an insertion site at location i on date d₁ (d₂), the time that the first (second) sample was drawn. It is important to monitor the relative abundances over time to detect clonal proliferation or see whether some clones are diminishing. The standard errors of the two fractions in (3) are determined from the Fisher Information under Equation (1), and a z-statistic is obtained from them and .

Typically, there are thousands of insertion sites under surveillance. When many significance tests of a similar kind are to be performed—called large-scale simultaneous testing (Efron, 2004)—it is often sensible to correct the standard error like that provided by likelihood methods from the shape of the frequency distribution of the test statistics. When the fraction of null hypotheses in a collection of tests is large, the central part of the distribution is mostly composed of statistics for null hypotheses and can be used to estimate the standard error under the null. The vector of relative abundances may contain thousands of (non-zero) elements, which may be monitored for change. If most do not change (or change only slightly), then the scale of the z-statistics from likelihood-based methods for the changes in relative abundance can be adjusted to compensate for possible mismatches between the model and the data to which it fits.

The locfdr package allows adjustment of the z-statistics by site and scale changes that are supposed to better match the null distribution, estimation of the fraction of insertion sites with changed relative abundance, and estimation of false discovery rates (FDR). It is applied to the z-statistics for the change in the relative abundance between sampling dates in each patient. The z-statistics comparing two dates poorly approximate a Gaussian distribution when θ_i1+θ_i2 > 10, rather like the well-known continuity issue in count date (Feller, 1945). So the adjustment factors for z-statistics are computed only on those z-statistics for which θ_id1+θ_id2 > 10.

2.8 Simulation

Simulation of insertion sites and their lengths uses a draw from a Poisson distribution with parameter, λ=θ_i to yield a count, s_i, for each site followed by a draw from the multinomial distribution with parameters, p=ϕ_j and N=s_i, yielding n_ij, j=1,…, J. If n_ij≥1, then w_ij is set to one, otherwise it is set to zero. Datasets that resemble sets which might be encountered in practice, must account for low abundance insertion sites that are unseen in our data. To do this, values of < 21 were rounded to the next lowest integer, then tabled, and then a mixture of 20 equally weighted, truncated Poisson distributions fit to the table. Each of the resulting 20 λ values was replicated enough times to match the expected and observed table totals, and combined with the values of of 21 and greater. Full details are provided in Section 9 in Supplementary Material.

2.9 Software

The R language and environment for statistical computing was used to perform the calculations. An R package called sonicLength was created to implement the algorithm of Section 2.3 and the simulations. The R packages locfdr, vegan, multicore, entropy, laeken and brew were used to carry out the computations and prepare this document and the Supplementary Material. Emacs org-mode was used to manage computations and prepare documents.

3 RESULTS

Data from 11 HTLV-1-infected patients were studied. Three samples taken from each patient were used, and the consecutive samples were taken at intervals ranging from 466 days to 1998 days with a mean of 1353 days. The patients are labeled A, B,…, K in the figures and the individual samples in each patient are numbered 1, 2, 3 in chronological order. On each of those days, three replicate subsamples were taken from the DNA pool of each sample.

The algorithm of Section 2.3 gave estimates of ϕ and θ. The glm fit used cubic B-splines (De Boor, 2001) for the fragment lengths with interior knots at 50 and 100. The boundary knots are placed at 1 and at 10 plus the largest observed length and counts of zero were used for unobserved lengths in that range.

Most results below are based on simultaneously fitting all three replicates of a single sample. However, in some instances fits are based on the separate replicates. Three iterations of the algorithm were required, and then the fit was deemed to have converged when the absolute value of gradients of the log-likelihood with respect to θ_i were all <10⁻⁵ when divided by and <0.01 in any case. Most samples had converged in the minimum three iterations, but one sample required 10 iterations to converge. Setting more stringent convergence criteria had negligible effect on the results.

3.1 Fitting ϕ

Figure 1 shows the graphs of for triplicate subsamples of a single sample from each of the two different patients (samples B2 and I1). As can be seen there is a substantial difference between the two patients and the curves for Patient I vary markedly among the triplicates. As a consequence, it seems unwise to try to find a common estimate 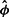to be applied across all the samples or even the subsamples.

Fig. 1.

versus Length. Estimates are provided for the replicates of sample I1 (solid lines) and sample B2 (dashed lines). The insert (dotted box) shows the corresponding calibration curves and an empirical calibration curve (thick line—see text).

The insert in Figure 1 shows the expected number of unique lengths, ∑_j=1^J(1−exp(−θϕ_j)), corresponding to each curve as a function of the number of parent fragments, θ. Estimates based on these curves approximate the maximum likelihood estimates. They can be compared with the empirical calibration curve of Gillet et al. (2011), which is seen to be quite different from these. Indeed, they are so different from one another that no one of them could adequately substitute for the others.

It is of some interest to see how the curves for 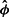vary by patient, by sample and by replicate. Supplementary Figure S3 shows the histogram of , the ratio of heights of the curve at length 60 and 100. Note that this portion of the curve reflects the typically geometric decline in the probability of shearing. The values vary by >3-fold. The analysis of variance (ANOVA) for with factors for patient and sample date (nested within patient) shows significant effects for patient (P <0.0001) and for date (P <0.0001). The variance components are estimated as 0.004 for patient, 0.028 for date and 0.019 for replicate. The variance component for patient is smallest and an order of magnitude smaller than the sum of the other two. So, most of the variation would seem to be tied to the sample preparation and processing.

The diagnostic plots of Section 2.6 shown in Section 11 of the Supplementary Material revealed a few sites whose curve for ϕ had sections where ϕ was much smaller than the estimate (or perhaps even zero). One such site at chr8:134994577F (by hg18) had no lengths between 88 and 102 but many outside that region. A repeat of ATGA covers 134 994 637 to 134 994 665 (or lengths 60–92), which complicates mapping the shear site. The shortfall in ϕ might be addressed by inspection of the original sequence reads for this site or by imputing the number apparently missed. Such corrective measures would be warranted if high abundance sites were affected.

3.2 Estimates of θ

3.2.1 Fitted values

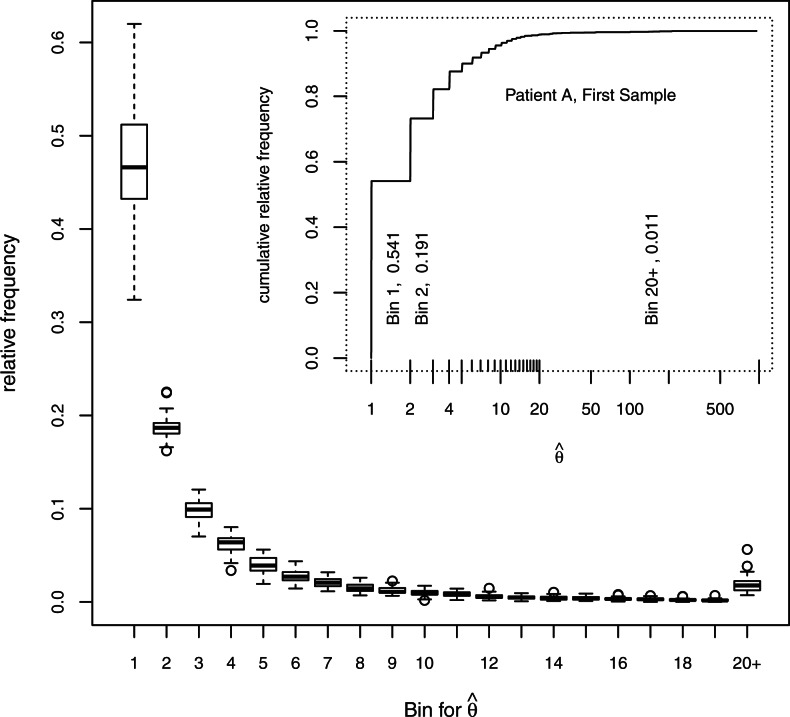
The distribution of in a single sample is shown in the insert in Figure 2. Most of the values are very close to 1.0, about one-fifth are very close to 2.0 and very few are >20. The values of near 1.0 mostly represent insertion sites for which only one shear event was recovered in the sample. The preponderance of such sites indicates that there are a substantial number of unseen integration sites, an issue which is treated in Section 8 in Supplementary Material. All the samples give a similar impression; their distributions are summarized by 20 boxplots showing the relative frequencies of 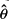according to the bins marked in the insert. The proportions in the bin for range from ~35% to 65%, those in the next bin range from ~15% to 25% and those in the last bin () range from ~ 1% to 6%.

Fig. 2.

Abundances of integration sites. The insert shows the cumulative frequency distribution for one sample, the bins used for relative frequencies in the larger plot enclosed by tick marks above the x-axis and the relative frequencies for three of the bins. Boxplots show the relative frequencies of each bin of for 33 samples. The box covers the first through third quartiles of the data, the central line of each box shows the median, the whiskers extend to the closer of the extreme or to 1.5 times the height of the box away from the box, and circles show points, if any, that lie beyond the whiskers.

Simulations were used to determine the bias of the estimates. For each of 33 setups mimicking the 33 samples here as described in Section 2.8, 100 runs were performed using the estimates of obtained here to sample the fragment lengths. Then values of and (and other estimands noted below) were estimated. For each of the simulated insertion sites, the average value of the was determined. Table 1 groups these according to the value of θ used in the simulation; the averages of the groups show excellent agreement between the estimates based on all three replicates and the parameter values used in the simulations. The agreement is also good for estimates based on a single replicate, but a modest upward bias is evident when θ> 512. The estimates based on empirical calibration also show good agreement for θ≤32, but the agreement is usually not as good for θ> 32 and shows a strong downward bias for θ> 1024. The impression that maximum likelihood estimates of θ have little bias is supported by the Supplementary Material, where plots of θ against the average of over 100 simulations hew closely to the line of identity (Supplementary Figs S6 and S7). However, some care is needed in fitting 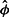. When 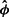was based on the relative frequencies (rather than fitting the quasi-Poisson glm) and a similar plot of average is prepared, divergence of the estimates from the true values is seen once the true values exceed 1000. As noted in Section 5.2 in Supplementary Material, the positive second partial of E(Y_ijr; θ_i, ϕ_jr) with respect to ϕ_jr suggests this bias when there is substantial variation in .

Table 1.

Average estimated value of θ

Category	Total	θ
(0,0.25]	34 964	0.17	0.17	0.17	0.17
(0.25,0.5]	69 970	0.36	0.36	0.36	0.36
(0.5,1]	40 875	0.68	0.68	0.68	0.68
(1,2]	15 140	1.47	1.47	1.48	1.47
(2,4]	24 271	2.8	2.8	2.81	2.79
(4,8]	8559	5.83	5.84	5.86	5.77
(8,16]	6461	9.89	9.91	9.94	9.74
(16,32]	1102	24.84	24.89	24.96	23.91
(32,64]	577	42.49	42.55	42.79	39.86
(64,128]	183	86.27	86.45	86.49	75.68
(128,256]	64	174.61	175.02	171.63	137.7
(256,512]	20	336.87	338.03	342.28	307.27
(512,1024]	11	763.09	766.73	822.16	777.5
> 1024	14	4749.68	4746.69	4906.33	2725.86

Each abundance parameter is assigned to an interval category. In each category, the average of the parameters is found (θ), of the estimates based on three replicates (), of the estimates based on single replicates (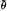) and of the average based on empirical calibration ().

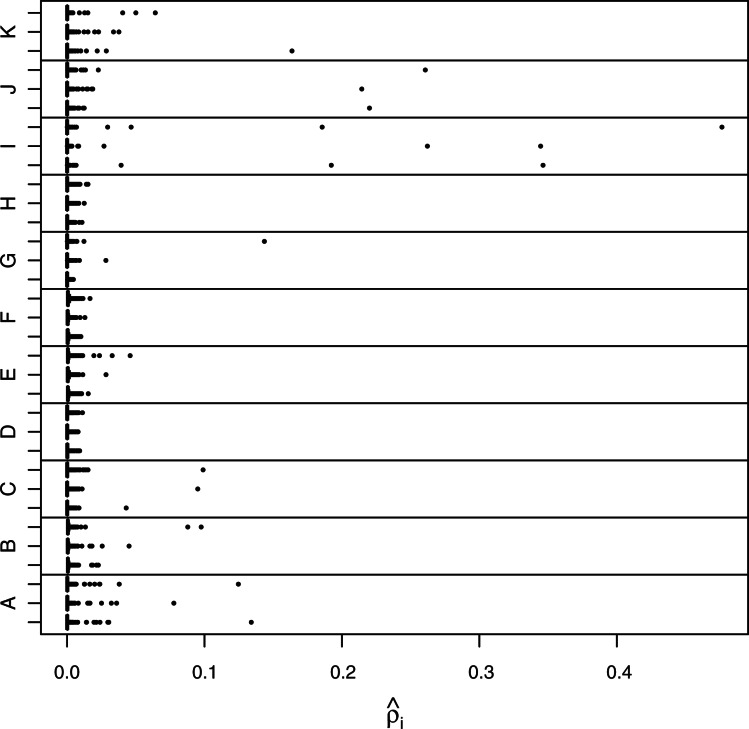
Figure 3 shows the relative abundance in each of 3 samples in each of 11 patients. The estimates use all three replicates taken for each sample. The samples are ordered according to date (earliest sample is lowest in each panel). It is evident that the pools of HTLV-1-infected cells differ substantially across patients; patient H has no single site accounting for >5% of , whereas patient I has two sites accounting for >50%.

Fig. 3.

Relative abundance of integration sites. A boxplot for the relative abundances of each sample is shown. The width of each box and its whiskers is quite narrow compared with the range of the data, and every sample has sites (seen as dots) that lie well beyond the box and whisker. The samples are in chronological order in each panel—lower is earlier.

3.2.2 Standard error of

The nominal standard errors in approximate those of the Poisson distribution (i.e. mean equals variance) when is not too large (less than ). For large values, however, the variation becomes quite a bit larger, and at , the variance is ≈ 10⁶—two orders of magnitude larger.

3.2.3 Extra model variation

According to the simulations carried out as described earlier, the asymptotic standard errors are in close agreement with the observed variation (Section 6.3 in Supplementary Material). However, these standard errors assume homogeneity of the fragment length distribution across all sites in a replicate. Evidence that the data contain more variation than predicted under this assumption was shown by fitting the three replicates of each sample separately, and computing the standard deviation for the values of for the insertion site that had the largest value when the triplicates were combined. When these values are compared with the value obtained from the likelihood (i.e. 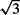times the asymptotic SD from the fit of the combined triplicates), it was seen that there were 32 instances in which the observed SD was greater, while 12.1 are expected assuming as usual that the sample variance follows a scaled χ_df² distribution with df=2. The conclusion to be drawn is that there is variation beyond that specified by the model. The likelihood method and standard errors developed here allowed explicit checking of the model; adjustment to account for overdispersion such as that in Section 3.3.1 is needed.

3.3 Tests for change between samples

3.3.1 Change in relative abundance

Tests for changes in relative abundance, δ_id1d2 could be based on the asymptotic standard errors. However, as noted earlier in Section 3.2.2 extra-model variation was seen among the individual replicates—making the theoretical standard errors too small. If it happens that most of the relative abundances have only negligible change, then the large-scale hypothesis testing framework (Efron, 2004) may be used for testing and calculation of false discovery rates. To ascertain whether this framework can be applied here, the z-statistics for change in relative abundance between date d₁ and date d₂ were calculated:

(4)

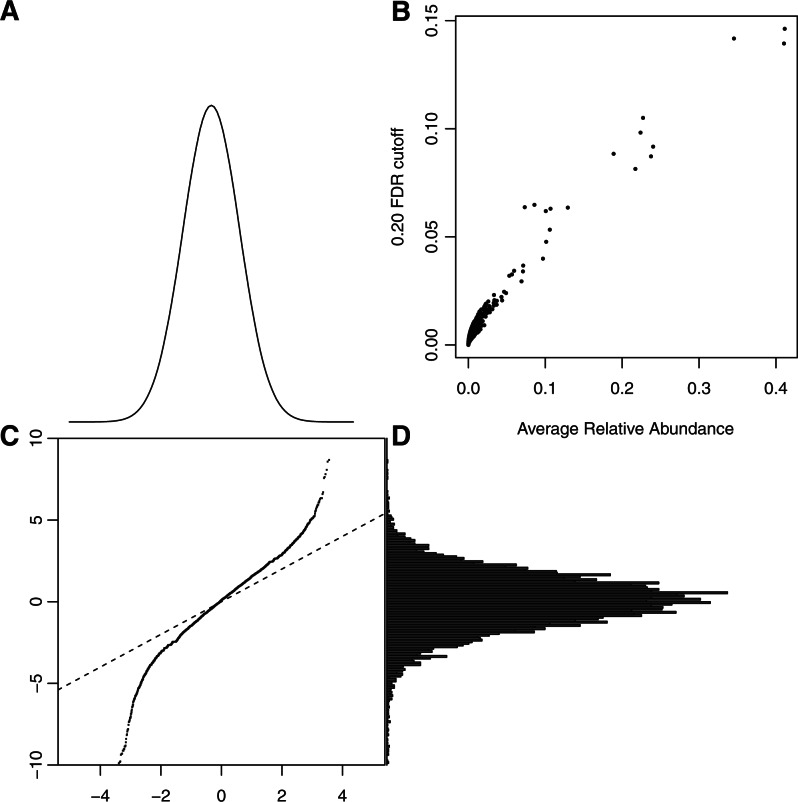
Inspection of histograms and Normal probability plots of the z-statistics for pairs of dates in individual patients (data not shown) revealed that the central part of the distribution matched the Normal probability law, but the tails were usually too long to match. This is consistent with the majority of sites having negligible change in relative abundance and a few having substantial changes. Figure 4 shows the results for all patients and pairs of times combined. The qq-plot is nearly linear through its central region and has a slope of about 1.5, which suggests variation beyond that in the model used to develop the z-statistics. The variation in was seen to grow rapidly for values of θ> 1000 and Figure 4B reflects this; there the cutoff in needed to declare a difference at FDR<0.20 is plotted against the average relative abundance of two samples, 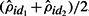, for 33 patient samples. For highly abundant sites that account for >10% of insertion bearing fragments, the difference needed to declare FDR<0.20 must be quite large. For example, when the average of two dates is 30%, the difference must exceed 12%. See the comment on this matter in Section 4.

Fig. 4.

Change statistics distribution. The Normal density (A) and the empirical distribution of change statistics (D) are used to form the Normal probability qq–plot (C). Linearity of the qq-plot is used to visually assess goodness-of-fit to the theoretical density. The plot would follow the line of identity in (C), if the data were Normal with unit variance. The linearity of the central portion is expected when there is a mixture of null and non-null hypotheses, but an adjustment is needed to match the null variance. (B) The cutoffs for a 20% FDR after accounting for the apparent null variance.

Figure 5 shows the relative abundances for each pair of dates for the samples of three patients (E, G and I). (Supplement Figs S17 and S18 show similar plots for all patients.) Those differences that achieve FDR<0.20 are marked with heavy lines (solid for adjacent pairs, dashed for first versus third). Two insertion sites of patient E were undetectable in 2000, then increased to moderately high levels in 2005 (although FDR > 0.20), and then increased again by 2008 to high levels. The most abundant site of patient G showed significant increases from 2001 to 2005 and again to 2008. Patient I has two very abundant sites, but the fairly large differences fail to attain FDR<0.20 even as more modest increases are discovered. In part, this is due to the larger standard errors associated with highly abundant sites as well as the rescaling needed to account for the overdispersion evident in Figure 4. In a patient with such abundant sites, increasing the number of replicates in the later samples would reduce the standard errors—yielding more accurate monitoring.

Fig. 5.

Changes in abundance. The relative abundances are plotted against sample date. The vertical axis uses a cube root scale for better visualization. Gray lines join the values between first and second samples and between the second and third samples.Black lines overlay adjacent pairs with abundances different at FDR <0.20. Dashed lines overlie both pairs when first and third samples differ at FDR<0.20.

In each panel, it is apparent that many sites are at undetectable levels for at least one visit as expected with many low abundance sites. Seventy percent are undetectable at some time for patient E, 77% for patient G and 82% for patient I. It is possible that some new insertions are established and existing insertions vanish.

Here, the z-statistics for each patient are calibrated separately to determine the scale factors and FDR cutoffs (which were used in Fig. 4B). The scale factors for the patients range from 1.251 to 1.977 with a mean of 1.576.

4 DISCUSSION

We addressed the problem of estimating the abundance of insertion sites from data on fragment lengths by a maximum likelihood approach. Simulations showed that the method works well, when the estimated probabilities of fragment lengths are not too variable. When a glm is used to fit the fragment length distribution, the abundance estimates have little bias and the asymptotic standard errors accurately portray the variability in simulated data.

These standard errors are available for single replicates, and provide a check on the model: empirical variations in triplicates from patient data varied more than expected, showing overdispersion of abundance estimates. Further, the z-statistics for the change in relative abundance have a broader distribution than the theory suggests. These observations emphasize the value of replication and mandate the use of standard errors derived empirically from replicates (as with a jackknife standard error) or by application of the large-scale hypothesis testing approach (Efron, 2004). Inspection of the data as histograms and as normal probability plots suggests that the large-scale hypothesis testing framework is suitable for testing changes in relative abundance.

The standard errors associated with relative abundances increase dramatically as the relative abundances increase >10% using the current setup. This makes it rather difficult to detect changes in the relative abundance of insertion sites that are highly abundant. For example, a change from 40% to 50% is below the limit of detection in data like those shown here in which there are three replicates. The standard errors of abundant sites would diminish if a sample were divided into more replicates.

Jackknife corrections for bias in the total number of insertion sites, the entropy of abundances and their Gini coefficient due to unseen insertion sites were successful in simulations (Sections 4, 7 and 8 in Supplementary Material) in spite of a large fraction of unseen sites. These corrections were enabled by the replicates, which also allowed the computation of jackknife standard errors.

Some heterogeneity of fragment lengths across sites was observed, the increase in power of added replicates to detect this also emphasizes the importance of replication. Even more replicates than the three used here may be needed for careful monitoring of patient status; the power to detect change in the abundance of highly abundant insertion sites is limited even with three replicates of each sample. In clinical monitoring in which highly abundant sites play a key role, an obvious way to increase power is to increase the number of replicates beyond the three replicates used here.

Going forward, these methods allow much more detailed assessment of clonal behavior during HTLV-1 infection. In the first analysis of these data, abundances could only be estimated roughly and standard errors had to be empirically determined. Using the methods described here, combined with ongoing data acquisition, it will be possible to relate much more fine grained information on clonal abundance to clinically relevant parameters such as viral gene expression and leukemogenesis.

Funding: National Institute of Allergy and Infectious Diseases (2R01 AI052845 and 5R01 AI082020); Wellcome Trust.

Conflict of Interest: N.G. is an employee of Illumina Inc, a public company that develops and markets systems for genetic analysis. The remaining authors declare no competing financial interests.