Abstract
Histone proteins are not only important due to their vital role in cellular processes such as DNA compaction, replication and repair but also show intriguing structural properties that might be exploited for bioengineering purposes such as the development of nano-materials. Based on their biological and technological implications, it is interesting to investigate the structural properties of proteins as a function of temperature. In this work, we study the spatial response dynamics of the histone H2AX, consisting of 143 residues, by a coarse-grained bond fluctuating model for a broad range of normalized temperatures. A knowledge-based interaction matrix is used as input for the residue-residue Lennard-Jones potential.
We find a variety of equilibrium structures including global globular configurations at low normalized temperature (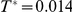 ), combination of segmental globules and elongated chains (
), combination of segmental globules and elongated chains (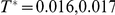 ), predominantly elongated chains (
), predominantly elongated chains (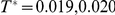 ), as well as universal SAW conformations at high normalized temperature (
), as well as universal SAW conformations at high normalized temperature (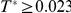 ). The radius of gyration of the protein exhibits a non-monotonic temperature dependence with a maximum at a characteristic temperature (
). The radius of gyration of the protein exhibits a non-monotonic temperature dependence with a maximum at a characteristic temperature (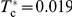 ) where a crossover occurs from a positive (stretching at
) where a crossover occurs from a positive (stretching at 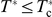 ) to negative (contraction at
) to negative (contraction at 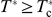 ) thermal response on increasing
) thermal response on increasing 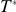 .
.
Introduction
Our perspective of proteins is more and more changing from static to dynamical entities [1]. Increasing efforts are undertaken to better understand the functioning of biological macromolecules with the aim of engineering them for technological applications [1]. In fact, proteins are powerful therapeutic agents [2], [3] and recent developments have stressed their impact on the bioengineering of nanomaterials, especially in biomedical imaging, drug delivery, biosensing and the design of functional nanocomposites [4], [5]. To this end, protein self-assembly in suitable media offers unique advantages in the fabrication of protein-based nanodevices and avoids cost-intensive manufacturing processes [1]. However, thermally stable proteins are essential for bionanotechnological applications [6]–[8]. Thus, based on the biological [9]–[12] and technological implications [1], [13], [14], it is interesting to investigate the structural properties of proteins as a function of temperature [15], [16].
Due to the unique sequence of residues a complex and specific structural response is expected. Consequently, the study of the structure of proteins has been of interest for many years, particularly exploiting computer simulations via idealized models [6], [7], [17]–[28]. However, despite considerable effort, a complete understanding of the fundamental issue of how proteins fold to its native structure still remains an open question from a first principle approach [6], [7], [17]–[28].
In this work, we explore how the protein H2AX, a variant of the histone H2A, conforms and responds to temperature changes. The protein H2AX plays a vital role in cellular functioning: Its serine 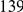 phosphorylated form,
phosphorylated form,  -H2AX [29], is one of the earliest repair responses to DNA double-strand breaks which can lead to mutations that in turn are a cause of cancer and hereditary disease [30]. Notably, it was found that
-H2AX [29], is one of the earliest repair responses to DNA double-strand breaks which can lead to mutations that in turn are a cause of cancer and hereditary disease [30]. Notably, it was found that  -H2AX increases in a variety of conditions in relation to double-strand break generation processes, including radiation and high temperature [31]. Moreover, a recent work has shown that postranslational modifications in histones underlie heat acclimation-mediated cytoprotective memory [32].
-H2AX increases in a variety of conditions in relation to double-strand break generation processes, including radiation and high temperature [31]. Moreover, a recent work has shown that postranslational modifications in histones underlie heat acclimation-mediated cytoprotective memory [32].
Regarding the above mentioned technological implications of proteins in general and the biological impact of the histone H2AX in particular the study of their temperature-dependent structural changes is worthwhile. Thus, we consider a coarse-grained model [18], [20] of this protein chain where knowledge-based residue-residue interactions [19], [33] are employed and effects of temperature are explored.
Analysis
The high dimensional space of protein conformations as well as the complexity of the energy surface make coarse-graining almost unavoidable in modeling the global structure and dynamics of proteins no matter whether one choses an all-atom approach, a minimalist description or a combination thereof [22]–[28].
In this work, we present a computer simulation study of the protein H2AX applying the bond-fluctuation method [34], which has been applied successfully to model the static and dynamical properties of polymer systems in several investigations [35]. It is a lattice algorithm with the advantage of avoiding non-ergodicity and its computational efficiency renders it more attractive than off-lattice models. The polymer evolves on a cubic lattice, where each monomer blocks eight lattice sites, which then cannot be occupied by other monomers. Monomers are connected by fluctuating bond vectors of lengths  ,
, 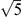 ,
, 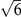 , 3 and
, 3 and 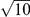 , leading to an average bond length of
, leading to an average bond length of 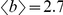 . A Monte Carlo move consists of randomly choosing one monomer to be moved to a randomly chosen lattice direction by one lattice unit. This trial motion is only accepted if neither the excluded volume constraint nor the restriction on the allowed range of bond lengths is violated. By additionally considering the Metropolis transition probability [35] for accepting or rejecting a move we include effects due to the finite interaction energies explained in the following [34]. Thus, the simulation method produces unbiased results, takes into account excluded volume interactions and ensures that no bond crossings can occur.
. A Monte Carlo move consists of randomly choosing one monomer to be moved to a randomly chosen lattice direction by one lattice unit. This trial motion is only accepted if neither the excluded volume constraint nor the restriction on the allowed range of bond lengths is violated. By additionally considering the Metropolis transition probability [35] for accepting or rejecting a move we include effects due to the finite interaction energies explained in the following [34]. Thus, the simulation method produces unbiased results, takes into account excluded volume interactions and ensures that no bond crossings can occur.
The H2AX protein consists of 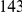 residues shown in Table 1. Each residue is described by a monomer of the bond-fluctuating protein chain [18], [20]. This is a simplified representation of a residue without the all-atom structural details but the specificity of each residue is captured via the applied residue-residue interactions [21]. Moreover, our approach has the advantage of computational efficiency allowing for the covering large (biological) scales. In fact, the bond-fluctuation method has recently been used to study the conformational relaxation into native structure of a general HP protein chain [36] and even a specific protein, sensory rhodopsin, without severe constraints [37].
residues shown in Table 1. Each residue is described by a monomer of the bond-fluctuating protein chain [18], [20]. This is a simplified representation of a residue without the all-atom structural details but the specificity of each residue is captured via the applied residue-residue interactions [21]. Moreover, our approach has the advantage of computational efficiency allowing for the covering large (biological) scales. In fact, the bond-fluctuation method has recently been used to study the conformational relaxation into native structure of a general HP protein chain [36] and even a specific protein, sensory rhodopsin, without severe constraints [37].
Table 1. Sequence of residues of the histone H2AX.
 M M |
 S S |
 G G |
 R R |
 G G |
 K K |
 T T |
 G G |
 G G |
 K K |
 A A |
 R R |
 A A |
 K K |
 A A |
 K K |
 S S |
 R R |
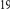 S S |
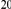 S S |
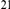 R R |
 A A |
 G G |
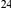 l l |
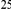 Q Q |
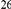 F F |
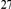 P P |
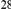 V V |
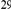 G G |
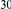 R R |
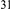 V V |
 H H |
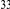 R R |
 L L |
 L L |
 R R |
 K K |
 G G |
 H H |
 Y Y |
 A A |
 E E |
 R R |
 V V |
 G G |
 A A |
 G G |
 A A |
 P P |
 V V |
 Y Y |
 L L |
 A A |
 A A |
 V V |
 L L |
 E E |
 Y Y |
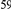 L L |
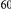 T T |
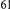 A A |
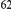 E E |
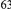 I I |
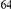 L L |
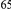 E E |
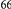 L L |
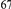 A A |
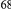 G G |
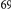 N N |
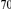 A A |
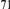 A A |
 R R |
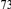 D D |
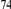 N N |
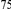 K K |
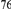 K K |
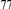 T T |
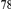 R R |
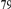 I I |
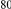 I I |
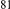 P P |
 R R |
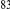 H H |
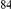 L L |
 Q Q |
 L L |
 A A |
 I I |
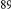 R R |
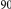 N N |
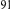 D D |
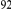 E E |
 E E |
 L L |
 N N |
 K K |
 L L |
 L L |
 G G |
 G G |
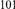 V V |
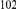 T T |
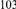 I I |
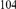 A A |
 Q Q |
 G G |
 G G |
 V V |
 L L |
 P P |
 N N |
 I I |
 Q Q |
 A A |
 V V |
 L L |
 L L |
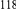 P P |
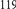 K K |
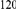 K K |
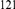 T T |
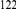 S S |
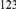 A A |
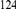 T T |
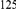 V V |
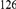 G G |
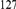 P P |
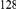 K K |
 A A |
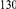 P P |
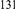 S S |
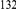 G G |
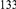 G G |
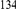 K K |
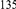 K K |
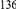 A A |
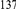 T T |
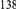 Q Q |
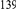 A A |
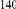 S S |
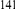 Q Q |
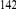 E E |
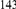 Y Y |
Hydrophobic residues are pink, polar residues are gold and electrostatic ones are blue.
Apart from excluded volume interactions, each residue interacts with the neighboring residues within the range 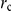 using a generalized Lennard-Jones (LJ) potential
using a generalized Lennard-Jones (LJ) potential
| (1) |
where 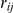 is the distance between the residues
is the distance between the residues  and
and 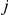 and
and 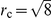 and
and  in units of the lattice constant. The strength of the pair potential
in units of the lattice constant. The strength of the pair potential 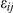 is unique for each pair of residues with appropriate positive (repulsive) or negative (attractive) values (for more detail on the force field see [19], [38]). In contrast to our recent study of a HIV protease with a coarse-grained approach involving the relative hydropathy index of each amino acid as well as results from all-atom simulations [18], in this work, we use a knowledge-based interaction matrix for the residue-residue pair interactions. The knowledge-based interaction potential matrix is derived from an ensemble of a large number of protein structures in the protein data bank (PDB). A number of such interaction tables are frequently used to investigate a range of questions related to protein structure including protein folding which has been studied extensively with a variety of models and methods involving all-atom details to minimalist coarse-grained descriptions [22]–[28], [39]–[44]. We resort here to the classic residue-residue contact interaction table [19] which is employed in studying scaffolding of short peptides [20].
is unique for each pair of residues with appropriate positive (repulsive) or negative (attractive) values (for more detail on the force field see [19], [38]). In contrast to our recent study of a HIV protease with a coarse-grained approach involving the relative hydropathy index of each amino acid as well as results from all-atom simulations [18], in this work, we use a knowledge-based interaction matrix for the residue-residue pair interactions. The knowledge-based interaction potential matrix is derived from an ensemble of a large number of protein structures in the protein data bank (PDB). A number of such interaction tables are frequently used to investigate a range of questions related to protein structure including protein folding which has been studied extensively with a variety of models and methods involving all-atom details to minimalist coarse-grained descriptions [22]–[28], [39]–[44]. We resort here to the classic residue-residue contact interaction table [19] which is employed in studying scaffolding of short peptides [20].
Even though the knowledge-based matrix elements 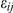 are simplified estimates derived from residue-residue contacts we are confident that the phenomenological interaction matrix implicitly takes into account the secondary and tertiary structure of the proteins [45], [46]. In fact, several factors need to be considered for the crystallization of a protein sample subject to an X-ray christallograpy study, which include protein purity, pH, concentration of the protein, the temperature, and precipitants. X-ray crystallographic images of several thousands of proteins from the PDB are used to derive the residue-residue interaction matrix which is applied as an input for our potential. In such a huge ensemble of proteins, residues in secondary and tertiary structures are expected be well represented by effective residue-residue interactions at various temperatures when applying a coarse-grained protein model.
are simplified estimates derived from residue-residue contacts we are confident that the phenomenological interaction matrix implicitly takes into account the secondary and tertiary structure of the proteins [45], [46]. In fact, several factors need to be considered for the crystallization of a protein sample subject to an X-ray christallograpy study, which include protein purity, pH, concentration of the protein, the temperature, and precipitants. X-ray crystallographic images of several thousands of proteins from the PDB are used to derive the residue-residue interaction matrix which is applied as an input for our potential. In such a huge ensemble of proteins, residues in secondary and tertiary structures are expected be well represented by effective residue-residue interactions at various temperatures when applying a coarse-grained protein model.
Each randomly selected residue performs its stochastic movement according to the Metropolis algorithm subject to excluded volume constraints and the limits on changes in the covalent (i.e. peptide) bond length as in our previous studies [18], [20]. A randomly selected residue at a site  is moved to one of its randomly selected neighboring lattice sites
is moved to one of its randomly selected neighboring lattice sites 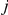 with the Boltzmann probability
with the Boltzmann probability 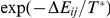 , where
, where 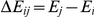 is the change in energy between the attempted
is the change in energy between the attempted 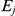 and current
and current 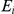 configuration [35].
configuration [35].
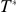 is the normalized temperature in units of the Boltzmann constant
is the normalized temperature in units of the Boltzmann constant 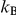 and the energy
and the energy 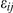 . Due to the lack of calibration with experimental data it is not possible to quantitatively relate the temperature
. Due to the lack of calibration with experimental data it is not possible to quantitatively relate the temperature 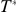 to physical temperature values. However, since the interresidue contact energies
to physical temperature values. However, since the interresidue contact energies 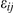 allow for the calculation of realistic conformational energies of amino acids sequences in a number of different folds [38] we are able to relate temperature changes qualitatively to changes in the structural properties of proteins. Thus, our coarse-grained protein model provides a (qualitative) framework for understanding the temperature-dependent response of proteins which can so far not be gained by experimental testing.
allow for the calculation of realistic conformational energies of amino acids sequences in a number of different folds [38] we are able to relate temperature changes qualitatively to changes in the structural properties of proteins. Thus, our coarse-grained protein model provides a (qualitative) framework for understanding the temperature-dependent response of proteins which can so far not be gained by experimental testing.
Initially, the protein chain is placed in a random conformation with excluded volume constraints. Simulations are then performed for a sufficiently long time (typically 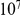 time steps) with
time steps) with 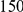 independent samples. While one can monitor (thermodynamic) quantities (such as the radius of gyration or the energy) in a simulation in order to make sure that the system has reached asymptotic steady state, one has to take into account that the protein may or may not be in equilibrium due to the possibility of metastability (caused by frustration). Gerstman and Chapagain [47] provide an estimate for the time which is required for a protein to undergo the transition from a random coil to its native state. Using a simplified coarse-grained model and introducing a propensity energy to constrain appropriate segmental structures they suggest that
independent samples. While one can monitor (thermodynamic) quantities (such as the radius of gyration or the energy) in a simulation in order to make sure that the system has reached asymptotic steady state, one has to take into account that the protein may or may not be in equilibrium due to the possibility of metastability (caused by frustration). Gerstman and Chapagain [47] provide an estimate for the time which is required for a protein to undergo the transition from a random coil to its native state. Using a simplified coarse-grained model and introducing a propensity energy to constrain appropriate segmental structures they suggest that 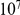 time steps (corresponding to about 0.01 sec) is large enough for a protein to reach its native structure. In our simulation, the protein chain is initially in a random coil configuration (with excluded volume constraints) and it takes about
time steps (corresponding to about 0.01 sec) is large enough for a protein to reach its native structure. In our simulation, the protein chain is initially in a random coil configuration (with excluded volume constraints) and it takes about 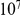 time steps to reach an equilibrium conformation. Thus, while one has to take into account that this approximation might fail when considering additional details such as an effective medium etc., the time scale by Gerstman and Chapagain could be a rough estimate of the order of magnitude for our simulation. Different lattice sizes are used to test for finite size effects. Most of the data presented here are generated on a lattice of size
time steps to reach an equilibrium conformation. Thus, while one has to take into account that this approximation might fail when considering additional details such as an effective medium etc., the time scale by Gerstman and Chapagain could be a rough estimate of the order of magnitude for our simulation. Different lattice sizes are used to test for finite size effects. Most of the data presented here are generated on a lattice of size 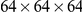 since the qualitative results for different lattice sizes do not show significant differences.
since the qualitative results for different lattice sizes do not show significant differences.
Results
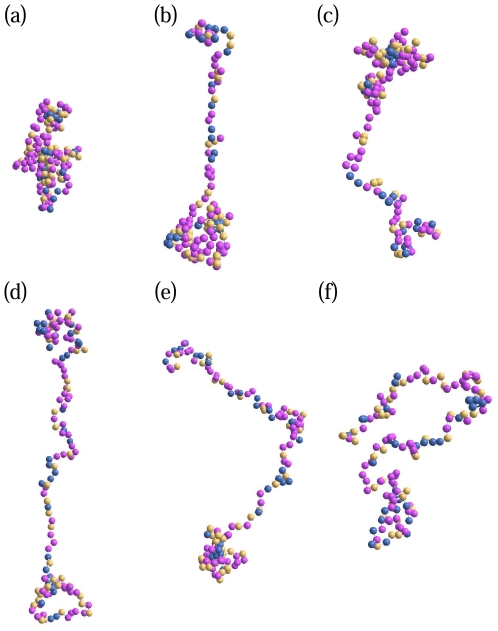
Fig. 1 illustrates snapshots of the histone H2AX for different representative temperatures (in reduced units) in the range of 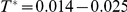 . Some of the general conformational characteristics such as globular structure formation (global aggregation of the intra-chain residues,
. Some of the general conformational characteristics such as globular structure formation (global aggregation of the intra-chain residues, 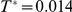 ), local segregation of selective residues (
), local segregation of selective residues (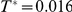 ), large-scale stretching (
), large-scale stretching (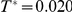 ), onset of randomization (
), onset of randomization (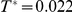 ) and thermal mixing (
) and thermal mixing (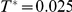 ) are already apparent in the “snapshot” configurations. The interplay between the cooperative and competing interactions among the residues and the temperature constrained by the peptide bonds leads to a rich ensemble of protein structures. While a detailed analysis of such a structural ensemble in an in vivo system still remains an open challenge, our approach offers some insights into the overall structural pattern changes that are so far inaccessible to experiment. Moreover, simulation studies (such as ours) preceding experimental tests may help e.g. in assessing the applicability of proteins for the design and fabrication of biomolecular devices in the bionanotechnology.
) are already apparent in the “snapshot” configurations. The interplay between the cooperative and competing interactions among the residues and the temperature constrained by the peptide bonds leads to a rich ensemble of protein structures. While a detailed analysis of such a structural ensemble in an in vivo system still remains an open challenge, our approach offers some insights into the overall structural pattern changes that are so far inaccessible to experiment. Moreover, simulation studies (such as ours) preceding experimental tests may help e.g. in assessing the applicability of proteins for the design and fabrication of biomolecular devices in the bionanotechnology.
Figure 1.
Snap shots of the histone H2AX at (a) 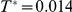 , (b)
, (b) 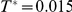 , (c)
, (c) 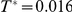 , (d)
, (d) 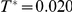 , (e)
, (e) 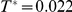 and (f)
and (f) 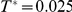 . Hydrophobic residues are shown in pink, polar residues in gold and electrostatic ones in blue. We find globular configurations at low temperature (
. Hydrophobic residues are shown in pink, polar residues in gold and electrostatic ones in blue. We find globular configurations at low temperature (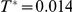 ), combination of segmental globules and elongated chains (
), combination of segmental globules and elongated chains (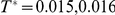 ), predominantly elongated chains (
), predominantly elongated chains (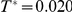 ), as well as universal SAW conformations at high temperature (
), as well as universal SAW conformations at high temperature (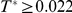 ).
).
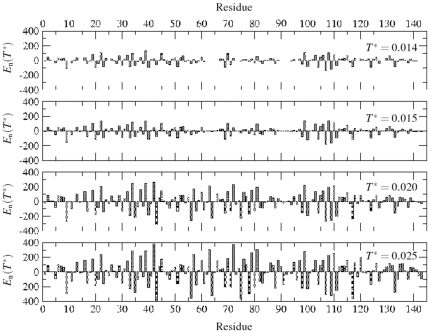
Fig. 2 and Fig. 3 show the energy and mobility profile of each residue. The energy of a residue is its interaction energy with neighboring residues within the range of interaction. The mobility of a residue is defined by the number of successful moves per unit MC time step. Note the contrasts in profiles at relatively low (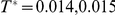 ) and high (
) and high (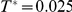 ) temperature. Residues along the histone backbone appear to possess an isotropic distribution of (almost in equal number) attractive (cohesive, negative) and repulsive (positive) energy. The magngitude of the repulsive and the attractive energy and their differences in consecutive segments increases with temperature which is manifested in the segmental configuration as well as in the global (coil-to-globule) structure of the protein.
) temperature. Residues along the histone backbone appear to possess an isotropic distribution of (almost in equal number) attractive (cohesive, negative) and repulsive (positive) energy. The magngitude of the repulsive and the attractive energy and their differences in consecutive segments increases with temperature which is manifested in the segmental configuration as well as in the global (coil-to-globule) structure of the protein.
Figure 2. Energy 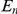 of each residue of histone H2AX at normalized temperatures
of each residue of histone H2AX at normalized temperatures 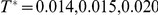 , and
, and 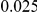 .
.
The energy of a residue is its interaction energy with neighboring residues within the range of interaction. The magnitude of the repulsive and the attractive energy and their differences in consecutive segments increases with temperature which is manifested in the global (coil-to-globule) structure of the protein. At low temperatures (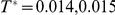 ), residues with the lowest mobility consist of 36R, 37K, 57E, 62E, 65E, 72R, 73D, 75K, 76K, 78R, 89R, 90N, 91D, 92E, 93E, 95N, 96K, 119K, 120K, 134K, 135K, 141Q and 142E. Nearly all the electrostatic residues (D, E, K, R) along with a few polar groups (Q,N) act as anchor/seed for segmental aggregation.
), residues with the lowest mobility consist of 36R, 37K, 57E, 62E, 65E, 72R, 73D, 75K, 76K, 78R, 89R, 90N, 91D, 92E, 93E, 95N, 96K, 119K, 120K, 134K, 135K, 141Q and 142E. Nearly all the electrostatic residues (D, E, K, R) along with a few polar groups (Q,N) act as anchor/seed for segmental aggregation.
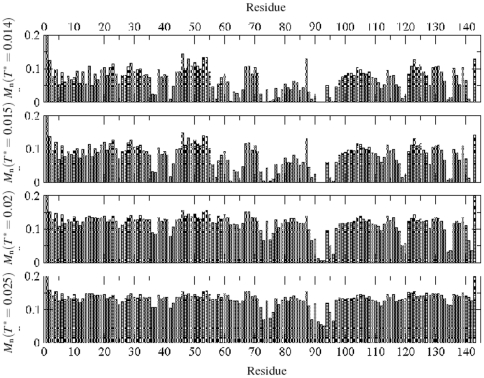
Figure 3. Mobility 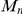 of each residue (number of successful moves per unit time step) of the histone H2AX at temperatures
of each residue (number of successful moves per unit time step) of the histone H2AX at temperatures 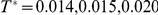 , and
, and 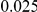 .
.
The mobility of a residue is defined by the number of successful moves per unit MC time step. With exceptions the mobility profile of the residues follows the energy profile relatively closely where the lower segmental energy differences translate into lower segmental mobility. Interestingly, some residues, 42E and 57E, show a low mobility despite their positive energy.
The mobility profile of the residues follows the energy profile relatively closely where the lower segmental energy differences translate into lower segmental mobility. At low temperatures (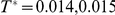 ), residues with the lowest mobility consist of 36R, 37K, 57E, 62E, 65E, 72R, 73D, 75K, 76K, 78R, 89R, 90N, 91D, 92E, 93E, 95N, 96K, 119K, 120K, 134K, 135K, 141Q and 142E. Nearly all the electrostatic residues (D, E, K, R) along with a few polar groups (Q,N) act as anchor/seed for segmental aggregation. Note that the pair interaction potentials of these residues have the largest well depth [19]. Most of these residues become more mobile when raising the temperature (i.e. see the segments 91D, 92E, 93E).
), residues with the lowest mobility consist of 36R, 37K, 57E, 62E, 65E, 72R, 73D, 75K, 76K, 78R, 89R, 90N, 91D, 92E, 93E, 95N, 96K, 119K, 120K, 134K, 135K, 141Q and 142E. Nearly all the electrostatic residues (D, E, K, R) along with a few polar groups (Q,N) act as anchor/seed for segmental aggregation. Note that the pair interaction potentials of these residues have the largest well depth [19]. Most of these residues become more mobile when raising the temperature (i.e. see the segments 91D, 92E, 93E).
It should be pointed out that some residues (e.g. 42E and 57E) have surprisingly low mobility despite their positive energy while others with low energy have a high mobility index. In fact, conformational energy of the amino acids sequence (the interaction energy) does not determine the local structure and mobility alone. Physical (covalent bonding) or topological (trapping) constraints also play an important role in the cooperative response.
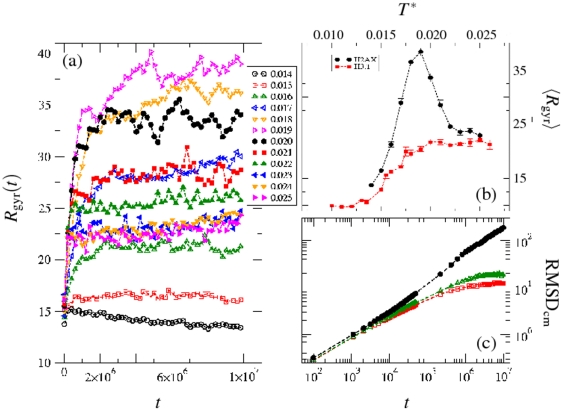
With respect to biotechnological applications it is interesting to study how the entire range of temperatures affects a protein's size and shape. The temporal variation of the radius of gyration 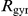 shows that it has reached its equilibrium at all temperatures except for the lowest one (
shows that it has reached its equilibrium at all temperatures except for the lowest one (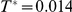 ) where the relaxation is too slow. Equilibration implies that the protein chain has explored a sufficient amount of conformations in structural phase space. The average value of the equilibrium radius of gyration can be evaluated from the asymptotic data sets at each temperature.
) where the relaxation is too slow. Equilibration implies that the protein chain has explored a sufficient amount of conformations in structural phase space. The average value of the equilibrium radius of gyration can be evaluated from the asymptotic data sets at each temperature. 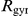 shows a non-monotonic dependence on temperature as can be seen in Fig. 4 with a maximum at a characteristic temperature
shows a non-monotonic dependence on temperature as can be seen in Fig. 4 with a maximum at a characteristic temperature 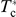 which is a “unique” property of the studied biomaterial. The radius of gyration increases on increasing the temperature (
which is a “unique” property of the studied biomaterial. The radius of gyration increases on increasing the temperature (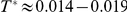 ) from the low end until around
) from the low end until around 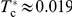 followed by a linear decay (
followed by a linear decay (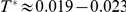 ) before reaching its saturation at high temperature
) before reaching its saturation at high temperature 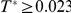 .
.
Figure 4.
(a) Dependence of the radius of gyration 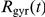 on MC time steps
on MC time steps  for various temperatures
for various temperatures 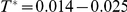 ; (b) temperature-dependent behavior of the mean radius of gyration
; (b) temperature-dependent behavior of the mean radius of gyration 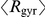 of the protein H2AX compared to the protein H3.1 where the same interaction parameters and normalized simulation temperature have been applied; (c) root mean squared displacement of the protein's center of mass
of the protein H2AX compared to the protein H3.1 where the same interaction parameters and normalized simulation temperature have been applied; (c) root mean squared displacement of the protein's center of mass 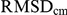 as a function of MC time steps
as a function of MC time steps  . The crossover from a positive thermal response of
. The crossover from a positive thermal response of 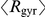 at low temperature to a negative thermal response at high temperature with a well-defined transition temperature
at low temperature to a negative thermal response at high temperature with a well-defined transition temperature 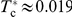 appears to be a specific characteristic of the H2AX protein structure.
appears to be a specific characteristic of the H2AX protein structure.
We examine how the competition between residue-residue interactions and thermal fluctuations leads to the observed non-monotonic temperature dependence of the radius of gyration. The attractive inter-residue interaction induces self-assembly of the protein segments towards a global globular structure (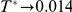 ) as the residues undergo their stochastic motion. As discussed above the highly interacting electrostatic residues act as an anchor collecting even those tethered residues that are repulsive. Thus, cooling down the protein leads to a conformational collapse into its globular conformation. The self-organized protein structure in its globular conformation begins to break on raising the temperature even by a small amount (
) as the residues undergo their stochastic motion. As discussed above the highly interacting electrostatic residues act as an anchor collecting even those tethered residues that are repulsive. Thus, cooling down the protein leads to a conformational collapse into its globular conformation. The self-organized protein structure in its globular conformation begins to break on raising the temperature even by a small amount (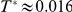 ) as the constitutive residues dissociate while some local assembly (held together by non-covalent interactions) still persists. The local assembly de-segregates on further increasing the temperature (
) as the constitutive residues dissociate while some local assembly (held together by non-covalent interactions) still persists. The local assembly de-segregates on further increasing the temperature (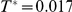 ) which stretches the corresponding segments resulting in a larger radius of gyration. Stretching of the protein continues until the characteristic temperature (
) which stretches the corresponding segments resulting in a larger radius of gyration. Stretching of the protein continues until the characteristic temperature (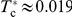 ) is reached beyond which the protein chain begins to contract. The chain segments fluctuate introducing randomness into a relatively stable elongated structure as the onset of thermal fluctuations sets in. The process can be described as a “thermal-driven contraction” emerging due to the cooperative effect of segmental interaction (looping) and conformational entropy. Note that the protein H2AX expands (positive) on heating in the low temperature regime (
) is reached beyond which the protein chain begins to contract. The chain segments fluctuate introducing randomness into a relatively stable elongated structure as the onset of thermal fluctuations sets in. The process can be described as a “thermal-driven contraction” emerging due to the cooperative effect of segmental interaction (looping) and conformational entropy. Note that the protein H2AX expands (positive) on heating in the low temperature regime (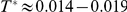 ) and contracts (negative) at the higher temperatures (
) and contracts (negative) at the higher temperatures (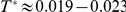 ).
).
The crossover from a positive thermal response in low temperature to a negative thermal response in high temperature regimes with a well-defined transition temperature (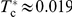 ) appears to be a specific characteristic of the H2AX protein structure. The results of another protein from histone family H3.1 provides additional support to our finding that histone H2AX shows a unique peak in its
) appears to be a specific characteristic of the H2AX protein structure. The results of another protein from histone family H3.1 provides additional support to our finding that histone H2AX shows a unique peak in its 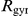 -temperature profile. The same interaction parameters and normalized simulation temperature are applied in the study of H3.1, which is of comparable size and does not show any peak in its
-temperature profile. The same interaction parameters and normalized simulation temperature are applied in the study of H3.1, which is of comparable size and does not show any peak in its 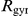 -temperature profile but exhibits a continuous transition from coil-to-globule on reducing the temperature. The difference in thermal response of H2AX and H3.1 however leads us to believe that this is due to the specific sequence of amino acids which might be exploited in technological applications requiring a material with such a distinct temperature response. Eventually, the radius of gyration saturates on further increasing the temperature beyond
-temperature profile but exhibits a continuous transition from coil-to-globule on reducing the temperature. The difference in thermal response of H2AX and H3.1 however leads us to believe that this is due to the specific sequence of amino acids which might be exploited in technological applications requiring a material with such a distinct temperature response. Eventually, the radius of gyration saturates on further increasing the temperature beyond 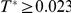 , where the protein conforms to a thermal-driven random (coil) structure.
, where the protein conforms to a thermal-driven random (coil) structure.
The size of the protein as measured by its radius of gyration 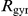 can be compared at a low temperature (
can be compared at a low temperature (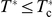 ) in the positive thermal response regime and at a higher temperature (
) in the positive thermal response regime and at a higher temperature (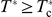 ) in the negative thermal response regime. One has to point out that, despite having the same magnitude of
) in the negative thermal response regime. One has to point out that, despite having the same magnitude of 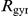 , the structure of the protein at these temperatures is very different. In particular, as shown in Fig. 1 we observe a local segmental segregation at low temperature while random configuration at high temperature dominate.
, the structure of the protein at these temperatures is very different. In particular, as shown in Fig. 1 we observe a local segmental segregation at low temperature while random configuration at high temperature dominate.
Although the radius of gyration can provide insight into the spatial extension of the protein, the specific dynamics of local structures are difficult to quantify with this measure. Thus, we have analyzed the root mean squared displacement of the center of mass of the protein with as a function of time for the entire temperature range. Fig. 4 shows these results for representative temperatures. The protein continues to diffuse at high temperatures while its motion slows down on reducing the temperature showing sub-diffusive asymptotic dynamics. At very low temperatures, 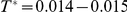 , the dynamics are too slow since the protein is localized into its globular conformation.
, the dynamics are too slow since the protein is localized into its globular conformation.
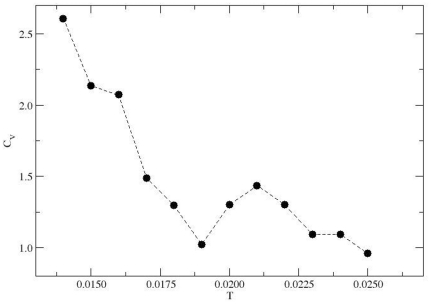
The question has to be raised whether there is another property such as the specific heat 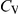 for which
for which 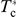 has a special significance.
has a special significance. 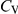 is evaluated from the fluctuation in the energy
is evaluated from the fluctuation in the energy 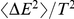 and Fig. 5 shows that the specific heat
and Fig. 5 shows that the specific heat 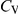 does not show a peak characteristic per se. This can be understood by noting that the characteristic temperature
does not show a peak characteristic per se. This can be understood by noting that the characteristic temperature 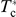 is related to the maximum thermal response in the spatial extension and not to the identification of a phase transition. However, we see that
is related to the maximum thermal response in the spatial extension and not to the identification of a phase transition. However, we see that 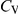 decays rather fast with increasing temperature before reaching a weave-like saturation. The undershoot in
decays rather fast with increasing temperature before reaching a weave-like saturation. The undershoot in 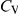 occurs around
occurs around 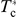 followed by an overshoot (
followed by an overshoot (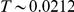 ) which could be seen as a minimum and maximum, respectively, in the temperature profile of
) which could be seen as a minimum and maximum, respectively, in the temperature profile of 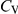 . The thermal phase transition in general is associated with the divergence of the thermal correlation length at the critical point. The relaxation of the protein here is not only controlled by the competition between residue-residue interactions and temperature (i.e. the thermal fluctuation) but also by the steric constraints imposed by the peptide bonds (entropic barrier which is hard to evaluate). Moreover, the size of the protein is too small to identify the second order phase transition generally identified in macroscopically large (i.e. infinitely long ideal) chain systems. Thus, the thermal response in
. The thermal phase transition in general is associated with the divergence of the thermal correlation length at the critical point. The relaxation of the protein here is not only controlled by the competition between residue-residue interactions and temperature (i.e. the thermal fluctuation) but also by the steric constraints imposed by the peptide bonds (entropic barrier which is hard to evaluate). Moreover, the size of the protein is too small to identify the second order phase transition generally identified in macroscopically large (i.e. infinitely long ideal) chain systems. Thus, the thermal response in 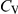 is expected to be different from that of the radius of gyration which is a result of both interaction (thermal) and entropic contributions and therefore more reliable as a direct measure.
is expected to be different from that of the radius of gyration which is a result of both interaction (thermal) and entropic contributions and therefore more reliable as a direct measure.
Figure 5.
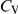 is evaluated from the fluctuation in the energy
is evaluated from the fluctuation in the energy 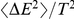 and shows a minimum in
and shows a minimum in 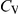 around
around 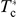 .
.
In fact, the relaxation of the protein is not only controlled by the competition between residue-residue interactions and temperature but also by the steric constraints imposed by the peptide bonds.
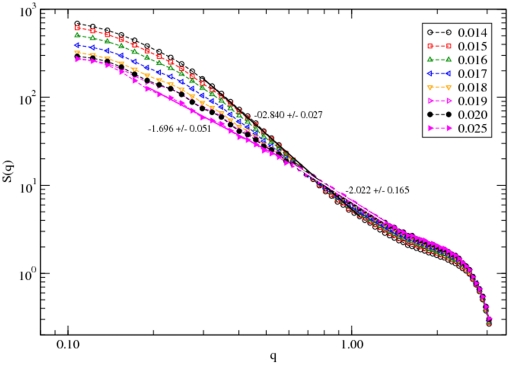
The structure factor 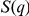 provides the spatial scaling of the distribution of constitutive elements
provides the spatial scaling of the distribution of constitutive elements
| (2) |
where 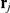 is the position vector of each residue and
is the position vector of each residue and 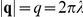 is the average spherical wave vector of wave length
is the average spherical wave vector of wave length 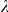 . For the protein, the structure factor is useful in understanding the structural details over a range of length scales. Fig. 6 shows the variation of
. For the protein, the structure factor is useful in understanding the structural details over a range of length scales. Fig. 6 shows the variation of 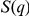 with the wave vector on a log-log scale. Since the radius of gyration
with the wave vector on a log-log scale. Since the radius of gyration 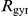 is a measure of the residue spread, the distribution of residues in the range of
is a measure of the residue spread, the distribution of residues in the range of 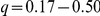 provides information about the global conformation of the protein. From the power-law scaling of the structure factor with the wave vector,
provides information about the global conformation of the protein. From the power-law scaling of the structure factor with the wave vector, 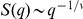 , we can estimate the distribution of the protein segments
, we can estimate the distribution of the protein segments 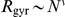 . We have estimated the slope of the power-laws in the appropriate range of the wave vector
. We have estimated the slope of the power-laws in the appropriate range of the wave vector 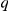 in Fig. 6:
in Fig. 6:
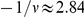 at
at 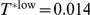 and
and 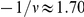 at
at 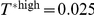 which provides
which provides 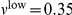 and
and 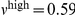 , respectively. Thus, the protein has an effective dimension
, respectively. Thus, the protein has an effective dimension 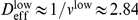 (almost solid, a globular structure) at
(almost solid, a globular structure) at 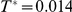 and
and 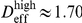 (a ramified, tenuous SAW structure) at
(a ramified, tenuous SAW structure) at 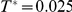 . As shown in Fig. 6 a systematic change in the mass distribution of the protein is clearly seen on increasing the temperature (
. As shown in Fig. 6 a systematic change in the mass distribution of the protein is clearly seen on increasing the temperature (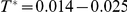 ). On the lower spatial scale (higher
). On the lower spatial scale (higher 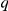 ) there are minor modifications in the mass distribution at
) there are minor modifications in the mass distribution at 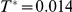 while the protein segments appear like an ideal chain with
while the protein segments appear like an ideal chain with 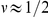 at
at 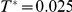 .
.
Figure 6. Structure factor 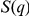 versus wave vector
versus wave vector 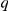 .
.
The effective dimension of the protein is 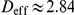 (almost solid, a globular structure) at
(almost solid, a globular structure) at 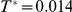 and
and 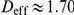 (a ramified, tenuous SAW structure) at
(a ramified, tenuous SAW structure) at 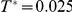 .
.
Discussion
In summary, a coarse-grained protein model is used to study the structural dynamics of the histone H2AX which consists of 143 residues tethered in a bond fluctuating chain on a cubic lattice. Although the atomistic details of residues are ignored, their specificity is captured via a knowledge-based interaction matrix as well as a LJ pair potential for residue-residue interactions. Each residue executes its stochastic motion according to the Metropolis criterion.
We have analyzed a number of local and global physical quantities such as the energy and mobility of each residue as well as the root mean squared displacement of the protein's center of mass, its radius of gyration, and its structure factor. The impact of temperature on these quantities is investigated and might be exploited for the design of biomaterials.
Our approach allows for the identification of segmental characteristics such as active regions and anchoring sites of the protein. We find that the electrostatic residues (e.g. 72R, 73D, 91D, 92E, 93E, 134K, 135K, etc.) are critical in orchestrating the segmental conformation, their self-assembly and de-segregation from the low to the moderately high temperature regime (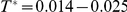 ). These highly interacting residues at their specific positions in the protein sequence appear to determine specificity and multi-scale structures. Accordingly, we observe global globular configurations at low (
). These highly interacting residues at their specific positions in the protein sequence appear to determine specificity and multi-scale structures. Accordingly, we observe global globular configurations at low (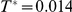 ), a combination of chains segments and smaller segmental globules at intermediate (
), a combination of chains segments and smaller segmental globules at intermediate (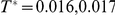 ), and elongated structures at moderately high temperatures (
), and elongated structures at moderately high temperatures (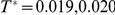 ). As expected, the specificity of residues vanishes at high temperatures (
). As expected, the specificity of residues vanishes at high temperatures (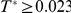 ) where the mobility of most residues becomes considerably high and comparable. In this thermal-driven structural regime, the residues become indistinguishable leading to a SAW chain conformation.
) where the mobility of most residues becomes considerably high and comparable. In this thermal-driven structural regime, the residues become indistinguishable leading to a SAW chain conformation.
The radius of gyration of the protein shows a non-monotonic dependence on the temperature with a maximum at a characteristic temperature which is determined by the competition between inter-residue interactions and temperature. The protein H2AX expands (positive thermal response) on heating in the low temperature regime (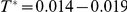 ) and contracts (negative thermal response) at higher temperatures (
) and contracts (negative thermal response) at higher temperatures (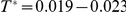 ). The crossover from a positive to negative thermal response occurs at a well-defined transition temperature (
). The crossover from a positive to negative thermal response occurs at a well-defined transition temperature (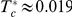 ) which may be a specific characteristic of the histone H2AX and particularly interesting for bioengineering purposes. The variation in the global conformation of the protein is explained in the framework of self-assembly at the local scale.
) which may be a specific characteristic of the histone H2AX and particularly interesting for bioengineering purposes. The variation in the global conformation of the protein is explained in the framework of self-assembly at the local scale.
Based on the analysis of the structure factor 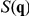 , we find that the radius of gyration scales with its molecular weight
, we find that the radius of gyration scales with its molecular weight 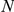 as
as 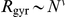 , where
, where 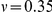 and
and 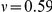 at
at 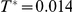 and
and 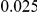 , respectively. The effective dimension of the protein is therefore
, respectively. The effective dimension of the protein is therefore 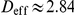 (almost solid, a globular structure) at
(almost solid, a globular structure) at 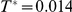 and
and 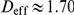 (a ramified, tenuous SAW structure) at
(a ramified, tenuous SAW structure) at 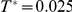 . A systematic change in the mass distribution is clearly seen with an increase in temperature (
. A systematic change in the mass distribution is clearly seen with an increase in temperature (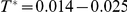 ).
).
Our coarse-grained protein model allows for a deeper understanding of local and global properties, which can so far not be gained by experimental testing. Besides the biological importance of proteins such as H2AX, we are able to provide a framework for analyzing potential candidates for the bioengineering of nano-materials. To this end, future experiments measuring physical quantities such as the spatial extension (radius of gyration) as a function of temperature would allow for the calibration of the temperature scale.
Footnotes
Competing Interests: The authors have declared that no competing interests exist.
Funding: Support from the Air Force Research Laboratory and Alexander von Humboldt foundation is gratefully acknowledged. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.
References
- 1.Renugopalakrishnan V, Garuňo-Juárez R, Narasimhan G, Verma CS, Wei X, et al. Rational design of thermally stable proteins: Relevance to bionanotechnology. J Nanosci Nanotech. 2005;5:1759–1767. doi: 10.1166/jnn.2005.441. [DOI] [PubMed] [Google Scholar]
- 2.Wang N, Mattis DM, Sundberg EJ, Schlievert PM, Kranz D. A single, engineered protein therapeutic agent neutralizes exotoxins from both staphylococcus aureus and streptococcus pyogenes. Clinical and Vaccine Immunology. 2010;17:1781–1789. doi: 10.1128/CVI.00277-10. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Kobsa S, Saltzman W. Bioengineering approaches to controlled protein delivery. Pediatric Research. 2008;63:513–519. doi: 10.1203/PDR.0b013e318165f14d. [DOI] [PubMed] [Google Scholar]
- 4.Asuri P, Bale SS, Karajanagi SS, Kan R. The protein-nanomaterial interface. Curr Opinion Biotechnology. 2006;17:562–568. doi: 10.1016/j.copbio.2006.09.002. [DOI] [PubMed] [Google Scholar]
- 5.Kane RS, Stroock A. Nanobiotechnology: Protein-nanomaterial interactions. Biotechnology Progress. 2007;23:316–319. doi: 10.1021/bp060388n. [DOI] [PubMed] [Google Scholar]
- 6.Korkegian A, Black ME, Baker D, Stoddard BL. Computational thermostabilization of an enzyme. Science. 2005;308:857. doi: 10.1126/science.1107387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Liang HK, Huang CM, Ko MT, Hwang JK. Amino acid coupling patterns in thermophilic proteins. Proteins. 2005;59:58. doi: 10.1002/prot.20386. [DOI] [PubMed] [Google Scholar]
- 8.Das R, Gerstein M. The stability of thermophilic proteins: a study based on comprehensive genome comparison. Functional and Integrative Genomics. 2000;1:76. doi: 10.1007/s101420000003. [DOI] [PubMed] [Google Scholar]
- 9.Paull TT, Rogakou EP, Yamazaki Y, Kirchgessner CU, Gellert M, et al. A critical role for histone h2ax in recruitment of repair factors to nuclear foci after dna damage. Curr Biol. 2000;10:886–895. doi: 10.1016/s0960-9822(00)00610-2. [DOI] [PubMed] [Google Scholar]
- 10.Fernandez-Capitello O, Chen HT, Celeste A, Ward I, Romanienko PJ, et al. Dna damageinduced g2-m checkpoint activation by histone h2ax and 53bp1. Nature Cell Biol. 2002;4:993–997. doi: 10.1038/ncb884. [DOI] [PubMed] [Google Scholar]
- 11.Bewersdorf J, Bennett BT, Knight KL. H2ax chromatin structures and their response to dna damage. PNAS. 2006;103:18137–18142. doi: 10.1073/pnas.0608709103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Ikura T, Tashiro S, Kakino A, Shima H, et al. Dna damage-dependent acetylation and ubiquitination of h2ax enhances chromatin dynamics. Mol And Cell Biol. 2007;27:7028–7040. doi: 10.1128/MCB.00579-07. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Van den Burg B, de Kreij A, van der Veek P, Manfeld J, Venema G. Characterization of a novel stable biocatalyst obtained by protein engineering. Biotech Appl Biochem. 1999;30:35. [PubMed] [Google Scholar]
- 14.Graddis TJ, Remmele RL, McGrew JT. Designing proteins that work using recombinant technologies. Curr Pharm Biotechnol. 2002;3:285. doi: 10.2174/1389201023378148. [DOI] [PubMed] [Google Scholar]
- 15.Somero GN. Proteins and temperature. Annu Rev Physiol. 1995;57:43–68. doi: 10.1146/annurev.ph.57.030195.000355. [DOI] [PubMed] [Google Scholar]
- 16.Smerdon M, Isenberg I. The effect of temperature on histone grk aggregation. Biochemical and Biophysical Research Communications. 1973;55:1029–1034. doi: 10.1016/0006-291x(73)91245-x. [DOI] [PubMed] [Google Scholar]
- 17.Eickholt J, Wang Z, Cheng J. A conformation ensemble approach to protein residue-residue contact. BMC Struct Biol. 2011;11:1–8. doi: 10.1186/1472-6807-11-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Pandey RB, Farmer BL. Globular structure of a human immunodeficiency virus-1 protease (1difa dimer) in an effective solvent medium by a monte carlo simulation. J Chem Phys. 2010;132:125101–125105. doi: 10.1063/1.3358340. [DOI] [PubMed] [Google Scholar]
- 19.Miyazawa S, Jernigan RL. Estimation of effective interresidue contact energies from protein crystal structures: quasi-chemical approximation. Macromolecules. 1985;18:534–552. [Google Scholar]
- 20.Eby DM, Johnson GR, Farmer BL, Pandey RB. Supramolecular assembly of a biomineralizing antimicrobial peptide. Phys Chem. 2011;13:1123–1130. doi: 10.1039/c0cp01364a. [DOI] [PubMed] [Google Scholar]
- 21.Feng J, Pandey RB, Berry RJ, Farmer BL, Naik RR, et al. The mechanism of adsorption conforms to soft epitaxy observed for peptides on metal surfaces. Soft Matter. 2011;7:2113–2120. [Google Scholar]
- 22.Pandey RB, Farmer BL. Phys Rev E. 2008;77:031902–031910. doi: 10.1103/PhysRevE.77.031902. [DOI] [PubMed] [Google Scholar]
- 23.Lyubartsev A, Laaksonen A. Calculation of effective interaction potentials from radial distribution functions: A reverse monte carlo approach. Phys Rev E. 1995;52:3730–37. doi: 10.1103/physreve.52.3730. [DOI] [PubMed] [Google Scholar]
- 24.Izvekov S, Voth G. J Phys Chem B. 2005;109:2469–73. doi: 10.1021/jp044629q. [DOI] [PubMed] [Google Scholar]
- 25.Zhou J, Thorpe I, Izvekov S, Voth G. Coarse-grained peptide modeling using a systematic multiscale approach. Biophys J. 2007;92:4289–03. doi: 10.1529/biophysj.106.094425. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Zhou J, Chen S, Jiang S. Orientation of adsorbed antibodies on charged surfaces by computer simulation based on a united-residue model. Langmuir. 2003;19:3472. [Google Scholar]
- 27.Marrink S, de Vries A, Mark A. Coarse grained model for semi-quantitative lipid simulations. J Phys Chem B. 2004;108:750–60. [Google Scholar]
- 28.Marrink S, Risselada H, Yefimov S, Tieleman D, de Vries A. The martini force field: coarse grained model for biomolecular simulations. J Phys Chem B. 2007;111:7812–24. doi: 10.1021/jp071097f. [DOI] [PubMed] [Google Scholar]
- 29.Rogakou EP, Pilch DR, Orr AH, Ivanova VS, Bonner WM. Dna double-stranded breaks induce histone h2ax phosphorylation on serine 139. J Biol Chem. 1998;273:5858–5868. doi: 10.1074/jbc.273.10.5858. [DOI] [PubMed] [Google Scholar]
- 30.Ayoub N, Jeyasekharan AD, Bernal JA, Venkitaraman AR. Hp1-beta mobilization promotes chromatin changes that initiate the dna damage response. Nature. 2008;453:682–686. doi: 10.1038/nature06875. [DOI] [PubMed] [Google Scholar]
- 31.Kongruttanachok N, Phuangphairoj C, Ponyeam W, Mutirangura A. Replication independent dna double-strand break retention may prevent genomic instability. Science Asia. 2008;34:253–257. doi: 10.1186/1476-4598-9-70. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Tetievsky A, Horowitz M. Posttranslational modifications in histones underlie heat acclimation-mediated cytoprotective memory. J Appl Physiol. 2010;109:1552–1561. doi: 10.1152/japplphysiol.00469.2010. [DOI] [PubMed] [Google Scholar]
- 33.Knowledge-based potential server for proteins at coarse grained level. Available: http://gor.bb.iastate.edu/potential/. Accessed 2010 Nov.
- 34.Carmesin I, Kremer K. The Bond Fluctuation Method: A New Effective Algorithm for the Dynamics of Polymers in All Spatial Dimensions. Macromolecules. 1988;21:2819–2823. [Google Scholar]
- 35.Binder K, Heermann DW. Monte Carlo Simulation in Statistical Physics: An Introduction. Berlin: Springer Verlag, 5 edition; 2010. [Google Scholar]
- 36.Bjursell J, Pandey RB. Relaxation to native conformation of a bond-uctuating protein chain with hydrophobic and polar nodes. Phys Rev E. 2004;70:052904. doi: 10.1103/PhysRevE.70.052904. [DOI] [PubMed] [Google Scholar]
- 37.Chen CM, Chen CC. Computer simulations of membrane protein folding: structure and dynamics. Biophys Journal. 2003;84:1902. doi: 10.1016/S0006-3495(03)74998-4. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Miyazawa S, Jernigan RL. Residue-residue potentials with a favorable contact pair term and an unfavorable high packing density term, for simulation and threading. J Mol Biol. 1996;256:623–644. doi: 10.1006/jmbi.1996.0114. [DOI] [PubMed] [Google Scholar]
- 39.Behringer H, Degenhard A, Schmid F. Coarse-grained lattice model for molecular recognition. Phys Rev Lett. 2006;97:128101–128104. doi: 10.1103/PhysRevLett.97.128101. [DOI] [PubMed] [Google Scholar]
- 40.Skepo M, Linse P, Arnebrant T. Coarse-grained modeling of proline rich protein 1 (prp-1) in bulk solution and adsorbed to a negatively charged surface. J Phys Chem. 2006;110:12141–12148. doi: 10.1021/jp056033o. [DOI] [PubMed] [Google Scholar]
- 41.Zhou Y, Karplus M. Interpreting the folding kinetics of helical proteins. Nature. 1999;400:400–403. doi: 10.1038/43937. [DOI] [PubMed] [Google Scholar]
- 42.Shen M, Freed KF. All-atom fast protein folding simulations: the villin headpiece. Proteins. 2002;49:439–445. doi: 10.1002/prot.10230. [DOI] [PubMed] [Google Scholar]
- 43.Wei Y, Nadler W, Hansmann UHE. Backbone and side-chain ordering in a small protein. J Chem Phys. 2008;128:025110–025115. doi: 10.1063/1.2819679. [DOI] [PubMed] [Google Scholar]
- 44.Chapagain PP, Gertsman B. Removal of kinetic traps and enhanced protein folding by strategic substitution of amino acids in a model alpha-helical hairpin peptide. Biopolym. 2006;81:167–178. doi: 10.1002/bip.20388. [DOI] [PubMed] [Google Scholar]
- 45.Wang Y, Feng S, Voth G. Transferable coarse-grained models for ionic liquids. Chem Theory Comput. 2009;5:1091–98. doi: 10.1021/ct800548t. [DOI] [PubMed] [Google Scholar]
- 46.Carbone P, Varzaneh H, Chen X, Müller-Plathe F. Transferability of coarse-grained force fields: The polymer case. J Chem Phys. 2008;128:064904. doi: 10.1063/1.2829409. [DOI] [PubMed] [Google Scholar]
- 47.Gerstman BS, Chapagain PP. Self-organization in protein folding and the hydrophobic interaction. J Chem Phys. 2005;123:054901–6. doi: 10.1063/1.1990110. [DOI] [PubMed] [Google Scholar]