Rotational Model for Actin Filament Alignment by Myosin

Abstract

Dynamics of the actomyosin cytoskeleton regulate cellular processes such as secretion, cell division, cell motility, and shape change. Actomyosin dynamics are themselves regulated by proteins that control actin filament polymerization and depolymerization, and myosin motor contractility. Previous theoretical work has focused on translational movement of actin filaments but has not considered the role of filament rotation. Since filament rotational movements are likely sources of forces that direct cell shape change and movement we explicitly model the dynamics of actin filament rotation as myosin II motors traverse filament pairs, drawing them into alignment. Using Monte Carlo simulations we find an optimal motor velocity for alignment of actin filaments. In addition, when we introduce polymerization and depolymerization of actin filaments, we find that alignment is reduced and the filament arrays exist in a stable, asynchronous state. Further analysis with continuum models allow us to investigate factors contributing to the stability of filament arrays and their ability to generate force. Interestingly, we find that two different morphologies of F-actin arrays generate the same amount of force. We also identify a phase transition to alignment occurs when either polymerization rates are reduced or motor velocities are optimized. We have extended our analysis to include a maximum allowed stretch of the myosin motors, and a non-uniform length for filaments leading to little change in the qualitative results. Through the integration of simulations and continuum analysis, we are able to approach the problem of understanding rotational alignment of actin filaments by myosin II motors in a truly unique way.

1. Introduction

Filamentous actin or F-Actin and its associated motor protein myosin II are fundamental cytoskeletal proteins essential to the physiological function of cells, establishment and maintenance of cell shape, and enabling cell motility. Actomyosin regulates cell shape and cell motility by restricting contractility to specialized regions in the cell such as the apical cell cortex [1], or the trailing edge of migrating cells [2, 3]. In these cases the role of actomyosin is experimentally tested by perturbing either the assembly of F-actin or the cross-linking and contractility of myosin II. However, given the ubiquity of actomyosin within non-muscle cells it has been difficult to resolve the specific role of actomyosin and related regulatory proteins within multicellular tissues. Actin rotation is believed to play a role in stress fiber formation, formation of the cytokinetic actin ring, initiation of filopodia, and podosome extension[4, 5].

Recent advances in mathematical and biophysical models of cytoskeletal filaments and motors have provided an important framework in which to analyze the dynamic properties of the cytoskeleton. Theoretical studies of cytoskeletal dynamics of microtubules and their associated motor protein kinesin [6, 7] have been used to elucidate the formation and function of spindles during mitosis. In vitro studies of the rheology of purified protein have found a multiple stage aggregation process by which myosin motors organize actin filaments into contracted states [8]. Similar models of the actin cytoskeleton have been used to study the role of actin polymerization in powering intracellular movement of Listeria monocytogenes [9]. Although there are many theoretical models for actomyosin dynamics [10, 11, 12, 13], these analyses have used “agent-based” computer simulations in which discrete elements, individual filaments, and structural elements are modeled within a complex geometry. Such models create a virtual assembly of “agents” with association rules and biochemical rates describing all interactions mediated by simple physics of diffusion, chemistry, and mechanics. To simplify the physically and biochemically complex cytoskeleton a range of alternative theoretical approaches have been adopted to break the complex biology of actomyosin into simpler systems whose behaviors can be explored analytically rather than computationally [14, 15, 16]. However, few of these studies have investigated the role of polymerization and motor contractility in aligning filaments. Given that filament alignment may be involved in diverse processes that reorganize F-actin, we developed theoretical models to directly explore these processes.

We hold the filaments pinned at their minus ends in order to prevent translational movements of filaments and expose mechanisms which play a role in aligning filaments. The polarity of the actin filament and its motor protein myosin II is a critical property and distinguishes the cytoskeleton from more generic types of polymer gels. In order to understand the complex behavior of actomyosin in complex morphologies we must consider the polarity and assembly of actin filaments, actin filament bending, the dual role of myosin motors as cross- linkers, and how motors shape and contribute to the mechanical properties of solid-like multi-filament structures. Through our simulations and analysis we found that filaments will always align and the time needed for alignment to occur depends on an optimal velocity for the myosin motors. We also investigated what mechanisms would inhibit alignment, and found that actin polymerization is a natural source of noise to destabilize alignment. We found that a phase transition to strong alignment occurs when either polymerization rates are reduced or the velocity for the myosin motor is changed toward an optimum.

2. Model and Methods

2.1. Simple geometry of actin-myosin interaction

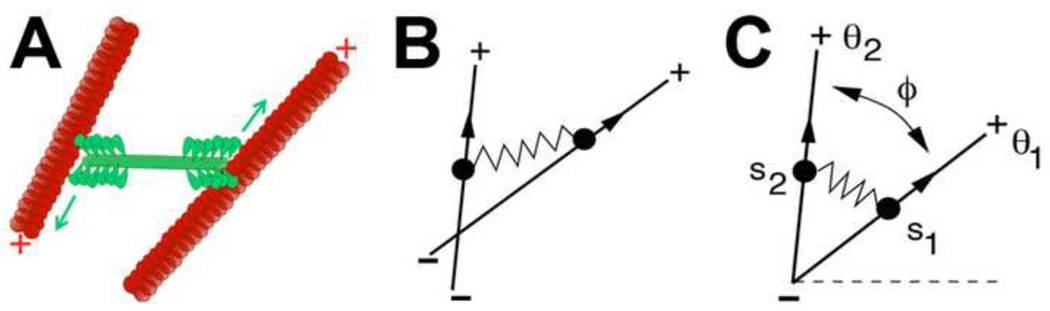
Within the cell cortex actin filaments are present with arbitrary orientations and myosin motors attach to the filaments, move toward filament plus-ends exerting a force which acts to align the filaments. If confined to a two dimensional plane each actin filament has three degrees of freedom: the position of its center of mass in the plane, and its orientation with respect to that center of mass. We first consider a simplified actomyosin array of one motor and two filaments (Figure 1A). In the cell, myosin II is organized into anti parallel arrays of bundled motors [17]. In our model we represent a single bundle as a mini thick filament and refer to such a bundle as a single “motor.” Filaments are only allowed to change their orientation. Minus ends which remained pinned at a fixed location we call the “origin.” Motors first attach at the pinned minus ends of a pair of filaments move toward the plus end, exerting a spring-like force on the filament pair (Figure 1B). We can define the angle of orientation for each filament (θ₁ and θ₂), and the distance from the minus-end to the attached motor (s₁ and s₂). The position of the two motors can be written in a Cartesian frame of reference as (s₁ cos θ₁, s₁ sin θ₁) and (s₂ cos θ₂, s₂ sin θ₂). As motors move to filament plus-ends, we assume they move with a constant velocity, υ. As the two ends of the myosin motor move apart toward the plus-ends of their respective filaments the myosin acts as a dynamic spring exerting forces on each filament in the pair [18, 19, 20], resulting in movement and rotation of both filaments.

Figure 1. Description of geometry, method, parameters, and variables.

(A) Cartoon depicting the biological interaction between actin filaments (red) and myosin II motors (green). (B) Simplified depiction of interaction between two actin filaments and one motor. (C) Idealized geometry for the motor-filament configuration used in our models. We refer interested readers to the supplementary material for simulation details.

From this biophysical description of motors, actin filaments, and their interactions we can describe the life-cycle of a myosin motor. The motor begins its life-cycle unattached to any filaments, waiting at the origin until it chooses to attach to a random pair of filaments. Once the motor attaches to a pair of filaments, the motor walks toward the plus-ends of the filament pair, generating force which pulls the filaments towards each other. The motor can detach from the filament pair as a result of a random stochastic process, and if the motor detaches, returns to the pool of unattached motors at the origin. On the other hand, if the motor reaches the end of the filament pair, it will fall off and return to the origin.

We have also simulated actin filament polymerization and depolymerization by allowing randomly selected filaments to disappear and be replaced by polymerization at the same time at a new angle. Polymerization rates represented by a rate per filament which allows the random, stochastic removal of a filament and placement of a new filament during our Monte Carlo simulations. In the event that a motor is attached to a depolymerizing filament, the motor will detach.

2.2. Equations of motion for the myosin motor and filament pair

Based on these rules we derive and compute the equations of angular motion for the filament pair as a myosin motor draws them into alignment. To extend the equations to the N filaments and M motors case, we only need to consider that the forces sum linearly. We derive the equations of motion for two filaments and one motor (Equation 1), where k is the spring constant and m is the mass of the motor.

$$\begin{array}{c}{\mathit{\theta ̇}}_1=\frac{k}{\mu }{s}^2\text{ sin}({\theta }_2-{\theta }_1)\hfill \\ {\mathit{\theta ̇}}_2=\frac{k}{\mu }{s}^2\text{ sin}({\theta }_1-{\theta }_2).\hfill \end{array}$$ (1)

More generally, we can define the change in angle for filament i from N total filaments as the sum of forces exerted by each motor m from the pool of motors (M(i)) which are all attached to filament i (Equation 2).

$${\mathit{\theta ̇}}_i=\frac{k}{\mu }{\displaystyle \sum _{m\in M(i)}}{s}_m^2\text{ sin}({\theta }_{p(m,i)}-{\theta }_i)$$ (2)

Since we have to calculate the change in angle between the filament pair to which the motor, m, is attached, we define the index for one filament to be i and the other filament’s index to be p(m, i).

From these equations of motion we can evaluate the mean of the distance the motor travels along the filament, s, squared. This term can be related to the mean rate of alignment and the average force exerted by the system (Equation 3).

$$\langle s^2\rangle =\frac{k}{\mu }\frac{1}{T}{\displaystyle {\int }_0^T}{s}^2(t)\mathit{\text{ dt}}.$$ (3)

We can also describe the morphology of the resulting actin array with an order parameter (Z), a measure of alignment of the filaments in our system. Z is defined as follows:

$$\begin{array}{cc}\hfill S(t)& ≔\frac{1}{N}{\displaystyle \sum _{i=1}^N}\text{sin}({\theta }_i(t))\hfill \\ \hfill C(t)& ≔\frac{1}{N}{\displaystyle \sum _{i=1}^N}\text{cos}({\theta }_i(t))\hfill \\ \hfill Z& ≔\underset{T\to \mathrm{\infty }}{\text{lim}}\frac{1}{T}{\displaystyle {\int }_0^T}\sqrt{S^2(t)+C^2(t)}\mathit{\text{ dt}}.\hfill \end{array}$$ (4)

In the statistics of circular or periodic distributions (1 − Z) is often called the circular variance [21]. The order parameter can be determined explicitly in the case of two filaments (Equation 5), where the difference in the angle between the filament pair, φ(t), is defined for −π to π.

$$Z=\underset{T\to \mathrm{\infty }}{\text{lim}}\frac{1}{T}{\displaystyle {\int }_0^T}\left|\text{cos}\frac{\varphi (t)}{2}\right|\mathit{\text{ dt}}$$ (5)

The order parameter as it relates to our Monte Carlo simulations describes the degree to which a set of filaments is co-aligned. For instance, in the case where the order parameter is one (Z = 1), all filaments are perfectly co-aligned with the same orientation angle. Alternatively, when the order parameter is zero (Z = 0), the filaments will have orientation angles uniformly distributed around the circle.

2.3. Biophysical properties of actin filaments and myosin motors

All of the parameters and their associated most commonly used value for the Monte Carlo simulations are found in table form with the supplementary information (TableS1), along with all of the variables (TableS2). The Monte Carlo simulations were carried out using MATLAB and the algorithm, represented as a simple flow chart (FigureS1), has been included in the supplementary information.

Actin filament polarity and length (L)

Actin microfilaments or F-actin vary from minimal lengths of a few G-actin subunits to more than 10 µm with a distinct polarity of plus- and minus- ends. For the majority of our simulations and continuum analyses we set filament length to 1 µm. This may be considered either the fixed length of a stable filament or the dynamic length of a tread-milling filament.

Myosin motor geometry and velocity (υ)

Each functional myosin II subunit is assembled from two heavy chains, two essential light chains, and two regulatory light chains. Myosin II mini thick filaments are assembled from multiple subunits into an antiparallel array with the globular ATPase head domains at the opposite ends of the filament and the rod-like domain of the subunits bound in antiparallel arrays in the center bare region of the mini-filament. The composition and length of mini thick filaments vary from cell type to cell type of ~20 myosin II complexes and are approximately ~350 nm in length [22]. Little is known experimentally about the force-producing capabilities of mini thick filaments but they can stretch and act like springs [19, 20, 18, 23]. We assume that ATP levels are high and myosin II motor ATPase activity is maximized.

Model time (t)

Model time is reported in seconds and the Monte Carlo simulations are advanced with individual time-steps of 0.01 seconds.

Motor attachment rate (r₀)

In the cell, the rate of motor attachment would reflect several factors including the rate of diffusion of myosin mini-filaments, the volume each mini-filament can search, and the relative density of F-actin binding sites. In our unique geometry the situation is considerably simplified since all unbound motors are held within binding range of F-actin at their minus-end. Thus, for a majority of our simulations we fix the motor attachment rate at 0.7 per second.

Myosin detachment rate(r₁)

Myosin motors are highly processive but do occasionally dissociate from filaments before reaching the plus-end. Since these rates are poorly characterized in vivo we choose detachment rates that range from 0.1 to 0.8 per second. This rate may also vary based on the amount that the motor is stretched; e.g. load (Section 3.5).

Depolymerization rate (r₂)

Actin filaments within cells are constantly being turned over so we introduce a depolymerization rate per filament. This rate may be dependent on the length of the filament and may be controlled within the cell. Polymerization rates are allowed to vary from 0.01 to 0.2 per second. In vivo, the polymerization / depolymerization rates may control actin abundance, however, within our simulations we enforce constant F-actin density and promptly polymerize a new filament when one filament depolymerizes.

Viscosity (μ)

In the cell, filaments experience viscous drag forces as they rotate through the cytoplasm. By contrast, myosin mini thick filaments, due to their smaller size, do not experience such drag forces. In our model, we only consider the viscous drag of water and explicitly simulate filament-filament interactions that would contribute to cytoplasmic viscosity. If we increase the viscosity parameter, we would see that the time it would take to align would increase since the increase in viscosity would make it more difficult for the filaments to rotate through the space. The viscosity of water is defined as 1 × 10⁻³ Pa s.

Motor stiffness (k)

As the two ends of the myosin II motor mini-filaments move apart on pairs of actin filaments the mini-filament exerts spring-like forces on the two filaments. Thus, our simulations include a motor spring stiffness term k. Myosin mini-filament stiffness has been measured from 1.7 to 5.0 pN/nm [24, 19, 20, 18].

(μ/k)

For our equations of motion and continuum analysis, we do not use separate values of μ and k but instead use the ratio of stiffness to viscosity. Due to uncertainty in the exact value of this term, ranging from 0.2 to 0.6 (s/m²) we set this ratio to 1.

3. Results

3.1. Two filaments, one motor

For simplicity, we first consider two filaments and one motor. The two filaments lie at specific angles (θ₁ and θ₂) and may be bound together at a distance, s, from their origin by a motor. We found it advantageous to consider the angle between the two filaments (φ := θ₂ − θ₁) rather than the orientation angle of each filament. We found a single equation of motion could replace the two equations defined previously (see Section 2.2, Equation 1):

$$\mathit{\varphi ̇}=-2s^2\frac{k}{\mu }\text{sin }\varphi .$$ (6)

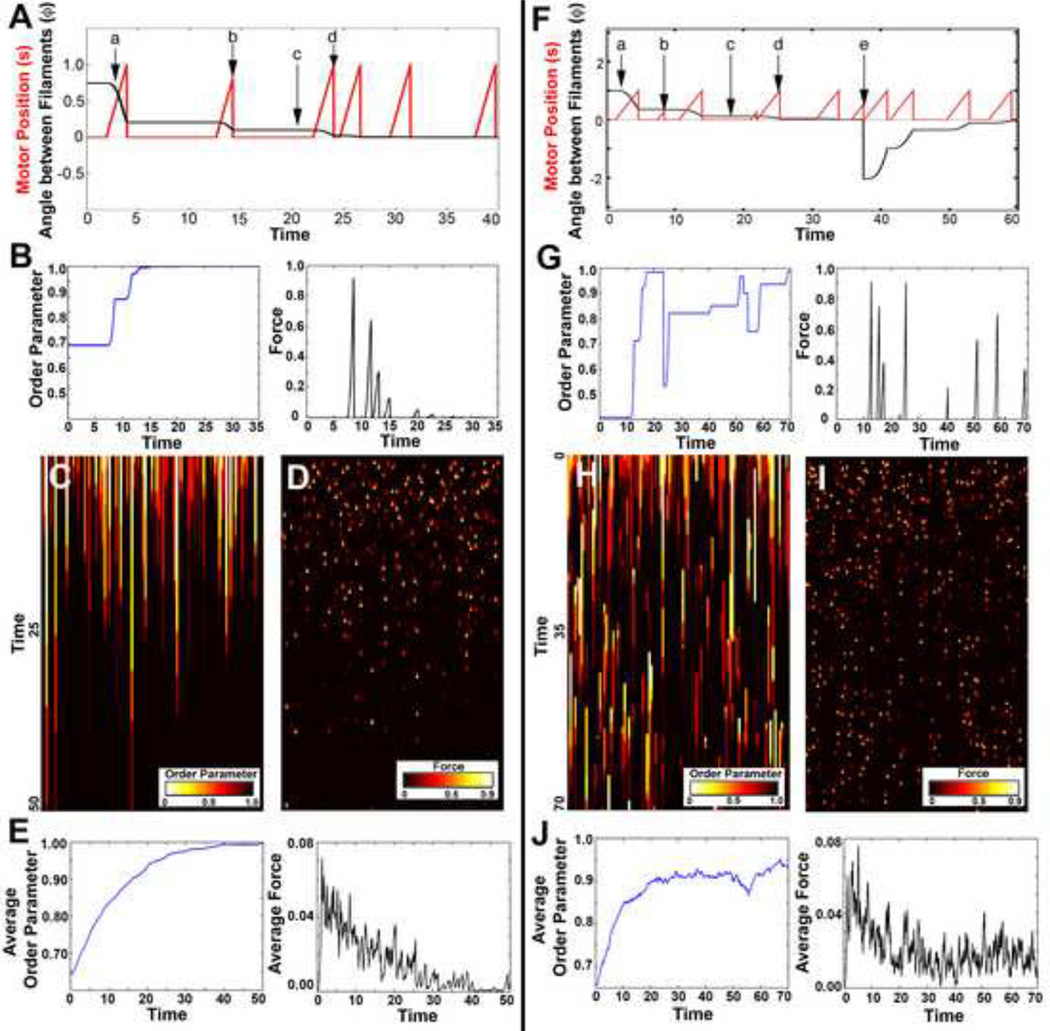
For the case of two filaments and one motor, we used this equation of motion to follow events that occurred during a typical simulation (Figure 2A): (a) the motor attached to the filament pair and started to pull filaments together as the motor traveled down the filament at a fixed velocity, (b) the motor fell off the filaments before it reached the ends of the filament pair, (c) the motor spent time waiting to attach to the filament pair, (d) the motor reached the plus-end of the filament and fell off. For all simulations perfect alignment is guaranteed since there were no other processes which could cause the difference in filament angle (φ) to increase. Thus, the changing morphology of the system could be followed as the order parameter (Equation 5) increased to a value of one and force-generated by the motor decreased to zero (Figures 2B–F).

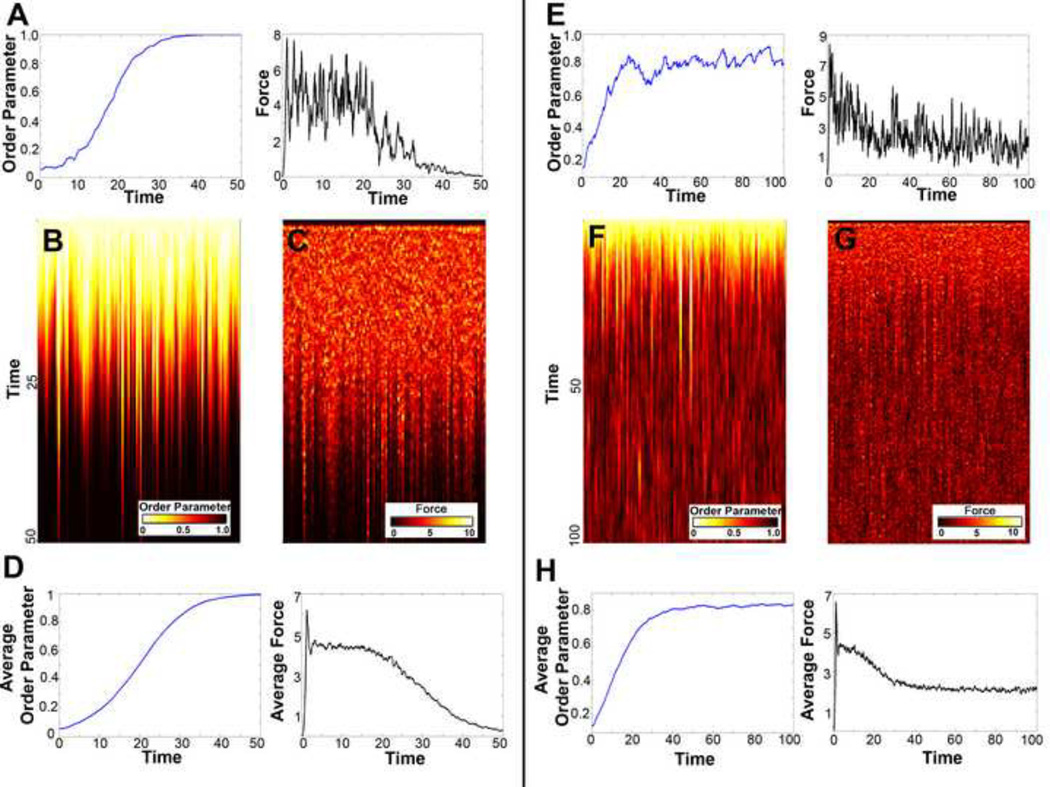
Figure 2. Monte Carlo Simulations for two filaments and one motor.

(A) Visual of one Monte Carlo simulation time course for motor movement (red) and the resulting change in angle of the filament pair (black) without polymerization: (a) motor attaches to the filament pair, (b) motor falls off before it reaches the end of the filaments, (c) motor waits to attach, (d) motor falls off when it reaches the end of the filaments. (B) Plots of order parameter (blue), and force generated (black) for one Monte Carlo simulation. (C) Color evolution plot of the order parameter for 100 Monte Carlo simulations. Given enough time, the two filaments become aligned by the motor. (D) Color evolution plot for the force generated by the motor for the 100 Monte Carlo simulations in C. (E) Average order parameter (blue) and average force generated (black) for the 100 Monte Carlo simulations shown in C and D. (F) One Monte Carlo simulation time course for motor movement (red) and the change in angle of the filament pair (black) with polymerization: (a) motor attaches to the filament pair, (b) motor falls off before it reaches the end of the filaments, (c) motor waits to attach, (d) motor falls off when it reaches the end of the filaments, (e) one filament depolymerizes and a new filament instantaneously polymerizes at a new angle. (G) Plots of order parameter (blue), and force generated (black) for one Monte Carlo simulation with polymerization. (H) Color evolution plot of the order parameter for 100 Monte Carlo simulations. In contrast to C, the addition of polymerization impedes long term alignment of the two filaments. (I) Color evolution plot for the force generated for the 100 Monte Carlo simulations in H. (J) Average order parameter (blue) and average force generated (black) for the 100 Monte Carlo simulations shown in H and I.

However, actomyosin in cells rarely assumes the form of static bundles and we turned to investigate processes that could destabilize or prevent formation of aligned bundles. Since actin filaments are constantly turning over in the cell we introduced the processes of polymerization and depolymerization. These processes introduced a form of noise into our simulations; by contrast, thermal noise could also prevent perfect alignment, but for filaments in a viscous media this source of noise is negligible.

Allowing filaments to undergo depolymerization and polymerization resulted in more complex dynamics for the two filament case. We considered the events along a typical time course (Figure 2F): (a) the motor attached to the filament pair and pulled filaments together as the motor traveled down the filament at a fixed velocity, (b) the motor spontaneously fell off the filaments, (c) the motor spent time waiting to attach, (d) the motor fell off once it reached the end of the filaments, (e) a filament depolymerized while a new filament polymerized at a new angle, discontinuously changing the value of the angle difference (φ). The motor worked to reduce the angle difference between filaments only to have that angle reset by a depolymerization and polymerization event. By including polymerization, perfect alignment is no longer possible. We described the degree of imperfect alignment through the time-evolution of the order parameter and the forces generated (Figures 2G–J). During the course of a single representative simulation run, the order parameter could rise to one and forces generated by a shared motor dropped to zero as filaments were completely aligned. However, once a filament depolymerized, the order parameter decreased and the motor again generated force.

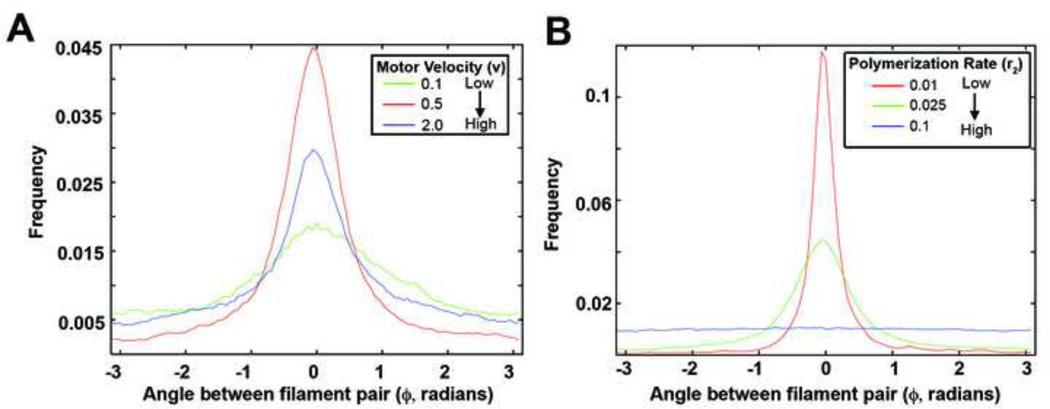
Even though depolymerization destabilizes the actomyosin system, we found that the angle difference between filaments in a population was still reduced over time. To understand this effect, we considered a histogram for the angle difference between filaments (φ). The distribution of angles for a long Monte Carlo simulation for two-filaments, one-motor showed a large number of perfectly aligned filament pairs and that depended on motor function (Figure 3A). As the rate of depolymerization increased, however, the angle distribution in the population became flatter with more filament pairs having larger filament angles.

Figure 3. Comparing effects of parameters on order with Monte Carlo simulations for two filaments, one motor.

(A) Distribution of the angle between the two filaments, ϕ, as the polymerization rate, r₂, increased. (B) Distribution of the angle between filaments as motor velocity increased. (C) Average force as a function of velocity for different rates of attachment, r₀, and detachment, r₁. (D) Order parameter (black) and average force (red) for the Monte Carlo simulations as motor velocity varied. r₀=0.4/s, r₁=0.1/s, r₂=0.05/s.

When we varied the motor velocity instead of the rate of depolymerization, we also observed a non- monotonic dependence of filament alignment on motor velocity (Figure 3B). In this case, both low and high motor velocities acted to flatten the distribution of angle differences. In order to understand the relationship between motor velocity and the difference in filament angles, we considered the average force generated (〈s²〉) for a large number of simulations as we varied motor velocity (Figure 3C). We found that average force reaches a maximum value at a unique motor velocity and this velocity in turn depends on the rates of motor attachment and detachment.

These effects could be understood if one took the perspective of a myosin motor. For any given set of motor filament interactions, e.g. rates of attachment and detachment, the most rapid alignment occurred when the motor spent the largest fraction of its life-cycle bound to the filament pair. For example, if the rate at which an unbound motor attached was reduced (that is, it took longer for the motor to attach), then the percent of the motor’s life-cycle devoted to aligning the filament pair was also reduced (compare red and black curves in Figure 3C). In order to increase the time devoted to aligning the filament pair the motor needed to slow down so it would not reach the end of the filament and fall off. As a correlate, if the rate of the motor spontaneously falling off was increased, then the velocity required for optimal alignment increased (compare red and green curves in Figure 3C). Thus, the ability of myosin motors to align filaments depended on both its velocity as well as its rates of attachment and detachment.

Intriguingly, motor velocities that produced maximal average force generation (〈s²〉) also produced the most aligned filament pairs (Figure 3D). The functional dependence of morphology and force production on motor velocity suggested we might be able to analytically derive these functions from a continuum representation of the dynamics of the two filament, one motor system.

3.2. Recasting the stochastic model of two filaments and one motor as a continuum model

In order to understand the relationship between actin filament alignment and forces generated by the motor we derived continuum equations which described the two filament, one motor dynamical system. Motor activity within a two filament network could be thought of as an example of a ‘two-state process’: either the motor was detached and waiting to attach to a filament at the minus end (P₀), or the motor was moving toward the plus ends of the two filaments and pulling the pair into alignment (P₁). We considered the time evolution of populations of motors in each of these two states:

$$\begin{array}{ccccc}\frac{\partial P_0(\varphi ,t)}{\partial t}=\hfill & \upsilon P_1(\varphi ,L,t)\hfill & +r_1{\displaystyle {\int }_0^L}{P}_1(\varphi ,s,t)\mathit{\text{ ds}}\hfill & -r_0{P}_0(\varphi ,t)\hfill & +\frac{r_2}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }}{\displaystyle {\int }_0^L}{P}_1(\psi ,s,t)\mathit{\text{ ds }}d\psi \hfill \\ \hfill & \text{Lost from plus-end}\hfill & \text{Randomly detach}\hfill & \text{Attach}\hfill & \text{Detach after depolymerization}\hfill \end{array}$$ (7)

The population or density of motors not bound to any filaments (P₀, Equation 7) changed by: 1) motors falling off the plus-end of any filament (from the group of filaments with attached motors, P₁), 2) motors randomly detached as they moved toward the filament’s plus-end, 3) motors bind to filament minus-ends, and 4) motors fell off filaments that depolymerized. Since motors could detach at any distance, s, along a filament’s length (defined from 0 to L), the second term in Equation 7 was integrated over all possible motor positions. We noticed that the first three terms in Equation 7, the loss and gain of motors, were independent of the filament pair’s orientation; only the last term depended explicitly on the rate of depolymerization. It was important to note that while filaments without attached motors could depolymerize, the last term of this equation only considered depolymerization of filaments with bound motors. The time evolution of motors bound to filament pairs was similar but we needed to include the density of motors at various positions along the length of the filament pairs:

$$\begin{array}{ccccc}\frac{\partial P_1(s,\varphi ,t)}{\partial t}=\hfill & -\upsilon \frac{\partial P_1(s,\varphi ,t)}{\partial s}\hfill & +\frac{k}{\mu }{s}^2\frac{\partial }{\partial \varphi }(\text{sin }\varphi P_1(s,\varphi ,t))\hfill & \hfill -r_1{P}_1(s,\varphi ,t)& \hfill -r_2{P}_1(s,\varphi ,t)\\ \hfill & \hfill \text{Motor movement}& \text{Filament movement}\hfill & \hfill \text{Randomly detach}& \hfill \text{Detach after depolymerization}\end{array}$$ (8)

The density of motors attached to filaments must include movement of motors: 1) as motors moved toward the plus-ends of the filament pair, 2) as motors moved with the angular movement of filaments, 3) as motors randomly detached from filaments, and 4) as motors detached when filaments depolymerized.

We investigated solutions which led to stable assemblies of filament systems, i.e. the steady state solution which yielded the stationary distribution of filaments over filament angles, φ, and motor positions, s. We began by defining a distribution, Q, which denoted the stationary solution and obtained expressions for force and the order parameter:

$$\langle s^2\rangle ={\displaystyle {\int }_{-\pi }^{\pi }}{\displaystyle {\int }_0^L}{Q}_1(\varphi ,s)s^2\mathit{\text{ ds }}d\varphi$$

Furthermore, we were able to derive an equation for the steady state marginal distribution of the distance along the filaments, ${\displaystyle {\int }_{-\pi }^{\pi }}{Q}_1(\phi ,s)d\phi$ and thus compute 〈s²〉 (Equation 9; see Appendix B).

$$\langle s^2\rangle =\frac{r_0}{r_1^2}\frac{2{\upsilon }^2-e^{-r_1/\upsilon }(2{\upsilon }^2+2\upsilon r_1+r_1^2)}{r_1+r_0(1-e^{-r_1/\upsilon })}.$$ (9)

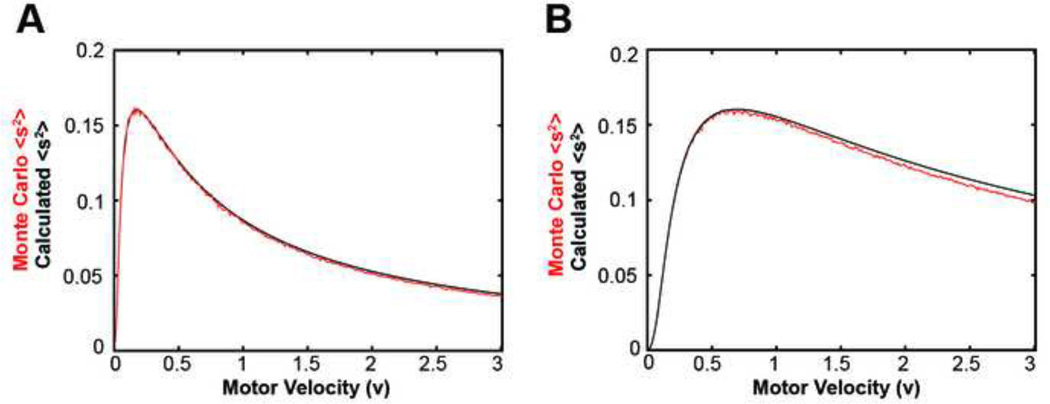
With this exact solution we calculated analytically how force generation depended on motor velocity, rates of motor attachment and detachment, and rates of filament polymerization (Figures 3D and 4). We found that our continuum equations were able to exactly replicate the Monte Carlo simulations for the two filament, one motor actomyosin system (Figure 4). In addition, the continuum solution was able to validate our Monte Carlo simulations of the two filament, one motor actomyosin system. For instance, we previously considered the density of steady state angles from our Monte Carlo simulations (Figures 3A and 3B) and the continuum equations showed us exactly how these densities depended on the parameters of the model.

Figure 4. Monte Carlo simulations and continuum solution.

(A) Plot of the continuum solution’s calculation of <s²> (black) compared to the Monte Carlo simulation calculation of <s²> (red) for r₀=0.4/s, r₁+r₂=0.15/s. (B) Plot of the continuum solution’s calculation of <s²> (black) compared to the Monte Carlo simulation calculation of <s²> (red) for r₀=1.4/s, r₁+r₂=0.6/s.

Further analysis of these equations and their steady state solutions (see Appendix B) allowed us to investigate exact relationships between rates of motor-filament attachment and detachment, motor velocities, polymerization rates, filament morphology, and force generation. For instance, as the rate of attachment decreased, the motor spent more time off the filaments and so the motor velocity must have been chosen so it maximized the amount of time the motor spent attached to the filaments.

3.3. Multiple Motors, Multiple Filaments

In order to understand more complex actomyosin networks we investigated the behavior of multiple-motors and multiple-filaments arranged with the same geometry as the simpler two filament, one motor system discussed previously. Initially, we suspected that the competition between multiple motors attached to the same filament might impede the progress of filament alignment. To test this hypothesis we returned to Monte Carlo simulations. These simulations started with multiple filaments randomly distributed around 360° and multiple motors all in an unbound state waiting to attach to the filament minus-ends. Each simulation was run for 400,000 steps with a time step of 0.01s. In order to compare steady state rates of filament alignment in each simulation, we averaged the order parameter over the last 300,000 steps. The reason for this, was that once the simulation started, if given enough time, the filaments would get closer and closer to their natural alignment, e.g. filament dynamics approached steady state.

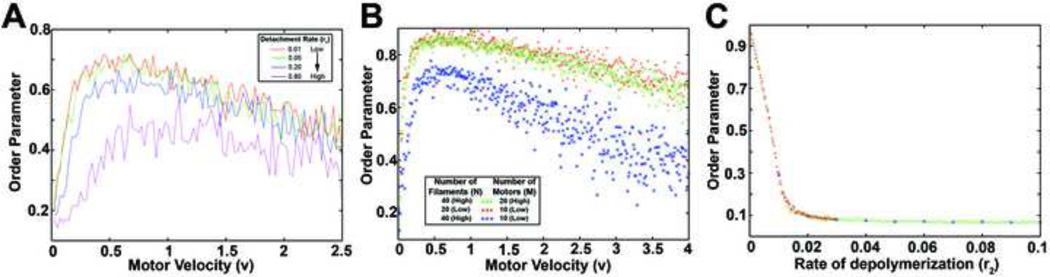
Interestingly, we found that filaments aligned in a manner analogous to the two filament, one-motor case (Figures 5 and 6) and exhibited the same dependence on parameters that were observed previously. For example, as we allowed the rate at which the motors spontaneously fell off the filaments to increase, the velocity at maximal alignment also increased which was accompanied by a decrease in the magnitude of alignment (Figure 5A). Thus, the process of filament alignment is slowed as motors spend less time bound to the filaments. Furthermore, we found that the velocity which produced maximal alignment was independent of filament density(Figure 5B). When the ratio of filaments to motors had fewer motors, however, the maximal degree of alignment decreased, even though the optimal motor velocity remained the same.

Figure 5. Same behavior for multiple filament, multiple motor case, as previously for two filaments, one motor.

(A) Plot showing the dependence of the order parameter on the rate of detachment (r₀) for 40 filaments and 20 motors. As expected, an increase in detachment resulted in a decrease in order. r₀=0.7/s, r₂=0.05/s. (B) Plot examining the relationship between the relative densities of motors to filaments. When the ratio of filaments to motors was the same, the same amount of order is expected; however, the optimal motor velocity required to achieve maximum alignment was independent of filament and motor density. r₀=0.7/s, r₁=0.1/s, r₂=0.05/s. (C) Plot showing the sensitivity of the order parameter of the system to the rate of depolymerization (r₂). Blue shows a larger discretization than green, with red being the most fine discretization of sampling order.

Figure 6. Monte Carlo Simulations: multiple filaments, multiple motors.

(A) Order parameter (blue) and force generated (black) for one Monte Carlo simulation with multiple filaments and multiple motors without polymerization. Note the same characteristics as seen in Figure 2B. (B) Color evolution plot of order parameter for 100 Monte Carlo simulations without polymerization. (C) Color evolution plot for force generated by the 100 Monte Carlo simulations shown in B. (D) The average order parameter (blue) and average force generated (black) by the 100 Monte Carlo simulations in B and C. (E) Order parameter (blue) and force generated (black) for one Monte Carlo simulation with polymerization. (F) Color evolution plot of order parameter for 100 Monte Carlo simulations with polymerization. (G) Color evolution plot for force generated by the 100 Monte Carlo simulations shown in F. (H) The average order parameter (blue) and average force generated (black) by the 100 Monte Carlo simulations in F and G.

When we considered the rate of depolymerization, we found that the order or alignment of our system was extremely sensitive to the rate of depolymerization (Figure 5C) and that depolymerization is the only stochastic process capable of impeding the progress of filament alignment. Furthermore, the extremely steep decrease in alignment with a small increase in the rate of depolymerization suggested that a phase transition from a completely disordered (in this case a perfectly uniform distribution of filaments) to an ordered or aligned state may occur.

From our parameter analysis, we concluded that the motor velocity and depolymerization rate of filaments are key parameters that control alignment of actin filaments. In order to draw a more descriptive conclusion as to how these two parameters effect the alignment of our system, we next considered the density angles between two filaments (Figure 7). In the case where filaments of the system were mostly aligned, the distribution has a tall, sharp peak about the angle difference of zero and flattens after the motor velocity is shifted from this optimal value (Figure 7A), or after the rate of depolymerization is increased (Figure 7B). To investigate the behavior of our actin network near this phase transition we turned from the Monte Carlo simulations to a continuum representation for our multiple filament, multiple motor system.

Figure 7. Effects of motor velocity and rate of polymerization (r₂) on multiple filament and multiple motor alignment.

(A) The distribution of the difference in angle between all filaments compared to filament #1. As motor velocity decreased from high (blue) to low (green), there was an intermediary velocity which caused the sharpest peak in the distribution, and thus the most alignment (red). (B) The distribution of the difference in angle between all filaments compared to filament #1. As polymerization rate increased from low (red) to high (blue), note the quick flattening of the distribution peak which suggested a phase transition dependent on the rate of polymerization.

3.4. Mean field analysis of multiple filaments and multiple motors

We considered an array of a large number of filaments, N, where each filament was at a discrete angle (θ_i) with a large number of motors, M. From this discrete model we calculated forces experienced by a single filament:

$$f({\theta }_i)=\frac{k}{\mu }{\displaystyle \sum _{j=1}^N}{\displaystyle \sum _{r=1}^M}{p}_{\mathit{\text{ijr}}}{s}_r^2\text{ sin}({\theta }_j-{\theta }_i)$$ (10)

The average force on a filament was found by linearly summing all the forces exerted by the motors which were attached to that filament. An attached motor, r, connects filament i and j. The term p_ijr was the probability that motor r was attached to filaments i and j. Since motors may contact any 2 out of N filaments, and connections are chosen randomly this probability factor was 1/(N(N − 1)).

In order to compute a mean field equation for the network of motors and filaments, we let the number of motors and filaments grow to infinity, keeping the ratio of motors to filaments as a fixed number, c. When we did this, the sum in Equation 10 became an integral (Equation 11).

$$f({\theta }_i,t)=\frac{\mathit{\text{kc}}}{\mu }{\displaystyle {\int }_{-\pi }^{\pi }}{\displaystyle {\int }_0^L}{s\prime }^2\text{ sin}(\theta \prime -{\theta }_i)P_1(\theta \prime ,s\prime ,t)\mathit{\text{ ds}}\prime d\theta \prime .$$ (11)

Next, we returned to the two-state model for myosin motors within a much larger F-actin array. Recall the definitions of P₁ and P₀ from the two filament, one motor case before where P₁ was the density of motors attached to filaments, and P₀ was the density of unbound motors. The time-evolution of motor density within these two states was:

$$\begin{array}{cccc}\frac{\partial P_1(s,\varphi ,t)}{\partial t}=\hfill & -\upsilon \frac{\partial P_1(s,\varphi ,t)}{\partial s}\hfill & -\frac{\partial }{\partial \theta }(P_1(s,\varphi ,t)f(\theta ))\hfill & \hfill -(r_1+r_2)P_1(s,\varphi ,t)\\ \hfill & \text{Motor movement}\hfill & \text{Filament movement}\hfill & \hfill \text{Detachment}\end{array}$$ (12)

$$\begin{array}{ccccc}\frac{\partial P_0(s,t)}{\partial t}=\hfill & \upsilon P_1(L,\theta ,t)\hfill & -r_0{P}_0\hfill & +{\displaystyle {\int }_0^L}{r}_1{P}_1(s\prime ,\theta ,t)\mathit{\text{ds}}\prime \hfill & +\frac{1}{2\pi }{\displaystyle {\int }_0^L}{\displaystyle {\int }_{-\pi }^{\pi }}{r}_2{P}_1(s\prime ,\theta \prime ,t)d\theta \prime \mathit{\text{ ds}}\prime \hfill \\ \hfill & \text{Lost from plus-end}\hfill & \text{Attach}\hfill & \text{Randomly detach}\hfill & \text{Detach after depolymerization}\hfill \end{array}$$ (13)

In contrast to the density functions for the simple case of two filaments and one motor, we considered the actual angle rather than the difference of angles. Since forces depend on the density of motor-bound filaments we found a nonlinear term that represented the movement of motors as filaments moved. Thus, unlike the two filament case, the density equations were nonlinear due to the fact that f(θ) was itself a function of P₁.

Since motors can only attach to filaments at the minus ends, we enforced a boundary condition that related motors leaving the pool of unbound motors with the motors attached at the minus-end of the filament pairs.

$$P_1(\theta ,0,t)=\frac{r_0}{\upsilon }{P}_0(\theta ,t).$$ (14)

Readers familiar with the analysis of coupled oscillators will see a strong similarity between Equation (E.1) and the Kuramoto equation [25] (see Appendix E). Because this was a nonlinear equation, there was no simple closed form solution; however, we used these equations to investigate the transition driven by high rates of depolymerization from a completely disordered state to an aligned state (referred to as the “asynchronous state” in coupled oscillators).

When we considered the density distribution of relative filament angles and increasing rates of depolymerization, we concluded that there existed a solution which was uniform in the filament angle, θ (Figure 7B; see Appendix C). These solutions were the marginal densities of the distance traveled for attached motors, $W_1(s)={\displaystyle {\int }_{-\pi }^{\pi }}{Q}_1(\phi ,s)d\phi$, and the density of unattached motors, $W_0={\displaystyle {\int }_{-\pi }^{\pi }}{Q}_0(\phi )d\phi$ (see Appendix C).

$$\begin{array}{cc}\hfill P_1(\theta ,s,t)& =\frac{1}{2\pi }{W}_1(s)\hfill \\ \hfill P_0(\theta ,t)& =\frac{1}{2\pi }{W}_0\hfill \end{array}$$

Returning with these solutions to our continuum equation for the force on a single filament we found:

$$f(\theta )=\frac{\mathit{\text{kc}}}{\mu }\frac{1}{2\pi }{\displaystyle {\int }_0^L}{s}^2{W}_1(s){\displaystyle {\int }_{-\pi }^{\pi }}\text{sin}(\theta \prime -\theta )d\theta \prime \mathit{\text{ds}}=0$$

The term f(θ) represented the angular flux of filaments moving under the influence of bound motors. As the array of filaments approached steady state this term disappeared and we were left with a steady state analogous to that found in our earlier analysis of two filaments and one motor.

This equilibrium solution corresponded to a completely disordered state in which the distribution of the filament angles was uniform. Since the equations for the two filament, one motor case were linear they do not include the integration of angular filament flux, and the completely disordered state was never a solution. The equation which described arrays of multiple filaments and multiple motors was nonlinear, so there may be more than one possible steady state. The most direct method to determine if there were other possible stationary distributions of motors was to examine the stability of the disordered state as parameters, such as the motor velocity, were varied.

We searched for a possible nonlinear phase transition by investigating the stability of different periodic modes of the disordered state (see Appendix D). If the fully disordered state was unstable with respect to perturbations to the distribution of filaments, then this mode would grow and the distribution might remodel into a single peak. With this approach we linearized the full equations about the trivial steady state and then solved the resulting linear system.

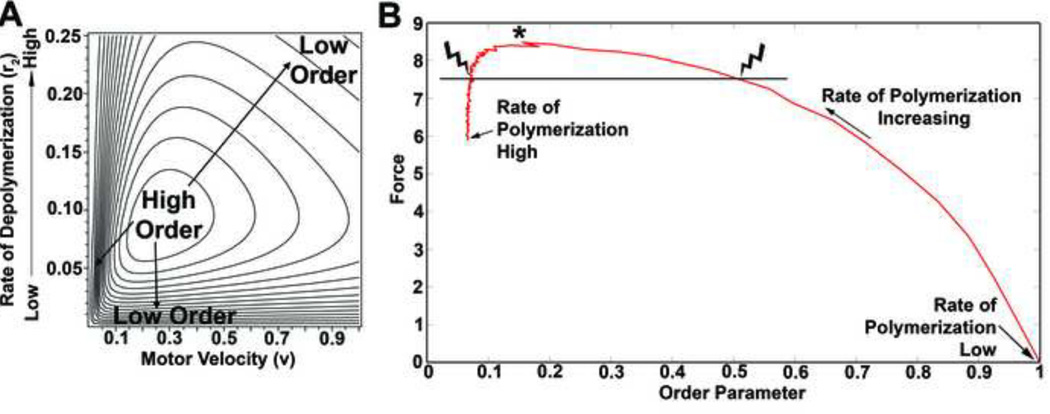
We discovered that F-actin morphology alone was not a predictive indicator of force production. Whereas a unique filament array morphology that did produce a unique level of maximal force (see asterisk in Figure 8B). Force production at even slightly lower levels produced by two distinct filament morphologies (see “arrow heads” in Figure 8B). One, a tightly aligned and another, a disorganized filament arrays produced identical levels of force. Thus, morphology alone was not a sufficient index for the assessment of force production within arrays of actin filaments which were free to rotate.

Figure 8. Examining the relationship between polymerization, motor velocity, order, and force with the continuum model.

(A) Contour plot for the continuum equation’s solutions show the domains of high and low order as a result of the polymerization rate (r₂) and the motor velocity (v). (B) Solutions predicted from the continuum model for force and order as the rate of polymerization increases. We observed that there exists a region where two differently ordered morphologies generate the same force.

3.5. Biological Complexities: How does the behavior of this simplified system change as more realistic conditions are introduced?

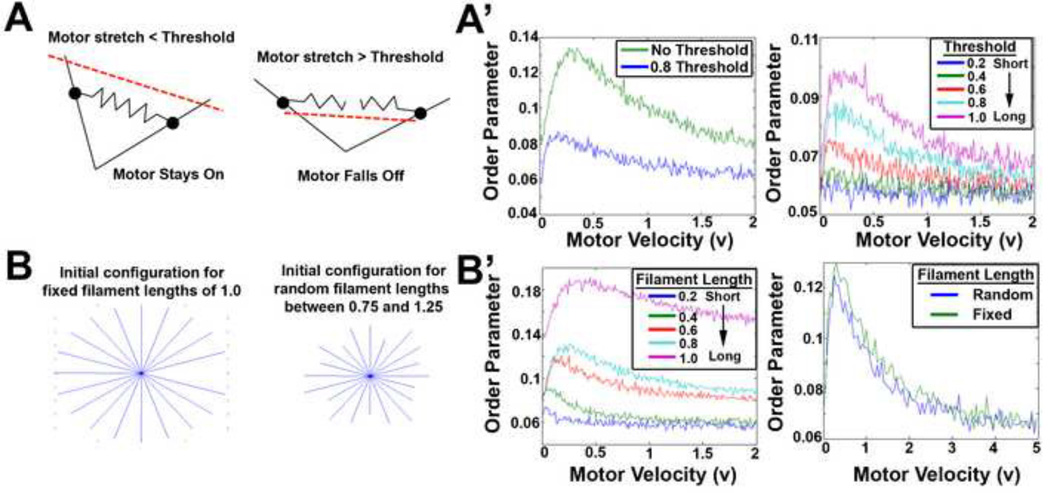
Thus far, our simulations and analysis did not limit the length that myosin motors could stretch between pairs of actin filaments. To test the importance of this assumption, we ran simulations where motors detached once they exceeded a threshold length (Figure 9A). This change lowered the motor velocity needed for optimal alignment of the filaments (Figure 9A’). Simulations where we introduced a threshold of myosin detachment behaved as if we had simply increased the rate of detachment of the motor (e.g. increased r₁). Alternatively, when we increased the threshold we found that the filaments aligned more strongly and the motor velocities needed for optimal alignment also increased.

Figure 9. Introducing complexities to the model yields the same results.

(A, A') The model allowed motors to stretch as far as necessary in order to stay attached to the filament pair; however, in vivo, it is more likely that the motor is limited in its stretch. We restricted the distance the motors can stretch which reduced the order of the system. (B, B') We assumed filaments had fixed lengths of one for our Monte Carlo simulations. We introduced complexity by varying the fixed length, which resulted in a decrease in order for a shortened filament length. To increase complexity even further, we considered filaments with random lengths that had an average length of one and found both the fixed length of one and random lengths with average length one, had the same order.

Up to this point our simulations used filaments of uniform length (Figure 9B); to test the importance of this assumption we ran simulations with filaments having different fixed lengths. With increased filament length, we found that filaments aligned to a greater degree and that the motor velocity needed to optimally align filaments also increased (Figure 9B’). If we allowed filaments to have random lengths between 0.75 and 1.25, so their average length would be 1.0. We found almost no change in the velocity needed to optimally align filaments, however, the magnitude of alignment decreased slightly (Figure 9B’).

4. Concluding remarks

Actomyosin networks shape a diverse array of cellular structures. Many of these, such as the alignment of actin filaments into the cytokinetic furrow or into the base of dynamic filopodia are likely to involve filament rotation. To understand the principles that shape these networks we have constructed a set of theoretical models to study the evolution of F-actin morphology and dissected the relative contributions of F-actin polymerization and myosinmotor based alignment to changes in filament morphology and force production. Monte Carlo simulations and continuum models identified regimes where actin filaments are stably bundled and other regimes where actin filament depolymerization leads to an asynchronous state where actomyosin forms a perpetually contractile array. The models suggest biophysical mechanisms through which myosin activity and F-actin polymerization reshape the cytoskeleton and drive cell shape change.

We first derived the equations of motion for a simple system of two filaments and one myosin II motor complex and defined a statistical property of circularly distributed actin filaments, the order parameter, to assess the morphology of arbitrarily large filament-motor arrays. Implementing simple stochastic processes that allow motors to bind or detach from filament-pairs, walk toward filament plus-ends, and pull filaments together, we performed Monte Carlo simulations in order to understand how these processes shape the morphology of filament pairs.

We found that maximal alignment of the filament pair occurred at a unique motor velocity and depended on both the rates of the stochastic processes and the length of the filaments. Motors aligned filaments more rapidly when they spent the largest fraction of their duty-cycle actively contracting the two filaments. At one extreme, if a motor traveled too slowly it would fall off the filament pair before reaching the end; and, at the other extreme, a motor that traveled too rapidly spent too much time waiting to bind to the pair of filaments.

These relationships suggested the existence of an underlying biophysical principle so we simplified the motor-filament interaction slightly and re-cast the problem using continuum equations for a “two-state process and investigated the evolution of the filament-motor system as density functions. These equations were solved explicitly, reproduced the findings from our Monte Carlo simulations and provided a direct link between parameters governing motor-filament interactions, the resultant filament morphology, and contractile strength. Remarkably, this analysis demonstrated that no matter how many motors or filaments there are, the density of motor positions is always the same.

In order to generalize these two-filament one-motor systems to systems with multiple filaments and motors we returned to Monte Carlo simulations. These systems reproduced the same general behaviors seen in the simpler system, namely, that filaments rapidly align over a wide range of model parameters and that the alignment peaks for conditions where motors spend the largest fraction of their duty cycle contracting filament-pairs.

Rapid alignment of filaments underlie a range of cellular processes such as the formation of the cytokinetic furrow in dividing cells and the convergence zone at the rear of lamellipodia in migratory cells. During the initial steps of cytokinesis, myosin II motors bind disordered actin filaments within the cortex and reorient those filaments aligning them within the cytokinetic furrow [26, 27]. Retrograde flowing actin filaments within lamellipodia first encounter myosin II at the rear of the lamellipodia. In this region, named the convergence-zone, filaments are anisotropically contracted, reoriented perpendicular to the direction of the flow, and are rapidly depolymerized [28, 29].

However, other cellular processes driven by actomyosin dynamics progress without alignment, for instance actomyosin assemblies at the rear of migrating cells, and a range of processes that direct cell shape change during morphogenesis in embryos [30, 3, 31, 32, 33]. To investigate processes that might destabilize filament alignment we modified our models to include filament polymerization/depolymerization. Both our two-filament, one-motor and multiple filament, multiple motor models revealed that the rate of depolymerization can alter the speed of alignment but could also produce morphologically stable arrays of permanently contractile filaments.

These models revealed that motor activity and polymerization underlie the ability of F-actin networks to undergo a phase-transition from organized aligned filaments into dynamically disorganized, permanently contractile arrays. This transition could be controlled by both the motor velocity and the frequency or rate of depolymerization. We propose that cells manipulate the state of actomyosin by controlling this phase transition. Actomyosin interactions can result in distinct patterns of force generation in addition to altering the morphology of filament arrays. In the absence of F-actin polymerization, myosin II quickly align filaments into tight bundles. However, such bundled filaments no longer generate contractile forces. In contrast, once polymerization is introduced, arrays of filaments can achieve some alignment, but instead of forming stable bundles, they form a dynamically disorganized contractile array. Polymerization, or rather depolymerization, allows the actin network to continuously generate contractile force. Thus, actin filament alignment combined with polymerization and depolymerization allows the cytoskeleton to remain continuously contractile even as its morphology is continuously changing.

To build our intuition about the performance of actomyosin we intentionally omitted numerous details of both actin filament and myosin II function. As we explored the behavior of the simple system we extended our models to include many of these omitted details and test their relevance as a more “realistic” biology. For instance, after allowing varying or random length filaments we found we could interpret the results in the context of our simpler model. Our greatest simplification for the model was fixing the minus-ends of filaments together in the center of an array. This simplification allowed us to investigate the complex interactions between polymerization and myosin motor function without the confounding effects of filament translocation or lateral movement. Clearly, more realistic models will require complex geometries of free-associating actin filaments. However these future efforts will to be able to build on both the Monte Carlo models and continuum-level theory that we developed here.

Highlights.

• Alignment of the actomyosin network is maximized by an optimal motor velocity.

• Filament depolymerization destabilizes alignment and bundling of action networks.

• A phase transition between aligned and disordered networks exists.

• Continuum analysis shows that two different morphologies generate the same force.

• Coupling of alignment and depolymerization optimizes the forces generated by myosin.

Supplementary Material

01. Figure S1. Algorithm flow chart for Monte Carlo simulations.

Pictorial flow chart describing the Monte Carlo simulation code used in the paper.

02. Table S1. Parameters and values used most often in the code.

Table illustrating the Monte Carlo simulation code’s parameters and the associated values used most often.

03. Table S2. Variables for the code.

Table illustrating all possible variables in the Monte Carlo simulation code.

Appendix

Appendix A. Deriving the equations of motion

We begin with the vector defining the position of the motor along filament j (x_j = s(cos θ_j, sin θ_j) for j = 1, 2), and derive the potential and kinetic energy for the system (Equation A.1), where k is the spring constant and m is the mass of the motor.

$$\begin{array}{cc}\hfill \mathrm{P}.\mathrm{E}.& =k{\Vert {\overrightarrow{x}}_1-{\overrightarrow{x}}_2\Vert }^2={\mathit{\text{ks}}}^2[1-\text{cos}({\theta }_2-{\theta }_1)]\hfill \\ \hfill \mathrm{K}.\mathrm{E}.& =\frac{1}{2}m\left({\Vert \dot{{\overrightarrow{x}}_1}(t)\Vert }^2+{\Vert \dot{{\overrightarrow{x}}_2}(t)\Vert }^2\right)=\frac{1}{2}{\mathit{\text{ms}}}^2[{\mathit{\theta ̇}}_1^2+{\mathit{\theta ̇}}_2^2]+\frac{1}{2}{m\upsilon }^2.\hfill \end{array}$$ (A.1)

In order to obtain equations of motion from the potential and kinetic energy equations, we consider the Lagrangian equations (Equation A.2).

$$\frac{\partial }{\partial t}\left(\frac{\partial \mathrm{K}.\mathrm{E}.}{\partial {\mathit{\theta ̇}}_i}\right)-\frac{\partial \mathrm{K}.\mathrm{E}.}{\partial {\theta }_i}=\frac{\partial \mathrm{P}.\mathrm{E}.}{\partial {\theta }_i}$$ (A.2)

We assume that motors operate without a drag force, based on the known sizes of myosin. However, we do consider a viscous damping term (μ) which opposes the movement of actin filaments and is analogous to the friction the filaments might experience when moved through water. Substituting into the potential and kinetic energies equations for filaments 1 and 2, we can explicitly derive our Lagrangian equations (Equation A.3).

$$\begin{array}{c}\hfill {\mathit{\text{ms}}}^2{\mathit{\theta ̈}}_1+\mu {\mathit{\theta ̇}}_1={\mathit{\text{ks}}}^2\text{sin}({\theta }_2-{\theta }_1)\hfill \\ \hfill {\mathit{\text{ms}}}^2{\mathit{\theta ̈}}_2+\mu {\mathit{\theta ̇}}_2={\mathit{\text{ks}}}^2\text{sin}({\theta }_1-{\theta }_2)\hfill \end{array}$$ (A.3)

Since the masses of the motor and filaments are small, we ignore the momentum term and solve for the equations of motion for the change in filament angle (Equation A.4; Equation 1 in the main text).

$$\begin{array}{c}\hfill {\mathit{\theta ̇}}_1=\frac{k}{\mu }{s}^2\text{sin}({\theta }_2-{\theta }_1)\hfill \\ \hfill {\mathit{\theta ̇}}_2=\frac{k}{\mu }{s}^2\text{sin}({\theta }_1-{\theta }_2).\hfill \end{array}$$ (A.4)

Appendix B. Solving the coupled integro-partial differential equations

For the distribution Q_j which denotes a stationary solution, we can write an equation for force (〈s²〉) and the order parameter (Z):

$$\begin{array}{c}\hfill \langle s^2\rangle ={\displaystyle {\int }_{-\pi }^{\pi }}{\displaystyle {\int }_0^L}{Q}_1(\varphi ,s)s^2\mathit{\text{ds}}\hfill \\ \hfill Z={\displaystyle {\int }_{-\pi /2}^{\pi }}\text{cos}\varphi /2\left({\displaystyle {\int }_0^L}{Q}_1(\varphi ,s)\mathit{\text{ds}}+Q_0(\varphi )\mathit{\text{ds}}\right)d\varphi \hfill \end{array}$$

The histogram of the values of the angle difference, ϕ, is a plot of $Q_M(\varphi )=Q_0(\varphi )+{\displaystyle {\int }_0^L}{Q}_1(\varphi ,s)\mathit{\text{ds}}$, the marginal distribution of the angles. These stationary solutions are represented by a pair of coupled integro-partial-differential equations and are generally difficult to solve numerically or analytically. However, in this case we can get a closed expression for the filament distributions and thus an exact expression for our torque-like term, 〈s²〉 (Equation 10). We can then use this distribution to approximate the dependence on the difference in angles, ϕ, and estimate the order parameter Z.

The marginal densities with respect to the motor distance down the filament pair, s, is found by integrating Q_0,1 with respect to ϕ:

$$\begin{array}{c}0={\displaystyle {\int }_{-\pi }^{\pi }}\left(-\upsilon {\partial }_s{Q}_1(\varphi ,s)+\frac{k}{\mu }{\partial }_{\varphi }[\text{sin}\varphi Q_1(\varphi ,s)]-(r_1+r_2)Q_1(\varphi ,s)\right)d\varphi \hfill \\ 0={\displaystyle {\int }_{-\pi }^{\pi }}\left(\upsilon Q_1(\varphi ,s)+{\displaystyle {\int }_0^L}\left[r_1{Q}_1(\varphi ,s)+\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }}{Q}_1(\theta ,s)d\theta \right]\mathit{\text{ ds}}-r_0{Q}_0(\varphi )\right)d\varphi .\hfill \end{array}$$ (B.1)

Let

$$\begin{array}{c}\hfill W_1(s)={\displaystyle {\int }_{-\pi }^{\pi }}{Q}_1(\varphi ,s)d\varphi \\ \hfill W_0(s)={\displaystyle {\int }_{-\pi }^{\pi }}{Q}_0(\varphi )d\varphi \end{array}$$

denote the marginal densities. Then from Equation B.1, we see that

$$0=-\upsilon W_1^{\prime }-(r_1+r_2)W_1$$ (B.2)

$$0=\upsilon W_1(L)-r_0{W}_0+(r_1+r_2){\displaystyle {\int }_0^L}{W}_1(s)\mathit{\text{ ds}}$$ (B.3)

$$W_1(0)=\frac{r_0}{\upsilon }{W}_0.$$ (B.4)

Finally, we must have the normalization:

$$W_0+{\displaystyle {\int }_0^L}{W}_1(s)\mathit{\text{ ds}}=1.$$

Remarkably, the marginal density for the motor position involves no unknown integrals with respect to ϕ and so we can solve it exactly. Furthermore, we can easily compute 〈s²〉. To save on some notational headaches, we set L = 1 without loss in generality. We also note that as far as the marginal motor position is concerned, r₁ and r₂ serve only to dislodge the motors; this is evident by the observation that they always appear as a sum r₁ + r₂. For the moment, we absorb the effects of r₂ into an effective r₁ to simplify the algebra. That is, if r₁ = 0.1 and r₂ = 0.05, as was the case in Figure 3 from the paper, then the effective r₁ is 0.15, the sum. Equation (B.2) and the boundary condition in Equation B.4 imply

$$W_1(s)=\frac{r_0}{\upsilon }{W}_0\text{ exp }\left(-\frac{r_1}{\upsilon }s\right).$$

Normalization allows us to solve for W₀:

$$W_0=\frac{r_1}{\upsilon (r_1+r_0(1-e^{-r_1/\upsilon }))},$$

So that

$$W_1(s)=\frac{r_0{r}_1}{\upsilon }\frac{e^{-r_{1}s/\upsilon }}{r_1+r_0(1-e^{-r_1/\upsilon })}.$$ (B.5)

We can now integrate Equation B.5 against s² to compute (Equation 10; Equation 13 from the text):

$$\langle s^2\rangle =\frac{r_0}{r_1^2}\frac{2{\upsilon }^2-e^{-r_1/\upsilon }(2{\upsilon }^2+2\upsilon r_1+r_1^2)}{r_1+r_0(1-e^{-r_1/\upsilon })}.$$ (B.6)

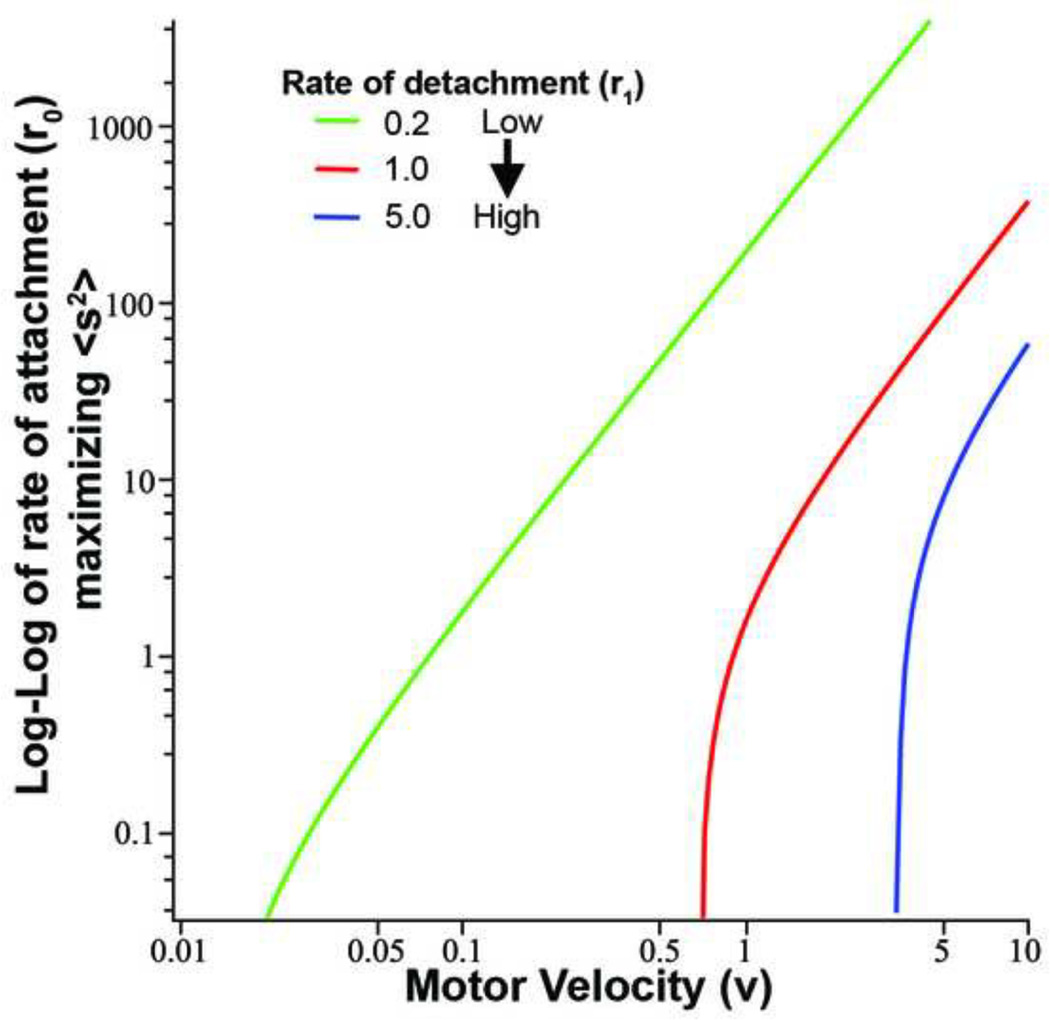
Equation B.6 allows us to see how the optimal velocity depends on the parameters. If we set the derivative of Equation B.6 to zero, we get an expression to determine the maximum. It is not possible to solve the resulting derivative for υ since the equation involves a mix of exponentials and rational functions. However, we can solve the resulting equation for r₀ and thus we obtain an expression, r₀ = ρ₀(υ, r₁) such that Equation B.6 is maximal. Figure B.1 shows plots of this expression for three different values of r₁. The way to interpret this plot is to, say, fix r₀ = 1, r₁ = 1 then observe that this corresponds to a value of υ ≃ 0.8 on the red curve (which corresponds to r₁ = 1). As r₀ → 0, the three curves appear to intersect the υ-axis at values which depend on r₁. In the loglog plot (Figure B.1), all three curves asymptote with the same slope, the translation depends only on r₁. The intersection with the υ-axis can be found by letting r₀ tend to zero in the expression for ∂F/∂υ; we find that this expression vanishes when

$$\text{exp}(r_1/\upsilon )=1+r_1\upsilon +(1/2){(r_1/\upsilon )}^2+(1/4){(r_1/\upsilon )}^3.$$

Figure B.1. Examining the relationship between attachment and detachment rates on optimal motor velocity for maximizing force.

The curves depict the maximal values of force (Equation 28) for two filaments and one motor with varying rates of detachment and attachment, and the resulting optimal motor velocity. The green curve depicts a small rate of detachment (r₁=0.2/s), the red curve a medium rate of detachment (r₁=0/s), and the blue curve a high rate of detachment (r₁=5/s). For the curves we do not consider the rate of polymerization, but we are able to deduce the relationship between all the variables that affect force.

There is a unique positive root, r₁/υ ≃ 1.45, so we see that for r₀ small, the optimal velocity is linearly proportional to r₁. We can also understand this intuitively. As r₀ tends to zero, this means we spend a great deal of time with the motor unattached to the filaments. We thus want to choose υ to maximize the amount of time spent on the filaments and in particular, we want to choose υ so that we get as far out as possible toward the ends of the filaments where the most work is done. Since the expected time to remain on the filament is 1/r₁, then by choosing υ ≃ r₁, we can get to the end of the filament before falling off while at the same time, not going so fast that we reach the ends. The linear asymptotes in the loglog plot can also be easily found by letting υ → ∞ whence, we find that $\upsilon ~\sqrt{r_1{r}_0}/2$. This is satisfying since it says that for large rates, the optimal velocity is the geometric mean of the rate of falling off and the rate of attaching.

Appendix C. Calculating the marginal density of the angle differences

We now turn to the marginal density of the angle differences. To obtain an equation for this, we integrate Equation B.1 with respect to s. Let S₀(ϕ) = Q₀(ϕ) and let $S_1(\varphi )={\displaystyle {\int }_0^L}{Q}_1(\varphi ,s)\mathit{\text{ds}}$. Note that S_0,1(ϕ) are the densities for the angle between the filaments when the motors are off, on respectively and independent of the motor position. S₁(ϕ) satisfies

$$0=\upsilon [Q_1(\varphi ,0)-Q_1(\varphi ,L)]+{\displaystyle {\int }_0^L}{s}^2\frac{k}{\mu }\frac{\partial \text{ sin }\varphi Q_1(\varphi ,s)}{\partial \varphi }\mathit{\text{ ds}}-(r_1+r_2)S_1(\varphi ).$$

Unfortunately, this expression does not just involve S₁, but also requires knowledge of the joint distribution, Q₁(ϕ, s). We now make an approximation; we suppose that Q₁(ϕ, s) = S₁(ϕ)W₁(s). That is, we assume that the variables s and ϕ are independent.While it is true that the value of s is independent of ϕ (which is why we could solve for the marginal density, W₁(s)), the angle difference, ϕ should depend on s as this governs the effective strength of the spring. With this approximation, we get

$$0=\upsilon [W_1(0)-W_1(L)]S_1(\varphi )+\frac{k\langle s^2\rangle }{\mu }[\text{sin }\varphi S_1(\varphi )]\prime -(r_1+r_2)S_1(\varphi )$$ (C.1)

$$0=\upsilon W_1(L)S_1(\varphi )+r_1{S}_1(\varphi )-r_0{S}_0(\varphi )+r_2\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }}{S}_1(\psi )d\psi$$ (C.2)

$$\upsilon S_1(\varphi )W_1(0)=r_0{S}_0(\varphi )$$ (C.3)

Equation C.3 is the approximate boundary condition. Let ${\mathit{S̄}}_1=1/(2\pi ){\displaystyle {\int }_{-\pi }^{\pi }}{S}_1(\varphi )d\varphi$ and X₂ ≔ 〈s²〉. Then we can solve Equation C.2 to get

$$r_0{S}_0=\upsilon W_1(L)S_1(\varphi )+r_1{S}_1(\varphi )+r_2{\mathit{S̄}}_1$$

and use Equation C.3 to obtain a single equation for S₁(ϕ):

$$\frac{d}{d\varphi }[\text{sin }\varphi S_1]=\frac{\mu r_2}{{\mathit{\text{kX}}}_2}[S_1-{\mathit{S̄}}_1]$$ (C.4)

For notational simplicity, let r = (μr₂)/(kX₂). In order to solve Equation C.4, we observe that it is symmetric about zero, and singular at −π, 0, and π. So we just have to solve it in the interval (0, π), and then can reflect this solution about zero to obtain the solution for the interval (−π, 0). Then, we must take appropriate limits. We remark that it is not necessary that S₁(ϕ) has a well-defined limit as ϕ → 0; we only require integrability. For simplicity we let S₁(π/2) = 1, which we can always scale later since Equation C.4 is linear and homogeneous in S₁. (The actual value will come about from normalization). Solving the ODE, we obtain

$$S_1(\varphi )=\left[1-r{\mathit{S̄}}_1{\displaystyle {\int }_{\frac{\pi }{2}}^{\varphi }}{\left(\frac{1-\text{cos }\psi }{\text{sin }\psi }\right)}^{-r}d\psi \right]{\left[\frac{1-\text{cos }\varphi }{\text{sin }\varphi }\right]}^r\frac{1}{\text{sin }\varphi }$$ (C.5)

We rewrite the expression for S₁ as

$$\begin{array}{cc}\hfill S_1(\varphi )& =F(\varphi ){\left(\text{tan }\frac{\varphi }{2}\right)}^r\frac{1}{\text{sin }\varphi }\hfill \\ \hfill F(\varphi )& \hfill =1-\mathit{\text{ra }}{\displaystyle {\int }_{\frac{\pi }{2}}^{\varphi }}{(\text{cot }\frac{\psi }{2})}^{r}d\psi \\ \hfill m& ={\mathit{S̄}}_1\hfill \end{array}$$

We notice that ${\left(\text{tan}\frac{\varphi }{2}\right)}^r\frac{1}{\text{sin }\varphi }$ goes towards infinity like the function (π − ϕ)^−(r+1) as ϕ goes to π, which is not integrable on our interval of (0, π). So in order for S₁(ϕ) to be integrable on the interval of (0, π), F(π) must go to zero as ϕ goes to π. We choose a to make F(ϕ) → 0. Then, applying L’Hopital’s rule it is easy to show that lim_ϕ→π S₁(ϕ) is finite. Next, we need to address the case of ϕ going to zero. We can approximate the behavior of F(ϕ) as ϕ → 0 as the function k₁ϕ^1−r + k₂, and tan(ϕ/2)^r/ sin ϕ as the function ϕ^r−1. Then S₁(ϕ) ≈ k₁ + k₂ϕ^r−1, which is singular for 0 < r < 1 near ϕ = 0, but is integrable. So if we integrate S₁(ϕ) from zero to π, we find, using integration by parts the following:

$${\displaystyle {\int }_0^{\pi }}{S}_1(\varphi )d\varphi =\frac{1}{r}{\left[{\left(\text{tan }\frac{\varphi }{2}\right)}^r\left(1-\mathit{\text{ra }}{\displaystyle {\int }_{\pi /2}^{\varphi }}\text{ cot }{\left(\frac{\psi }{2}\right)}^{r}d\psi \right)\right]}_0^{\pi }-\frac{1}{r}{\displaystyle {\int }_0^{\pi }}\frac{{\left(\text{tan }\frac{\varphi }{2}\right)}^r}{r}\left(-\mathit{\text{ra}}\text{cot}{\left(\frac{\varphi }{2}\right)}^r\right)d\varphi =0+a\pi =a\pi .$$

We use L’Hopital’s rule to show the first expression is zero. This integration shows that ${\displaystyle {\int }_{-\pi }^{\pi }}{S}_1(\varphi )=2\pi a$ so that S̄₁ = a as required for self-consistency. We can rewrite the expression and use Equation C.2 to write:

$$S_1(\varphi )=\frac{1}{\text{sin }\varphi }{\text{tan}}^r\frac{\varphi }{2}{\displaystyle {\int }_{\varphi }^{\pi }}{\text{ cot}}^r\frac{\psi }{2}d\psi$$ (C.6)

$$S_0(\varphi )=\frac{1}{r_0}[(\upsilon W_1(L)+r_1)S_1(\varphi )+r_{2}a].$$ (C.7)

Appendix D. Determining the stability of the trivial state

We write P₁(θ, s, t) = (1/2π)W₁(s) + p₁(θ, s, t) and P₀(θ, t) = (1/2π)W₀ + p₀(θ, s, t) and find that to linear order:

$$\frac{\partial p_1}{\partial t}=-\upsilon \frac{\partial p_1}{\partial s}-K\frac{W_1(s)}{2\pi }\frac{\partial }{\partial \theta }\left({\displaystyle {\int }_0^L}{\displaystyle {\int }_{-\pi }^{\pi }}\text{ sin}(\theta \prime -\theta )s^2{p}_1(\theta \prime ,s,t)\mathit{\text{ ds }}d\theta \prime \right)-(r_1+r_2)p_1$$ (D.1)

$$\frac{\partial p_0}{\partial t}=\upsilon p_1(\theta ,L,t)-r_0{p}_0+{\displaystyle {\int }_0^L}\left(r_1{p}_1(\theta ,s\prime ,t)+\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{\pi }}{r}_2{p}_1(\theta \prime ,s\prime ,t)d\theta \prime \right)\mathit{\text{ ds}}\prime$$ (D.2)

$$p_1(\theta ,0,t)=\frac{r_0}{\upsilon }{p}_0(\theta ,t).$$ (D.3)

Where $K=\frac{\mathit{\text{kM}}}{\mu N}$, M is the number of motors and N is the number of filaments. In addition, we must have the normalization of the perturbation

$${\displaystyle {\int }_0^L}{\displaystyle {\int }_{-\pi }^{\pi }}{p}_1(\theta ,s,t)+p_0(\theta ,t)d\theta \mathit{\text{ ds}}=0.$$

Equation D.1 is a convolution in θ and is homogeneous with respect to t and θ, so that we can look for solutions of the form

$$\begin{array}{cc}\hfill p_1(\theta ,s,t)& ={\psi }_1(s)e^{\mathit{\text{im}}\theta }{e}^{\lambda t}\hfill \\ \hfill p_0(\theta ,t)& ={\psi }_0{e}^{\mathit{\text{im}}\theta }{e}^{\lambda t}\hfill \end{array}$$

where m is an integer and ψ_j are unknown. If, for some m, the real part of λ is positive, then solutions will grow with respect to that mode, m, and the completely disordered state will be unstable. We plug this form into Equations D.1–D.3 to get a sequence of linear eigenvalue problems. We consider three distinct cases: m = 0, m = 1, and m ≥ 2. First, we will address the first and last cases, and then turn to the more difficult m = 1 case. The cases for which m ≠ 1 are simplest because the integral term in Equation D.1 vanishes since the convolution over θ involves only sin θ.

Appendix D.1

Case 1: m = 0

When m = 0, the eigenvalue problem is

$$\begin{array}{c}\lambda {\psi }_1=-\upsilon {\psi }_1^{\prime }-(r_1+r_2){\psi }_1\hfill \\ \lambda {\psi }_0=\upsilon {\psi }_1(L)-r_0{\psi }_0+(r_1+r_2){\displaystyle {\int }_0^L}{\psi }_1(s\prime )\mathit{\text{ds}}\prime .\hfill \end{array}$$

The solution to the first equation along with the boundary condition implies

$${\psi }_1(s)=\frac{r_0{\psi }_0}{\upsilon }{e}^{-(\lambda +r_1+r_2)s/\upsilon }.$$

We exploit a special property of m = 0. The normalization implies that

$${\psi }_0+{\displaystyle {\int }_0^L}{\psi }_1(s\prime )\mathit{\text{ds}}\prime =0.$$

Plugging the formula for ψ₁(s) into the normalization yields

$${\psi }_0+{\psi }_0\frac{r_0}{\lambda +r_1+r_2}[1-\text{exp}(-[\lambda +r_1+r_2]L/\upsilon )]=0.$$

Dividing by ψ₀ and rearranging, we get

$$(\lambda +r_1+r_2+r_0)e^{\lambda L/\upsilon }=r_0{e}^{-(r_1+r_2)L/\upsilon }$$

Multiply both sides by L/υ and call z = λL/υ to obtain

$$e^{z}z+{\mathit{\text{ae}}}^z=b$$

where a = (r₁ + r₂ + r₀)L/υ and b = r₀ (L/υ) exp(−(r₁ + r₂)L/υ). We rewrite one more time as

$$-{\mathit{\text{ae}}}^z+b-{\mathit{\text{ze}}}^z=0.$$

Bellman and Cooke [34] prove that all roots, z to this equation have negative real parts if and only if −a < 1, −a < −b, and one more condition that requires that −b be less than a positive number. Clearly all three conditions hold since a > b > 0. Thus, we conclude that with respect to perturbations with m = 0, the trivial state is stable.

Appendix D.2

Case 2: m > 1

When m > 1, then the eigenvalue equation is

$$\begin{array}{l}\lambda {\psi }_1=-\upsilon {\psi }_1^{\prime }-(r_1+r_2){\psi }_1\hfill \\ \lambda {\psi }_0=\upsilon {\psi }_1(L)-r_0{\psi }_0+r_1{\displaystyle {\int }_0^L}{\psi }_1(s\prime )\mathit{\text{ds}}\prime .\hfill \end{array}$$

As in the m = 0 case, we have

$${\psi }_1(s)=\frac{r_0{\psi }_0}{\upsilon }{e}^{-(\lambda +r_1+r_2)s/\upsilon }.$$

Unfortunately, we can no longer make use of the normalization condition since ${\displaystyle {\int }_{-\pi }^{\pi }}{e}^{\mathit{\text{im}}\theta }d\theta =0$ for m ≠ 0. We now plug this into the second equation to obtain

$$\lambda =-r_0\left(1-\frac{r_1}{\lambda +r_1+r_2}\right)(1-e^{-(\lambda +r_1+r_2)L/\upsilon }).$$

There are no positive values of λ that satisfy this equation since the righthand side will be negative. We can rewrite the equation as

$$\frac{\lambda (\lambda +r_1+r_2)}{\lambda +r_2}=-r_0(1-e^{-\lambda L/\upsilon }{e}^{-(r_1+r_2)L/\upsilon }).$$ (D.4)

For L/υ large enough, there can be no roots with positive real parts since the right-hand side goes to −r₀ and thus, we must have

$$\lambda (\lambda +r_1+r_2)+r_0(\lambda +r_2)=0$$

which has only roots with negative real parts. Thus, as L/υ gets smaller, the only way to get positive real parts is that a root must have a zero real part. Since we have eliminated any possible real zero roots, we must then have an imaginary root, iω. In this case we substitute λ = iω into Equation D.4 and obtain

$$\frac{r_1{\omega }^2}{r_2^2+{\omega }^2}+i\frac{\omega (r_2{r}_1+r_2^2+{\omega }^2)}{r)2^2+{\omega }^2}=-r_0(1-e^{-(r_1+r_2)L/\upsilon }{e}^{i\omega L/\upsilon }).$$

As ω varies, the right-hand side traces out a circle centered on the real axis and entirely in the left-half plane. The left-hand side traces out a curve that is in the right-half plane. Thus, there can never be an intersection so that there can never be an imaginary root. Thus there is no way to get roots with a positive real part as L/υ varies and we conclude that all roots to Equation D.4 must have negative real parts.

Appendix D.3

Case 3: m = 1

We finally turn to the most interesting case. So far, we have seen that perturbations in modes of the form exp(imθ) where m ≠ 1 decay exponentially. For m = 1, the linear equation is

$$\begin{array}{cc}\hfill \lambda {\psi }_1& =-\upsilon {\psi }_1^{\prime }-(r_1+r_2){\psi }_1+\frac{K}{2}{W}_1(s){\displaystyle {\int }_0^L}s{\prime }^2{\psi }_1(s\prime )\mathit{\text{ ds}}\prime .\hfill \\ \hfill \lambda {\psi }_0& =\upsilon {\psi }_1(L)-r_0{\psi }_0+r_1{\displaystyle {\int }_0^L}{\psi }_1(s\prime )\mathit{\text{ ds}}\prime \hfill \\ \hfill {\psi }_1(0)& =\frac{r_0}{\upsilon }{\psi }_0.\hfill \end{array}$$

One could solve these linear equations explicitly to find an equation for the eigenvalues, λ. However, the resulting equation is very complicated and offers little analytic insight. Thus, rather take the difficult approach, we make the following observations. First, if K = 0, then the eigenvalue equations are the same as for the m ≥ 2 case and we know that there are no eigenvalues with positive real parts. Thus, we can ask if increasing K can cause some of these “stable” eigenvalues to cross the imaginary axis. There are two ways that this can happen: (i) a negative real eigenvalue becomes a positive real eigenvalue; or (ii) a pair of complex conjugate eigenvalues crosses at an imaginary eigenvalue. Our numerical simulations show that the alignment seems to always produce a stationary peak rather than a peak that rotates at a constant velocity. This empirical fact suggests that the loss of stability of the uniform state occurs through a real eigenvalue crossing zero as in the second case, time periodic (rotating) solutions would be expected. Thus, we will ask if there is a value of K such that there is a zero eigenvalue. Hence we must solve

$$\begin{array}{cc}\hfill 0& =-\upsilon {\psi }_1^{\prime }-(r_1+r_2){\psi }_1+\frac{K}{2}{W}_1(s){\displaystyle {\int }_0^L}s{\prime }^2{\psi }_1(s\prime )\mathit{\text{ ds}}\prime .\hfill \\ \hfill 0& =\upsilon {\psi }_1(L)-r_0{\psi }_0+r_1{\displaystyle {\int }_0^L}{\psi }_1(s\prime )\mathit{\text{ ds}}\prime \hfill \\ \hfill {\psi }_1(0)& =\frac{r_0}{\upsilon }{\psi }_0.\hfill \end{array}$$

There is one differential equation and two algebraic conditions, so we cannot expect there to be a nonzero solution for any K. However, picking the correct K will tell us the critical value, K above which there will be alignment and below which there will be a uniform distribution of filament angles. For notational simplicity, we write ψ₁(s) = ψ₀ϕ(s), σ ≔ (r₁ + r₂)/υ, and W₁(s) = A exp(−σs). Let

$$D≔{\displaystyle {\int }_0^L}{s}^2\varphi (s)\mathit{\text{ ds}}.$$

Then ϕ(s) satisfies

$$\frac{d\varphi }{\mathit{\text{ds}}}=-\sigma \varphi +\frac{\mathit{\text{KAD}}}{2\upsilon }{e}^{-\sigma s}$$

which with the boundary condition yields

$$\varphi (s)=\left(\frac{r_0}{\upsilon }+\frac{\mathit{\text{KAD}}}{2\upsilon }s\right)e^{-\sigma s}.$$

Let

$${\mu }_n≔{\displaystyle {\int }_0^L}{s}^n{e}^{-\sigma s}\mathit{\text{ ds}}.$$

Then the unknown constant, D satisfies

$$D={\displaystyle {\int }_0^L}{s}^2\varphi (s)\mathit{\text{ ds}}=\frac{r_0{\mu }_2}{\upsilon }+D\frac{\mathit{\text{KA}}{\mu }_3}{2\upsilon }$$

or

$$D=\frac{2r_0{\mu }_2}{2\upsilon -\mathit{\text{KA}}{\mu }_3}.$$

We finally use the equation for ψ₀ to obtain:

$$0=-r_0{\psi }_0+\upsilon {\psi }_0\varphi (L)+r_1{\displaystyle {\int }_0^L}{\psi }_0\varphi (s)\mathit{\text{ ds}}.$$

Dividing this by ϕ₀, we obtain an equation of the form:

$$0=-r_0+r_0{e}^{-\sigma L}+\frac{r_0{r}_1}{r_1+r_2}(1-\text{exp}(-\sigma L))+\frac{\mathit{\text{KAD}}}{2\upsilon }(\upsilon {\mathit{\text{Le}}}^{-\sigma L}+r_1{\mu }_1).$$

A final bit of rearranging and use of the definition of D yields

$$\frac{r_0{r}_2}{(r_1+r_2)(L\upsilon e^{-\sigma L}+r_1{\mu }_1)}(1-e^{-\sigma L})=\frac{{\mathit{\text{KAr}}}_0{\mu }_2}{\upsilon (2\upsilon -\mathit{\text{KA}}{\mu }_3)}.$$ (D.5)

The lefthand side is strictly positive. The righthand side is a function of K which vanishes when K = 0 and tends to infinity as K tends to 2υ/(Aμ₃). Thus, for any parameters, we can find a unique value of K, call it K_crit solving Equation D.5:

$$K_{\mathit{\text{crit}}}=\frac{2z{\upsilon }^2}{A(z\upsilon {\mu }_3+r_0{\mu }_2)}$$ (D.6)

where the lefthand side of Equation D.5 is abbreviated as z. Since all of these functions and constants are known, we can plot K_crit as a function of any parameter, in particular, υ.

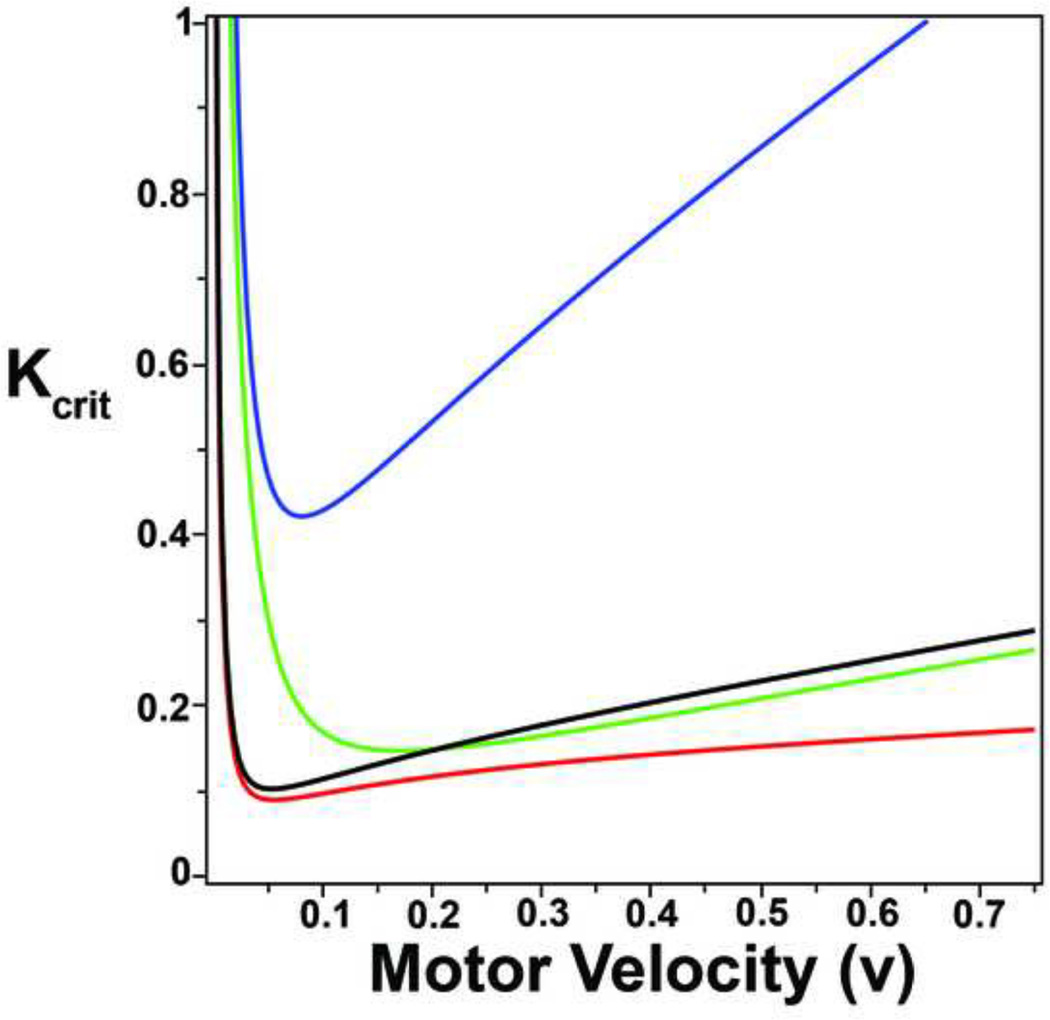
Figure D.1 shows the value of K_crit as the velocity of the motors varies. If K > K_crit, then there is a real positive eigenvalue and the uniformly distributed orientation is unstable. That is, we expect to see the beginnings of alignment along a single direction. First, note that in all cases the curve has a single minimum value at a particular velocity. K_crit goes to infinity as υ goes to both 0 and infinity. We can interpret the curves as follows. Suppose for example, that K = 0.6, r₀ = 0.7, r₁ = 0.1, r₂ = 0.1. Then for a band of velocities between 0.05 and 0.35, K > K_crit so that we expect to see alignment only when the velocity is in this narrow band.

Figure D.1. Determining how K_crit is a function of motor velocity.

K_crit, shown in Equation 41 depends on all the variables of the model: motor velocity, and rates of attachment, detachment, and polymerization. The curves specifically show how K_crit depends on motor velocity, but also how it depends on the three variable rates. The blue curve shows a low rate of attachment (r₀=0.7), a low rate of detachment (r₁=0.1), and a high rate of polymerization (r₂=0.1). The rest of the curves are as follows: green (r₀=0.7 (low), r₁=0.4 (high), r₂=0.025 (low)), black (r₀=0.7 (low), r₁=0.1 (low), r₂=0.025 (low)), and red (r₀=2.8 (high), r₁=0.1 (low), r₂=0.025(low)). Notice that the minimum value of K_crit depends most on the sum of the rate of detachment and polymerization. The asymptotic approximation yields the range of motor velocities for which maximal alignment is expected.

The position of the minimum of K_crit is most dependent on r₁ + r₂ (compare black, green, and blue curves). The parameter r₀ tends to pull down the right part of the curve; large r₀ makes K_crit independent of υ for large velocities. This is because, when r₀ is large, you spend almost all your time on the filaments so the velocity doesn’t matter so much, there is no “penalty” for going fast.

We can use MAPLE to compute an asymptotic approximation for K_crit at the extremes of υ → 0 and υ → ∞. We find that as υ → 0,

$$K_{\mathit{\text{crit}}}~\frac{r_2(r_2+r_1)(r_2+r_1+r_0)}{r_0}\frac{1}{\upsilon },$$

and as υ → ∞,

$$K_{\mathit{\text{crit}}}~\frac{6r_2}{r_0}\upsilon .$$

The latter is independent of r₁, which makes sense for when υ is very large, the probability of ever falling off the filament is virtually zero and the key parameters are the waiting time r₀ and the depolymerization, r₂. We note that for small r₂, both of the asymptotic expressions are proportional to r₂; the more orientation “noise”, the larger is the spring strength needed to overcome it. The asymptotic expansions can be added together to get a qualitatively good approximation of the true curve:

$$K_{\mathit{\text{approx}}}=\frac{r_2(r_2+r_1)(r_2+r_1+r_0)}{r_0}\frac{1}{\upsilon }+\frac{6r_2}{r_0}\upsilon .$$

This simple function has a minimum at

$$\upsilon ={\upsilon }_{\mathit{\text{min}}}≔\sqrt{(r_1+r_2)(r_0+r_1+r_2)/6}$$

which is a reasonable approximation of the minimum of K_crit. What the minimum tells us is the velocity for which the weakest motors (lowest value of K) could cause some alignment. We emphasize that the analysis here is a linearized analysis, so that it does not necessarily tell us about what happens far from the onset of the alignment instability. Thus, we cannot necessarily infer the optimal velocity from this calculation; we can only determine the range of velocities for which alignment is possible.

Appendix E. Kuramoto Model Similarities

$$\frac{\partial P_1(s,\varphi ,t)}{\partial t}=-\upsilon \frac{\partial P_1(s,\varphi ,t)}{\partial s}-\frac{\partial }{\partial \theta }(P_1(s,\varphi ,t)f(\theta ))-(r_1+r_2)P_1(s,\varphi ,t)$$ (E.1)

$$\frac{\partial P_0(s,t)}{\partial t}=\upsilon P_1(L,\theta ,t)-r_0{P}_0+{\displaystyle {\int }_0^L}{r}_1{P}_1(s\prime ,\theta ,t)\mathit{\text{ds}}\prime +\frac{1}{2\pi }{\displaystyle {\int }_0^L}{\displaystyle {\int }_{-\pi }^{\pi }}{r}_2{P}_1(s\prime ,\theta \prime ,t)d\theta \prime \mathit{\text{ds}}\prime$$ (E.2)

Equations E.1 and E.2 (Equations 16 and 17 from the paper) bear a close resemblance to the well-studied Kuramoto model for synchronization of a pool of globally coupled oscillators.

$$\frac{d{\theta }_i}{\mathit{\text{dt}}}={\omega }_i+\frac{K}{N}{\displaystyle \sum _{j=1}^N}\text{sin}({\theta }_j-{\theta }_i)+\omega {\xi }_i$$

In the Kuramoto model, θ_i represents the phase of the ith oscillator, K the coupling strength, ω_i, the uncoupled frequencies of the oscillators and σξ_i the external noise. In the limit as N goes to infinity, we write an equation for the density, ρ(θ, ω, t) of the oscillators:

$$\frac{\partial \rho }{\partial t}=-\frac{\partial }{\partial \theta }\left(\rho (\theta ,\omega ,t)\left[\omega +K{\displaystyle {\int }_{-\mathrm{\infty }}^{\mathrm{\infty }}}g(\omega ){\displaystyle {\int }_0^{2\pi }}\text{sin}(\varphi -\theta )\rho (\varphi ,\omega t)d\varphi d\omega \right]\right)+\frac{{\sigma }^2}{2}\frac{{\partial }^2\rho }{\partial {\theta }^2}$$

Here g(ω) is the density for the distribution of oscillator frequencies. There are two sources of disorder in the Kuramoto model, extrinsic noise, σ, and the heterogeneity of the frequencies. In our model, the noise comes from the de/polymerization of the filaments and since the new filaments occur at any angle, the noise does not appear locally as phase diffusion as in the Kuramoto model. Both our equations and the Kuramoto equations have a similar nonlinearity and both equations admit a completely disordered state as a solution. In our analysis and the Kuramoto analysis, the key to the onset of order (synchronization in the Kuramoto model) is that this disorder state becomes unstable as some parameter increases. Thus, while the two equations come from completely different motivating systems, they bear a close resemblance simply because they both describe dynamics of systems which lie on the circle.