Impact of Endothelium Roughness on Blood Flow

Abstract

Cell free layer (CFL), a plasma layer bounded by the red blood cell (RBC) core and the endothelium, plays an important physiological role. Its width affects the effective blood viscosity as well as the scavenging and production of nitric oxide (NO). Measurements of the CFL and its spatio-temporal variability are highly uncertain, exhibiting random fluctuations. Yet traditional models of blood flow and NO scavenging treat the CFL’s bounding surfaces as deterministic and smooth. We investigate the effects of the endothelium roughness and uncertain (random) spatial variability on blood flow and estimates of effective blood viscosity.

1 Introduction

The distribution of nitric oxide (NO) in the microcirculation is determined, in large part, by the balance between NO production and consumption in the blood and tissue compartments. A key mechanism of this balance is the gradient of NO concentration at the interface between blood and tissue, a complex sub-microscopic region generally free of red blood cells (RBCs). It is termed the “cell free layer” (CFL). The CFL is bounded by the surface of the endothelium and the surface of the moving RBC column, a configuration that can be modeled as a two layer system. Analysis of this model can be approximated by assuming a Newtonian fluid and a parabolic profile velocity within the CFL which mergers into plug flow and non-Newtonian flow properties in the central RBC core (17, 18). Several studies used this approach to estimate the velocity gradient in the CFL and to estimate shear stress at the vessel wall. The level of shear stress determines the rate of NO production by the endothelium (5). The width of the CFL modulates the rate of NO scavenging by RBCs, since it determines the distance from the source of NO to its major sink on the blood side (2, 6, 18, 22).

Shear stress is determined by the effective viscosity, the velocity gradient, the nature of the flow and the flow boundary geometry. NO bioavailability and oxygen transfer is determined by the shear stress, flow conditions, hematocrit (Hct) and the CFL width. The relation between NO production and shear stress has been analyzed experimentally and theoretically (13, 15). Theoretical studies reveal that the CFL width and shear stress are primary factors in determining NO bioavailability in the vessel wall (19). These studies assume that the interface between the RBC column and plasma is a smooth deterministic surface. However this surface is formed by RBC that deform and aggregate forming an irregular boundary (8, 9), affecting flow and shear stress on the endothelium. Likewise, the endothelium surface exhibits (random) spatial variability.

The endothelium is exposed to a flow field that transmits a distribution of shear stresses to its surface. These forces have a heterogeneous spatial distribution evidenced by the difference of response levels even in contiguous cells are often noted in neighboring cells. This variability was proposed (3) to be in part the consequence of the cell surface geometry. The latter was quantified in living endothelium by means of atomic force microscopy measurements (1).

A deterministic characterization of this undulating surface (16), which treated its profile as a sinusoid, relied on two parameters: the length in flow direction divided by the width transverse to flow, and the height-to-length ratio. These parameters were used to determine the maximum shear stress and shear stress gradient developed by flow by mean of an analytic linearized solution to the governing equations. The analysis in (16) revealed that shear stress gradients at the surface of the endothelium are very large, a consequence of the small dimension over which changes occur.

The topographic variability of the endothelial surface is not well established, rendering their deterministic descriptions problematic. It is known that the endothelial surface is affected by both blood flow and the physiological condition. Various factors, such as endothelial swelling and dehydration (14) and endothelial contractility (7), are modulators of the surface topography that remain unexplored. The study (1) showed that flow also changes the surface from a smooth and uniform sinusoid-like variation to the appearance of fibrous structures embedded in the surface. Such a variety of features suggests that the surface be described by means of stochastic variables and treated as a random boundary characterized by a correlation length (of its variability) in the direction of flow, a mean perturbation height and a standard deviation of this mean height.

Spatial variability of the CFL width is highly uncertain (8, 9). To quantify the impact of this uncertainty on measured and observed flow characteristics (e.g., shear stress on endothelium walls), we treat the CFL surface as a random field. A problem formulation, which describes blood flow in a flow chamber with randomly varying aperture, is presented in Section 2. In Section 3 we use a Karhunen-Loève expansion (e.g., 12) as a means of statistical parameterization of this random boundary. A numerical algorithm for solving the Stokes flow equations in the resulting random domain is described in Appendices A and B. Biophysical implications of our analysis are discussed in detail in Section 4 and summarized in Section 5.

2 Problem Formulation

Consider viscous (low Reynolds number) steady-state blood flow between two plates, one of which is smooth (deterministic) and the other is rough (random). Let μ denote the kinematic viscosity of blood. Then flow velocity u = (u₁, u₂)^T and pressure distribution p at every point x in the flow domain D are governed by the Stokes and continuity equations,

$$\mu {\nabla }^2\mathbf{u}=\nabla p,\nabla \cdot \mathbf{u}=0\mathbf{x}\in \mathcal{D}.$$ (1)

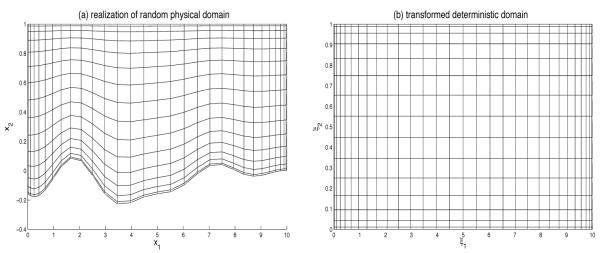
The lower boundary, s(x₁), of the flow domain D = {(x₁, x₂): 0 ≤ x₁ ≤ L_x, s(x₁) ≤ x₂ ≤ L_y} is uncertain. This uncertainty is conceptualized by allowing s to vary randomly in space, i.e., by treating it as a random field s(x₁ ω) where ω ∊ Ω indicates a realization (“coordinate”) in probability space Ω. A typical realization of the random flow domain D(ω) is shown in Figure 3a below.

Figure 3.

(a) A typical realization of the random flow domain D(ω) and (b) its mapping onto a deterministic domain.

The flow is driven by an externally imposed pressure gradient, such that

$$p(0,x_2)=P_l,p(L_x,x_2)=P_r,s\le x_2\le L_y.$$ (2a)

The normal components of the pressure gradient on the two walls is zero,

$$\mathbf{n}\cdot {\nabla }_p(x_1,s)=0,\frac{\partial p}{\partial x_2}(x_1,L_y)=0.$$ (2b)

We assume the bounding surfaces to be impermeable,

$$\mathbf{n}\cdot \mathbf{u}(x_1,s)=0,v(x_1,L_y)=0,$$ (3a)

and impose no-slip boundary conditions,

$$\mathbf{s}\cdot \mathbf{u}(x_1,s)=0,u(x_1,L_y)=0.$$ (3b)

Here n and s denote the unit normal and tangential vectors to the random surface s(x₁,ω), respectively.

3 Statistical Representation of Random Surfaces

Let us employ the Reynolds decomposition, s(x₁, ω) = s̄(x₁) + s’(x₁, ω), to represent the random surface s(x₁,ω) as the sum of its ensemble mean s̄(x₁) and zero-mean fluctuations s’(x₁,ω) about this mean. We assume that available data, such as that reported in (9), are sufficient to estimate the relevant statistics of s(x₁,ω), specifically its mean s̄, standard deviation σ_s, and a two-point correlation function ρ_s(x₁, y₁). Then the random field s(x₁,ω) can be represented via a Karhunen-Loève expansion,

$$s(x_1,\omega )=\stackrel{‒}{s}\left(x_1\right)+{\sigma }_s\sum _{m=1}^{\infty }\sqrt{{\lambda }_m}{f}_m\left(x_1\right)Y_m\left(\omega \right).$$ (4)

Here Y_m(ω) (m ≤ 1) are independent random variables, and λ_m and f_m(x₁) are eigenvalues and eigenfunctions of the Fredholm equations,

$${\int }_0^{L_x}{\rho }_s(x_1,y_1)f_m\left(y_1\right)\mathrm{d}{y}_1={\lambda }_m{f}_m\left(x_1\right),m\ge 1.$$ (5)

For an exponential correlation function,

$${\rho }_s(x_1,y_1)={\mathrm{e}}^{-\mid x_1-y_1\mid ∕l_s}$$ (6)

with the correlation length l_s > 0, the eigenvalue problem in Eq. 5 admits an analytical solution (e.g., 11),

$${\lambda }_m=\frac{2l_s}{l_s^2{\omega }_m^2+1},m\ge 1$$ (7)

and

$$f_m\left(x\right)=\frac{l_s{\omega }_m\cos \left({\omega }_{m}x\right)+\sin \left({\omega }_{m}x\right)}{\sqrt{(l_s^2{\omega }_m^2+1)L_x∕2+l_s}}.$$ (8)

Here the constants ω_m (m ≥ 1) are solutions of the transcendental equation $(l_s^2{\omega }_m^2-1)\sin \left({\omega }_m{L}_x\right)=2l_s{\omega }_m\cos \left({\omega }_m{L}_x\right)$.

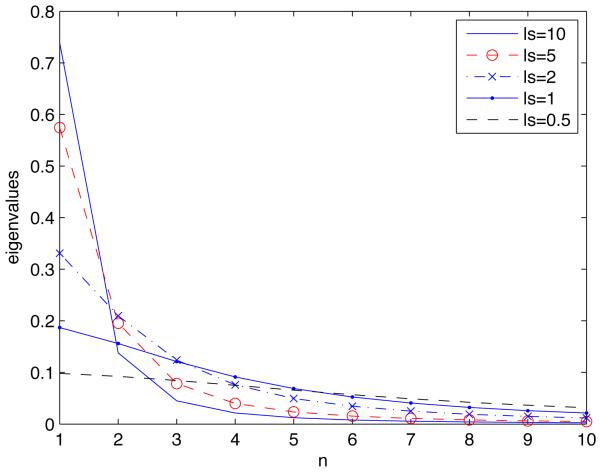
Practical implementation of Karhunen-Loève expansions requires one to truncate the infinite summation in Eq. 4. The resulting truncation error depends on the correlation length l_s. The larger the correlation length, the fewer terms in Eq. 4 are necessary to represent the random surface s₁(x₁, ω) with a given degree of accuracy. Figure 1 shows how the decreasing correlation length l_s affects the decay of the eigenvalues λ_m for the exponential correlation function in Eq. 6.

Figure 1.

Decay of eigenvalues λ_n with n for several correlation lengths l_s.

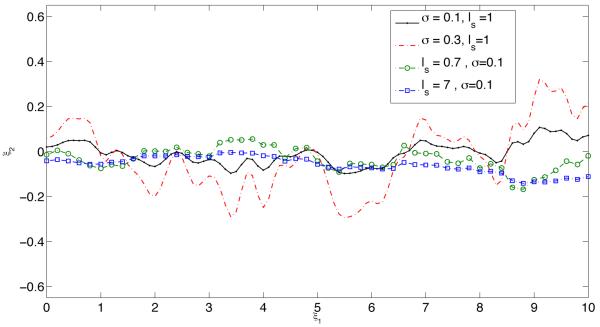
Within the statistical framework adopted here, the endothelium roughness is characterized by two parameters: the standard deviation σ_s and the correlation length l_s. Typical realizations of the uncertain (random) endothelium surface s(x₁, ω) for several values of the standard deviation σ_s and the correlation length l_s are shown in Figure 2.

Figure 2.

Typical realizations of the uncertain (random) endothelium surface s(x₁, ω) for several values of standard deviation σ_s and correlation length l_s.

A numerical algorithm for solving the Stokes flow equations in the resulting random domain is described in Appendix A. It follows a procedure introduced in (10, 21, 24) and consists of two steps. First, the random flow domain is mapped onto a deterministic domain with smooth boundaries (Section A.1), the transformed Stokes equations become stochastic. Second, a generalized polynomial chaos expansion (23) is used in Section A.3 to solve these equations.

4 Simulation Results and Discussion

The mean p̄(x) and variance ${\sigma }_p^2\left(\mathrm{x}\right)$ of pressure p(ξ, ω) were computed as

$$\stackrel{‒}{p}\left(\mathrm{x}\right)=p_0\left(\mathrm{x}\right),{\sigma }_p^2\left(\mathrm{x}\right)=\sum _{k=1}^M{p}_k^2\left(\mathrm{x}\right)\overline{{\Psi }_k^2},$$ (9)

where ${\left\{{\Psi }_m\left(\mathbf{Y}\right)\right\}}_{m=0}^M$ is a set of multidimensional orthogonal polynomials and ${\left\{p_m\left(\mathbf{x}\right)\right\}}_{m=0}^M$ are corresponding deterministic expansion coefficients, both of which are introduced in Section A.3. The identical procedure was used to compute the means and variances of the velocity components u₁(ξ, ω) and u₂(ξ, ω). These means and variances serve respectively to predict the average behavior of, and to quantify predictive uncertainty for, blood pressure and velocity (Section 4.1) and shear stress on the endothelium (Section 4.2). In Section 4.3 we investigate the impact of endothelium roughness on the estimation of effective blood viscosity.

4.1 Blood pressure and velocity

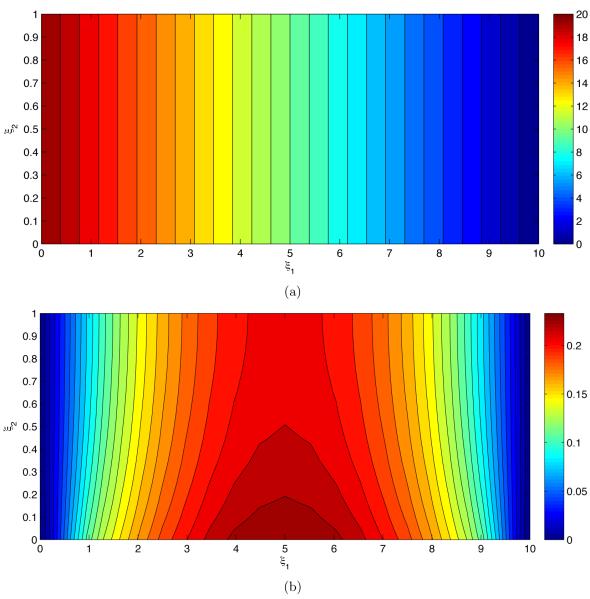
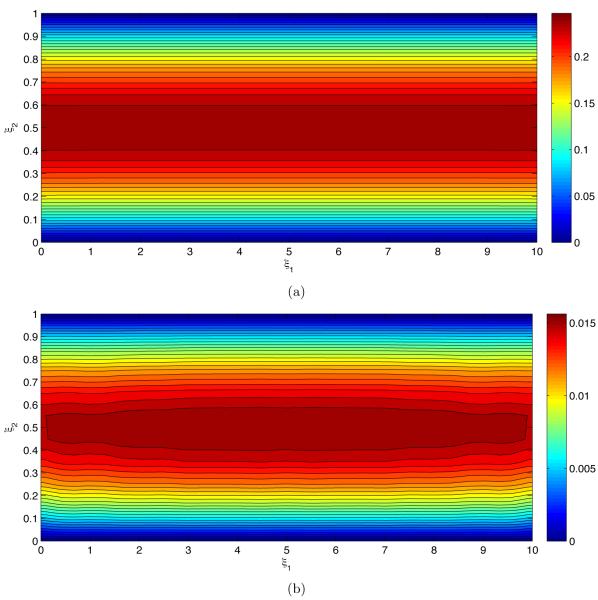
Figure 4 exhibits the pressure statistics resultant from uncertain geometry of the endothelium wall s(x₁). The mean pressure p̄ in Figure 4a decreases linearly from left to right between the two pressure values imposed on the inlet and outlet of the flow chamber. In other words, the mean pressure gradient is constant and unaffected by the endothelium roughness. The uncertain geometry of the endothelium manifests itself in pressure fluctuations about the mean, as quantified by the standard deviation σ_p in Figure 4b. Predictive uncertainty increases with the distance from the inlet and outlet, where pressure is certain, reaching its maximum in the middle of the flow chamber (ξ₁ = L_x/2). It also decreases with the distance from the uncertain endothelium surface (ξ₂ = 0).

Figure 4.

(a) Average pressure p̄ and (b) deviations from the mean (standard deviation) σ_p.

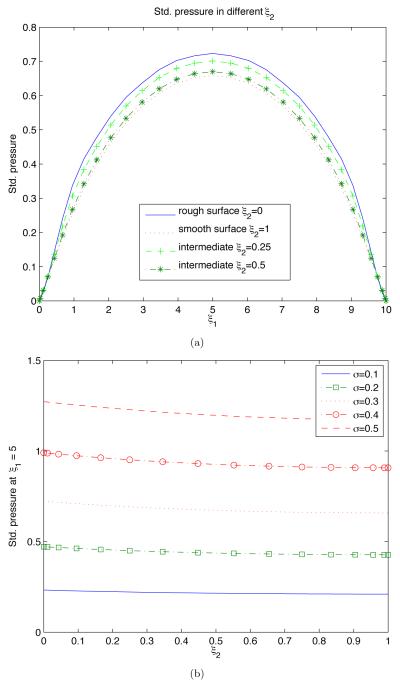
Figure 5 highlights these observations further by presenting several crosssections of the standard deviation of pressure σ_p. In particular, it reveals that the dependence of σ_p on the distance from the uncertain endothelium surface is relatively mild (Figure 5b). This dependence becomes more pronounced as the degree of uncertainty about the endothelium geometry (σ_s) increases.

Figure 5.

Standard deviation of pressure, σ_p, along several horizontal cross-sections ξ₂ = c (a) and vertical cross-section ξ₁ = L_x/2 (b).

The mean flow velocity ū and the standard deviation σ_u1 of the horizontal component of the flow velocity u₁ induced by randomly fluctuating pressure gradient ▽_ξp are shown in Figure 6. The flow is horizontal in the mean (Figure 6a). The no-slip boundary conditions at the walls imply that the horizontal component of flow velocity at the walls is known with certainty (u₁ = 0 at ξ₂ = 0 and ξ₂ = 1), so that σ_u1 = 0. Predictive uncertainty (σ_u1) increases with the distance from the walls, reaching its maximum in the middle of the flow chamber, ξ₂ = 0.5.

Figure 6.

(a) Average flow velocity ū and (b) deviations from the mean of the horizontal component of the flow velocity (its standard deviation) σ_u1.

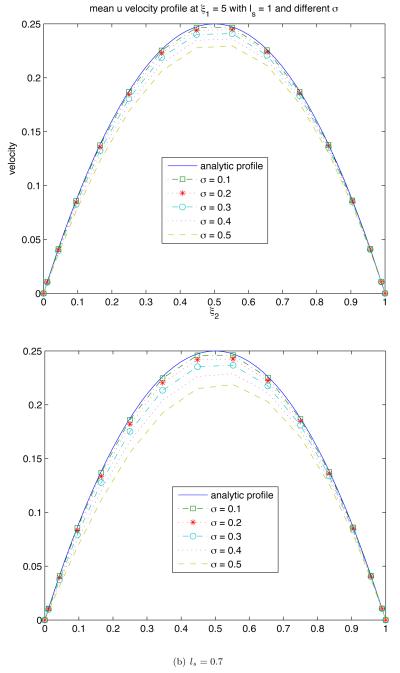
Figure 7 reveals how the endothelium roughness (as quantified by σ_s and l_s) affects the mean flow velocity ū. The overall effect is to reduce the mean flow velocity relative to its counterpart corresponding to the assumption of smooth endothelium (σ_s = 0). For a given σ_s, the mean velocity decreases as l_s becomes smaller, i.e., the endothelium surface becomes more irregular.

Figure 7.

Mean velocity profiles ū(L_x/2, ξ₂) for several degrees of endothelium roughness (σ_s and l_s).

4.2 Flow rate and wall shear stress

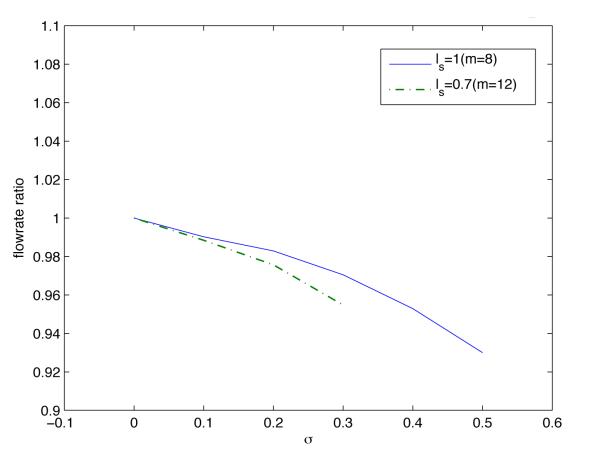
The decrease in mean velocity with increasing endothelium roughness (Figure 7) translates into the corresponding decrease in the volumetric flow rate $Q={\int }_0^1{u}_1\mathrm{d}{\xi }_2$. It is well known that, for a given pressure gradient, Q decreases as the wall roughness increases. Figure 8 quantifies this effect in terms of the observable statistics of endothelium roughness, σ_s and l_s. The flow rate decreases as the roughness amplitude (standard deviation) σ_s increases and/or the correlation length l_s decreases.

Figure 8.

The volumetric flow rate, normalized with its counterpart in the flow chamber with smooth walls, as a function of the statistical parameters σ_s and l_s characterizing endothelium roughness.

Another quantity of physiological significance is the shear stress on the endothelium wall s(x₁, ω),

$${\tau }_w({\xi }_1,s;\omega )=\mu \frac{\partial u_1({\xi }_1,s;\omega )}{\partial {\xi }_2}.$$ (10)

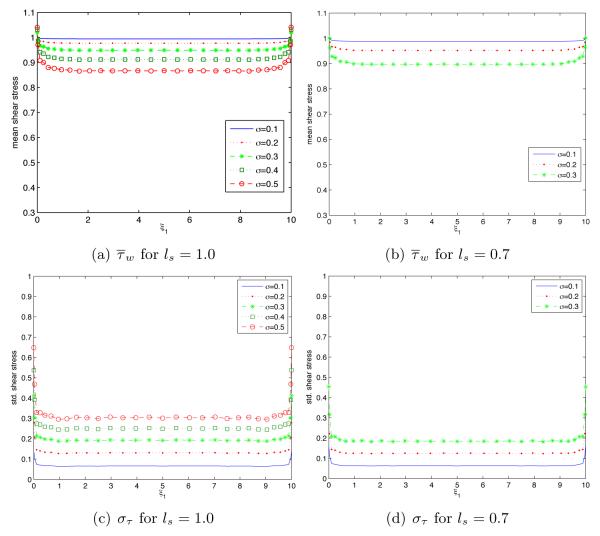
Spatial variability of the mean, ${\overline{\tau }}_w\left({\xi }_1\right)$, and standard deviation, σ_τ(ξ₁), of the endothelium shear stress τ_w is shown in Figure 9 for several degrees of endothelium roughness (σ_s and l_s). The mean shear stress ${\overline{\tau }}_w$ increases with both the magnitude of the endothelium fluctuations (its standard deviation σ_s) and its correlation length l_s. Predictive uncertainty (as quantified by σ_τ) increases with σ_s anddecreases with l_s. Boundary effects (deviation from the fully-developed flow regime, wherein the shear stress statistics are constant) extend further inside the flow chamber as σ_s increases and/or l_s decreases.

Figure 9.

Spatial variability of the mean shear stress ${\overline{\tau }}_w({\xi }_1,{\xi }_2)$ and its standard deviation σ_τ(ξ₁, ξ₂) along the endothelium wall ξ₂ = 0 for several degrees of endothelium roughness (σ_s and l_s).

4.3 Effective blood viscosity

A classical treatment of blood flow in arteries whose walls are modeled as smooth surfaces relies on the Poiseuille law to relate the volumetric flow rate Q to the pressure gradient dp/dx,

$$Q=-\frac{L_y^3}{12\mu }\frac{\mathrm{d}p}{\mathrm{d}x}.$$ (11)

Accounting for (random) endothelium roughness requires one to replace the Poiseuille law in Eq. 11 with its “effective” or “equivalent” counterpart,

$$\overline{Q}=-\frac{L_y^3}{12{\mu }_e}\frac{\mathrm{d}\stackrel{‒}{p}}{\mathrm{d}x},$$ (12)

wherein μ_e denotes the effective viscosity.

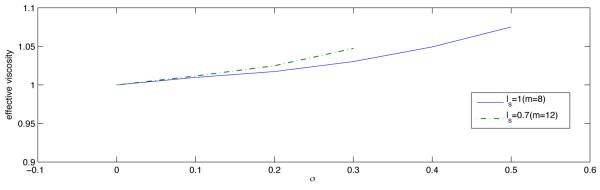
Figure 10 demonstrates that μ_e, the blood viscosity inferred from in vivo experiments via the Poiseuille law depends not only on blood properties but also on the statistical parameters characterizing the endothelium roughness (σ_s and l_s). The effective viscosity μ_e increases as σ_s increases and/or l_s decreases.

Figure 10.

Effective blood viscosity μ_e, normalized with its counterpart corresponding to the smooth wall approximation, as a function of the endothelium roughness parameters σ_s and l_s.

5 Conclusions

We developed a computational framework to quantify the impact of uncertainty in the cell free layer (CFL) width on measured and observed flow characteristics (e.g., shear stress on endothelium walls). This is accomplished by treating the CFL surface as a random field with zero mean, standard deviation σ_s and correlation length l_s. This surface is represented via a Karhunen-Loève expansion. The Stokes equations defined on the resultant random domain are solved in two steps. First, the random flow domain is mapped onto a deterministic domain with smooth boundaries, which renders the transformed Stokes equations stochastic. Second, a generalized polynomial chaos expansion is used to solve these equations.

Our analysis leads to the following major conclusions.

• The mean pressure gradient is constant and unaffected by the endothelium roughness. Uncertainty in (randomness of) the endothelium surface manifests itself in pressure fluctuations about the mean, as quantified by the standard deviation σ_p.

• The overall effect of endothelium roughness is to reduce the mean blood flow velocity relative to its counterpart corresponding to the assumption of smooth endothelium (σ_s = 0). For a given σ_s, the mean velocity decreases as l_s becomes smaller, i.e., the endothelium surface becomes more irregular.

• The decrease in mean velocity with increasing endothelium roughness translates into the corresponding decrease in the volumetric flow rate. The volumetric flow rate decreases as the roughness amplitude (standard deviation) σ_s increases and/or the correlation length l_s decreases.

• The mean shear stress increases with both the magnitude of the endothelium fluctuations (its standard deviation σ_s) and its correlation length l_s. Boundary effects (deviation from the fully-developed flow regime, wherein the shear stress statistics are constant) extend further inside the flow chamber as σ_s increases and/or l_s decreases.

• The blood viscosity, inferred from in vivo experiments via the Poiseuille law, depends not only on blood properties but also on the statistical parameters characterizing the endothelium roughness (σ_s and l_s). The effective blood viscosity increases as σ_s increases and/or l_s decreases.

Appendix

A Solving Stokes Equations on Random Domain

A two-step approach to solving differential equations on random (uncertain) domains is described and implemented below.

A.1 Stochastic mapping onto a deterministic domain

Let us introduce a new coordinate system (ξ₁, ξ₂), in which the original stochastic flow domain D takes the form of a deterministic rectangle E = {(ξ₁, ξ₂) : 0 ≤ ξ₁ ≤ L_x, 0 ≤ ξ₂ ≤ L_y}. A mapping D → E is accomplished by a transformation of coordinates ξ_i = ξ_i(x₁, x₂ (i = 1, 2). For the relatively simple flow domain under consideration, such a mapping can be defined analytically, for example, as ξ₁ = x₁ and ξ₂ = (L_y − x₂)/[L_y − s(x₁, ω)]. For more complex geometries, a stochastic mapping ξ_i = ξ_i(x₁, x₂) (i = 1, 2) and its inverse x_i = x_i(ξ₁, ξ₂) (i = 1, 2) are constructed (e.g., 10, 24) by solving Laplace’s equations,

$$\frac{{\partial }^2{x}_i}{\partial {\xi }_1^2}+\frac{{\partial }^2{x}_i}{\partial {\xi }_2^2}=0,({\xi }_1,{\xi }_2)\in E,i=1,2$$ (13)

subject to the boundary conditions

$$x_1(0,{\xi }_2)=0,x_1(L_x,{\xi }_2)=L_x,x_1({\xi }_1,0)={\xi }_1,x_1({\xi }_1,L_y)={\xi }_1;$$ (14a)

$$x_2(0,{\xi }_2)={\xi }_2,x_2(L_x,{\xi }_2)={\xi }_2,x_2({\xi }_1,0)=s,x_2({\xi }_1,L_y)=L_y.$$ (14b)

Uncertainty (randomness) in domain geometry, s(x₁, ω), manifests itself in the mapping problem through the boundary condition in Eq. 14. To facilitate numerical solution of the mapping problem given by Eqs. 13-14, one has to truncate the infinite series in the Karhunen-Loève expansion [4] after K terms. For a given accuracy, the smaller the correlation length l_s, the higher the value of K (see, e.g., 23, 24).

Solutions of Eqs. 13-14 can now be approximated by a series

$$x_i({\xi }_1,{\xi }_2,\omega )=\sum _{k=0}^K{\widehat{x}}_{i,k}({\xi }_1,{\xi }_2)Y_k\left(\omega \right),i=1,2.$$ (15)

Substituting Eq. 15 into Eq. 13 and taking a Galerkin projection yields 2(K + 1) Laplace’s equations for the coefficients ${\widehat{x}}_{i,k}({\xi }_1,{\xi }_2)$,

$$\frac{{\partial }^2{\widehat{x}}_{i,k}}{\partial {\xi }_1^2}+\frac{{\partial }^2{\widehat{x}}_{i,k}}{\partial {\xi }_2^2}=0,({\xi }_1,{\xi }_2)\in E,i=1,2,k=0,\dots ,K.$$ (16)

For k = 0, Eqs. 16 are subject to boundary conditions

$$x_{1,0}(0,{\xi }_2)=0,x_{1,0}(L_x,{\xi }_2)=L_x,x_{1,0}({\xi }_1,0)={\xi }_1,x_{1,0}({\xi }_1,L_y)={\xi }_1;$$ (17a)

$$x_{2,0}(0,{\xi }_2)={\xi }_2,x_{2,0}(L_x,{\xi }_2)={\xi }_2,x_{2,0}({\xi }_1,0)=\stackrel{‒}{s},x_{2,0}({\xi }_1,L_y)=L_y.$$ (17b)

For k ≥ 1, these boundary conditions are replaced with their homogeneous counterparts,

$$x_{1,k}(0,{\xi }_2)=0,x_{1,k}(L_x,{\xi }_2)=0,x_{1,k}({\xi }_1,0)=0,x_{1,k}({\xi }_1,L_y)=0;$$ (17c)

$$x_{2,k}(0,{\xi }_2)=0,x_{2,k}(L_x,{\xi }_2)=0,x_{2,k}({\xi }_1,L_y)=0,$$ (17d)

except for the boundary conditions

$$x_{2,k}({\xi }_1,0)={\sigma }_s\sqrt{{\lambda }_k}{\psi }_k\left({\xi }_1\right).$$ (17e)

We use a Chebyshev spectral method to solve Eqs. 16-17. A typical outcome of such calculations is shown in Figure 3 for one realization of the random surface s(x₁, ω).

A.2 Transformed Stokes equations

The procedure outlined above enables one to compute, among other things, a transformation Jacobian,

$$J({\xi }_1,{\xi }_2,\omega )\equiv \frac{\partial ({\xi }_1,{\xi }_2)}{\partial (x_1,x_2)}=J[{\xi }_1,{\xi }_2,Y_1\left(\omega \right),\dots ,Y_K\left(\omega \right)].$$ (18)

For an arbitrary twice-differentiable function f(x) defined on D,

$${\nabla }_x^{2}f\equiv {\nabla }_{\mathrm{x}}\cdot \mathbf{F}=\frac{1}{J}\left(\frac{\partial F^1}{\partial {\xi }_1}+\frac{\partial F^2}{\partial {\xi }_2}\right)\equiv \frac{1}{J}{\nabla }_{\xi }\cdot \mathbf{F}$$ (19a)

and

$${\nabla }_{\mathrm{x}}f=\frac{1}{J}\left[\left(\frac{\partial x_2}{\partial {\xi }_2}\mathbf{i}-\frac{\partial x_1}{\partial {\xi }_2}\mathbf{j}\right)\frac{\partial f}{\partial {\xi }_1}-\left(\frac{\partial x_2}{\partial {\xi }_1}\mathbf{i}-\frac{\partial x_1}{\partial {\xi }_1}\mathbf{j}\right)\frac{\partial f}{\partial {\xi }_2}\right],$$ (19b)

where i and j are the normal vectors of the (ξ₁, ξ₂) coordinate system. The contravariant components F¹ and F² of the transformed vector F(ξ) are given by

$$F^1=A\frac{\partial f}{\partial {\xi }_1}-B\frac{\partial f}{\partial {\xi }_2},F^2=-B\frac{\partial f}{\partial {\xi }_1}+C\frac{\partial f}{\partial {\xi }_2}$$ (19c)

with

$$A=\frac{1}{J}\left[{\left(\frac{\partial x_2}{\partial {\xi }_2}\right)}^2+{\left(\frac{\partial x_1}{\partial {\xi }_2}\right)}^2\right],B=\frac{1}{J}\left(\frac{\partial x_2}{\partial {\xi }_1}\frac{\partial x_2}{\partial {\xi }_2}+\frac{\partial x_1}{\partial {\xi }_1}\frac{\partial x_1}{\partial {\xi }_2}\right),C=\frac{1}{J}\left[{\left(\frac{\partial x_2}{\partial {\xi }_1}\right)}^2+{\left(\frac{\partial x_1}{\partial {\xi }_1}\right)}^2\right].$$ (19d)

Using Eqs. 19 to rewrite the Stokes Eqs. 1 in the (ξ₁, ξ₂) coordinate system, we obtain

$$\frac{\partial }{\partial {\xi }_1}\left(A\frac{\partial u_1}{\partial {\xi }_1}-B\frac{\partial u_1}{\partial {\xi }_2}\right)-\frac{\partial }{\partial {\xi }_2}\left(B\frac{\partial u_1}{\partial {\xi }_1}-C\frac{\partial u_1}{\partial {\xi }_2}\right)=\frac{1}{\mu }\left(\frac{\partial x_2}{\partial {\xi }_2}\frac{\partial p}{\partial {\xi }_1}-\frac{\partial x_2}{\partial {\xi }_1}\frac{\partial p}{\partial {\xi }_2}\right)$$ (20a)

and

$$\frac{\partial }{\partial {\xi }_1}\left(A\frac{\partial u_2}{\partial {\xi }_1}-B\frac{\partial u_2}{\partial {\xi }_2}\right)-\frac{\partial }{\partial {\xi }_2}\left(B\frac{\partial u_2}{\partial {\xi }_1}-C\frac{\partial u_2}{\partial {\xi }_2}\right)=\frac{1}{\mu }\left(\frac{\partial x_1}{\partial {\xi }_2}\frac{\partial p}{\partial {\xi }_2}-\frac{\partial x_1}{\partial {\xi }_2}\frac{\partial p}{\partial {\xi }_1}\right).$$ (20b)

The Stokes and continuity Eqs. 1 imply that ${\nabla }_{\mathrm{x}}^{2}p=0$. When written in the (ξ₁, ξ₂) coordinate system, this equation takes the form

$$\frac{\partial }{\partial {\xi }_1}\left(A\frac{\partial p}{\partial {\xi }_1}-B\frac{\partial p}{\partial {\xi }_2}\right)-\frac{\partial }{\partial {\xi }_2}\left(B\frac{\partial p}{\partial {\xi }_1}-C\frac{\partial p}{\partial {\xi }_2}\right)=0.$$ (21)

The transformed flow Eqs. 19-21 are stochastic, i.e., have random co-efficients. The theory of stochastic differential equations defined on deterministic domains is relatively mature. Their solutions can be obtained with a variety of well-established techniques, including perturbation-based moment equations (20), stochastic finite elements (4), and stochastic collocation methods (11, and the references therein). In the subsequent numerical simulations we employ a stochastic finite element method, which is also known as the generalized polynomial chaos expansion (24).

A.3 Solution of stochastic flow equations

Let ${\left\{{\Psi }_m\left(\mathbf{Y}\right)\right\}}_{m=0}^M$ denote a set of multidimensional orthogonal polynomials of the random vector Y(ω) (Y₁, …, Y_K)^T of the K independent random variables Y₁(ω), …, Y_K(ω) introduced in Eqs. 4 and 15. The polynomials are chosen to have the ensemble means ${\overline{\Psi }}_0=1$ and ${\overline{\Psi }}_k=0$ (k ≥ 1) and satisfy the orthogonality condition

$$\overline{{\Psi }_i{\Psi }_j}=\overline{{\Psi }_i^2}{\delta }_{ij},\overline{{\Psi }_i{\Psi }_j}\equiv \int {\Psi }_i\left(\mathbf{Y}\right){\Psi }_j\left(\mathbf{Y}\right)W\left(\mathbf{Y}\right)\mathrm{d}{Y}_1\dots \mathrm{d}{Y}_K,$$ (22)

where δ_ij is the Kronecker delta and W(Y) is a weight function corresponding to a given polynomial type.

The size of the polynomial set, M, is determined by the “stochastic dimension” K and the order P of polynomials Ψ_k, according to

$$M=\frac{(K+P)!}{K!P!}-1.$$ (23)

Polynomial chaos expansions (PCEs) represent a system state, e.g., pressure p(ξ, ω), a random field whose ensemble statistics are to be determined, as a series

$$p(\xi ,\omega )=\sum _{k=0}^M{\widehat{p}}_k\left(\xi \right){\Psi }_k\left[\mathbf{Y}\left(\omega \right)\right].$$ (24)

Similar expansions are employed for the other two state variables, u₁(ξ, ω) ≡ u(ξ, ω) and u₂(ξ, ω) ≡ v(ξ, ω). Following the Galerkin projection procedure outlined in the Appendix, we obtain a set of deterministic equations for the coefficients ${\left\{{\widehat{p}}_k\left(\xi \right)\right\}}_{k=0}^M,{\left\{{\widehat{u}}_k\left(\xi \right)\right\}}_{k=0}^M$ and ${\left\{{\widehat{v}}_k\left(\xi \right)\right\}}_{k=0}^M$,

$$\sum _{j,k=0}^M{\mathcal{C}}_{ijk}\left[\frac{\partial }{\partial \xi }\left({\widehat{A}}_k\frac{\partial {\widehat{u}}_j}{\partial \xi }-{\widehat{B}}_k\frac{\partial {\widehat{u}}_j}{\partial \eta }\right)+\frac{\partial }{\partial \eta }\left({\widehat{C}}_k\frac{\partial {\widehat{u}}_j}{\partial \eta }-{\widehat{B}}_k\frac{\partial {\widehat{u}}_j}{\partial \xi }\right)\right]=\frac{1}{\mu }\sum _{j,k=1}^M{\mathcal{C}}_{ijk}\left({\widehat{D}}_k\frac{\partial {\widehat{p}}_j}{\partial \xi }-{\widehat{E}}_k\frac{\partial {\widehat{p}}_j}{\partial \eta }\right)$$ (25)

$$\sum _{j,k=0}^M{\mathcal{C}}_{ijk}\left\{\frac{\partial }{\partial \xi }\left({\widehat{A}}_k\frac{\partial {\widehat{v}}_j}{\partial \xi }-{\widehat{B}}_k\frac{\partial {\widehat{v}}_j}{\partial \eta }\right)+\frac{\partial }{\partial \eta }\left({\widehat{C}}_k\frac{\partial {\widehat{v}}_j}{\partial \eta }-{\widehat{B}}_k\frac{\partial {\widehat{v}}_j}{\partial \xi }\right)\right\}=\frac{1}{\mu }\sum _{j,k=0}^M{\mathcal{c}}_{ijk}\left(-{\widehat{F}}_k\frac{\partial {\widehat{p}}_j}{\partial \xi }+{\widehat{G}}_k\frac{\partial {\widehat{p}}_j}{\partial \eta }\right)$$ (26)

$$\sum _{j,k=0}^M{\mathcal{C}}_{ijk}\left\{\left({\widehat{D}}_k\frac{\partial {\widehat{u}}_j}{\partial \xi }-{\widehat{E}}_k\frac{\partial {\widehat{u}}_j}{\partial \eta }\right)+\left(-{\widehat{F}}_k\frac{\partial {\widehat{v}}_j}{\partial \xi }+{\widehat{G}}_k\frac{\partial {\widehat{v}}_j}{\partial \eta }\right)\right\}=0$$ (27)

$$\sum _{j,k=0}^M{\mathcal{C}}_{ijk}\left[\frac{\partial }{\partial \xi }\left({\widehat{A}}_k\frac{\partial {\widehat{p}}_j}{\partial \xi }-{\widehat{B}}_k\frac{\partial {\widehat{p}}_j}{\partial \eta }\right)+\frac{\partial }{\partial \eta }\left({\widehat{C}}_k\frac{\partial {\widehat{p}}_j}{\partial \eta }-{\widehat{B}}_k\frac{\partial {\widehat{p}}_j}{\partial \xi }\right)\right]=0.$$ (28)

Here $C_{ijk}\equiv \overline{{\Psi }_i{\Psi }_j{\Psi }_k}$, $A={\Sigma }_k^M{\widehat{A}}_k{\Psi }_k$, and ${\widehat{B}}_k$, ${\widehat{C}}_k$, ${\widehat{D}}_k$, ${\widehat{E}}_k$, ${\widehat{F}}_k$, ${\widehat{G}}_k$ are coefficients in the similar expansions of B, C, D, E, F, and G, respectively.

Algebraic Eqs. 25-28 were solved by using a spectral collocation method.

B Stochastic Galerkin Method

A good introduction to stochastic finite elements can be found in (4). Here we provide a brief description. Let L(ξ, ω; u) denote a stochastic differential operator acting on u(ξ, ω). Consider a stochastic partial differential equation (PDE)

$$\mathcal{L}(\xi ,\omega ;u)=f(\xi ,\omega ),$$ (29)

where f is a (random) source function. Substituting the polynomial chaos expansion of u, Eq. 24, into Eq. 29 yields

$$\mathcal{L}\left(\xi ,\omega ;\sum _{k=0}^M{\widehat{u}}_k{\Psi }_k\right)=f(\xi ,\omega ).$$ (30)

Multiplying both sides of Eq. 30 with ψ_i and taking the mean, while accounting for the orthogonality condition in Eq. 22, yields a Galerkin projection onto the i-th basis polynomial ψ_i,

$$\langle \mathcal{L}\left(\xi ,\omega ;\sum _{k=0}^M{\widehat{u}}_k{\Psi }_k\right),{\Psi }_i\rangle =\langle f(\xi ,\omega ),{\Psi }_i\rangle ,i=0,\dots ,M.$$ (31)

Here the inner product 〈a, b〉 between two functions a(Y) and b(Y) is defined in terms of the ensemble average $\overline{ab}$ in Eq. 22. Equation 31 gives rise to a system of M + 1 deterministic PDEs for ${\widehat{u}}_k\left(\mathbf{x}\right)$ (k = 0, …, M).