Economic Analysis of the Use of Facemasks During Pandemic (H1N1) 2009

Abstract

A large-scale pandemic could cause severe health, social, and economic impacts. The recent 2009 H1N1 pandemic confirmed the need for mitigation strategies that are cost-effective and easy to implement. Typically, in the early stages of a pandemic, as seen with pandemic (H1N1) 2009, vaccines and antivirals may be limited or non-existent, resulting in the need for non-pharmaceutical strategies to reduce the spread of disease and the economic impact. We construct and analyze a mathematical model for a population comprised of three different age groups and assume that some individuals wear facemasks. We then quantify the impact facemasks could have had on the spread of pandemic (H1N1) 2009 and examine their cost effectiveness. Our analyses show that an unmitigated pandemic could result in losses of nearly $832 billion in the United States during the length of the pandemic. Based on present value of future earnings, hospital costs, and lost income estimates due to illness, this study estimates that the use of facemasks by 10%, 25%, and 50% of the population could reduce economic losses by $478 billion, $570 billion, and $573 billion, respectively. The results show that facemasks can significantly reduce the number of influenza cases as well as the economic losses due to a pandemic.

1. Introduction

On June 11, 2009, the World Health Organization (WHO) declared the outbreak of novel influenza A (H1N1) (referred to as pandemic (H1N1) 2009 per WHO nomenclature) a pandemic. The emergence of an unexpected or novel strain of influenza poses problems in combating the spread of infection. Vaccines are typically the first line of defense against influenza viruses (Germann et al., 2006), however, in the case of novel viruses vaccines may not be readily available. In addition to vaccines, public health campaigns encouraging good hygiene have been used to reduce the spread of influenza.

During the pandemic (H1N1) 2009 outbreak several non-pharmaceutical mitigation strategies were used including school closures, social distancing, and facemasks (Condon and Sinha, 2009). Influenza spreads through person-to-person contact via airborne particles as well as by direct and indirect (e.g., via fomites) contacts. Several studies have shown that facemasks can be an effective mitigation strategy. A recent study on facemasks and hand hygiene showed a 10 – 50% transmission reduction for influenza-like illnesses (Aiello et al., 2010). Other studies have also shown that facemasks can not only act as a barrier (Del Valle et al., 2010) but they can redirect and decelerate exhaled air flows to prevent them from entering the breathing zones of others (Tang and Settles, 2009). Several laboratory studies on mask effectiveness have shown that N95 respirators are 21.5% effective in protecting against the inhalation of nanoparticles, while surgical masks were only 2.4% effective (an Lee et al., 2008). However, a study by Loeb et al. (Loeb et al., 2009) found that surgical masks and N95 respirators offered about the same percentage of protection for nurses in hospitals. Although several studies have shown that both surgical masks and N95 provide similar protection against influenza, a recent editorial by Killingley (Killingley, 2011) discusses two studies and argues that the results are still inconclusive and that more research is needed. For our model we will focus on N95 respirators since we are interested in analyzing optimal interventions, however, our analyses may be applicable to surgical masks based on Loeb et al. (Loeb et al., 2009) results.

Using a mathematical model, Tracht et al. (Tracht et al., 2010) analyzed the effectiveness of facemasks in reducing the spread of pandemic (H1N1) 2009. They compared the impact that surgical and N95 masks could have on reducing the spread of influenza. Their results showed that facemasks can be an effective intervention strategy for mitigating an airborne disease. We expand upon that model by dividing the population into three age groups and quantifying the impact of facemasks (also referred to as N95 respirators) have on the spread of the disease as well as their cost effectiveness.

2. Methods

Following the approaches developed in (Del Valle et al., 2005) and (Tracht et al., 2010), the population is divided into two subgroups: a mask-wearing group (subscript M) and a non-mask wearing group. People alternate between mask and non-mask groups based on the number of individuals infected with pandemic (H1N1) 2009. We also separate the population into three different age group classifications: children between ages 0–17 (superscript 1), adults between ages 18–64 (superscript 2), and seniors older than 65 (superscript 3). Individuals are characterized by their epidemiological status: susceptible, S^k and $S_M^k$, exposed, E^k and $E_M^k$ (i.e., people who are infected but not yet fully contagious), and infectious individuals, I^k and $I_M^k$, where k = 1 (ages 0–17), 2 (ages 18–64) and 3 (ages 65+). Definitions of the epidemiological classes are summarized in Table 1 and the transfers are shown diagrammatically in Figure 1. Because we are evaluating the potential economic impact of masks during the pandemic (H1N1) 2009 outbreak, we use a closed system with no migration in or out; births and natural deaths are not included in the model.

Table 1.

State variables and definitions for the model.

Variable	Definition
Sk	Number of susceptible individuals not wearing a mask in age group k
$S_M^k$	Number of susceptible individuals wearing a mask in age group k
Ek	Number of exposed individuals not wearing a mask in age group k
$E_M^k$	Number of exposed individuals wearing a mask in age group k
Ik	Number of infected individuals not wearing a mask in age group k
$I_M^k$	Number of infected individuals wearing a mask in age group k
Hk	Number of hospitalized individuals in age group k
Rk	Number of recovered individuals in age group k
Dk	Number of dead individuals in age group k

Figure 1. Schematic relationship between mask wearing and non-mask wearing individuals for pandemic (H1N1) 2009.

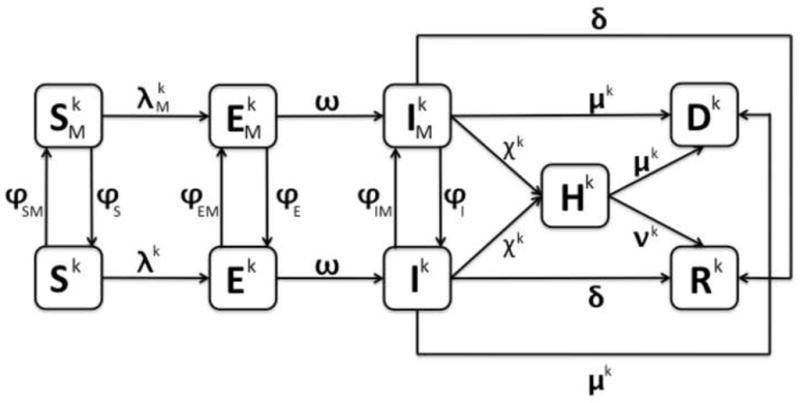
Note there are three different diagrams represented: k = 1 (ages 0–17), 2 (ages 18–64), and 3 (ages 65+). The arrows connecting the boxed groups represent the movement of individuals from one group to an adjacent one. Susceptible individuals (S^k or $S_M^k$) can either become exposed (E^k or $E_M^k$) or move between the non-mask wearing (S^k) or mask wearing ( $S_M^k$) susceptible groups. Exposed individuals (E^k or $E_M^k$) can either become infectious (I^k or $I_M^k$) or move between the non-mask wearing (E^k) and mask wearing ( $E_M^k$) exposed groups. Infectious individuals (I^k or $I_M^k$) can recover (R^k), die (D^k), be hospitalized (H^k), or move between non-mask wearing (I^k) and mask wearing ( $I_M^k$) infectious groups. Hospitalized individuals can either recover (R^k) or die (D^k).

As seen in Figure 1, the transfer rates from the exposed classes, E^k and $E_M^k$, to the infectious classes, I^k and $I_M^k$, are ωE^k and $\omega E_M^k$, respectively. Infectious individuals can move to group D^k at rate μ^kI^k and ${\mu }^k{I}_M^k$ when they die from infection to group R^k, at rate δI^k and $\delta I_M^k$ upon recovery, or to group H^k at rate of χ^kH^k and ${\chi }^k{H}_M^k$ if they are hospitalized. Those individuals who are hospitalized either recover at a rate of ν^kH^k or die at a rate of μ^kH^k. The mean times in the infectious classes, I^k and $I_M^k$, are 1/(μ^k+δ+χ^k). Hence, the infectious fraction δ/(μ^k+δ+χ^k) recovers and the infectious fraction μ^k/(μ^k+δ+χ^k) dies as a consequence of the disease.

We assume homogenous mixing within each age group and heterogeneous mixing between groups; the mixing matrix containing the average number of daily contacts an individual from group k has with group j is shown in Table 2. We also assume that contact levels remain normal throughout the epidemic, except that the average number of daily contacts for hospitalized individuals is reduced by 1/3. We define t₀ as the beginning of the epidemic. Movement of individuals between mask and non-mask groups depends upon the number of pandemic (H1N1) 2009 cases in the population, that is, a specified percentage of the population starts wearing masks as the number of infected people increases.

Table 2. Mixing matrix.

The average number of daily contacts age group k has with age group j (Del Valle et al., 2007).

Age	Children (0–17)	Adults (18–64)	Seniors (65+)
Children (0–17)	23.3824	31.7305	1.9396
Adults (18–64)	7.9593	37.1030	3.4924
Seniors (65+)	3.1534	21.8981	7.6981

We define ϕ_SMS^k, ϕ_EME^k, and ϕ_IMI^k to be the transfer rates from the S^k, E^k, and I^k classes to the $S_M^k,E_M^k$, and $I_M^k$ classes, respectively; similarly ${\varphi }_S{S}_M^k,{\varphi }_E{E}_M^k$, and ${\varphi }_I{I}_M^k$ are the transfer rates from the $S_M^k,E_M^k$, and $I_M^k$ to the S^k, E^k, and I^k, respectively.

The rate coefficients are modeled by step-functions of the number of infectious individuals in the population:

$${\varphi }_r=\{\begin{array}{ll}{a}_r,\hfill & 0\le \sum _{k=1}^n(I^k+I_M^k)\le \tau \hfill \\ b_r,\hfill & \tau <\sum _{k=1}^n(I^k+I_M^k)\hfill \end{array}$$ (1)

for $r=S^k,E^k,I^k,S_M^k,E_M^k$, and $I_M^k$ and k = 1 (ages 0–17), 2 (ages 18–64) and 3 (ages 65+), where the parameters a and b are positive constants that determine the rate of movement and τ is the number of pandemic (H1N1) 2009 cases that determines when masks are implemented.

Using the transfer diagram shown in Figure 1, we obtain the following system of differential equations:

$$\begin{array}{l}\frac{{dS}_M^k}{dt}=-({\varphi }_S+{\lambda }_M^k)S_M^k+{\varphi }_{S_M}{S}^k\\ \frac{{dE}_M^k}{dt}=-({\varphi }_E+\omega )E_M^k+{\lambda }_M^k{S}_M^k+{\varphi }_{E_M}{E}^k\\ \frac{{dI}_M^k}{dt}=-({\varphi }_I+{\mu }^k+\delta +{\chi }^k)I_M^k+\omega E_M^k+{\varphi }_{I_M}{I}^k\\ \frac{{dS}^k}{dt}=-({\varphi }_{S_M}+{\lambda }^k)S^k+{\varphi }_S{S}_M^k\\ \frac{{dE}^k}{dt}=-({\varphi }_{E_M}+\omega )E^k+{\lambda }^k{S}^k+{\varphi }_E{E}_M^k\\ \frac{{dI}^k}{dt}=-({\varphi }_{I_M}+{\mu }^k+\delta +{\chi }^k)I^k+\omega E^k+{\varphi }_I{I}_M^k\\ \frac{{dH}^k}{dt}=-({\mu }^k+{\nu }^k)H^k+(I_M^k+I^k){\chi }^k\\ \frac{{dR}^k}{dt}=(I_M^k+I^k)\delta +{\nu }^k{H}^k\\ \frac{{dD}^k}{dt}=(I_M^k+I^k){\mu }^k+{\mu }^k{H}^k\end{array}$$ (2)

where k = 1, 2, and 3. Note that there is a system of nine equations for each of the three age groups, resulting in a system of 27 differential equations.

Here λ^k (non-mask groups) and ${\lambda }_M^k$ (mask groups) are the forces of infection and λ^kS^k and ${\lambda }_M^k{S}_M^k$ are the transfer rates from the susceptible classes, S^k and $S_M^k$, to the exposed classes, E^k and $E_M^k$. There are six different infection rates, λ^k and ${\lambda }_M^k$ for each of the three age groups, which incorporate the probability of transmission per contact from an individual in age group k to an individual in age group j (β^kj); the reduced infectiousness due to incubation (α), and 1 − η_t (t = i or s), which accounts for the effectiveness of the mask in reducing either susceptibility (η_s) or infectivity (η_i). The transmissibility, β^kj, is defined as the susceptibility of the population, multiplied by the infectivity of the disease, multiplied by the average number of contacts an individual has per day. The definitions of the parameters are summarized in Table 3. The forces of infection for the non-mask group and mask group are given by:

$$\begin{array}{r}{\lambda }_l^k(t)=\sum _{j=1}^n{\lambda }_l^{kj}(t)\\ l=\{\begin{array}{ll}\text{No}\text{Mask},\hfill & {\eta }_s=0\hfill \\ \text{Mask},\hfill & {\eta }_s\ne 0\hfill \end{array}\end{array}$$ (3)

Table 3.

Parameter values and descriptions

Parameter	Description	Units	Baseline	Range	Reference
N1	Population of age group 1 (0–17)	People	73,000,000	1–100 million	36
N2	Population of age group 2 (18–64)	People	191,000,000	1–250 million	36
N3	Population of age group 3 (65+)	People	38,000,000	1–50 million	36
${\mathfrak{R}}_{\mathit{unc}}^1$	Effective reproduction number (uncontrolled) for age group 1 (0–17)	1	1.3 & 1.35 & 1.4	0–2	35; 32; 40; 29
${\mathfrak{R}}_{\mathit{unc}}^2$	effective reproduction number (uncontrolled) for age group 2 (18–64)	1	1.25 & 1.3 & 1.35	0–2	35; 32; 40; 29
${\mathfrak{R}}_{\mathit{unc}}^3$	effective reproduction number (uncontrolled) for age group 3 (65+)	1	1.2 & 1.25 & 1.3	0–2	35; 32; 40; 29
${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}$	Average effective reproduction number (uncontrolled)	1	1.25 & 1.3 & 1.35	0–2	35; 32; 40; 29
βkj	Transmission rate from age group k to age group j	1	See Text	0–1	See Text
κkj	Average number of contacts age group k has with age group j	$\frac{\mathit{People}}{\mathit{Day}}$	See Text	0–40	16
ξk	Infectivity of age group k	1	See Text	0–1	See Text
ιj	Susceptibility of age group j	1	1	0–1	8; 39
ω	Incubation relative rate	Day−1	0.25	0–1	35; 10
δ	Non-hospitalized recovery relative rate	Day−1	0.20	0–1	10
ν1	Hospitalized recovery rate relative for age group 1 (0–17)	Day−1	$\frac{1}{5}$	0–1	27
ν2	Hospitalized recovery rate relative for age group 2 (18–64)	Day−1	$\frac{1}{8}$	0–1	27
ν3	Hospitalized recovery rate relative for age group 3 (65+)	Day−1	$\frac{1}{10}$	0–1	27
μ1	Death relative rate for age group 1 (0–17)	Day−1	0.0000192	0–1	11; 32
μ2	Death relative rate for age group 2 (18–64)	Day−1	0.0008224	0–1	11; 32
μ3	Death relative rate for age group 3 (65+)	Day−1	0.00008102	0–1	11; 32
χ1	Hospitalization relative rate for age group 1 (0–17)	Day−1	0.00435	0–1	11
χ2	Hospitalization relative rate for age group 2 (18–64)	Day−1	0.00457	0–1	11
χ3	Hospitalization relative rate for age group 3 (65+)	Day−1	0.0045	0–1	11
θ	Reduced contacts due to hospitalization	1	$\frac{1}{3}$	0–1	See Text
α	Reduced infectiousness due to incubation	1	0.5	0–1	See Text
ηi	Decrease in infectivity because of mask	1	0.20	0–1	24; 1
ηs	Decrease in susceptibility because of mask	1	0.50	0–1	24; 1
τ	Number of infectious individuals at which masks are implemented	People	30,200	30,200	See Text
ar	Positive constant that determines the rate of movement between mask and non-mask classes	1	0	0–1	See Text
br	Positive constant that determines the rate of movement between mask and non-mask classes	1	0.1	0–1	See Text
ϕr	Movement rate between mask and non-mask classes, r = S, SM, E, EM, I, IM	1	See Text	0–1	See Text, 13
I1/N1	Initially infected fraction of population of age group 1	1	$\frac{1,800}{73,000,000}$	0–1	15
I2/N2	Initially infected fraction of population of age group 2	1	$\frac{2,000}{191,000,000}$	0–1	15
I3/N3	Initially infected fraction of population of age group 3	1	$\frac{100}{38,000,000}$	0–1	15

We define ${\lambda }_l^{kj}$ in (3) as the product of the transmissibility of a disease, β^kj, and the fraction of contacts that are infected. β^kj is the product of the average number of contacts per unit time that each individual in age group k has with age group j, κ_kj; the susceptibility of the population, which is set to 1 for children and adults and 0.85 for seniors (Center for Disease Control and Prevention, 2009b; Xing and Cardona, 2009), ι_j; and the infectivity of the disease for age group k, ξ_k. That is:

$$\begin{array}{c}{\lambda }_l^{kj}=\left(\begin{array}{c}\text{Number}\text{of}\\ \text{Contacts}\text{per}\\ \text{Unit}\text{Time}\end{array}\right)X\left(\begin{array}{c}\text{Susceptibility}\\ \text{of}\text{the}\\ \text{Population}\end{array}\right)X\left(\begin{array}{c}\text{Infectivity}\\ \text{of}\text{the}\\ \text{Disease}\end{array}\right)X\left(\begin{array}{c}\text{Fraction}\text{of}\\ \text{Contacts}\text{that}\\ \text{are}\text{Infected}\end{array}\right)\\ {\lambda }_l^{kj}(t)=({\kappa }_{kj})\text{x}({\iota }_j)\text{x}({\xi }_k)\text{x}\left[(1-{\eta }_s)\left(\frac{I^j+\alpha E^j+(1-\theta )H^j}{N}\right)+(1-{\eta }_s)(1-{\eta }_i)\left(\frac{I_M^j+\alpha E_M^j}{N}\right)\right]\end{array}$$ (4)

where N is the total population.

3. Effective Reproduction Number, ℜ_eff

The effective reproduction number, ℜ_eff, is the average number of secondary cases produced by a typical infectious individual during the infectious period (Hethcote, 2000; van den Driessche and Watmough, 2002). The success of mitigation strategies is measured by their ability to reduce the spread of disease. In an epidemic model the magnitude of the effective reproduction number, ℜ_eff, determines whether an epidemic occurs and its severity (Del Valle et al., 2005). When ℜ_eff > 1, the disease will spread and an epidemic will occur, however, when ℜ_eff < 1, the disease will die out (Del Valle et al., 2005; Tracht et al., 2010).

Each individual age group has a unique initial effective reproduction number denoted ${\mathfrak{R}}_{\mathit{eff}}^k$, however, when we average these three values, we obtain an average effective reproduction number, ${\mathfrak{R}}_{\mathit{eff}}^{\mathit{avg}}$, for the entire model. Without any intervention strategies in place, the model has an initial average effective reproduction number (uncontrolled), ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}$.

The ‘next generation operator’ approach (van den Driessche and Watmough, 2002) can be used to find an expression for the effective reproduction number (controlled), ℜ_con, to determine the effectiveness of masks as an intervention strategy. This is done by linearizing the system of equations (3) around the disease-free equilibrium (DFE). The DFE has E^k, $E_M^k$, I^k, $I_M^k$, and H^k equal to zero with S^0_k, $S_M^{0_k}$, and R^0_k positive, where k = 1, 2, and 3. The resulting 15-dimensional linearized system is of the form $\frac{dX}{dt}=(F-V)X$, where

$$X={[\begin{array}{ccccccccccccccc}{E}^1& E_M^1& I^1& I_M^1& H^1& E^2& E_M^2& I^2& I_M^2& H^2& E^3& E_M^3& I^3& I_M^3& H^3\end{array}]}^T$$

The F matrix is a 15 × 15 matrix that can be described in blocks of 5 × 5 with the first two rows having nonzero entries in every column and the third, fourth, and fifth rows containing all zeros. The first two rows are of the form:

$$\frac{1}{\sigma }\left[\begin{array}{lllll}{\beta }^{kj}{S}^{0_k}\alpha \hfill & {\beta }^{kj}{S}^{0_k}\alpha m_i\hfill & {\beta }^{kj}{S}^{0_k}\hfill & {\beta }^{kj}{S}^{0_k}{m}_i\hfill & {\beta }^{kj}{S}^{0_k}(1-\theta )\hfill \\ {\beta }^{kj}{S}_M^{0_k}\alpha m_s\hfill & {\beta }^{kj}{S}_M^{0_k}\alpha m_s{m}_i\hfill & {\beta }^{kj}{S}_M^{0_k}{m}_s\hfill & {\beta }^{kj}{S}_M^{0_k}{m}_s{m}_i\hfill & {\beta }^{kj}{S}_M^{0_k}{m}_s(1-\theta )\hfill \end{array}\right]$$

where k and j represent the three age group classifications, k = 1, 2, and 3 and j = 1, 2, and 3, m_s = 1 − η_s, m_i = 1 − η_i, and $\sigma =S^{0_1}+S_M^{0_1}+S^{0_2}+S_M^{0_2}+S^{0_3}+S_M^{0_3}$. The V matrix is block diagonal with 5 × 5 blocks of the form:

$$B=\left[\begin{array}{ccccc}{\varphi }_{E_M}+\omega & -{\varphi }_E& 0& 0& 0\\ -{\varphi }_{E_M}& {\varphi }_E+\omega & 0& 0& 0\\ -\omega & 0& {\varphi }_{I_M}+{\mu }^k+\delta & -{\varphi }_I& 0\\ 0& -\omega & -{\varphi }_{I_M}& {\varphi }_I+{\mu }^k+\delta & 0\\ 0& 0& -{\chi }^k& -{\chi }^k& {\mu }^k+{\nu }^k\end{array}\right]$$

which has an inverse of the form:

$$B^{-1}=\left[\begin{array}{ccccc}\frac{{\varphi }_E+\omega }{{\gamma }_1\omega }& \frac{{\varphi }_E}{{\gamma }_1\omega }& 0& 0& 0\\ \frac{{\varphi }_{E_M}}{{\gamma }_1\omega }& \frac{{\varphi }_{E_M}+\omega }{{\gamma }_1\omega }& 0& 0& 0\\ \frac{{\varphi }_E+\omega }{{\gamma }_1{\gamma }_2}+\frac{{\varphi }_I}{{\gamma }_2{\gamma }_3}& \frac{{\varphi }_E}{{\gamma }_1{\gamma }_2}+\frac{{\varphi }_I}{{\gamma }_2{\gamma }_3}& \frac{{\varphi }_I+{\mu }^k+\delta }{{\gamma }_2{\gamma }_3}& \frac{{\varphi }_I}{{\gamma }_2{\gamma }_3}& 0\\ \frac{{\varphi }_{E_M}}{{\gamma }_1{\gamma }_2}+\frac{{\varphi }_{IM}}{{\gamma }_2{\gamma }_3}& \frac{{\varphi }_{E_M}+\omega }{{\gamma }_1{\gamma }_3}+\frac{{\varphi }_{I_M}}{{\gamma }_2{\gamma }_3}& \frac{{\varphi }_{I_M}}{{\gamma }_2{\gamma }_3}& \frac{{\varphi }_{I_M}+{\mu }^k+\delta }{{\gamma }_2{\gamma }_3}& 0\\ \frac{{\chi }^k}{{\gamma }_3{\gamma }_4}& \frac{{\chi }^k}{{\gamma }_3{\gamma }_4}& \frac{{\chi }^k}{{\gamma }_3{\gamma }_4}& \frac{{\chi }^k}{{\gamma }_3{\gamma }_4}& \frac{1}{{\gamma }_4}\end{array}\right]$$

where γ₁ = ϕ_E+ϕ_EM+ω, γ₂ = ϕ_IM+ϕ_I+μ^k+δ, γ₃ = μ^k+δ, and γ₄ = ν^k+μ^k.

FV⁻¹ will have zeros in rows 3, 4, 5, 8, 9, 10, 13, 14, and 15, so the eigenvectors must also have zeros in these rows. Thus, the 15 × 15 matrix consists of the rows 5(f − 1) + 1, 2 and columns 5(g − 1) + 1, 2. This matrix E = FV⁻¹ will have fg blocks of 5 × 5, with entries given by:

$$\left[\begin{array}{lllll}{\rho }_1\left(\frac{\alpha }{\omega }{\psi }_1+\frac{{\psi }_1}{{\gamma }_2}+{\psi }_2+\epsilon \right)\hfill & {\rho }_1\left(\frac{\alpha }{\omega }{\psi }_{1M}+\frac{{\psi }_{1M}}{{\gamma }_2}+{\psi }_2+\epsilon \right)\hfill & {\rho }_1({\psi }_3+\epsilon )\hfill & {\rho }_1({\psi }_{3M}+\epsilon )\hfill & {\rho }_1\epsilon \hfill \\ {\rho }_2\left(\frac{\alpha }{\omega }{\psi }_1+\frac{{\psi }_1}{{\gamma }_2}+{\psi }_2+\epsilon \right)\hfill & {\rho }_2\left(\frac{\alpha }{\omega }{\psi }_{1M}+\frac{{\psi }_{1M}}{{\gamma }_2}+{\psi }_2+\epsilon \right)\hfill & {\rho }_2({\psi }_3+\epsilon )\hfill & {\rho }_2({\psi }_{3M}+\epsilon )\hfill & {\rho }_2\epsilon \hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \\ 0\hfill & 0\hfill & 0\hfill & 0\hfill & 0\hfill \end{array}\right]$$

where ${\rho }_1=\frac{{\beta }^{kj}{S}^{0_k}}{\sigma },{\rho }_2=\frac{{\beta }^{kj}{S}_M^{0_k}(1-{\eta }_s)}{\sigma },{\psi }_1=\frac{{\varphi }_E+\omega +{\varphi }_{E_M}(1-{\eta }_i)}{{\gamma }_1},{\psi }_{1_M}=\frac{{\varphi }_E+(1-{\eta }_i)({\varphi }_{E_M}+\omega )}{{\gamma }_1},{\psi }_2=\frac{{\varphi }_I+{\varphi }_{I_M}(1-{\eta }_i)}{{\gamma }_2{\gamma }_3},{\varphi }_3=\frac{{\varphi }_I+{\mu }^k+\delta +{\varphi }_{I_M}(1-{\eta }_i)}{{\gamma }_2{\gamma }_3},{\varphi }_{3_M}=\frac{{\varphi }_I+({\varphi }_{I_M}+{\mu }^k+\delta )(1-{\eta }_i)}{{\gamma }_3{\gamma }_3}$, and $\epsilon =\frac{(1-\theta ){\chi }^k}{{\gamma }_3{\gamma }_4}$.

The effective reproduction number ℜ_con is the largest eigenvalue of the matrix E = FV⁻¹ (van den Driessche and Watmough, 2002). We cannot obtain an explicit form of the ℜ_con for our model, thus we estimated ℜ_con numerically for a specific set of parameter values and initial population size for the three different age groups. The resulting ℜ_con is an average of the three different age groups ℜ_con, thus we refer to it as ${\mathfrak{R}}_{\mathit{con}}^{\mathit{avg}}$.

4. Estimation of Parameter Values

While the use of facemasks and our model can be applicable to other viral respiratory infections, we use pandemic (H1N1) 2009 parameter values. The epidemiology of pandemic (H1N1) 2009 has been estimated by several researchers since the outbreak in May 2009 (Tuite et al., 2010; Tang et al., 2010; Yang et al., 2009; Pourbohloul et al., 2009; Center for Infectious Disease Research and Policy, 2010; Centers for Disease Control and Prevention, 2010; Xing and Cardona, 2009; Center for Disease Control and Prevention, 2009b). The parameter values shown in Table 3 were selected based on the most recent and best available data. The incubation period for pandemic (H1N1) 2009 has been reported to be one to four days with a mean of four days (Tuite et al., 2010; Center for Infectious Disease Research and Policy, 2010). The mean time in the exposed classes, E^k and $E_M^k$, corresponding to the incubation period has been assumed to be 4 days, making the transfer rate to the infectious classes, I^k and $I_M^k$, constant at ω=1/4.

The infectious period is believed to be between one and seven days, with an average of five days (Tuite et al., 2010; Center for Infectious Disease Research and Policy, 2010). Thus making the baseline value for the recovery rate constant at δ=1/5. The fatality rate of pandemic (H1N1) 2009 varies depending on age and is thought to be in the range of 0.001%–0.3% for all age groups, with a mean of 0.0064% for ages 0–17, 0.02734% for ages 18–64, and 0.027% for ages 65+ (Centers for Disease Control and Prevention, 2010; Tuite et al., 2010; Writing Committee of the WHO Consultation on Clinical Aspects of Pandemic (H1N1) 2009 Influenza, 2010; Tang et al., 2010). The case fatality rate for our model is μ^k/(μ^k+δ), setting this equal to 0.0064%, 0.02734%, and 0.027% results in μ¹=0.0000192, μ²=0.0008224, and μ³=0.00008102, respectively.

The estimates for the transmission of pandemic (H1N1) 2009 indicate that one infected person typically infected one to two people (Tuite et al., 2010; Tang et al., 2010; Yang et al., 2009; Pourbohloul et al., 2009). The transmissibility, β^kj, is the product of the susceptibility of the population, the infectivity of the disease, and the average number of daily contacts (Stroud et al., 2006; Chowell et al., 2006). The susceptibility of the population is set to one for children (0–17) and adults (18–64), as pandemic (H1N1) 2009 was a novel virus, and at 0.835 for seniors (65+), since it is believed about 33% of the senior population has existing immunity that correlates to a 50% reduction in susceptibility to pandemic (H1N1) 2009 (Xing and Cardona, 2009; Center for Disease Control and Prevention, 2009b). The number of contacts an individual from age group k has with age group j can be found in Table 2, (Del Valle et al., 2007). The infectivity of the disease is estimated numerically.

Consistent with the U.S. Census Bureau, the baseline population size, N, for the model is set at 302 million people, all of whom are initially in the susceptible class, S^k, depending on age group classification. The model uses a baseline population of 73 million for children (ages 0–17), N₁; 191 million for adults (ages 18–64), N₂; and 38 million for seniors (ages 65+), N₃. The initially infected fractions I¹/N₁, I²/N₂, and I³/N₃ are set at 1,800/73,000,000, 2,000/191,000,000, and 100/38,000,000 respectively. We assume that individuals start wearing masks after there are 30,200 (or 0.001% of the population) cases of pandemic (H1N1) 2009 present in the population. We analyze the impact of mask implementation when 10%, 25%, and 50% of the population wear masks. We use a baseline value of η_s=0.2 and η_i=0.5 for the effectiveness of N95 respirators (Tracht et al., 2010). Individuals in the exposed classes, E^k and $E_M^k$, are thought to be less infectious due to incubation than those individuals who are in the infectious classes, I^k and $I_M^k$, so we set a=0.5 (Hayden et al., 1998; Atkinson and Wein, 2008).

5. Results

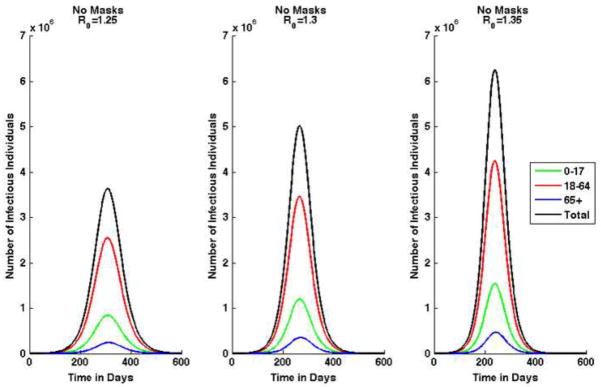
We use this model to analyze three different scenarios, using different values for ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}:1.25,1.3,\text{and}1.35$. We also analyze three variations in mask effectiveness and evaluate each case with 10%, 25%, and 50% of susceptible and exposed individuals wearing facemasks. When 10%, 25%, and 50% of susceptible and exposed individuals are wearing masks, the fraction of infectious individuals wearing masks is 30%, 40%, and 50%, respectively. All simulations assume that there are 1,800 infectious children, 2,000 infectious adults, and 100 infectious seniors in a total population of 302 million at the beginning of the epidemic, and all other individuals are susceptible. Note that in Tracht et al. (Tracht et al., 2010) we analyzed the impact of varying the number of index cases and showed that the number of initially infected individuals can have a major impact on the epidemic size. Masks are implemented after after 30,200 cases of pandemic (H1N1) are reported. For sensitivity analysis on the impact of delays in the implementation of masks, see Tracht et al. (Tracht et al., 2010). Figure 2 shows the epidemic curve for each of the three initial uncontrolled effective reproduction numbers when there are no intervention strategies in use.

Figure 2. Epidemic curves by age group and combined total for pandemic (H1N1) 2009 when there are no masks worn.

Results shown for three scenarios: the average uncontrolled effective reproduction number, ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.25,{\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3,\text{and}{\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.35$.

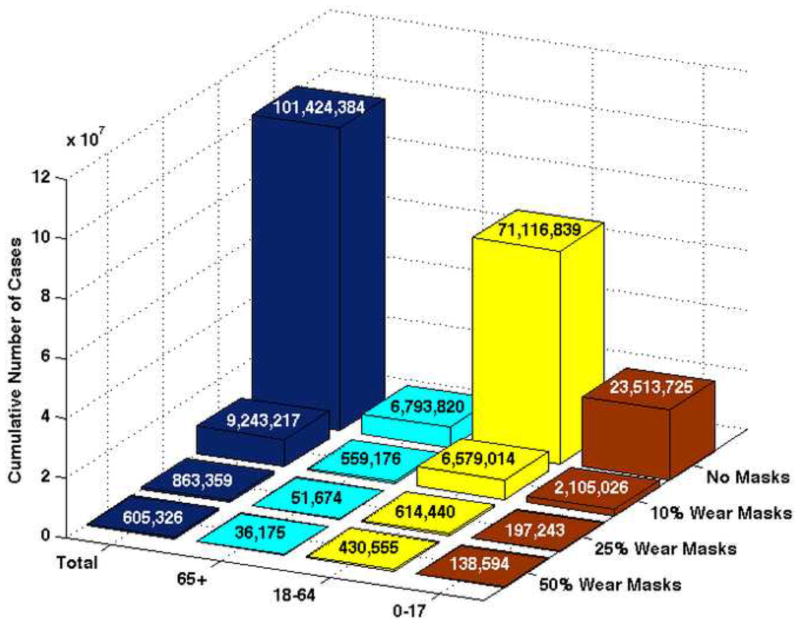
Table 4 shows the numerical results for the number of cumulative cases, deaths, and hospitalizations for each scenario when there are no interventions (no masks worn). The results when the N95 respirator is 20% effective in reducing susceptibility and 20% effective in reducing infectivity are shown in Table 5.

Table 4. Baseline results.

Cumulative number of cases, deaths, and hospitalizations in the absence of masks for three initial values of ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.25,1.3,\text{and}1.35$.

Category	Age Group	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$
Cases	0–17	23,513,725	28,084,081	31,912,371
	18–64	71,116,839	81,223,927	88,372,676
	65+	6,793,820	8,365,016	9,758,304
	Total	101,424,384	117,673,024	130,043,351
Deaths	0–17	2,257	2,695	3,063
	18–64	281,319	321,299	349,578
	65+	2,660	3,276	3,821
	Total	286,236	327,270	356,462
Hospitalizations	0–17	500,489	597,769	679,255
	18–64	2,482,884	2,835,751	3,085,333
	65+	292,243	359,830	419,764
	Total	3,275,616	3,793,350	4,184,352

Table 5. Cumulative number of cases, deaths, and hospitalizations for 10%, 25%, and 50% of the population wearing N95 respirators when they are 20% effective in reducing susceptibility and infectivity.

The results from three different initial average effective reproduction numbers uncontrolled are shown: ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.25,1.3,\text{and}1.35$.

N95 Respirator: ηi=0.2 and ηs=0.2
Category	Age Group	10%			25%			50%
		${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$
Cases	0–17	2,105,026	4,715,016	7,431,064	197,243	317,591	731,988	138,594	170,448	227785
	18–64	6,579,014	13,987,270	20,886,048	614,440	942,665	2,061,786	430,555	504,214	639348
	65+	559,176	1,275,281	2,042,594	51,674	84,198	196,065	36,175	44,965	60605
	Total	9,243,216	19,977,567	30,359,706	863,357	1,344,454	2,989,839	605,324	719,627	927738
Deaths	0–17	202	452	713	18	30	70	13	16	21
	18–64	26,024	55,329	82,619	2,430	3,728	8,155	1,703	1,994	2529
	65+	219	499	799	20	32	76	14	17	23
	Total	26,445	56,280	84,131	2,468	3,790	8,301	1,730	2,027	2573
Hospitalizations	0–17	44,805	100,357	158,170	4,198	6,759	15,580	2,949	3,627	4848
	18–64	229,689	488,319	729,189	21,451	32,911	71,982	15,031	17,603	22321
	65+	24,053	54,855	87,864	2,222	3,621	8,433	1,556	1,934	2607
	Total	298,547	643,531	975,223	27,871	43,291	95,995	19,536	23,164	29776

Table 4 shows that when ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.25,1.3,\text{and}1.35$, the percentage of the total population infected with pandemic (H1N1) 2009 is 33.5%, 38.9%, and 43%, respectively. When 10% of the population wears masks that are 20% effective in reducing susceptibility and infectivity, the results show a reduction in the number of total cumulative cases: 9,243,217 (9.1% of the population is infected), 19,977,568 (16.9%), and 30,359,707 (23.3%) for each of the three values of ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}$, respectively. Figure 3 represents graphically the cumulative number of pandemic (H1N1) 2009 cases when ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.25$ and the mask is 20% effective in reducing both infectivity and susceptibility.

Figure 3. Cumulative number of pandemic (H1N1) 2009 cases when ${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$ and the N95 respirator is 20% effective in reducing both infectivity and susceptibility.

Three cases are shown when 10%, 25% and 50% of the total population wears masks.

An intervention strategy is measured by its ability to lower the effective reproduction number below 1. In some scenarios in which facemasks are worn the reproduction number is reduced to less than 1. For the mid-level severity scenario, ℜ_unc=1.3, the effective reproduction number is reduced to 0.9462, when masks are 20% effective in reducing both susceptibility and 50% effective in reducing infectivity with 25% of the population wearing masks. An effective reproduction number that is very close to one implies that the epidemic may continue to spread. Therefore, other intervention strategies in addition to facemasks should be implemented in order to halt the spread of the epidemic.

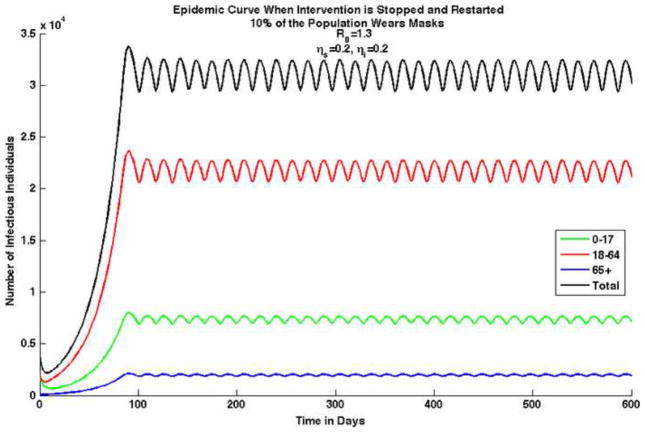
We also analyzed a scenario in which the mask intervention is temporarily halted and then restarted. It is possible that once the perceived risk decreases, the population stops using facemasks. We implemented masks when there were 30,200 cases of reported pandemic (H1N1) 2009 in the population, however, once the number of infections decreases below this number, individuals stop wearing masks. This results in an epidemic that never dies out, but remains oscillating, as shown in Figure 4.

Figure 4. Epidemic curves for each age group and combined total for pandemic (H1N1) 2009 with an initial average uncontrolled effective reproduction number, ${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$, in which N95 respirators are worn by 10% of the population and are 20% effective in reducing susceptibility and 50% effective in reducing infectivity.

In this case, waves are produced because the intervention strategy is temporarily halted and restarted, e.g., if the number of infectious individuals drops below 30,200 reported cases, people stop wearing masks. Once the number of infectious individuals reaches 30,200 cases people start to wear masks again. Note that in this scenario the epidemic never dies out and the number of infectious individuals continues to oscillate between 29,400 and 32,500.

6. Sensitivity Analysis

The results presented above used assumptions based on the best available information, however, in order to better understand the model and its sensitivity to certain parameters, we analyzed different parameter values and scenarios. This sensitivity analysis examines the effects of age-specific compliance rates, which age groups wear masks, limiting the number of available masks, and limiting the amount of money spent on masks.

Age-specific compliance

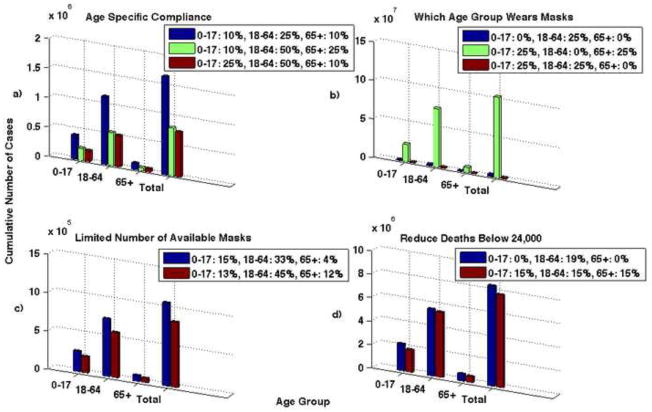
Higher compliance rates from the adult group can reduce the cumulative number of cases. Here we analyzed three scenarios for compliance: 1) 10% of children, 25% of adults, and 10% of seniors wear masks; 2) 10% of children, 50% of adults, and 25% of seniors wear masks; 3) 25% of children, 50% of adults, and 10% of seniors wear masks. We used a ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3$ and η_i=0.2 and η_s=0.2. The results are shown graphically in Figure 5, Part a.

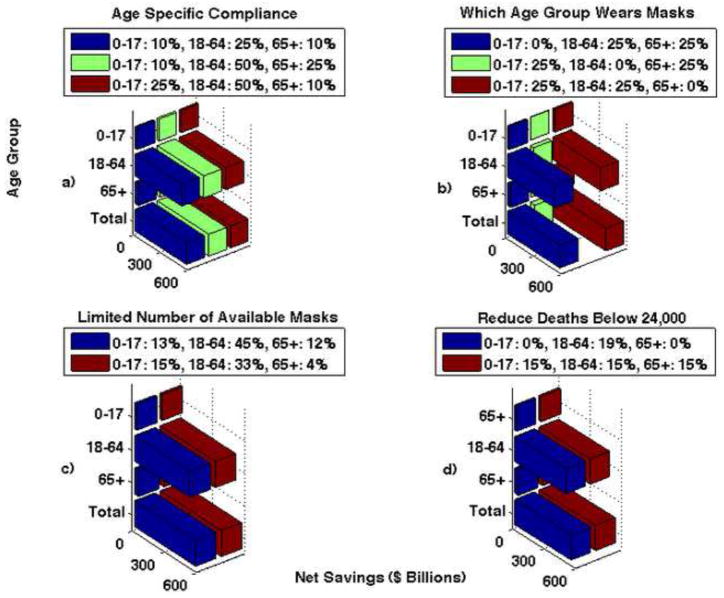
Figure 5. The number of cumulative cases for ${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$ when N95 respirators are 20% effective in reducing both susceptibility and infectivity.

Part a shows the results for age specific compliance. Three different scenarios are shown: 1) 10% of children, 25% of adults, and 10% of seniors wear masks (blue bar), 2) 10% of children, 50% of adults, and 25% of seniors wear masks (green bar), 3) 25% of children, 50% of adults, and 10% of seniors wear masks (red bar). Note that the compliance rates of the children and seniors do not appear to decrease the disease spread, but the compliance rates of adults greatly reduces the number of cases. If only 25% of adults comply compared to 50% the number of cases nearly doubles. Part b shows the results when one group is not wearing masks and 25% of the other two remaining groups wearing masks. Note that if children or seniors do not wear masks the results are very similar, however, there is a large increase in the number of cases if adults do not wear masks. Part c shows the results when there is a limited number of masks available. The blue bar shows the number of cases if there are 75,500,000 masks available and the red bar shows if there are 100,000,000 masks available. Note that the goal in distributing the masks is to reduce the total number of deaths. Part d shows the results when the objective is to reduce the number of deaths below 24,000. The blue bars represent when 19% of adults wear N95 respirators and 0% of children and seniors wear them. The red bars represent when 15% of all age groups wear masks. Note that the number of cumulative cases is lower when 15% of the entire population; while it is important for the adult age group to wear masks, better results are seen when all age groups comply.

Which age group wears masks

The simulation results are most sensitive to the adult group. The results show that if the adult population wears masks, the epidemic can be mitigated. We analyzed three cases: 1) children do not wear masks, 2) adults do not wear masks, and 3) seniors do not wear masks; in each case we assumed the remaining two age groups have a 25% compliance rate. Figure 5, Part b shows the results for these three scenarios for ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3$ and η_i=0.2 and η_s=0.2.

Limit on the number of available masks

During a pandemic there may be a limited number of masks available. If this situation arises, we need to know how to effectively distribute the masks in order to minimize the number of deaths. We analyzed two scenarios: 1) there are 75,500,000 masks available (e.g., enough for about 25% of the population); and 2) there are 100,000,000 masks available (e.g., enough for about 1/3 of the population). We assumed ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3$ and masks to be 20% effective in reducing susceptibility and infectivity. We performed an optimization analysis to determine how best to distribute the limited number of masks to reduce the number of deaths. If only 75.5 million masks are available, 14.5% of them should go to children (ages 0–17), 83.5% to adults (ages 18–64), and 2% to seniors (ages 65+). In other words, 15% of children, 33% of adults, and 4% of seniors should wear masks. This combination results in the lowest number of deaths (3,004). If there are 100 million masks available, 9.5% should go to children, 86% to adults, and 4.5% to seniors, or in other words, 13% of children, 45% of adults, and 12% of seniors should wear masks. This combination results in the lowest number of deaths (2,352). These results are shown in Figure 5, Part c.

Reduce deaths below 24,000

Seasonal influenza typically results in 24,000 deaths per year (Center for Disease Control and Prevention, 2010). In an influenza pandemic, the number of deaths could dramatically increase. We examined the level of intervention necessary to reduce the number of deaths during pandemic (H1N1) 2009 to less than that of typical seasonal influenza. To reduce the number of pandemic (H1N1) 2009 deaths to below 24,000, we considered two scenarios: 1) what percentage of adults need to wear masks and 2) what percentage of the entire population would need to wear masks. If ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3$ and masks are 20% effective in reducing both susceptibility and infectivity, 19% of adults would need to wear masks to reduce the number of deaths to less than 24,000; the total number of deaths in this scenario is 22,820. If ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3$ and masks are 20% effective in reducing both susceptibility and infectivity, 15% of all age groups would need to wear masks to reduce the number of deaths below 24,000; in this scenario deaths are reduced to 22,192. Even if 100% of children and seniors wear masks, but adults to do not wear masks, the number of deaths is still greater than 24,000. It is important that the adult age group wears masks. Figure 5, Part d shows the number of cumulative cases that result from both scenarios.

7. Economic Analysis

An influenza pandemic has the potential to have a tremendous impact on the economy; several loss estimates have been predicted (Ewers and Dauelsberg, 2007). The Congressional Budget O3ce estimated a 4.25% reduction in Gross Domestic Product (GDP) as the result of a severe pandemic similar to the 1918 Spanish Influenza pandemic, and a 1% drop in GDP for a more mild pandemic (Arnold et al., 2006). While there are many mitigation strategies that can be used to reduce the impact of a pandemic, such as vaccines, school closures, and social distancing, these options can be very costly and are not necessarily economically efficient. The potential cost of school closures for pandemic (H1N1) 2009 was estimated at $10 billion to $47 billion (Lempel et al., 2009). The U.S. spent an estimated $6.4 billion dollars on an immunization program (Morgan, 2009).

To estimate one measure of the benefits of facemasks, we use the results from our model to estimate the net savings that could be gained by a percentage of the population wearing facemasks, a potentially cheaper alternative to other mitigation strategies such as vaccines and school closures. We do not, however, compare estimated savings from facemasks to the benefits obtained from other options. We define three sources of savings from the use of face-masks: 1) avoided hospitalization costs, 2) reductions in lost future income due to fatalities, and 3) reductions in lost earnings due to illness. Finally, we subtract the estimated costs of the masks from this equation to arrive at the net savings estimate. These three measures are presented in Equation 5 with the parameter values and their decriptions given in Table 6.

Table 6. Parameter values and descriptions used to calculate the net savings from using masks.

Monetary values are expressed in year 2010 U.S. dollars. k represents the different age groups.

Economic Analysis Parameters and Descriptions Used to Calculate Net Savings
Parameter	Description	Units	Baseline	Range	Reference
HPk	Number of hospitalizations prevented in age group k	People	See Text	See Text	See Text
DPk	Number of deaths prevented in age group k	People	See Text	See Text	See Text
CPk	Number of cases prevented in age group k	People	See Text	See Text	See Text
WMk	Number of individuals wearing masks in age group k	People	See Text	0–50%	See Text
LFk	Percentage of population in the labor force	1	64.7%	60–70%	6
AHD1	Average hospital duration for children	Days	5	1–10	7
AHD2	Average hospital duration for adults	Days	8	1–10	7
AHD3	Average hospital duration for seniors	Days	10	1–10	7
AHC1	Average hospital cost for children	$\frac{U.S.\$}{\mathit{Day}}$	4,235.31*	1,000–10,000	27
AHC2	Average hospital cost for adults	$\frac{U.S.\$}{\mathit{Day}}$	8,678.35*	1,000–10,000	27
AHC3	Average hospital cost for seniors	$\frac{U.S.\$}{\mathit{Day}}$	9,890.09*	1,000–10,000	27
AI	Average income	$\frac{U.S.\$}{\mathit{Day}}$	165.36	100–500	5
PV1	Present value earnings lost for children	$\frac{U.S.\$}{\mathit{Person}}$	1,465,771*	3–10 million	27
PV2	Present value earnings lost for adults	$\frac{U.S.\$}{\mathit{Person}}$	1,496,890*	3–10 million	27
PV3	Present value earnings lost for seniors	$\frac{U.S.\$}{\mathit{Person}}$	94,972*	3–10 million	27
AA	Average absenteeism due to influenza-like illness	Days	1.3	0–5	2
CM	Cost of N95 respirator (5 Pack)	$\frac{U.S.\$}{5\mathit{Masks}}$	$9.00	15–35	14

^*Adjusted to U.S. 2010 dollars.

$$\text{Net}{\text{Savings}}_k={\text{HP}}_k\ast {\text{AHD}}_k\ast ({\text{AHC}}_k+\text{LF}\ast \text{AI})+{\text{DP}}_k\ast {\text{PV}}_k+{\text{CP}}_k\ast \text{AA}\ast \text{LF}\ast \text{AI}-\text{WM}\ast \text{CM}$$ (5)

where k = 1, 2, and 3 (corresponding to children, adults, and seniors, respectively). We assume that seniors do not work, thus, their average income (AI) is set to zero. We also assume that at least one parent of sick children take o3 from work to care for them.

A baseline estimate of the hospitalization costs, losses in future income due to fatalities, and lost earnings, due to an unmitigated pandemic could cost nearly $832 billion in the U.S. It is against this baseline estimate of unmitigated losses due to pandemic influenza that we look at the potential savings from facemasks, and we do so in four ways. The first estimates savings that depend on the effective reproduction number, the percentage of each age group that wears facemasks, and the effectiveness of the masks (in term of susceptibility and infectivity). The second considers the effects of age specific compliance rates on net savings. The third examines the impacts of one group no wearing masks. The fourth addresses net savings when the number of masks available is limited and the objective is to reduce fatalities.

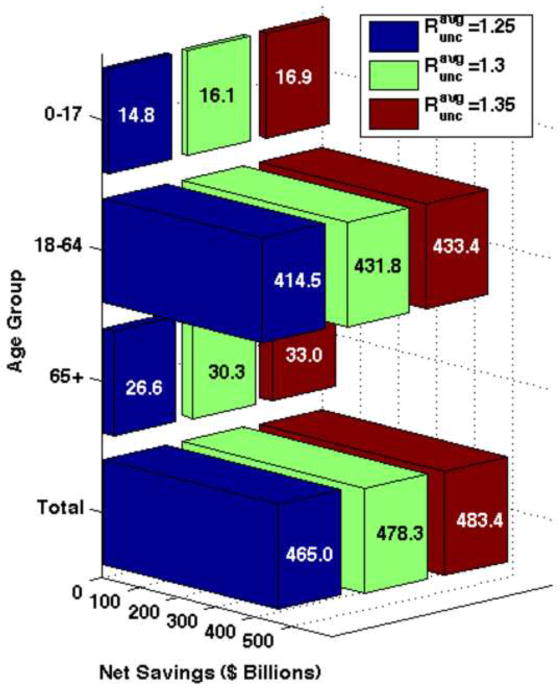
For the first analysis, if facemasks are worn by 10% of the population and they are 20% effective in reducing both susceptibility and infectivity and ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}=1.3$, the net savings would amount to approximately $478 billion. Under comparable assumptions, if 50% of the population wears masks, the net savings increases to $573 billion. As one might expect, net savings increases with higher rates of mask use and effectiveness for each value of ${\mathfrak{R}}_{\mathit{unc}}^{\mathit{avg}}$. In all cases, the greatest net savings result when the adult age group (18–64) wears masks, while the lowest net savings occur when children wear masks. Table 7 summarizes the net savings from all scenarios and Figure 6 shows the total net savings and the net savings for each age group for 10% of the population wearing masks when masks are 20% effective.

Table 7.

Net savings gained by a percentage of the population wearing N95 Respirators.

Net Savings: N95 Respirator (2010 U.S. Dollars in Billions)
Category	Age Group	10%			25%			50%
		${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.25$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$	${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.35$
Net Savings ηi = 0.2, ηs = 0.2	0–17	14.81	16.16	16.93	16.13	19.21	21.57	16.17	19.31	21.92
	18–64	414.55	431.89	433.49	452.82	515.63	554.37	453.91	518.37	563.42
	65+	26.67	30.33	33.00	28.83	35.41	40.89	28.88	35.56	41.46
	Total	456.03	478.38	483.43	497.77	570.25	616.83	498.96	573.24	626.80
Net Savings ηi = 0.5, ηs = 0.2	0–17	16.15	19.30	21.91	16.20	19.36	22.01	16.21	19.37	22.02
	18–64	453.51	518.12	563.29	454.87	519.89	565.83	455.05	520.10	566.08
	65+	28.87	35.57	41.47	28.94	34.71	41.62	28.94	35.67	41.62
	Total	498.54	572.99	626.67	500.01	573.97	629.46	500.20	575.14	629.73
Net Savings ηi = 0.5, ηs = 0.5	0–17	16.18	19.34	21.99	16.21	19.37	22.02	16.21	19.38	22.03
	18–64	454.50	519.32	565.30	455.15	520.23	566.21	455.24	520.33	566.33
	65+	28.93	35.64	41.59	28.96	35.69	41.64	28.95	35.68	41.64
	Total	499.61	574.30	628.88	500.31	575.29	629.88	500.40	575.38	630.00

Figure 6. Net savings when 10% of the population is wearing N95 respirators and they are 20% effective in reducing both susceptibility and infectivity.

Three different pandemic severity scenarios are shown. The greatest net savings for the length of the pandemic are seen when the adult (18–64) age group wears masks.

For the second analysis, we considered the effect of age-specific compliance rates on net savings. We examined the net savings under three different scenarios in which all age groups have different compliance rates: 1) 10% of children, 25% of adults, and 10% of seniors wear masks, 2) 10% of children, 50% of adults, and 25% of seniors wear masks, and 3) 25% of children, 50% of adults, and 10% of seniors wear masks. All three scenarios result in nearly the same net savings: $568.8 biliion, $573 billion, and $573.2 billion, respectively. The results are shown numerically in Table 8 and graphically in Figure 7, Part a.

Table 8.

Net savings for age specific compliance rates for ${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$, η_s =0.2, and η_i=0.2.

		Compliance Rates Children – 10% Adults - 25% Seniors - 10%	Compliance Rates Children - 10% Adults - 50% Seniors - 25%	Compliance Rates Children - 25% Adults - 50% Seniors - 10%
Net Savings (In billions)	0–17	19.14	19.28	19.28
	18–64	514.39	518.17	518.36
	65+	35.31	35.55	35.56
	Total	568.85	573.01	573.21

Note that the only significant difference is when the adult population has a lower compliance rate; varying the percentage of children and seniors wearing masks does not effect net savings much.

Figure 7. Net savings when the population wears N95 respirators that are 20% effective in reducing both infectivity and susceptibility, with an ${\mathfrak{R}}_{\mathrm{unc}}^{\mathrm{avg}}=1.3$.

Part a shows the net savings for the age specific compliance scenario. There are three scenarios shown: 1) 10% of children, 25% of adults, and 10% of seniors wear masks (blue bar), 2) 10% of children, 50% of adults, and 25% of seniors wear masks (green bar), and 3) 25% of children, 50% of adults, and 10% of seniors wear masks (red bar). Part b shows the net savings when one group is not wearing masks and 25% of the other two remaining groups wearing masks. If adults do not wear facemasks, net savings are reduced. Part c shows net savings when there are a limited number of masks available. Similar net savings are seen in both cases; the goal is to distribute masks effectively to reduce the total number of deaths. Part d shows the net savings when the objective is to reduce the number of deaths below 24,000. Note that similar net savings are seen in both cases; the goal is to distribute masks effectively to reduce the total number of deaths to less than 24,000.

These results also suggest that net savings will increase with higher adult compliance rates, but at a decreasing rate. For example, doubling the adult compliance rate (from 25% to 50%), increasing children’s compliance rate (from 10% to 25%) and holding the senior compliance rate constant (at 10%) increases net savings to adults by about $4.4 billion, a far smaller increase in net savings than occurs when the compliance rate of adults is increased from 0% to 25%.

For the third analysis, we examined the effect of one age group not wearing masks, while the other two age groups maintained a 25% compliance rate. When children or seniors do not wear masks, the net savings are not significantly different. However, if the adult age group does not wear masks the net savings is significantly reduced. The net savings when children, adults, and seniors do not wear masks is $563.7 billion, $47.5 billion, and $569.6 billion, respectively. The results are shown graphically in Figure 7, Part b and numerically in Table 9.

Table 9.

Net savings for for when one age group does not wear masks and 25% of the other two age groups does wear masks, ${\mathfrak{R}}_{\text{unc}}^{\text{avg}}=1.3$, η_s=0.2, and η_i=0.2.

		Compliance Rates Children - 0% Adults - 25% Seniors - 25%	Compliance Rates Children - 25% Adults - 0% Seniors - 25%	Compliance Rates Children - 25% Adults - 25% Seniors - 0%
Net Savings (In billions)	0–17	18.91	3.92	19.17
	18–64	509.74	36.53	515.13
	65+	35.06	7.09	35.34
	Total	563.72	47.55	569.64

Note that when the adult population does not wear masks the net savings is significantly lower, however net savings does not change if either children or seniors do not wear masks.

Comparing the results across adult compliance rates for children and seniors reveals the importance of adult compliance rates. For example, when the adult compliance rate is 25%, increasing compliance rates of children (from 0% to 25%) or reducing the compliance rate of seniors (from 25% to 0%) has little effect on estimated net savings for either group. In contrast, reducing the adult compliance rate (from 25% to 0%) while increasing the compliance rate of children (from 0% to 25%) actually reduces the net savings for children from $18.9 billion to $3.9 billion.

For the final analysis, we calculated the optimal distribution of masks if there is a limited supply; Figure 7, part c shows the net savings for two scenarios in which the number of masks is limited. During a pandemic, one of the most important goals is to reduce the number of deaths, thus we also considered an objective of minimizing deaths. Figure 7, part c shows the net savings gained from two different scenarios that reduce the number of deaths to less than 24,000 (e.g., below typical seasonal influenza mortality rates (Center for Disease Control and Prevention, 2010)).

8. Discussion

The standard pharmaceutical mitigation strategies used during an influenza outbreak are vaccines and antivirals. In the case of a novel virus these strategies may not be readily available and can be very costly, thus, there is a need for non-pharmaceutical interventions to reduce disease spread. In the absence of vaccines, non-pharmaceutical interventions, such as hand washing and facemasks, become the first line of defense. We used a mathematical model with three different age groups to examine the effect facemasks could have had on disease spread during the pandemic (H1N1) 2009. We then used these results to evaluate the cost effectiveness of the use of facemasks.

The numerical simulations results indicate that without any intervention strategies in place, a large percentage of the population could be infected with pandemic (H1N1) 2009; approximately 33%–43% of the population could become infected. If 10% of the population wears masks with an effectiveness of 20% in reducing susceptibility and infectivity, there is a large reduction in the cumulative number of cases.

We used present value of future earnings, hospital costs, and lost income estimates due to illness to estimate the economic losses resulting from pandemic (H1N1) 2009. Our model estimates that without any intervention strategies economic losses could be in the range of $662 billion to $832 billion (2010 dollars). The model suggests that wearing masks could result in significant savings.

If 10% of the population wears facemasks and they are 20% effective in reducing both susceptibility and infectivity, there is the potential for net savings in the range of $456 billion to $483 billion (2010 dollars), depending on the value of the initial effective reproduction number. Net savings increases greatly if N95 respirators are 50% effective in reducing susceptibility and infectivity. If 10%, 25%, and 50% of the total population wears masks, there is a $500.4 billion, $575.3 billion, and $630 billion (2010 dollars) net savings, respectively.

The highest net savings result when the adult age group wears masks, partially due to this age group having the largest population and to the fact that they contribute most to the economy. It is most important for the adult population to wear masks during a pandemic in order to reduce economic losses and the total number of deaths. Facemasks can provide economic savings not only from diverted losses caused by death and illness, but other measures such as social distancing and school closures can pose a large economic burden.

Evidence shows that people would be willing to wear masks during an epidemic (Condon and Sinha, 2009; kum Tang and yan Wong, 2004). During pandemic (H1N1) 2009, Mexico City officials required the use of facemasks for bus and taxi drivers and suggested their use for passengers. Condon and Sinha found a compliance rate for bus and taxi drivers to be 20–90% and for passengers 8–55% during the beginning of the pandemic (Condon and Sinha, 2009). However, for facemasks to be effective in reducing the spread of disease they need to be: (1) available, (2) affordable, (3) worn properly, (4) replaced or sanitized daily, and (5) fit-tested (if using N95 respirators) (Tracht et al., 2010).

Only 25% of the adult population would have to wear masks in order to achieve significant net savings. One of the policy implications of our results is that people should consider wearing masks, as it is typically done in some Asian countries, to prevent the spread of airborne viruses. Facemasks are not only inexpensive, but are easy to implement and less costly than most other mitigation strategies. N95 respirators come in varying sizes, ranging from extra small to large, thus is would be feasible for people to buy them based on their face size. Although we used N95 respirators as the basis for out analyses, recent studies (Loeb et al., 2009) have shown that surgical masks and N95 respirators can provide similar protection. We can conclude from our model that facemasks are an effective intervention strategy in reducing the spread of pandemic (H1N1) 2009 and are an extremely cost-effective tool to reduce economic losses due to illness.

Highlights.

• We model an influenza epidemic where three age groups wear facemasks.

• We analyze the cost effectiveness of the use of facemasks during an epidemic.

• Facemasks can reduce the number of influenza cases as well as economic losses.

• Our analyses show facemasks could reduce economic losses by $570 billion.