Abstract
The topographic distribution of ventilation in the lungs is determined by the interaction of several factors, including lung shape, airway tree geometry, posture, and tissue deformation. Inter-species differences in lung structure-function and technical difficulty in obtaining high resolution imaging of the upright human lung mean that it is not straightforward to experimentally determine the contribution of each of these factors to ventilation distribution. We present a mathematical model for predicting the topological distribution of inhaled air in the upright healthy human lung, based on anatomically-structured model geometries and biophysical equations for model function. Gravitational deformation of the lung tissue is predicted using a continuum model. Air flow is simulated in anatomically-based conducting airways coupled to geometrically simplified terminal acinar units with varying volume-dependent compliances. The predicted ventilation distribution is hence governed by local tissue density and elastic recoil pressure, airway resistance and acinar compliance. Results suggest that there is significant spatial variation in intrinsic tissue properties in the lungs. The model confirms experimental evidence that in the healthy lungs tissue compliance has a far greater effect than airway resistance on the spatial distribution of ventilation, and hence a realistic description of tissue deformation is essential in models of ventilation.
Keywords: Ventilation distribution, Tissue deformation, Structure-function
1. Introduction
The human lung typically operates in the upright posture, yet imaging modalities that are used to study lung function are usually restricted to acquiring data in horizontal positions (Hopkins et al., 2007b; van Beek and Hoffman, 2008; Sá et al., 2010), or use relatively low resolution methods to measure function in the upright lung (Amis et al., 1984). A recent study has tried to address this limitation by administering contrast when upright and then imaging when supine (Petersson et al., 2009). However this is still not a precise image of the upright ventilation distribution. The alternative option of studying animals is confounded by species differences in airway and lung geometry which will impact on resistance and on functional differences between normal postures. A mathematical model that is predictive of ventilation distribution in the human in the upright posture would therefore have obvious application in relating experimental or clinical imaging-based measurements of lung function (supine or prone) to upright lung function, and additionally in providing a framework for in silico experiments.
Heterogeneity that is present in the distribution of inhaled air to different regions of healthy human lungs impacts on the function of the organ. Specifically, heterogeneous ventilation in the presence of heterogeneous and poorly correlated perfusion reduces gas exchange efficiency. Large scale effects lead to preferential ventilation of lung tissue (parenchyma) in gravitationally-dependent regions compared with non-dependent regions during tidal breathing (Glenny, 2009). Due to the combined effects of the asymmetrically branching structure of the lung airways and regionally varying tissue compliance, a large degree of variability is superimposed on this dependent to non-dependent ventilation distribution. Although ventilation is heterogeneous, it exhibits an important spatial correlation as a result of the structure of the lung: low-ventilation regions neighbour other low-ventilation regions and vice versa (Altemeier et al., 2000). In addition, the complex interaction of the shape of the lungs and chest wall and motion of the lobes could be important in determining the ventilation distribution (Glenny et al., 2000). A mathematical model that is predictive of the ventilation distribution in the lung must therefore include a description of airway anatomy and its relationship to air flow resistance, as well as tissue deformation and local elasticity in response to gravity. Ultimately it should also include interaction with the chest wall and diaphragm.
Early computational modelling studies of ventilation distribution attributed regional differences in ventilation to a pleural pressure gradient in the lungs and hence to the effects of the nonlinear pressure-volume relationship of the tissue, but did not attempt to incorporate airway or lung structure (Milic-Emili et al., 1966). More recently, Tawhai et al. (2006) proposed a model that couples tissue deformation and flow, however this model was limited to using the local tissue deformation as a flow boundary condition, which negates its use in studies where resistance is important. Models have been developed that incorporate airway resistance in idealised symmetric airway geometries, which neglect ventilation heterogeneity due to airway structure (Lambert et al., 1982; Wiggs et al., 1990; Venegas et al., 2005). Campana et al. (2009) presented a model in an anatomically-based asymmetric airway tree (Tawhai et al., 2004), but assumed uniform compliance and hence did not introduce the effect of gravity acting on the tissue. This inherently assumes that airway resistance is dominant in determining the distribution of ventilation, which is a reasonable assumption in the context of that study where major bronchoconstriction was simulated. However, experimental and theoretical studies have shown that in the normal lung, compliance dominates over airway resistance in determining ventilation distributions (Milic-Emili et al., 1966; Otis et al., 1956). Therefore a representation of tissue mechanics must be included in theoretical models of ventilation to capture the balance between resistance and compliance.
The current study presents a theoretical model of ventilation that integrates each of 1) an anatomically based structure, 2) tissue deformation due to gravity (and hence the effect on local tissue compliance) and 3) airway resistance. It is the first theoretical model to concurrently describe each of these important contributing features and so is the only existing model that can explain how these factors interact to influence the function of the airways. Model results support experimental findings that the effect of airway resistance on ventilation distribution in normal breathing is likely to be minor in comparison to the gradient of transpulmonary pressure, and hence compliance (Milic-Emili et al., 1966). In addition, this integrated model suggests that conventional estimates for acinar compliance that are used in mathematical models (i.e. constant or linear compliance distributions) are insufficient to give rise to the significant heterogeneity in the distribution of ventilation that has been observed experimentally (Altemeier et al., 2000; Robertson et al., 2005; Musch et al., 2002).
2. Methods
The ventilation model presented here combines the results of previously published models of the structure of the lungs and conducting airways (Tawhai and Burrowes, 2003; Tawhai et al., 2004) and lung tissue mechanics (Tawhai et al., 2009) with a model of airflow. The airflow model couples flow in the conducting airways (based on measurements made by Pedley et al. (1970)) and an equation of motion which drives flow into the acinus via a temporally changing pleural pressure. The model of the acinus is similar in its translation of physical processes to the classic single compartment model (Ben-Tal, 2006); however, each acinus is now represented by an individual compartment, resulting in ~32,000 individual expanding and contracting compartments plus ~64,000 airways that comprise the conducting airway tree. The model is implemented in CMISS (www.cmiss.org) – an in-house mathematical modelling environment.
2.1. Structural model
Subject-specific structural models for the lungs and conducting airways as described in detail in previous studies (Tawhai and Burrowes, 2003; Tawhai et al., 2004) were used to define geometries in which to solve functional models of tissue mechanics and air flow. In brief, finite element models of the lungs and central airways were geometry fitted to MDCT (multidetector-row computed tomography) imaging of the lungs of a healthy volunteer male. Imaging was acquired supine at 90 % of vital capacity, which is assumed close to TLC (total lung capacity). Imaging data were provided by the University of Iowa Comprehensive Lung Imaging Center (I-Clic) under the Human Lung Atlas project. Imaging of subjects in this study has been approved by the University of Iowa Institutional Review Board and Radiation Safety Committees. The subject and model used in the current study was also used in a prior study of lung soft tissue mechanics (Tawhai et al., 2009).
Airways additional to the segmented central airways were generated using a volume-filling branching algorithm, to fill the lung-shaped volumetric mesh. The algorithm uses the central airways as initial conditions and the lung shape as a boundary condition for “growth” of a space-filling tree geometry. The supine TLC models were scaled to the subject’s upright FRC (functional residual capacity) volume obtained from pulmonary function tests (PFTs) whilst seated (4.47 L). This assumed no change in shape of the chest wall or diaphragm with the change in posture between supine and upright lungs, but allowed for lung volume differences between the supine and upright postures.
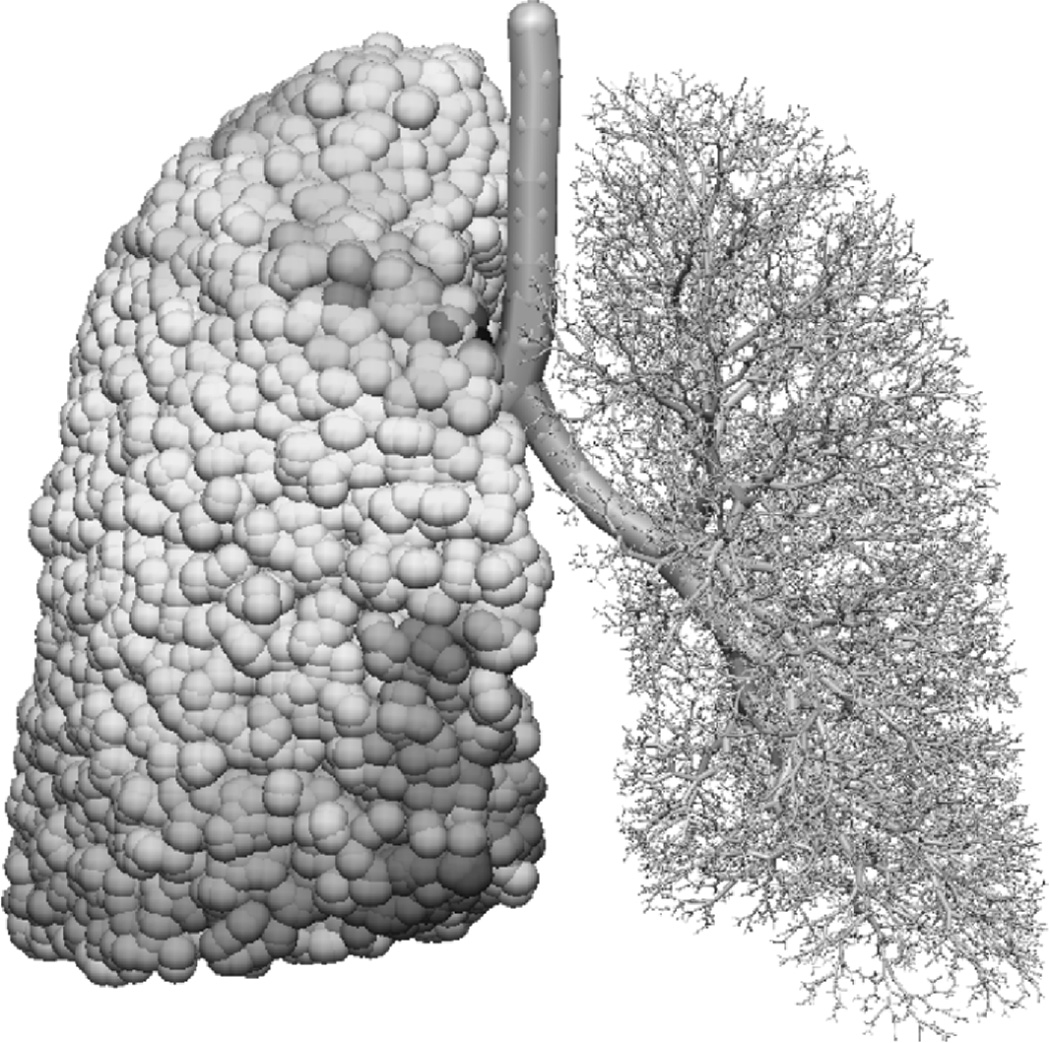
To construct models of airway function, the proportion of the measured lung volume that resides in the conducting airways and the respiratory airways must be calculated. Conducting airway radii were assigned using the subject’s FRC tracheal radius (7.26 mm, calculated from the mean tracheal cross-sectional area from FRC imaging and assuming a circular cross-section) and a Horsfield diameter ratio (RdH) of 1.152. The Horsfield diameter ratio was selected such that the model’s mean length to diameter ratio was close to 2.8 (Horsfield et al., 1976). Using this conducting airway geometry the volume of the conducting airways including and distal to the trachea was 102 ml. An additional 80 ml was included to account for the volume of the upper airways (proximal to the trachea), based on the predictive equation from Hart et al. (1963) for total anatomical dead space as a function of body height. Alveolar volume at FRC was then 4.29 L (the PFT measured volume minus the volume of all conducting airways). To obtain the volume of a single acinus this value was divided by the number of acinar units in the model (31,800) resulting in a mean acinar volume, defined as VFRC, of 135 mm3. Figure 1 shows the model geometry: the right lung is shown with spheres representing acinar units and the left lung is shown with the conducting airways only.
Figure 1.
Model lung and airway geometry viewed from the front. The right lung is shown with spheres representing acinar units and the left lung is shown with the conducting airways only.
2.2. Tissue deformation and compliance
The pre-inspiratory (FRC) model geometry and regional distribution of compliance were estimated using finite deformation elasticity, using the methods previously presented by Tawhai et al. (2009) for the left lung of two supine human subjects including the subject considered here. As this component of the functional model has been reported previously, details are provided as an appendix. In brief, the lungs and air were assumed to comprise a compressible, homogeneous, isotropic material, with the non-linear relationship between tissue stress and strain defined by a strain energy density function (W):
| (1) |
where J1 and J2 are the first and second invariants of the Green-Lagrangian finite strain tensor, and ξ, a, and b are constant coefficients1. The lungs were assumed free to slide within a rigid pleural cavity during introduction of gravity loading, and enforced to remain in contact with the cavity surface. Tissue deformation in this subject has previously been validated for the supine posture only (Tawhai et al., 2009). In the current study the model was positioned upright; that is, with gravity (9.81 ms−2) oriented in the cranial-caudal direction. Direct validation data for the upright posture in this subject are not available.
Predictions of the geometric displacement of the lungs from the model of Tawhai et al. (2009) were used to calculate the displacement of the airways and acini under gravity, and an initial distribution of stress. The results of the soft tissue mechanics were used to calculate deformed acinar volumes (V), Pe, and the compliance ℂ of each acinus at FRC. To do this, airways and acini were assumed to displace as material points within the lung continuum model. Their spatial positions were then updated based on the deformed configuration of the respective volume elements in which they were located. Local deformed acinar volume was calculated by multiplying the undeformed acinar volume (V0 = VFRC/2) by the ratio of deformed to undeformed volume (V/V0), where V/V0 is the square root of the determinant of the right Cauchy-Green strain tensor as calculated using the model of Tawhai et al. (2009).
The acini were assumed to expand isotropically during subsequent incremental changes in volume, allowing estimation of Pe and ℂ from the finite deformation stress tensors:
| (2) |
| (3) |
where λ is (isotropic) stretch from undeformed reference volume, and . Derivation of these equations is given in the appendix. Note that Eq. 3 holds for λ ≥ 1.15 (see appendix), which is the case for all acini in the quiet breathing simulations from FRC volume considered here.
2.3. Air flow model
Movement of air into the lungs is driven by expansion of the alveolar tissue. Expansion of the tissue is driven by increase in volume of the thoracic cavity and transmission of more negative pleural pressure (Ppl) from the pleural surface to the internal tissue of the lung. The rate of local tissue expansion is limited by the resistance of the airways that supply the tissue. In reality this is a tightly coupled system, where air flow and tissue expansion occur simultaneously and with feedback. This bi-directional tissue-flow interaction is significant in, for example, severe bronchoconstriction. However, in the current study we considered only quiet breathing in a normal healthy lung in which we assumed that alveolar air pressure was small enough that it did not make a significant contribution to the balance of forces that determined the tissue deformation as predicted by Tawhai et al. (2009). The ventilation model presented here used the soft tissue mechanics model to define the initial pre-inspiratory configuration of the lung and airway tree as well as the elastic recoil pressure of each acinus, but for subsequent inhalation-exhalation the model operated independently of the soft tissue mechanics model.
Airflow in conducting airways
Flow in all conducting airways (distal to and including the trachea) was assumed to be Poiseuille flow with additional energy losses incurred by flow disturbances at the airway bifurcations, as determined experimentally by Pedley et al. (1970) from studies of resistance in physical models of the bronchial tree incorporating up to four bifurcations. The models had a constant area ratio between parent and daughter branches and a fixed branching ratio. The study also assumed fully developed flow with negligible axial flow (as in the assumptions of Poiseuille resistance) and that disturbances to flow originated from non-viscous sources, but were dissipated into daughter airways via viscosity (evidence for this assumption is given by Schroter and Sudlow (1969)).
The assumptions of Poiseuille flow require flow to be fully developed and laminar. The governing equations for airflow in the conducting airway tree were therefore conservation of flow at bifurcations, and a modified Poiseuille’s equation. Pedley et al. (1970) proposed that - ignoring kinetic energy changes - the ratio of actual airway resistance (Raw) to its Poiseuille flow equivalent (RP) can be approximated by:
| (4) |
where Re is the Reynolds number, r and l are the radius and length of the airway, respectively, and KPe = 1.85 is a constant. The Reynolds number is Re = (2Qρ)/(π r μ), where ρ and μ are the density (1.51×10−6 g.mm−3) and viscosity (1.92×10−5 Pa.s) of air, respectively. Limitations in the experimental study means that there is uncertainty in KPe. KPe may be dependent on distance through an airway, the diameter of an airway, branch angles, the ratio of parent to daughter diameter, the number of bifurcations in a system and whether flow is inspiratory or expiratory. These conditions were not examined further in the original work, however the authors stated that their sources of error would likely cause underestimation in KPe and so it is possible that airway resistance would be increased compared with the relationship used here. Sensitivity of the model to KPe is examined in a later section.
The resistance of each airway was calculated as the Poiseuille resistance multiplied by ZPe, and the pressure-flow relationship for each conducting airway is:
| (5) |
where Paw2 and Paw1 are the air pressures at the proximal and distal ends of the airway segment, respectively.
Acinar airflow
Previous modelling studies have used an equation of motion that relates airway resistance, air flow, tissue compliance, and the rate of change of internal and external pressures to model the mechanics of ventilation, with the lung treated as a single lumped unit (Ben-Tal, 2006) or multiple units (VijaySekhar et al., 2010). Here we use an equivalent general equation of motion as these previous studies, but parameterised to the compliance of the pulmonary acinus. That is, each acinus was modelled as a compliant unit subtending a terminal bronchiole. Assuming isotropic expansion of each acinus, the equation of motion is:
| (6) |
where subscripts aw and A correspond to the terminal bronchiole and the acinus, respectively; Paw and Q are the pressure and flow in the terminal bronchiole; Raw is the resistance of the terminal bronchiole; VA and ℂA are the volume and compliance of the acinar unit; I is the inertance of the unit; and Pl is the local pressure acting to expand the unit as calculated by the tissue deformation model (Pl = −Pe under static conditions at FRC). This equation, which balances forces acting on the acinus, can be thought of as the equation of motion for an expanding balloon that contains air, attached to an airway, where total resistance to airflow is a function of airway resistance, tissue compliance and inertia (the resistance of the fluid to any change in its motion). This equation of motion, if properly parameterised, can be applied at multiple spatial scales in the lung, for example to the whole lung as in Ben-Tal (2006).
To simplify equation 6 we note that inertial forces can be neglected if the term IdQ/dt is small compared with the other terms in that equation, i.e. that fluid acceleration is negligible. Ben-Tal (Ben-Tal, 2006) showed in their whole lung model that inertial forces can be neglected during quiet breathing. We assume here that the rate of change of airflow in each individual acinus is small enough that inertial terms can also be neglected.
Using the relation that flow into an acinar unit (Q) is equal to the volume change of the unit (dVA/dt), then the time derivative of Eq. 6 rearranged in terms of Q is:
| (7) |
The air pressure at the proximal end of the trachea was assumed to be constant and equal to atmospheric pressure throughout the breathing cycle. Initial conditions (at the start of a breath) assume zero flow in all airways. Ppl was then varied sinusoidally over the duration of a breath. The change in Ppl from FRC was assumed to be equal at all locations, and additive to the local acinar value of Pl.
Solving the system of governing equations over a model with 60,000 airways takes on the order of one day using the RADAU5 solver to numerically integrate Eq. 7 simultaneously for all acini. To accommodate solving the model over a large domain and multiple breaths in a reasonable time period, we implemented the simplest numerical method for Eq. 7 which was a finite difference scheme. The asymmetric branching structure of the lungs can lead to solution instability under certain conditions using this approach. To improve solution stability a “flow-predictor ” scheme, which is a modification to a standard finite difference scheme, was used to numerically integrate Eq. 7 (Coleman et al., 1977). Over a suitably small time interval (Δt = tn −tn−1) the rate of change of pressures acting within or on the acinus were assumed to be constant, such that dPaw/dt = υ and dPl/dt = β, so:
Integrating with respect to t using Qn−1 = Q(tn−1) as an initial condition gives:
| (8) |
where
The flow at the end of the time period Qn = Q(tn) can then be calculated as:
| (9) |
Qn for each acinus was used as a boundary condition to update the flow distribution in the conducting airways over time. For each acinus, the acinar compliance was the acinar tissue compliance component summed in parallel with the chest wall compliance component:
| (10) |
where ℂA(tissue) is calculated using Eq. 3, and ℂA(CW) is taken as the mean acinar tissue compliance, such that the total compliance of the chest wall was equal to the total tissue compliance (sum of acinar tissue compliances; decreasing compliance with inflation volume). Note that ℂA was updated at each time step using Eq. 10 and Eq. 3, because it is dependent on the current state of tissue expansion (λn = λ(tn)). Solutions were obtained using Δt = 0.01 s, which was confirmed as a sufficiently small time step size to achieve convergence in the solution (less than a 1 % difference with the solution at Δt = 0.005 s).
2.4. Model parameters and simulation conditions
As shown in Table 1, which lists the model parameters and their sources, the model is defined by seven parameters: three that relate to the lung geometry (VFRC, tracheal radius, RdH), three that define the tissue elasticity (ξ, a, and b), and one that contributes to the airway resistance (KPe). VFRC and tracheal radius are specific to the subject (not free parameters) and RdH is constrained by morphometric data on the relationship between airway diameter and length, whereas the remainder of the parameters are assumed - but not confirmed - to be representative of the population.
Table 1.
Model and simulation parameters, and their sources
| Description | Value | Source | |
|---|---|---|---|
| VFRC | The mean FRC volume of an acinus | 135 mm3 | PFTs (see text) |
| ξ | Strain energy density function coefficient | 2500 Pa | Tawhai et al. (2009) |
| a | Strain energy density function coefficient | 0.433 | Kowalczyk and Kleiber (1994) |
| b | Strain energy density function coefficient | −0.661 | Kowalczyk and Kleiber (1994) |
| KPe | Pedley correction factor | 1.85 | Pedley et al. (1970) |
| ρ | Air density | 1.15×10−6 g.mm3 | Ideal gas law (37 C) |
| μ | Air viscosity | 1.92 ×10−6 | Sutherland’s formula (37 C) |
| Trachea radius | 7.26 mm | From imaging (see text) | |
| RdH | Horsfield diameter ratio | 1.152 | See text |
The elasticity constants ξ, a, and b were assigned values of 2500 Pa, 0.433, and −0.611, respectively. The values of the a and b coefficients were taken from a previous study (Kowalczyk and Kleiber, 1994). Their appropriateness for the in vivo lung and the value of the ξ were determined by Tawhai et al. (2009) based on three reference points during zero gravity inflation. These were a zero stress and strain state at 50% of FRC volume, inflation pressure of approximately 0.49 kPa (5 cmH2O) at FRC volume, and inflation pressure of approximately 2.94 kPa (30 cmH2O) at TLC volume. In the previous study this parameter set was shown sufficient for predicting tissue density distribution in two supine humans (including the subject used in this study) with quite different lung function Tawhai et al. (2009).
The mean pleural pressure was oscillated between −0.49 kPa (−5.0 cmH2O) at FRC and −0.80 kPa (−8.2 cmH2O) at peak inspiration in order to obtain a tidal volume of 0.6 L (this is at the high end of the normal range due to the subject’s relatively large lung volume). Normal quiet breathing was simulated with a breath duration of 5.0 s with equal inspiratory and expiratory periods.
3. Results
The Human Lung Atlas imaging data and PFTs do not include measurements of airway resistance or tissue compliance against which the predictive model could be compared. While the ideal would be to have subject specific data for each measure comparison, in this study comparisons can only be made against population data to confirm whether the model functions within a physiologically reasonable range. These comparisons show that the model is able to predict function as adequately as previous theoretical models of ventilation (Campana et al., 2009; Lambert et al., 1982; Wiggs et al., 1990; Milic-Emili et al., 1966; Tawhai et al., 2006; Venegas et al., 2005).
3.1. Airway resistance and tissue compliance
The minimum and maximum total airway resistance (excluding the upper airway) over a breath was 28 Pa.mm−3.s−1 (0.29 cmH2O.L−1.s−1) and 118 Pa.mm−3.s−1 (1.21 cmH2O.L−1.s−1), respectively, compared with literature values of approximately 59–234 Pa.mm−3.s−1 (0.6 – 2.4 cmH2O.L−1.s−1) in healthy adult lungs including the upper airway (Butler et al., 1960). The total lung compliance (not including the chest wall) was 2.1×103 mm3.Pa−1 (0.21 L.cmH2O−1) and 1.8×103 mm3.Pa−1 (0.18 L.cmH2O−1) at end-expiration and end-inspiration, respectively. This compares with accepted normal values of approximately 2.0×103 mm3.Pa−1 (0.20 L.cmH2O−1) in human lungs (Harris, 2005).
Figure 2 shows the series pathway resistance from the trachea to each acinus, against vertical location of the acinus in the upright lung. The airway pathways are longer to the apex and base of the lungs, and hence the mean series resistance is higher to these regions. Asymmetry in airway structure leads to heterogeneity in pathway resistance.
Figure 2.
Resistance of all pathways from trachea to acini plotted against vertical location of acinus, shown as mean and standard deviation of 1 cm iso-gravitational slices.
3.2. Distribution of acinar volumes and acinar ventilation
The model presented here is the first to couple a predicted distribution of acinar compliance from a model of tissue deformation with a predictive model of ventilation. The non-uniform distribution of initial (FRC) acinar volumes calculated from the tissue deformation model is shown in figure 3. Iso-gravitational non-uniformity of the FRC acinar volumes arises due to the curvilinear lung shape. That is, computing the deformation in a linear cuboid geometry would give zero in-plane heterogeneity. For the 0.6 L tidal volume, the mean acinar ventilation was 3.8±0.26 mm3.s−1, with a minimum of 2.5 and maximum of 4.1 mm3.s−1. As the flow rates in the airways vary over a breath, the acinar ventilation was calculated as the inspired acinar volume change divided by the inspiration time.
Figure 3.
Distribution of acinar volumes at FRC. Due to the gravitational deformation of the lung tissue, acini in the apical region are on average more expanded, whereas acini in the basal region are less expanded.
Predicted ventilation to dependent regions was greater than ventilation to non-dependent regions and an iso-gravitational heterogeneity is imposed on this gravitationally-oriented distribution. This can be seen in figure 4, which shows the ventilation distribution in a cranial-caudal slice of the lung geometry viewed from the front. There was a decrease in acinar ventilation in the most dependent lung region. This decrease was proportional to the small increase in tissue expansion in this region that is visible in figure 3, with a small contribution from airway path resistance. This increase in acinar volume (reduction in acinar ventilation) is due to deformation of a nonlinearly elastic tissue within an irregularly shaped geometry: deformation of a linear material within a cuboid shape does not have this same feature, whereas a linear material in an irregular (lung-shaped) geometry or a nonlinear material in the cuboid shape both have this behavior.
Figure 4.
Topology of acinar ventilation. A cranial-caudal slice of the lungs is viewed from the front with each sphere representing an acinar unit. The colour spectrum goes from low ventilation in blue (minimum=2.8 mm3.s−1) to high ventilation in red (maximum=4.6 mm3.s−1).
3.3. Ventilation gradient and heterogeneity
The lung geometry was divided into 1 cm3 “voxels” and the acinar ventilation data was aggregated in these voxels using interpolation based on the acinar volumes. Thus the “voxel” data contains the effect of geometric deformation of the airways (more acini per unit volume in the dependent region compared to the nondependent region) as well as the distribution of actual ventilation. The overall coefficient of variation (CV) for the voxel-aggregated data was 20.9%. The lung model was divided into 1 cm thick iso-gravitational slices, and the mean and standard deviation of the 1 cm3 voxel data were determined for each iso-gravitational slice. A linear fit to the means yielded a gradient of 1.5% per cm; a linear fit to all of the ventilation data gave a gradient of 1.4% per cm. These gradients quantify the gravitational component of the ventilation distribution, due directly to deformation of the lung tissue via the “Slinky” effect (Hopkins et al., 2007a), and the resulting gravitational distribution of tissue compliance.
The sensitivity of the ventilation gradient and flow heterogeneity to the energy dissipation equation (Eq. 4) was assessed by simulating flow distribution for 10% step changes in KPe (to 50% and 150% of its original value), and by comparing results with those obtained using Poiseuille flow (no additional energy dissipation term). Decreasing KPe decreased the flow gradient and the flow heterogeneity from baseline by less than 0.25% for all values of KPe; increasing KPe decreased the flow gradient (by maximum 1.57% at 150% KPe) and increased the flow heterogeneity (by maximum 3.84% at 150% KPe). Neglecting the additional energy dissipation had a very small effect on the flow gradient and heterogeneity when simulating under baseline conditions or for doubling the breath duration (differences of less than 0.4%). The ventilation gradient was reduced by 2.95% when assuming Poiseuille flow with double the tidal volume, and the heterogeneity was reduced by 8.16% when the breath duration was halved.
3.4. Important contributors to ventilation distribution
To analyse the importance of including a model of tissue deformation, or whether a more simple assumption regarding the distribution of compliance would be adequate, three simulations are compared. The first and most simple simulation assumed a uniform distribution of tissue compliance such that all acini had the same initial volume. This is analogous to a lung with zero variability in tissue properties that is ventilating in zero gravity. The second simulation assumed a linear increase in compliance in the cranial-to-caudal direction, using a similar magnitude for the gradient to that obtained from the tissue deformation model, but with no iso-gravitational heterogeneity. The third simulation used soft tissue mechanics predictions of the volumetric strains in the lung volume to set the distribution of acinar volumes at FRC. In this case, both the gravitationally-oriented distribution of tissue density and iso-gravitational heterogeneity were included. A comparison of the ventilation distributions from these three model cases is shown in figure 5. For the first case (uniform compliance) ventilation is distributed uniformly relative to the other two cases, with a very small amount of in-plane heterogeneity. In this case the acinar compliance was equal at all locations, therefore the small heterogeneity is a result of the non-uniformity of airway resistance. The linear compliance gradient of the second case induces a ventilation gradient that is close to linear over the top 60% of the model, and with a small degree of curvature in the lower 40%. This curvature is exaggerated in the final case (tissue mechanics), with a small region of ventilation increase in the most apical two slices, and a clear region of flow decrease in the most basal three slices. The final case also has marked in-plane heterogeneity due to complex deformation of the curvilinear lung model under gravity causing heterogeneity in volumetric strain and hence in local tissue compliance.
Figure 5.
Comparison of the resultant ventilation distribution using different initial volume distributions: (1) baseline model predictions of the tissue deformation; (2) linear initial volume distribution; (3) uniform initial volume distribution. The small iso-gravitational heterogeneity is not visible for the case of linear and uniform initial distributions due to the scale on the abscissa. Plots show a mean and standard deviation for each solution.
In order to quantify the relative contributions of resistance and compliance to the ventilation distribution in this healthy lung model, the correlations between pathway resistance and ventilation, and between acinar compliance and ventilation were calculated. Figures 6b and 6a plot the pathway resistance (from trachea to an acinus) and the acinar compliance, respectively, against the ventilation received by that acinus. There is high correlation between compliance and the resultant ventilation, whereas there is a very low correlation between resistance and ventilation. The Pearson correlation coefficients, which indicate whether a linear correlation is present, for the two data sets are 0.99 and −0.21, respectively. This implies that resistance has only a small effect on ventilation distribution in healthy subjects, likely because of the low viscosity of air. In comparison, pathway resistance is an important determinant in the distribution of perfusion in the pulmonary vasculature due to the relatively higher viscosity of blood (Clark et al., 2011).
Figure 6.
(a) Correlation between acinar ventilation and acinar compliance. (b) Correlation between acinar ventilation and resistance of the pathway from trachea to acinus. There is a high correlation between compliance and the resultant ventilation, whereas the resistance has little effect due to the low viscosity of air.
4. Discussion
We have presented a novel mathematical model of the spatial distribution of ventilation in an anatomically based geometric model of a normal human lung during quiet breathing. The model employs pragmatic simplifications to enable a coupling between gravitational parenchymal deformation and a model for airflow in an extensive system of model airways. In comparison with previous ventilation models, the new model includes an estimation of the spatial distribution of acinar compliance that is based on soft tissue deformation mechanics rather than an idealised distribution. In simulations of normal breathing, the modelling presented here shows that traditional modelling assumptions regarding the distribution of tissue mechanics produce significantly reduced ventilation heterogeneity when compared with a coupled ventilation-tissue mechanics approach. In addition, the model shows that assuming a uniform pulmonary tissue compliance during normal breathing is insufficient to predict a gravitational distribution of ventilation as is observed experimentally across different postures (Amis et al., 1984; Petersson et al., 2009).
4.1. Distribution of acinar volumes and acinar ventilation
Imaging data show both a heterogeneity of, and a gravitational gradient in, lung tissue density. Heterogeneity in tissue density arises partly due to the complexity of the arrangement of the physical structures within the lung, and partly due to incomplete separation of air and blood from tissue during post-processing of the imaging, but also because the driving (pleural) pressure required to inflate the lung is not transmitted uniformly through the lung to each ventilatory unit. That is, there is both a structural and functional component to the heterogeneity. The gravitational gradient arises because the lung deforms - much like a Slinky™- under gravity (Hopkins et al., 2007a). Tawhai et al. (2009) presented a computational model of lung tissue deformation which was able to predict the MDCT-imaged distribution of lung tissue density with respect to gravity that was obtained for the subject considered here. The model further predicted a heterogeneity in lung tissue density as a result of the irregularity of the lung shape causing a non-uniform transmission of stress and therefore of local tissue expansion. The model heterogeneity was smaller than observed in imaging due to 1) an assumption of a homogeneous continuum of lung tissue rather than distinct air, blood and tissue regions and 2) an inherent lack of noise, or partial voluming effects, in the model. The heterogenous transmission of pressures as modelled by Tawhai et al. (2009) translates in the current model to a non-uniform FRC acinar volume distribution with (on average) more inflated acinar units at the apex of the upright lung at FRC; this is illustrated in Figure 3. The differentially inflated acinar units each have a locally defined compliance, which in terms of the model of ventilation employed here results in heterogeneity and gravitational gradients in ventilation as seen in Figures 4 and 5. Gravitational distributions of ventilation are in agreement with current understanding of the ventilation distribution in the upright human lung (Petersson et al., 2009; West, 2000). However, ventilation in this subject was not imaged directly, so exact comparisons can not be made. In order to assess heterogeneity, the lung geometry was divided into 1 cm3 “voxels” and the acinar ventilation data was aggregated in these voxels using interpolation based on the acinar volumes. Thus the “voxel” data contains the effect of geometric deformation of the airways (more acini per unit volume in the dependent region compared to the nondependent region) as well as the distribution of actual ventilation. The overall coefficient of variation (CV) for the voxel-aggregated data was 20.9%. There is a wide range of reported CV values for different imaging modalities, experimental protocols, lung volumes, subjects and species. Here we compare with a study that has a similar voxel resolution because the CV is strongly dependent on the spatial resolution: as voxel size decreases, the CV normally increases. A study that imaged humans using PET found the CV to be 24% (prone) to 36% (supine) at a 0.9 cm3 voxel resolution (Musch et al., 2002). The CV calculated here is comparable, although low, reflecting in part the lower heterogeneity in the soft tissue mechanics model (Tawhai et al., 2009). Without including the tissue mechanics component the heterogeneity is greatly reduced (Figure 5).
4.2. Important contributors to ventilation distribution
The important physiological mechanisms that dictate the topology of the ventilation distribution in healthy lungs are gravitational deformation of the tissue within a curvilinear geometry, spatial variation in airway resistance, and underlying variation in the inherent tissue properties. This new model confirms current experimentally- and theoretically-based understanding, that at normal breathing frequencies in the healthy lung the ventilation distribution is dominated by the tissue compliance and effects of airway resistance are minimal due to the low viscosity of air (Milic-Emili et al., 1966; Otis et al., 1956). The airways branch asymmetrically which means that there is a small degree of heterogeneity in ventilation due to variability in pathway resistance, even when each acinus has an equal compliance (compare the baseline case with the uniform case in figure 5). However no correlation can be seen between ventilation levels and upstream airway resistance when the tissue compliance is not uniform (figure 6b). While resistance affects the dynamics of ventilation – that is, the temporal distribution – a normal breath in healthy lungs is long enough such that the time lag introduced by varying resistances does not affect the spatial topology.
As tissue compliance appears to be the dominant mechanism in determining the ventilation distribution, it is important to have a heterogeneous (and physiologically based) distribution of the tissue compliance. It is well understood that at the start of an inspiration acini in non-dependent (apical) regions of the upright human lungs are more expanded than acini in dependent (basal) regions due to the weight of the lung tissue. Non-linear tissue compliance means that they are also less compliant. However there is also significant iso-gravitational heterogeneity which arises due to the shape of the lungs and the propagation of stresses through the tissue. Although it is assumed here that the lung tissue is a continuum with uniform material properties, simulations of tissue deformation in a curvilinear geometry can give rise to a considerable degree of heterogeneity. Including this model of tissue deformation in a ventilation model clearly predicts more physiologically consistent ventilation distributions than simply assuming that tissue compliance is constant or proportional to lung height (figure 5). Therefore we conclude that it is an essential feature in functional computational models of ventilation which aim to describe ventilation and perfusion matching or changes in ventilation distribution with disease. The ventilation distribution predicted using a linear approximation to the initial acinar volume distribution has a similar overall trend to that from using model predictions of the tissue deformation (baseline), but it does not adequately predict heterogeneity. Thus a linear approximation to tissue density may be satisfactory for some studies, for example, those wishing to focus on redistribution between dependent and non-dependent regions.
4.3. Limitations on model validation
The model comprises three sub-models that each require validation: 1. Anatomically-based model geometry, 2. Soft tissue mechanics, 3. Flow model comprising equations for airway resistance, flow conservation, and balance of pressure and flow in peripheral elastic tissue units. The model geometry is specific to the CT-imaged geometry of the subject used here in terms of lobe shape and central airway location and size. The proportion of the tree that was derived from a deterministic algorithm is consistent with multiple morphometric studies of the human airway tree, as described in Tawhai et al. (2004). Deformation predicted by the soft tissue mechanics model has been compared against CT imaging from the same subject in the supine posture, and compares well (Tawhai et al., 2009). However, there is no upright data against which this individual subject’s tissue deformation could be compared, hence in the absence of direct validation data we have established that the predicted ventilation distribution is reasonable when compared with measurements in other subjects from the literature. Validation of other aspects of the model (e.g. resistance as an output of the flow model) were similarly limited to comparing against generally accepted functional values from the literature to show that the model is not inconsistent with these data. Data defining the ventilation distribution in the upright posture are not available for this subject, and are very limited in other subjects; a direct subject-specific validation of the upright model is therefore not possible without acquiring new data. The experimental methods of Petersson et al. (2009) - in conjunction with CT imaging to define the lung anatomy - show the most promise for providing this sort of validation data.
4.4. Major assumptions and study limitations
There are several limitations in the modelling approach that could be improved through further development: 1. the model assumes that each acinus is mechanically independent of its neighbours; 2. the supine thoracic cavity shape is used to simulate the upright posture; 3. the change in pleural pressure is assumed equal at all locations; and 4. the model assumes laminar flow with flow disturbance at the bifurcations as described by Pedley’s model.
In reality the acini do not function as independent elastic balloons; they are physically coupled through fibrous scaffolding and shared septa. Neglecting this physical interdependence could become inappropriate when considering significant airway constriction, during which the reduced expansion or dynamic hyper-inflation of a tissue unit (due to increased airway resistance) could increase or limit the expansion of neighbouring tissue units. Related to this, bronchoconstriction could also effectively stiffen the parenchymal tissue in the neighbourhood of the constricted airway. The feedback from the airways to the tissue elasticity that would be required to mimic this interaction has not been included in the current model. The tissue deformation model is used to initialise the volumes of the acinar tissue units pre-inspiration and their elasticity based on the assumption of isotropic expansion; there is no further interaction with the tissue mechanics during the ventilation simulation. The approach presented here neglects anisotropy of the tissue deformation during the transition to the flow model; non-uniformity of the tissue stretch could be important in non-baseline ventilation, e.g. during airway closure or high rates of ventilation. Ideally the tissue deformation and flow models would be solved concurrently as a coupled system, however this is a challenging problem that has not yet been addressed hence in the interim it is necessary to prescribe a weaker coupling between the two models. The simplest coupling (and the weakest) is to initialise the flow model using the tissue mechanics model, and to assume isotropic expansion in the flow model which retains the simplicity of the equation of motion. That is, we do derive a new formulation for the tissue component, which would be necessary if the anisotropy of the tissue mechanics deformation were to be retained. Without simulating the initial deformation via the mechanics model we would have to make an assumption about the pre-inspiratory distribution of the airway tree, and as we have demonstrated, simplistic assumptions for this distribution have a significant effect on the ventilation distribution.
The supine lung shape was used because MDCT imaging of the upright lung is not available. The main difference in shape that would be expected with a move to upright is a caudal shift in the diaphragm due to displacement of the abdominal contents with gravity. We have tested whether a difference in lung shape would affect the predictions of the current model (results not shown here), and have found that shape per se. has little effect in comparison to the subject’s mean tissue density and tissue density gradient at FRC. Stretch in the cranial-caudal axis would effectively increase the tissue stiffness in that direction, potentially reducing the magnitude of the predicted ventilation gradient. This however would be counteracted by improving upon another simplification in the model, which is the assumption of a uniform change in pleural pressure. If the change in pleural pressure was largest in the basal region compared with the apex, this would drive greater ventilation to the base of the lung and increase the ventilation gradient. While it is possible to impose arbitrary distributions of the increment in pleural pressure, the robust approach to this problem would be to explicitly model the structures of the chest wall and diaphragm, and include their influence on the lung by simulating their volume change during breathing. However this would require data to describe the shape change of these structures during breathing.
Flow in the largest airways is turbulent, not laminar, in part due to the presence of a turbulent laryngeal jet (Lin et al., 2007). Flow in the smaller airways is also not laminar, as it is disturbed by passing through the airway bifurcations and the shortness of the airways is insufficient for it to become fully developed. We have adopted the model of Pedley et al. (1970) to account for this latter feature of the flow, however we have not included any approximation to the effect of the turbulent laryngeal jet. We believe it is unlikely that neglecting turbulence in the largest airway of our model would have any significant effect on the distribution of flow to the smallest airways.
Our comparison of ventilation distribution and flow heterogeneity against a model that assumes only Poiseuille resistance shows that the Pedley et al. (1970) model makes a very small contribution to the flow distribution under the conditions that we have considered here: it was necessary to halve the breath duration or double the tidal volume to have a significant difference with the Poiseuille-based ventilation gradient or heterogeneity. The validity of the Pedley et al. (1970) model for airflow in the conducting airways (equations 4 and 5) is dependent on the size of the airway in question, the rate of airflow, and the branching angle between a parent airway and each of its daughter branches. Pedley et al. (1970) derived their expression for energy dissipation based on inspiratory flow experiments using physical models with straight tubular bifurcations of constant cross-section, a single bifurcation angle, and in-plane branching. The expression has not been validated for the wide range of flows, branching angles, and branch plane angles that exist in the lung, nor for expiratory flow. However for the moderate ventilation conditions considered here the air flow resistance makes only a very small contribution to the distribution of ventilation, hence the baseline distributions of flow are not sensitive to the adoption of the Pedley et al. (1970) model, nor to uncertainty in its parameterisation.
4.5. Summary
This study presents structure-based modelling of the ventilation distribution in healthy lungs and provides an important building block for physiological modelling of more complex pulmonary phenomena, such as gas transport and exchange. The use of anatomical geometries enables retention of important spatial information. We have shown that there is likely to be significant variation in inherent tissue properties which acts to compound ventilation heterogeneity. In addition, we have clearly illustrated that the tissue compliance distribution requires a realistic description in models of the ventilation topology. The techniques described here bring subject-specific modelling of pulmonary function a step closer, particularly in conjunction with a recently developed model of pulmonary perfusion within the same anatomically-based structure (Clark et al., 2011). However, not all model parameters are available on a subject specific basis, and model validation in the upright posture remains a significant challenge. Importantly, the development of a modelling framework that allows a relatively straightforward construction of models of structure (Burrowes et al., 2005; Tawhai et al., 2004), tissue deformation (Tawhai et al., 2009), perfusion (Clark et al., 2011) and now ventilation provides the required theoretical tools to achieve subject specificity. The challenge now is to obtain suitable imaging and functional data sets that can translate agreement with population measures - as achieved in the current study - to subject-specific validation.
Highlights.
-
>
We model the ventilation distribution in upright healthy human lungs
-
>
Anatomically-accurate geometries are used to include spatial information
-
>
Tissue deformation simulations are coupled to the air-flow simulations
-
>
Results compare well with whole lung measures and expected distribution patterns
-
>
Inclusion of realistic compliance distributions is essential in ventilation models
Acknowledgements
This research was supported by a University of Auckland Doctoral Scholarship, NIH grant HL-103405, and MSI grant 20959-MTS-UOA.
Appendix
A. Derivation of compliance and elastic recoil pressure
For an isotropic material, the deformation gradient can be expressed uniquely in terms of the principal stretches or in terms of the invariants of the right Cauchy-Green deformation tensor. For the lung tissue deformation model, the strain energy density function is defined as (Burrowes and Tawhai, 2010):
| (A.1) |
where J1 and J2 are the invariants of the Green-Lagrangian finite strain tensor, and are related to the invariants of the right Cauchy-Green deformation tensor (C) with: . Therefore, W can also be written as:
| (A.2) |
where I1 and I2 are the invariants of C.
Local elastic recoil pressure
The 2nd Piola-Kirchoff stress tensor is defined as:
| (A.3) |
The derivatives of the invariants of C are (Zienkiewicz and Taylor, 2000):
| (A.4) |
Using Eq. A.2, the derivatives of W are:
| (A.5) |
| (A.6) |
| (A.7) |
where . Substituting the derivatives into Eq. A.3:
| (A.8) |
The invariants of C can also be written in terms of the principal stretches with: . Assuming an isotropic stretch (λ1 = λ2 = λ3 = λ), Eq. A.8 is:
| (A.9) |
In terms of the stretches, .
The Cauchy stress tensor is used to estimate the local Pe, and is related to S by:
| (A.10) |
where F is the material deformation gradient; and JF is the Jacobian of F and is a measure of the volume change of a material element. For an isotropic expansion, F is:
Therefore, the Jacobian is: JF = λ3. The local Pe is estimated with the Cauchy stress, and hence is given by:
| (A.11) |
Tissue compliance
The compliance (ℂ) is defined as the change in volume (dV) divided by the change in pressure (dPe) required to effect that volume change:
| (A.12) |
Expressing the change in pressure and volume in terms of the stretch:
| (A.13) |
The deformed volume (V) of a material element undergoing an isotropic expansion is related to the undeformed volume (V0):
| (A.14) |
As derived above, the Pe effecting the volume change is given by the Cauchy stress. Using Eqs. A.9 and A.11 the derivative of the pressure is:
| (A.15) |
The compliance is equal to dV/dPe and is hence derived from Eqs. A.14 and A.15
| (A.16) |
Compliance is a monotonic decreasing function of inflation (the bigger the acinus the harder it is to inflate). The function ℂ is non-monotonic at very low acinar volumes, so the functional form derived here becomes an invalid representation of compliance. This does not affect the current study as volumes are not low enough for this representation of compliance to give non-physical results. A non-physical form for compliance is avoided if λ ≥ 1.15 at all times, which is true of the results of this study, which considers normal quiet breathing. In terms of normal lung function a value of λ = 1.15 would correspond to a deformed-to-undeformed volume ratio of approximately 1.5. Recall that the undeformed reference volume is half of measured FRC volume; therefore, a subject would need to be breathing at approximately 75% of their measured FRC volume to be within this range.
At very low acinar volumes (λ < 1.15) where the derived compliance relationship is not valid, a linear relationship may give a satisfactory relationship between λ and compliance
| (A.17) |
where ℂ* is the compliance value at λ = 1.15. This would need to be taken into account in simulations at very low breathing volumes and experimental validation may be required to validate this type of relationship.
Footnotes
Publisher's Disclaimer: This is a PDF file of an unedited manuscript that has been accepted for publication. As a service to our customers we are providing this early version of the manuscript. The manuscript will undergo copyediting, typesetting, and review of the resulting proof before it is published in its final citable form. Please note that during the production process errors may be discovered which could affect the content, and all legal disclaimers that apply to the journal pertain.
Note that the strain energy density function in Tawhai et al. (2009) is written incorrectly; the correct version - as used here - appears in Burrowes and Tawhai (2010)
References
- Altemeier WA, McKinney S, Glenny RW. Fractal nature of regional ventilation distribution. J Appl Physiol. 2000;88(5):1551–1557. doi: 10.1152/jappl.2000.88.5.1551. [DOI] [PubMed] [Google Scholar]
- Amis TC, Jones HA, Hughes JM. Effect of posture on inter-regional distribution of pulmonary ventilation in man. Respir Physiol. 1984 May;56(2):145–167. doi: 10.1016/0034-5687(84)90100-2. [DOI] [PubMed] [Google Scholar]
- Ben-Tal A. Simplified models for gas exchange in the human lungs. J. Theor. Biol. 2006;238(2):474–495. doi: 10.1016/j.jtbi.2005.06.005. [DOI] [PubMed] [Google Scholar]
- Burrowes KS, Hunter PJ, Tawhai MH. Anatomically based finite element models of the human pulmonary arterial and venous trees including supernumerary vessels. J Appl Physiol. 2005;99:731–738. doi: 10.1152/japplphysiol.01033.2004. [DOI] [PubMed] [Google Scholar]
- Burrowes KS, Tawhai MH. Coupling of lung tissue tethering force to fluid dynamics in the pulmonary circulation. Int. J. Numer. Meth. Biomed. Engng. 2010 Published online in Wiley InterScience ( www.interscience.wiley.com). [Google Scholar]
- Butler J, Caro CG, Alcala R, DuBois A. Physiological factors affecting airway resistance in normal subjects and in patients with obstructive respiratory disease. J Clin Invest. 1960;34(4) doi: 10.1172/JCI104071. 584591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Campana L, Kenyon J, Zhalehdoust-Sani S, Tzeng Y-S, Sun Y, Albert M, Lutchen KR. Probing airway conditions governing ventilation defects in asthma via hyperpolarized MRI image functional modeling. J Appl Physiol. 2009;106(4):1293–1300. doi: 10.1152/japplphysiol.91428.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Clark AR, Tawhai MH, Hoffman EA, Burrowes K. The interdependent contributions of gravitational and structural features to perfusion distribution in a multi-scale model of the pulmonary circulation. J Appl Physiol. 2011;110:943–955. doi: 10.1152/japplphysiol.00775.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Coleman TG, Mesick HC, Darby RL. Numerical integration. a method for improving solution stability in models of the circulation. Annals of Biomedical Engineering. 1977;5(4):322–328. doi: 10.1007/BF02367312. [DOI] [PubMed] [Google Scholar]
- Glenny RW. Determinants of regional ventilation and blood flow in the lung. Intens Care Med. 2009;35(11):1833–1842. doi: 10.1007/s00134-009-1649-3. [DOI] [PubMed] [Google Scholar]
- Glenny RW, Bernard SL, Robertson HT. Pulmonary blood flow remains fractal down to the level of gas exchange. J Appl Physiol. 2000;89(2):742–748. doi: 10.1152/jappl.2000.89.2.742. [DOI] [PubMed] [Google Scholar]
- Harris RS. Pressure-volume curves of the respiratory system. Respir Care. 2005;50:78–98. [PubMed] [Google Scholar]
- Hart MC, Orzalesi MM, Cook CD. Relation between anatomic respiratory dead space and body size and lung volume. J. Appl. Physiol. 1963;18(3):519–522. doi: 10.1152/jappl.1963.18.3.519. [DOI] [PubMed] [Google Scholar]
- Hopkins SR, Henderson AC, Levin DL, Yamada K, Arai T, Buxton RB, Prisk GK. Vertical gradients in regional lung density and perfusion in the supine human lung: the Slinky effect. J Appl Physiol. 2007a;103(1):240–248. doi: 10.1152/japplphysiol.01289.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hopkins SR, Levin DL, Emami K, Kadlecek S, Yu J, Ishii M, Rizi RR. Advances in magnetic resonance imaging of lung physiology. J Appl Physiol. 2007b;102(3):1244–1254. doi: 10.1152/japplphysiol.00738.2006. [DOI] [PubMed] [Google Scholar]
- Horsfield K, Relea FG, Cumming G. Diameters, lengths, and branching ratios in the bronchial tree. Respir Physiol. 1976;26(3):351–356. doi: 10.1016/0034-5687(76)90005-0. [DOI] [PubMed] [Google Scholar]
- Kowalczyk P, Kleiber M. Modeling and numerical-analysis of stresses and strains in the human lung including tissue-gas interaction. Eur J Mech A-Solid. 1994;13:367–393. [Google Scholar]
- Lambert RK, Wilson TA, Hyatt RE, Rodarte JR. A computational model for expiratory flow. J Appl Physiol. 1982;52(1):44–56. doi: 10.1152/jappl.1982.52.1.44. [DOI] [PubMed] [Google Scholar]
- Lin C-L, Tawhai MH, McLennan G, Hoffman EA. Characteristics of the turbulent laryngeal jet and its effect on airflow in the human intra-thoracic airways. Resp Physiol Neurobi. 2007;157:295–309. doi: 10.1016/j.resp.2007.02.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Milic-Emili J, Henderson JA, Dolovich MB, Trop D, Kaneko K. Regional distribution of inspired gas in the lung. J Appl Physiol. 1966;21(3):749–759. doi: 10.1152/jappl.1966.21.3.749. [DOI] [PubMed] [Google Scholar]
- Musch G, Layfield JDH, Harris RS, Melo MFV, Winkler T, Callahan RJ, Fischman AJ, Venegas JG. Topographical distribution of pulmonary perfusion and ventilation, assessed by PET in supine and prone humans. J Appl Physiol. 2002;93(5):1841–1851. doi: 10.1152/japplphysiol.00223.2002. [DOI] [PubMed] [Google Scholar]
- Otis AB, McKerrow C, R.A B, Mead J. Mechanical factors in distribution of pulmonary ventilation. J. Appl. Physiol. 1956;8:427–443. doi: 10.1152/jappl.1956.8.4.427. [DOI] [PubMed] [Google Scholar]
- Pedley TJ, Schroter RC, Sudlow MF. Energy losses and pressure drop in models of human airways. Respir Physiol. 1970;9(3):371–386. doi: 10.1016/0034-5687(70)90093-9. [DOI] [PubMed] [Google Scholar]
- Petersson J, Rohdin M, Sanchez-Crespo A, Nyren S, Jacobsson H, Larsson SA, Lindahl SG, Linnarsson D, Neradilek B, Polissar NL, Glenny RW, Mure M. Regional lung blood flow and ventilation in upright humans studied with quantitative SPECT. Respir Physiol Neurobiol. 2009;166(1):54–60. doi: 10.1016/j.resp.2009.01.008. [DOI] [PubMed] [Google Scholar]
- Robertson HT, Kreck TC, Krueger MA. The spatial and temporal heterogeneity of regional ventilation: Comparison of measurements by two high-resolution methods. Respir Physiol Neurobiol. 2005;148(1–2):85–95. doi: 10.1016/j.resp.2005.05.008. [DOI] [PubMed] [Google Scholar]
- Sá RC, Cronin MV, Cortney Henderson A, Holverda S, Theilmann RJ, Arai TJ, Dubowitz DJ, Hopkins SR, Buxton RB, Kim Prisk G. Vertical distribution of specific ventilation in normal supine humans measured by oxygen-enhanced proton MRI. Journal of Applied Physiology. 2010;109(6):1950–1959. doi: 10.1152/japplphysiol.00220.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Schroter RC, Sudlow MF. Flow patterns in models of the human bronchial airways. Respir Physiol. 1969;7(3):341–355. doi: 10.1016/0034-5687(69)90018-8. [DOI] [PubMed] [Google Scholar]
- Tawhai MH, Burrowes KS. Developing integrative computational models of pulmonary structure. Anat Rec B New Anat. 2003;275B(1):207–218. doi: 10.1002/ar.b.10034. [DOI] [PubMed] [Google Scholar]
- Tawhai MH, Hunter P, Tschirren J, Reinhardt J, McLennan G, Hoffman EA. CT-based geometry analysis and finite element models of the human and ovine bronchial tree. J Appl Physiol. 2004;97(6):2310–2321. doi: 10.1152/japplphysiol.00520.2004. [DOI] [PubMed] [Google Scholar]
- Tawhai MH, Nash MP, Hoffman EA. An imaging-based computational approach to model ventilation distribution and soft-tissue deformation in the ovine lung. Acad. Radiol. 2006;13(1):113–120. doi: 10.1016/j.acra.2005.09.088. [DOI] [PubMed] [Google Scholar]
- Tawhai MH, Nash MP, Lin C-L, Hoffman EA. Supine and prone differences in regional lung density and pleural pressure gradients in the human lung with constant shape. J Appl Physiol. 2009;107(3):912–920. doi: 10.1152/japplphysiol.00324.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Beek EJ, Hoffman EA. Functional imaging: CT and MRI. Clin. Chest Med. 2008;29(1):195–216. doi: 10.1016/j.ccm.2007.12.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Venegas JG, Winkler T, Musch G, Vidal Melo MF, Layfield D, Tgavalekos N, Fischman AJ, Callahan RJ, Bellani G, Scott Harris R. Self-organized patchiness in asthma as a prelude to catastrophic shifts. Nature. 2005;434(7034):777–782. doi: 10.1038/nature03490. [DOI] [PubMed] [Google Scholar]
- VijaySekhar H, Wassim M, Li H, Bailey JM. Limit cycle stability analysis and adaptive control of a multi-compartment model for a pressure-limited respirator and lung mechanics system. Int J Control. 2010;83(5):940–955. [Google Scholar]
- West JB. Respiratory Physiology: The Essentials. 6th Edition. Philadelphia: Lippincott Williams and Wilkins; 2000. [Google Scholar]
- Wiggs BR, Moreno R, Hogg JC, Hilliam C, Pare PD. A model of the mechanics of airway narrowing. J Appl Physiol. 1990;69(3):849–860. doi: 10.1152/jappl.1990.69.3.849. [DOI] [PubMed] [Google Scholar]
- Zienkiewicz OC, Taylor RL. Solid Mechanics, 5th Edition. Vol. 2 of The Finite Element Method. Oxford: Butterworth-Heinemann; 2000. [Google Scholar]