Early Mathematics Achievement Trajectories: English-Language Learner and Native English-Speaker Estimates, Using the Early Childhood Longitudinal Survey

Abstract

This study used data from the Early Childhood Longitudinal Survey, Kindergarten Class of 1998 –1999, to (a) estimate mathematics achievement trends through 5th grade in the population of students who are English-language proficient by the end of kindergarten, (b) compare trends across primary language groups within this English-language proficient group, (c) evaluate the effect of low socioeconomic status (SES) for English-language proficient students and within different primary language groups, and (d) estimate language-group trends in specific mathematics skill areas. The group of English-language proficient English-language learners (ELLs) was disaggregated into native Spanish speakers and native speakers of Asian languages, the 2 most prevalent groups of ELLs in the United States. Results of multilevel latent variable growth modeling suggest that primary language may be less salient than SES in explaining the mathematics achievement of English-language proficient ELLs. The study also found that mathematics-related school readiness is a key factor in explaining subsequent achievement differences and that the readiness gap is prevalent across the range of mathematics-related skills.

Findings from the Nation’s Report Card (i.e., the National Assessment of Educational Progress [NAEP]) reveal persistent mathematics-related achievement discrepancies related to income and race (National Mathematics Advisory Panel, 2008). One third of students in US schools are considered culturally or linguistically diverse, and in many urban schools, minority students represent a majority of the student population (Yates & Ortiz, 2004). In addition, of the more than 3.5 million children who are English-language learners (ELLs; Nieto & Bode, 2008), 75% speak Spanish as their primary language (Yates & Ortiz, 2004). The achievement gap between ELLs and their native English-speaking peers is well documented. However, the extent and the nature of the gap are less understood, in part because the data sources that underlie such estimates are generally limited for purposes of reliably estimating population values or for accurately comparing the progress of ELLs with native English-speaking students (D’Angiulli, Siegel, & Maggi, 2004; Genesee, Lindholm-Leary, Saunders, & Christian, 2005). Many such data sources represent efforts to satisfy federal and state reporting requirements, include all available cases, or are subject to few quality controls (Lesaux, Rupp, & Siegel, 2007). Also, differences in assessments and in definitions of English-language proficient make it difficult to compare students across data sets and all but eliminate the possibility of consolidating across state-level efforts. Even well-maintained data from rigorously monitored collection programs are generally not appropriate for building population-level models because of the challenge of managing factors that condition initial case selection and continuing inclusion (Albus, Thurlow, & Liu, 2002; Fry, 2007).

Data sets that rely on probability sampling may minimize some of the above limitations. However, these data sources can be misleading, as well, to the extent that they reassign English-language proficiency status at each measurement point (Albus et al., 2002; de Jong, 2004), a common approach that distorts the achievement patterns of ELLs by removing their test scores from ELL-specific achievement trends as they become increasingly skillful users and consumers of English. This bias may be evident both in reading and math but is likely to be more marked in literacy-related tasks, given the relationship of reading ability and linguistic background. For example, on the NAEP, which reassigns English-proficiency status at each administration, 75% of White (presumably native English-speaking) fourth graders and 80% of White eighth graders scored at or above the basic level on the reading measure. In the ELL group, 28% of fourth graders and 29% of eighth graders scored at or above basic performance levels. The gap between the two groups is both large and relatively stable, reflecting the prominent role of second-language proficiency (Kieffer, 2008; Roberts, Mohammed, & Vaughn, 2010) on measures of English reading. It is presumable that, if language status had not been reassigned based on proficiency, the percentage of ELLs scoring at or above basic levels would have been higher in eighth grade than in fourth grade to the extent that English-language skills within the group improved during the intervening years. A language-related achievement gap is evident in the NAEP mathematics data, as well, although the within-group stability of the reading data is not. For example, whereas 89% of White fourth graders and 79% of White eighth graders scored at a basic level or above, 54% of ELL fourth graders and only 29% of ELL eighth graders scored at or above basic levels. Students identified on the NAEP as being Asian/Pacific Islanders scored at levels comparable to White students in both mathematics and reading.

Roberts et al. (2010) estimated primary language differences in early reading achievement using the Early Childhood Longitudinal Survey, Kindergarten Class of 1998 –1999 (ECLS-K) for the group of students who were proficient in oral English by the end of kindergarten. Their findings suggest that English-proficient students make generally comparable progress through fifth grade, regardless of primary language, when socioeconomic status (SES) differences are controlled. Indeed, when language-diverse students enter school with comparable levels of reading readiness and English-language proficiency, they often outperform native speakers of similar SES over time. There is less clarity concerning patterns of early mathematics achievement and their relationship to primary language and SES, although the NAEP (National Assessment of Educational Progress, 2004) trends and prior research suggest that mathematics and reading may differ in substantive ways. The present study considers this possibility for the ECLS-K sample of English-language proficient students used in Roberts et al. (2010). For clarity, the group of bilingual students who speak a language other than English at home are referred to as ELLs in this article. The group of students whose primary home language is English (and who may or may not be bilingual) are referred to as native speakers of English.

Primary Language and Achievement in Mathematics

On average, individual differences in mathematics ability appear early, often before the start of school, and become increasingly disparate over time (Jordan, Kaplan, Locuniak, & Ramineni, 2007). Williamson, Appelbaum, and Epanchin (1991), for instance, found a positive correlation between students’ initial level of mathematics achievement and subsequent achievement in a longitudinal study of students through eighth grade. B. Muthén, Khoo, and Francis (1998) drew a similar conclusion, based on longitudinal data from seventh through 12th graders. At the primary grade level, Aunola, Leskinen, Lerkkanen, and Nurmi (2004) found that mathematics performance in Finnish primary grade students was highly stable, although increasingly dispersed over time, with more rapid growth among those with higher initial skill levels. Bodovski and Farkas (2007) reported a similar pattern in the ECLS-K data, with the lowest achieving kindergarten students making fewer gains through third grade than their peers, despite receiving more instructional time (the effect of additional instruction was moderated by teacher-reported levels of student engagement).

Further, although skill levels tend to disperse over time, early mathematics competence appears to hinge on a relatively small set of skills. The bulk of research suggests that counting and number sense (Geary, 1993; Gelman & Gallistel, 1978), discriminating between relative sizes or quantities (e.g., Ackerman & Dykman, 1995; Barrouillet, Fayol, & Lathulière, 1997; Bull, Johnston, & Roy, 1999; Geary, 1993, 2004; Geary, Widaman, Little, & Cormier, 1987; Hanich, Jordan, Kaplan, & Dick, 2001; Rourke, 1993), establishing ordinality and sequence (Gelman & Gallistel, 1978), and adding and subtracting simple whole numbers (Bryant et al., 2008; Gersten, Jordan, & Flojo, 2005) are critical and significantly predictive of subsequent success. General cognitive structures are also associated with mathematics development, including working memory (Geary, 2004), processing speed (Bull et al., 1997), phonological processing (Fuchs et al., 2005, 2006), and memory, both long- and short-term (Fuchs et al., 2006).

Primary language and culture may also interact to influence mathematics achievement (Chen & Stevenson, 1995; Flynn, 1991; Kao, 1995). For example, Asian-influenced communities, more so than Western societies, tend to associate educational attainment with student effort, rather than ability (Chen & Stevenson, 1995), and parents from Asian backgrounds generally have higher academic expectations for their children and provide more encouragement to achieve in school (Hao & Bonstead-Bruns, 1998). Systematic group differences in parental attitudes and expectations are associated with similar differences in students’ achievement in mathematics and otherwise (Fan & Chen, 2001). Finally, the vast majority of work in this area has involved students who struggle with mathematics, including those with mathematics disabilities or cognitive deficits (Jordan et al., 2007). Normative patterns of overall mathematics ability and discrete mathematics-related skills have been less thoroughly investigated, particularly in a longitudinal framework, for both the group of ELLs and for the group of native speakers of English.

SES, Primary Language, and Mathematics Achievement

Although poverty is correlated with achievement for all student groups (Aikens & Barbarin, 2008), regardless of ethnicity or primary language, its greater prevalence in homes, schools, and communities where ELL children live and learn suggests a potential confound of its effect with that of language in describing achievement trends of language-diverse groups (effect is used throughout this article in its statistical sense; it does not denote causal relationships). In the general population, SES’s relationship with early achievement may largely be due to its link with learning opportunities (Phillips, Brooks-Gunn, Duncan, Klebanov, & Crane, 1998; Stipek & Ryan, 1997). Students living in low-SES settings have fewer literacy- and mathematics-related preschool opportunities, on average, than children from more advantaged circumstances. Low-SES students also are less likely than their peers to attend enriching preschool programs (Magnuson, Meyers, Ruhm, & Waldfogel, 2004; National Center for Education Statistics, 2003), to have repeated exposures to models of oral reading or simple counting (Coley, 2002; Evans, 2004; Hart & Risley, 1995; Jordan, Huttenlocher, & Levine, 1994), and to have access to print-and number-rich environments (Evans, 2004; Neuman & Celano, 2001). Students living in low-SES settings begin formal schooling, on average, with fewer mathematics-related early skills than students from more advantaged backgrounds, a difference that is generally reflected in lower levels of readiness and lower achievement scores in kindergarten and first grade (National Assessment of Educational Progress, 2004).

Although low SES is associated with lower levels of achievement in all groups, the extent of its influence on reading achievement may differ (e.g., an interaction or moderating effect) for ELL groups compared with native English-speaking populations (see D’Angiulli et al., 2004; Krashen & Brown, 2005; Kieffer, 2008). SES differences in mathematics have been noted as well (Ginsburg & Golbeck, 2004). Saxe, Guberman, and Gearhart (1987) found that students from low- and middle-income families differed in their performance on measures of counting, ordinality and sequence, and simple addition and subtraction, although there were no differences in discriminating among relative sizes or quantities. Several studies (Jordan et al., 2007; Jordan, Kaplan, Oláh, & Locuniak, 2006) have suggested that kindergarten students from lower income families demonstrate relatively flat learning trajectories on early number-related tasks, such as counting, discriminating among relative sizes or quantities, and identifying ordinality and sequence. However, the interaction of primary language and SES on math trajectories has not been considered. This study addresses this gap in the literature.

Purposes of This Study

Poverty and achievement level at the end of kindergarten (i.e., also discussed as readiness in this article) are known correlates of learning trends in mathematics. Their respective and joint effects, however, are poorly understood, particularly across the population of elementary-aged students and within different primary language groups. This study used the ECLS-K to estimate the relationship of primary language and mathematics achievement by comparing the growth trajectories of three groups—students who speak English at home, students who speak Spanish at home but are English-language proficient, and students who speak an Asian-influenced language at home but are English-language proficient—while modeling and/or controlling for the confounding influences of SES (Kennedy & Park, 1994; Kieffer, 2008; Weber & Longhi-Chirlin, 2001). The relationship of readiness and subsequent mathematics achievement was also estimated as a way of describing variation in achievement over time as a function of initial ability (Aunola et al., 2004). Language-related effects on this relationship, if any, were represented by differences in the groups’ respective regressions of slope (growth) on intercept (initial status). Language-group assignments were maintained from initial sampling through fifth grade to avoid problems associated with reassignment, and the sample was restricted to students who passed the English-language screening measure in kindergarten as a means of uncoupling the influence of English-language proficiency and primary language. Although this restriction did not necessarily yield equivalent groups in terms of oral English proficiency— because the related measure was used only as a screening instrument and only with ELLs—it did offer a general marker for oral English ability. Specific research questions in this area included the following:

Question 1: To what extent do primary language differences moderate mathematics achievement trajectories in English language proficient students?

Question 2: To what extent does primary language moderate the relationship of readiness and achievement?

The second overall aim of this study was to untangle the often-confounded influences of primary language and SES on mathematics achievement. Building on results from the first research aim, SES effects were estimated within each language group and compared across groups to identify language-specific differences, if any, in the inter-relationship of poverty and mathematics progress. The relationship of readiness and ongoing achievement, and the possibility that this relationship varies by language and/or SES, was also considered. Specific research questions in this area included the following:

Question 3: To what extent do SES differences moderate mathematics achievement trajectories?

Question 4: To what extent does the interaction of SES and primary language moderate mathematics achievement trajectories?

Finally, the inter-relationship of important mathematics skills was an area of interest, given prior research on the effect of initial status on subsequent growth and the possibility that specific skills reliably characterize mathematics competence. The ECLS-K measures nine skill clusters on each of four occasions. Achievement patterns within each skill area can be modeled overall and for each language group, and group-specific trends can be compared as a way of identifying specific areas that may underlie more general language-related mathematics differences. This area has been the subject of very little, if any, inquiry from a longitudinal perspective. The specific research question in this area (Question 5) is the following:

To what extent does primary language moderate the achievement trajectories within each of the three language groups, and to what extent do any differences predict later mathematics achievement?

Method

Participants

The ECLS-K follows a cohort of children beginning kindergarten in the fall of 1998. Data were first collected from a nationally representative sample (approximately 21,000 students from about 1,000 public and private kindergarten programs) during the fall of the cohort’s kindergarten year. Since then, students have been evaluated in the spring of kindergarten, the fall and spring of first grade, and in the spring of third and fifth grades. Data are currently available through 2003–2004, the cohort’s fifth-grade year. The ECLS-K uses a multistage probability sample design, with the base year primary sampling unit (PSU), region, consisting of counties or groups of counties selected by probability proportional to size (PPS), and with size determined by the number of resident 5-year-olds (Asian/Pacific Islanders were oversampled). One hundred PSUs were initially selected, with the 24 largest designated as self-representing and included by default in the final sample. The 76 remaining PSUs were grouped into substrata based on size (i.e., number of 5-year-olds), percentage minority, and average SES. Two PSUs were selected from each of these substrata by PPS without replacement, using Durbin’s (1967) method.

Public and private schools offering kindergarten programs were selected in the second stage. Within each PSU, public and private schools were considered as unique strata, providing reliable sample representation across other variables. A total of 1,280 schools were sampled from the original frame (student N at sampling = 19,173), including 936 public schools (student N at sampling = 15,229) and 346 private schools (student N at sampling = 3,944). An additional 133 schools were added as part of the spring of 2000 sample freshening to include first-graders not enrolled in kindergarten in 1998 –1999. The final sampling stage was students who were selected using equal probability systematic sampling within each stratum, with oversampling of Asian/Pacific Islander to allow for reliable within-group estimates. The target number of students at any given school was 24. The refreshed sample had 21,357 students after the base year, 15,985 native English speakers and 5,372 ELLs. Of the total, 16,143 were available for the fifth-grade sample (11,771 native English speakers and 4,372 ELLs).

Student-level analyses of ECLS-K data are reliably generalized to all students enrolled in public school kindergarten in the fall of 1998 (NCES, 2003) to the extent that the sample used for analysis accounts for differences in the probability of selection due to clustering and stratification. The ECLS-K dataset includes sampling weights and school- and PSU-level identifiers for this purpose. Missing data can also introduce sampling bias and compromise external validity (Graham, Cumsille, & Fisk, 2003; Hofer, Flaherty, & Hoffman, 2006), with differential rates of attrition in longitudinal analyses often posing the most challenging scenario (Allison, 2002; Cohen, 1991). In accordance, a full information maximum likelihood (FIML) estimator, with robust (to non-normality and nonindependence of observations) standard errors and chi-square test statistics (when applicable), was used for estimation.

Latent variable growth modeling uses covariance structures as input, and the FIML estimator provides a missing data matrix as part of the output file. The missing data matrix (in this case, a 4 × 4 matrix with measurement occasions as the variables) indicates the percentage of data used (i.e., covariance coverage) for each input covariance in the analysis. The default minimum coverage in Mplus is .10. The 48 coverage values (16 in each of three matrices) in the data used for this analysis ranged from .985 to .632, with an average coverage value of .860. Approximately 97% (.973) of Time 1 cases were available at Time 2 (97% for native English speakers, 97% for Spanish-speaking ELLs, and 98% for Asian-language-speaking ELLs). Approximately 84% (.841) of Time 1 cases had valid test scores at Time 3 (82% for native English speakers, 86% for Spanish-speaking ELLs, and 85% for Asian-language-speaking ELLs). At Time 4, the group-specific coverage values were 65% for native English speakers, 75% for Spanish-speaking ELLs, and 68% for Asian-language-speaking ELLs. The Time 4 values differ significantly (z = 3.25 when the native English speakers are compared with the combined ELL group) and may represent different rates of attrition. However, to the extent that the ECLS-K data set represents the population of US public school students beginning kindergarten in 1998, different rates of attrition across the groups are normative and may not represent bias in the traditional sense.

Students who were proficient in oral English by the end of kindergarten, including students who became proficient during the course of their kindergarten year, were included in the study sample. Primary language was identified as the language spoken at home during the student’s kindergarten year. Because the public-use version of the ECLS-K data suppresses data on sparsely populated variables as a means of protecting participants’ identity, primary language was not directly indicated for students speaking a language other than Spanish or English at home. Asian-language status was assumed for students identified as ELLs and coded as Asian in the race/ethnicity fields. Greater specification within the group of Asian languages (e.g., Japanese, Chinese, Korean) was not possible. Students attending private schools were excluded from the analysis. Although private school estimates are of interest, students in these settings seem to represent a qualitatively distinct population (Bryk, Lee, & Holland, 1993; Coleman, Hoffer, & Kilgore, 1982), especially in the context of ELLs. The final analysis sample had 12,012 cases with data on at least one measurement occasion, 10,812 coded as native English speakers, 736 coded as English-proficient Spanish-speaking ELLs, and 464 as English-proficient Asian-language-speaking ELLs.

Measures

ECLS-K measure of mathematics

The mathematics measure used in the ECLS-K is a unique assessment based on the Mathematics Framework for the 1996 NAEP (National Assessment Governing Board, 1996). The assessment includes five content strands (number sense, properties, and operations; measurement; geometry and spatial sense; data analysis, statistics, and probability; and patterns, algebra, and functions) that encompass the range of skills taught in elementary school mathematics. Although the proportion of items from each content strand varies across grade levels, the majority of items on the kindergarten and first-grade measures address number sense, properties, and operations. Items on the third- and fifth-grade levels are allocated as follows: 40% involve the number sense, properties, and operations strand; 20% address the measurement strand; 15% measure the geometry and spatial sense strand; 15% address the patterns, algebra, and functions strand; and 10% address the data analysis, statistics, and probability strand.

Tests were individually administered, using an adaptive approach that tailored item difficulty to each student’s current performance level (a 17-item routing test was administered to identify initial difficulty levels), thereby improving score reliability at each measurement occasion and increasing the utility of trend estimates over time. Individually assessing young children maximizes the odds of securing accurate estimates, and customizing question difficulty to accommodate different performance levels can prevent boredom and/or fatigue. This adaptive process yields a vertical scale useful for comparing achievement and significantly shortens the time needed to test individual students. Item response theory (IRT) was used to calculate the predicted probability of each item being answered correctly by students of similar ability levels. As a result, the overall IRT-based mathematics scores represent the estimated number of items test takers would have answered correctly at each measurement point if all questions from the first- and second-stage tests had been administered. Estimates of internal consistency reliability for the ECLS-K measures ranged from .93 to .96 (Pollack, Atkins-Burnett, Najarian, & Rock, 2005), and the overall score was highly correlated (r = .83) with the Woodcock-McGrew-Werder Mini-Battery of Achievement (Woodcock, McGrew, & Werder, 1994). Validity of the measures, according to the ECLS-K authors, was established by judgments of technical and substantive experts, by the considerable match between the hypothesized and actual patterns of correlations between IRT scores across rounds and by subjects, and by the high degree of similarity between the ECLS-K and NAEP, in terms of subgroup gaps (Black/White, ELL/native English speaker, etc.).

The ECLS-K measures of specific mathematics-related abilities are organized around nine proficiency levels that are assumed to follow a hierarchical Guttman model, where mastery of later skills assumes success in prerequisite skill areas. The mathematics proficiency levels are labeled as follows in the ECLS-K: (1) count, number, and shape; (2) relative size; (3) ordinality and sequence; (4) add and subtract; (5) multiply and divide; (6) place value; (7) rate and measurement; (8) fractions; and (9) area and volume. For each, several score types are provided, including total correct scores and proficiency scores, which are dichotomous indicators of mastery status. Proficiency probability scores are also provided. These scores are IRT-based estimates of a student’s likelihood of mastering a given skill area (or proficiency level) on different measurement occasions. A score of 1 indicates mastery, and once achieved, it is carried forward. For example, if a student answered correctly all items on count, number, and shape in the spring of kindergarten, his or her score would be 1.00 for the kindergarten measurement occasion and for all subsequent occasions, reflecting the hierarchical and conditional nature of early mathematics skills. Split-half reliabilities for these proficiency probability scores ranged from .40 to .85, depending on the measure and occasion. The low split-half reliabilities are concentrated in the early skill areas, where the skill specific measures are only four to five items in length. Split-half reliability estimates for these are based on two to three items.

This approach yielded data structures with significant ceiling and floor effects, often described as censored data. In the case of count, number, and shape, for example, the ECLS-K data are censored from above because most students will be at or near 1 after the first measurement occasion. For midlevel skills such as rate and measurement, the data are censored from below for the first several occasions because most students score at or close to 0 in kindergarten and perhaps first grade but are more normally distributed at later measurement points. For higher level skills, such as area and volume, the data are censored from below on most occasions because a large majority of students do not master these levels. Because proficiency probability scores are continuous-level data, growth mixture modeling was possible within each of the proficiency levels, providing a mechanism for identifying primary language-related differences in developing subskills and estimating group-specific trends in mathematics skills.

ECLS-K indicators of SES

A student- or family-level measure of SES is provided in the ECLS-K dataset. It is a composite variable computed by ECLS-K to reflect the SES of the household at the time of data collection in the spring of kindergarten. The components used to create the variable include (a) father/male guardian’s education; (b) mother/female guardian’s education; (c) father/male guardian’s occupational prestige, based on the 1989 General Social Survey (Davis, Smith, & Hodge, 1991); (d) mother/female guardian’s occupational prestige, based on the 1989 General Social Survey; and (e) household income. The five variables are standardized with a mean of 0 and a standard deviation of 1. The composite variable is treated as continuous and ranges from −4.75 to 2.75. The percentage of students who qualified for free or reduced lunch (FRL) in the fall of 1999 was used to identify school-wide SES.

Oral Language Development Scale

The Oral Language Development Scale (OLDS) is used in the ECLS-K to identify English-language proficiency of students identified as ELLs. The OLDS is a screening tool that measures children’s listening comprehension, vocabulary, and ability to understand and produce language. It uses subtests from the Pre-Language Assessment Scales 2000 (Duncan & De Avila, 1998), the most widely used instrument during the last 20 years for classifying school children according to English-language proficiency. Children in households speaking languages other than English were given the English-language OLDS. Those scoring below the cut point were administered the Spanish OLDS if the school noted the home language as Spanish. Internal consistency reliabilities for the English Pre-Language Assessment Scales 2000 range from .86 to .90 (Duncan & DeAvila, 1998).

Plan for Analysis

The research questions were addressed using an integrated modeling approach, with each analysis providing a foundation for subsequent models. Question 1 (“To what extent do primary language differences moderate mathematics achievement trajectories in English language proficient students?”) and Question 2 (“To what extent does primary language moderate the relationship of readiness and achievement?”) were addressed using latent growth models to estimate mathematics achievement for native English-speaking students and for the ELL subgroups of interest. Multilevel models were also constructed to estimate the relative effects (effects as used in its statistical sense) of student- and school-level SES and to more precisely calculate the effects of primary language. Question 3 (“To what extent do SES differences moderate mathematics achievement trajectories?”) used mixture modeling for censored variables to estimate multigroup growth models within the different subskill areas. Mplus (L. K. Muthén & Muthén, 2007) was used for analyses. Mplus models longitudinal data using a multivariate approach, meaning that two-level models are analogous to three-level models in hierarchical linear modeling (HLM) and single-level Mplus models with longitudinal data are akin to the two-level HLM model with occasions at Level 1 and individual at Level 2.

Unconditional models

Unconditional growth models of mathematics achievement, including a baseline multilevel model, were estimated using measures administered in the spring of kindergarten, and the first, third, and fifth grades. Growth was conceptualized in terms of three parameters: (a) intercept calculated from the total covariance structure (i), which corresponds to a student’s status in the spring of kindergarten (y₀); (b) slope, which reflects the change from one time point to another; and (c) a higher order term (q) representing the shape of the trend (Bollen & Curran, 2006). The multilevel baseline model included three additional growth-related parameters: (a) a between-school intercept (i_b), which is the average school-level mean; (b) the school-level average for slope (s_b); and (c) a school-level estimate of “curve” (i.e., the quadratic term). Per convention, the coefficients for the intercept growth factor for the within-groups model were fixed at one, residual variances for the outcomes were constrained as equal over time, and residual variances of the growth factors were freely estimated (L. K. Muthén & Muthén, 2007). The growth factor residuals were correlated as the default because they do not influence other variables in the model, aside from their own indicators (L. K. Muthén & Muthén, 2007). In the between-groups model, the residual variances and the intercepts of the outcome at the four time points were fixed to zero, and the growth factor intercepts were estimated as the default. The sampling weights that the ECLS-K provided were used to adjust for clustering effects and to correctly estimate model parameters, fit indices, and unbiased standard errors. Properly adjusted parameter estimates (adjusted for nonindependence due to clustering) can be derived from the single-level longitudinal model in Mplus if the appropriate sample-related weights are applied. The added value of the multilevel approach is that it allows modeling of cluster-related nonindependence (e.g., group-specific estimates of a model’s parameters) while also providing a mechanism for identifying parameters that may vary at the school level, apart from sampling-related clustering. In this study, the relative effects of school-level SES were of interest, although language differences in this respect were not estimated.

Mathematics achievement conditioned on primary language and student-level SES

Multigroup models were fit to estimate the effect of primary language and to evaluate its conditional relationship with SES in predicting group-specific parameters. Although the effect of language was conceptualized as a student-level variable, its significance was evaluated by fitting and comparing separate single-level models for the three groups (the two ELL subgroups and the native English speakers), rather than by creating a dummy-coded “language” covariate, because the multigroup approach offered greater analytic flexibility (Bovaird, 2007). School-level effects were not specifically modeled as a function of primary language, as suggested above. Instead, parameter estimates were adjusted for cluster-related nonindependence, using sample weights and other sampling-related controls provided in the ECLS-K database.

Censored data models

To estimate achievement in the nine ECLS-K proficiency levels, weighted average proficiency probabilities were calculated for each group at each measurement occasion for each skill cluster. Given the censored nature of many of these data and the interest in multigroup analyses, longitudinal mixture modeling (L. K. Muthén & Muthén, 2007) was used to identify and compare trends within each of the nine proficiency levels. Mixture modeling is distinguished by the use of categorical latent variables and is particularly useful for censored data types when multiple groups are involved. Censored models assume that the observed range (i.e., the range covered by the measure in question) of an underlying trait represents only one part of the true distribution, and trends across the “true range” are estimated by using observable data. An iterative, integrated modeling approach as described for Questions 1 and 2 was used for these analyses, as well. Two sets of models were fit: one not adjusted for student-level SES effects and the other with student-level SES modeled and constrained across primary language groups.

Evaluating group differences

Difference testing of nested models with scaled chi-sqaured values was used to compare dissimilar parameter estimates across the ELL and native English-speaking groups. Difference testing, in this case, involved constraining the ELL subgroups and the native English-speaking group as equal on the parameter in question (e.g., intercept) and then comparing the fit of the constrained and the fully specified models. If the ELL subgroups and the native English-speaking group were comparable on the parameter of interest, the fit for the constrained and full models did not significantly differ. Constraints resulting in less adequate fit suggested significant group differences on the relevant parameter. Means and variances for the ELL and native English-speaking groups were compared on intercept, slope, and shape.

Results

The nonlinear nature of the achievement trends is evident in the weighted raw scores over time (see Table 1). Across the total sample, the average weighted IRT scores were 32.32 at kindergarten, 56.69 at first grade, 90.38 at third grade, and 110.80 at fifth grade. Note that the interval between these occasions varies: Time 1 to Time 2 is a 12-monthinterval, and Time 2 to Time 3 and Time 3 to Time 4 are 24-month intervals. Thus, the 24.37 average scale score increase from Time 1 to Time 2 represents a 12-month period of development, and the 33.69- and 19.42-point gains for the other two intervals reflect change over 2 years, a pattern that highlights the nonlinear nature of the overall trend. A similar pattern is evident across the three language groups, as indicated by the weighted mean scores in Table 1. Group-specific estimates for student- and school-level SES are summarized in Table 1, as well, with Spanish-speaking ELLs overrepresented in the lower SES levels.

Table 1.

Weighted Descriptive Statistics for L1 and ELL Groups

Language	Kindergarten (Time 1)	First grade (Time 2)	Third grade (Time 3)	Fifth grade (Time 4)	% male	Student SES	School FRL (%)	School LEP (%)	School ≥ grade level (%)
English	32.89 (11.47)	57.39 (16.71)	91.11 (22.20)	111.28 (22.54)	48	−.05	35	7	58
Spanish	26.95 (9.29)	50.45 (13.21)	83.53 (21.02)	105.29 (22.52)	51	−.62	53	29	46
Asian	34.74 (12.64)	59.05 (16.87)	98.67 (21.69)	119.63 (21.38)	49	.02	36	21	58

Note. L1 = ; ELL = English-language learner; SES = socioeconomic status; FRL = free or reduced lunch; LEP = limited English proficiency. Means (and standard deviations in parentheses) are provided for the four time points.

As anticipated, the linear unconditional model of mathematics achievement did not adequately represent the data, χ²(12) = 2427.09, confirmative fit index (CFI) = .57, root-mean-square error of approximation (RMSEA) = .179, and a follow-up model with freely estimated time scores for the third and fourth observations (L. K. Muthén & Muthén, 2007) confirmed this conclusion (time scores of 3 and 5, reflecting the actual times of measurement, would have suggested a linear trend; actual estimates were 2.38 and 3.22) and supported the curvilinear hypothesis. The addition of a quadratic term yielded a well fit unconditional baseline model, χ²(2) = 34.23, scaling correlation factor (SCF) = 7.274, CFI = .99, Tucker-Lewis index (TLI) = .98, RMSEA = .036, when the residual variance for the observed fifth-grade measure was fixed at 0 (overriding the equal-residuals-over-time default did not affect growth parameter estimates). For this baseline model, the mean intercept was 32.42, with a standard error of .32 and variance of 115.67. The mean slope was 25.32 (SE = 0.24), and its variance was 42.70. The deceleration (i.e., quadratic) mean was −1.93 (SE = 0.038) and its variance was 0.89. The correlation of intercept and slope was .56. Intercept and the quadratic term correlated at −.54. The slope and quadratic correlation was −.88. Appropriate case-level weights from the ECLS-K database were used with the single-level model to account for the stratified and clustered nature of ECLS-K data and to estimate unbiased standard errors. A multilevel baseline model was fit as well, as a check on these estimates and as a prelude to estimating models with school-level variables. Adjustments to the single-level model were applied to the within-groups part of the multilevel model (i.e., residuals for the last observed measure fixed at 0), which fit the data extremely well, χ²(3) = 14.85, SCF = 2.659, CFI = .99, TLI = .99, RMSEA = .018, and yielded growth estimates nearly identical to those of the single-level model adjusted for cluster effects (see Table 2). The within-group correlation of intercept/slope was .59, and the between-group estimate was .55.

Table 2.

Fit Indices, Growth Parameter Estimates, and Group Differences for Unconditional Single-Level and Multi-Group Models Using IRT Measure of Overall Math Ability

Model	χ2/df (SCR)	CFI/TLI	RMSEA	I (SE)	Intercept σ2a	S (SE)	Slope σ2a	Q (SE)	Q σ2a
Single group	34.23/2 (7.274)	.99/.98	.036	32.42 (0.32)	115.67	25.32 (0.24)	42.70	−1.93 (0.038)	0.89
Two-level	14.85/3 (2.659)	.99/.99	.018	32.46 (0.34)	74.84 (40.50)	25.33 (0.24)	28.21 (13.95)	−1.93 (0.038)	0.66 (0.22)
Multigroup	54.61/6 (4.568)	.99/.99	.045
English				32.99 (0.35)a	117.5ef	25.48 (0.26)c	42.6g	−1.96 (0.04)d	0.89h
Spanish				27.17 (0.78)b	59.4e	24.23 (0.70)c	32.2g	−1.72 (0.09)d	0.51h
Asian				34.74 (1.01)a	159.1f	26.14 (0.67)c	58.5g	−1.83 (0.11)d	1.34h

Note. IRT = item response theory; SCR = scaling correction factor, used in MPLUS to compare nested models; CFI = comparative fit index; TLI = Tucker-Lewis index; RMSEA = root-mean-square error of approximation; I = intercept; S = slope; Q = quadratic. Estimates with the same superscripted letters do not differ significantly. Estimates with different superscripts differ significantly at p < .01 or greater. For example, English and Asian do not differ on mean intercept, whereas Spanish differs from both. Within/between variance estimates are provided for the two-level model.

^aValues in parentheses in these columns are variance estimates.

Question 1: To What Extent Do Primary Language Differences Moderate Mathematics Achievement Trajectories in English-Language Proficient Students?

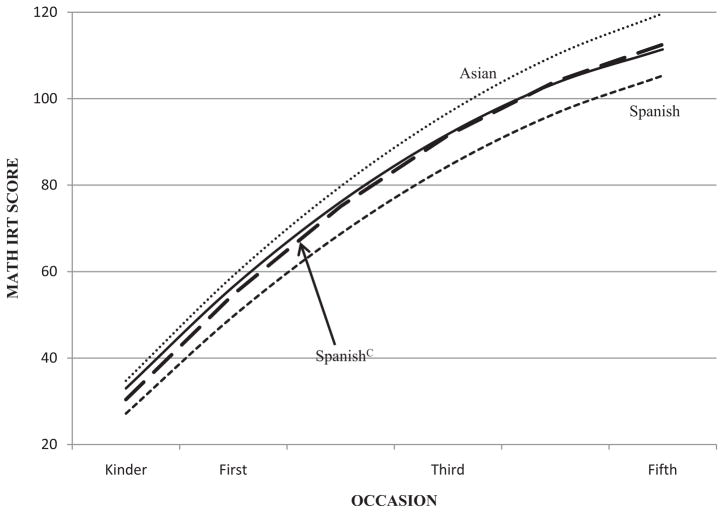
To assess the effect of primary language on subsequent mathematics achievement, a multigroup model was estimated, χ²(6) = 54.61, SCF = 4.568, CFI = .99, TLI = .99, RMSEA = .045, followed by a series of nested-model comparisons. The results, summarized in Table 2, indicate that groups differed in their respective levels of readiness (i.e., intercept), with the Spanish-speaking ELL group scoring lower than both the native English-speaking group (p < .05) and the Asian language-speaking ELL group (p < .001). There were differences, as well, in the variance estimates for intercept. In this case, the Asian language-speaking ELL group had significantly greater variation at Time 1 than did the Spanish-speaking ELL group (p < .01). There were no statistically significant group differences related to slope or the quadratic term. The nested model comparisons reflected in Table 2 are based on the serial manipulation of single parameters (e.g., intercept was constrained across groups, whereas all other growth parameters were allowed to vary across groups, then slope was constrained). When all parameters were simultaneously constrained as equal, there were differences between the Spanish-speaking ELL group and the native English-speaking group, Δχ²(4) = 12.34, p < .05, and between the Spanish-speaking and Asian-language-speaking ELL subgroups, Δχ²(4) = 23.96, p < .001. There were no differences between native English-speaking group and Asian-language-speaking ELL group, Δχ²(4) = 6.29. The values plotted in Figure 1 represent average trends for each group.

Figure 1.

Average achievement trajectories for English-language-learner subgroups and L1 (first language) group. Note that the dashed line with the largest sized segments (labeled as Spanish^c) represents the Spanish-language trend when socioeconomic status effects are constrained as equal across groups. The solid line represents the native English-speaking group.

Question 2: To What Extent Does Primary Language Moderate the Relationship of Readiness and Achievement?

The relationship of readiness and achievement and the possibility that primary language moderates this relationship was evaluated by regressing slope on intercept within the multigroup model (the quadratic term was fixed as equal across groups). The unstandardized coefficients were .465 for the native English speakers, .675 for the Spanish-speaking ELLs, and .407 for the Asian-language-speaking ELLs. The only statistically significant difference was between the Asian-language-speaking and Spanish-speaking ELLs, with initial status being more predictive of later achievement in the Spanish-speaking ELL group (p < .05). Although not statistically significant, the difference between Spanish-speaking ELLs and native English speakers was sizable as well (see Table 3).

Table 3.

Fit Indices, Growth Parameter Estimates, and Group Differences for SES-Conditioned Models Using IRT Measures of Overall Math Ability

Model	χ2/df (SCR1)	CFI/TLI	RMSEA	I (SE)	I σ2a	S (SE)	S σ2a	Q (SE)	Q σ2 (variance estimate)	I on SESa	S on SESa	Q on SESa
Single group	33.74/3 (6.937)	.99/.98	.029	33.12 (0.28)	98.83	25.72 (0.22)	36.26	−1.98 (0.04)	0.79	5.42	3.29	−0.40
Two-level	13.44/5 (2.874)	.99/.99	.012	35.46 (0.54)	69.1 (27.6)	27.60 (0.38)	26.4 (8.1)	−2.26 (0.07)	0.64 (0.12)	4.20 (−0.06)	2.53 (−0.05)	−0.32 (0.006)
Multigroup	59.81/9 (4.37)	.99/.98	.038
English				33.29 (0.30)a	100.2f	25.67 (0.23)c	36.0h	−1.99 (0.04)d	0.79i	5.40i	3.37j	−0.40k
Spanish				28.68 (0.86)b	56.9f	25.61 (0.79)c	30.1h	−1.88 (0.12)d	0.48i	2.43i	2.24j	−0.26k
Asian				34.67 (0.97)a	148.4g	26.09 (0.63)c	52.5h	−1.82 (0.10)d	1.2i	3.83i	2.82j	−0.48k

Note. SES = socioeconomic status; IRT = item response theory; SCR = scaling correction factor, used in MPLUS to compare nested models; CFI = comparative fit index; TLI = Tucker-Lewis index; RMSEA = root-mean-square error of approximation; I = intercept; S = slope; Q = quadratic. The two-level model includes both within and between estimates for variance and for the SES-related regression coefficients (the last three columns). The within-school regression coefficients represent change per standard deviation increase in SES, whereas the between-school estimates represent change per percentage point increase in school-wide FRL. All SES-related coefficients (in the last three columns) differed significantly from zero at p < .01 or better. In the multigroup model, estimates with the same superscripted letters do not differ significantly. Estimates with different superscripts differ significantly at p < .01 or greater. For example, the intercept mean for the Spanish-speaking group is significantly less than in the English and Asian groups. Similarly, intercept variance is significantly greater in the Asian group than in the English or Spanish groups, which do not differ from one another.

^aValues in parentheses in these columns are variance estimates.

Question 3: To What Extent Do SES Differences Moderate Mathematics Achievement Trajectories?

The effect of student-level poverty in the total sample was evaluated by regressing intercept, slope, the quadratic, and the coefficient for the intercept/slope correlation on SES, χ²(3) = 33.38, SCF = 6.937, CFI = .99, TLI = .98, RMSEA = .029. SES had a statistically significant effect (p < .001) on all growth factors (see Table 3). The coefficients represent change in scale score per one standard deviation change in student-level SES. For example, across all language groups, intercept increased (or decreased) by 5.42 scale score points for each standard deviation increase (or decrease) in SES.

The same relationships (i.e., regressions of growth factors onto student-level SES) were estimated in the multigroup model, χ²(9) = 59.81, SCF = 4.365, CFI = .99, TLI = .98, RMSEA = .038, and nested comparisons were used to evaluate differences in the relationship of SES and mathematics achievement. Although not statistically significant, several of these differences were relatively large (e.g., 5.40 for native English speakers on intercept vs. 2.43 for Spanish-speaking ELLs). Specifically modeling these effects altered the group-specific parameter estimates for the Spanish-speaking ELL group somewhat, although the pattern of group differences did not change (see Table 3). However, when SES effects were constrained as equal across the three groups, the Spanish-speaking ELL readiness estimate no longer differed from those for the other groups. The Spanish-speaking ELL group intercept in the constrained model was 30.41, the slope was 26.28, and the quadratic was −1.97. Estimates for the other groups were largely unchanged. The line labeled “Spanish^c” in Figure 1 depicts average Spanish-speaking ELL achievement when differences in the prevalence and effect of poverty are removed from the equation. The notion that English-proficient Spanish-speaking ELLs achieve at levels comparable to those of native English-speaking students is consistent with earlier studies on the relationship of bilingualism and early reading achievement across similar levels of SES.

Question 4: To What Extent Does the Interaction of SES and Primary Language Moderate Mathematics Achievement Trajectories?

The two-level model of language and SES effects, χ²(5) = 13.44, SCF = 2.874, CFI = .99, TLI = .99, RMSEA = .012, fit the data extremely well (i.e., a one-group model so language effects are not estimated), providing an apparently better fit than the single-level, one-group model of student-level SES effects (Akaike information criterion [AIC] = 357932.15 for the two-level model, and AIC = 396804.08 for the single-level model) and suggesting a significant role of school-level SES factors in students’ mathematics achievement (23% of the variance in slope was at the school level, and 29% of the variance in intercept). The regression coefficients for the between- and within-school SES effects are presented in Table 3. Within schools, the values represent change in scale score per standard deviation of student-level SES (e.g., there was an average difference of 4.20 scale score points between students from average-SES homes and those from homes one standard deviation above the mean). The between-school estimate is the average change in the school-level mathematics scale score per percentage point increase in school-wide FRL (e.g., .6-point average score increase on intercept per increase of 1 percentage point in school-wide FRL, or about 1.5 scale score point quartile). The six SES-related effects in Table 3 differed significantly from zero at p < .01. A nested, multigroup, multilevel model with SES effects specified at the school and student levels (i.e., the interaction of student-level SES, school-level SES, and primary language) was not viable, given the cross-classified structure of the data.

Question 5: To What Extent Does Primary Language Moderate the Achievement Trajectories Within Each of the Three Language Groups, and to What Extent Do Any Differences Predict Later Mathematics Achievement?

ECLS-K items and their order of presentation reflect a typical progression for most students and schools, with counting and number sense predominating at the preschool and kindergarten levels, basic operations becoming more prevalent in Grades 1–3, and fractions and simple geometry beyond that. Weighted average proficiency probabilities were calculated for each group at each measurement occasion for each skill cluster, using the FIML estimator. These probabilities are summarized in Table 4. The values can be interpreted as the average likelihood that students will score at or above the proficiency level in the area in question on the occasion in question. The values can be also be conceptualized as the percentage of students likely to score at or above proficiency within each primary language group. The pattern reflects the structure of the different subskill measures, which is hierarchical and conditional in nature. Probabilities for lower level skills increase rapidly across the early grade levels, approaching 1.00 in some cases, and the probabilities for higher level skills remain very small in the early grades and increase in the later grades. Because skill measures are aligned with typical curricula, item difficulties are constrained by the grade level at which a skill is typically taught and/or mastery is expected (e.g., instruction in and mastery of addition and subtraction is a hallmark of the primary grades; thus, most students would be expected to “pass” these items by the third-grade measurement occasion).

Table 4.

Estimated Proficiency Probabilities Across Math Subskills for Language Subgroups

Language subgroup	Count, number, shape	Relative size	Ordinality, sequence	Add and subtract	Multiply, divide	Place value	Rate, measurement	Fractions	Area, volume
English
K	.99	.85	.54	.16	.01	.00	.00	.00	.00
1st	.99	.99	.95	.71	.22	.03	.00	.00	.00
3rd	.99	.99	.99	.96	.76	.42	.13	.01	.00
5th	.99	.99	.99	.99	.91	.72	.42	.13	.02
Spanish
K	.97	.72	.32	.07	.00	.00	.00	.00	.00
1st	.99	.99	.92	.60	.11	.01	.00	.00	.00
3rd	.99	.99	.99	.94	.66	.29	.07	.00	.00
5th	.99	.99	.99	.99	.88	.66	.33	.06	.01
Asian
K	.97	.87	.58	.20	.03	.01	.00	.00	.00
1st	.99	.99	.97	.74	.24	.07	.01	.00	.00
3rd	.99	.99	.99	.98	.82	.54	.21	.01	.00
5th	.99	.99	.99	.99	.95	.83	.59	.25	.05

Note. K = kindergarten.

The probabilities in Table 4, when considered across grade levels and language groups, suggest that Asian-language-speaking ELLs and native English-speaking students outperformed Spanish-speaking ELLs, on average, with the Spanish-speaking group appearing to lag increasingly behind as the skills grow more sophisticated (the estimates are not adjusted for SES). Multigroup growth mixture models (described earlier) were estimated to determine the extent to which apparent differences may, in fact, represent the data, while also accounting for the censored nature of the data. Table 5 summarizes growth parameters for the respective models within each language group and identifies statistically significant differences across the groups for all skill areas, except (a) count, number, and shape; (b) fractions; and (c) area and volume, which were censored to such an extreme degree that relevant growth modeling results were not interpretable.

Table 5.

Fit Indices, Growth Parameter Estimates, and Group Differences for Unconditional Models Using Proficiency Probability Scores

Group	Relative size			Ordinality and sequence			Add and subtract			Multiply and divide			Place value			Rate and measurement
	I	S	Q	I	S	Q	I	S	Q	I	S	Q	I	S	Q	I	S	Q
English	.833a	−.066c	.429d	.528a	.612c	.062e	.155a	.536c	−.063d	−.221a	.456c	−.039d	−.512a	.330c	−.012d	−.142a	.002b	.021c
Spanish	.730b	.111c	.360d	.298b	.763d	.030e	−.004b	.570c	−.065d	−.355b	.448c	−.035d	−.671b	.323c	−.008d	−.156a	−.042b	.026c
Asian	.917a	−.099c	.487d	.573a	.584c	.094e	.196a	.550c	−.064d	−.190a	.464c	−.036d	−.503a	.358c	−.010d	−.130a	−.001b	.028c

Note. I = intercept; S = slope; Q = quadratic. Italicized estimates do not differ significantly from zero at p < .05. Within a skill area, parameter estimates with the same superscripted letters do not differ significantly. Estimates with different superscripts differ significantly at p < .01 or greater.

The importance of readiness (i.e., intercept) is clearly indicated in these results. With the exception of place value, the Spanish-speaking ELL group scored significantly lower at Time 1, on average, than the other two groups. The significantly greater slope on the measure of ordinality and sequence for Spanish-speaking ELLs suggests a closing of this initial gap. In the other areas, however, initial differences appear relatively stable across time and across the groups. To the extent that the observed data reliably estimate scores outside of the observable range (i.e., scores above 1.0), the Spanish-speaking ELL group appears to continue to lag behind the other groups, as evidenced by its much lower readiness level and relatively comparable rates of progress across the grade levels (i.e., there are no slope advantages for Spanish-speaking ELLs, other than in ordinality and sequence). It should also be noted that the nested model comparisons summarized in Table 5 are based on the serial manipulation of single parameters. For example, the nested model comparison for intercept represents a statistical test of group differences in average readiness when achievement and deceleration freely estimated. When all parameters were simultaneously constrained as equal, there were large differences between the Spanish-speaking ELL group and the other two groups on all skill measures. Even on rate and measurement, where there were no apparent differences in the individual parameter estimates, there was a very large overall difference between the native English-speaking and Spanish-speaking ELL groups (Δχ² = 35.84, p < .001). In the analysis of total scores, intercept was more predictive of slope in the Spanish-speaking ELL group and marginally so for the native English-speaking group.

Results in Table 6 reflect the same analyses summarized in Table 5 but with student-level SES’s effect on intercept, slope, and shape explicitly modeled and constrained across language groups, thus adjusting mean estimates for differences in the effect of student-level SES. The findings, in terms of the pattern of statistically significant group differences, were virtually identical to those in Table 5 when individual parameters were evaluated serially. However, model comparisons involving simultaneous constraints across all parameters resulted in the expected pattern of findings when compared with the non-SES-adjusted results described above; controlling student-level SES attenuated both the prevalence and magnitude of language-group differences. For example, with SES controlled, the earlier difference between native English speakers and Spanish-speaking ELLs on rate and measurement (Δχ² = 35.84, p < .001) was no longer evident (Δχ² = 2.01, p < .57).

Table 6.

Fit Indices, Growth Parameter Estimates and Group Differences for Unconditional Models Using Proficiency Probability Scores With Student-Level SES Controlled Across Primary Language Groups

Group	Relative size			Ordinality and sequence			Add and subtract			Multiply and divide			Place value			Rate and measurement
	I	S	Q	I	S	Q	I	S	Q	I	S	Q	I	S	Q	I	S	Q
English	.891a	−.062c	.429d	.538a	.616c	.064e	.159a	.551c	−.066d	−.224a	.466c	−.040d	−.521a	.341c	−.013d	−.168a	.019b	.019c
Spanish	.806b	.071c	.386d	.408b	.737d	.044e	.084b	.579c	−.068d	−.286b	.481c	−.040d	−.618b	.376c	−.015d	−.183a	.013b	.022c
Asian	.917a	−.107c	.489d	.570a	.589c	.095e	.189a	.567c	−.068d	−.204a	.476	−.038d	−.522a	.366c	−.011d	−.130a	.013b	.026c

Note. SES = socioeconomic status; I = intercept; S = slope; Q = quadratic. Italicized estimates do not differ significantly from zero at p < .05. Within a skill area, parameter estimates with the same superscripted letters do not differ significantly. Estimates with different superscripts differ significantly at p < .01 or greater.

Discussion

Lesaux (2006) proposed three subgroups for organizing research and policymaking related to ELLs: (a) language-minority students who continue to meet local criteria for formal limited English proficiency or other designation for language support, (b) language-minority students who met local criteria at earlier points but whose current oral English proficiency levels no longer warrant language support, and (c) language-minority students who have never received language support services due to their sufficiently developed oral English proficiency at school entry. This study addressed Lesaux’s third category. The group of native English speakers was also a focus. The findings suggest that primary language may be less salient than SES in explaining the mathematics achievement of ELLs in is this group. The study also found mathematics-related school readiness to be the area most correlated with SES across the range of mathematics-related skills for both ELLs and for the group of native speakers of English. The findings highlight the potential pitfalls of overgeneralizing ELLs, given the considerable within-ELL group differences, and suggest a need for an even more nuanced approach to recognizing diversity in ELLs. Several findings are worth noting in this respect.

First, the more prominent relationship of readiness and achievement in the Spanish-speaking ELL group compared with the Asian-language-speaking ELL group (and compared with the native English-speaking group) suggests that change in the Spanish-speaking group during the elementary school years may be more constrained than in other ELL language groups. The Spanish-speaking ELLs not only began school less ready than the other ELL group, but their initial status, on average, was more predictive of later achievement. Although controlling SES partly eliminates differences between the Spanish-speaking ELL and native English-speaking groups, significant language-related effects remain within the ELL group (i.e., between the subgroups of Asian-language-speaking ELLs and Spanish-speaking ELLs)—that is, a Spanish-speaking ELL and an Asian-language-speaking ELL matched on SES and on initial mathematics status nonetheless differ in rates of achievement through fifth grade, on average, in the ECLS-K data. This finding suggests that improving the average initial mathematics status of Spanish-speaking ELLs may (the survey nature of the ECLS-K precludes more definitive conclusions in this respect) in itself be inadequate for closing the language-related achievement gap with Asian-language-speaking ELLs (see Kennedy & Park, 1994). At the least, the finding makes clear that pathways to mathematics achievement differ for the two most prevalent subgroups of ELLs (Fry, 2007).

Second, these findings (particularly the within-ELL variability) underscore important distinctions between language-related differences in mathematics processing and mathematics achievement. Research and theory on mathematics processing naturally assume a cognitive perspective (e.g., Ashcraft, 1992; J. I. D. Campbell, 1994; Dehaene, 1992; Deloche & Seron, 1987; Denes & Signorini, 2000; Hurford, 1987; McCloskey, 1992; Wang, Lotus, Kuhl, & Hirsch, 2007). The general view is that different mathematics-related functions— understanding numerals, retrieving numerical facts, performing calculations or numerical operations, or producing results in spoken or written forms— overlap in areas but are also distinct in key respects (J. I. D. Campbell & Epp, 2004; Dehaene, 1992; Hirsch, Moreno, & Kim, 2001), with language playing an important role, although there is some variety of opinion on the extent and nature of its effect. Encoding-complex models (Bernardo, 2001; J . I. D. Campbell, 1994; J. I. D. Camp-bell & Epp, 2004) emphasize language dependence across all aspects of mathematics processing, with efficiency conditioned on the degree of proximity between the language of instruction, measurement, or query (i.e., the prompt) and the student’s native language. Triple-code models (Dehaene, 1992, 1997; Dehaene, Molko, Cohen, & Wilson, 2004; Dehaene, Spelke, Pinel, Stanescu, & Tsivkin, 1999) assume a language component as well but also include abstract and language-independent mechanisms. Dehaene (1992), for example, suggested that understanding of relative magnitude and success with abstract quantity-based operations are language-independent, whereas code-recognition processes that are necessary for retrieval of mathematics facts and problem solving are language-dependent. Although different in their details, both models, encoding complex and triple code, suggest that mathematics and language-processing systems are integrated and interdependent.

However, results of the present study, notably the achievement advantage of Asian-language-speaking ELLs, do not align with key hypotheses suggested by cognitive-processing models. For example, an encoding-complex model would suggest an advantage for Spanish-speaking ELLs compared with Asian-language-speaking ELLs, given the dissimilarity of English and Asian-related languages, particularly nonalphabetic Asian languages (e.g., Chinese, Japanese, several Korean forms), compared with the shared features of English and Spanish. This inconsistency may stem from one (or more) of several factors. The bilingual nature of the sample may have a role, assuming that the relationship of primary language and mathematics achievement varies according to students’ comfort with the language of instruction and measurement (i.e., an ELL’s second language in the ECLS-K data). The unavailable data on Asian ELLs first language also introduces a degree of ambiguity, given that several alphabetic Asian languages are more similar to Spanish than English in their consistency of sound to letter correspondences. A more compelling explanation (perhaps) is that cognitive-processing theories are poorly equipped for anticipating population-level achievement trends or for explaining group differences in outcomes. Although language may be directly (i.e., at the individual or cognitive level) implicated in mathematics-related differences, large-sample parameter estimates and hypotheses about broad group differences may be better informed by theories that operate at a similarly broad level, with language representing a proxy for factors that directly influence achievement (Goyette & Xie, 1999).

In this context, the earlier-mentioned research on the relationship of language and culture (Chen & Stevenson, 1995; Flynn, 1991; Kao, 1995) is instructive. Indeed, even within the group of Asian-language-speaking ELLs, the relationship of parental expectation and student achievement appears salient (Chen & Stevenson, 1995; Huntsinger, Jose, Liaw, & Ching, 1997; Parmar, Harkness, & Super, 2004). For example, Goyette and Xie’s (1999) analysis of the National Educational Longitudinal Survey found large differences in the achievement expectations of parents from different groups within the Asian American community (as measured by years of expected education) and corresponding patterns in the mathematics scores of students from the same groups. When SES and generational status were controlled (e.g., SES and status as a member of a first generation both have direct effects on parents’ achievement expectations but are confounded with ethnic group), these differences were attenuated in all groups except Chinese Americans and Southeast Asian Americans. Parents in these two groups had higher expectations than did Caucasian parents and parents from the other Asian-language ethnic groups, and children in these two groups significantly outperformed students from other Asian-language groups on the NAEP mathematics test.

A similar pattern may be evident in the ECLS-K data. Although distinct Asian-language groups were not compared, the significantly greater variation in the Time 1 scores of Asian-language-speaking ELLs, compared with both native English speakers and Spanish-speaking ELLs, suggests the presence of distinct subgroups within the group of Asian-language-speaking ELLs. The greater variance in estimates of slope for the Asian-language group (although not statistically significantly so) are also consistent with the possibility of distinct subgroups.

Skill-Specific Trajectories

Trends for specific mathematics skills were estimated (a) without constraints on SES and (b) with the effects of SES specifically modeled and constrained across groups. SES’s effect was similar across these two analyses, in terms of specific parameters. However, comparisons involving simultaneous constraints across all growth parameters were more similar in outcome to results using the ECLS-K total mathematics score (see Figure 1): In general, controlling student-level SES attenuated both the prevalence and magnitude of readiness differences between ELLs and native English speakers. This finding underscores the importance of early intervention and high-quality preschool opportunities for all students from low-SES settings (see F. Campbell, Pungello, Miller-Johnson, Burchinal, & Ramey, 2001) and particularly for low-income Spanish-speaking ELLs.

However, as suggested elsewhere, enhanced preschool opportunities alone may not be sufficient to narrow the language-related mathematics achievement gap, given the presence of significant school-level SES effects and the fact that later success in mathematics, whether basic arithmetic or higher level mathematics, is dependent on the acquisition and application of prerequisite knowledge and skills (Aunola et al., 2004; Rittle-Johnson, Steigler, & Alibali, 2001). For example, fluency with whole numbers, including automatic recall of multiplication and division facts, is critical to success in pre-algebra and algebra (National Mathematics Advisory Panel, 2008). In accordance, the sizable number of fifth-grade students not proficient in these areas (9%, 12%, and 5% of native speaking, Spanish-speaking ELLs, and Asian-language ELLs, respectively) is a real concern for school professionals. It may also represent an opportunity. If math skills are more instructionally determined and structurally hierarchical than literacy-related abilities, they may also be more sensitive to systematic, explicit instruction and repeated practice, particularly rote skills such as the recall of basic math facts. They may also be less likely than reading skills to flourish in the absence of quality instruction, a particular concern for students in low-SES schools, where instructional quality may be an issue, and for ELLs, who may benefit less from early mathematics instruction because of language- and literacy-related barriers and are thus more likely than native English speakers not to acquire essential early skills (Abedi, 2004; Abedi & Lord, 2001; Brown, 2005; Carey, Fennema, Carpenter, & Franks, 1995) and to experience long-term difficulties as a result.

Future Research

As suggested, SES is thought to reflect differences in children’s early and ongoing opportunities to participate in and benefit from events and activities that build early number sense. Less clear, however, is the extent to which low SES is experienced differently by different language groups, because of cultural or other differences (e.g., do the damaging aspects of poverty or the supporting features of high SES vary across groups?). Like SES, language represents a more comprehensive and multifaceted construct. Classification as ELL varies widely, both across states and within states across school settings or contexts. There is lack of consensus in the literature and in practice on who should be considered an ELL and on factors that best regulate the duration of such a classification. For example, no clear guidelines exist for classifying students whose home language is a nonstandard dialect of English, students who come from truly multilingual home-language settings (whether or not one of those languages is English), and students who have become proficient English speakers and readers after years of instruction but whose home language is still other than English. Meaningful distinctions within the Asian-language group also generally go unacknowledged. This variation in classification may represent significant differences and, thus, conditions the reliability of policy and practice recommendations derived from studies that use broad definitions of ELL status as a grouping variable.

The correlates of school-level SES, their relationship with early mathematics outcomes, and their interaction with school-wide reform efforts that target improved outcomes for ELLs should be considered in more detail as well. Schools that “beat the odds” are the subject of considerable inquiry (see Borman, 2005). However, the notion of “odds” suggests a degree of external validity that is sometimes not apparent in this research, because of the lack of reliable achievement estimates on which to base expectations for different SES and language demographics. National probability data like the ECLS-K may be useful for validating and perhaps even augmenting these more descriptive studies by establishing reliable markers against which to compare and evaluate school-level performance. Models that account for the increasingly skillful use of oral English in ELLs are needed as well, particularly as a means for differentiating instructional options. The inter-relationship of reading competence, English language proficiency, and mathematics performance also needs additional study.

Summary

Although these results do not support a causal argument for the effects of primary language or low SES, they are externally reliable in that they represent the population of English-proficient students beginning kindergarten in 1998. The findings suggest that primary language may be less salient than SES in explaining the mathematics achievement of Spanish-speaking and Asian-language-speaking ELLs who are English-language proficient. The study also found mathematics-related school readiness to be the area most correlated with SES. Findings suggest significant gaps in levels of performance across the range of mathematics-related skills and considerable variation within the ELL group and within the Asian-language-speaking subgroup of ELLs.