Simultaneous Measurement of Cerebral Blood Flow and Transit Time with Turbo Dynamic Arterial Spin Labeling (Turbo-DASL): Application to Functional Studies

Abstract

A turbo dynamic arterial spin labeling (Turbo-DASL) method was developed to simultaneously measure cerebral blood flow (CBF) and blood transit time with high temporal resolution. With Turbo-DASL, images were repeatedly acquired with a spiral readout after small-angle excitations during pseudo-continuous ASL and control periods. Turbo-DASL experiments at 9.4 T, without and with diffusion gradients were performed on rats anesthetized with isoflurane or α-chloralose. We determined blood transit times from carotid arteries to cortical arterial vessels (TT_a) from data obtained without diffusion gradients, and to capillaries (TT_c) from data obtained with diffusion gradients. Cerebral arterial blood volume (CBV_a) was also calculated. At the baseline condition, both CBF and CBV_a in the somatosensory cortical area were 40–50% less in rats with α-chloralose than in rats with isoflurane, while TT_a and TT_c were similar for both anesthetics. Absolute CBF and CBV_a were positively correlated, while CBF and TT_c were slightly negatively correlated. During forepaw stimulation, CBF increase was 15±3% (n=7) vs. 60±7% (n=5), and CBV_a increase was 19±9% vs. 46±17% under isoflurane vs. α-chloralose anesthesia, respectively; and CBF vs. CBV_a changes were highly correlated. However, TT_a and TT_c were not significantly changed during stimulation. Our results support that arterial CBV increase plays a major role in functional CBF changes.

INTRODUCTION

Arterial spin labeling (ASL) MRI (1–4) can be used to quantify in vivo tissue perfusion, such as cerebral blood flow (CBF), without using a contrast agent. With this technique, water proton nuclear spins in arterial blood are magnetically labeled and used as freely diffusible tracers to observe perfusion rates with MRI. Arterial spin labeling can be achieved by either continuous ASL, in which a long RF pulse, on the order of seconds, inverts the proton magnetization in the carotid arteries (1), or by pulsed ASL in which a relatively short RF pulse, on the order of milliseconds, changes the longitudinal magnetization of the arterial blood in a slab proximal to the imaging section of interest (2–4). Following spin labeling, arterial blood travels from the labeling plane to capillaries where it exchanges with tissue water, resulting in a change in tissue proton magnetization. The arterial blood transit time (TT) from the labeling plane to the vascular compartment within an imaging pixel is an important parameter for determining CBF (5), and may be sensitive to vascular viability and related to disease pathology (6–7). Thus, it is crucial to measure the arterial blood transit time in normal and pathological subjects.

With pulsed ASL measurements, repeated acquisitions of ASL images with small flip angle excitations can be performed after the ASL pulse (8–12), allowing the rapid detection of multiple spin labeling time points. These methods include Look-Locker flow-sensitive alternating inversion-recovery (LL-FAIR) (8), inflow turbo-sampling FAIR (ITS-FAIR) (9), turbo transfer insensitive labeling (Turbo-TILT) (10), and rapid acquisitions after signal targeting with alternating radio frequency (STAR) ASL (11, 12). With pulsed ASL models (8–12), arterial blood transit time and CBF have been successfully determined in humans; however, low sensitivity limits its application in rodent models. With continuous ASL measurements, transit times can be determined by varying the post-labeling delay (7, 13, 14) or by using the dynamic ASL (DASL) technique (15, 16). With DASL, images are acquired during repeated on-and-off periods of a long ASL pulse (i.e., three times longer than T₁ of tissue). To improve temporal resolution of ASL signals, the onset time of each ASL pulse is shifted relative to MRI data collection. DASL has been used to simultaneously measure arterial blood transit time and CBF in rats (15, 16), but the long experimental time limits its utility for dynamic studies, such as fMRI.

Arteries and arterioles that supply blood to capillaries near active neurons actively dilate during functional stimulation (17, 18). If we model blood flow according to the Poiseuille’s equation describing the relationship between flow, resistance, and pressure of a Newtonian fluid in a long straight tube, a 10% increase of vessel diameter (i.e., 21% CBV increase) should induce a 46% increase in blood flow. This relationship also suggests that increased arterial CBV (CBV_a) will also result in shorter arterial blood transit times. This expectation appears to be supported by human fMRI measurements (8, 10, 12, 14, 19), where increases in functional CBF are accompanied by shorter transit times. However, in our previous functional measurements during somatosensory stimulation in isoflurane-anesthetized rats (20), relative changes in CBF and CBV_a were similar, suggesting that there was no significant change in the arterial blood transit time. Thus, direct measurement of arterial blood transit times with high temporal resolution is necessary to determine if stimulation leads to changes in arterial blood transit times in rodent models, and if our previous observation resulted from the use of isoflurane.

In this work, a modified dynamic ASL method was implemented with rapid repetition of data collection during pseudo-continuous ASL and control periods, which we refer to as turbo dynamic arterial spin labeling (Turbo-DASL). Turbo-DASL experiments at 9.4 T with a temporal resolution of 4 s were performed on isoflurane- and α-chloralose-anesthetized rats during forepaw stimulation. Studies have shown that isoflurane increases the baseline CBF and blunts the evoked CBF response, while α-chloralose has a lower baseline CBF and exhibits a higher CBF response (20, 21). To measure blood transit times from carotid arteries to cortical arterial vessels (TT_a) and to capillaries (TT_c), Turbo-DASL was performed without and with flow-crushing bipolar diffusion gradients. Cerebral arterial blood volume (CBV_a) was also calculated from ASL signals acquired with and without diffusion gradients (22). Baseline and evoked CBF, TT_a, TT_c and CBV_a in the somatosensory cortex were measured and compared in rats under isoflurane or α-chloralose anesthesia.

THEORY

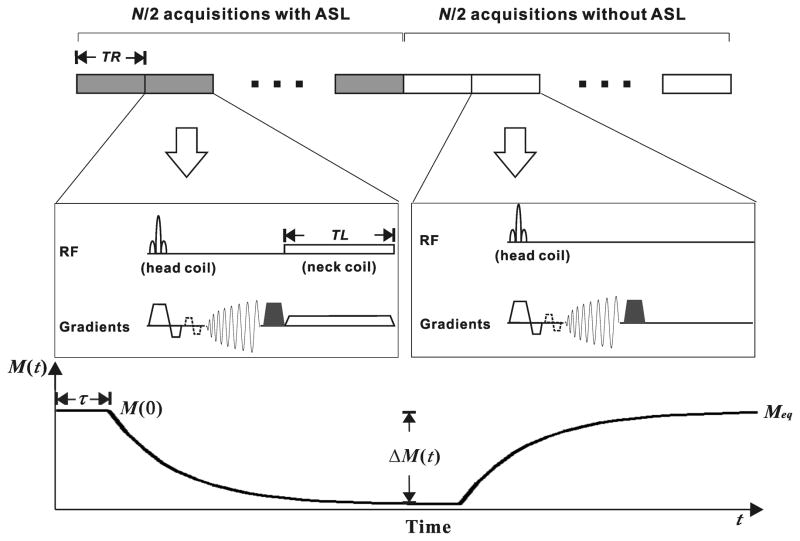
The Turbo-DASL technique was implemented with rapid repetition of spiral data acquisition for improved temporal resolution. Figure 1 shows the schematics of the imaging protocol, pulse sequence and expected MRI signal. In one Turbo-DASL cycle consisting of N images with a repetition time, TR, the first half of the images are acquired with ASL, and the second half of the images are acquired without ASL as a control. A spin labeling pulse with duration TL is applied between each spiral image acquisition and subsequent excitation pulse. To minimize the magnetization transfer effect in imaging slices, actively-decoupled neck and head coils can be used for spin labeling and for data acquisition, respectively. The time-dependent magnetization during one Turbo-DASL cycle is dependent on perfusion and the apparent longitudinal relaxation rate (R_1app) in the presence of repeated excitations (see Fig. 1 expected time course). R_1app = R₁−ln(cosθ)/TR where R₁ is the spin-lattice relaxation rate of tissue water and θ is the flip angle of the excitation pulses (9). The magnetization at time t, M(t) is described as

Figure 1.

Schematic diagrams of the Turbo-DASL pulse sequence (top) and the expected signal response (bottom). A cycle of N images with repetition time (TR) consists of N/2 acquisitions with ASL and the other N/2 without ASL. Spiral data collection is applied after a low flip angle excitation RF pulse for obtaining short-TE images, and followed by a magnetization-dephasing gradient pulse (filled trapezoid). Diffusion gradients (dashed trapezoids) are optionally applied to eliminate arterial blood signal and to measure blood transit time to capillaries. Arterial spin labeling pulse with labeling time (TL) is applied using a neck labeling coil along with z-axis gradient around the carotid arteries. The signal M(t) varies with respect to time t. τ is the cerebral blood transit time from the carotid arteries to vasculature in the imaging slice, and M(0) and M_eq are the signal intensities at t = 0 and steady-state in the presence of repetitive excitations, respectively. ΔM(t) is the signal difference between labeling and control periods with respect to time t.

$$M(t)=M(0)e^{-t\cdot R_{1\mathit{app}}^{\prime }}+M_{eq}(1-e^{-t\cdot R_{1\mathit{app}}^{\prime }})-\mathrm{\Delta }M(t),$$ [1]

where M(0) is the magnetization at t = 0; M_eq is the magnetization at the steady-state condition; ΔM(t) is the perfusion-induced magnetization due to ASL; and $R_{1\mathit{app}}^{\prime }=R_{1\mathit{app}}+f/\lambda$ where f is the cerebral blood flow and λ is the brain-to-blood partition coefficient. ΔM(t) can be solved using the general kinetic model proposed by Buxton et al. (23), in which blood tracer (spin) delivery function c(t) is convolved with tracer decay (i.e., magnetization relaxation) m(t) and residual function r(t).

When t is shorter than the blood transit time from the labeling position to the imaging pixel τ, ΔM(t) is zero and M(t) is constant if M(0) = M_eq. When the arterial signal contribution is significant, a two-compartment (tissue and artery) model is valid. For simplicity, a one-compartment ASL model is applied here with the assumption that blood exchanges with extravascular tissue water rapidly. When t ≥ τ, ΔM(t) is

$$\mathrm{\Delta }M(t)=\frac{2M_{0}f}{\lambda }{\int }_0^{t}c(t^{\prime })\cdot r(t-t^{\prime })m(t-t^{\prime }){dt}^{\prime }$$ [2]

where M₀ is the fully-relaxed tissue magnetization. The delivery function c(t) = α₀e^−τ·R_1a is the degree of spin-labeling at the labeling position and R_1a is the spin-lattice relaxation rate of arterial blood water. Since pseudo-continuous ASL is proposed in Fig. 1, α₀ is (TL/TR) of the spin labeling efficiency measured with continuous ASL, assuming that the labeled spins in arterial vasculature are not perturbed by excitation RF pulses before they exchange with tissue spins. The residual function r(t) = e^−t·f/λ, and the tracer decay function m(t) = e^−t·R_1app. Eq. [2] can be rewritten as

$$\mathrm{\Delta }M(t)=\{\begin{array}{ll}0\hfill & t<\tau \hfill \\ \frac{2M_0{\alpha }_0{e}^{-\tau \cdot R_{1a}}f}{\lambda R_{1\text{app}}^{\prime }}[e^{-max(t-\mathrm{\Delta }-\tau ,0)R_{1\text{app}}^{\prime }}-e^{-(t-\tau )\cdot R_{1\text{app}}^{\prime }}]\hfill & t\ge \tau \hfill \end{array},$$ [3]

where the max function returns the larger of the two values, and Δ= (N/2)·TR. During the first set of N/2 images, with ASL, the magnetization decays according to ( $1-e^{-(t-\tau )\cdot R_{1\mathit{app}}^{\prime }}$) at t > τ. During the second set of N/2 images, the magnetization begins to recover to M_eq at t > Δ+ τ. In order to obtain CBF (f) and blood transit time from the Turbo-DASL data using Eqs. [1] and [3], α₀, M₀ and $R_{1\mathit{app}}^{\prime }$, need to be determined. The spin labeling efficiency is measured in the usual manner, and M₀ and $R_{1\mathit{app}}^{\prime }$ can be determined from a fit of signal decay, M(t), obtained with the same imaging parameters, but without ASL. M(0), M_eq, f and τ are then determined from one Turbo-DASL cycle (see Fig. 1). τ is the blood transit time from the labeling plane to the cortical arterial vessels (TT_a) in the absence of flow crushing gradients, and to the capillaries (TT_c) when flow-crushing gradients are applied before data acquisition.

MATERIALS AND METHODS

Animal Preparation

This study used thirteen male Sprague-Dawley rats weighing 350–450 g (Charles River Laboratories, Wilmington, MA, USA), and all procedures were approved by the University of Pittsburgh Institutional Animal Care and Use Committee. Animals were initially induced with 5% isoflurane in a mixture of medical air and O₂ gases, then intubated and mechanically ventilated. The femoral artery was catheterized for blood sampling and pressure monitoring. During the imaging experiments, animals were maintained with an air: O₂ mixture such that the fraction of inspired oxygen was 30%. Animals were anesthetized with 1.5% isoflurane (n = 8), or an infusion of α-chloralose (an initial 55 mg/kg i.v. bolus followed by 25 mg/kg/hr) (n = 5). Blood gases were sampled intermittently. The arterial blood pressure and the breathing pattern were recorded with a multi-trace recorder (AcKnowledge, Biopak, CA). End-tidal CO₂, blood gases and blood pressure were kept within normal physiology ranges and body temperature was maintained at 37.5°C using a circulating water pad.

Imaging Experiment

All MRI experiments were performed on a 9.4 T, 31-cm-bore MRI system (Varian, Palo Alto, CA), equipped with an actively shielded 12-cm inner diameter gradient insert (Magnex, Abingdon, UK), which operates at a maximum gradient strength of 400 mT/m and a rise time of 120 μs. Two actively-decoupled coils were used: a neck coil for arterial spin labeling and a surface coil for imaging brain. Localized shimming was performed over a volume covering the imaging region to yield a water spectral line-width of less than 30 Hz. Anatomical T₁-weighted images were acquired with a conventional Turbo Fast Low Angle SHot (TurboFLASH) using an inversion time of 1.4 s. A single 2-mm thick coronal slice covering the primary somatosensory cortex was selected according to anatomical images, multi-slice scout fMRI data, and rat brain atlas (24).

All Turbo-DASL images were acquired with a single-shot spiral read-out (25). The imaging parameters were as follows: flip angle in the contralateral primary somatosensory cortex=21^o–27^o, measured by the B₁ mapping method with doubling of the RF power (26); TE = 6 ms; matrix size = 64 × 64; field of view = 2.56 cm × 2.56 cm; off-resonance frequency for ASL = 8500 Hz; and z-axis gradient strength for ASL = 1 G/cm. To determine M₀ and $R_{1\mathit{app}}^{\prime }$, 20 images were acquired with the same imaging parameters used for Turbo-DASL, but without the ASL pulse. To determine whether f and τ are sensitive to experimental parameters, Turbo-DASL experiments (without stimulation) were performed in one isoflurane-anesthetized animal with TR = 100 and 200 ms with TL = 70 and 170 ms respectively, and N = 40 and 80.

For functional studies in seven isoflurane-anesthetized and five α-chloralose-anesthetized animals, Turbo-DASL experiments with N = 40 images, TR = 100 ms and TL = 70 ms were performed without and with flow-crushing diffusion gradients (b = 50 s/mm²), which minimizes arterial blood signals (22). The flow-crushing gradients were simultaneously applied to all three axes to minimize the duration of the gradient pulse and consequently TE. Somatosensory stimulation was performed on one forepaw by repeated electric pulses with the parameters optimized under isoflurane anesthesia (pulse duration: 1 ms, current: 1.3–1.4 mA and frequency: 6 Hz) (27–28), or under α-chloralose anesthesia (pulse duration: 0.3 ms, current: 2.0 mA and frequency: 3 Hz) (21). One fMRI run consisted of 5 baseline (20 s), 5 stimulation (20 s), and 10 baseline (40 s) cycles, with inter-run delay of > 2 min. About 50 runs were repeated.

Data Processing and Analysis

All image reconstruction and computations were carried out off-line with MATLAB (Mathworks, Natick, MA) scripts. All repeated fMRI runs with the same imaging parameters were combined to obtain one averaged fMRI run for each subject. No image coregistration, spatial smoothing, or temporal and spatial filtering was conducted. M₀ (M(0) in Eq. [1]) and $R_{1\mathit{app}}^{\prime }$ were determined from 20 images without ASL using Eq. [1] without theΔM(t) term. Since the degree of spin-labeling in the labeling position, measured with the method as described in (29), was 0.7 with our setup, the labeling efficiency, α₀, was assumed to be 0.7×(TL/TR). R_1a is 0.43 s⁻¹ at 9.4 T (30). With these parameters and using a brain-to-blood partition coefficient, λ, of 0.9 g/ml, f,τ, M(0), and M_eq were determined for each Turbo-DASL cycle with a pixel-by-pixel or region-by-region fit using Eqs. [1] and [3]. Data were recorded as the mean ± SD for statistical analysis.

To determine the effects of imaging parameters TR and N on the fitted parameters (i.e., CBF and TT) of Turbo-DASL, data sets from one animal without stimulation were analyzed. All repeated Turbo-DASL cycles with the same imaging parameters were averaged, resulting in one Turbo-DASL cycle for each experimental condition. Then, somatosensory cortical and large vessel regions of interest (ROI) were chosen, based on the brain atlas and anatomic images. Time courses from one Turbo-DASL cycle were obtained from these ROIs.

For fMRI data (n = 12), baseline CBF and TT maps were obtained from one averaged pre-stimulus Turbo-DASL cycle for each animal. Time-dependent CBF and TT maps were also determined on a Turbo-DASL cycle-by-cycle basis, and functional maps were generated using a boxcar cross-correlation method with a cross-correlation threshold of 0.5 and the number of cluster pixels of 3. Then, the percent signal changes were calculated from active pixels.

To compare quantitative CBF and TT values between baseline and stimulation periods, we selected one contralateral somatosensory ROI with 3 × 3 pixels, based on the anatomical T₁-weighted image and stereotaxic coordinates of forelimb area (24). We obtained several pieces of information. First, time courses of CBF and TT were determined from ROI-based Turbo-DASL data. Second, baseline values were calculated from one averaged pre-stimulus Turbo-DASL cycle. Third, physiological values during stimulation were calculated from one averaged stimulation Turbo-DASL cycle except the transition period 0–4 s after the onset of stimulation. In addition, we calculated CBV_a from the signals acquired with and without diffusion gradients as (22)

$${\mathit{CBV}}_a=\lambda \frac{\mathrm{\Delta }M(0)/M_0(0)-\mathrm{\Delta }M(b)/M_0(b)}{2{\alpha }_a\cdot \xi -\mathrm{\Delta }M(b)/M_0(b)},$$ [4]

where ΔM(0) and ΔM(b) are the differences between the first and last (i.e., N/2 image) signals during ASL in each Turbo-DASL cycle acquired without and with diffusion gradients, respectively; M₀(0) and M₀(b) are the fully-relaxed initial magnetization M₀ values acquired without and with diffusion gradients, respectively; α_a is α₀·exp(−TT_a·R_1a) that is the effective labeling efficiency considering the arterial blood magnetization relaxation during TT_a; and ξ= exp[− (R_2a^* − R_2t^*)·TE] in which R_2a^* and R_2t^* are the apparent transverse relaxation rates (i.e., R₂^*) of arterial blood and tissue, respectively, and ξ is considered to be 1, because of the short TE (i.e., 6 ms) used here (22).

RESULTS

Baseline Turbo-DASL without stimulation

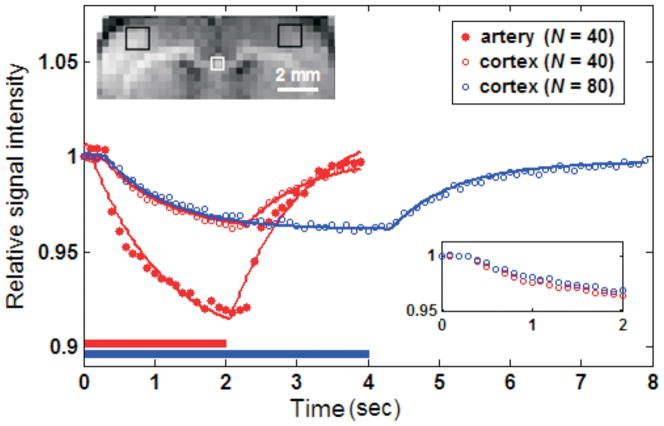
Figure 2 shows the time-dependent Turbo-DASL signal from a single isoflurane-anesthetized rat with different imaging parameters. Data is shown from tissue ROIs in the somatosensory cortex and an artery-containing ROI. Signals exponentially decreased during the ASL period (indicated by horizontal bars), then recovered during the control period. In the artery-containing ROI (white square in the inset image), the signal decrease was more rapid and greater as compared with the somatosensory cortex (filled vs. open red circles). Fitting of the experimental data with Eq. [1] was quite good for the somatosensory cortex (open red and blue circles for N = 40 and N = 80, respectively), but not for areas with a large arterial contribution (filled red circles), indicating that the single-compartment ASL model is reasonable for ROI with a minimal arterial contribution, such as the cortex. To determine the effect of Turbo-DASL imaging parameters on CBF and TT quantification, CBF and TT_a determined from the somatosensory ROI were compared across four different conditions (TR = 100 ms and 200 ms, with N = 40 or 80). Turbo-DASL data with TR = 100 ms and N = 40 and 80 yielded CBF of 1.20 and 1.30 ml/g/min and TT_a of 286 and 310 ms, respectively. When TR was increased to 200 ms, the measured CBF values were 1.34 and 1.51 ml/g/min and the TT_a values were 295 and 302 ms, for N = 40 and 80, respectively. Although TT_a was insensitive to the Turbo-DASL parameters, the measured CBF values slightly increased with TR and N. Our data indicates that the duration of control and labeling periods affected the fitting convergence. When the ASL period is longer (e.g., increased N and/or TR), the steady-state condition is better satisfied and the calculated CBF is likely to be more accurate.

Figure 2.

Regional MR signals during one averaged Turbo-DASL cycle acquired with different imaging parameters without diffusion gradients, from one isoflurane-anesthetized animal. Turbo-DASL data were obtained from somatosensory cortex regions (black boxes in the inset image) and artery-containing ROI (white box), and were fitted with Eq. [1] (see solid lines). The single-compartment model fits very well to the cortical data, but not to data containing significant signal from large arteries. Bars underneath Turbo-DASL time courses indicate ASL durations. Inset time courses show 0 to 2 s data points of the somatosensory ROI for better visualization.

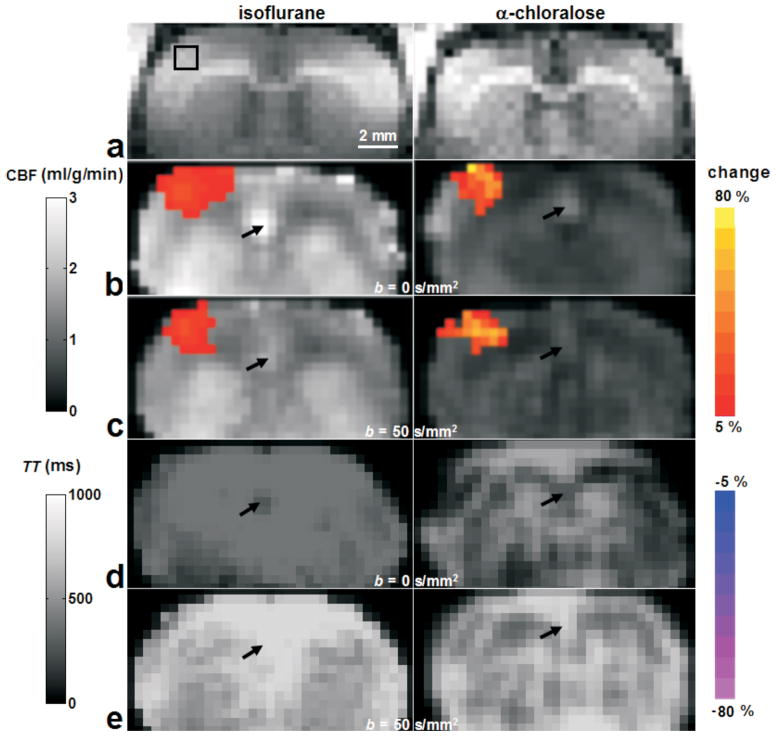
Baseline CBF and TT maps were calculated from Turbo-DASL data with TE = 100 ms and N = 40 for isoflurane- and α-chloralose-anesthetized animals (Fig. 3 gray-scale background images). CBF values determined without diffusion gradients were 20–30% higher than those with flow-crushing gradients (Fig. 3b vs. 3c background), and CBF values in rats under α-chloralose anesthesia (right column) were about 50–60% of that measured in rats under isoflurane anesthesia (left column). Baseline TT values obtained without and with diffusion gradients were 300–400 ms (Fig. 3d) and 500–700 ms (Fig. 3e), respectively. The diffusion gradients had a major impact on pixels that contained signal from large vessels (indicated by black arrows) by reducing computed CBF and increasing calculated TT to values of neighbor tissue pixels.

Figure 3.

Baseline and functional Turbo-DASL results from two rats, anesthetized with isoflurane (left) and α-chloralose (right). Gray scale background maps (except the anatomical T₁-weighted image a) were quantitative CBF values obtained without and with diffusion gradients (b and c, respectively), and TT values without and with diffusion gradients (d and e, respectively). Color maps overlaid on baseline images were percent changes of active pixels responding to forepaw stimulation. On the anatomical T₁-weighted images (a), the black box indicates the 3×3 pixel ROI in the contralateral area, which will be used for further data analysis. Arrows indicate one large arterial vessel region, where the diffusion gradient of 50 s/mm² changed the computed baseline CBF and TT.

Baseline CBF, TT_a, TT_c and CBV_a determined from the contralateral somatosensory ROI (black square in Fig 3a) were tabulated in Table 1. Note that CBF was determined from data with a diffusion gradient to minimize arterial blood contributions. Baseline CBF and CBV_a in rats under α-chloralose anesthesia were 50–60% of those in rats anesthetized with isoflurane (p < 0.05). Baseline TT_a and TT_c values were not statistically different for isoflurane vs. α-chloralose anesthesia.

Table 1.

Turbo-DASL results of isoflurane-anesthetized (n = 7) and α-chloralose-anesthetized (n = 5) rats, in baseline and somatosensory stimulation conditions^a

	Absolute values in baseline condition		Absolute values in stimulation (Functional percentage changes)
Anesthetic	isoflurane	α-chloralose	isoflurane	α-chloralose
CBF (ml/g/min)b	1.05±0.25	0.66±0.14*	1.21±0.28† (15±3%)	1.06±0.23† (60±7%)
TTa (ms)	381±86	396±48	376± 86 (−1±3%)	383±44 (−3±3%)
TTc (ms)	636±83	714±37	627± 92 (−2±3%)	698±40 (−2±2%)
CBVa (ml/100g)	0.59±0.26	0.30±0.14*	0.69±0.29† (19±9%)	0.44±0.19† (46±17%)

^aAll values were obtained from contralateral somatosensory cortical ROIs with 3×3 pixels (mean ± SD). TT_a: arterial blood transit time from the carotid arteries to cortical arteries; TT_c: arterial blood transit time from carotid arteries to capillaries; CBV_a: cerebral arterial blood volume.

^bCBF was measured with diffusion gradients (b = 50 s/mm²).

^*Significantly different from values in the baseline condition under isoflurane anesthesia (p < 0.05, independent two sample t-test).

^†Significantly different from values in the baseline condition under the same anesthesia (p < 0.05, paired two-tailed t-test).

Functional responses in isoflurane- and α-chloralose-anesthetized animals

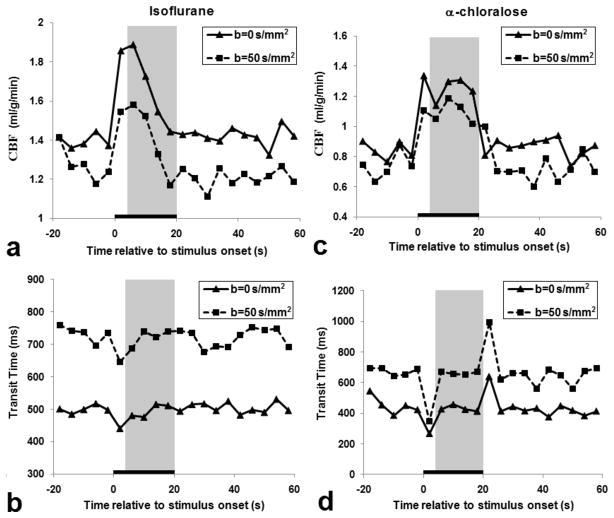
During forepaw stimulation, localized CBF changes were observed in the contralateral somatosensory cortex of animals under both anesthetics, while no significant changes in TT_c and TT_a were detected (see Fig. 3 color maps). Time courses of the contralateral somatosensory ROI were obtained from the same animals shown in Fig. 3 and then plotted in Fig. 4. Time courses of CBF and TT were similar with (dashed lines) vs. without diffusion gradients (solid lines), although there were different baseline values. Under α-chloralose anesthesia (Fig. 4c), functional changes in CBF were much larger and more constant than those under isoflurane (Fig. 4a). However, no significant changes in TT were observed, except during stimulus-on and -off transition periods. Since dynamic changes in CBF and TT during the transition periods between baseline and stimulation conditions (e.g., 0–4 s) introduce errors in CBF and TT quantification from Turbo-DASL data, transition data points were excluded for quantitative ROI analysis.

Figure 4.

Time courses of CBF and transit time in the contralateral somatosensory ROI from two rats shown in Figure 3 under isoflurane (a, b) and α-chloralose (c, d) anesthesia, measured without (b = 0 s/mm²) and with diffusion gradients (b = 50 s/mm²). The black bar indicates the 20 s stimulus period, while the gray-highlighted region indicates the stimulation time period (i.e., 4–20 s) used for further data analysis in Figures 5–6 and Table 1.

Quantitative CBF, TT_a, TT_c and CBV_a determined from the contralateral somatosensory ROI (black square in Fig 3a) during stimulation were tabulated in Table 1. Note that CBF was calculated from data with diffusion gradients to minimize arterial blood contributions, even though relative changes in blood flow measured without and with diffusion gradients were similar (data not shown). Significant increases in CBF and CBV_a were detected under isoflurane and α-chloralose anesthesia (p < 0.05). However, TT_a and TT_c did not change significantly during stimulation under both anesthetic conditions (p > 0.05).

Relationship between CBF, TT and arterial CBV

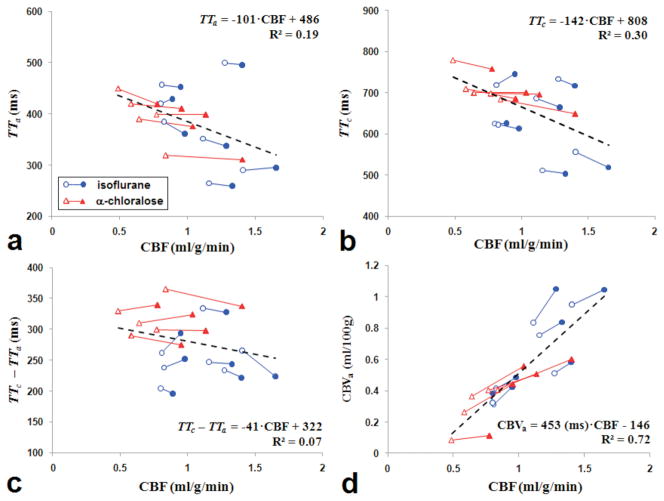
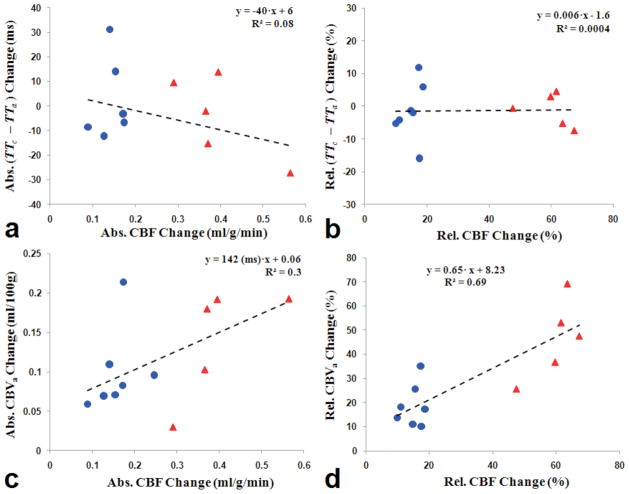
Data from each subject during baseline and stimulation periods were plotted in Figure 5, and the change in transit times and CBV_a were plotted against the corresponding change in CBF in Figure 6. As shown in figures 5a–c, shorter TT_a, TT_c and blood transit time from arteries to capillaries (i.e., TT_c –TT_a) were accompanied by higher CBF values during baseline and stimulation conditions under both anesthetics, albeit weakly correlated. Similarly, functional change of (TT_c –TT_a) was poorly or not correlated with CBF change (Figs. 6a and 6b). As expected, the absolute CBF value was highly correlated with the absolute CBV_a (R² > 0.7) (Fig. 5d), and functional CBF change was highly correlated to functional CBV_a response (Figs. 6c and 6d).

Figure 5.

Inter-animal relationships between physiological parameters obtained from Turbo-DASL data. CBF values measured with diffusion gradients (b = 50 s/mm²) at baseline (open symbols) and stimulation (filled symbols) in each animal (connected line) were plotted against corresponding TT_a (a), TT_c (b), TT_c – TT_a (c), and CBV_a (d). Blue circles with blue lines and red triangles with red lines represent data measured from animals anesthetized with isoflurane and α-chloralose, respectively. The dash lines show a linear fit for all points on each plot. When CBV_a is linearly correlated with CBF (d) with zero intercept, CBV_a (ml/100g) = 320 (ms) · CBF (ml/100g/min).

Figure 6.

Absolute (Abs.) and relative (Rel.) functional changes in CBF vs. TT_c – TT_a (a and b), and CBF vs. CBV_a (c and d). CBF values were measured with diffusion gradients (b = 50 s/mm²). Blue circles and red triangles represent data obtained from isoflurane and α-chloralose anesthetized rats, respectively. The dash lines show a linear fit for all points on each plot. When functional CBF vs. CBV_a relationship was obtained with zero intercept, ΔCBV_a (ml/100g) = 244 (ms) · ΔCBF (ml/100g/min) and ΔCBV_a (%) = 0.82 · ΔCBF (%).

DISCUSSION

Technical aspects of Turbo-DASL

Using the Turbo-DASL method, CBF and TT were obtained with high temporal resolution, facilitating hemodynamic measurements. This approach relies on several assumptions: i) the one-compartment ASL model is appropriate, ii) no dynamic changes of CBF and TT occur during one Turbo-DASL cycle, and iii) the arterial blood signals are not affected by repeated excitations. As mentioned in the Results section, fitting Turbo-DASL data with Eq. [1] is also dependent on ASL and control durations. Due to the use of a 2-s ASL duration for fMRI studies, our calculation yields a slightly underestimated CBF.

In our application, we adopted the single-compartment model. When tissue-dominant pixels are chosen, the single-compartment model fits the data well, as seen in the cortex (see Fig. 2). However, when arterial blood signals contribute significantly (as shown in the artery ROI in Fig. 2 and indicated by arrows in Fig. 3), the single-compartment model is not appropriate; short TT_a and high CBF values were observed when fitting data with Eq. [1]. For this data, a two-compartment (blood and tissue) ASL model can be used to determine CBF, TT_a and TT_c, but the accuracy of these parameters is poor due to limited number of data points.

Dynamic changes in physiological parameters during one Turbo-DASL cycle will generate errors in the calculated CBF and TT because the ASL model assumes a steady-state condition, as seen in Figure 4. Even if CBF and TT do not change during a 4-s period, dynamic change in BOLD signals (in this case M(0)≠M_eq) will induce errors in CBF and TT estimations. In our computer stimulations with baseline CBF and TT values shown in Table 1, the calculated transit time would decrease up to 7% if the BOLD signal linearly increased to 1% during 4 s without CBF and TT changes. When large, rapid, hemodynamic changes occurred in the transition periods between baseline and stimulation periods, large erroneous changes in TT were observed (especially in Fig. 4d). This error can be reduced by shortening each Turbo-DASL cycle; however, the sensitivity of ASL-induced signals is reduced, leading to larger errors in fitting. To take into account these dynamic changes, a more complex model needs to be established with varying TT and other hemodynamic changes with different onset times; however, the limited number of data points available for fitting precludes the use of a more complex model. Thus, in our study these transition periods were excluded from the calculations.

Quantification of CBF and CBV_a values is closely dependent on accuracy of arterial spin labeling efficiency. The assumption of no arterial blood signal saturations by repeated excitations is not likely valid. Arterial blood travels within arterial vasculature during TT_c – TT_a (e.g., ~300 ms) before it enters into the capillaries, and will experience repeated RF excitations at every TR of 100 ms, consequently reducing the spin labeling efficiency. Although the exact saturation level of arterial blood signals is related to RF flip angle, TR and TT_c – TT_a, it is pretty clear that our spin labeling efficiency value was overestimated, resulting in an underestimation of CBF and CBV_a values. However, the relative changes in CBF and CBV_a are valid because the errors canceled each other out. Also, the determination of TT is independent of the accuracy of the spin labeling efficiency, although TT_a (381 ms) in the somatosensory cortex determined under isoflurane anesthesia is slightly longer than that previously obtained under halothane anesthesia (223 ms) (7) or isoflurane anesthesia (260 ms) (16).

Baseline physiological parameters under different anesthetics

The CBF values obtained with Turbo-DASL, 1.05 ml/g/min in rats under isoflurane and 0.66 ml/g/min in rats under α-chloralose, are slightly lower than or similar to CBF values previously obtained, 1.5 ml/g/min under isoflurane (20, 31) and 0.6–0.91 ml/g/min under α-chloralose (30, 32–34). The CBV_a value under isoflurane obtained from Turbo-DASL (0.59 ml/100 g) is less than the reported value with the same animal model, 0.8–1.1 ml/100 g (20, 35). If the same error between the CBV_a values under isoflurane obtained from Turbo-DASL and the previous reports (20, 35) also occurred under α-chloralose, the expected CBV_a is 0.41 – 0.56 ml/100 g under α-chloralose.

As expected, rats anesthetized with the two different anesthetics exhibited different baseline CBF and CBV_a values. CBF and CBV_a with α-chloralose were ~60% and ~50% of that found with isoflurane, respectively. However, the measured transit times were similar for both anesthetic conditions. When all animals were compared together, higher absolute CBF values were associated with higher CBV_a (Fig. 5d) and lower TT (Fig. 5b). These results agree with previous studies during global CO₂ modulation where CBF is positively correlated with CBV_a (20, 32), and CBF is inversely correlated with TT (15, 16). This indicates that higher CBF accompanies a higher blood velocity and a shorter blood transit time from the carotid arteries to cortical vessels.

The difference between TT_c and TT_a is the time that blood has spent in the cortical arterial vasculature, which is referred to as the mean transit time (MTT) of blood throughout the arterial vasculature. This can be also determined by the central volume principle MTT = CBV_a/CBF. The baseline MTT of arterial vasculature calculated from CBV_a and CBF is about 337 ms for rats under isoflurane and about 272 ms rats under α-chloralose, which is similar to 255 ms and 318 ms (TT_c – TT_a in Table 1), respectively. Note that the definition of conventional MTT differs from MR-measured TT_a or TT_c.

Physiological changes induced by forepaw stimulation under two different anesthetics

During neural stimulation, CBF and CBV_a increased 15% and 19% for rats under isoflurane anesthesia, and increased 60% and 46% for rats under α-chloralose anesthesia, respectively. Our observation that an increase in CBF is mostly due to an increase in CBV_a (see Figs. 5d, 6c and 6d) agrees well with our lab’s previous CBF and CBV_a measurements using the same animal model under isoflurane anesthesia (20, 36). Although changes in CBF and CBV_a depend on different stimulus parameters and different animal physiological conditions, our findings with these anesthetics show similar trends to previous measurements using isoflurane (28) and α-chloralose (21). Under isoflurane, CBF was not maintained during the 20-s stimulation period unlike under α-chloralose (Fig. 4a vs. 4c). This is not due to methodological problems, but due to genuine vascular responses. Neural activities and CBF responses quickly decrease during the stimulation period due to neural adaptation effects (28). The dynamic functional CBF change during the stimulation period is closely dependent on the physiological condition of the animal and isoflurane level (37).

During stimulation, TT_a and TT_c slightly decreased in most animals (Figs. 5a and 5b), albeit the decrease was statistically insignificant (Table 1), and a higher CBF increase appeared to have a larger MTT change (Fig. 6a). In several previous studies in rodents, a CO₂ challenge resulted in a significant decrease in TT_a while CBF increased (15, 16, 38). This apparent difference can be due to different vascular regulation mechanisms of local neural activity vs. a global CO₂ challenge, and due to the different stimulation periods. In our forepaw stimulation studies, the 20-s stimulation period led mostly to only dilation of the arterial vessels (36, 39) because venous vessels dilate slowly and passively. A long stimulation period is often used for CO₂ studies; therefore, both arterial and venous vessels dilate (32), which reduces the venous resistance and consequently increases the upstream arterial blood velocity.

Our functional TT_a and TT_c data differ from human studies in which significant transit time decreases were detected during stimulation (8, 10, 12, 14, 19). In visual cortex, Francis et al. (8) reported that TT_a and TT_c decreased 14–20%, while CBF increased 86%; and Ho et al. (12) reported that TT_c decreased 15–25% from 780 ms while CBF increased 42–66%. In motor cortex, Yang et al. (19) reported that TT_a decreased 17% from 650 ms while CBF increased 80%. With a motor and visual task, Gonzalez-At et al. observed a significant decrease in TT_a, about 150 ms from 850 ms, while CBF increased 30% during stimulation (14). Since baseline TT is much larger in the human brain than in small animals, a change in transit time is more easily detectable in humans relative to small animals. Potentially important confounding effects are stimulation duration and type, which will determine arterial vs. venous CBV change and consequently arterial blood velocity change (36).

There are numerous non-MR measurements of blood velocity and/or arterial-to-venous transit time of blood during stimulation. Capillary blood velocity changes have been measured by laser Doppler (40) and by two-photon laser scanning microscopy (41–42). There are two common observations in literature: increasing capillary velocity (41–43) and shortening arterial-to-venous MTT during stimulation (44). During a 20-s somatosensory stimulation, arterial vessels dilate significantly (20, 36, 39) with little or small arterial blood velocity increase, while capillaries and venous vessels do not dilate much (39), consequently increasing blood velocity. Thus, capillary blood velocity increases, and arterial-to-venous MTT is shortened during stimulation. These non-MR findings do not disagree with our Turbo-DASL data.

CONCLUSION

In summary, we have developed a novel Turbo-DASL technique to rapidly measure arterial blood transit time and blood flow, and applied it without and with diffusion gradients to anesthetized rats. Baseline CBF and CBV_a were much less in rats under α-chloralose than under isoflurane, while TT_a and TT_c were similar for both anesthetic conditions. During forepaw stimulation, relative CBF and CBV_a changes in the somatosensory cortex were higher for rats under α-chloralose than under isoflurane. However, TT_a and TT_c were not significantly changed. These results indicate that there is minimal arterial blood velocity change during somatosensory stimulation, and support the hypothesis that arterial dilation plays an important role in functional CBF increase.