In glucose-limited continuous culture the minimum substrate concentration for growth, s_min, is crucial in the competition between the enterobacterium Escherichia coli and Chelatobacter heintzii, an environmentally abundant bacterium

Abstract

The competition for glucose between Escherichia coli ML30, a typical copiotrophic enterobacterium and Chelatobacter heintzii ATCC29600, an environmentally successful strain, was studied in a carbon-limited culture at low dilution rates. First, as a base for modelling, the kinetic parameters μ_max and K_s were determined for growth with glucose. For both strains, μ_max was determined in batch culture after different precultivation conditions. In the case of C. heintzii, μ_max was virtually independent of precultivation conditions. When inoculated into a glucose-excess batch culture medium from a glucose-limited chemostat run at a dilution rate of 0.075 h⁻¹ C. heintzii grew immediately with a μ_max of 0.17±0.03 h⁻¹. After five transfers in batch culture, μ_max had increased only slightly to 0.18±0.03 h⁻¹. A different pattern was observed in the case of E. coli. Inoculated from a glucose-limited chemostat at D=0.075 h⁻¹ into glucose-excess batch medium E. coli grew only after an acceleration phase of ∼3.5 h with a μ_max of 0.52 h⁻¹. After 120 generations and several transfers into fresh medium, μ_max had increased to 0.80±0.03 h⁻¹. For long-term adapted chemostat-cultivated cells, a K_s for glucose of 15 μg l⁻¹ for C. heintzii, and of 35 μg l⁻¹ for E. coli, respectively, was determined in ¹⁴C-labelled glucose uptake experiments. In competition experiments, the population dynamics of the mixed culture was determined using specific surface antibodies against C. heintzii and a specific 16S rRNA probe for E. coli. C. heintzii outcompeted E. coli in glucose-limited continuous culture at the low dilution rates of 0.05 and 0.075 h⁻¹. Using the determined pure culture parameter values for K_s and μ_max, it was only possible to simulate the population dynamics during competition with an extended form of the Monod model, which includes a finite substrate concentration at zero growth rate (s_min). The values estimated for s_min were dependent on growth rate; at D=0.05 h⁻¹, it was 12.6 and 0 μg l⁻¹ for E. coli and C. heintzii, respectively. To fit the data at D=0.075 h⁻¹, s_min for E. coli had to be raised to 34.9 μg l⁻¹ whereas s_min for C. heintzii remained zero. The results of the mathematical simulation suggest that it is not so much the higher K_s value, which is responsible for the unsuccessful competition of E. coli at low residual glucose concentration, but rather the existence of a significant s_min.

Introduction

Growth kinetics

Microbial growth kinetics describes the relationship between the specific growth rate (μ) and the concentration of a growth-limiting substrate (s). It has been proposed already early that μ increases with s in a ‘saturation-type'-like dependence until bacteria attain their maximum specific growth rate (Penfold and Norris, 1912; Hinshelwood, 1946). This was confirmed by Monod and until today his empirical relationship (1) is the most widely used model to describe the kinetics of microbial growth (Monod, 1942; for parameter definitions see Table 1):

Table 1. Parameters and variables used in this study and their definitions.

Abbreviation	Definition
a	Specific maintenance rate (h−1)
D	Dilution rate (h−1)
De	Dilution rate (h−1), where coexistence of competitors is possible
F	Flow rate (l h−1)
Ks	Monod saturation constant (μg l−1)
P	Population composition based on cell number (%)
s	(Steady-state) substrate concentration in continuous culture (μg l−1)
se	Substrate concentration (μg l−1), at which coexistence is possible
sin	Substrate concentration in medium feed (mg l−1)
smin	Predicted substrate concentration at D=0 h−1 (μg l−1)
S	Substrate (mg l−1)
t	Time (h)
x	Biomass concentration (mg l−1)
X	Biomass (mg l−1)
μ	Specific growth rate (h−1)
μmax	Maximum specific growth rate (h−1)
q	Specific uptake rate (mg glucose·mg dry weight −1 · min−1))
qexcess	Uptake rate at substrate excess conditions without any adaptation (mg glucose·mg dry weight −1·min−1)
qmax	Maximum specific uptake rate (mg glucose·mg dry weight −1·min−1)
YX/S	Growth yield (gram dry biomass formed·(gram substrate consumed)−1)

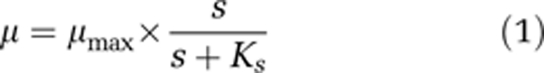Various other models (Blackman, 1905; Powell, 1967; Westerhoff et al., 1982; Koch, 1999) or modifications of the Monod model (Contois, 1959; Powell, 1967; Shehata and Marr, 1971; Dabes et al., 1973; Pirt, 1975; Baloo and Ramkrishna, 1991; Alexander, 1994) have been proposed, in which specific cases can describe selected experimental data equally well or even better. The success of the Monod model is partly due to its simplicity, the similarity to the well-established Michaelis–Menten enzyme kinetics, the biologically meaningful interpretation of the model constants μ_max and K_s, and their experimental accessibility.

Microbial maintenance and its quantification using a minimum substrate concentration (s_min)

As an extension of the Monod model, the concept of maintenance metabolism was proposed in the sixties and critically reviewed recently (van Bodegom, 2007). Microbial maintenance can be quantified and described by different concepts such as the specific maintenance rate (Marr et al., 1963), a maintenance coefficient (Pirt, 1965), and maintenance reflected in a minimum substrate concentration (s_min). Recently, van Bodegom (2007) introduced an additional conceptual model that differentiates between growth and non-growth components of maintenance. In several studies, existence of an s_min has been observed in continuous culture systems (Kovárová et al., 1996; Tros et al., 1996a; Füchslin et al., 2003). In glucose-limited chemostat culture, Kovárová et al. (1996) experimentally examined the growth kinetics of E. coli ML30 (the strain also used in this study) and proposed to expand the Monod model by the additional term of s_min. It was suggested that the phenomenon of s_min is caused by the maintenance energy demand (Pirt, 1965), limiting diffusion kinetics (Schmidt et al., 1985; Bosma et al., 1996) or by the minimum concentration required for enzyme induction (Lechner and Straube, 1984). The extended form of the Monod equation (2) predicts a finite threshold substrate concentration, s_min, at zero growth rate. The specific maintenance rate, a, describes the same phenomenon; it is defined as a negative relative growth rate, in which the product of the specific maintenance rate and the microbial biomass equals the loss of cell material through maintenance (Marr et al., 1963). Maintenance rate a and s_min can be easily related (3). However, as pointed out recently one has to be very cautious in relating the three mathematical parameters as they are based on different assumptions and experimental determination relies on different methods (van Bodegom, 2007).

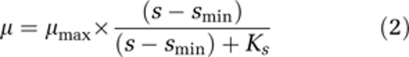Based on mathematical modelling, it is assumed that s_min is especially important during slow growth at low substrate concentrations (Münster, 1993; Kovárová-Kovar and Egli, 1998) as they are normally found in the environment. This hypothesis was experimentally tested here. As an experimental system, we used two strains with differing s_min for growth with glucose, studied the growth and competition of both strains in glucose-limited chemostat culture, and modelled the results with the classical Monod model as well as the model expanded by s_min.

Different experimental approaches have been described in the literature to determine K_s and μ_max and there is no consensus on which of the proposed methods is superior and whether or not all of them (should) lead to the same values (Grady et al., 1996; Kovárová-Kovar and Egli, 1998). In practice, unfortunately, kinetic constants of microbial populations are not always ‘constant' (Grady et al., 1996). The most important reasons for this variability, although rarely quantified, are probably differing cultivation conditions, culture history (Powell, 1967; Kovárová-Kovar and Egli, 1998), or physiological adaptation resulting from a switch between substrate transport systems of different affinity (Harder and Dijkhuizen, 1982; Tros et al., 1996b). Furthermore, when cultivated for extended periods in the same environment populations can evolve through a selection of mutants with increased fitness (Hartl and Dykhuizen, 1979; Wick et al., 2002). Consequently, adaptation processes must be taken into account when competition between different microorganisms for a common substrate is studied. Evolution and composition of a microbial consortium and the environmental concentration of growth-limiting substrates are, therefore, intimately linked. Hence, competition and kinetics are of crucial importance for microbial processes in ecosystems (Gottschal, 1993).

Linking competition experiments at low growth rates with kinetics is connected with several difficulties. The most important one is the very low residual substrate concentrations under which this competition takes place; they are usually in the range of a few μg per litre, that is, below detection limit. Therefore, in contrast to earlier studies at higher growth rates (Senn et al., 1994; Kovárová et al., 1996; Lendenmann et al., 2000), K_s can usually not be determined by measuring the residual concentration of the growth controlling substrate. Another aspect is that slow-growing cells (for example, from a low D in continuous culture) are usually not able to immediately increase the rate of growth when transferred to substrate excess conditions. One has to distinguish between the ‘intrinsic' μ_max achieved after adaptation to substrate excess conditions, and the ‘extant' μ_max achieved without any adaptation phase by originally slowly growing cells just after they had been exposed to substrate excess (see Grady et al., 1996 and Wick et al., 2002).

Competition

The simplest case of competition between microbial strains for a common resource has been defined as ‘pure and simple'. ‘Simple' because only one single nutrient controls the growth rate and ‘pure' because competition for this nutrient is the only interaction between the competitors (Frederickson and Stephanopoulos, 1981). Although it is questionable whether such ‘pure and simple' competition is very common in nature it represents the most extensively experimentally studied interaction among microbes in the laboratory; it is also commonly applied for explaining microbial interactions observed in ecosystems. Numerous ‘pure and simple' ecological scenarios have been put forward (Gottschal, 1993), the most successful of them is the scenario of the ‘opportunist' and the ‘gleaner' for heterotrophic competitors (Veldkamp and Jannasch, 1972; Grover, 1990). Competition between ‘gleaner' and ‘opportunist' for a common single substrate is based on the original Monod kinetic model and its interpretation to competitive scenarios (Herbert et al., 1956). Opportunists have a high μ_max but low substrate affinity (high K_s), which allows them to utilise nutrients in an opportunistic way when they become rapidly available, for example, by a sudden flush of nutrients, or rapid elimination of competitors. In contrast, gleaners are characterised by a low μ_max and high affinity (low K_s) and are designed to operate in oligotrophic ecosystems with scarce organic resources. Their main physiological characteristics are high efficiency of nutrient assimilation and economical metabolism. However, concerning μ_max they are inferior to opportunists.

E. coli and C. heintzii as a model system

E. coli is the standard indicator bacterium for assessing microbial quality of drinking water and potential faecal contamination (World Health Organization, 1996). Therefore, there is considerable interest in understanding its survival and competitiveness in the natural environment. In temperate climates and unpolluted sites, E. coli cells shed into the environment are assumed to be unable to survive and to die quickly (Korhonen and Martikainen, 1991; Bogosian et al., 1996). However, it has been reported that under mesotrophic to eutrophic conditions and (sub)tropical temperatures between 15 and 45 °C this enterobacterium can not only survive but also grow (Hazen and Toranzos, 1990; Tassoula, 1997; Solo-Gabriele et al., 1999). This conflicts with the use of E. coli as a general hygiene indicator for water. As a competition partner for E. coli, we chose the environmentally successful Chelatobacter heintzii (also listed now as Aminobacter heintzii). This gram-negative bacterium is present in quite high numbers not only in activated sludge (up to 1% of the total microbial population), but also in surface waters and soil (0.01–0.1% of total population) (Wilberg et al., 1992; Bally, 1994). It has been studied extensively in our laboratory and was found to be nutritionally versatile and suitable for cultivation in continuous culture (Bally et al., 1994; Bally and Egli, 1996).

The goal of this study was to investigate the competition of E. coli with C. heintzii at environmentally relevant (low) growth rates. However, mostly the kinetic parameters of microbial cultures are determined at elevated specific growth rates because of analytical difficulties. For example, in our chemostat study (Senn et al., 1994; Lendenmann et al., 1996; Kovárová, 1997; Kovárová-Kovar and Egli, 1998) kinetic parameters for E. coli with glucose were collected at dilution rates normally not lower than 0.2 h⁻¹. Hence, it is unknown whether such kinetic properties can be extrapolated to situations of slow growth. Therefore, for both strains the kinetic parameters (extant and intrinsic) were first experimentally determined during slow growth with glucose using different experimental approaches. Then, competition experiments were carried out between C. heintzii and E. coli at low dilution rates in glucose-limited continuous culture. Finally, obtained results were mathematically modelled based on the experimentally determined kinetic Monod parameters.

Materials and methods

Organisms and chemicals

Escherichia coli ML30 (DSM 1329) and Chelatobacter heintzii (ATCC 29600) were used in all experiments. Chemicals were purchased from either Fluka (Buchs, Switzerland) or Merck (Darmstadt, Germany).

Growth media and cultivation conditions

Batch medium

The mineral medium contained, per litre: 275 mg NH₄Cl, 75 mg MgSO₄·7H₂O, phosphate buffer (see below), glucose (see below), and the following trace elements: 5 mg CaCl₂·H₂O, 35 mg KCl, 1.5 mg FeCl₂, 60 μg H₃BO₃, 100 μg MnCl₂·4H₂O, 120 μg CoCl₂·6H₂O, 70 μg ZnCl₂, 25 μg NiCl₂·6H₂O, 15 μg CuCl₂·2H₂O, 25 μg Na₂MoO₄·2H₂O, 5.2 mg EDTA·Na₄(H₂O)₄. To prepare one litre of medium, NH₄Cl and MgSO₄ were dissolved in 900 ml of deionised water and heat sterilised at 121 °C. After cooling down to room temperature, the mineral medium was supplemented with glucose (⩾98%, Fluka) as the only source of carbon and energy (always for a final concentration of 500 mg of carbon per litre) by 0.22 μm filtration using sterile disposable filters (type GVWP, Millipore, Billerica, MA, USA). Also added by sterile filtration after heat sterilisation was 100 ml of phosphate buffer (Na₂HPO₄·2H₂O/KH₂PO₄, 0.56 M with respect to phosphate, pH 7.5), 1 ml of trace element solution (1000 times concentrated, see above) and 0.05 ml of vitamin stock solution with a composition according to Egli et al. (1988).

Determination of μ_max in batch culture

In batch cultures with glucose as sole source of carbon and energy, the ‘extant' maximum specific growth rate, μ_max, of E. coli and C. heintzii was determined by OD₅₄₆ measurements at 30 °C after different precultivation conditions. The μ_max in batch culture was extracted from the linear part of an ln(OD₅₄₆) versus time plot.

Continuous culture medium

The same mineral medium and vitamin stock solution were used as for batch cultivation, except that phosphorus was added in the form of 1.25 ml H₃PO₄ (85%) per litre. The complete mineral medium with all mineral components combined (including trace elements) had a pH of 3–4 and was sterilised by autoclaving at 120 °C for 1 h. After autoclaving and cooling down to room temperature, the mineral medium was supplemented with glucose, lactose or mixtures of the two sugars as the only source of carbon and energy using sterile disposable 0.22 μm filters (Millipore). The concentration of sugars was in total 50 mg of C per litre. In addition, 0.25 ml of vitamin stock solution was added per litre of medium by sterile filtration as described above.

Continuous cultivation

Continuous cultivation was performed in a 3.5-l bioreactor (MBR, Wetzikon, Switzerland) with a working volume of 2.8 l. The bioreactor was equipped with both pH (7.50±0.05) and temperature control (30±0.1 °C). For pH control, a mixture of sterile 0.5 M NaOH and 0.5 M KOH was used. The impeller speed control was set to 1000 revolutions per minute and the oxygen saturation was always kept >90% air saturation. Cultures were regularly checked for wall growth to avoid artefacts as reported earlier (Pirt, 1975).

Chemostat (that is, steady state) conditions were typically reached after >5 volume changes and confirmed by constant biomass concentration (either via optical density or dry cell weight).

Analysis of mixed microbial cultures

In continuous culture competition experiments, the composition of mixed cultures was followed using fluorescence in-situ hybridisation directed against E. coli in combination with cell surface antibodies specific for C. heintzii. For population analysis, cells were collected on a 0.20-μm GTPB microscopy black filter membrane (Millipore) and then stained. The two methods were absolutely specific and no cross-reaction was observed. Samples were first specifically stained either by specific antibodies or by 16S rRNA probe; and subsequently, all cells were stained with 4,6-diamidino-2-phenylindole (DAPI) in order to determine the total bacterial number. For every sample, two measurements in triplicates were made, one for the determination of the fraction of C. heintzii and one for E. coli.

Fluorescence in-situ hybridisation for E. coli

A specific 17-base long 5′-end CY3-labelled 16S rRNA probe against E. coli was designed earlier (Wick et al., 2001) with the oligonucleotide sequence (ACTTTACTCCCTTCCTCCC). Whole cell hybridisation was done according to the procedure described by Manz et al. (1992).

Immunodetection of C. heintzii

The method used was adapted and modified from Bally (1994). All aqueous solutions were filtered before use (0.2 μm pore size) and all glassware was cleaned carefully with detergents, acid and ethanol to avoid any contamination before use. To ∼2 ml of culture sample, one drop (20 μl) of formaldehyde solution (37%) was added. The sample was vortexed for 1 min and kept in the refrigerator for 3 h. Subsequently, the sample was centrifuged (3 min, 10 000 g), the pelleted cells were washed three times with phosphate-buffered saline (PBS: 14.4 g l⁻¹ Na₂HPO₄·2H₂O, 3.2 g l⁻¹ NH₂PO₄·2H₂O, 5.9 g l⁻¹ NaCl, pH 7.5) and finally resuspended in 2 ml of 50% ethanol/50% PBS (vol/vol) and stored at −20 °C. Then, 30 μl of C. heintzii ATCC 29600 strain-specific serum (polyclonal from rabbit; Bally, 1994), diluted 100 times with PBS, was placed on a glass slide and the membrane filter was placed upon the serum. This allowed the serum to diffuse through the membrane filter without disturbing the homogeneous distribution of microbial cells on the filter surface. Slides were incubated for 30 min in a moist atmosphere at 25 °C in the dark. Unbound antibodies were then removed by carefully rinsing the filter with 50 ml of PBS on a glass filtration fritte. The procedure was repeated using 30 μl of 50 times diluted fluorescein isothiocyanate-anti-rabbit-serum (F-0382, commercially available from Sigma, St Louis, MO, USA).

DAPI staining

To determine the total cell number, the cells were fixed on the filter and stained with either the specific antibody or 16S rRNA probe, the filters were covered with 30 μl of aqueous DAPI solution (10 μ) and incubated for 10 min. Subsequently, the cells were washed once with PBS in order to remove excess DAPI from the cells.

Microscopy and determination of mixed microbial cultures

The black filter membrane (Millipore) was placed on a glass slide with 20 μl of PBS. It was covered with a glass slide suitable for fluorescent microscopy. The samples were examined within 5 h after staining using an Olympus BH-2 RFCA microscope ( × 100 DplanApo 100UVPL objective lens, × 10 eyepiece) equipped for epifluorescence microscopy using immersion oil (Olympus, Volketswil, Switzerland).

The total (DAPI stained) cell number was counted by excitation with UV light (360 nm), fluorescein isothiocyanate-positive cells were enumerated using blue light (495 nm) excitation and cells stained with the CY3-labelled 16S rRNA probe using red light (540 nm) excitation in combination with cutoff filter HQ-CY3 61241007 (AF Analysentechnik, Tübingen, Germany). Ten randomly chosen microscopic fields on filters with an appropriate number of total cells (50–200) were counted at each wavelength and the fraction of a specific strain given in % of the total population (P) was calculated.

Biomass and yield determination

Biomass measured as cell dry weight was determined by filtration through 0.2 μm pore size polycarbonate membrane filters (Sterico AG, Dietikon, Switzerland). Cells collected on preweighed filters were washed once with 50 ml of distilled water and filters were dried at 105 °C to constant weight. Optical density was determined in a 1-cm cuvette at 546 nm with a Uvikon 860 spectro-photometer (Kontron, Zürich, Switzerland). The growth yield was expressed as gram of cell dry weight formed per gram of glucose consumed.

Sugar analysis

To avoid significant consumption of sugars during sampling the biomass was immediately (<0.5 s) separated from the culture liquid by filtration. Filtered samples were desalted by electrodialysis and subsequently the concentration of glucose and lactose was determined by HPLC separation, post-column reaction with alkaline copper(II) bisphenanthroline and amperometric detection. The method for sugar analysis and its validation has previously been published in detail (Lendenmann, 1994; Senn et al., 1994). Despite fast separation of the cells from the culture liquid, the residual sugar in the medium is partly consumed by the cells (see Lendenmann, 1994); therefore, the effective detection limit is higher than the technical detection limit. Reliable glucose and lactose determinations, which were not affected by the on-going sugar consumption during sampling, were achieved at concentrations >30 μg l⁻¹. Whereas the determinations of lactose concentrations were not problematic because of its high residual concentration, the residual glucose concentration was frequently below the effective detection limit.

Glucose uptake by whole cells

Concentration-dependent uptake of ¹⁴C-glucose was assayed by a rapid filtration method. Cells from the culture (2 ml) were collected by centrifugation (10 000 g, 2 min) at 4 °C and the supernatant was discarded. In order to keep disturbance of the cells at a minimum the samples were diluted with filtered (0.2 μm pore size) spent chemostat cultivation medium without any detectable residual glucose. The cell suspension in spent medium was incubated for 5 min at 30 °C to assure that remaining glucose was consumed to very low level before -glucose-UL-¹⁴C (Sigma) was added at a defined concentration to start the uptake experiment. As a function of time (15, 30, 45, 60, 90, 120, 150 and 180 s), aliquots of 200 μl were withdrawn from the assay mixture and immediately filtered through cellulose nitrate filters with a pore size of 0.25 μm (Sartorius AG, Göttingen, Germany). Without delay, the filters were washed with 20 ml of PBS buffer containing 50 μ unlabelled glucose. Then, the filters were placed in scintillation vials and 3 ml of scintillation liquid (FilterCount, Packard Instrument B.V., Groningen, The Netherlands) was added. Finally, radioactivity was determined with a BETAmatic I liquid scintillation counter (Kontron Analytical). Uptake rates were calculated from the linear part of the uptake curve and are mean values of three independent transport assays (standard deviation is indicated). In our study, the uptake rate of C. heintzii corresponded well with the measured maximum specific growth rate. Converting the observed q_max (0.0070 mg glucose · mg dry weight ⁻¹ · min⁻¹) into specific growth rate (Equation 4) a μ_max of 0.19 h⁻¹ was obtained, which is close to μ_max observed in batch culture (0.16–0.18 h⁻¹). In contrast, in the case of E. coli the experimentally determined q_max (0.0050 mg glucose · mg dry weight⁻¹ · min⁻¹) was significantly lower than the q_excess measured in our pulse experiment (0.0144±0.0005 mg glucose·mg dry weight⁻¹·min⁻¹). In a previous study, Hunter and Kornberg reported a similar discrepancy between uptake rates for labelled glucose and q_max and these authors used a correction factor of 3.333. When multiplying our q_max calculated from the ¹⁴C-glucose uptake with this factor we obtain a value of 0.01667 mg substrate·mg dry weight⁻¹·min⁻¹, which is very close to the q_excess determined in our pulse experiment (see above). Obviously, a considerable proportion of the glucose taken up was oxidised and lost as ¹⁴CO₂ depending on the physiological state of the cells and assay conditions (Hunter and Kornberg, 1979).

Competition experiments

To perform competition experiments for glucose in continuous culture, E. coli and C. heintzii were first cultivated separately for 10 days in a glucose-limited chemostat at a dilution rate of 0.05 h⁻¹ in order to allow sufficient time for the adaptation of both strains to low glucose concentrations. After 10 days, 100 ml of culture liquid was removed from each chemostat and cross-inoculated to start the competition for glucose between the two strains.

Theoretical wash-in and wash-out curves

The hydraulic behaviour of an ideal flow-through system is described by the theoretical wash-out (5) and wash-in (6) curves and were calculated by the following equations (Pirt, 1975):

Modelling

For mathematical calculations and modelling, the program AQUASIM was used (Reichert, 1998). In earlier work on the growth of E. coli in glucose-limited chemostat culture at 37 °C (Senn et al., 1994), we found that s=f(D) three kinetic models fitted the data with similar quality (Monod, Shehata and Marr, Westerhoff). Extending this work to suboptimal and superoptimal temperatures (17, 28 and 40 °C), we experimentally observed a clear indication for the existence of a finite glucose concentration at zero growth rate, and when extending the classical Monod model with an s_min, the obtained kinetic data could be fitted well and statistically better than with any other model of similar complexity (Kovárová et al., 1996). Hence, the original (1) and the extended Monod model (2) were the obvious model of choice to be applied to our competition experiments. A more extensive search for better fitting models seems presently not justified. Based on this, the following differential equations were used to describe population dynamics and substrate concentrations in the competition experiments:

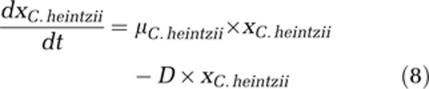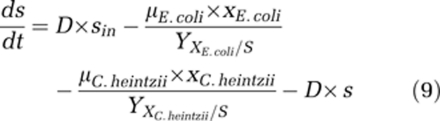Values for K_s, μ_max and Y were determined experimentally (see Results). With the parameter estimation tool of AQUASIM substrate concentration and s_min were inferred. A weighted least squares parameter estimation was performed for s and s_min by fitting calculated mixed culture composition data to measured composition based on cell counts. This was done by minimising χ² values using the secant method and non-linear regression. For the estimation, the standard deviation (σ) was set to 10% if not experimentally determined. It was assumed that the ratio of biomass to cell number of E. coli and C. heintzii, respectively, remained constant during competition experiments.

Results

Determination of μ_max

In batch culture, C. heintzii exhibited a rather constant μ_max independent of cultivation history. When cultivated in continuous culture at D=0.05 h⁻¹ for at least 10 days (ca. 26 generations) and transferred into a batch culture with excess glucose this strain achieved a μ_max of 0.17±0.03 h⁻¹ after a short acceleration phase of 2 h. After repeatedly transferring cells from the exponential growth phase into fresh batch medium only a minor improvement of μ_max from 0.17 to 0.18±0.03 h⁻¹ was recorded after 120 generations, suggesting that for this bacterium extant and intrinsic μ_max are similar under the conditions tested.

A different behaviour was observed for E. coli. When cultured in a glucose-limited chemostat at D=0.05 h⁻¹ (as C. heintzii above) and transferred into a batch culture with excess glucose, linear growth was recorded during the first 3.5 h. After this adaptation phase, exponential growth started and an extant μ_max of 0.54 h⁻¹ was finally reached. Repeated subculturing under excess glucose conditions lead to an increase of μ_max reaching a value of 0.72±0.03 h⁻¹ after 62 generations and 0.80±0.02 h⁻¹ after 120 generations (corresponding to the intrinsic μ_max).

In order to determine the potential μ_max (that is, the ‘extant' μ_max) of slowly growing E. coli, we also determined the q_excess for glucose by pulsing excess glucose directly into a continuous culture of cells that had been growing at D=0.075 h⁻¹ for at least 10 days (26 generations). The pulse of glucose injected was chosen such that the initial concentration was around 1 mg l⁻¹; this is well above the K_s of the culture for glucose (Wick et al., 2002) but did not lead to a significant change in biomass concentration. The medium supply was shut off immediately after the pulse and the decrease in glucose concentration was measured (Supplementary Figure S1). The linear decrease of glucose observed confirmed that the pulsed glucose concentration was significantly higher than K_s, reducing the relationship q_excess=q_max·s/(s+K_s) to q_excess≈q_max. The q_max determined in this way was 0.0144±0.0005 mg glucose·(mg CDW·min)⁻¹. Converting this into specific growth rate (4), assuming that the yield of 0.38 mg CDW (mg glucose)⁻¹ measured during continuous cultivation remained constant, an extant μ_max of 0.33±0.011 h⁻¹ was obtained. We suggest that this extant value is the most appropriate to simulate growth kinetics under the slow and transient growth conditions applied in our competition experiments (D=0.05 or 0.075 h⁻¹). In summary, and as expected for a typical environmental gleaner, C. heintzii exhibited a considerably lower μ_max than the enterobacterium E. coli.

Determination of K_s from glucose uptake rates

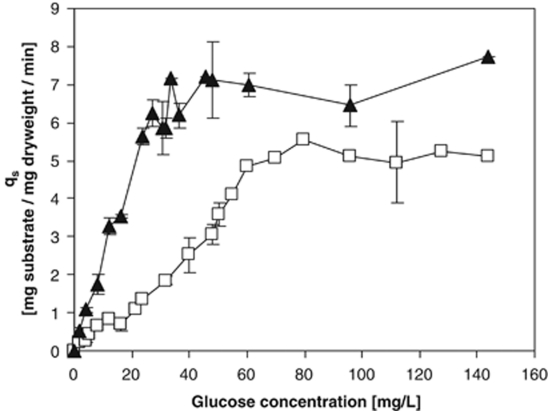
At the low growth rates used it was not possible to reliably determine the steady-state concentration of glucose in chemostat cultures (it was clearly below 30 μg l⁻¹) and to deduce K_s (or s_min) from the Monod equation. Therefore, an alternative approach was taken to determine K_s for glucose of the two strains, namely by monitoring glucose uptake rates of cells at different glucose concentrations (see Figure 1) using ¹⁴C-labelled glucose. For this, cells of E. coli and C. heintzii were cultivated in glucose-limited chemostat culture at D=0.075 h⁻¹ for at least 10 days (26 generations) before samples were taken. To circumvent effects on glucose uptake capacity due to abrupt environmental changes (see Hunter and Kornberg, 1979) harvested cells were resuspended and diluted with 0.2 μm-filtered spent chemostat medium. The q_glucose as a function of glucose concentration is shown in Figure 1 for C. heintzii and E. coli, respectively. For C. heintzii, the q_glucose increased almost linearly up to a glucose concentration of 30 μg l⁻¹. Although this pattern is closer to Blackman than Monod kinetics one can estimate a half saturation constant of 15 μg glucose per litre at 0.5 q_max. The pattern of dependence of q_glucose of E. coli on substrate concentration was similar to that observed for C. heintzii. The cells reached q_max at ∼70 μg glucose per litre and the estimated K_s for glucose is 35 μg l⁻¹, which corresponds well with the intrinsic K_s reported earlier in a glucose-limited chemostat (Kovárová et al., 1996).

Figure 1.

Uptake rate (q_s) of ¹⁴C-glucose by E. coli (□) and C. heintzii (▴) at 30 °C as a function of the glucose concentration in the assay mixture. The cells had been cultivated in glucose-limited continuous culture with a feed of 50 mg of carbon glucose per litre, at D=0.075 h⁻¹ and 30 °C.

Competition for glucose during continuous culture at low dilution rates

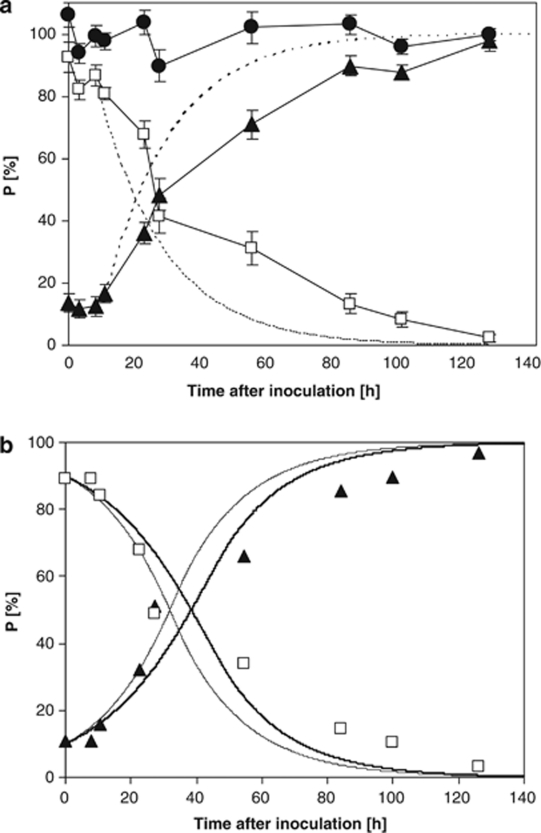
When cells from E. coli and C. heintzii, adapted first to growth in glucose-limited chemostat culture at D=0.05 h⁻¹, were cross-inoculated E. coli was unable to compete with C. heintzii. The results obtained for the competition of E. coli transferred into the C. heintzii chemostat culture are shown in Figure 2a. At each time point, the sum of E. coli plus C. heintzii cells added up to 97.9±3.7% and corresponded well with the cell number determined by DAPI. A lag phase of 8 h was observed before C. heintzii started to displace E. coli and the concentration of E. coli cells decreased slightly slower than predicted by the theoretical wash-out curve. The fact that the displacement of E. coli follows almost wash-out indicates that the enterobacterium was virtually unable to grow, and that cells of C. heintzii exhibited a considerably better competition properties for glucose. Also in the complementary competition experiment (E. coli cells inoculated into the C. heintzii chemostat) the enterobacterium was unable to compete (data not shown). In both chemostat cultures, the residual glucose concentration remained always below the detection limit of 30 μg l⁻¹. In general, higher growth rates favour opportunistic strains; therefore, the competition experiment was repeated at a slightly higher D of 0.075 h⁻¹ (Figure 3a). Because quantification of C. heintzii proved to be very reliable the fraction of E. coli was not determined in this competition experiment.

Figure 2.

(a) Population dynamics (P) of E. coli (□) and C. heintzii (▴) in relation to cell number during competition for glucose in a glucose-limited continuous culture at dilution rate of 0.05 h⁻¹. As a control, the sum of both strains is also given (•). For comparison, the theoretical wash-in () and wash-out () curves are shown assuming a lag phase of 8 h. (b) Prediction of competition for glucose for a mixed culture of E. coli (□) and C. heintzii (▴) in a glucose-limited continuous culture at a dilution rate of 0.05 h⁻¹ using the fits for the different s_min are shown, namely for s_min=18.0 μg l⁻¹ () from Kovárová et al. (1996) and for s_min=12.6 μg l⁻¹ (), a value obtained by parameter estimation.

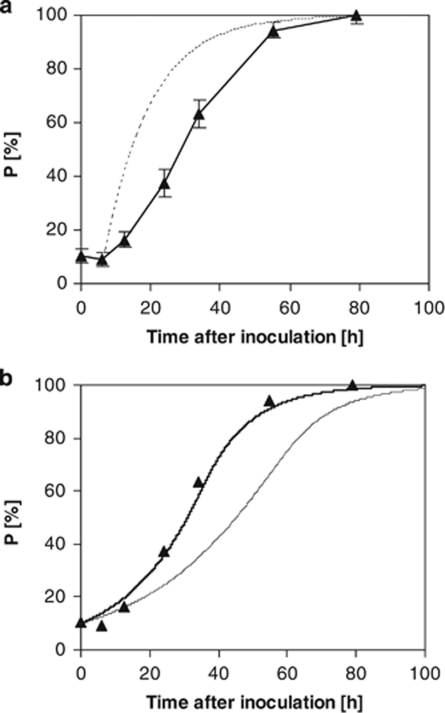
Figure 3.

(a) Population dynamics C. heintzii (▴) in relation to cell number during competition for glucose with E. coli in a glucose-limited continuous culture at a dilution rate of 0.075 h⁻¹ with a glucose feed of 50 mg carbon per litre at 30 °C. For comparison, the theoretical wash-in curve is shown assuming a lag phase of 7 h. (b) Prediction of competition for glucose for a mixed culture of C. heintzii (▴) and E. coli in a glucose-limited continuous culture at a dilution rate of 0.075 h⁻¹. The fits for the different s_min are shown, namely for s_min=18.0 μg l⁻¹ () from Kovárová et al. (1996) and for s_min=34.9 μg l⁻¹ (—), a value obtained by parameter estimation.

Even at this dilution rate C. heintzii was able to outcompete E. coli. Also, here a short lag phase was observed before displacement of E. coli started. However, the deviation of the C. heintzii cell concentration from the theoretical wash-in curve was significantly more pronounced indicating that E. coli was more competitive at this higher dilution rate. Again, it was not possible to reliably determine the residual glucose concentration before and during the competition experiment.

Competition for mixtures of glucose and lactose

In the two previously described experiments, E. coli was virtually unable to withdraw glucose from the common pool and was rapidly displaced by C. heintzii. This raises the question whether or not interactions other than only competition for glucose took place. To test whether C. heintzii negatively affected growth of E. coli (for example, by excreting an inhibitory metabolite), the mixed population was cultivated with different mixtures of glucose and lactose at a D of 0.075 h⁻¹. In contrast to glucose, which serves as a carbon source for both strains, only E. coli is able to consume lactose (Egli et al., 1988). Hence, we tested whether or not kinetics and stoichiometry of growth of E. coli with lactose was affected in the presence of C. heintzii.

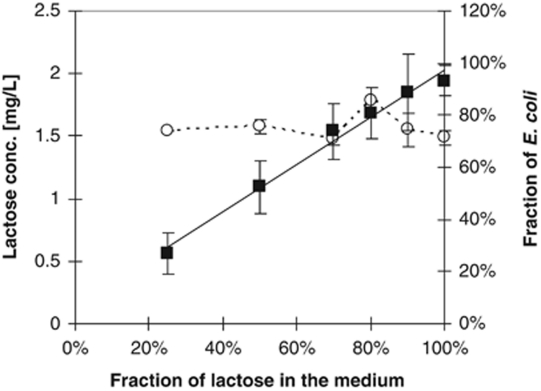
The composition of the bacterial population and the residual lactose concentration determined as a function of the glucose/lactose mixture in the feed medium is shown in Figure 4. The steady-state fraction of E. coli cells increased linearly with increasing parts of lactose in the feed medium. The fact that the contribution of E. coli cells to the total population corresponded perfectly to the fraction of lactose in the feed indicates that E. coli was virtually excluded from the consumption of glucose by C. heintzii and that it grew primarily with lactose. This confirms that E. coli has a substantially lower competitiveness for glucose than C. heintzii under the conditions tested. During growth with all mixtures, the glucose steady-state concentration was always below the detection limit and that of lactose remained constant at 1.5 mg l⁻¹ and was independent of the composition of the feed and the composition of the population. The unaffected lactose utilisation is a strong hint that growth of E. coli was not negatively influenced by the presence of C. heintzii, suggesting that in the two experiments shown in Figures 2 and 3 competition for glucose was ‘pure and simple', that is, the only interaction between the two strains.

Figure 4.

Growth of mixed population of C. heintzii and E. coli in relation to cell number with defined mixtures of lactose and glucose in a carbon-limited continuous culture at D=0.075 h⁻¹ and 30 °C with a total carbon feed of 50 mg l⁻¹. Percentage of E. coli in the bacterial population (▪) and steady-state lactose concentration (○) is shown as a function of the percentage of lactose in the feed medium.

Simulation

The competition performance in glucose-limited continuous culture of the two bacterial strains was simulated using the kinetic parameters (Table 2) determined for C. heintzii and E. coli in pure culture. Both the classical Monod model (Eq. 1) and Monod's model extended with s_min (Eq. 2) were used, the latter because E. coli was reported earlier to exhibit a significant s_min during growth with glucose in continuous culture (Kovárová et al., 1996).

Table 2. Model parameters and their values used for the simulation of growth and competition for glucose in carbon-limited continuous cultures at 30 °C.

	μmaxa	Ks	YX/Sb	smin (at D=0.05 h−1)	smin (at D=0.075 h−1)
E. coli	0.33 h−1a	35 μg l−1	0.38	12.6 μg l−1	34.9 μg l−1
C. heintzii	0.17 h−1	15 μg l−1	0.45	0 μg l−1	0 μg l−1

μ_max, K_s, and Y_X/S were experimentally determined (see Results or Materials and methods) whereas s_min was assessed during modelling by parameter estimation.

^aq_max was measured and μ_max calculated by μ_max=q_max × Y_X/S.

^bY_X/S was determined in the pure culture chemostat just before the competition experiment was started.

Using the experimentally determined parameters, the original Monod model predicts a stable culture of the two strains when competing at a dilution rate 0.05 h⁻¹, at D=0.075 h⁻¹ it predicts that E. coli would win the competition for glucose (compare Figure 5b). This is in contradiction to the experimental outcome. To check whether or not this difference may be due to inaccuracies in the determination of the kinetic parameters, we analysed the sensitivity of the different parameters on the outcome of the competition using the original and the modified Monod equation (Table 3). Whereas both K_s and μ_max can vary considerably without affecting the competitiveness significantly, minor changes in s_min can already lead to the dominance (⩾90%) of one of the strains after 120 h of competition. The sensitivity analysis indicates that only with major changes in the measured kinetic parameters, C. heintzii would win the competition in the simulation. Changes of the size required cannot be explained by inaccuracies in the experimental determination of the kinetic parameters used in the simulation.

Figure 5.

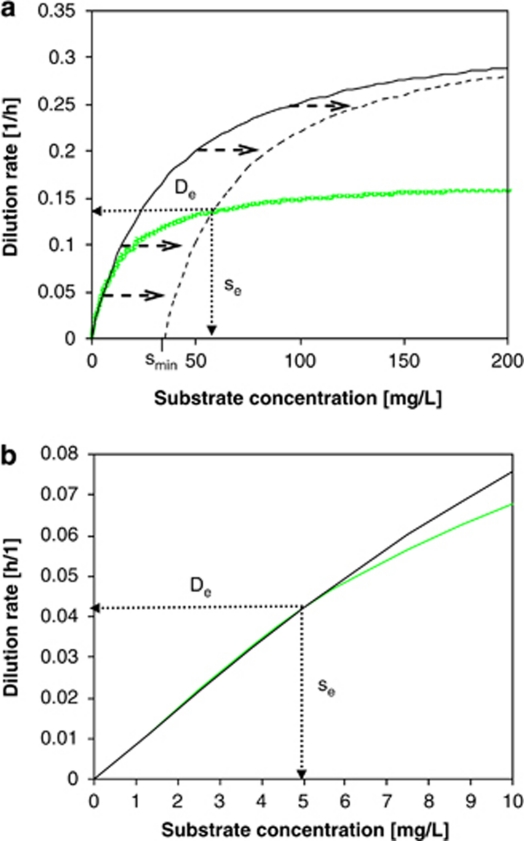
(a) μ–s relationship of E. coli (using original Monod model (—) and Monod model extended with s_min (- - -)) and C. heintzii (Monod model ()). All parameters were determined at D=0.075 h⁻¹. C. heintzii will outcompete E. coli at s<s_e, whereas E. coli will outcompete C. heintzii at s>s_e. Coexistence is theoretically possible at D_e with a steady-state substrate concentration s_e. Kinetic parameters of the two competitors are listed in Table 2. (b) Zoom into the 0–10 μg l⁻¹ concentration range of Figure 5a. At very low substrate concentration (0–5 μg l⁻¹), the classical Monod kinetics predicts for both strains virtually the same specific growth rates and s_e is 5.0 μg l⁻¹ suggesting coexistence, which is in contradiction to the competition experiments shown in Figure 2a.

Table 3. Sensitivity analysis of parameters based on the original (middle column) and the Monod model extended by s_min (right and left column).

Parameters	Dominance of E. colia	Coexistenceb	Dominance of C. heintziia
	⩾0.52 h−1	0.33 h−1	⩽0.22 h−1
	⩽20.6 μg l−1	35 μg l−1	⩾57.5 μg l−1
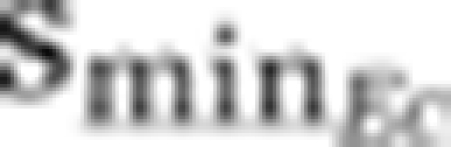	N.p.c	0 μg l−1	⩾2.8 μg l−1
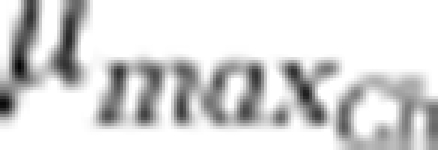	⩽0.11 h−1	0.17 h−1	⩾0.24 h−1
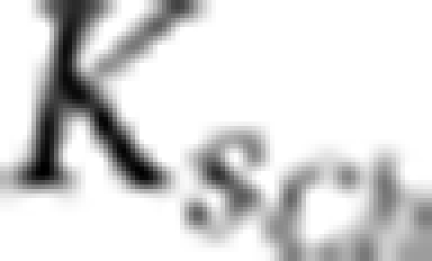	⩾25.5 μg l−1	15 μg l−1	⩽9.1 μg l−1
	⩾2.9 μg l−1	0 μg l−1	N.p.c

For testing sensitivity of the population composition to minor changes in the kinetic parameters, the range of individual parameters was varied while maintaining all other parameters constant. The same substrate supply was used for the simulation as for the competition experiment for glucose in a glucose-limited continuous culture at dilution rate of 0.05 h⁻¹. Equations and default parameters were used as described in Materials and methods.

^aDominance was arbitrarily defined as the cell number of a strain >90% after 120 h of continuous cultivation.

^bKinetic parameters used from Table 2.

^cN.p.=not possible; i.e., dominance of a strain obtained only when s_min set to values <0 μg l⁻¹.

At low growth rates, maintenance energy can have a significant role and is known to affect competition and kinetics (Pirt, 1975; Kovárová-Kovar and Egli, 1998). Hence, we tested whether the Monod model extended with s_min is able to predict the outcome of the two competition experiments, using the same values for the kinetic parameters K_s and μ_max as in the simulations shown in Figures 2b and 3b. As it was not possible to measure s_min directly, the value of s_min was adjusted such that simulation and experimental data were in best agreement for the two competition experiments. For the results obtained at a dilution rate of 0.05 h⁻¹, the values obtained for s_min determined by parameter estimation were 12.6 μg l⁻¹ for E. coli and 0 μg l⁻¹ for C. heintzii. At the higher dilution rate of D=0.075 h⁻¹, the value of s_min for E. coli increased to 34.9 μg l⁻¹ whereas that for C. heintzii remained zero. These values are quite close to the s_min of 18 μg l⁻¹±2, reported by Kovárová et al. (1996) for the growth of E. coli in glucose-limited chemostat culture at 28.4 °C.

Discussion

We started out from the (commonly accepted) assumption that it is possible to predict and explain ‘pure and simple' competition of two bacterial strains for a single resource from Monod kinetic parameters determined in pure culture. This was tested here for an environmental ‘gleaner' (C. heintzii) and an ‘opportunist' (E. coli) at low growth rates in a glucose-limited continuous culture system. It turned out that the classic Monod kinetic parameters μ_max and K_s were not sufficient to explain the observed competition results and both modelling and experimental data suggest that an additional parameter, the maintenance-related minimum substrate concentration for growth, s_min, determines the competitive properties of microbial strains during slow growth considerably more than μ_max and K_s.

The initial determination of the two Monod ‘constants' in pure culture supported earlier suggestions (Grady et al., 1996; Kovárová-Kovar and Egli, 1998) that these ‘constants' may not be constant but may vary considerably depending on growth conditions and the method used for their determination. Grady et al. (1996) proposed to distinguish between ‘extant' and ‘intrinsic' values of kinetic parameters, leading to the question of which values should be used under what conditions. In the attempt to determine relevant values of μ_max and K_s for growth with glucose in our competition scenario, we observed that the two strains behaved very differently with respect to the ability to reach their (intrinsic) μ_max. Populations of E. coli cultivated at low dilution rates in glucose-limited chemostat culture were only able to achieve an (extant) μ of 0.33 h⁻¹ during the first hours after transfer to excess glucose conditions, whereas the intrinsic μ_max of ‘batch-trained' populations was in the range of 0.80 h⁻¹. Only repeated growth cycles in batch culture resulted in a continuous increase of their extant μ_max until the intrinsic μ_max of 0.80 h⁻¹ was approached after some 150 generations. This phenomenon had been reported already earlier, where fully batch-‘adapted' cultures of E. coli ML30 exhibited a μ_max of 0.92 h⁻¹ at 37 °C (Lendenmann, 1994; Senn et al., 1994). Similar findings were reported for other E. coli strains in both glucose-excess (Novak et al., 2006) and glucose-limited chemostat cultures (Wick et al., 2002). It seems that by (so far unknown) mutations and selection the μ_max of E. coli strains can be significantly increased and that the (extant) μ_max is dependent on culture conditions as well as culture history. Consequently, the extant μ_max of 0.33 h⁻¹ was used for simulation of the kinetic behaviour of E. coli in our competition scenario. In contrast, C. heintzii was able to speed up growth quickly and reached its intrinsic μ_max within the first 2 h. Affinity for glucose exhibited by chemostat-adapted populations of both strains was not significantly affected by a transfer to excess or transient conditions, as determined in labelled glucose uptake assays under the conditions used subsequently in our competition experiments (Figure 1). Surprisingly, only a minor difference in K_s for glucose was observed between the enterobacterium and the environmentally successful C. heintzii. The glucose K_s value of 15 μg l⁻¹ determined for C. heintzii is an average value compared with values reported for other environmental bacterial strains, which range from 5 μg l⁻¹ for a lake isolate (Hobbie and Wright, 1965) to 33 μg l⁻¹ for the widespread Aeromonas hydrophila (Van der Kooij et al., 1980). The obtained half saturation constant of 35 μg glucose·l⁻¹ for E. coli corresponds well with K_s values reported earlier for this strain (Kovárová et al., 1996).

Employing the determined kinetic parameters (using the extant μ_max for E. coli) and the original Monod model predicted a virtually stable mixed culture at D=0.05 h⁻¹ and a successful competition of E. coli at D=0.075 h⁻¹. The lower glucose affinity exhibited by E. coli was theoretically easily ‘neutralised' by its higher extant μ_max (Figure 5b). This clearly contradicts the experimentally observed success of C. heintzii in all our competition experiments. A sensitivity analysis suggested that the observed difference between model prediction and experimental results is not caused by inappropriate determination of the kinetic parameters (Table 3). Also, the fact that growth of E. coli with lactose was not affected by the presence of C. heintzii strongly suggests that a negative influence of the presence of C. heintzii is very unlikely (Figure 4) and that competition for glucose was the only interaction between the two strains in our experiments.

All this indicated that the original Monod model is unable to appropriately describe growth and competition during slow growth. Since maintenance requirements are considered to be particularly important during slow growth we also tested whether or not extension of the Monod model by s_min, as used earlier for the growth of E. coli over an extended temperature range (Kovárová et al., 1996), would result in an improved fit of model to experimental data. Indeed, applying this extended Monod model allowed to simulate the outcome of our competition experiments. The enormous impact of s_min on growth kinetics, and consequently on competition at low growth rates, is visualised in Figure 5. The plot demonstrates that in the absence of an s_min for E. coli, C. heintzii would win the competition only at glucose concentrations <5.0 μg l⁻¹. However, existence of an s_min of 35 μg l⁻¹ for E. coli provides C. heintzii with a competitive advantage already at glucose concentrations <58.0 μg l⁻¹ (Figure 5; Table 3). Therefore, especially during slow growth microbial strains affected by significant maintenance requirement should be distinctly disadvantaged in their competitive properties. Importantly, this disadvantage cannot be counteracted by an improved affinity or specific growth rate.

In view of its role for competition during slow growth we have to point out that it is difficult to experimentally determine s_min; values reported so far for cells cultivated in carbon-limited continuous culture vary over a wide range from 6545.5 to 12.0 μg l⁻¹ dependent on strain, substrate and growth conditions (Kovárová et al., 1996; Tros et al., 1996a; Füchslin et al., 2003). For glucose-controlled chemostat cultures of E. coli ML30, Kovárová and co-workers reported a temperature dependence of s_min, with a minimum of 12 μg glucose l⁻¹ at 37 °C, the optimum temperature for growth. Our experiments suggest also a growth rate dependence of s_min as the value obtained for s_min for E. coli determined by parameter estimation increased from 12.6 μg l⁻¹ at D=0.05 h⁻¹ to 34.9 μg l⁻¹ at D=0.075 h⁻¹, respectively. This would be in agreement with the literature reviewed by van Bodegom (2007) according to which a great body of experimental data suggest that maintenance rate increases with increasing growth rates.

The importance of s_min for microbial growth in the environment remains to be elucidated further. Most information reported so far originates from single substrate-limited systems. Average free glucose concentrations in aqueous systems are in the range of 1–10 μg l⁻¹ (Wright and Hobbie, 1966; Egli, 1995). Thus, it seems obvious that E. coli with a significant s_min is hardly able to gain access to enough substrate to satisfy its maintenance energy needs. However, under environmental conditions the pool of available carbon substrates does not consist only of one single compound but of a complex mixture of carbon compounds all present at low concentrations (Münster, 1993). Under such conditions, microbial cells are expected to perform so-called ‘mixed substrate growth', that is, they use multiple carbon sources simultaneously (Egli, 1995). Mixed substrate growth allows a more efficient use of individual carbon substrates at low concentrations (Egli, 1995). Hence, one would expect that s_min for individual carbon substrates would be lower under environmental conditions than during growth in artificial systems with single substrates, which was indeed observed by Tros et al. (1996a). In fact, in growth studies in drinking water distribution systems E. coli had definitely more difficulties to cope with low nutrient concentrations compared with the autochthonous freshwater bacteria, suggesting the existence of an s_min for the growth of E. coli. The enterobacterium did not grow with assimilable organic carbon levels <54 μg l⁻¹ (LeChevalier et al., 1987), whereas environmental bacterial strains were able to grow down to 10 μg l⁻¹ levels (Van der Kooij et al., 1982; Van der Kooij and Hijnen, 1985; Van der Kooij, 1987).

Still, an explanation for the significant s_min of E. coli and its virtual absence in C. heintzii remains to be found. Up to now, due to its difficult experimental accessibility, s_min has been mainly neglected in kinetic studies. Further investigations are needed to show whether or not the significant s_min observed here is a general property of enterobacteria or copiotrophs, and whether this is one of the important differences to oligotrophic bacteria. Such information would be crucial for a better understanding of microbial growth and degradation processes in the environment.