Dimerization of Helical β-Peptides in Solution

Abstract

Molecular simulations are used to examine the aggregation behavior of several β-peptides in explicit water. The particular peptides considered here adopt a helical, rodlike conformation in aqueous solution. Four distinct molecular sequences are considered. Earlier experimental studies have revealed the formation of ordered and disordered aggregates for such molecules, depending on sequence. The simulations reported here, which are conducted by resorting to metadynamics techniques, lead to free energy surfaces for dimerization of the peptides in water as a function of separation and relative orientation. Such surfaces are used to identify the molecular origins for the behaviors observed in the experiments.

Introduction

Oligomers of β-amino acids, known as β-peptides, are a class of synthetic proteinlike molecules that have received considerable attention as a result of their ability to form well-defined secondary structures. Compared to the α-amino acids found in proteins, β-amino acids have one additional backbone carbon atom. That additional backbone carbon atom increases the palette of available residues, and offers the possibility of introducing ring containing structures into the peptide backbone. Certain β-peptides form highly stable and predictable helical secondary structures (1–7). In particular, introducing five membered cyclic residues into the β-peptide stabilizes a helical secondary structure known as the 14-helix, in which each hydrogen-bonded ring has 14 members. In this type of helix, each β-amino acid forms a hydrogen bond with the β-amino acids located three residues away. Fig. 1 illustrates a typical β-peptide helix for a 10-residue long β-peptide, and shows typical dimensions for the helix. These helices are highly stable, and form with a lower minimum number of residues than the helices of natural peptides (8).

Figure 1.

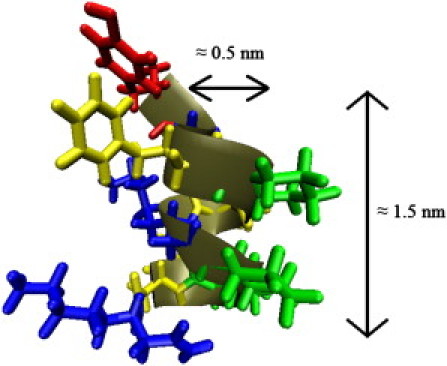
A 14-helical β-peptide. The residues are colored (red, β³-hTyr ; green, ACHC; blue, β³-hLys; yellow, β³-hPhe).

Beyond their ability to form stable secondary structures, β-peptides also exhibit a rich self-assembly behavior. In this regard, β-peptides are particularly attractive in that one can control their secondary structure and ensure that it is preserved throughout the aggregation process. Furthermore, one can also control the three-dimensional presentation of the molecules' various functional groups and examine the role of structure on intermolecular interactions. This feature is illustrated in Fig. 2, which provides a schematic representation of the four β-peptides considered in this work. The four peptides have two sets of residues, and there are two isomers of each. In one isomer, referred to as the globally amphiphilic isomer, each side of the helix contains either only hydrophobic or only hydrophilic groups. In the nonglobally amphiphilic isomer, each face of the helix contains both types of residue. The ability to present distinct chemical moieties on a particular face of the molecule is of interest in fundamental studies of peptide association in solution because it allows one to extract unambiguous conclusions about the role of sequence on association. A notable example is provided by recent work in which distinct sequences of short β-peptides induced the formation of liquid crystalline phases (9). More generally, different types of aggregates have been observed depending on sequence. Some β-peptides form globular aggregates, whereas others form fibers (10). One fiber aggregate formed by a β-peptide sequence was characterized as consisting of hollow cylinders (11).

Figure 2.

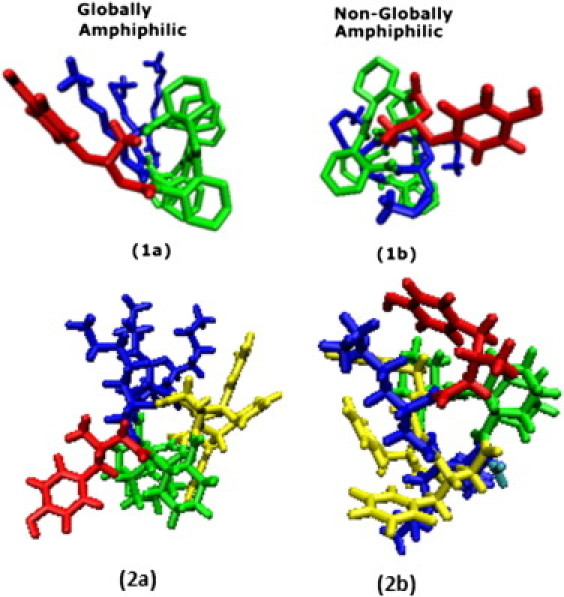
Illustration of the four peptides studied showing globally amphiphilic and nonglobally amphiphilic display of hydrophobic and hydrophilic groups.

Recent experiments have revealed a broad range of self-assembling behaviors of the four peptide sequences considered here, shown in Fig. 3. The β-amino acids contained in these β-peptide sequences are analogs of the α-amino acids tyrosine (β³-hTyr), lysine (β³-hLys), phenylalanine (β³-hPhe), as well as a β-amino acid with a six membered ring, trans-2-aminocyclohexanecarboxylic acid (ACHC). The four peptides consist of two globally amphiphilic β-peptides, and nonglobally amphiphilic isomers of each of these. Experimentally, the peptide with sequence labeled 1a in Fig. 3 exhibits a liquid crystal phase, whereas its nonglobally amphiphilic isomer (1b) does not. However, in the case of β-peptide 2, the pattern is reversed: the globally amphiphilic isomer (2a) does not form a liquid crystal phase, but the nonglobally amphiphilic does.

Figure 3.

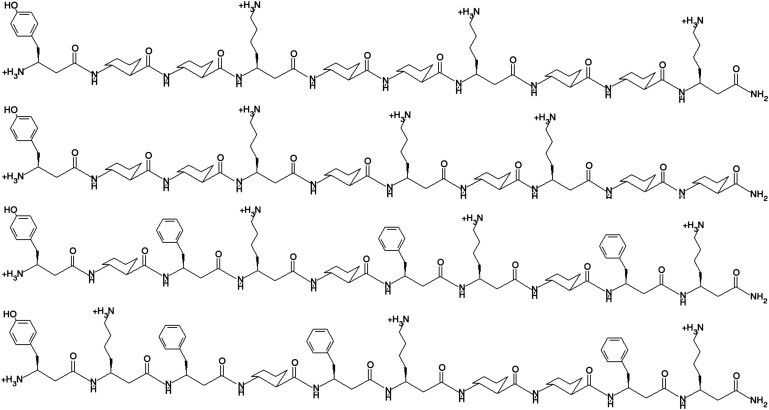
Structures of the four β-peptides.

According to Onsager Theory, a liquid crystal phase can be formed by large anisotropic molecules due to excluded volume effects (12). Small molecules can also form a liquid crystal phase in a similar manner if they self-assemble into larger, highly anisotropic aggregates. This self-assembly process has been extensively studied for the case of globally amphiphilic molecules. In such molecules, the hydrophobic faces tend to aggregate, leading to anisotropic structures such as lamellae or rod-shaped micelles (13). The causes of a liquid crystal phase formed from nonglobally amphiphilic small molecules are less well understood.

The aim of this article is to gain an understanding of how β-peptide sequence influences aggregation and ultimately the formation of the liquid crystal phase by examining the free energy of interaction between two molecules in solution. We do so by resorting to molecular simulations of atomistic models of these four peptides. The resulting potential of mean force can be used to interpret aggregation experiments, and it can also serve as a guide to formulate coarse-grain models for study of aggregation in solution. Previous computational studies of β-peptide aggregation have involved calculation of the potential of mean force as a function of distance between two peptides. Miller et al. (14) calculated the potential of mean force for the four peptides mentioned above using constraint-force simulations of atomistic representations of the molecules. Subsequent simulations of the same molecules by Mondal et al. (15) found global minima for all the peptides using umbrella sampling. Although the models adopted in these studies were slightly different, the results of these two studies are not fully consistent with each other. Furthermore, Mondal et al. (15) found that the different force field parameters in use for β-peptides gave similar aggregation behavior in their umbrella sampling simulations.

Pomerantz et al. (10) characterized the phase behavior of the four peptides studied here and proposed that highly anisotropic aggregates are responsible for the liquid crystal forming behavior of the two peptides that formed this phase. These authors, however, could not propose a molecular level explanation for the different specific interactions leading to particular aggregation behaviors of the peptides. Because a high degree of anisotropy is required in the proposed aggregates, it is therefore important to determine how the faces of these β-peptides approach each other to gain a detailed understanding of the aggregation behavior.

As mentioned above, past computational studies relied only on unidimensional calculations of the potential of mean force along the separation between the centers of mass of two molecules. To investigate the role of relative orientation on the interaction between two molecules and identify the source of discrepancies between previous calculations, in this work we introduce a second variable along which to sample interactions and we generate free energy surfaces as a function of both distance and orientation. More specifically, we define a helix angle variable with a vector across the helix on each peptide, and control the angle between these two vectors. This is illustrated in Fig. 4; a precise definition is given in the Materials and Methods. Recently proposed metadynamics simulations are used to facilitate sampling of configurational space (16). Our results indicate that the peptides that show both a strong tendency to aggregate and a strong conformational preference for certain helix angles form liquid crystal phases, whereas the others do not. Our results also show that past simulations might have been hampered by the existence of deep local minima within the corresponding two-dimensional free energy surfaces, thereby explaining the inconsistencies between different literature reports.

Figure 4.

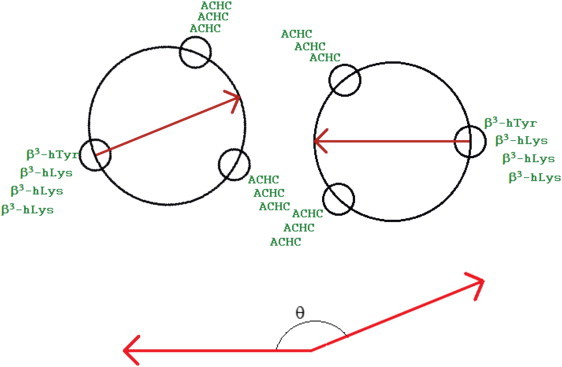
Illustration of the definition of the helix angle. In this figure, peptide 1a is represented schematically. Here the two peptides align with their end-to-end vectors parallel. A vector is defined between two fixed atoms on the helix backbone for each peptide (the α-carbon of the fifth residue and the β-carbon of the sixth residue). In this case, the angle is near 180°.

Materials and Methods

The chemical structures of the peptides considered in this work are given in Fig. 3. For completeness, their sequences are given in Table 1, along with key characteristics describing their tendency to aggregate. Most of our simulations were performed in cubic boxes of side length 5.4 nm, and included ∼5200 water molecules. A 200-ns simulation was also performed for peptide 1a with a larger box size, 6 nm on each side and 7015 water molecules, to examine finite size effects. Initial structures for each peptide were generated by using 14-helical β-peptide structures for the four peptides taken from earlier simulations (4). The peptides were then replicated, so that two identical peptides were initially placed at an arbitrarily selected separation of 2 nm. For that separation the interactions between the molecules are small. The system was then solvated with TIP3P water and counterions to preserve electroneutrality, and equilibrated during 4 ns of molecular dynamics simulations at constant pressure and temperature. These structures were used as the initial configuration for NPT metadynamics simulations.

Table 1.

Summary of β-peptides studied

1a	(β3-hTyr)-[ACHC-ACHC-(β3-hLys)]3	Forms liquid crystal phase, aggregates.
1b	(β3-hTyr)-[ACHC-ACHC-(β3-hLys)]-[ACHC-(β3-hLys)-ACHC]-[(β3-hLys)-ACHC-ACHC]	Does not form liquid crystal phase, does not aggregate.
2a	(β3-hTyr)-[ACHC-(β3-hPhe)-(β3-hLys)]3	Forms aggregates, but not liquid crystal.
2b	(β3-hTyr)-[(β3-hLys)-(β3-hPhe)-ACHC]-[(β3-hPhe)-(β3-hLys)-ACHC]-[ACHC-(β3-hPhe)-(β3-hLys)]	Forms liquid crystal with cylindrical structure.

Description of the four β-peptides studied: The first column gives the abbreviations used in this article. The second column gives a β-amino-acid sequence. The β-amino acids are abbreviated as follows: β³-hTyr = β³ homotyrosine, ACHC = trans-2-aminocyclohexanecarboxylic acid, β³-hLys = β³ homolysine, and β³-hPhe = β³ homophenylalanine. Chemical structures for each of these amino acids are represented in the structure of peptide 2a in Fig. 1, which contains all of the β-amino acids mentioned.

Four replicas of each of the systems were created, for use in the bias exchange implementation discussed later. The CHARMm27 all-atom force field was used (17), with parameters developed for β-peptides from Rathore et al. (5). This force field was developed based on an approach that optimized parameters with respect to ab initio and experimental data, with parameters specifically designed to capture aromatic interactions in the case of aromatic amino acids (18). A particle-mesh Ewald sum was used for long-range electrostatic interactions with a short range cutoff of 10 Å and a maximum relative error of 10⁻⁵ (19). A cutoff of 10 Å was also used for Lennard-Jones interactions. Bonds were constrained with the LINCS algorithm, and a time step of 0.002 ps was used. The velocity rescaling thermostat was used for temperature coupling (20), with a temperature coupling parameter of 0.2 ps. The pressure was maintained at 1 bar using the Berendsen barostat with a time constant of 1 ps and a compressibility of 4.5·10⁻⁵ bar⁻¹.

All simulations were performed using the GROMACS (21) simulation package. The PLUMED (22) metadynamics plugin was used to enhance sampling. Hills were deposited every 200 time steps with a height of 0.1 kJ/mol. A wall potential was employed on the reaction coordinate at 2.5 nm to avoid sampling a region with artifacts arising from the periodic boundary conditions. We adopted a bias exchange implementation in which four replicas of the system are simulated (23). Two order parameters were considered in these simulations: the distance between the α-carbon of the fifth residue of each peptide, and the helix angle between two molecules. As illustrated in Fig. 4, the helix angle is provided by the angle between vectors defined on each peptide. The vector on each peptide points from the α-carbon of the fifth residue to the β-carbon of the sixth residue. The helix angle is the angle between the vectors of the two peptides. The four replicas of the system consisted of one in which the biasing potentials for both reaction coordinates are excluded, one in which only the distance coordinate potential is used, one in which only the angle coordinate potential is used, and one in which the potentials for both order parameters are used. Only this last box is actually analyzed for results. Periodically, a swap between the configurations in the boxes is proposed. The swap between boxes a and b is accepted with probability

$$p_{ab}=\text{min}\left(1,\beta \left[V_{bias}^a\left(x^a,t\right)+V_{bias}^b\left(x^b,t\right)-V_{bias}^a\left(x^b,t\right)-V_{bias}^b\left(x^a,t\right)\right]\right).$$ (1)

Swap moves were proposed every 200 steps, consistent with the range of swap frequencies that has been used successfully in past simulations of protein systems with these methods (23,24). For each peptide, simulations were performed for 200 ns. The free energy was calculated from the first 150 ns of data, and recalculated after an additional 50 ns. The free energy minima did not change location or change magnitude by >3 kJ/mol, indicating good convergence.

Results and Discussion

Fig. 5, left, shows results from the two-dimensional bias exchange simulations for peptide 1a. Peptide 1a is the globally amphiphilic peptide with six cyclic ACHC groups that is experimentally found to form a liquid crystal phase. For peptide 1a, the free energy surface exhibits two distinct minima of approximately equal depth as a function of the helix angle, with angles close to 0 and 180° being preferred. The configuration at the minimum near 180° is similar to that represented in Fig. 4, with a representative frame shown later in Fig. 6. The minimum near 0° is related, with the hydrophobic groups facing one another, but the peptides' end-to-end vectors align in an antiparallel configuration, with the N-terminus of one peptide near the C-terminus of the other. Fig. 5, right, shows results for peptide 1a performed on a larger box size, 6 nm, under the same conditions. A comparison between Fig. 5, left and right, indicates that our simulations do not appear to suffer from finite size effects. The two free energy surfaces are very similar, with differences that are well within the statistical uncertainty of our results and had a root mean square difference of 0.4 RT.

Figure 5.

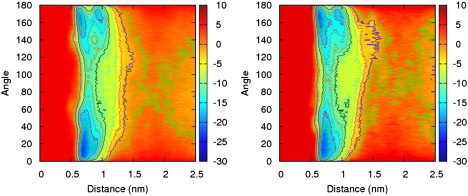
Free energy surface for peptide 1a as a function of distance and helix angle in units of kJ/mol. There are two deep free energy minima at a separation of ∼0.7 nm, one with a high helix angle corresponding to a parallel configuration of the end-to-end vectors and one with a low helix angle corresponding to antiparallel end-to-end vectors. Free energy surface for peptide 1a as a function of distance and helix angle in units of kJ/mol using a larger box size of 6 nm. The results are consistent with the results for a simulation with a box size of 5.4 nm.

Figure 6.

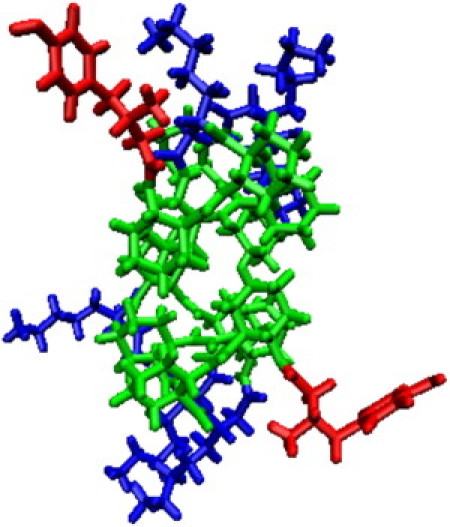
Representative configuration of the free energy minimum structure for peptide 1a with the hydrophobic groups facing each other and the end-to-end vectors nearly parallel.

Peptide 1b is the nonglobally amphiphilic isomer of peptide 1a. Experimentally, it is not found to form a liquid crystal phase. The free energy surface for this peptide is shown in Fig. 7. Peptide 1b exhibits only a weak minimum in free energy, 5 kJ/mol at its deepest, which is much less than the free energy minimum for peptide 1a as a function of either distance or angle.

Figure 7.

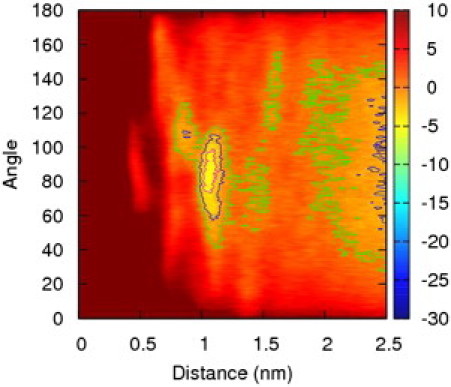
Free energy surface for peptide 1b as a function of distance and helix angle in units of kJ/mol. There is only a single shallow minimum in the free energy.

The magnitude of the free energy minima can be quantified from the free energy function, G(r), by evaluating the ratio

$$\frac{\int \int \begin{array}{c}r=2.5,\theta =180\\ r=0,\theta =0\end{array}{e}^{-\frac{G\left(r\right)}{kT}}drd\theta }{2.5\text{nm}-180}.$$

Mathematically, this represents the ratio of the average probability per nanometer that the peptides are within a distance of 2.5 nm to the probability per nanometer that the peptides are far from each other (where G(r) = 0). For peptide 1b, this ratio is just 0.7, compared to 100 for peptide 1a. The magnitude of the free energy ratio for peptide 1b is also smaller than for peptide 2b, where the ratio is 1.4, and for peptide 2a, where the probability ratio is 20. This weakness of the free energy minimum likely explains the absence of a liquid crystal phase for peptide 1b, where the maximum depth of the free energy minimum is 5 kJ/mol, or ∼2 RT. Because the barrier to dissociation is relatively low, it is not a likely candidate to form highly ordered aggregates.

Peptides 2a and 2b are the globally amphiphilic and nonglobally amphiphilic isomers, respectively, of a β-peptide sequence similar to 1a and 1b, but with three ACHC residues replaced by β₃-homophenylalanine (β³hPhe). The results for the peptide isomers 2a and 2b, shown in Figs. 8 and 9, are surprising at first. The free energy surface for peptide 2a exhibits a free energy minimum that is narrow in the peptide distance parameter, but very wide in the angle parameter. The free energy minima as a function of angle at the free energy minimum distance are very shallow compared to those encountered in peptide 1a. The free energy surface for peptide 2b, however, exhibits one deep minimum at ∼1.3 nm, and the range of the angle parameter is small and that minimum is highly localized at an angular value of 60°. There are two shallower minima at 0.6 nm, localized to 60° and 120°. This seems to indicate that the angle is a more significant variable for the nonglobally amphiphilic peptide than the globally amphiphilic one—just the opposite result from what was observed for peptides 1a and 1b.

Figure 8.

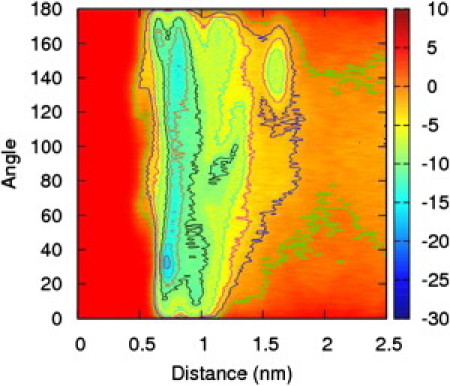
Free energy surface for peptide 2a as a function of distance and helix angle in units of kJ/mol. Here the preference for helix angles near 0° or 180° is greatly reduced compared to peptide 1a.

Figure 9.

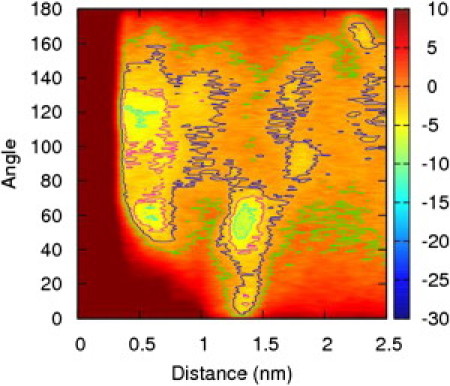
Free energy surface for peptide 2b as a function of distance and helix angle in units of kJ/mol. The free energy minimum is significantly deeper than in the case of peptide 1b, and the angular preference is strong.

This stark difference in behavior is due to the higher degree of conformational freedom of the β³hPhe residue compared with the cyclic ACHC residues. The ACHC residues have their rings incorporated into the peptide backbone, whereas the β³hPhe cyclic groups are connected to the backbone by a bond to an intervening carbon atom that is free to rotate. This ability of the hydrophobic phenyl groups to reorient introduces a tolerance for imperfect alignment of the backbones into the free energy surface. Because the phenyl groups can rearrange themselves to compensate for changes in the helix angle, the dependence of the free energy on angle is considerably reduced compared to that of peptide 1a.

The situation for the nonglobally amphiphilic peptide 2b is also drastically changed from the behavior of the corresponding peptide 1 isomer by the conformational freedom introduced by the β³hPhe residues. Peptide 1b failed to show any deep free energy minima, presumably because no relative orientation of the peptide produces a highly favorable set of interactions. However, with three of the ACHC residues replaced by β³hPhe residues, the hydrophobic groups can rearrange themselves into a favorable configuration, while still presenting the β³-hLys residues to the solvent. There is a strong, narrow global free minimum corresponding to one configuration that achieves this balance well. A representative frame from this free energy minimum is illustrated in Fig. 10. The helices orient with the end-to-end vectors nearly aligned antiparallel, with a slight offset. There is a 60° angle between the helices. The free energy minimum is highly localized at this angle, and slight changes in angle result in steep increases in free energy.

Figure 10.

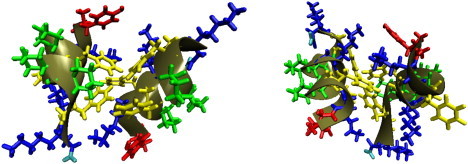
Typical frame of the free energy minimum configuration of peptide 2b (right) shown from two angles.

The formation of the anisotropic aggregates proposed by Pomerantz et al. (10) that lead to the formation of a lyotropic liquid crystal depends on both the propensity for aggregation, and the ability of the mode of aggregation, to produce long-range order. Because aggregation with random orientation could not produce long-range order, one would expect liquid crystal formation when aggregation is energetically favorable and the dependence of free energy on orientation is high. This is what is observed in these simulations.

Comparison of Metadynamics and Constraint Force Methods

The results of two-dimensional simulations using metadynamics show a free energy minimum as a function of distance for all four of the peptides. This result is consistent with the unidimensional potentials of mean force by Mondal et al. (15), although some quantitative differences persist.

The free energy from the metadynamics simulations is generally lower at close distances than that generated in short constraint-force calculations. The length of the simulations by Miller et al. (4,14) included a brief equilibration of <1 ns, followed by production runs of 5 ns for peptides 1b and 2a, and 10 ns for peptides 1a and 2b. A problem with the constraint-force method for molecules of this size is the slow timescale of rotational kinetics at close distances due to stearic effects. To examine these effects, we performed 20-ns simulations of peptide 1a using the constraint-force method with the distance constrained to 0.65 nm and a unidimensional metadynamics simulation starting from the same configuration, and examined the rotational kinetics. Fig. 11 shows how the peptide distance and angle vary as a function of time for the metadynamics simulation, whereas Fig. 12 shows the angle as a function of time for the constraint-force simulation.

Figure 11.

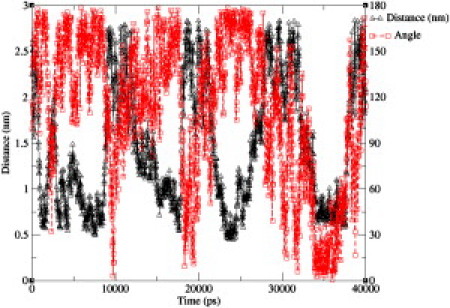
Distance and helix angle tracked over 40 ns of a metadynamics calculation.

Figure 12.

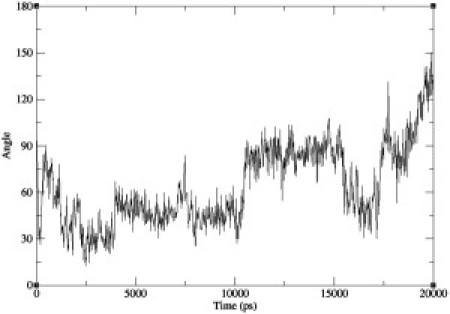
Helix angle as a function of time for a 20-ns constraint force simulation.

It can be seen that, after 10 ns, the peptide has not undergone a full rotation in the constraint force case, whereas a wide range of angles is sampled by metadynamics. At the end of the 20-ns constraint-force simulation, the peptide has transitioned to a higher angle. The slowness of the rotational kinetics at short distances systematically underestimates the free energy at these points. The metadynamics simulations overcome this difficulty by causing the peptides to approach one another along many essentially independent trajectories. In the two-dimensional case, the biasing potential ensures that the full range of possible angles is sampled. The umbrella sampling method used by Mondal can mitigate this problem to some extent because the peptides need not remain at very close distances for the entire simulation, but the kinetics of rotation will still be slow when the peptides are close together. Metadynamics leads to enhanced sampling of orientational space, and more reliable results.

Conclusions

Metadynamics simulations were used to examine the free energy of aggregation of four distinct β-peptides in water. The results of these simulations present a considerable improvement over earlier one-dimensional potentials of mean force generated by earlier simulations.

The free energy surfaces presented here were determined as a function of the separation between molecules and their relative angles. These surfaces provide a more complete understanding of peptide dimerization than that obtained from the one-dimensional potentials of mean force in the literature, including those of our group, and demonstrate that, depending on the sequence of residues along the backbone, β-peptides can exhibit a wide variety of interactions, ranging from only slightly attractive to highly attractive, with sometimes intricate orientational dependencies. Our results are consistent with the predictions of the experimentalists who suggested that highly anisotropic aggregates were responsible for liquid crystal phase behavior in that peptides that exhibit a very weak attraction or low angular dependence fail to exhibit any liquid crystal phase in experiments. In contrast, peptides that exhibit strong free energy minima and a strong orientational dependence exhibit liquid crystalline behavior and fiber formation in experiments.