Determining the Gaussian Curvature Modulus of Lipid Membranes in Simulations

Abstract

The Gaussian curvature modulus $\overline{\kappa }$ of lipid bilayers likely contributes more than 100 kcal/mol to every cellular fission or fusion event. This huge impact on membrane remodeling energetics might be a factor that codetermines the complex lipid composition of biomembranes through tuning of $\overline{\kappa }$. Yet, its value has been measured only for a handful of simple lipids, and no simulation has so far determined it better than a factor of two, rendering a systematic investigation of such enticing speculations impossible. Here we propose a highly accurate method to determine $\overline{\kappa }$ in computer simulations. It relies on the interplay between curvature stress and edge tension of partially curved axisymmetric membrane disks and requires determining their closing probability. For a simplified lipid model we obtain $\overline{\kappa }$ and its relation to the normal bending modulus κ for membranes differing both in stiffness and spontaneous lipid curvature. The elastic ratio $\overline{\kappa }/\kappa$ can be determined with a few percent statistical accuracy. Its value agrees with the scarce experimental data, and its change with spontaneous lipid curvature is compatible with theoretical expectations, thereby granting additional information on monolayer properties. We also show that an alternative determination of these elastic parameters based on moments of the lateral stress profile gives markedly different and unphysical values.

Introduction

Lipid bilayer membranes are quasi-two-dimensional fluid sheets that, in aqueous solution, assemble spontaneously from their lipid constituents. Because thermal energy can hardly stretch but easily bend them, their important soft modes are curvature deformations. Hence, on length scales barely exceeding their thickness (∼4 nm), such membranes follow a quadratic curvature-elastic continuum theory (1–3). Within the well-established mathematical framework developed by Helfrich (2), the energy of a membrane patch 𝒫, amended by a contribution due to its boundary $\partial \mathcal{P}$ (4), is expressible as

$$E\left[\mathcal{P}\right]=\underset{\mathcal{P}}{\int }\text{d}A\left\{\frac{1}{2}\kappa {\left(K-K_0\right)}^2+\overline{\kappa }{K}_{\text{G}}\right\}+\underset{\partial \mathcal{P}}{\oint }\text{d}s\gamma .$$ (1)

Here, K = c₁ + c₂ is the total curvature (the sum of the two local principal curvatures c₁ and c₂) and K_G = c₁c₂ is the Gaussian curvature (5,6). We also have four material parameters: The bending modulus κ, the Gaussian curvature modulus $\overline{\kappa }$, the spontaneous curvature K₀, and the edge tension γ (the excess free energy of an open edge). The bending modulus κ can be experimentally obtained by flicker spectroscopy (7–12), the low-tension stress-strain relation (13), x-ray scattering (14–17), or neutron spin-echo measurements (18–20) (albeit with some caveats (21)). An alternative method not based on fluctuations relies on pulling thin membrane tethers (22–24). In simulations, both monitoring undulations (25–34) and measuring tensile forces in tethers (35,36) have been successfully employed. The edge tension can be extracted—both in experiments (37–40) as well as in simulations (28–32)—mainly by studying pores. In simulations, one can even stabilize a straight open edge through periodic boundary conditions (41–44). Finally, if the two bilayer leaflets are identical, K₀ = 0 by symmetry, and we will henceforth also restrict it to this frequent special case.

We are left with the Gaussian curvature modulus $\overline{\kappa }$. It is so difficult to measure (Table 1 lists the few available results from the literature) due to the famous Gauss-Bonnet theorem (5,6), which states that the surface integral over the Gaussian curvature K_G depends only on the topology and the boundary of the membrane patch 𝒫 in question, meaning one needs to change either one to get an experimental signal that is sensitive to $\overline{\kappa }$. This statement can be viewed as both a blessing and a curse. A blessing, because if neither topology nor boundary change, the value of $\overline{\kappa }$ is strictly irrelevant: the term $\overline{\kappa }{K}_{\text{G}}$ can be eliminated from Eq. 1 right from the start. A curse, because in the remaining situations in which topology or boundary changes matter, we have no simpler way to obtain $\overline{\kappa }$ other than precisely via such situations, which tend to involve hard-to-control processes—both in experiments and in simulations.

Table 1.

Summary of experimental or simulational results pertaining to the Gaussian curvature modulus

System	$-\overline{\kappa }/\kappa$	Layer	Ref.
Egg lecithin	0.83 ± 0.12	Bi∗	(88)
DOPE-Me†	0.83 ± 0.08	Mono	(74)
DOPE-Me	0.90 ± 0.09	Mono	(78)
DOPE	0.92 ± 0.11	Mono	(46)
DOPC	0.84 ± 0.17	Mono	(46)
DOPC/Chol (1:1)	0.76 ± 0.10	Mono	(46)
GMO/DOPC/DOPE‡	0.75 ± 0.08	Mono	(89)
DOPC:SM:Chol§	0.9 ± 0.38	Bi	(53)
DOPC:SM:Chol¶	0.31…0.63	Bi	(54)
CG lipid model (90)	0.54‖	Mono	(91)
CG lipid model (79)	0.03‖	Mono	(92)

Note that the “Layer” column indicates whether the elastic ratio $\overline{\kappa }/\kappa$ refers to monolayers or bilayers.

^∗Measured value of $\overline{\kappa }$ is an apparent value.

^†Abbreviations: DOPE-Me, monomethylated DOPE; DOPE, dioleoyl-sn-glycero-3-phosphatidylethanolamine; DOPC, dioleoyl-sn-glycero-3-phosphatidylcholine; Chol, cholesterol; GMO, glycerolmonooleate; SM, sphingomyelin.

^‡Mixing ratio: 58:38:4.

^§The authors studied various mixing ratios. The value of $\overline{\kappa }/\kappa$ is not quoted in Baumgart et al. (53), but follows if one assumes that the elastic ratio is the same in the liquid-ordered and liquid-disordered phase.

^¶Mixing ratio: 30:50:20.

^‖The error is difficult to estimate and probably dominated by systematics rather than statistics.

Still, a number of important cases fall into this latter category. Most obvious are fusion and fission events, which are ubiquitous in cell biology: ER remodeling, Golgi biogenesis, vesicular transport, endocytosis, cell division, pathogene infection, and countless other processes evidently involve topology changes in membranes (45). During fusion, the topological change alone requires the energy to increase from the initial to the final state by −4π$\overline{\kappa }$ ∼ 200–250 k_BT (where k_BT = 0.6 kcal/mol is the thermal energy); here we have used κ ≈ 20 k_BT and assumed $\overline{\kappa }/\kappa$ ∼ −0.9 (from Table 1). The Gaussian curvature modulus also matters in continuum theories of fission and fusion processes, because it affects the energy of fusion intermediates (such as catenoidal fusion pores or stalks), and thus the height of barriers that have to be crossed (46). In living cells, such events are of course coupled to and driven by active processes (such as ATP hydrolysis) (45), but equilibrium thermodynamics remains useful by predicting the free energy differences or barriers cells need to cope with. Because the energetics depends on $\overline{\kappa }$, which can be affected not only by the lipid composition but also by adding suitable proteins (47), it is tempting to speculate that tuning its value might conceivably be one factor influencing how cells choose the composition of their biomembranes. However, without efficient ways to measure $\overline{\kappa }$ in experiment or predict it from simulation, this hypothesis remains untestable. Finally, the case of boundary changes also includes the contact between phase-segregated lipid domains. Not only can the line tension between domains induce budding (48,49), but the difference in Gaussian curvature moduli between the two phases affects the equilibrium shape (50–54) through the boundary term in the Gauss-Bonnet theorem (5,6): The associated boundary conditions change the line tension and exert torques around the phase boundary. This adds a further aspect to the notion of membrane rafts (55–57).

Here we propose a method to accurately determine the Gaussian curvature modulus $\overline{\kappa }$ in a simulation. The key idea is to quantify the probability with which a partially bent circular membrane patch closes up to form a vesicle—a process first studied by Helfrich (4), but for a different reason: He wanted to predict the size of vesicles formed by ultrasonication and assumed a value for the Gaussian modulus. We turn the argument around and measure the critical system size, hence we can infer $\overline{\kappa }$ if all other material parameters are known. As it turns out, the necessary simulations are easy to perform, computationally not too expensive, result in a very clean signal, and thus permit the determination of $\overline{\kappa }$ with high accuracy.

We note that an alternative strategy that has been used in the past to gain information about curvature moduli is to compare differently curved surfaces (planes, cylinders, spheres), and extract the moduli (or how they change upon modifying the surface) by expanding the free energy in terms of surface curvature. This path has been followed in theory (58–62), experiment (63), and simulation (62) for a number of different systems, but it has so far not been successfully applied to lipid (mono- or bi-) layers.

Theory

Let us outline the theoretical framework. Consider a flat circular bilayer patch of area A. It has no bending energy, but an edge energy proportional to its circumference. If this patch assumes the shape of a spherical cap of mean curvature c, the line energy decreases, but now bending energy arises. From Eq. 1 and simple geometry one finds the excess energy ΔE of such a curved patch (4,64),

$$\frac{\Delta E\left(x,\xi \right)}{4\pi \left(2\kappa +\overline{\kappa }\right)}=\Delta \tilde{E}\left(x,\xi \right)=x+\xi \left[\sqrt{1-x}-1\right],$$ (2)

where we scaled ΔE by the bending energy of a complete spherical vesicle and defined

$$x={\left(Rc\right)}^2,\xi =\frac{\gamma R}{2\kappa +\overline{\kappa }},\text{and}R=\sqrt{\frac{A}{4\pi }}.$$ (3)

The reaction coordinate x varies from x = 0 (flat patch) to x = 1 (closed vesicle of radius R). The functional form of this excess energy depends on the parameter ξ (see inset in Fig. 1): At ξ = 1, the closed vesicle has the same energy as the flat disk, and for smaller ξ the flat disk is stable. For 1 < ξ < 2, the closed vesicle is more stable, but an initially flat disk must surmount an energy barrier located at x^∗ = 1 – (ξ/2)² of height $\Delta {\tilde{E}}^{\ast }$ = (1 – ξ/2)² to close up. For ξ > 2, no barrier is left and a flat disk is always unstable against vesiculation. The transition energetics is thus fully determined by the parameter ξ, which itself depends on A, γ, κ, and $\overline{\kappa }$. Of these, all except $\overline{\kappa }$ can be predetermined by simple means. Hence, if we choose a suitable area A and measure the functional form of the barrier, we can deduce $\overline{\kappa }$.

Figure 1.

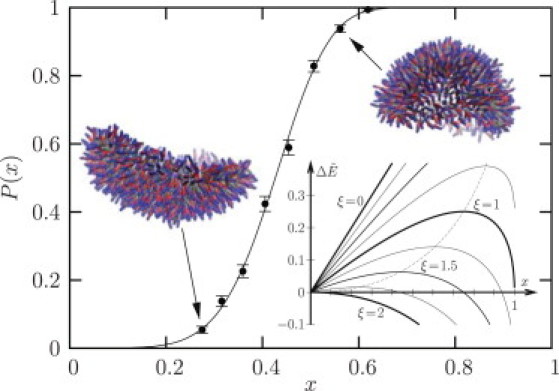
Closing probability of a precurved bilayer patch as a function of x (the parameters correspond to system 1). Averages were extracted from 500 independent simulations, with error bars following from Bernoulli statistics. (Solid line) Fit to Eq. 4, which yields ξ = 1.503 ± 0.003, with mean and error determined by Monte Carlo resampling of the raw data. (Inset) Shape of the energy barrier $\Delta \tilde{E}$(x,ξ) from Eq. 2 as a function of x for various values of ξ. Two simulation snapshots for x = 0.28 and x = 0.56 are also shown.

We note that even though we will encounter fairly strong curvatures (see the Supporting Material for a more detailed discussion), no complications due to 1), spontaneous bilayer curvature or 2), area difference elasticity will arise. Although it is true that the two monolayers individually have a spontaneous curvature and their respective neutral surfaces do not coincide with the bilayer midplane, this does not induce an overall spontaneous curvature but instead “renormalizes” the bilayer Gaussian curvature modulus in a well-known way (see Eq. 5 below). And because lipids can move between leaflets across the open edge, no area difference elasticity can build up.

Simulation

We now apply this strategy to measure the Gaussian curvature modulus for a specific example system, namely, the coarse-grained (CG) membrane model due to Cooke et al. (31,32). We choose the CG level for two reasons: First, elastic moduli are macroscopic membrane observables, and we wish to see how universal their properties are (e.g., the elastic ratio $\overline{\kappa }/\kappa$ and its dependence on lipid curvature). And second, a CG model permits us to study a wide range of specific examples with excellent statistics, which we will use to argue that the underlying analysis is sound. However, because our method 1), proves so efficient and 2), makes no use of any specific property of the Cooke model (for instance the absence of solvent), we are confident that it will work well for other membrane models at a higher resolution, at a larger but still manageable computational effort.

Briefly, in the Cooke model a lipid is represented by three linearly connected beads, one for the head and two for the tail. Lipids aggregate due to an effective tail-attraction, whose range w_c and depth ε can be varied (31,32). We choose k_BT/ε = 1.1 and explore a range of values for w_c to scan the bending rigidity κ. We also change the size of the head bead, thus modifying the spontaneous lipid curvature. Despite its simplicity, this model has been successfully applied to a variety of biophysical and biological problems, such as lipid sorting in curvature gradients (65), insertion mechanisms for antimicrobial peptides (66), lipid-composition-driven protein interactions (67), and protein-driven membrane vesiculation (68). Simulations were done with the ESPResSo package (69).

In the simulation the function $\Delta \tilde{E}$(x,ξ) arises as a free energy barrier, but it proves unnecessary to invoke numerical free energy calculation techniques to measure it: The system closely follows the path assumed by the theory (i.e., it stays part of a spherical cap), so we can map $\Delta \tilde{E}$(x,ξ) by creating intermediate states—precurved membrane patches at different values of x—and follow their evolution. For this simple dynamics to hold, the bilayer patch must be small enough so that undulations and their contribution to the free energy barrier $\Delta \tilde{E}$(x^∗,ξ) are negligible. From Eq. 3 and ξ ∼ 𝒪(1) we see that this equivalently limits the length $\left(2\kappa +\overline{\kappa }\right)/\gamma$ (see also the Supporting Material). This might get problematic for bilayers with a very low edge tension (due to, say, a high lipid curvature), but for the cases studied by us the assumption holds. Note also that we do not need to worry about any complications due to hydrodynamics, because the Cooke model is solvent-free.

Following this closing-up process many times, we sample the probability P(x) of such precurved caps closing up, which is a monotonically increasing function of x that changes most rapidly in the neighborhood of x = x^∗. We can link this to the underlying theory by asserting that the reaction coordinate x follows a diffusion process in the potential from Eq. 2. The closing-up probability then coincides with the so-called splitting probability, which measures what fraction of the trajectories starting at a given initial value of x will end up at x = 1. For this an analytical expression exists (70),

$$P_{\xi ,\tilde{D}}\left(x\right)=\frac{\underset{0}{\overset{x}{\int }}\text{d}y{\text{e}}^{\Delta \tilde{E}\left(y,\xi \right)/\tilde{D}}}{\underset{0}{\overset{1}{\int }}\text{d}y{\text{e}}^{\Delta \tilde{E}\left(y,\xi \right)/\tilde{D}}},$$ (4)

where $\tilde{D}$ is an effective diffusion constant. Due to the simple form of $\Delta \tilde{E}$ the integrals can actually be done analytically, giving us a lengthy but closed expression for $P_{\xi ,\tilde{D}}\left(x\right)$ (see the Supporting Material). This can be used to fit the measured P(x), using ξ and $\tilde{D}$ as fitting parameters. Fig. 1 illustrates this for one particular example. Notice that the excellent fit confirms our supposition that simulation and theory follow the same reaction coordinate, i.e., that our analysis is applicable.

Results and Discussion

In our simulations we systematically varied system size, bending rigidity, and spontaneous lipid curvature; all results are collected in Table 2. Let us now discuss what we learn from them. To begin with, note that the elastic ratio $\overline{\kappa }/\kappa$ hovers in the range −0.95 ± 0.1, in accord with the most accurate experimental values from Table 1. However, many of these data refer to monolayers, and their interpretation requires more care: whereas κ = 2κ_m, the “naïve” Gaussian modulus $2{\overline{\kappa }}_{\text{m}}$ for a bilayer is shifted because the two monolayers generally have 1), a spontaneous (lipid) curvature K_0m and 2), a surface of inextension a distance z₀ away from the bilayer midplane. One then finds (71–75)

$$\overline{\kappa }=2\left({\overline{\kappa }}_{\text{m}}-2z_0{K}_{0\text{m}}{\kappa }_{\text{m}}\right).$$ (5)

A more thorough comparison thus requires extra information. Fortunately, the accuracy of our results is high enough to probe deeper, but before that, let us point out two more immediate observations.

Table 2.

List of all simulated systems

No.	Nlipids	A[σ2]	Nx/Nsim	b [σ]	wc[σ]	γ[kBT/σ]	ξ	κ[kBT]	$-\overline{\kappa }$[ kBT]	$-\overline{\kappa }/\kappa$
1	900	541.7	8|500	0.95	1.6	3.043 ± 0.060	1.503 ± 0.003	12.44 ± 0.26	11.59 ± 0.57	0.93 ± 0.03
2	1000	601.9	8|500	0.95	1.6	3.043 ± 0.060	1.568 ± 0.003	12.44 ± 0.26	11.46 ± 0.57	0.92 ± 0.03
3	1100	662.0	11|500	0.95	1.6	3.043 ± 0.060	1.631 ± 0.003	12.44 ± 0.26	11.34 ± 0.58	0.91 ± 0.03
4	900	511.2	8|500	0.95	1.7	4.558 ± 0.061	1.439 ± 0.002	18.36 ± 0.29	16.51 ± 0.65	0.90 ± 0.02
5	1000	568.2	8|500	0.95	1.7	4.558 ± 0.061	1.477 ± 0.002	18.36 ± 0.29	15.97 ± 0.65	0.87 ± 0.02
6	1100	624.7	8|500	0.95	1.7	4.558 ± 0.061	1.534 ± 0.002	18.36 ± 0.29	15.77 ± 0.65	0.86 ± 0.02
7	900	559.6	8|250	0.95	1.55	2.478 ± 0.054	1.541 ± 0.004	10.10 ± 0.32	9.46 ± 0.68	0.94 ± 0.04
8	720	416.8	8|250	0.92	1.6	3.767 ± 0.054	1.703 ± 0.004	11.72 ± 0.23	10.71 ± 0.50	0.91 ± 0.03
9	740	437.0	8|250	0.935	1.6	3.495 ± 0.058	1.559 ± 0.004	11.82 ± 0.27	10.42 ± 0.59	0.88 ± 0.03
10	1050	644.4	8|200	0.965	1.6	2.676 ± 0.057	1.469 ± 0.005	12.43 ± 0.36	11.81 ± 0.78	0.95 ± 0.04
11	1430	895.7	8|250	0.98	1.6	2.208 ± 0.045	1.529 ± 0.005	11.87 ± 0.40	11.54 ± 0.83	0.97 ± 0.04
12	1660	1070.3	8|200	1.00	1.6	1.657 ± 0.048	1.407 ± 0.006	11.41 ± 0.37	11.95 ± 0.80	1.05 ± 0.04

N_lipids is the number of lipids; A is the area of patch (in units of σ², where σ ≈ 1 nm is the diameter of a lipid tail bead, error is much less than 1%); N_x is the number of different x values investigated for each system; N_sim is the number of folding simulations for each value of x; b is the diameter of a lipid head bead; w_c is the attractive range of the interaction potential in the Cooke model; γ is the edge tension; ξ is the parameter in the energy barrier from Eq. 2, determined by fitting the closing-up probabilities via Eq. 4; κ is the bending modulus, determined through simulating tethers (35); and $\overline{\kappa }$ is the Gaussian curvature modulus, inferred from ξ, κ, γ, and $R=\sqrt{A/4\pi }$.

First, in Systems 1–3 and 4–6 we study different system sizes (at two bending rigidities, tuned by changing the tail attraction parameter w_c). In each case, $\left|\overline{\kappa }/\kappa \right|$ appears to very slightly decrease for bigger systems. It is conceivable that this originates from higher order (quartic) curvature corrections, because particularly for the small systems the curvatures are substantial; and yet, within the error bars the effect is hardly significant. Hence, we will ignore this in the following and average over the three sizes.

Second, Systems 1–3, 4–6, and 7 probe three different bending elasticities for the same lipid shape (same headgroup size b = 0.95σ, but different w_c; see Table 2). In this case there is a clear trend that stiffer membranes have a larger value for $\overline{\kappa }/\kappa$ (i.e., closer to 0). One might at first think that increasing the tail attraction increases the lipid spontaneous curvature K_0m, but according to Eq. 5 this effect should result in a change in the opposite direction. Instead, we propose the following tentative explanation: Increasing w_c reduces the area per lipid and stiffens the membrane. This not only reduces the area compressibility, but also the degree to which it can be compressed any further. Recall now that in simple thin plate continuum theory one can derive $\overline{\kappa }/\kappa$ = ν – 1 (76), where ν is the Poisson ratio of the material (which can vary in the range −1 ≤ ν ≤ 1/2). The largest value ν = 1/2 corresponds to the incompressible limit. Hence, a less compressible membrane has a larger Poisson ratio and thus a larger value for $\overline{\kappa }/\kappa$—in line with our observation. The same physics might be responsible for the fact that measurements on the mixed systems DOPC/Chol and GMO/DOPC/DOPE (see Table 1) lead to elastic ratios bigger than those of the pure systems. We hasten to add, though, that this argument is difficult to make more quantitative, because membranes are not really homogeneous and isotropic continuum elastics (they have important nonisotropic internal structure (77)), so it seems best to leave these observations at a cautious semiquantitative level.

Third, in Systems 1–3, 8, 9, 10, 11, and 12 we vary the headgroup size of the lipid, b/σ ∈ {0.92, 0.935, 0.95, 0.965, 0.98, 1.0}, and thereby the spontaneous lipid curvature K_0m. Over this range, κ changes by merely 4%, while at the same time the elastic ratio changes by ∼17%, as shown in Fig. 2. A straight line fit gives $\overline{\kappa }/\kappa$ = (0.69 ± 1.49) – (1.71 ± 1.56)b/σ (with strongly anticorrelated errors determined from Monte Carlo resampling the data). A simple geometric model suggests that the spontaneous lipid curvature can be written as K_0m = α/R ≃ α(b/b_t – 1)/2σ, where b_t is the size of the tail bead (see inset in Fig. 2). The prefactor α would have the value 2 if only geometry mattered, but because this neglects the entropy of lipid tail-bending fluctuations, its actual value should be smaller. We will assume that 1 ≤ α ≤ 2 constitutes a meaningful range, but the precise value of α will not matter in what follows. Inserting this geometric model into Eq. 5 leads to

$$\frac{\overline{\kappa }}{\kappa }=\left(\frac{{\overline{\kappa }}_{\text{m}}}{{\kappa }_{\text{m}}}+\frac{\alpha z_0}{\sigma }\right)-\left(\frac{\alpha z_0}{b_{\text{t}}}\right)\frac{b}{\sigma },$$ (6)

supporting the linear relation observed in Fig. 2. From the corresponding fit, we can further determine αz₀ and ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\mathrm{m}}$, provided we are willing to make two more assumptions: 1), b/b_t predominantly affects K_0m and not the monolayer elastic ratio ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\mathrm{m}}$; and 2), the effective tail bead size in the Cooke model is b_t = 0.95σ, meaning that the spontaneous curvature of the standard lipid with b = 0.95σ is zero. The former is supported by the observation that over the wide temperature range 55..90°C, the value of ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\mathrm{m}}$ for DOPE-Me appears to be roughly constant (78), whereas the spontaneous curvature K_0m changes by ∼13% (74,78). The latter is plausible because the head bead size b has deliberately been taken to be 5% smaller than the nominal tail bead size σ to ensure that, after tail compression due to cohesion, the lipids are effectively straight (recall that heads only repel but tails attract) (31,32). If we assume both items, we can deduce from Eq. 6 and the fit that αz₀ ≈ (1.63 ± 1.48)σ and ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\mathrm{m}}$ ≈ −0.93 ± 0.03. The value for αz₀ unfortunately carries a large error bar, because the slope of the line in Fig. 2 cannot be determined more precisely, despite the fact that every single elastic ratio is known at unprecedented accuracy. Because also α can only be estimated within a factor of 2, this method is not a practical way to find z₀.

Figure 2.

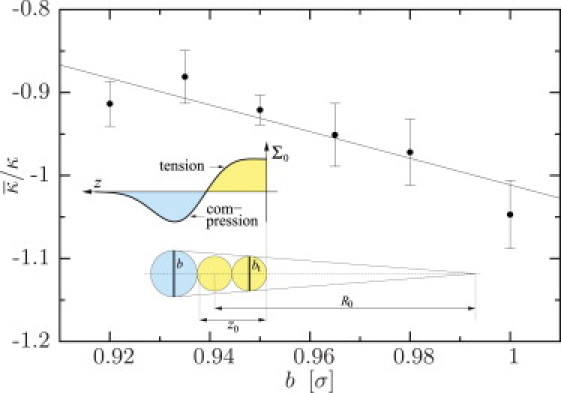
Elastic ratio as a function of head bead size b for w_c = 1.6σ (Systems 1–3, 8, 9, 10, 11, and 12 from Table 2). The straight line is a fit to the data points. (Inset) Definitions of the distance of inextension, z₀; the bead sizes b and b_t; and the geometric curvature radius R₀ ≃ 2σ/(b/b_t − 1). The lateral stress profile ${\Sigma }_0$ (z) of the Cooke model is also indicated above the sketched model lipid.

In contrast, the statistical error for ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\mathrm{m}}$ is remarkably small (note that the anticorrelated errors in slope and intercept cancel); however, the result still depends on our assumption that b = 0.95σ is the head bead size at which the spontaneous lipid curvature in the Cooke model vanishes (where ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\text{m}}=\overline{\kappa }/\kappa$, according to Eq. 6). If we more conservatively estimate that this special size lies somewhere between 0.92σ and 0.98σ, we find the more realistic accuracy ${\overline{\kappa }}_{\text{m}}/{\kappa }_{\mathrm{m}}$ ≈ −0.93 ± 0.05. These monolayer values are compatible with the experimental monolayer values measured for DOPE-ME, DOPE, and DOPC (see Table 1).

Real membranes and most simulation models are not infinitely thin surfaces but are structured across their width. It has often been pointed out that the lateral stress profile ${\Sigma }_0$(z) of the flat membrane contains information about elastic parameters entering the Helfrich level of Eq. 1. Specifically, if the membrane is tensionless, the first and second moment taken over one leaflet are (71–73)

$$-{\kappa }_{\text{m}}{K}_{0\text{m}}=\underset{0}{\overset{d}{\int }}\text{d}z\left(z-z_0\right){\Sigma }_0\left(z\right),$$ (7)

$${\overline{\kappa }}_{\text{m}}=\underset{0}{\overset{d}{\int }}\text{d}z{\left(z-z_0\right)}^2{\Sigma }_0\left(z\right),$$ (8)

where d is a distance sufficiently far out in the bulk that the membrane stresses have vanished. The elastic parameters for the complete bilayer are obtained by taking the integrals over the entire membrane and setting z₀ = 0; Eq. 5 is thereby rediscovered as a special consequence. Note that for a symmetric and tensionless bilayer, the result of Eq. 7 does not depend on the value of z₀ because the integral of ${\Sigma }_0$ (z) vanishes.

The stress profile can in principle be obtained in simulations (34,79–85), suggesting an alternative route toward $\overline{\kappa }$, but there are caveats:

• 1.The unique definition of a local stress is subject to ambiguities (87).
• 2.${\Sigma }_0$ (z) for CG models might be unrealistic; it certainly is so in the Cooke model (see inset in Fig. 2).
• 3.The stress-tensor-route toward $\overline{\kappa }$ has never been tested against other approaches, simply because no accurate alternatives were available.

We have calculated ${\Sigma }_0$ (z) for the Systems 1–3 (see the Supporting Material) and found κ_m K_0m ≃ 3.75 k_BT/σ and $\overline{\kappa }$ ≃ −21.7 k_BT, without any assumptions on z₀. The first implies the extremely high lipid curvature K_0m ≃ 0.67/σ (given κ_m = κ/2 = 6.2 k_BT), the second the highly unusual (but still permissible) elastic ratio $\overline{\kappa }/\kappa$ ≃ −1.7. Our estimated monolayer Gaussian modulus ${\overline{\kappa }}_{\text{m}}$ = −0.93 κ_m = −5.8 k_BT would require the very small value z₀ ≃ 0.68σ. Furthermore, for ${\overline{\kappa }}_{\text{m}}$ to stay negative, z₀ has to be <1.45 σ, which is inconsistent with the common expectation that z₀ locates near the hydrophobic-hydrophilic interface ($z\simeq 2\sigma$ in the Cooke model). Unlike the values determined from closing a bilayer patch, these results are neither plausible nor in agreement with experiment. We therefore conclude that the stress tensor route suffers from deficits.

A potential breakdown of the relation between stress profile and material parameters is both distressing and disappointing, because calculating $\overline{\kappa }$ from ${\Sigma }_0$ (z) would be easier than the patch-closure approach we have described here. And whereas the unphysical nature of ${\Sigma }_0$ (z) in the Cooke model might seem the most obvious culprit, we emphasize that Eqs. 7 and 8 can be based entirely on mechanical reasoning and elastic continuum theory (71,72). As such, their validity does not depend on any specific physical assumptions or interpretation of the actual stress distribution. On the other hand, these equations neglect local correlations, such as lipid packing and local alignment of tails. These must also affect the free energy and hence the stress distribution, and this is not captured on a purely mechanical level. Gompper and Klein (77) have illustrated that when one attempts to recapture such correlations using an empirical Ginzburg-Landau theory, corrections to Eqs. 7 and 8 appear that depend on the local order parameter distribution and the new coupling parameters. Because the latter cannot be easily measured, this precludes a straightforward numerical test or correction. If the discrepancy arises due to correlations along the bilayer normal, one could argue that the coarse nature of the Cooke model is to blame and more highly resolved bilayer models will fare better. However, if lateral correlations also matter, then these are not necessarily shorter ranged in a higher resolved model, because the area per lipid is essentially matched. In that case, there would be no reason to expect the stress profile even of an atomistic simulation to yield $\overline{\kappa }$. We will leave this question open here, but in light of the observations we make in this article, we submit that the validity of Eqs. 7 and 8 should not uncritically be taken for granted.

Using a CG model, we showed that we can, with great accuracy, measure the Gaussian curvature modulus of lipid membranes and probe several of its generic properties. Although the model is not precise enough to predict $\overline{\kappa }$ for an actual lipid, the strategy we have proposed is very efficient and trivial to parallelize. We believe that it remains feasible for more sophisticated models that require more computational effort. For instance, the folding-up simulations we did for System 1 took ∼2000 CPU hours, which takes a few days on a small cluster. We could even have restricted our efforts to 200 simulations per starting curvature (see System 10), given that the total error is dominated by κ and γ. For a more finely resolved lipid model, for instance the MARTINI model (29), we estimate that a few months should suffice to determine $\overline{\kappa }$, assuming that κ and γ have already been determined.