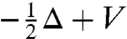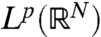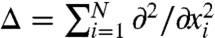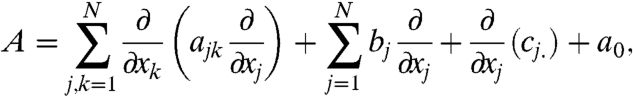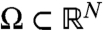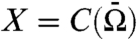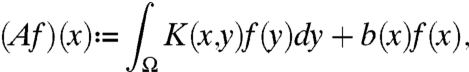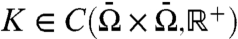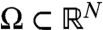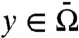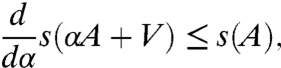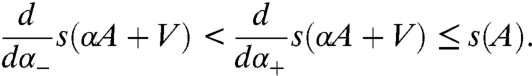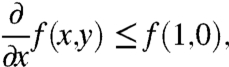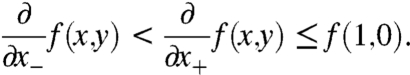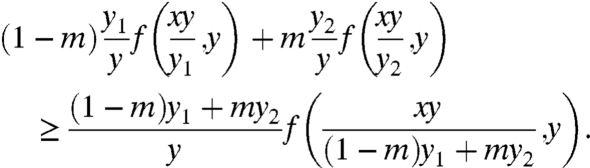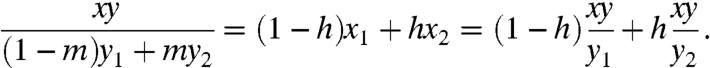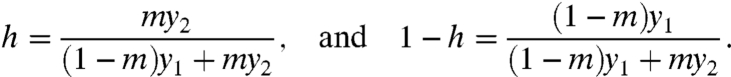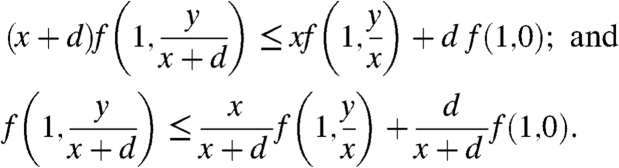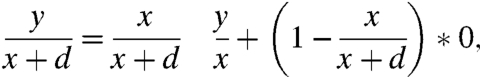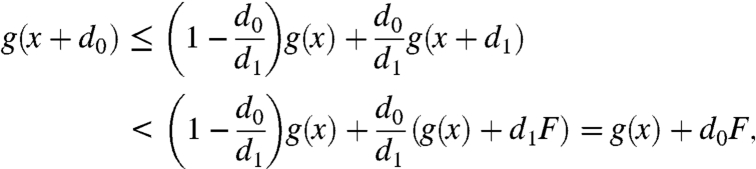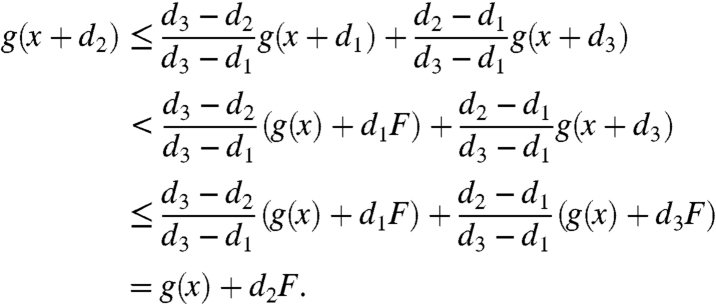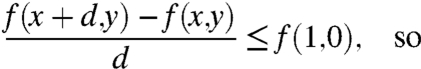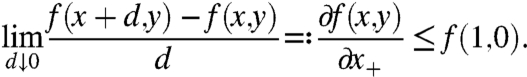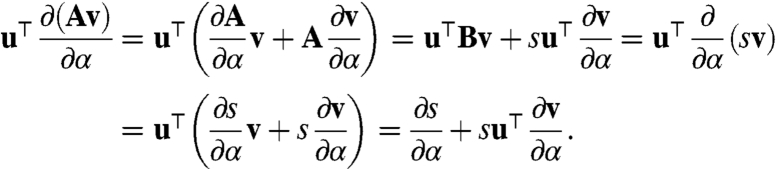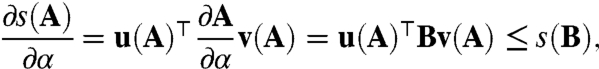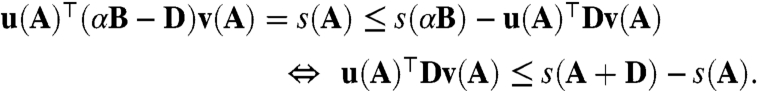Resolvent positive linear operators exhibit the reduction phenomenon

Abstract

The spectral bound, s(αA + βV), of a combination of a resolvent positive linear operator A and an operator of multiplication V, was shown by Kato to be convex in 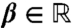. Kato's result is shown here to imply, through an elementary “dual convexity” lemma, that s(αA + βV) is also convex in α > 0, and notably, ∂s(αA + βV)/∂α ≤ s(A). Diffusions typically have s(A) ≤ 0, so that for diffusions with spatially heterogeneous growth or decay rates, greater mixing reduces growth. Models of the evolution of dispersal in particular have found this result when A is a Laplacian or second-order elliptic operator, or a nonlocal diffusion operator, implying selection for reduced dispersal. These cases are shown here to be part of a single, broadly general, “reduction” phenomenon.

The main result to be shown here is that the growth bound, ω(αA + V), of a positive semigroup generated by αA + V changes with positive scalar α at a rate less than or equal to ω(A), where A is also a generator, and V is an operator of multiplication. Movement of a reactant in a heterogeneous environment is often of this form, where V represents the local growth or decay rate, and α represents the rate of mixing. Lossless mixing means ω(A) = 0, while lossy mixing means ω(A) < 0, so this result implies that greater mixing reduces the reactant’s asymptotic growth rate, or increases its asymptotic decay rate. Decreased growth or increased decay are familiar results when A is a diffusion operator, so what is new here is the generality shown for this phenomenon. At the root of this result is a theorem by Kingman on the “superconvexity” of the spectral radius of nonnegative matrices (1). The logical route progresses from Kingman through Cohen (2) to Kato (3). The historical route begins in population genetics.

In early theoretical work to understand the evolution of genetic systems, Feldman, colleagues, and others kept finding a common result from each model they examined (4–14)—be they models for the evolution of recombination, or of mutation, or of dispersal. Evolution favored reduced levels of these processes in populations near equilibrium under constant environments, and this result was called the Reduction Principle (11).

These results were found for finite-dimensional models. But the same reduction result has also been found in models for the evolution of unconditional dispersal in continuous space, in which matrices are replaced by linear operators. This finding raises the questions of whether this common result, discovered in such a diversity of models, reflects a single mathematical phenomenon. Here, the question is answered affirmatively.

The mathematical underpinnings of the reduction principle for finite-dimensional models were discovered by Sam Karlin (15, 16) [although he did not realize it, and he had earlier proposed an alternate to the reduction principle—the mean fitness principle (17), which was found to have counterexamples (18)]. Karlin wanted to understand the effect of population subdivision on the maintenance of genetic variation. Genetic variation is preserved if an allele has a positive growth rate when it is rare, protecting it from extinction. The dynamics of a rare allele are approximately linear, and of the form

[1]

where x(t) is a vector of the rare allele’s frequency at time t among different population subdivisions, α is the rate of dispersal between subdivisions, P is the stochastic matrix representing the pattern of dispersal, and D is a diagonal matrix of the growth rates of the allele in each subdivision. The allele is protected from extinction if its asymptotic growth rate when rare is greater than 1. This asymptotic growth rate is the spectral radius,

[2]

where σ(A) is the set of eigenvalues of matrix A.

Karlin discovered that for M(α)≔[(1 - α)I + αP], the spectral radius, r(M(α)D), is a decreasing function of the dispersal rate α, for arbitrary strongly connected dispersal pattern:

Theorem 1. (Karlin's Theorem 5.2)

[(16), pp. 194–196] Let P be an arbitrary nonnegative irreducible stochastic matrix. Consider the family of matrices

Then for any diagonal matrix D with positive terms on the diagonal, the spectral radius

is decreasing as α increases (strictly provided D ≠ dI).

Karlin’s Theorem 5.2 means that greater mixing between subdivisions produces lower r(M(α)D), and if it goes below 1, the allele will go extinct. While this theorem was motivated by the issue of genetic diversity in a subdivided population, its form applies generally to situations where differential growth is combined with mixing. D could just as well represent the investment returns on different assets and P a pattern of portfolio rebalancing. Or D could represent the decay rates of reactant in different parts of a reactor, and P a pattern of stirring within the reactor. In a very general interpretation, Theorem 5.2 means that greater mixing reduces growth and hastens decay.

If the dispersal rate α is not an extrinsic parameter, but is a variable which is itself controlled by a gene, then a gene which decreases α will have a growth advantage over its competitor alleles. The action of such modifier genes produces a process that will reduce the rates of dispersal in a population. Therefore, Theorem 5.2 also means that differential growth selects for reduced mixing.

In the evolutionary context, the generality of the mixing pattern P in Karlin’s Theorem 5.2 makes it applicable to other kinds of “mixing” besides dispersal. The pattern matrix P can just as well refer to the pattern of mutations between genotypes, and then α refers to the mutation rate. Or P can represent the pattern of transmission when two loci recombine, and then α represents the recombination rate. The early models for the evolution of recombination and mutation that exhibited the reduction principle in fact had the same form as Eq. 1 for the dynamics of a rare modifier allele. Once this commonality of form was recognized (19–21), it was clear that Karlin’s theorem explained the repeated appearance of the reduction result in the different contexts, and generalized the result to a whole class of genetic transmission patterns beyond the special cases that had been analyzed.

The dynamics of movement in space have been long modeled by infinite-dimensional models, where space is continuous and the concentrations of a quantity at each point are represented as a function. The dynamics of change in the concentration are modeled as diffusions, where the Laplacian or elliptic differential operator or nonlocal integral operator takes the place of the matrix P in the finite-dimensional case. When the substance grows or decays at rates that are a function of its location, the system is often referred to as a reaction diffusion. In reaction-diffusion models for the evolution of dispersal, the reduction principle again makes its appearance (22) (23, Lemma 5.2) (24, Lemma 2.1) (25). In nonlocal diffusion models, again the reduction principle appears (26). This repeated occurrence points to the possibility of an underlying mathematical unity.

Here, a broad characterization of this “reduction phenomenon” is established by generalizing Karlin’s theorem to linear operators. The reduction results previously found for various linear operators are, therefore, seen to be special cases of a general phenomenon.

This result is actually implicit in Kato’s generalization (3) of Cohen’s theorem (2) on the convexity of the spectral bound of essentially nonnegative matrices with respect to the diagonal elements of the matrix. It is educed from Kato’s theorem here by means of an elementary “dual convexity” lemma.

Kato’s goal in ref. 3 was to generalize, from matrices to linear operators, Cohen’s convexity result (2):

Theorem 2. (Cohen)

(2) Let D be diagonal real n × n matrix. Let A be an essentially nonnegative n × n matrix. Then s(A + D) is a convex function of D.

Here, s(A + D) is the spectral bound—the largest real part of any eigenvalue of A + D. A synonym for the spectral bound used in the matrix literature is the spectral abscissa (27, 28). When the spectral bound is an eigenvalue, it is also referred to as the principal eigenvalue (29), dominant eigenvalue (30), dominant root (31), Perron-Frobenius eigenvalue (32), or Perron root (33). “Essentially nonnegative” means that the off-diagonal elements are nonnegative. Synonyms include “quasi-positive” (34), “Metzler,” “Metzler-Leontief,” “ML” (32), and “cooperative” (35).

Cohen’s proof relied upon the following theorem of Kingman:

Theorem 3. (Kingman)

(1) Let A be an n × n matrix whose elements, A_ij(θ), are nonnegative functions of the real variable θ, such that they are “superconvex,” i.e., for each i, j, either log A_ij(θ) is convex in θ [A_ij(θ) is log convex], or A_ij(θ) = 0 for all θ. Then the spectral radius of A is also superconvex in θ.

Kato generalized Cohen’s result to linear operators by first generalizing Kingman’s theorem. Before presenting Kato’s theorem, some terminology needs to be introduced:

X represents an ordered Banach space or its complexification.

X₊ represents the proper, closed, positive cone of X, assumed to be generating and normal (see ref. 3).

B(X) represents the set of all bounded linear operators A: X → X.

A is a positive operator if AX₊⊂X₊.

The resolvent of A is R(ξ,A)≔(ξ - A)^-1, the operator inverse of ξ - A, .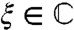

The resolvent set 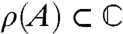are those values of ξ for which ξ - A is invertible.

The spectrum of A∈B(X), σ(A), is the complement of the resolvent set, ρ(A).

The spectral bound of closed linear operator A, not necessarily bounded, is

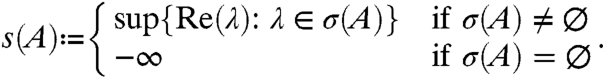The type (growth bound) of an infinitesimal generator, A, of a strongly continuous (C₀) semigroup, {e^tA: t > 0}, is

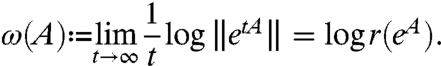Generally, -∞ ≤ s(A) ≤ ω(A) < ∞, but conditions for s(A) = ω(A) or s(A) < ω(A) are part of a more involved theory for the asymptotic growth of semigroups (see refs. 36–38).

Definition 1:

Operator A is resolvent positive if there is ξ₀ such that (ξ₀,∞)⊂ρ(A) and R(ξ,A) is positive for all ξ > ξ₀ (39).

The relationship of the resolvent positive property to other familiar operator properties includes the following list of key results:

1. If A generates a C₀-semigroup T_t, then T_t is positive for all t≥0 if and only if A is resolvent positive (ref. 38, p. 188).

2. If A is a resolvent positive operator defined densely on X = C(S), the Banach space of continuous complex-valued functions on compact space S, then A generates a positive C₀-semigroup [(38), Theorem 3.11.9].

3. If A is resolvent positive and its domain, D(A)⊂X, is dense in X, then for every f∈D(A²), there exists a unique solution, u(t)∈D(A) for all t≥0, u∈C¹([0,∞),X), to the Cauchy problem (39, Theorem 7.1)

   

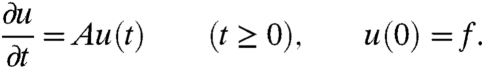
4. If A is resolvent positive then: s(A) < ∞; if σ(A) is nonempty; i.e., -∞ < s(A), then s(A)∈σ(A); if 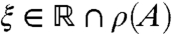yields R(ξ,A)≥0 then ξ > s(A) (3) (38, Proposition 3.11.2).

5. Differential operators higher than second order are never resolvent positive (40, Corollary 2.3) (41).

6. Well-known examples of resolvent positive operators include the following (for details see the sample references):

   1. Schrödinger operators on , where is the Laplace operator, and V is an operator of multiplication with constraints depending on p (see refs. 42–44).
   2. Second-order elliptic operators on L^p(Ω),

      

      where is open, coefficients are measurable and bounded, ellipticity conditions apply to a_jk(x), and appropriate additional conditions hold for the coefficients, domain and boundary (45), also e.g., (3, 46, 47).
   3. Linear integral operators A on defined by

      

      where , is bounded, and K(x,y) > 0, b(x) are measurable functions for x, (26, 48, 49). A resolvent positive combination of integral and differential operator is analyzed in ref. 50.

Kato’s generalization of Cohen’s theorem is as follows:

Theorem 4. (Generalized Cohen’s Theorem)

(3) Consider X = C(S) (continuous functions on a compact Hausdorff space S) or X = L^p(S), 1 ≤ p < ∞, on a measure space S, or more generally, let X be the intersection of two L^p-spaces with different p’s and different weight functions. Let A: X → X be a linear operator which is resolvent positive. Let V be an operator of multiplication on X represented by a real-valued function v, where v∈C(S) for X = C(S), or v∈L^∞(S) for the other cases. Then s(A + V) is a convex function of V. If in particular A is a generator of a C₀ semigroup, then both s(A + V) and ω(A + V) are convex in V.

Kato’s theorem is further generalized to Banach lattices by Arendt and Batty (51) as follows:

Theorem 5. (Generalized Kato’s Theorem)

[(51), Theorem 3.5] Let A be the generator of a positive semigroup on a Banach lattice X, and let refer to the “center” of X. Then the functions V↦s(A + V) and V↦ω(A + V) from Z(X) into [-∞,∞) are convex.

Results

Theorem 6. (Generalized Karlin’s Theorem)

Let A be a resolvent positive linear operator, and V be an operator of multiplication, under the same assumptions as Theorem 4 (or let A and V be as in Theorem 5). Then for α > 0 :

1. s(αA + V) is convex in α;

2. For each α > 0, either

   1. ∀ d > 0, or
   2. ∀ d > 0;

3. In particular, when s(A) = 0 then s(αA + V) is nonincreasing in α (the reduction phenomenon), and when s(A) < 0 then s(αA + V) is strictly decreasing in α;

4. For each α > 0,

   [3]

   except possibly at a countable number of points α, where the one-sided derivatives exist but differ:

   [4]

If A is a generator of a C₀-semigroup, then the above relations on s(αA + V) also apply to the type ω(αA + V).

Proof:

We consider the general form

[5]

where α > 0, . Kato (3) explicitly shows that ϕ(1,β) is convex in β (which he points out is equivalent to varying V). Kato's result is shown to imply the properties claimed for s(αA + V) = ϕ(α,1) with respect to variation in α, by Lemma 1, to follow.

Lemma 1. (Dual Convexity)

Let and . Let have the following properties:

[6]

[7]

Then:

1. f(x,y) is convex in x;

2. For each , either

   1. (a) f(x + d,y) < f(x,y) + d f(1,0) ; or
   2. (b) .

   For y ≠ 0, if f(x,y) is strictly convex in y, then f(x,y) is strictly convex in x, and .
3. For each ,

   

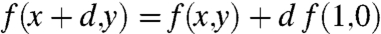
   except possibly at a countable number of points x, where the one-sided derivatives exist but differ:

   

   The lemma holds if we substitute or or both.

Proof:

1. f(x,y) is convex in x.

   The relation (f is homogeneous of degree one) allows a set of rescalings that transform convexity in y into convexity in x. It is perhaps worth noting that this relation is actually a homomorphism, which can be put into a more familiar form by defining a product x⋆y ≔f(x,y), and function ψ(x)≔αx, which gives ψ(x)⋆ψ(y) = ψ(x⋆y).

   For the case y = 0, Eq. 6 gives f(αx,0) = αf(x,0), so f is trivially convex in x.

   For y ≠ 0, the following derivations have the constraints y, y₁, , y, y₁, y₂ ≠ 0, and 0 < m < 1, so that {y,y₁,y₂,m,1 - m,(1 - m)y₁ + my₂} are nonzero and their ratios and reciprocals are always defined, and ratios of y_i terms always positive. These constraints keep the arguments of f within their domains throughout the rescalings.

   Convexity of f(x,y) in y gives

   [8]

   for m∈(0,1), y₁ ≠ y₂. Applying [6] to [8], with respective substitutions α = y₁/y, α = y₂/y, and α = [(1 - m)y₁ + my₂]/y in the three f terms, yields:

   [9]

   Let x₁≔xy/y₁ and x₂≔xy/y₂ represent the rescaled first arguments for f on the left side of [9] (so x, x₁, ). We try the ansatz that x₁ and x₂ can be combined convexly to yield the third rescaled argument on the right side of [9]:

   

   The ansatz has solution

   

   Note that h∈(0,1) is assured because y₁ and y₂ have the same sign, y₁ ≠ y₂, and m∈(0,1).
   Define ϕ≔[(1 - m)y₁ + my₂]/y. Then ϕ > 0 because y, y₁, and y₂ all have the same sign. Substitution gives (1 - m)y₁/y = (1 - h)ϕ, and my₂/y = hϕ, and [9] becomes:

   

   After dividing both sides by ϕ > 0,

   [10]

   which is convexity in x [for each (x₁,x₂,h),∃(y₁,y₂,m)]. The case of strict convexity follows by substituting > for ≥ throughout.

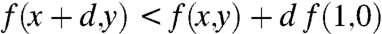
2. Either , or .

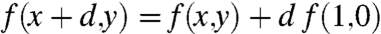
   If y = 0, then case 2b in Lemma 1 holds by [6]:

   

   For y ≠ 0, the strategy will be to show first that . Next, it is shown that if for any , then it is true for all .
   The steps are shown here only for x, , but they are readily applied to . By [6], for x, d > 0, the following are equivalent:

   [11]

   [12]

   Because 0 < d/(x + d), x/(x + d) < 1, the second arguments for f in [12] are related by convex combination,

   

   so [12] is just a statement of the convexity of f(x,y) in y, as hypothesized. Strict convexity of f(x,y) in y replaces ≤ with < throughout [11] and [12], yielding case 2a in Lemma 1.
   Now, with x > 0, suppose that for some d₁ > 0,

   [13]

   We shall see that convexity then prevents f(x + d,y) from ever returning to the line for d > 0.
   We consider five points:

   [14]

   For readability, write g(x) ≡ f(x,y) and F ≡ f(1,0). By convexity [10], and hypothesis [13],

   

   and, by [10], [13], and [11] (line 3 below),

   

   For the case where , the direction of inequalities in [14] needs to be reversed, and all the subsequent relations are preserved.

3. For each , ∂f(x,y)/∂x ≤ f(1,0), except possibly at a countable number of points x, where the one-sided derivatives exist but differ: .

   Rearrangement of [11] gives

   [15]

   [16]

   For y = 0, equality holds in [15] for all d > 0. For y ≠ 0, because f(x,y) is convex in x on the open interval , the left-sided and right-sided derivatives always exist, and differ at most at a countable number of points, at which the right-sided derivative [16] is greater than the left-sided derivative [(52) Proposition 17, pp. 113–114].

A concavity version of the lemma may be trivially produced by reversal of the convexity inequalities.

Remark 1:

It would be clearly desirable to characterize the conditions for strict convexity in Kato’s theorem, so that by Lemma 1, one would obtain strict convexity in Theorem 6, item 1, and strict monotonicity in items 3 and 4. Item 2 is the best that can be offered in the way of strict inequality without strict convexity. But the problem is more technical and is deferred to elsewhere.

It is reasonable, nevertheless, to conjecture that the properties which produce strict convexity in the matrix case (ref. 53, Theorem 4.1) (ref. 54, Theorem 1.1) extend to their Banach space versions: i.e., for a > 0, when resolvent positive operator A is irreducible (ref. 55, p. 250) (ref. 51, p. 41), then s(αA + βV) is strictly convex in β if and only if V is not a constant scalar.

The conjectured sharpening of Theorem 6 to strict inequality would have application to continuous-space models for the evolution of dispersal, and show populations to be invadable by less-dispersing organisms when they experience spatially heterogeneous growth rates (a “selection potential” as defined in ref. 20). This invasibility result is a key element of the Reduction Principle, and is first stated generally for finite matrix models in refs. 19, pp. 118, 126, 137, 195, 199 and 20, Results 2, 3. The invasibility result's primary implication is that for a population to be non-invadable, it must experience no spatial heterogeneity of growth rates where it has positive measure, and this points toward ideal free distributions (defined to be those which spatially equalize the growth rates when this is possible), as the evolutionarily stable states. For reviews and recent developments, see refs. 56–60.

A Third Proof of Karlin’s Theorem 5.2.

Karlin’s proof is based on the Donsker-Varadhan variational formula for the spectral radius (62). Kirkland, et al. (56) recently discovered another proof using entirely structural methods. A third distinct proof of Karlin’s theorem is seen as follows by application of Lemma 1 to Cohen’s theorem, combined with Friedland’s equality condition [(53), Theorem 4.1] (see also refs. 53 and 62 for other proof methods).

The expression in Karlin’s Theorem 5.2 can be put into the form used in Theorem 6:

where A = (P - I)D, α∈(0,1), and β = 1. Because M(α)D is a nonnegative matrix when α∈(0,1), by Perron-Frobenius theory its spectral bound s(M(α)D) equals its spectral radius r(M(α)D).

Cohen’s theorem gives that s(αA + βD) is convex in β, and thus by Lemma 1, s(αA + βD) is convex in α > 0 and

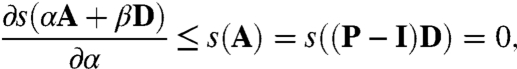[17]

the right identity seen because e^⊤(P - I)D = (e^⊤ - e^⊤)D = 0, where e is the vector of ones, and e^⊤ is its transpose.

Strict convexity in β is shown by Friedland (ref. 53, Theorem 4.1) to occur when P is irreducible and D ≠ cI, for any c > 0. Strict convexity in β implies, by Lemma 1, that r(M(α)D) = s(M(α)D) is strictly convex and decreasing in α.

Remark 2:

The core of Kirkland, et al.’s (56) proof of Theorem 1 is their Lemma 4.1, which can be expressed as

with equality only when e^⊤A = s(A)e^⊤, where u(A)^⊤ and v(A) are the left and right eigenvectors of A associated with the Perron root s(A), and u∘v is the Schur-Hadamard (elementwise) product.

Kirkland, et al.’s (55) result, except for the equality condition, is a special case of ref. 63 Theorem 3.2.5 that x^⊤Ay≥s(A) for any x,y≥0: x∘y = u(A)∘v(A). To obtain the equality condition requires an approach Kirkland, et al.’s (55) distinct proof provides.

Remark 3:

Schreiber and Lloyd-Smith [(64) Appendix B, Lemma 1] followed the reverse path and extended Kirkland, et al’s result on s(M(α)D) to the form s(αA + D), where A is essentially nonnegative and D any diagonal matrix.

Remark 4:

Kato (3) notes that the Donsker-Varadhan formula provides another route besides Kingman’s theorem to his generalization of Cohen’s theorem (but with more restrictive conditions). Indeed, Friedland (53) uses the Donsker-Varadhan formula to prove Cohen’s theorem augmented by strict convexity. The dual convexity relationship shown here between Cohen’s and Karlin’s theorems means that both routes of proof apply as well to Karlin’s theorem. Given these parallels, the relationship between the theorem of Kingman and the theorem of Donsker and Varadhan invites deeper study.

Lemma 1 combined with Cohen’s theorem can also be used to give a new proof of an inequality of Lindqvist, the special case considered in ref. 65, Theorem 2, pp. 260–261.

Theorem 7. (Lindqvist)

[(65), Theorem 2, subcase ] Let A be an irreducible n × n real matrix such that (i) A_ij≥0 for i ≠ j, and (ii) The left and right eigenvectors of A, u(A)^⊤ and v(A), associated with eigenvalue s(A), satisfy u(A)^⊤v(A) = 1. Let D be an n × n real diagonal matrix. Then

[18]

Proof:

Because A is an irreducible essentially nonnegative matrix, s(A) is an eigenvalue of multiplicity 1. Consider the representation A = αB - D, where B is essentially nonnegative and α > 0. Write s ≡ s(A). Because A is irreducible, it has unique u ≡ u(A) and v ≡ v(A) given u^⊤v = e^⊤v = 1, and all the derivatives exist (28) in the following derivation [(66), Sec. 9.1.1]:

Cancellation of terms su^⊤∂v/∂α gives

the inequality derived as in Eq. 17. Scaling by α, subtracting D, and substituting αB = A + D, we get

A Key Open Problem.

In some physical systems, and in biological applications especially, there may be multiple, independently varied operators acting on a quantity [e.g., diffusion with independent advection (ref. 67, eq. 2.9)], or the variation may not scale the mixing process uniformly [e.g., conditional dispersal (68, 69)], so that variation is not of the form αA + V but rather αA + B, where B is a linear operator other than an operator of multiplication. Examples are known where departures from reduction occur; i.e., ds(αA + B)/dα > s(A). Results for the form αA + B have been obtained for symmetrizable finite matrices in models of multilocus mutation (70), and dispersal in random environments (71). Some results for Banach space models have also been obtained (67–69, 72–77).

A key open problem, then, is to find necessary or sufficient conditions on Banach space operators, B, such that ∂s(αA + βB)/∂α ≤ s(A) (which may depend on A, β/α, domain, and boundary conditions). A sufficient condition is that s(αA + βB) be convex in β, by Lemma 1. Thus, the dual problem is to ask: for which B is s(αA + βB) convex in β? Some results towards this problem are in ref. 78. Kato obtained Theorem 4 with operators of multiplication, V, because the family of operators e^βV is semigroup-superconvex in β (definition in ref. 3), but this semigroup-superconvexity approach faces the challenge that, “It is in general difficult to find a nontrivial semigroup-superconvex family B(h)” (3).