The distribution of ligand-binding pockets around protein-protein interfaces suggests a general mechanism for pocket formation

Abstract

Protein-protein and protein-ligand interactions are ubiquitous in a biological cell. Here, we report a comprehensive study of the distribution of protein-ligand interaction sites, namely ligand-binding pockets, around protein-protein interfaces where protein-protein interactions occur. We inspected a representative set of 1,611 representative protein-protein complexes and identified pockets with a potential for binding small molecule ligands. The majority of these pockets are within a 6 Å distance from protein interfaces. Accordingly, in about half of ligand-bound protein-protein complexes, amino acids from both sides of a protein interface are involved in direct contacts with at least one ligand. Statistically, ligands are closer to a protein-protein interface than a random surface patch of the same solvent accessible surface area. Similar results are obtained in an analysis of the ligand distribution around domain-domain interfaces of 1,416 nonredundant, two-domain protein structures. Furthermore, comparable sized pockets as observed in experimental structures are present in artificially generated protein complexes, suggesting that the prominent appearance of pockets around protein interfaces is mainly a structural consequence of protein packing and thus, is an intrinsic geometric feature of protein structure. Nature may take advantage of such a structural feature by selecting and further optimizing for biological function. We propose that packing nearby protein-protein or domain-domain interfaces is a major route to the formation of ligand-binding pockets.

At one point or another, virtually all biological processes are dependent on protein-protein and/or protein-ligand interactions (1). Since these interactions are ubiquitous for biological activity and are important to drug design, intense research efforts have been dedicated to elucidating their structural basis. This has resulted in the deposition of thousands of protein-protein and protein-ligand complexes in the PDB (2). From a structural prospective, protein surface regions directly contacting other proteins are known as protein-protein interfaces, whereas binding-sites for small molecule ligands are referred to as ligand-binding pockets.

Using insights gleaned from high resolution structures, numerous studies have characterized protein-protein interfaces (3–6) and ligand-binding pockets (7, 8). Protein interfaces are usually large, with a buried solvent accessible area of over 1,000 Å² (3). With the exception of intertwined interface structures, most protein interfaces have planar shapes (4, 9, 10). Although there are in principle millions of ways of forming protein-protein interfaces, a recent study has revealed that the structural space of protein interfaces is surprisingly small, primarily attributed to limited ways of protein secondary structural packing and the flatness of interfaces (10). This affords the possibility of convergent evolution for common biological functions. In contrast to protein interfaces, ligand-binding pockets are smaller, typically covering several hundred Ų. Although very large ligands may be located on a more planar surface, to increase interaction strength, the majority of pockets are concave in shape so that they can firmly grasp or partially envelop their cognate ligands; hence, the name “pocket” (7, 8). A very recent comparison between experimental and artificial quasispherical structures of single-domain proteins has proposed that packing by hydrogen-bonded secondary structures is crucial for the formation of protein interfaces and ligand-binding pockets (9).

Due to their importance, protein interfaces and ligand-binding pockets have been the focus of many computational studies aimed at predicting their exact location using sequence and structural information (11). With regard to protein interfaces, information such as residue conservation and complementary physicochemical properties are commonly used or combined in these prediction methods (12–19). While geometry alone is not sufficient to identify protein interface residues, it is more useful for locating ligand-binding pockets; e.g., by looking for the largest pocket on protein surface (7, 20). Both geometry and energy based methods are commonly used for predicting ligand-binding sites (21, 22). In general, predicting whether a ligand interacts with a given a target protein and, if so, where it binds, are much more challenging than merely predicting interaction sites given a known interacting ligand-protein pair. The former problem is better addressed by knowledge-based methods that use existing well-characterized proteins as templates for comparative prediction (12, 23, 24). These template-based methods are practical for large-scale, proteome-wide applications, albeit they cannot make novel predictions for features absent in the template library.

Despite the many studies mentioned above, to the best of our knowledge, the structural relationship between ligand-binding pockets and protein interfaces has been overlooked. In particular, how do ligand-binding pockets distribute around protein interfaces? Previous studies have examined internal cavities surrounded by protein interfacial residues (25, 26). Here, we are not only interested in cavities, but also the general ligand-binding pockets nearby protein interfaces. It is important to realize that many interfacial residues are partially exposed; i.e., they are “rim” residues (3). Do these rim residues have a dual role as participants in both protein-ligand and protein-protein interactions? Do interfacial residues have the same chance of coordinating ligand binding compared to other surface residues? To address these questions, we present a comprehensive analysis of the distribution of pockets around protein-protein interfaces. Consistent with this distribution, small molecule ligands are frequently found in the neighborhood of protein interfaces. To further explain this observation, we demonstrate that pockets of similar size and location can be generated through docking of artificial protein structures. Moreover, we show that domain-domain interfaces of multi-domain proteins provide structural pockets that interact with ligands. These results suggest that many pockets are geometric in origin and arise from the intrinsic physical properties of proteins without the requirement of evolution. Evolution plays a role in optimizing their sequence properties to enable a specific biochemical function. Finally, we propose that packing of proteins or domains is a general mechanism for creating ligand-binding pockets.

Results

Distribution of Pockets in Protein Complexes.

We first investigate how pockets distribute within protein complexes, using experimentally solved crystal structures of 1,611 representative protein-protein complexes from previous studies (13, 27). To characterize the distance between a detected pocket and a protein interface, we introduce R_min, the minimum of all distances between the geometric center of the pocket and heavy atoms of protein-protein interfacial residues (see Methods). Each pocket is also assigned a volume in units of grid points, as reported by the grid-based pocket detection program LIGSITE^CSC (20). Unless specified otherwise, we consider pockets of a volume larger than 100 grid points, each with a grid spacing of 1 Å. This cutoff is arbitrary and covers about 80% of pockets occupied by ligands. Nevertheless, changing the cutoff values does not qualitatively affect the results presented below.

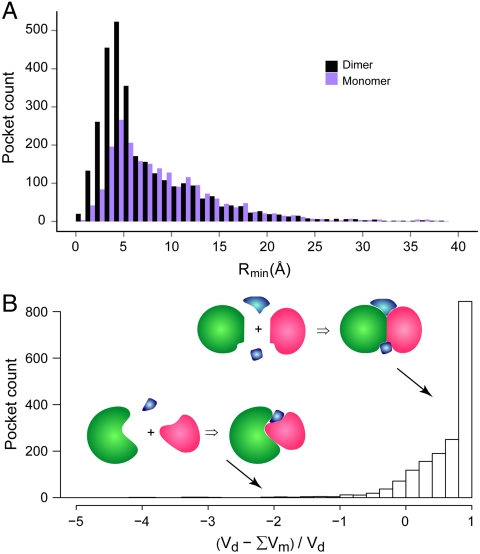
A total of 3,045 pockets were detected in 1,211 dimeric complexes larger than the cutoff. A prominent peak of pocket count emerges at a R_min of 5 Å (Fig. 1A). Consequently, 57% of all pockets can be found within a R_min of 6 Å. Therefore, the majority of pockets that have a potential to bind ligands are distributed immediately adjacent to protein-protein interfaces. To examine whether these pockets are formed upon protein complexation, we separated all protein complexes into individual monomers and repeated the same pocket detection procedure for each monomer. A total of 2,129 pockets were detected in 1,598 monomers from 905 dimers, or about 30% fewer pockets than in dimers. Fig. 1A displays that the dominant reduction occurs within a 6 Å R_min, from 1,797 in dimers to 796 in monomers, whereas the numbers are similar at 1,298/1,331 if the pockets are more than 6 Å away from protein interfaces. This result suggests that the formation of the protein complex dramatically enlarges the collection of pockets.

Fig. 1.

Distribution of pockets from protein-protein interfaces. Pockets are calculated using dimeric complex structures (denoted as “dimer”) and individual monomeric structures, respectively. (A) Histograms of pockets versus the distance from the protein interface. The width of the distance bins is 1 Å; few cases with extreme values > 40 Å are not shown. Definition of R_min is given in the text. (B) Statistics of volume changes for interfacial pockets with a R_min < 6 Å. The volumes of a pocket found in dimers and separated monomers are denoted as V_d and V_m, respectively. The summation is over all monomer pockets associated with each dimer pocket (see text). Insets are diagrams that depict ligand-binding pockets formed upon protein-protein complexation. Ligands are colored in blue and the two proteins are colored in green and red.

Not only does complexation create more pockets, it also more likely generates larger pockets nearby protein interfaces than those found in the separated monomeric structures. Fig. 1B shows the statistics of the volume change of a dimer pocket identified in complexes within a 6 Å R_min, relative to the sum of the volumes of all associated monomer pockets. A monomer pocket is associated with a dimer pocket if the monomer pocket has a volume of at least 30 grid points and > 10% of its pocket lining residues are also found in the dimer pocket, regardless of the distance from the monomer pocket to the protein interface. The vast majority (90%) of these interfacial dimer pockets have a larger volume than their associated monomer pockets combined. In 69% of cases, it is at least double that of the sum of the isolated monomer pockets, whereas in only 3.5% of cases are the monomer pockets 50% larger than their dimer counterpart.

Consistent with the above observations, the pocket lining residue density f_int at the interfaces in the complex structures is 18.1%, compared to 8.32% for the density f_nint in noninterface regions. In the separated monomeric structures, the value of f_int dramatically drops to 5.47%, essentially the same as the pocket residue density f_nint of 5.51%. In other words, interfacial regions have the same chance of participating in pocket formation as noninterfacial regions in the separated monomers, and this chance is increased by over more than a factor of two upon complexation.

Distribution of Ligands in Protein Complexes.

We next examine whether small molecule ligands preferably bind to the pockets adjacent to protein interfaces. Here, a ligand refers to a molecule with more than five heavy atoms that is not a peptide, DNA or RNA. In our dataset, we identified 741 complexes with at least one such ligand. A total of 2,255 ligands are bound to these protein complexes. To describe the geometrical distribution of these ligands, we define D_min, the minimum of heavy-atom distances between ligand and protein interfacial residues, analogous to R_min. We also introduce the ratio ρ, which measures the fraction of buried surface area of a bound ligand due to contacts with protein interfacial residues versus with all protein surface residues (see Methods).

Among all ligands bound to protein complexes, 1,210 (54%) contact at least one side of the protein interface, and 782 (35%) of them contact both sides of the protein interface (Table 1). The numbers are 528 (71%) and 383 (52%), if we consider the ligand closest to the interface in each complex. In other words, over half of protein complexes bind to at least one ligand in the immediate neighborhood of a protein interface. The median of D_min is 4.2 Å for all ligands and 3.0 Å for the closest ligands, respectively. Analysis of the set of the closest ligands contacting both sides of protein interface yields a mean ρ value of 52%. That is, on average about half of buried surface area of such a ligand is attributed to interactions with interfacial residues.

Table 1.

Statistics of ligands bound to protein-protein complexes

	All	Closest
N	2,255	741
n1	1,210 (54%)	528 (71%)
n2	782 (35%)	383 (52%)
	4.2 Å	3.0 Å

Closest denotes the ligand that has the minimum distance D_min to the protein-protein interface among all ligands bound to the complex. N, n₁, and n₂ are the total number of all ligands, ligands contacting at least one side of protein interface, and ligands contacting both sides of interface. is the median of D_min.

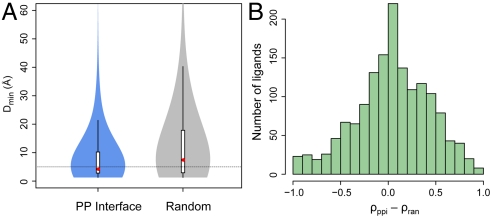
Compared with random protein surfaces of the same solvent accessible area, protein-protein interfaces are statistically closer to ligands. As shown in Fig. 2A, random surfaces give median/mean D_min values of 7.4/12.2 Å, in contrast to the much smaller values of 4.2/7.9 Å for protein interfaces (P < 2.2 × 10^-16, Wilcoxon paired one tailed test). Similarly, random surfaces make a contribution to burying ligand surfaces, as displayed in Fig. 2B. Protein interfaces make contacts to about 23% more ligands than randomly selected protein surfaces. On average, the difference in ρ values is 4.5% higher by protein interfaces than by random surfaces (P = 5.0 × 10^-8).

Fig. 2.

The distribution of ligands from protein-protein interfaces. (A) Violin plot of the minimal distance between ligand and protein interface/random surface patch. The plot is derived from a boxplot by scaling the width of the box, such that the area is proportional to the number of structures observed. A dotted horizontal line is located at a D_min of 5 Å. The white bars range from 25th to 75th percentile; and whiskers extend to a distance of up to 1.5 times the interquartile range. The red spheres represent the medians. The same violin plot schemes are employed in subsequent figures. (B) Histogram of the difference in the fraction of ligand contact surface area contributed by protein interface residues versus random surface residues. Only cases with nonzero values are shown.

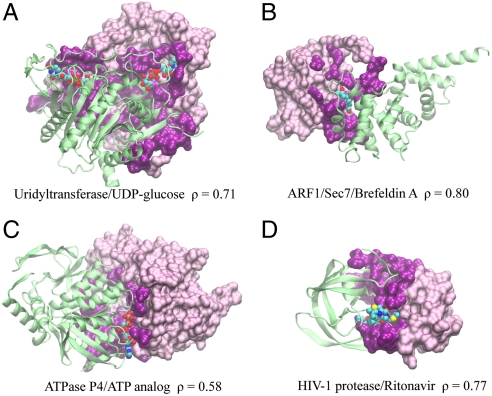
Fig. 3 shows four examples of ligands that extensively interact with protein-protein interfaces. The first example is Galactose-1-phosphate uridyltransferase, an enzyme catalyzing the transfer of a uridine 5′-phosphoryl group from UDP-glucose to galactose 1-phosphate during galactose metabolism (28). The proteins form a symmetric homodimer, and two UDP-glucose molecules are engulfed by the periphery residues of the protein interface (Fig. 3A). The second example is a heterodimer consisting of ARF1, a GTPase, and Sec7, a guanine nucleotide exchange factor that activates ARF1 (29). The activation is inhibited by a fungi metabolite Brefeldin A, which only binds to the ARF1/Sec7 complex, but not individual monomers. Not surprisingly, the binding site of the inhibitor is located at the protein interface formed by ARF1/Sec7 (Fig. 3B). The third example is the hexameric ATPase P4 from a dsRNA bacteriophage (30). This protein, belonging to the RecA family of ATPases, provides energy for packaging the genome of the virus through ATP hydrolysis. Fig. 3C shows a dimeric form of the protein, which binds to an ATP at the interface of the dimer. Such a binding-site arrangement at the protein interface is also seen in other types of ATPases, such as the rotary F-ATPases, which utilize heterodimeric interfaces instead to capture ATP/ADPs. The last example is HIV-1 protease, which is a prime drug target for treating AIDS caused by the virus (31). Fig. 3D shows that Ritonavir, an approved drug, binds to a channel-like structure formed by two protease monomers. Compatible with the symmetric shape of the binding sites, the drug molecule has a symmetric structure.

Fig. 3.

Examples of ligands bound at protein-protein interfaces. Protein and ligand are (A) Uridyltransferase/UDP-glucose (PDB code: 1guq), (B) ARF1/Sec7/Brefeldin A (1re0), (C) ATPase P4/ATP analog (1w48), (D) HIV-1 protease/Ritonavir (1rl8). In each snapshot, one protein monomer is shown in a surface representation, where interfacial/noninterfacial residues are shown in dark/light purple colors, respectively; for clarity, the other protein monomer is shown in a green cartoon representation. The ligand is shown in a van der Waals representation using the following color code: carbon (cyan), nitrogen (blue), oxygen (red), sulfur (yellow), and phosphate (tan). Molecular images were created with VMD (42).

Artificial Pockets at Protein Interfaces.

We hypothesize that pockets suitable for ligand-binding around protein interfaces may be generated through random protein-protein interactions, and hence, are predominantly a geometric effect. To test this hypothesis, we selected 363 artificial protein complexes from a previous study (10) (see Methods). Each of these artificial complexes corresponds to one of 363 native protein complexes with a bound ligand (not necessarily bound to the protein interface), such that each artificial/native pair have weak but statistically significant interface structure matches at a mean nonsequential IS-score [an interfacial similarity metric (10)] of 0.29 and a P-value < 0.05 for 89% of the pairs. We then followed the same procedure of detecting all pockets in the artificial complex structures and in their separated monomeric structures, respectively. Similar to that observed for native protein structures, one can immediate recognize a considerable pocket reduction from the complexes to the monomers in the proximity of protein interfaces (Fig. S1). A total of 553 pockets were found within a R_min of 6 Å in 305 artificial complexes, versus 426 pockets from their separated monomers. About 66% of these dimer pockets have volumes that are larger than their corresponding monomer pockets combined; and 35% of dimer pocket have at least double the total volume of their monomer counterparts. Likewise, the pocket residue density f_int and f_nint are 22.4% and 16.1% in the complexes, respectively. The value of f_int dramatically decreases to 12.6% in the monomers, which is very similar to the value of f_nint at 13.5%. These densities are higher than their counterparts in the native structures, mainly because the random sequences of the artificial structures contain more pockets arising from imperfect packing; the mean number of pockets is 3.8 per artificial complex versus 2.0 per native complex of comparable size. Nevertheless, it is clear that the artificial protein docking generate significantly more and larger pockets than their monomeric counterparts.

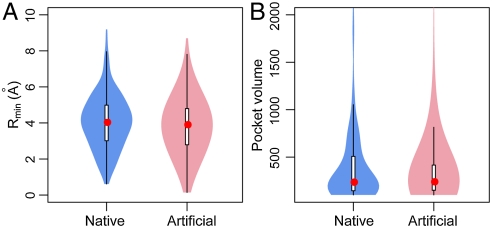
If we further consider pockets whose geometric centers are within 10 Å from both sides of protein interfaces, we found 359 pockets from 226 native dimers, and 530 pockets from 354 artificial dimers. The median/mean of pocket and interface distance R_min is 4.0/4.1 Å for native pockets, similar to 3.8/3.9 for artificial pockets (Fig. 4A). The median volume of native pockets is 234, almost the same as 238 for artificial pockets (Fig. 4B). However, native dimers have a higher chance of large pockets > 1,000, resulting in a larger mean size (402) than that (345) of artificial pockets. The mean sizes are 311/302 for native/artificial pockets, after removing 24/20 pockets larger than 1,000 grid points. The result suggests that pockets of similar sizes can be generated through artificial protein docking and arise owing to geometric effects.

Fig. 4.

Pockets of native complexes versus pockets of artificial complexes. (A) Distribution of pockets in the neighborhood of protein interfaces. (B) Comparison of pocket volume defined as the number of grid points.

Distribution of Ligands in Two-Domain Proteins.

Many monomeric proteins contain multiple domains. Except for their covalent linking, domain-domain interfaces are quite similar to protein-protein interactions. We expect that packing around the domain interfaces also creates pockets that are taken advantage by ligands, in a similar fashion to protein interfaces. To verify this, we performed analyses of both the pocket and the ligand distributions in 1,416 representative two-domain protein structures (see Methods). A total of 1,008 pockets were found in 813 structures. The number of pockets per structure is smaller than that of protein-protein complexes, mainly because of size effects. On average, two-domain structures are less than half the size of protein complexes. After splitting domains and analyzing single domains separately, we found 466 pockets from 426 structures. As shown in Fig. S2, about 87% of the pocket loss on separating the domains (from 683 to 176 pockets) are contributed by those pockets within R_min of 6.0 Å from the domain-domain interfaces. This is very similar to that observed for protein complexes. Moreover, it appears that interfacial pockets are prevalent in two-domain proteins, as also demonstrated by a very low pocket residue density f_int of 1.84% and f_nint of 2.36% for split domains, and a high f_int of 15.7% and f_nint of 5.63% for the full two-domain structures. The value of f_int is comparable to the f_int of 18.1% for protein-protein complexes. Overall, the results suggest that the vicinity of domain-domain interface is rich in pockets potentially for ligand recognition.

A subsequent analysis found 1,269 ligands bound to 630 two-domain proteins. Among all ligands identified, 735 (58%) interact with at least one residue of a domain-domain interface, and 544 (43%) interact with both sides of the domain interface. Among all 630 proteins, each interacting with at least one ligand, 482 (77%) have at least one ligand contacting at least one side of the domain interface, and 403 (64%) interact with at least one ligand contacting both sides of the interface. The percentage of ligands located in the immediate neighborhood of the interface is 12% higher than that of protein complexes, where about 52% bind to at least one ligand at both sides of the interfaces. The ligands that are the closest to and contact both sides of domain interfaces give a median D_min is 2.7 Å, and a mean ρ value of 51%.

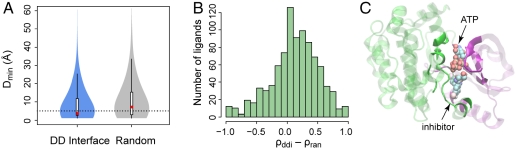
Compared to a randomly selected surface patch of the same surface area accessible to solvent, the domain interface region is favored by ligands, as shown in Fig. 5. Random surfaces give median D_min values of 7.1 Å, in contrast to much smaller values of 3.6 Å by protein interfaces (P < 2.2 × 10^-16). Similarly, random surfaces make a smaller contribution to the ligand surfaces. On average, the difference in ρ values is 12% higher by protein interfaces compared to random surfaces (P < 2.2 × 10^-16).

Fig. 5.

Ligand distributions around protein domain-domain interfaces. (A) The minimal distance from ligand to domain interface versus the distance to random surface patch. (B) The fraction of ligand contact surface area contributed by domain interface versus that of a random surface. (C) Example of a ligand bound to a protein domain interface. The N- and C-terminal domains of the protein kinase MEK1 are shown in purple and green cartoon representations, respectively. Two ligands cocrystallized are shown in a vdW representation. Protein residues contacting the ligands are displayed in solid colors, and other residues are dimmed for clarity.

One notable superfamily of multidomain proteins that have such a ligand-binding pocket at their domain-domain interface is protein kinases, enzymes that phosphorylate a target protein by transferring a phosphate group from ATP (32). Here, we focus on the highly conserved kinase catalytic subunit. The catalytic subunit has two domains (also referred to as “lobes” or “subdomains”). An example is the kinase MEK1 (33) shown in Fig. 5C. The protein binds to an ATP molecule at the interface of two domains, a conserved binding site across the superfamily of protein kinases. Both domains are directly involved in order to grasp and catalyze the molecule. In Fig. 5C, the pocket at the interface is large enough such that a second ligand is also bound to the interface. This ligand, which is a drug lead, deactivates the enzyme and serves as a noncompetitive inhibitor. This example illustrates that both cognate and noncognate ligands can bind to pockets formed at the domain interfaces.

Discussion

Through a comprehensive analysis, we demonstrate that protein-protein and protein-ligand interactions are often arranged in close geometric proximity. Among ligand-bound protein-protein complexes, most (52%) interact with at least one ligand using residues from both sides of the protein interface. These residues on average contribute to roughly half of the buried surface area of the corresponding ligand. Furthermore, compared to a random protein surface patch, the protein interfaces are closer to the small molecule ligands.

Why do ligands prefer binding sites around protein interfaces? A major reason is that packing at a protein interface is not perfect, especially around the periphery of the interface, leaving pockets as a natural harbor for ligand binding. This is supported by the distribution of binding pockets in protein complexes. Over half of pockets identified in dimeric proteins are located within 6 Å of the protein interface; these are called interfacial pockets. Many of these pockets are naturally formed by bringing the monomers into contact. They may also be the result of merging smaller pockets on the monomeric protein surfaces. The number and size of these interfacial pockets are significantly reduced if we consider protein monomers individually but freezing the location of the side chains as in the bound state, suggesting that protein complexation is essential for the pocket formation.

The prominent presence of interfacial pockets is mainly a structural consequence of packing, because similar sized pockets can be generated by docking entirely artificial protein complexes involving simulated monomers with random protein sequences. In other words, this is an effect that does not require evolutionary selection but is an intrinsic geometric feature of protein structures. Apparently, native interfacial pockets may be occupied by ligands without a biological function. For example, this can occur when certain compounds are added to assist crystallization by stabilizing the complex structure or to trap them in a desired state, such as 2-methyl-2,4-pentanediol (MPD), dithiothreitol (DTT), and 2-amino-2-hydroxymethyl-propane-1,3-diol (Tris). While most ligands found in interfacial pockets are endogenous, it is often not clear whether their presence is related to an intended in vivo functional role of the protein complex (34).

Since interfacial pockets are abundant in a system without evolutionary selection, it is quite likely that nature takes advantage of such geometric features to select for ones that recognize specific ligands. The presence of interfacial pockets offers a natural way to switch between substrate engagement and release through protein association and (partial) dissociation. One notable example is the ABC transporters, which use the interface of two nucleotide binding domains to capture and hydrolyze ATPs into ADPs (35). Hydrolysis drives conformational changes required for the transportation of substrates and also adjusts the interfacial structure to later dislodge ADP. Such ligand binding at an interfacial pocket is also observed in ATPases (Fig. 3C), though they do not seem to undergo conformational changes as dramatic as ABC transporters. Conversely, ligand binding may also be utilized to control protein-protein interactions and further regulate the biological function that the complex is responsible for. Common examples are inhibitors; e.g., Brefeldin A (Fig. 3B). These biological advantages of interfacial pockets may also contribute to their popularity.

Taking together, it is plausible that protein-protein packing creates confined physical spaces, mainly around the periphery of the protein interface and yield pockets that may accommodate ligands. Initially nonspecific protein-ligand interactions are produced. In some cases, cooperative protein-ligand and protein-protein binding may be required to enhance the stability of the complex. From these, functional interactions may be selected and further optimized through evolution. We propose that this is an important mechanism for a protein to acquire biologically relevant ligand-binding pockets. This is in agreement with the idea that many of the features required for protein function emerge from the structural properties of proteins (9).

The mechanism of packing induced pocket formation not only applies to interprotein pockets, but also to intraprotein pockets. The analysis of two-domain proteins suggests that the domain interfaces are also preferred by ligands. About 64% of ligand-bound, two-domain proteins interact with at least one ligand at their domain interface. Although the biological relevance of most of these ligands has not been verified, we found 340 cognate ligands from 173 two-domain enzymes in the PROCOGNATE database (34). And 115 (66%) of these enzymes have at least one cognate ligand located in the vicinity of domain interfaces. The number is very similar to that of all two-domain proteins examined.

The ligand-bound pockets at domain interfaces may be formed through the fusion of smaller proteins or segments. One possible example is protein kinases, whose ATP binding pockets are located within a cleft between the N- and C-terminal domains of the catalytic subunits (Fig. 5C). Similar ATP binding pockets are also found in the ATP-grasp fold proteins, which share the structurally similar C-terminal domains as the protein kinases. By contrast, the N-domains of these two families of proteins are diverse with different topologies (36). It is possible that they evolved from a common ancestor, who fused a small protein (segment) with two different proteins (or segments) separately. The fusions produce the ancient forms of kinases and ATP-grasp folds, and both further evolved into their current forms. Alternatively, the structural and functional similarity between protein kinases and ATP-grasp folds may be the consequence of convergent evolution. Either way, producing a domain interfacial pocket is crucial for fulfilling the ATP-binding and catalytic function of both the protein kinases and the ATP-grasp proteins.

Methods

Datasets.

A nonredundant set of 1,611 dimeric protein complexes was taken from previous studies (13, 27). None of these dimers shares with another dimer more than one pair of monomers at a sequence identity of 35% or higher. A nonredundant set of 1,416 two-domain proteins were taken from the protein classification database CATH version 3.4 (37). They share less than 35% sequence identity among each other. The domain boundaries were manually defined by CATH curators. The complete lists of these two datasets are available at http://cssb.biology.gatech.edu/ppipocket.

Analysis of Protein Interfaces, Pockets, and Ligands.

A heavy-atom distance cutoff of 4.5 Å is employed to define protein-protein and domain-domain interfacial contacts. A protein-protein/domain-domain interface is the collection of all residues with at least one interfacial contact between monomers/protein domains. Detection of pockets on a protein surface was conducted using the program LIGSITE^CSC (20), with a grid spacing of 1 Å. Detection of small molecule ligands was done using the program LPC (38). Ligands with five or less heavy atoms were discarded. A ligand is deemed bound to a protein if it contacts at least five residues of the protein according to LPC.

The distance between a pocket and a protein interface is defined as R_min = min (r_i), where r_i is the distance between the geometric center of the pocket (reported by LIGSITE^CSC) and the ith heavy atom of the interface. Analogously, the distance between a ligand and a protein interface is defined as D_min = min(d_ij), where d_ij is the distance between the ith and jth heavy atoms of the interface and the ligand, respectively. The ratio ρ is defined as BSA_int/BSA_all, where BSA_int and BSA_all are buried solvent accessible surface area of the ligand due to contacts with protein interfacial residues and contacts with all protein surface residues, respectively. A probe radius of 1.4 Å was employed.

The pocket residue densities f_int at protein interfacial and f_nint at noninterfacial regions are calculated as , where a is substituted by “int” (interface) or “nint” (noninterface), respectively, and are the numbers of pocket lining residues and of surface residues in the interfacial or noninterfacial regions of the ith structure, and N is the total number of structures with at least one pocket. The densities were calculated for the complex/two-domain structures and for their separated monomeric/domain structures, respectively. The pocket residues are surface residues with at least one heavy atom within an empirical cutoff of min (1.2 V^1/3, 15) Å from the center of predicted pocket, and V is the volume of the pocket.

Random Surface Patch.

To generate a surface patch of the same size as a protein interface, a surface residue is randomly chosen and added to the list of patch residues. All remaining surface residues within 5 Å from selected path residues are retained in a temporary list, from which one residue is randomly selected and added to the list of patch residues. The random surface patch grows until the total surface area of all selected patch residues is no less than the surface area of the corresponding protein interface accessible to solvent. The surface area is determined using the program NACCESS (39) at default parameters. One random surface patch was generated for each protein structure.

Artificial Protein-Protein Interfaces.

Artificial protein-protein interfaces were extracted from previously built artificial protein complexes (10). These artificial complexes were originally taken from a library of polyvaline structures generated with the protein structure prediction package TASSER (40). They were then converted to all-atom models using random protein sequences (10). From these structures, a total of 2,000 pairs of artificial structures were randomly chosen and rigid-body docking was subsequently conducted with FT-dock (41). For each docking pair, the top 10 cluster representative protein-protein complex models were retained. Since artificial complex structures have a size limit of 600 amino acids, we chose 363 native complexes within this size limit that are bound to at least one ligand for the comparative pocket analysis. For each native complex, we selected a unique artificial structure that has the best interface similarity according nonsequential alignment by the program iAlign (10, 27), yielding a total set of 363 artificial complexes for pocket analysis.