The molten globule state is unusually deformable under mechanical force

Abstract

Recently, the role of force in cellular processes has become more evident, and now with advances in force spectroscopy, the response of proteins to force can be directly studied. Such studies have found that native proteins are brittle, and thus not very deformable. Here, we examine the mechanical properties of a class of intermediates referred to as the molten globule state. Using optical trap force spectroscopy, we investigated the response to force of the native and molten globule states of apomyoglobin along different pulling axes. Unlike natively folded proteins, the molten globule state of apomyoglobin is compliant (large distance to the transition state); this large compliance means that the molten globule is more deformable and the unfolding rate is more sensitive to force (the application of force or tension will have a more dramatic effect on the unfolding rate). Our studies suggest that these are general properties of molten globules and could have important implications for mechanical processes in the cell.

Mechanical force plays an important role in many biological processes, and with recent advances in force spectroscopy, the mechanical properties of single proteins can now be investigated. Force spectroscopy can be used to control the folding and unfolding behavior of a single protein molecule and follow the single trajectory of the molecule, providing previously inaccessible information about the energetics, kinetics, mechanism, and mechanical sensitivity of these processes.

This force spectroscopy approach allows the determination of structural and mechanical properties of both native and partially folded states along a defined order parameter, the end-to-end extension of the molecule (Δx), which may serve as a good reaction coordinate depending on how well the states are separated along the observed order parameter (1–4). One property that can be defined along this coordinate, the distance to the transition state (Δx^‡), largely determines the effect of force on unfolding or refolding transitions and indicates how much the state can be deformed (in terms of its end-to-end distance) without crossing the transition state. A smaller Δx^‡ indicates the rate constant is less sensitive to force, whereas a larger Δx^‡ indicates the rate constant is more sensitive to the application of force (k ∝ exp[(FΔx^‡)/k_BT]).

All native proteins studied to date have a small distance to the transition state (less than 2 nm) (5–10), with small deformations resulting in unfolding (“brittle” behavior). However, many proteins populate partially folded molten globular states that are compact and contain secondary structure but lack the well-packed tertiary interactions characteristic of native proteins (11, 12); such species are difficult to characterize, and their structures and roles remain largely unknown. Previous work has suggested that molten globules, with this lack of well-packed tertiary interactions, may have a larger Δx^‡ and be more compliant, and thus are more deformable under, and less resistant to, force (13).

Here, we investigate the properties of a molten globule state using the protein sperm whale apomyoglobin. Sperm whale apomyoglobin is an excellent model system to study the molten globule state and compare it to the native state because both the native and molten globule states are easily accessible. Apomyoglobin populates the molten globule state both at equilibrium (under acidic conditions) and transiently during the folding process at neutral pH. The single site mutation, H36Q, is compatible with our experimental studies as it populates the equilibrium molten globule at pH 5.0 and transiently during folding at pH 7.0 (14, 15), thus providing a unique opportunity to study the mechanical properties of this state under both conditions.

We used optical trap force spectroscopy (Fig. 1A) to investigate the native and the molten globule states of apomyoglobin H36Q along two different pulling axes in order to determine the effect of the application of force and choice of pulling axis on the unfolding and folding behavior of the molecule. The pulling axes are defined by the placement of two cysteine residues, which serve as attachment points for dsDNA tethers through which the force is applied to the protein. One axis was defined by the N and C termini (N/C variant), and the second, orthogonal axis was defined by residue 53 (A53C) and the C terminus (53/C variant) (Fig. 1B). We find here that unlike natively folded proteins, the molten globule state is compliant (large distance to the transition state); and thus compared to native proteins, the molten globule is more deformable and the unfolding rate is more sensitive to force. These unique properties of molten globules likely play important roles in force-dependent processes in the cell.

Fig. 1.

Experimental setup (A) and structure of holomyoglobin (B). (A) The protein was tethered between two polystyrene beads through functionalized dsDNA attached to the protein at the engineered cysteine residue, thereby determining the axis along which the force was applied. One bead is held on a pipette tip by suction, and a dual beam counterpropagating optical trap manipulates the other. By monitoring the bead in the trap, the force on the tether and the relative extension of the tether were measured. (B) The structure of holomyoglobin (Protein Data Bank IDcode 1BZ6). The regions that are thought to be structured in the molten globule state are highlighted in red. The arrows indicate the pulling axis for the N/C variant (in green) and the 53/C variant (in blue) with the end-to-end distance between the pulling points as determined from the structure in parentheses.

Results and Discussion

The Native State of Apomyoglobin Unfolds Cooperatively Under Force with a Small Distance to the Transition State.

Fig. 1 illustrates the general setup of the optical trap and protein geometry. A single apomyoglobin protein was tethered between two polystyrene beads through functionalized dsDNA attached to the molecule at the sites of cysteine modification, thereby defining the axis along which the force was applied (Fig. 1A). These dsDNA “handles” (558 bp) provide space between both the bead surfaces and the molecule, preventing any nonspecific interactions with or between the beads from influencing the behavior of the molecule. In this experimental setup, one bead (2.1-μm diameter) is held in place on a pipette tip by suction, and a dual beam counterpropagating optical trap manipulates the other bead (3.2-μm bead diameter). By monitoring the bead in the trap, the force on the tether (dsDNA-Protein-dsDNA) and its relative extension of the tether were measured.

Unfolding and refolding events at pH 7 were evaluated through force-ramp experiments. At this neutral pH, the protein adopts its native state at equilibrium (14). Both the unfolding and refolding events for the N/C variant are cooperative, with a bimodal unfolding force distribution centered at 12.5 and 6.1 pN and a unimodal refolding force distribution centered around 4.5 pN (Fig. 2A); the measured extension changes for both transitions are consistent with the distances expected for unfolding from either the native state or the molten globule state (the N and C termini interact in both states, Fig. 1B). Because of the indistinguishable extension change between the native and molten globule states, direct observation and kinetic analysis of the folding of the intermediate to the native state was not possible. When the time between pulling cycles (the dwell time at low force) is increased, the distribution of unfolding forces is no longer bimodal and shows a unimodal distribution centered around 12.5 pN (Fig. S1). This result suggests that, as expected, the protein folds in a three-state process and the longer dwell time allows the protein to refold from the intermediate to the native state (which unfolds at approximately 12.5 pN), and the low force events (approximately 6.1 pN) observed at short dwell times result from unfolding of a transient, nonnative intermediate state. This behavior is similar to the behavior observed previously for RNase H (13). Constant force-jump experiments were carried out to determine the lifetime of the native state as a function of force and allowed calculation of the distance to the transition state for unfolding (Fig. 3A). The resulting distance to the transition state () is 1.2 ± 0.8 nm [95% confidence interval (C.I.); Table 1 and Fig. 3B], similar in magnitude to those of other native proteins (5–10).

Fig. 2.

Force-ramp traces of the N/C and 53/C variant at pH 7 and pH 5. Force-ramp experiments are depicted showing the force as a function of the trap position with the pulling traces shown in blue and the relaxation traces shown in red. Traces from the N/C variant are shown in A and C at pH 7 and pH 5, respectively. Traces from the 53/C variant are in B and D at pH 7 and pH 5, respectively. Histograms are shown of the unfolding (in blue) and refolding force (in red) distributions.

Fig. 3.

Force-jump experiments on the N/C and 53/C variant of apomyoglobin. (A) A sample trace of a force-jump unfolding experiment depicting the force and trap position as a function of time at the high force after the jump from the low force. After waiting several seconds to ensure complete refolding to the native state, the trap position was moved increasing the tension on the tether to the desired higher force and maintained constant by feedback. (B and C) Linear fit of the natural log of the unfolding rate constants as a function of force are shown for the N/C (B) and 53/C (C) variants. The distance to the transition state is determined from the slope of the lines using Bell’s model (Eq. 1).

Table 1.

Summary of the distances to the transition state and the normalized position of the transition state for apomyoglobin at pH 7.0 and pH 5.0

All errors are 95% confidence intervals.

Force-ramp experiments on the 53/C variant at pH 7.0 are similarly cooperative with unimodal unfolding and refolding force distributions centered around 12.0 and 6.5 pN, respectively (Fig. 2B); the extension changes are again consistent with models of both the native state and molten globule structures. Because both the unfolding force is lower and the refolding force is higher than for the N/C variant, there is less hysteresis for this variant, which likely masks a second, lower force unfolding transition, which arises from unfolding of the transient intermediate. The distance to the transition state corresponding to the high-force transition state () is 1.0 ± 1.0 nm (95% C.I.) as measured by constant force-jump experiments (Table 1 and Fig. 3C), similar to the other pulling axis and other native proteins.

The Molten Globule State of Apomyoglobin Unfolds Cooperatively Under Force with a Large Distance to the Transition State.

After initially characterizing an individual molecule at pH 7.0, the buffer was changed to pH 5.0 with the sample still held in the optical trap in order to populate the molten globule state at equilibrium (Fig. S2) (16). Under these conditions, unfolding and refolding events (I–U) of the N/C variant are cooperative and reversible, with both force distributions centered on 4.5 pN (Fig. 2C). The 53/C variant also shows cooperative unfolding and refolding events, with both force distributions centered on 6.5 pN (Fig. 2D). The total extension changes for both variants are consistent with those measured at pH 7.0.

The force-dependent unfolding and refolding rates of the pH 5 state were determined using constant trap position experiments. In these experiments, the trap is held at a fixed position and the force varies as the molecule spontaneously folds and unfolds, allowing for the state to be identified and the lifetimes of each state as a function of force to be measured (see Materials and Methods). [It should be noted that these hopping experiments were inaccessible for the native state because of the long lifetime of the native state (i.e., high barrier to unfolding) at low force.] The distances to the transition state for both folding and unfolding of both variants were determined by using Bell’s model (17) (see Fig. 4, Table 1, and Table S1). Other more detailed models that account for any potential movement of the transition state were not needed due to the limited force-range examined (18). The apparent deviations at the extreme forces are associated with more uncertainty due to the longer lifetimes and limited observations as well as a potential bias toward a smaller rate constant due to missed observations for the short-lived state. The distances from the molten globule state to the transition state () for both variants (6.1 ± 0.5 nm for the N/C variant; 3.4 ± 1.2 nm for the 53/C variant, 95% C.I.) are significantly larger than those from their respective native states (see above) and those measured previously for other natively folded proteins (5–10).

Fig. 4.

Constant trap position experiments on the N/C and 53/C variants. Typical 1-s trace of a constant trap position experiment with the force averaged down to 1,000 Hz (in blue) for the N/C variant (A) and the 53/C variant (C). The inferred trajectory of the molecule at 500 Hz is shown in red. The accompanying histogram is of the force measured over 1 min depicting the two observed populations. Linear fits of the natural logarithm of the rate constants as a function of force are shown for the N/C (B) and 53/C (D) variants. The distance to the transition state is determined from the slope of the lines using the Bell’s model.

For both pulling axes, the native state appears brittle (small distance to the transition state) while the molten globule state appears compliant (relatively large distance to the transition state). Each axis, however, represents a different reaction coordinate with a different total end-to-end distance change. To compare different reaction coordinates, we calculated a normalized distance to the transition state (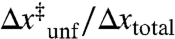), which is analogous to the Tanford β value used in chemical denaturant studies (19). Natively folded proteins have a “mechanical” Tanford β value of 0.05 to 0.1; in contrast, the molten globule state of apomyoglobin has a value of approximately 0.3 for both pulling axes (Table 1). The choice of pulling axis does not significantly alter these relative distances to the transition state or the apparently two state equilibrium behavior for these low force events. Previous mechanical studies on Escherichia coli ribonuclease H suggest a similar value for the molten globule-like folding intermediate of this protein (approximately 0.3) (13), providing further evidence that a large mechanical compliance may be a property common to molten globules.

This relatively large distance to the transition state, or compliance, has two important consequences. First, it implies that the molten globule state can undergo large fluctuations (end-to-end extension changes) without committing to cross the unfolding barrier. This ability to deform is likely to play an important functional role, such as in the incorporation of heme in the case of apomyoglobin (20). Second, the large distance to the transition state indicates that the unfolding rates for molten globules are more sensitive to force [the change in unfolding rate per unit force is greater (k ∝ exp[(FΔx^‡)/k_BT]) than the unfolding rates of native proteins]. Thus, in the cell, the application of small amounts of force that might be applied by other proteins by molecular machines will have a more dramatic effect on the probability of unfolding molten globules than natively folded proteins.

Recently, the role of force has become more evident in such cellular processes as transmembrane protein transport and protein degradation (21–24), stressing the importance of understanding how proteins resist force and the role of the distance to the transition state. Recent studies suggest that the molten globule plays an important role in cellular processes that involve mechanical unfolding. For example, in the case of anthrax lethal factor, translocation of the N-terminal domain across the membrane requires mechanical unfolding of the molten globule-like state (25). Similarly, the bacterial protease ClpXP targets truncated proteins (26), which are more likely than full-length proteins to lack specific tertiary interactions and resemble a molten globule. Our results suggest that the molten globule state, with its larger distance to the transition state and weaker resistance to mechanical force, is an easier and less energetically costly substrate for these motors to process (27, 28). In addition to its potential in vivo implications, the mechanical properties of this protein state could be exploited for bioengineering applications in synthetic biology and material science.

Conclusions

In sum, using single molecule force-spectroscopy, we have shown that the molten globule state of apomyoglobin is compliant with a large distance to the transition state. This distance is in sharp contrast to the distance measured for the native state of apomyoglobin and for other natively folded proteins. Further, the relative distance to the transition state is independent of the direction of the pulling axis and the applied force. These results indicate that the molten globule state is much more deformable and more susceptible to unfolding under an applied force. This deformable state has implications for both biological function and material sciences. It represents a previously uncharacterized class of protein materials and is likely to play an important role in cellular functions and therefore be an unrealized locus for evolutionary pressure.

Materials and Methods

Protein Construction, Purification, and Sample Preparation.

The plasmid, pMB413b, containing the myoglobin gene was provided by D. Barrick (Johns Hopkins University). Using a PCR Quikchange protocol (Stratagene), an N-terminal six histidine tag followed by a TEV protease site and the H36Q mutation were inserted into the gene. Two variants of this gene were produced with cysteines either added onto the N and C terminus (herein referred to as the N/C variant) or at residue 53 (A53C) and onto the C terminus (herein referred to as the 53/C variant) (Fig. 1B).

The plasmid was transformed into chemically competent BL21 (DE3) pLysS cells. The cells were grown in Luria Broth (200 ug/mL of ampicillin, 34 ug/mL chloramphenicol), and the protein was constitutively expressed for 24 h at 37 °C, allowing for the incorporation of the heme and production of the holo-protein. Cells were harvested by centrifugation and resuspended in 20 mM sodium phosphate, pH 8, 300 mM sodium chloride, and 0.5 mM tris(2-carboxyethyl)phosphine. The cells were lysed by sonication, and the soluble fraction was isolated by centrifugation followed by filtration through a 0.2-um filter. This lysate was purified over a nickel sepharose column followed by a step elution with 20 mM sodium phosphate, pH 8, 300 mM sodium chloride, 0.5 mM TCEP, and 250 mM imidazole. The elution was dialyzed overnight at 4 °C against 20 mM sodium phosphate, pH 8, 300 mM sodium chloride, and 0.5 mM TCEP in the presence of TEV protease (2 mg/L) to remove the N-terminal six histidine tag. The dialysate was then run over a second nickel sepharose column, and the flow-through was collected. Analysis by SDS-PAGE demonstrated that the protein was greater than 95% pure. The heme was removed by a Vydac C-18 reverse phase column using 0.1% trifluoroacetic acid (TFA) and eluting the protein with a linear gradient of 0.1% TFA and acetonitrile on a Shimadzu HPLC system. DNA handles were attached to both holo- and apo-myoglobin using previously reported methods (13, 29).

Optical Tweezer Instrumentation and Experiments.

The instrument used in this experiment was a dual beam counterpropagating optical trap (30). The spring constant of the trap was set to 0.05 pN/nm. A piezo actuator controlled the position of the trap and allowed position resolution to within 0.5 nm (30). Drift during constant trap position experiments was less than 1 nm per minute, allowing an average force to be maintained to within 0.05 pN over the course of a typical 1-min constant trap position measurement. Because of the limited force precision between fibers (± 0.5 pN), data could not be pooled before the analysis, and each fiber was therefore analyzed separately.

The molecule was characterized in two different buffers (10 mM Tris, pH 7, 250 mM sodium chloride, and 1 mM EDTA and 10 mM sodium acetate, pH 5.0, 250 mM sodium chloride, and 1 mM EDTA) and by three different types of experiments: force-ramp, force-jump, and constant trap position experiments. The unfolding and refolding behavior was first analyzed using force-ramp studies that involved moving the trap position in a cycle between 3 and 20 pN at a constant velocity of 100 nm/s. These force data were collected at 1,000 Hz (however, 2% of all data points were not collected due to hardware constraints). These data were smoothed with a sliding window of 10 ms, and the difference at intervals of 10 ms was determined. The standard deviation of the difference was then calculated, and a threshold for detection of an event was set based off the variance in this signal. A 99.9% confidence threshold (3.3σ) was set for the high signal-to-noise high-force events (greater than 7 pN), and a 90% confidence threshold (1.6σ) was used for the noisier low-force events (lower than 7 pN). The position with the highest difference signal was identified as the folding or unfolding event. From this experiment, the unfolding or folding force distribution as a function of the loading rate and the extension change of the molecule as a function of force could be measured.

For force-jump experiments (Fig. 3), the molecule was held at a low force of 3 pN for several seconds by force feedback to ensure that the molecule was in the native state. The force was then quickly increased to the specified force and held constant by feedback. When operating in constant force feedback mode, the feedback controlled the position of the trap, and therefore the force on the bead and molecule, with a frequency of 2 kHz and a step size proportional to 10% of the force difference between the two states. An average force could be maintained with a standard error of 0.01 pN of the set value with a standard deviation of 0.1 pN at 100 Hz. Using the position of the trap, unfolding events were detected using a t-test similar to previous methods (31) and used to determine the lifetime of the folded state of the molecule at the average force.

During constant trap position experiments, the molecule folded and unfolded, hopping between the two states, with many transitions observed for a single tether (Fig. 3). The force signal was used to identify the state (the higher force indicated the more compact, folded state) and determine its lifetime. Bypassing the limiting hardware and recording the data on a second computer, data was recorded at 50 kHz for 1 min at each trap position with a minimum of ten different trap positions collected per tether. The data were subsampled down to 1,000 Hz, a frequency below the corner frequency (i.e., a time scale slower than the response time of the trapped bead) to ensure the data within each state was independently sampled and not correlated. It should be noted that active constant force feedback experiments could not be used because the limitations of the feedback result in errors in the measured lifetimes and the subsequent analysis. In addition, at extreme forces, the measured rate constants are less precise because of the limited number of observations in a given state, and missed transitions to and from a state may introduce additional error and a bias toward lower rate constants.

Constant Trap Position Analysis with a Bayesian Hidden Markov Model.

We used a Bayesian hidden Markov model (BHMM) approach (32–35) to analyze the constant trap position optical tweezers data. This Bayesian extension of the standard machine learning approach of hidden Markov model (HMM) analysis (36) allows the experimental uncertainties to be directly quantified by sampling from the posterior of the model parameters (transition probabilities and Gaussian state observable distributions) given the data, rather than simply identifying the maximum-likelihood model parameters as in the traditional HMM approach. To do this, we augment the standard HMM likelihood function with a prior that enforces the physical detailed balance constraint in the transition matrix. Sampling from the posterior proceeds by a Gibbs sampling approach, alternating updates of the reversible transition matrix (37, 38), with updates of the hidden state sequence and the Gaussian state observable distributions using standard techniques (32–35).

The BHMM code we used here sampled two-state models over the measurement histories of force at constant trap positions, producing estimates of the average force characterizing each state and the transition probabilities among the states, as well as confidence intervals that characterize the uncertainty in these values due to finite-sample statistics. After subsampling the force data to 1,000 Hz to produce Markovian statistics (verified by examination of force-autocorrelation functions), the method samples models consistent with the data using a Gibbs sampling strategy that assumes the force measurements from each state (including measurement error) are normally distributed about the average force for that state. Here, the number of states was fixed to two after verifying the two-state nature of the data by inspection of the force traces. The first 50 BHMM samples after starting from the maximum-likelihood estimate were discarded, and 1,000 samples were subsequently generated to collect statistics on average forces and transition probabilities, as well as generate the 95% confidence intervals reported here. Matrices of rate constants K were computed from transition matrices T(τ) using the standard relationship T(τ) = exp[K(τ)] through use of the matrix logarithm, where K is the 2 × 2 matrix of rate constants k_ij and τ is the observation time.

The Matlab code used for the BHMM approach has been deposited and is freely obtained from http://simtk.org/home/bhmm/. Complete implementation and validation details of this code are described in an accompanying arXiv preprint (39).

Determination of the Distance to the Transition State and the Coincidental Rate Constants Using Bell’s Model.

For a given state, a linear fit of the natural log of the rate constants at each average force determined the distance to the transition state using Bell’s model (17, 40, 41),

[1]

where k_m represents the contribution of experimental parameters such as the bead size, trap stiffness, and handle length to the observed rate; k₀ is the intrinsic rate constant of the molecule in the absence of force; F is the force; Δx^‡ is the distance to the transition state; κ is the effective spring constant of the system; k_B is the Boltzmann constant; and T is the absolute temperature. For this notation, the applied force and effective spring constant of the system are positive and the distance to the transition state is positive from the folded state to the unfolded state and negative from the unfolded state to the folded state. The Bell’s model emphasizes that three parameters (k₀,k_m, and κ) determine the absolute rate constants and are not easily deconvoluted, making any interpretation of the absolute rate constants difficult. Because of this we only interpret the resulting distances to the transition state.

For the constant trap position experiments, the crossing point between the two fits determined the coincident rate constant and force. For the N/C variant, all reported fits had R² values greater than 0.9. Because of a lower signal-to-noise ratio for the 53/C variant, all fits had R² values greater than 0.7. The reported values in Table 1 were the average of at least five different fibers each analyzed separately. The results of the analysis for each individual fiber are shown in Table S1.

Distance Determination for Unfolding and Refolding Events.

The extension change of the molecule was inferred from the difference in the trap positions in the unfolded and folded state at the force at which the event occurred. As the force on the bead is the same in each state, the bead is at the same distance from the center of the trap. Therefore, any change in the position of the trap reflects the change in the end-to-end extension of the molecule. The measured extension change is the difference between the unfolded end-to-end extension and the folded end-to-end extension of the molecule:

[2]

Using a worm-like chain model (42) given the persistence length (P = 0.65 nm), contour length, and temperature, the end-to-end extension of the unfolded state at a given force can be calculated assuming a contour length. The contour length was calculated from the number of amino acids between the handle attachment points. With the measured extension change in the molecule and the calculated end-to-end extension of the unfolded state, the end-to-end extension of the folded state can be inferred. These distances were consistent with the structural models of the native and molten globule state.