Comparison of Pause Predictions of Two Sequence-Dependent Transcription Models

Abstract

Two recent theoretical models, Bai et al. (2004, 2007) and Tadigotla et al. (2006), formulated thermodynamic explanations of sequence-dependent transcription pausing by RNA polymerase (RNAP). The two models differ in some basic assumptions and therefore make different yet overlapping predictions for pause locations, and different predictions on pause kinetics and mechanisms. Here we present a comprehensive comparison of the two models. We show that while they have comparable predictive power of pause locations at low NTP concentrations, the Bai et al. model is more accurate than Tadigotla et al. at higher NTP concentrations. Pausing kinetics predicted by Bai et al. is also consistent with time-course transcription reactions, while Tadigotla et al. is unsuited for this type of kinetic prediction. More importantly, the two models in general predict different pausing mechanisms even for the same pausing sites, and the Bai et al. model provides an explanation more consistent with recent single molecule observations.

Introduction

Transcription elongation is a process by which RNA polymerase (RNAP) copies genetic information from DNA into RNA. During elongation, RNAP translocates on a DNA template and incorporates NTPs into the 3’ end of the nascent RNA. The rate of incorporation of each NTP is far from uniform, and is largely dictated by the DNA sequence being transcribed. In particular, at certain sequences known as pause sites, RNAP tends to dwell much longer than on average (for review see ref (1)). Pausing reflects the intrinsic kinetic properties of transcription elongation, and moreover, some pause sites have been found to play important regulatory functions in gene expression (2, 3). Therefore, establishing a correlation between the DNA sequence and pausing would be an essential step in understanding both the transcription mechanism and gene regulation.

Biochemical assays have shown that at some pause sites, RNAP reverse translocates by threading the 3’ RNA into its secondary channel, a phenomenon known as backtracking (4, 5). Backtracking can be viewed as a non-productive branch pathway that kinetically competes with the main pathway of NTP incorporation (1, 6). With improved spatial resolution to near bp level, recent single molecule experiments revealed that although pauses of longer duration could be induced by backtracking, pauses of shorter duration showed no or minimal backtracking (7, 8) and thus are likely caused by a different mechanism.

Based on a thermodynamic analysis of the transcription elongation complex (TEC) pioneered by Yager and von Hippel (9), a kinetic model developed by Bai et al. (10, 11) (referred to here as Model B) and later a related equilibrium model by Tadigotla et al. (12) (referred to here as Model T) now make it possible to predict pause locations and mechanisms for a given DNA sequence. These theoretical studies have provided important insights by predicting pause locations based on the free energy of the corresponding TEC, which depends strongly on the DNA sequence (9-13). Although the two models have similar energetic considerations, they treat the backtracking kinetics differently: in Model B, backtracking at most template positions is considered to be a slow process and therefore insignificant compared with NTP incorporation along the main pathway; while in Model T, RNAP was allowed to undergo fast backtracking until it encountered the first secondary structure formed in the nascent RNA. These are fundamental differences and consequently are expected to generate different predictions on pause locations, kinetics, and mechanism.

Since these two models serve as valuable tools to predict sequence-dependent pausing for future elongation kinetic studies, the transcription field will benefit from a careful evaluation of these two models against relevant experimental data. Although the two models were compared by Tadigotla et al. (12), the comparison was carried out with incorrect criteria for Model B and also only focused on predictions of pause locations at low NTP concentrations. Furthermore, the predicative power of Model B has been since improved by incorporating NTP-specific kinetic parameters (11).

In this work, we present a comprehensive comparison of Model B with Model T. a) In an effort to make a direct and fair comparison of the two models, we reproduced Model T and checked that it predicted essentially identical pause locations as those by Tadigotla et al. (12). b) We compared the predictive power of the two models by analyzing pause locations at different NTP concentrations. c) We simulated transcription gels with Model B and Model T and evaluated its kinetic predictions against corresponding experimental transcription gels. d) Finally we tested whether these models would provide explanations consistent with recent single molecule measurements of sequence-resolved pausing.

Results

Below we have briefly recapitulated Model T and Model B, described our reproduction of Model T, and then compared performance of the two models against various experimental data. Detailed experimental and simulation condition, model parameters, and temperature consideration can be found under Materials and Methods.

Brief recapitulation of the two models

Both models are based on a thermal ratchet mechanism for transcription elongation: RNAP translocates reversibly between different states under thermal activation, and NTP incorporation biases RNAP to move forward by 1 bp along the DNA template. Right after NTP incorporation, the TEC is in its pre-translocation state, and the RNAP needs to translocate 1bp downstream into the post-translocation state in order to incorporate the next NTP (first row in Figure 1A). As mentioned above, TEC can also potentially access the “backtracked” or “forward-tracked” states (second row in Figure 1A). During backtracking, RNAP translocates along the upstream DNA template while threading the 3’ end of the nascent RNA through its secondary channel. During forward-tracking, RNAP moves forward beyond the post-translocation state without NTP incorporation while shortening the DNA:RNA hybrid.

Figure 1. Overview of the two models.

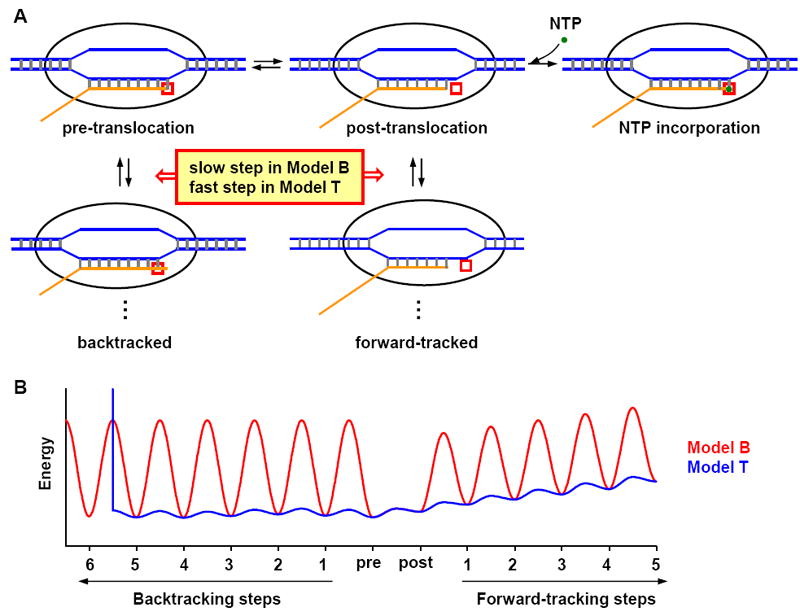
A) Cartoon of the transcription elongation pathway. During elongation, the RNA polymerase unwinds a stretch of dsDNA (blue), with one strand forming a double helix with the nascent RNA (orange). The transcription elongation complex (TEC) has different translocation states, which are defined by the relative locations between the RNA 3’ end and the RNAP active site (red box): in the pre-translocation state, the RNA 3’ end is inside the active site; in the post-translocation state, active site is empty and RNA 3’ end is in its immediate vicinity. Only in this position, TEC is able to bind and incorporate the incoming NTP (green dot); in the backtracked state, RNA 3’ end passes the active site into the secondary channel; in the forward-tracked state, RNA active site moved further downstream from the RNA 3’ end, resulting in a shortened DNA-RNA hybrid. The pathways used in the two models are almost identical, and as indicated in the plot, the main difference lies in the kinetic rates in the branch pathways (see text for detail). B) Typical translocation energy landscape in Model B (red) and Model T (blue). The troughs of the curves represent the TEC free energy in different translocation states, and the peaks in between neighboring troughs are the activation barriers that affect the translocation rate. In general, the energy barriers for backtracking and forward-tracking in Model B are much higher than those in Model T.

Because NTP incorporation can only take place in the post-translocation state, all the other states accessible to RNAP are effectively competitive inhibitors to the elongation reaction (6). The overall NTP incorporation rate is thus largely determined by the probability of RNAP being in the post-translocation state, which depends on the translocation energy landscape (typical examples shown in Figure 1B). The troughs in Figure 1B represent the free energy of TEC in different translocation states, and the peaks in between the neighboring troughs are the activation barriers for translocation. The two models incorporated essentially the same TEC free energy (Materials and Methods), whereas they have different assumptions about the activation barriers (Figure 1B).

The TEC free energy is calculated based on the free energy involved in ssDNA bubble and RNA-DNA hybrid formation, and its value strongly depends on the DNA sequence within the TEC, the TEC structure, and its translocation state (9, 10, 12). TEC containing shorter RNA-DNA hybrid tends to be less stable. Therefore, the forward-tracked (hybrid length <8) and post-translocation state (hybrid length: 8) on average is less stable than pre-translocation and backtracked states (hybrid length: 9). Such energy profile makes a simple equilibrium assumption problematic. If the TEC were to equilibrate among all translocation states, a significant portion of the RNAP would necessarily undergo extensive backtracking at a majority of the template positions, which would prevent efficient NTP incorporation during active elongation.

To reduce the probability of backtracking, the two models took different approaches. Model B assumes a large backtracking activation barrier for all the backtracking steps so that at majority of the template positions, backtracking occurs with a low probability (red curve in Figure 1B; 10). Model T assumes RNAP is capable of fast backtracking until it encounters the first secondary structure formed by the nascent RNA outside the RNAP, where the backtracking barrier is effectively infinite (blue curve in Figure 1B; in this particular case, RNAP encounters RNA secondary structure after 5bp backtracking). In other words, the most significant difference between the two models is the accessibility of RNAP to its backtracked states. Model B also assumes a higher forward-tracking barrier (Figure 1B), but since the forward-tracked states are unstable, the forward-tracking rates do not significantly affect the model prediction.

Model T consists of five alternative sub-models (12): four equilibrium models with and without the consideration of co-transcriptional RNA folding and thermal fluctuation of the TEC structure, and one kinetic model. These models are highly related, and are supposed to illustrate the contributions made by the various energetic components to the predictive power, within the same conceptual equilibrium model. The consideration of the folded RNA is a unique and important component of Model T but the fluctuations in the TEC structure have only a small quantitative effect on the model performance (12). Also, Model T’s kinetic sub-model produced predictions similar to its equilibrium counterpart. Therefore, in this work, we focus on the comparison of Model B with Model T’s “SBF” sub-model (single bubble with RNA folding, i.e., the equilibrium model with RNA folding and single TEC structure).

Replication of Model T

In order to make direct and valid comparisons of the two models, we reproduced Model T (the SBF sub-model) and checked for pause locations on the same 10 sequences as were used by Tadigotla et al. (12; Materials and Methods).

In Model T, because of the equilibrium assumption, the NTP incorporation at any site, n, follows single exponential kinetics with a rate constant k(n). A pause is defined when the k(n) falls below a threshold: k(n) < ξ max{k(n)}, where max{k(n)}, is the maximum k(n) on that template at a given NTP concentration. We tuned ξ to achieve maximum predictive power of pause locations, defined as the ratio of correct to incorrect pause location predictions. The optimized ξ is equal to 0.015, identical to that used in the original Model T, resulting in ~ 30% of the sequence being pause sites. The pause sites predicted by our implementation of Model T had ~ 95% overlap with those predicted by the original Model T (SI), and the overall predictive powers of the two versions were essentially identical (Figure 2A). Note that in Figure 2, we plotted the inverse of the predictive power, i.e., the ratio of incorrect to correct pause location predictions. This presentation follows the notation of Tadigotla et al. (12) in order to make a straightforward comparison with their Figure 2B.

Figure 2. Comparison of the predictive powers of pause locations of the two models.

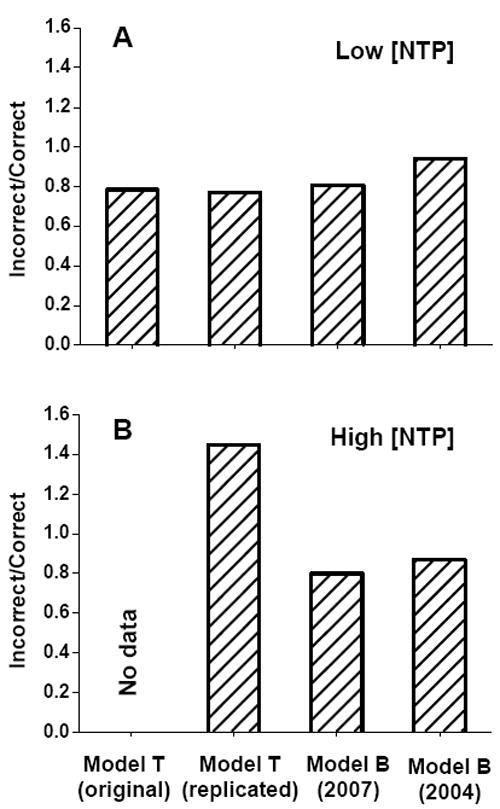
The statistics of the model predictions of pause locations are illustrated by the ratio of the number of incorrect to the number of correct predictions for all templates tested. The lower the ratio is, the better the model performance. A) Comparison at low [NTP] using the ten templates of Tadigotla et al. (12). B) Comparison at high [NTP] using pKA2, pTS147 (10), λtR1 (10), and his and ops templates (8). 1^st column: reported by Tadigotla et al. (12) (see their Figure 2D, only available for the low [NTP]). 2^nd column: by replicated Model T. 3^rd column: by Model B (2007). 4^th column: by Model B (2004).

This good agreement indicates that we have faithfully reproduced Model T. The minor differences in their pause predictions may be due to details of pause selection (Materials and Methods). In the following sections, we will only compare Model B with our implementation of Model T.

The two models have similar predictive power at low [NTP]

Previously, Tadigotla et al. (12) compared the two models for their predictions of the pause locations on ten templates, where the pauses were identified experimentally at low NTP concentrations (≤ 40 μM NTPs), and concluded that Model T had much better predictive power than Model B. However, the predictive power of pause locations in both models depends strongly on the pause criteria, which were optimized for Model T, but not for Model B. In addition, Model B recently incorporated NTP-specific kinetic parameters (11), which improved its accuracy in kinetic predictions. Therefore, we repeated the comparisons of Model T with Model B (2004) and Model B (2007) with pause criteria individually optimized for each model.

The pause criteria used in Model T can not be directly applied to Model B because in Model B backtracked states are not in equilibrium with pre- and post-translocation states, and thus NTP incorporation can not be simply characterized by a single rate constant. Instead, we set a threshold for the average RNAP dwell time at each template position, τ(n). By analogy with Tadigotla et al. (12), a pause is defined when $\tau (n)>\frac{1}{\eta }\min \left\{\tau (n)\right\}$, where min{τ(n)} is the shortest τ(n) on the template at a given NTP concentration. We tuned η for Model B to achieve maximum predictive power of pause locations for the same 10 DNA sequences as were used for Model T. The optimized η ~ 0.05 resulted in ~19% sequence coverage of pause sites.

With the optimized pause criteria, the two models generated largely overlapping predictions of pause sites (SI) and the overall predictive powers were very similar with only a slightly lower performance by Model B (2004) (Figure 2A). This result contradicts the results shown in Figure 2d of Tadigotla et al. (12), leading to the statement regarding “the poor performance of the model presented by Bai et al.” compared with Model T. In fact these similar results between the two models under low [NTP] reflect the overlap in the formulation of the two models: pause sites occur at unstable post-translocation states.

The pause criteria above could also be expressed as a threshold in the pause duration. The pause threshold for Model T is ~ 0.15 - 0.30 s using k_max = 700 s^-1 and K_d = 20 μM (same values as used by Tadigotla et al. (12)), whereas it is ~ 1.5 – 3.0 s for Model B. As discussed below, a pause threshold on the order of a second is more consistent with experimentally measured pause kinetics.

Model B has better predictive power at high [NTP]

Although the two models have similar performance for predictions of pause locations at low [NTP], it is possible for their performance to be different at higher [NTP]. Model T has a more stringent equilibrium assumption: Model T requires that all translocation states must reach equilibrium; whereas Model B only requires that pre- and post-translocations to be in equilibrium. The equilibrium assumption is less likely to be valid when the NTP incorporation cycle is fast at high [NTP] as has been pointed out by Tadigotla et al. (12). It would be interesting to examine how Model T and Model B perform at high [NTP].

We compared the predictive power of pause locations by both models with measurements at higher [NTP] (100 μM - 1 mM NTPs). These measurements included pauses identified on transcription gels of three templates derived from pKA2, pTS146 and λtR1 (transcription gels shown in (10)), as well as single molecule measurements on the his and ops templates (8). As for low [NTP], pause thresholds were individually optimized for Models T and B (SI). Model B showed similar predictive power at high [NTP] to that at low [NTP], whereas the predictive power of Model T was significantly lower at high [NTP] and was about half that of Model B (Figure 2B).

This indicates that at high [NTP], although post-translocation states may be considered in equilibrium in Model B, equilibrium among all translocation states, which is necessary for Model T, can not be achieved. As [NTP] increases, the equilibrium assumption in Model T begins to become less valid at some template positions. The point of transition for each template position depends on sequence-dependent TEC stability and NTP-specific kinetic parameters (11, 14-16). Figure 2 also shows that Model B (2007) performs better than Model B (2004) at both high and low [NTP].

Pause kinetics predicted by Model B, but not Model T, agrees with experiments

Pause location prediction provides a simple method to compare the two models; however, a more stringent comparison is the ability to predict pause kinetics. Conventionally pause kinetics has been assayed by time-course reactions using transcription gels. Previously we had simulated transcription gels using Model B (10) and shown that elongation and pause kinetics predicted by Model B were in good agreement with experimental transcription gels. Here using Model B (11), we simulated some of the transcription gels used in Tadigotla et al. (12), and two examples are shown in Figure 3 together with the corresponding experimental gels (D387 (A) and D167 (B) templates) (16). The simulated gels captured most features of the experimental gels, such as the pause positions and their intensity changes over time.

Figure 3. Prediction of transcription gels using Models T and B.

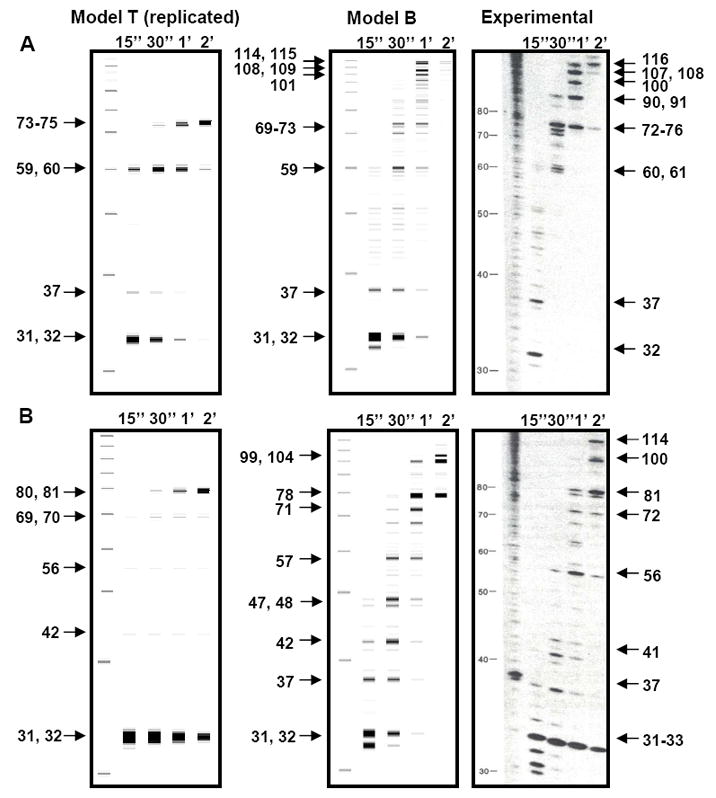
A, B) Transcription gels on D387 (A) and D167 (B) templates (16) and the corresponding simulations using Model T and Model B (2007). Predicted prominent pauses (marked on the left side) are at similar locations with similar durations as those of measured pauses (marked on the right side).

These simulations also provide verification for the pause thresholds used in Model B. Note the simulated gels had a time point interval of 15 s, but a pause does not have to be >15 s in duration to be detectable. In fact, the majority of the predicted pauses indicated in Figure 2 had durations shorter than 15 s and were typically 2-5 s (SI). Yet most of them (~ 91%) accumulated significant populations (> 2%) in at least one gel lane, which has been shown to be easily detectable in real transcription gels (for another example, see Figure 3 of (10)). Thus the ~1.5 s pause threshold used by Model B was experimentally verified, in spite of the concerns raised by Tadigotla et al. (12) that it was too short.

The simulated transcription gels on the same templates using Model T could not correctly match measurements (Figure 3). The predicted pause durations varied from ~ 0.2 s, which was too short to be detected in the corresponding gels, to ~ 20 minutes (SI), which was much longer than that estimated from the gel (< 1 min). It is important to note that the pause kinetics predicted by Model T can not be corrected by a simple linear rescaling of rates at all sites (e.g., using a different k_max), which does not change the dynamic range of k(n) (over six orders of magnitude). Nevertheless, it is likely that this dynamic range may decrease if the alternative “MBF” (multiple bubbles with RNA folding) and kinetic sub-models are used.

The two models predict different pause mechanisms

Because the two models have different treatments of translocation into backtracked states, they predict different translocation states that RNAP may explore prior to the next NTP incorporation. For a given template position n, the translocation states of RNAP may be characterized by the mean translocation state m̅∣_n (m < 0 for backtracked states, m = 0 / 1 for pre- and post-translocation states, and m > 1 for forward-tracked states; Materials and Methods).

Tadigotla et al. (12) assumed that RNAP may rapidly backtrack until it encounters a secondary structure in RNA. Because backtracked states in general are more stable than the post-translocation state, Model T predicts significant backtracking of RNAP, especially at pause sites. Over the ten templates used by Tadigotla et al. (12), Model T predicts that m̅∣_n = −1.6 ± 3.3 bp (mean ± s.d.) for all the template positions including pause and non-pause sites, and −4.2 ± 4.0 bp for pause sites alone (Figure 4A).

Figure 4. Comparison of the prediction of pause mechanism.

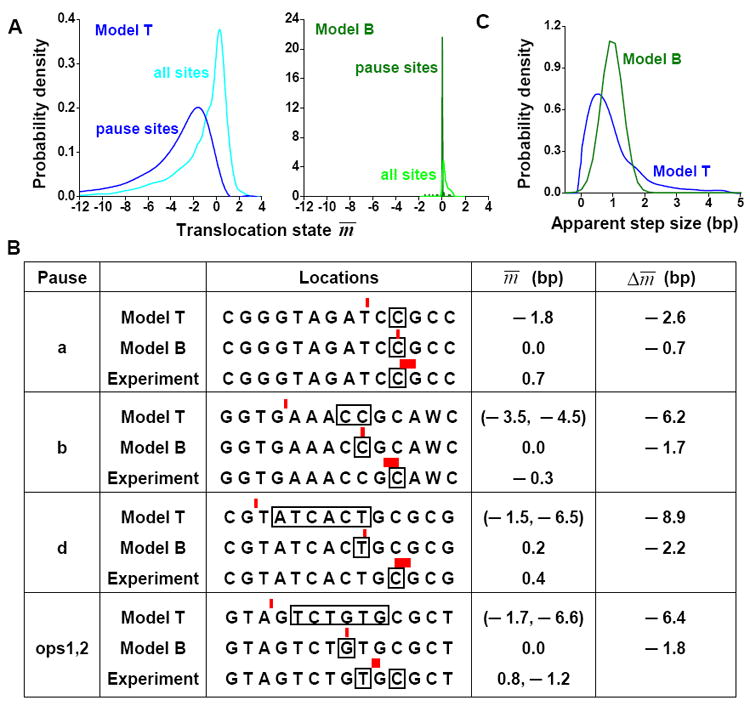
A) The predicted histogram of the mean translocation state m̅∣_n by Model T (left) and Model B (2007) (right) for all positions, or for pause sites alone, on the ten templates used in Tadigotla et al. (2006). B) Comparison of the predicted and measured (8) translocation states of the pause sites from the his and ops templates. For the experimental data, each red bar indicates pause position measured by single molecule techniques and the width of the bar indicates the uncertainty in the measurement; each black box indicates the location of the 3’end of the RNA during pausing as determined by a transcription gel. The distance between the bar and the box thus indicates the RNAP translocation state at the pause site. Similar notation is used for predictions by the two models. Model B predicted a single pause site with a single RNAP position on the DNA template for each sequence. On the other hand, Model T predicted multiple pause sites for some sequences but a single location of RNAP on the DNA template during pausing. The two columns on the right show the distance of the RNAP on the DNA template from the pre-translocation state, and the difference in the predicted and measured position of RNAP. C) RNAP apparent step size distributions predicted by Model T and Model B under 18 pN assisting force.

On the other hand, Model B predicted two different types of pauses (10), one involves backtracking and the other is caused by repetitive translocation between pre- and post-translocation states. Due to the high backtracking activation barrier in Model B, backtracking occurs with small probability. For instance, out of the 91 pauses predicted by Model B on the ten templates, only 15 had a backtracking probability > 5%. Accordingly, this low probability of backtracking results in m̅∣_n being close to the pre-translocation state. Over the ten templates, Model B predicts that RNAP is always located close to the pre-translocation state: m̅∣_n = 0.3 ± 0.3 bp for all template positions, and 0.0 ± 0.19 bp for pause sites (Figure 4A).

We compared predictions by the two models with single molecule measurements by Herbert et al. (8), where the m̅∣_n at certain pause sites were directly measured with near bp resolution. In total, six pause sites were examined and no significant RNAP backtracking were found at these pauses (Figure 4B; 8). Incorporating the 7 pN assisting force applied to the RNAP by tilting the energy landscape (11, 17), both models were able to predict 4 out of the 6 pause sites (Figure 4B). However, the m̅∣_n predicted from the two models are different: over the 4 pause sites, Model T predicted that RNAP can backtrack by as much as ~ 7 bp. This large backtracking distance resulted in a difference between the predicted and measured paused position of RNAP by as much as ~ 9 bp, much larger than the measurement uncertainty. In contrast, in agreement with the measurements, Model B predicted that m̅∣_n values at the pause sites are all close to 0 (no significant backtracking) (Figure 4B).

We have also compared the predicted apparent step size (m̅∣_n+1− m̅∣_n+1) distributions of RNAP during transcription elongation from the two models with single molecule measurements conducted at 18 pN assisting force (7). Both models have an intrinsic mean apparent step size of 1 bp; however they predict markedly different distributions (Figure 4C). On the template used by Shaevitz et al., Model T predicted an apparent step size variation of 1.0 bp (s.d.). This large variation is inconsistent with the experimental observation that RNAP took uniform 1 bp steps with variations ~ 0.2 bp. Model B, on the other hand, predicted an apparent step size variation of 0.4 bp, again more in accord with measurements.

Discussion

In this work, we have compared two recent models on sequence-dependent kinetics of transcription elongation. We conclude that Model B has an overall better performance than Model T in terms of predictive power of pause location, kinetics, and mechanism. Nonetheless, a major strength of Model T is its simplicity compared with Model B. It involves fewer model parameters that must be experimentally determined.

The two models share a large degree of similarity in their formulations. Their major differences lie in their different RNAP backtracking kinetics and how to consider the effect of co-transcriptional RNA folding on the elongation kinetics. Below we will elaborate on these two points and discuss the pros and cons for each model.

In Model B, the backtracking “entry step” (from the pre-translocation state to the first backtracked state) is in general assumed to be slow comparing to the NTP incorporation rate in the main reaction pathway so that backtracking happens with very low probability for most template positions. As a result, a majority of predicted pauses are pre-translocation pauses that occur along the main reaction pathway. In Model T, backtracking is assumed to be very rapid until RNAP encounters a kinetic barrier imposed by co-transcriptionally folded RNA. Thus most of the predicted pauses by this model are backtracked pauses.

Biochemical experiments indicate slow translocation kinetics into and out of a backtracked state: on some experimentally identified backtracked pause sites, RNAP only backtracked under prolonged NTP starvation of ~10 min, which is orders of magnitude longer than the NTP incorporation time scale (0.05 - 1 s) (4). In addition, single molecule experiments also indicate that most of the pauses are not caused by backtracking (7, 18). Taken together this indicates it is likely that backtracking indeed encounters a high activation barrier as is assumed in Model B. This high barrier may be imposed by the RNAP structure that requires the 3’ end of the nascent RNA chain to reverse thread through a narrow pore of the secondary channel (12–15 Å wide) that is tailored for NTP entry to the active site (19, 20). Nonetheless Model B’s assumptions that the barrier heights were sequence-independent and remained the same for all backtracked states are likely oversimplified. The nature of the activation barrier requires further elucidation.

The effect of co-transcriptional RNA folding on the elongation kinetics is considered in Model T, but is ignored in Model B. Secondary structures in the nascent RNA are known to play important roles in transcription kinetics. A strong RNA hairpin with a GC-rich stem, together with an adjacent downstream U-rich region, leads to termination. RNA hairpins may also induce pausing by interacting with the flap region of the RNAP (5, 21). Therefore, a more accurate description of sequence-dependent RNAP kinetics should consider contributions from RNA secondary structures. This consideration also provides a good starting point for future modeling of transcription termination.

As pointed out in Tadigotla et al. (12), the energetic consideration of the interplay between the backtracked RNAP and RNA secondary structure in Model T is oversimplified. More accurate modeling of RNA requires detailed knowledge of the kinetics of RNAP translocation and co-transcriptional RNA folding, which needs future effort in both experimental and theoretical work.

Although Model B has an overall better performance, RNAP kinetics might be best described by the essence of the two models: RNAP backtracks with a relatively slow rate so that at most of the template positions, backtracking occurs with low probability. Backtracked RNAP could be assisted by RNA folding to bias its motion in the forward direction. A more comprehensive description of transcription may even involve consideration of the interaction between the RNAP and downstream DNA (22), as well as RNAP conformational changes.

To test the extent of the RNA folding contribution to elongation kinetics, several experiments could be conducted. Potential pause sequences may be engineered into templates with and without strong upstream hairpins to examine the differences in pausing kinetics. RNA hairpin formation could also be eliminated to test whether backtracking is encouraged as a result. One recent single molecule study measured elongation kinetics by applying a large force on the nascent RNA to prevent formation of RNA secondary structures, and concluded that a RNA hairpin had no effect on the kinetics (23). However, a possible effect might have been masked by the large assisting force (~ 30 pN) applied to RNAP, which was previously shown to reduce backtracking (24, 25). Alternatively, RNA hairpins could be eliminated by degrading RNA with RNase, and the RNAP elongation rate measured in a single molecule assay.

There are alternative interpretations of pause mechanism. Herbert et al. (8) proposed an off-pathway “pause state” that does not involve backtracking. Biochemical studies also provided evidence that RNA 3’-end in TEC could “fray” from the template DNA and thus induce pausing off the main reaction pathway (26, 27). It should be noted that if the occurrence of such isomerization step is correlated with the equilibrium of pre/post-translocation state, it would not change the predicted pause sites from current Model B.

Our hope in the current work is to put forth a comprehensive comparison of the current models in an effort to clarify strengths and weaknesses of each model and to lay out a foundation for future theoretical and experimental work on the mechanism of sequence-dependent transcription pausing and elongation.

Materials and Methods

Experimental and simulation conditions

If not mentioned specifically, the NTP concentration used in the simulations are the same as the corresponding experiments: 1) low [NTP]: 10 μM for sequences D104, D111, D112, D123, D167, D387 (30°C; Levin and Chamberlin, 1987), 40 μM for sequence seq10, and 30 μM for sequences seq11–seq13 (30°C; 12), 2) high [NTP]: 1 mM for pKA2, 1 mM ACG, 200 μM U for pTS147, 100 μM for λtR1 (25°C; 10), and 1mM ACU, 250 μM G for his and ops templates (~25°C; 8), and 3) step size simulation: 5 μM A, 2.5 μM C, 10 μM G/UTP. These conditions are listed in a table in SI.

Temperature considerations

As shown above, experiments were conducted at different temperatures. Since model parameters including those relating to the thermodynamic stability of nucleic acids and kinetic rates are functions of temperature, these parameters should be chosen or tuned for the temperature of the corresponding experimental measurements. However, we found that pause location predictions by both Models were rather insensitive to model parameters, in agreement with Tadigotla et al. (12). On the other hand, we also found that pause kinetics was very sensitive to temperature. Therefore, the following treatments of temperature were taken in consideration of Model T and Model B.

In order to faithfully replicate Model T, we performed simulations of pause location data under low [NTP] for Model T using thermodynamic parameters for 37°C, which is different from the experimental temperature of 30°C but is the same as was used by Tadigotla et al. (12). We performed simulations of pause location data under high [NTP] using thermodynamic parameters for 25°C, same as experimental temperature.

Parameters for Model B have previously been optimized for 25°C (10,11). Here all pause location predictions were performed using the same parameters. Kinetic predictions, such as simulations of transcription gels, require more careful consideration of temperature. Since the experimental transcription gels shown in Figure 2 were taken under 30°C, to compensate for the increased transcription rate at 30°C, we increased the [NTP] from the experimental concentration of 10 μM to 25 μM.

Parameters used in the simulation

The same structure of TEC was used to for both models: a DNA bubble size of 12 bp, a DNA-RNA hybrid size of 9 bp, and 1 nt downstream ssDNA. For Model T, the k_max and K_d were the same as in Tadigotla et al: k_max: 700 s^-1, K_d: 20 μM. For Model B, the NTP-dependent k_max and K_d were the same as Bai et al. (11), the backtracking barrier height was 41.2 k_BT, and the rest of the parameters were the same as in Bai et al. (10).

Subtle differences in the model consideration

In Model B, we consider a dangling energy term for the post-translocation and forward-tracked state energies by assuming a 50% of terminal base pair energy for the ss template DNA nucleotide immediately adjacent to the 3’ end of the RNA in the transcription bubble (9,10). This term is not considered by Tadigotla et al. and its replicated model.

In Tadigotla et al., the TEC state energy includes the RNA folding energy. For a given product length n, RNA folding is only considered for pre- and backtracked states and a folded RNA structure does not unfold until after NTP incorporation. Therefore, RNAP will not move beyond the first hairpin encountered. In a sense, this is not an equilibrium model. Strictly speaking, were RNA also allowed to fold in forward-tracked states, RNAP would often become arrested or dissociated because of the lack of RNA unfolding assumed in the model. Even if the unfolding rate were assumed to be fast, the forward-tracked states would then be in equilibrium with all the other accessible states; there would be cases where RNAP would pause because forward-tracked states are energetically more favorable. These pauses were manually discarded by Tadigotla et al. because of the argument that RNAP’s transient presence in the forward states did not allow enough time for hairpin formation (personal communication). In order to faithfully reproduce Model T, we also did not allow hairpins to form in forward-tracked states so that the RNA folding energy stayed the same for the forward-tracked states as that of the post-translocation state. Because energetically favorable forward-tracked states are very rare, this treatment in energy calculation in Model T does not significantly affect its predictions.

Calculation of m̅∣_n

In Model T, the average translocation position at site n relative to the pre-translocation state was calculated as:

$${\overline{m}\mid }_n=\frac{\left(1+\frac{[\mathrm{NTP}]}{K_{\mathrm{d}}}\right)\exp \left(-\mathrm{\Delta }{G}_{n,1}/k_{\mathrm{B}}T\right)+\sum _{m\ne 1}m\exp \left(-\mathrm{\Delta }{G}_{n,m}/k_{\mathrm{B}}T\right)}{\left(1+\frac{[\mathrm{NTP}]}{K_{\mathrm{d}}}\right)\exp \left(-\mathrm{\Delta }{G}_{n,1}/k_{\mathrm{B}}T\right)+\sum _{m\ne 1}\exp \left(-\mathrm{\Delta }{G}_{n,m}/k_{\mathrm{B}}T\right)}.$$

In Model B, we used a Monte-Carlo method to simulate a large number of single molecule traces of RNAP position versus time. Then for a particular n, we analyzed the total time RNAP spent at each m, t(n, m), and calculate the m̅∣_n as: ${\overline{m}\mid }_n=\frac{\sum _{m}m·t(n,m)}{\sum _{m}t(n,m)}$.

Abbreviations

RNAP

RNA polymerase

TEC

Transcription Elongation Complex

ds

double stranded

ss

single stranded