Correction for Arterial-Tissue Delay and Dispersion in Absolute Quantitative Cerebral Perfusion DSC MR Imaging

Abstract

The singular value decomposition deconvolution of cerebral tissue concentration-time (C-T) curves with the arterial input function (AIF) is commonly used in dynamic susceptibility contrast (DSC) cerebral perfusion MR imaging. However, it is sensitive to the time discrepancy between the arrival of the bolus in the tissue C-T curve and the AIF signal. This normally causes inaccuracy in the quantitative perfusion maps due to delay and dispersion effects. A comprehensive correction algorithm has been achieved through slice-dependent time-shifting of the AIF, and a delay-dependent dispersion correction model. The correction algorithm was tested in 11 healthy subjects and 3 ischemic stroke patients scanned with a quantitative perfusion pulse sequence at 1.5T. A validation study was performed on 5 patients with confirmed cerebrovascular occlusive disease scanned with MRI and positron emission tomography (PET) at 3.0T. A significant effect (p<0.05) was reported on the quantitative cerebral blood flow and mean transit time measurements (up to 50%). There was no statistically significant effect on the quantitative cerebral blood volume values. The in vivo results were in agreement with the simulation results, as well as previous literature. This minimizes the bias in patient diagnosis due to the existing errors and artifacts in DSC imaging.

INTRODUCTION

The singular value decomposition (SVD) method is usually employed to deconvolve the tissue concentration-time (C-T) function with the arterial input function (AIF) in dynamic susceptibility contrast (DSC)-MRI analysis (1). This method is known to be sensitive to arterial-tissue delay (ATD), defined as the time discrepancy between the arrival of the bolus in the tissue C-T function and the AIF (2,3). The two major ATD problems can be distinguished as follows: (a) experimental ATD, due to the slice acquisition scheme, and (b) physiological ATD, due to collateral circulation or to the selection of the AIF signal near an occluded arterial branch (4,5). Dispersion of C-T signals occurs in the presence of physiological ATD, which limits the accuracy of the cerebral perfusion values obtained using DSC-MRI clinically. From a qualitative perspective, this usually does not lead to a misidentification of the hypoperfused brain areas. However, it is more of a problem when quantitative analysis is performed to characterize changes between the original and follow-up examinations for a certain patient (4), or to compare them to a well-defined ischemic threshold (9) in order to differentiate the “at-risk” tissue from the ischemic core and from tissue not at risk (10).

A block-circulant matrix for SVD deconvolution (cSVD) (3), a reformulated SVD (rSVD) (5,6) and a least-squares fitting method to determine tracer delay on a pixel-by-pixel basis (7,8), are all existing time-shifting techniques to remove the effect of delay on the quantification of cerebral perfusion. However, these techniques do not account for the dispersion effects that are expected to occur simultaneously in the ischemic brain region mainly, and the resulting perfusion measurements will tend to be underestimated (2).

In addition to approaches for quantification using non-contrast arterial spin-labeling (12–14), there have been a number of algorithms proposed to obtain quantitative images of cerebral blood volume (CBV, in ml/100g), cerebral blood flow (CBF, in ml/100g/min) and mean transit time (MTT, in s) using DSC. Quantitative CBF (qCBF), quantitative CBV (qCBV) and MTT, obtained from DSC perfusion images using the so-called “Bookend technique” (15,16), have been proven reproducible, reliable, and accurate (17). Delay and dispersion effects have been modeled via exponential vascular transport functions (2,4,11) which have produced promising results in predicting and correcting the peak shift and general shape of the C-T tissue and AIF signals.

In this analysis, we will use the recently reported Self-CALibrated Epi Perfusion Weighted Imaging (SCALE-PWI) MRI pulse sequence (18) which is a simplified approach to the “Bookend technique” (15,16). SCALE-PWI eliminates the need for additional T₁ scans from the original bookend protocol. With the inclusion of a fully-automated AIF selection and image reconstruction software that is part of the MRI scan console, the scan protocol used in this is clinically assessable. The purpose of this work is to test the hypothesis that a simple model-dependent approach can be used to improve the accuracy of quantitative cerebral perfusion measurements using DSC-MRI in a setting of delay and dispersion of the bolus of contrast agent between the sampled AIF and tissue-contrast curve. We will evaluate an algorithm correcting for both experimental and physiological ATDs, as well as the dispersion effects observed in DSC perfusion images based on a delay-dependent vascular transport model. The proposed algorithm will be tested and compared to the existing algorithms through numerical simulations across a large range of MTT, ATD and dispersion values of interest, in vivo experiments in healthy subjects and patients at 1.5T, and direct comparison to values obtained with positron emission tomography (PET) in patients at 3.0T.

MATERIALS AND METHODS

We have developed a post-processing algorithm to account for bolus delay and dispersion effects in the AIF that can result in incorrect perfusion values in vascular territories that are distal to the point where the AIF is sampled or, in case of occluded arteries, fed by collateral flow. We added an additional correction to the AIF which mitigates the effect of time shifts between the sampling function of the AIF and the tissue curves. The source of this shift results from the order in which individual 2D slices are acquired within a multi-slice 2D DSC perfusion acquisition.

Correction Algorithm

The correction algorithm was developed in MATLAB V7.2 (The Mathworks, Inc., Natick, MA, USA), and was integrated into the existing automatic image postprocessing algorithm of the bookend technique (17).

Global AIF Selection

The process of calculating a slice-resampled, delay-dispersion corrected AIF can be thought of as the determination of a voxel-specific local AIF. Prior to these calculations, we must derive an analytical expression for the “global” AIF. A number of voxels where the C-T curve falls within the adaptive threshold are selected, based on Carroll, et al. (19). Average AIF signals are computed using the signals from the voxels belonging to each slice separately. In each case, the corresponding C-T curve, AIF(t), is computed from the AIF signal, S(t), as follows:

$$\mathit{\text{AIF}}(t)=-\frac{k}{\mathit{\text{TE}}}\text{ln}\left(\frac{S(t)}{S_0}\right)$$ [1]

where S₀ is the pre-injection signal, TE is the echo time and k reflects the contrast agent relaxivity and properties of the pulse sequence (15). An analytical expression is determined for each of the computed AIFs, by fitting them to a gamma-variate model using the Levenberg-Marquardt least squares fit MATLAB built-in function, according to the indicator dilution curve (IDC) theory:

$$C_{\mathrm{\Gamma }}(t)=A_{\mathrm{\Gamma }}·t^{\alpha }·e^{-\frac{t}{\beta }}$$ [2]

where C_Γ (t) is the gamma-variate model of the IDC, α and β are the shape and scale parameters, respectively, and the factor A_Γ refers to the IDC amplitude (20–22). The initial guesses of the fit parameters(A_Γ, α, and β), are determined using a χ²-minimization grid search algorithm to ensure robust fitting and rapid convergence of the solution. The AIF with the best fit (i.e. the one with the smallest sum of the squared residuals) is chosen as a global AIF(t), to be used as input to the slice re-sampling and delay/dispersion corrections.

AIF Re-sampling Correction

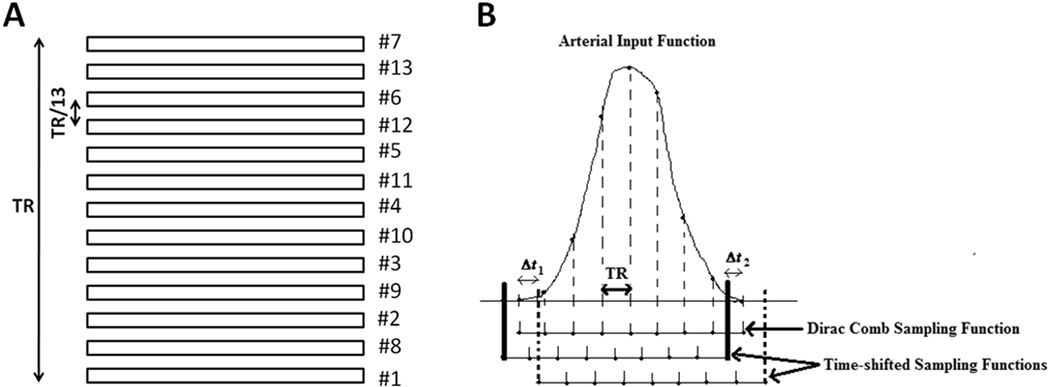
Several slices are acquired sequentially during one measurement of the DSC scan, with a time separation between 2 consecutive slices equal to the repetition time (TR) divided by the number of slices. When a global AIF is chosen in a single slice and used for deconvolution of tissue C-T curve in each slice, there is an acquisition time discrepancy between the AIF-chosen slice and the deconvolved slice, and it varies depending on the order of slice acquisition (ascending, descending or interleaved (odd/even)) (Figure 1).

Figure 1.

A) Interleaved (odd/even) order of slice acquisition of the DSC images of 13 contiguous brain slices: apparent changes, by fractions of TR (integer multiples of TR/13), in the arrival time of the contrast bolus to each brain slice with respect to the AIF are introduced. B) Time-shifting of the AIF sampling function by Δt₁ > 0 and Δt₂ < 0 (see Eq. [4]), corresponding to slices acquired after and before the slice where the AIF was selected, based on the interleaved order of slice acquisition. For instance, if 13 slices are acquired, and the AIF slice is #6 by counting from bottom to top (designated as #10 in order of acquisition), signals from tissues in slice #12 (#13 in order of acquisition) are acquired 3xTR/13 after the AIF, and signals from tissues in slice #13 (#7 in order of acquisition) are acquired 3xTR/13 before the AIF.

To correct this time shift, an appropriate sampling function of the global, fitted AIF(t) is created to obtain the time-shifted AIF corresponding to each slice. The fitted AIF(t) is a continuous-time signal which is defined over all time points (t > 0) (23). It is re-sampled through multiplication with a slice-specific Comb sampling function (see Eqs. [3] and [4]), to result in a discrete-time signal, AIF[n,T], i.e. sampled at discrete intervals of TR (23). AIF[n,T], defined for the “n^th” slice, is then used to deconvolve the sampled tissue curves of all the voxels in a given slice. This is described mathematically as:

$$\mathit{\text{AIF}}[n,T]=\mathit{\text{AIF}}(t)·\left\{{\displaystyle \sum _{i=0}^{K-1}}\delta (T-(i+\mathrm{\Delta }t)·\mathit{\text{TR}})\right\}$$ [3]

$$\mathrm{\Delta }t=(n-n_{\mathit{\text{AIFslice}}})·\mathit{\text{TR}}/N$$ [4]

where AIF(t) is the global AIF, i.e. the continuous-time AIF signal derived from an analytical fit of the sampled AIF signal extracted from a single 2D slice, and n is the slice number in order of slice acquisition. n_AIFslice is the AIF slice number following the order of slice acquisition, Δt is the fractional time shift of the Dirac comb sampling function, K is the number of samples of the discrete AIF signal, and N is the total number of brain slices being imaged. The resulting slice-specific AIF is used to deconvolve the C-T curves of all the voxels belonging to a given slice using SVD.

Tissue Delay and Dispersion Correction

This correction is a combination of a time-shifting technique based on the computed ATD, and the introduction of an exponential vascular transport function that models the dispersion of the contrast bolus as it moves from the sampling site to the tissue of interest. First, the bolus arrival time (BAT) and bolus recirculation time (BRT) in each voxel are determined via an algorithm based on adaptive thresholding that ensures a signal drop larger than 90% of the baseline signal prior to bolus arrival. Time-shifting is indirectly achieved by an ATD removal method, which multiplies the original C-T curve by a step function (see Eq. [5]):

$$\mathrm{\Pi }[i]=\{\begin{array}{cc}\hfill 1\hfill & \hfill \mathit{\text{if BAT}}\le i\le \mathit{\text{BRT}}\hfill \\ 0\hfill & \mathit{\text{otherwise}}\hfill \end{array}\mathit{\text{ for }}i=\mathit{1},\dots ,K$$ [5]

where K is the number of sample time points during the DSC scan, which are separated by TR.

We model the physiological ATD as:

$$\mathit{\text{ATD}}={\mathit{\text{BAT}}}_{\mathit{\text{VOI}}}-{\mathit{\text{BAT}}}_{\mathit{\text{AIF}}}$$ [6]

where BAT_VOI is the BAT value of the voxel-of-interest (VOI) and BAT_AIF is the BAT of the AIF of the slice to which the VOI belongs. In addition, we use a delay (ATD)-dependent dispersion model which consists of an exponential vascular transport function to correct for dispersion effects on the tissue C-T curve (24):

$$R_d(t)=\frac{A}{\mathit{\text{ATD}}+1}{e}^{-\beta \frac{t}{\mathit{\text{ATD}}}}$$ [7]

where R_d (t) is the dispersion residue function to be used for the correction, with amplitude $\frac{A}{\mathit{\text{ATD}}+1}$ and dispersion constant β, characteristic of the cerebral vasculature system (both A and β are real positive numbers that are determined via fitting). This transport function has been shown to be an appropriate model determined for the local AIF, as reported by Lee, et al (24).

We assume an individual’s brain microvasculature has a single dispersion characteristic constant (β).We determine the values of A and β based on a venous signal selected at the level of the sagittal sinus, since the delay of bolus arrival to the latter is within the range of physiological delays of interest. An average venous signal is determined by automatic segmentation of few blood voxels located in the sagittal sinus, based on adaptive thresholding and large drops in T₁ values due to contrast injection (17). A corresponding venous C-T curve is computed using Eq. [1] and fitted to Eq. [2] via least-squares fitting, by windowing with the venous BAT and BRT values. A venous residue function is then computed by deconvolving, via standard SVD method, the fitted venous C-T curve with the appropriately re-sampled AIF, to ensure the effect of multiple-slice shifting is removed simultaneously. The MTT dependence of the residue function is removed by first deconvolving the venous residue function with:

$$R(t)=e^{-\frac{t}{\mathit{\text{MTT}}}}$$ [8]

where R(t) is a simple model of the vasculature bed represented as a single, well-mixed compartment (25,26). The resulting residue function is then fitted into the dispersion model (Eq. [7]), with appropriate venous ATD value, to obtain A and β. We apply the values of A and β determined using the venous signal, with appropriate ATD, to determine a localized delay-dependent dispersion model for each voxel in the brain (see Eq. [7]).

We look at BAT and ATD maps (2) to identify brain regions with positive and negative ATD values. For positive ATD regions, the slice-specific AIF is convolved by the dispersion function (Eq. [7]) with appropriate ATD value for the VOI to create the necessary dispersion in the AIF signal prior to deconvolution. For negative ATD regions, the AIF is deconvolved with the appropriate dispersion function prior to deconvolving the VOI’s C-T curve.

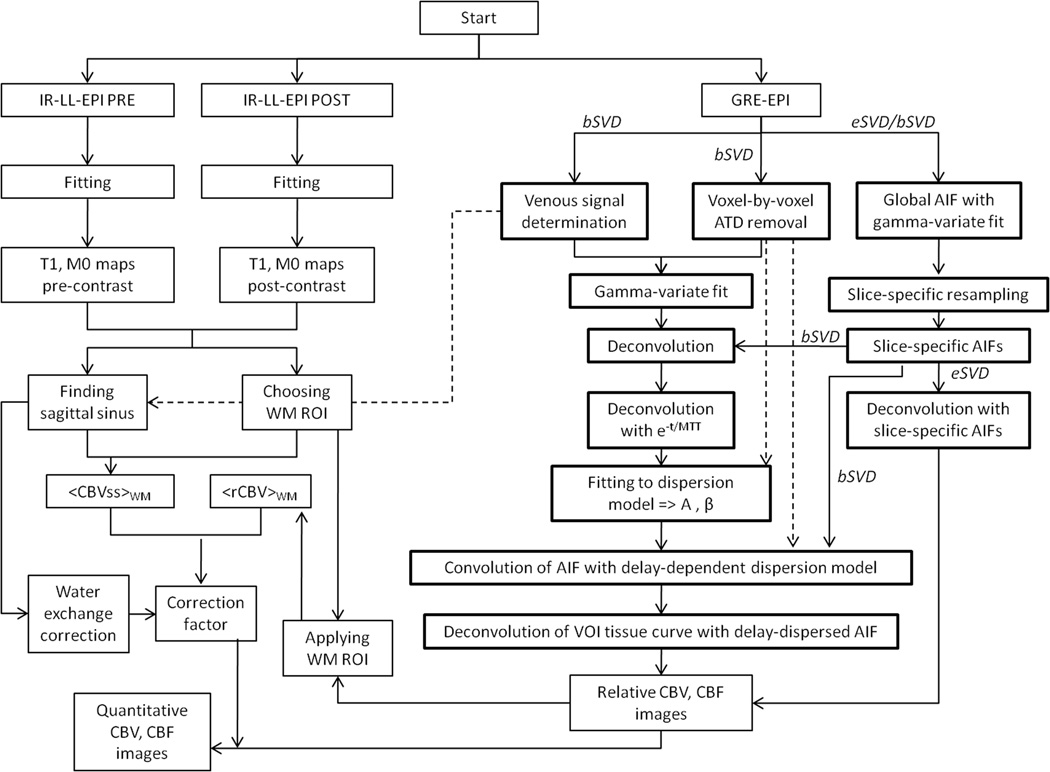
Figure 2 is a flowchart of the automatic postprocessing algorithm that itemizes the steps of eSVD, bSVD, determination of delay and dispersion, with final Bookend calibration. Note that the bSVD correction includes the eSVD method, and that the Bookend calibration takes place after performing the deconvolution analysis using eSVD alone or bSVD.

Figure 2.

Flowchart of the automatic postprocessing algorithm showing how eSVD, bSVD, determination of delay and dispersion, and Bookend calibration were put together to produce the absolute quantitative cerebral perfusion measurements. The postprocessing steps of the SCALE-PWI/Bookend algorithm involving the proposed correction have been marked in bold lines. eSVD refers to SVD with “experimental” delay correction only. bSVD refers to SVD with the added physiological delay and dispersion (“beta”) correction, which automatically includes eSVD.

Monte Carlo Simulations

A simulated AIF C-T was obtained using the standard simulation process described by Calamante, et al (2), for a typical AIF signal observed in adults, and TR = 1 sec. A single, well-mixed compartmental model of the residue function was assumed (25,26) resulting in a single exponential residue function (Eq. [8]). Sampled tissue C-T curves were obtained via numerical convolution of the AIF with the residue function.

AIF Re-sampling Correction

MATLAB-based computer simulations were performed to compare the size of the AIF sampling error in standard SVD (1), rSVD (5), cSVD (3), and SVD with and without the proposed experimental AIF resampling correction (eSVD), across a range of MTT (6 to 24 sec) and ATD (−0.9 to 0.9 sec) values. The ATD values were incremented by TR/N, which represents the incremental time delay observed among slices due to the slice acquisition scheme. T_OFFSET = −40 · TR was used for the rSVD technique (5).

Tissue Delay and Dispersion Correction

For the physiological ATD and ATD-dependent dispersion, simulations were performed to compare the accuracy of standard SVD (1), rSVD (T_OFFSET = −10 · TR) (5), cSVD (3), and SVD with the proposed ATD-dependent dispersion correction model (bSVD) across a range of MTT (6, 12 and 24 sec), ATD (0 to 6 sec, with increments of TR) and β (0.5 to 3 sec, with increments of 0.5 sec) values. These values were chosen based on the range of physiologically relevant delay and dispersion values.

Gaussian noise was added to simulate different signal-to-noise ratios (SNR = 5, 20 and 100), including typical values found in vivo (SNR ~ 20). The simulations were repeated 100 times in each case. The reconstructed CBF values were compared to computer-generated truth values by examining the ratio of the two values. Trends were examined to determine the region of validity of the different reconstruction techniques. These simulations served as a basis to evaluate the observed changes in the same imaging metric in the human data.

In vivo Studies

This investigation is fully Health Insurance Portability & Accountability Act (HIPAA)-compliant and was approved by the institutional review board. The proposed AIF re-sampling and delay-dispersion corrections were applied to the human data.

Healthy Volunteers

Eleven healthy subjects (7 males, 4 females, 29.18 ± 8.02 years old) were scanned with the SCALE-PWI pulse sequence for automatic brain perfusion quantification, on a 1.5T MR scanner (MAGNETOM Espree, Siemens AG Healthcare Sector, Erlangen, Germany). Written informed consent was obtained from each subject prior to being scanned in accordance with the internal review board at our institution. The SCALE-PWI imaging parameters were: TE = 34 ms, TR = 1090 ms, flip angle = 20°, field of view = 220 mm × 220 mm, slice thickness = 5 mm, matrix dimensions = 128 × 128, GRAPPA with acceleration factor = 2. A total of 50 DSC measurements were acquired for 13 contiguous brain slices with an interleaved order of slice acquisition (odd then even slices), during the passage of a single-dose injection of Gd-DTPA (0.1 mmol/kg) contrast agent, followed by a saline flush of 15 ml, at a rate of 4 ml/s.

Patient Data

Six patients (3 males, 3 females, 48.83 ± 16.63 years old) were enrolled from an ongoing clinical trial at Northwestern Memorial Hospital, and were scanned with the SCALE-PWI pulse sequence at 1.5T (Avanto, Siemens AG Healthcare Sector, Erlangen, Germany). The imaging parameters were identical to those used in the healthy volunteers’ study. Three of these patients were classified as having no known perfusion abnormality, and three other as suffering from an ischemic stroke by an experienced, board-certified neuroradiologist. The latter three included: 1) a 42-year-old female with a history of stroke and left middle cerebral artery (MCA) occlusion; 2) a 43-year-old male who suffered from occlusion of the M1 segment of the right MCA and acute stroke in the right deep nuclei; and, 3) a 47-year-old female who suffered from an acute stroke resulting in large right basal ganglia and right temporal lobe infarcts, and a severe stenosis of the M1 segment of the right MCA.

For direct validation, a subset of five patients (2 males, 3 females, 42.4 ± 13.8 years old), chosen from an ongoing study of MRI and PET cerebral perfusion imaging were analyzed. These subjects were chosen based on large perfusion deficits, resulting in MRI qCBF values that correlated poorly with PET reference values. All patients were enrolled at Washington University School of Medicine in the ongoing study based on angiographically confirmed chronic stable large artery cerebrovascular occlusive disease (CVD). Patients were scanned on the same day with the conventional Bookend MR technique (17) at 3T (Trio, Siemens) and with the gold standard of reference for perfusion imaging, [¹⁵O]-H₂O PET (27,28).

Region of Interest (ROI) Analysis

The paired difference t-test was used to determine whether the differences seen in the in vivo data (for the healthy subjects and ischemic stroke patients) due to the applied correction were statistically significant. Statistical significance was defined at the 5% level.

For the ischemic stroke patients scanned with SCALE-PWI, diffusion images with b = 1000 s/mm² were used to identify infarct ROIs and corresponding normal ROIs on the contralateral sides, by a board-certified neuroradiologist. A total of 14 ROIs were drawn over infarcted or hyperintense diffusion-weighted regions in MATLAB. ROIs included WM, GM, and cortical blood vessels (BV), at different levels in the brain, and corresponding ROIs were drawn on the contralateral side to each infarct ROI.

For the MR-PET patients, ROIs were drawn to cover hypoperfused areas with prompt (ΔBAT =0 to 1.5 s) and delayed (ΔBAT =1.5 to 9 s, resulting from vessel occlusion) bolus arrival for each patient. Pearson’s correlations were computed to compare MR to PET CBF values in these ROIs, with (bSVD) and without (SVD) applying the proposed delay and dispersion correction.

RESULTS

Numerical Simulations

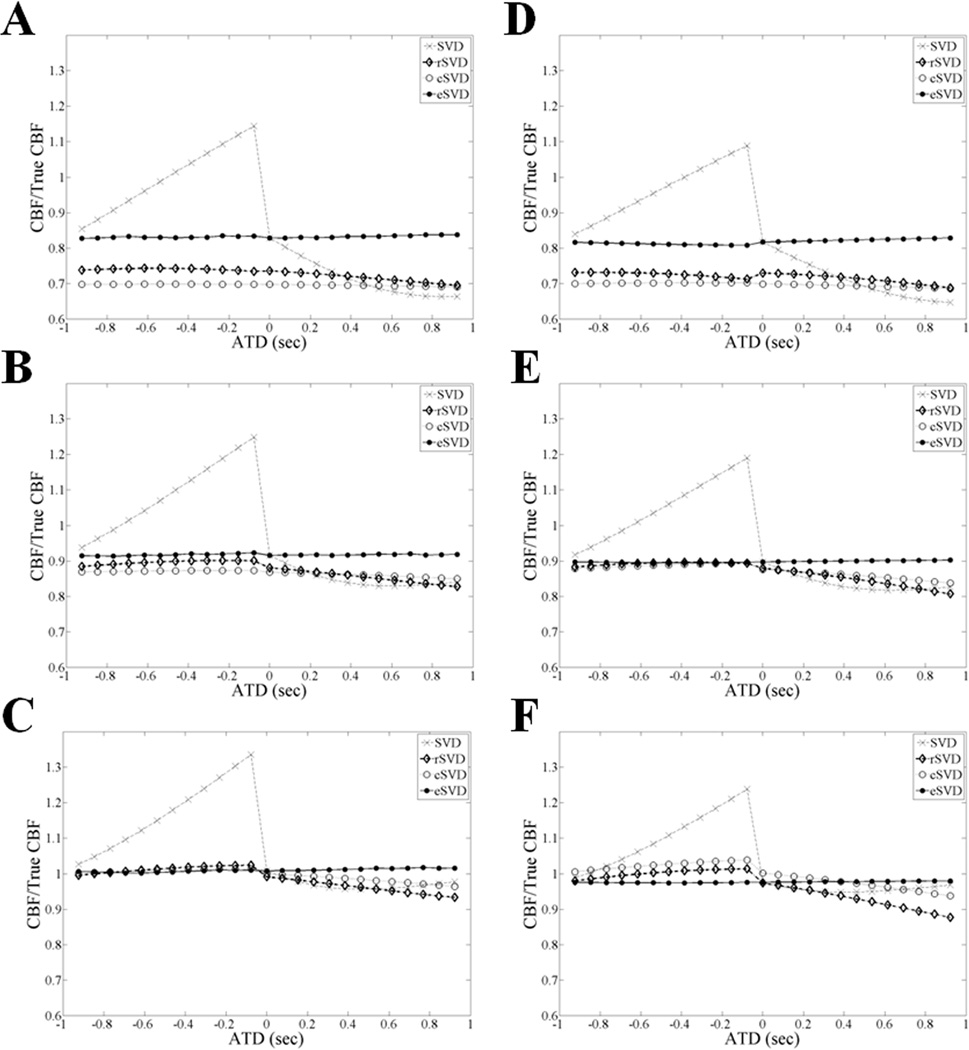
The ratio of measured CBF/True CBF shown in Figure 3 was determined using standard SVD, rSVD, cSVD and eSVD algorithms for MTT values between 6 and 24 s, and shows that the eSVD algorithm calculated CBF more accurately (close to one) and precisely (less variation) than the standard SVD, cSVD, and rSVD algorithms. This difference in the three approaches was most pronounced for short MTT (6 s). The accuracy of all three deconvolution techniques improved as MTT increased. A similar behavior is reported as the noise level increases, i.e. from the second (SNR = 20) to the first (SNR = 5) column of Figure 3, due to the optimal noise rejection threshold used for SVD (P_SVD = 0.2), which indicates the eSVD method is very robust in the presence of noise.

Figure 3.

The ratio of CBF/True CBF is compared for SVD, rSVD, cSVD, and eSVD methods, for a range of representative ATD and MTT values, with TR = 1 s and N = 13: A and D correspond to MTT = 6 s, B and E correspond to MTT = 12 s, and C and F correspond to MTT = 24 s, for SNR = 5 and 20, respectively. An oscillation threshold, P_SVD = 0.2, was used for all SVD methods. In these simulations, eSVD outperformed rSVD and cSVD for all MTT and SNR values.

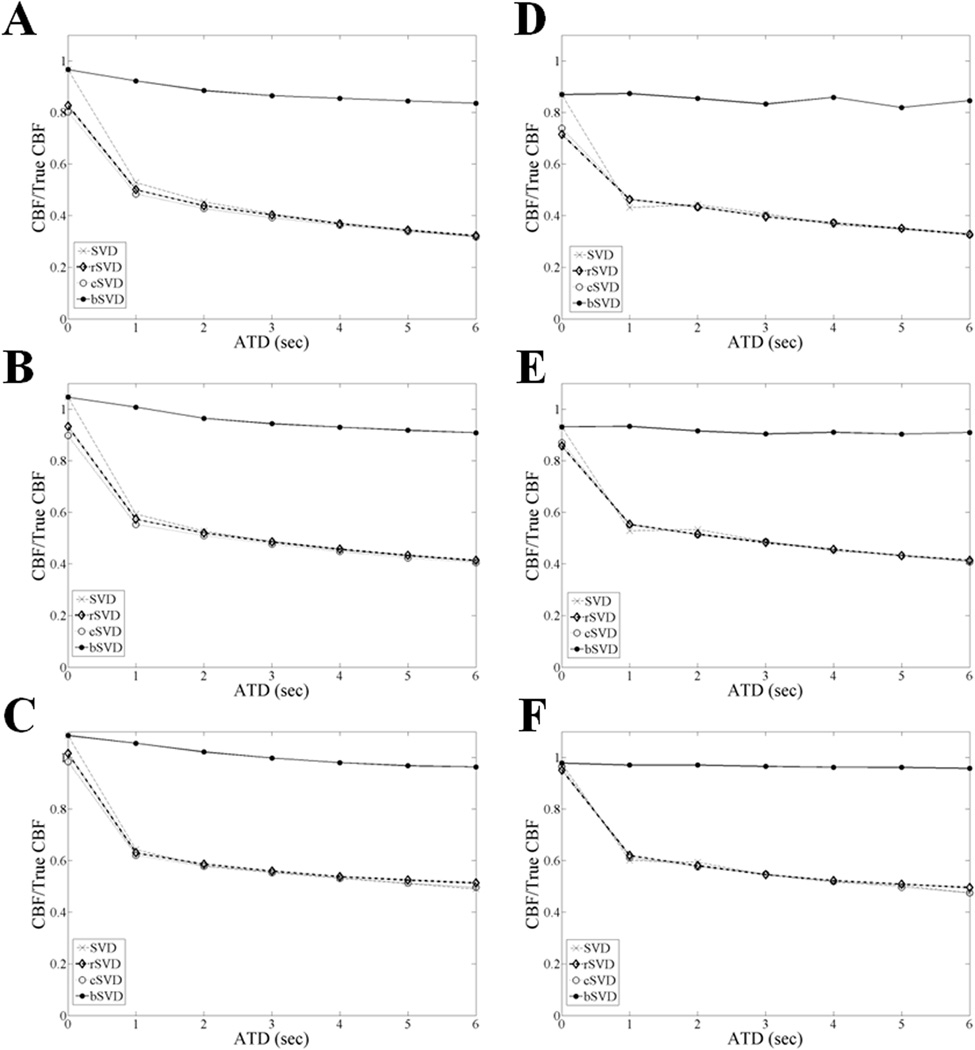
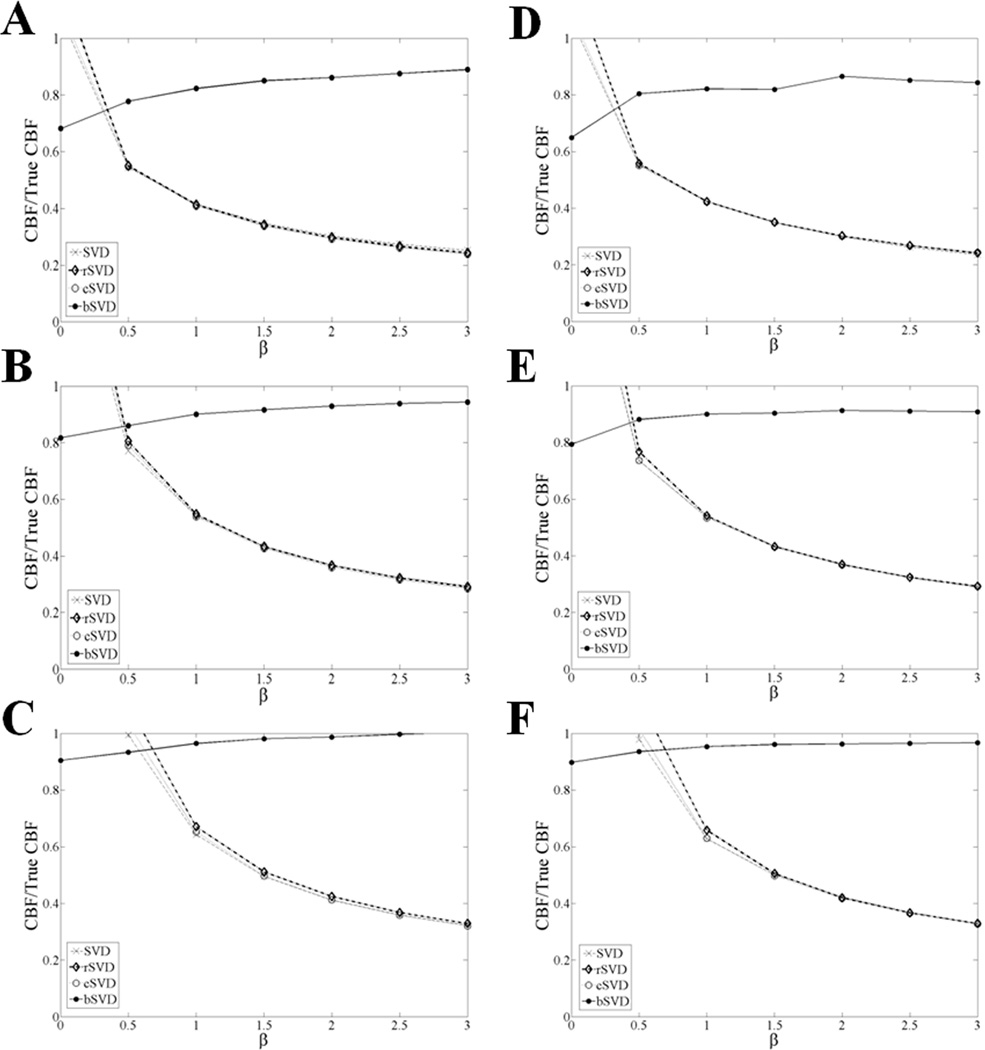
The same ratio (CBF/True CBF) is presented in Figures 3 and 4 for values obtained with SVD, rSVD, cSVD, and bSVD, for MTT values between 6 and 24 s, over a range of ATD values and dispersion constants (β), respectively. bSVD outperformed (accuracy > 0.8) all other deconvolution methods (accuracy < 0.6) in the presence of delay and delay-dependent dispersion. The measured inaccuracy in the computed CBF values via SVD, rSVD and cSVD increased with increasing ATD and dispersion (β), and the proposed bSVD method appeared to be stable over the ranges of ATD and β values of interest. Based on these simulations, a 20 to 50% correction of CBF values is expected using the bSVD method as compared to the existing deconvolution methods. Similar effects are reported for both SNR levels (5 and 20), which indicates the bSVD method is also less sensitive to noise.

Figure 4.

The ratio of CBF/True CBF is compared for SVD, rSVD, cSVD, and bSVD methods, for a range of representative ATD values with β = 1.5 at different MTT values: A and D correspond to MTT = 6 s, Band E correspond to MTT = 12 s, and C and F correspond to MTT = 24 s, for SNR = 5 and 20, respectively. These simulations assumed TR = 1 s and N = 13. An oscillation threshold, P_SVD = 0.2, was used for all SVD methods. bSVD outperformed rSVD and cSVD for all MTT and ATD values.

A similar behavior to that of SNR = 20 was reported for SNR = 100 in both cases (eSVD and bSVD), therefore, the latter plots are not shown.

In vivo Results

Experimental AIF Re-sampling Correction

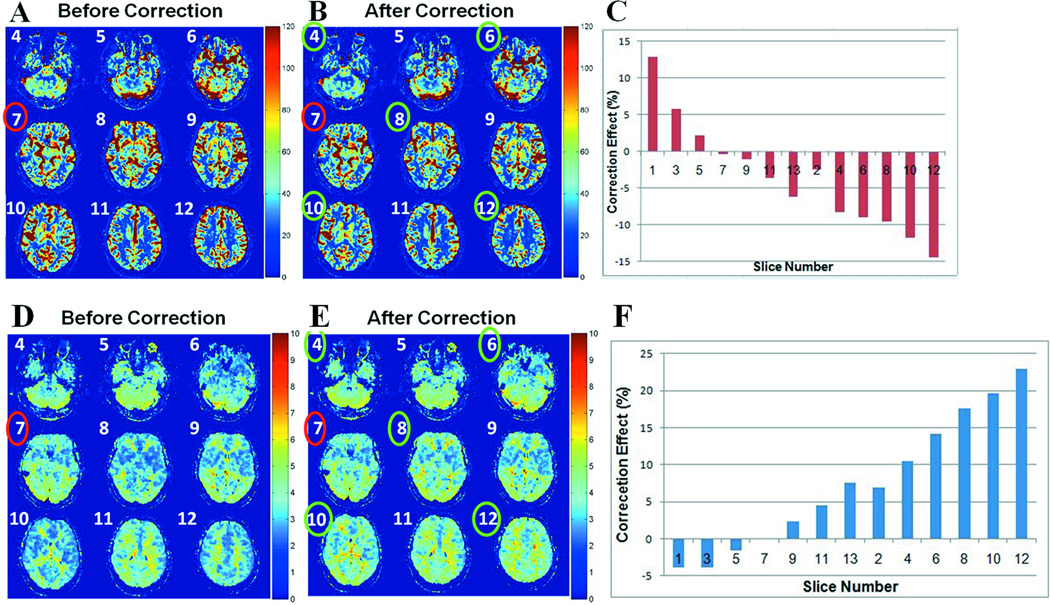
A qualitative comparison of qCBF and MTT maps, in a representative subject, obtained with (eSVD) and without (SVD) experimental ATD correction, is given in Figure 6. The quantitative correction effect increased by moving to slices acquired further away from the AIF slice based on the interleaved order of slice acquisition, due to more pronounced artifact (see Figure 6 (C, F). This was expected based on the simulations presented in Figure 3. There was no or minimal correction effect on the AIF slice. The correction algorithm eliminated the alternation in perfusion parametric image intensity among consecutive slices. The correction effect was similar for qCBF and MTT maps: total correction range of 27.3% and 26.8%, respectively. The correction method had a minimal effect on the qCBV maps with total range of correction being less than 1%.

Figure 6.

A and B are qCBF maps (in ml/100 g/min) for slices numbered 4 through 12, in a representative subject, before (SVD) and after (eSVD) applying the correction algorithm, respectively. C) Bar plot of the correction effect, measured as a percent change in mean qCBF value in each given slice due to the correction, when moving away from the slice where the AIF was selected (slice #7), based on the interleaved order of slice acquisition. D and E are MTT maps (in seconds) for slices numbered 4 through 12, for the same subject as in A and B, before (SVD) and after (eSVD) applying the correction algorithm, respectively. F) Bar plot of the correction effect, measured as a percent change in mean MTT value in each given slice due to the correction, when moving away from the AIF slice, based on the interleaved order of slice acquisition. The AIF slice is marked in red, and the slices where the correction effect is greatest are marked in green.

Table 1 shows that the differences depicted in the mean qCBF and MTT values due to the eSVD correction in all the slices, except the slice where the AIF was chosen (ATD = 0), were statistically significant. There were no statistically significant differences in the qCBV values of all slices due to the applied correction. Pearson’s correlation (r) values were greater than 0.95 in all cases.

Table 1.

Paired difference t-test comparing mean qCBF, qCBV, and MTT values obtained before (SVD) and after (eSVD) the AIF resampling correction in brain slices acquired at different fractional time delays (ATD) from the AIF slice.

ATD	−2*TR/13	−TR/13	0	TR/13	2*TR/13	3*TR/13	4*TR/13	5*TR/13
qCBF	3.6×10−6	1.9×10−5	0.38	1.9×10−5	6.6×10−7	1.7×10−7	1.5×10−5	0.01
qCBV	0.88	0.89	0.33	0.16	0.08	0.06	0.09	0.14
MTT	5.3×10−6	1.9×10−7	~1	9.9×10−8	3.1×10−8	9.0×10−8	3.7×10−6	0.01

Physiological ATD and Dispersion Correction

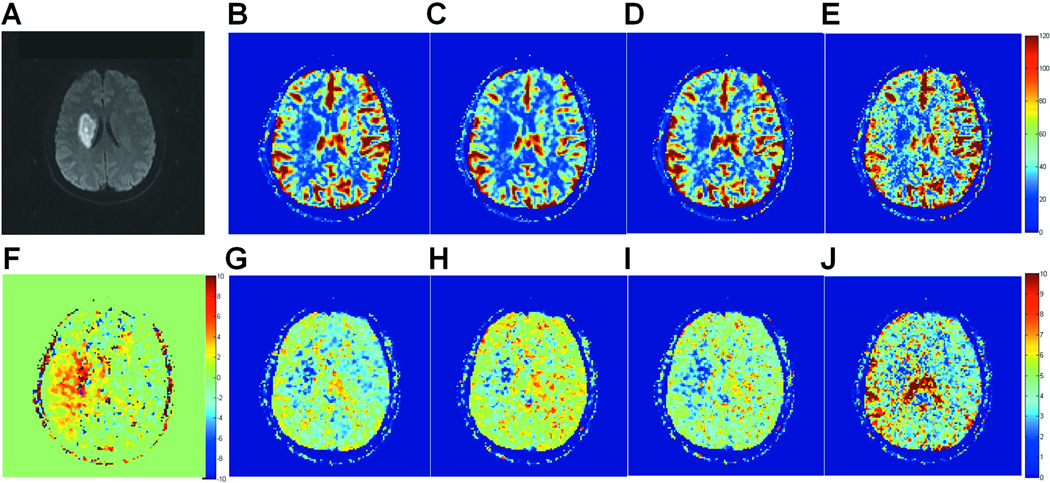
Figure 7 compares qCBF and MTT maps obtained with the different SVD deconvolution methods in a representative brain slice of the second patient included in this study. As expected from the simulations in Figure 4, qCBF values within and around the infarcted region (Figure 7A) increased with the bSVD method, as compared to existing methods of deconvolution (SVD, rSVD, and cSVD). Overall, the contrast in the MTT maps improved due to the bSVD correction, when compared to SVD, rSVD and cSVD, individually. The high MTT region in Figure 7J overlaps with the region on the side of the infarct that is suffering from major delays, prolonged MTTs and reduced blood flow, but not yet infarcted. The infarct core itself appears to have extremely low (blue) MTT values due to the absence of blood supply, based on the central volume theorem (29).

Figure 7.

A is a diffusion-weighted image of a representative brain slice showing a well-defined infarct area. B, C, D, and E are qCBF maps (in ml/100 g/min) of the same slice obtained with standard SVD, rSVD, cSVD, and bSVD, respectively. F is a ΔBAT map (in s), and G, H, I, and J are MTT maps (in s) of the same slice obtained with standard SVD, rSVD, cSVD, and bSVD, respectively.

For the quantitative analysis, mean qCBF values, measured in ROIs drawn around the infarcts and their corresponding, contralateral normal sides, computed with SVD, cSVD, rSVD, and bSVD, are presented in Table 2, for two representative patients with ischemic stroke. Table 3 presents mean MTT values for the same patients and ROIs, as computed with the 4 different methods. Patient 1 was characterized by positive ATD only, while patient 2 had both positive and negative ATD regions, with positive ATD dominance. SVD, cSVD and rSVD all resulted in underestimation of qCBF compared to the bSVD corrected values, for all the ROIs of Patient 1, and most of the ROIs of Patient 2. This was accompanied by overestimation of the MTT values in the respective ROIs. Note that qCBF underestimation of at least 15% resulted in overestimation of MTT for Patient 1, who suffered mainly from positive delay. In the case of Patient 2, the combination of positive and negative delay corrections demonstrated some cases of overestimation of qCBF and underestimation of MTT, which resulted from the correction of the dominant negative delay in some ROIs.

Table 2.

Mean and standard deviation of qCBF values (in ml/100 g/min) with standard SVD, cSVD, rSVD, and bSVD, in infarct and contralateral normal ROIs, for two of the patients under study.

Patient 1
ROI	ROI Type	Tissue Type	SVD	cSVD	rSVD	bSVD
1	Infarct	GM + BVa	50.2 ± 26.6	44.3 ± 19.9	37.2 ± 16.5	63.9 ± 37.7
1	Contrab	GM + BV	93.9 ± 32.2	70.6 ± 22.6	59.7 ± 18.7	130.4 ± 50.5
2	Infarct	GM + BV	27.0 ± 17.7	30.1 ± 20.2	26.2 ± 16.2	37.0 ± 25.1
2	Contra	GM + BV	49.7 ± 36.6	47.5 ± 27.0	38.9 ± 22.9	74.2 ± 59.6
3	Infarct	GM + WM + BV	15.9 ± 18.6	17.9 ± 20.0	15.7 ± 17.4	18.2 ± 19.2
3	Contra	GM + WM + BV	46.6 ± 30.7	41.9 ± 23.3	34.6 ± 19.8	53.7 ± 39.8
Patient 2
ROI	ROI Type	Tissue Type	SVD	cSVD	rSVD	bSVD
1	Infarct	Mid-Vent WM 1c	31.5 ± 10.6	35.3 ± 13.9	31.0 ± 10.6	37.5 ± 16.9
1	Contra	Mid-Vent WM 1	65.9 ± 27.4	47.4 ± 19.9	38.0 ± 13.1	60.1 ± 27.4
2	Infarct	Mid-Vent WM 2d	18.7 ± 8.9	19.8 ± 10.5	16.8 ± 7.4	24.1 ± 14.0
2	Contra	Mid-Vent WM 2	47.6 ± 18.9	41.4 ± 19.2	35.9 ± 12.1	51.4 ± 22.6
3	Infarct	Top-Vent WM e	32.4 ± 22.1	34.9 ± 26.6	29.2 ± 19.4	33.5 ± 18.0
3	Contra	Top-Vent WM	38.3 ± 12.9	33.8 ± 12.4	29.4 ± 8.6	41.0 ± 16.4

^aCortical blood vessels

^bContralateral to infarct

^cFirst white matter ROI at the mid-ventricular level

^dSecond white matter ROI at the mid-ventricular level

^eWhite matter ROI above the ventricle

Table 3.

Mean and standard deviation of MTT values (in sec) with standard SVD, cSVD, rSVD, and bSVD, in infarct and contralateral normal ROIs, for two of the patients under study.

Patient 1
ROI	ROI Type	Tissue Type	SVD	cSVD	rSVD	bSVD
1	Infarct	GM + BV	4.2 ± 1.2	4.6 ± 1.1	5.4 ± 1.0	3.7 ± 1.4
1	Contra	GM + BV	2.9 ± 0.3	3.9 ± 0.6	4.5 ± 0.5	2.3 ± 0.4
2	Infarct	GM + BV	5.4 ± 1.0	4.9 ± 1.0	5.5 ± 0.8	4.7 ± 1.4
2	Contra	GM + BV	3.9 ± 0.7	3.8 ± 0.6	4.6 ± 0.5	2.9 ± 0.8
3	Infarct	GM + WM + BV	5.5 ± 1.1	4.8 ± 1.1	5.5 ± 1.2	5.6 ± 1.9
3	Contra	GM + WM + BV	3.8 ± 0.8	4.0 ± 0.8	4.8 ± 0.6	3.6 ± 0.9
Patient 2
ROI	ROI Type	Tissue Type	SVD	cSVD	rSVD	bSVD
1	Infarct	Mid-Vent WM 1	4.9 ± 1.3	4.5 ± 1.3	4.9 ± 1.2	5.5 ± 2.2
1	Contra	Mid-Vent WM 1	3.5 ± 0.9	4.9 ± 1.3	5.8 ± 1.1	4.3 ± 1.6
2	Infarct	Mid-Vent WM 2	3.3 ± 1.4	3.3 ± 1.6	3.7 ± 1.6	4.2 ± 2.4
2	Contra	Mid-Vent WM 2	3.9 ± 0.9	4.7 ± 1.4	5.1 ± 1.2	3.8 ± 1.6
3	Infarct	Top-Vent WM	3.8 ± 1.3	3.6 ± 1.2	4.1 ± 1.4	6.5 ± 3.6
3	Contra	Top-Vent WM	4.2 ± 1.0	4.9 ± 1.5	5.4 ± 1.4	4.2 ± 1.7

A paired difference t-test performed over a total of 28 ROIs obtained from the 3 patients under study showed no significant difference between qCBV values obtained before (SVD) and after (bSVD) applying the delay-dispersion correction.

MR-PET Validation

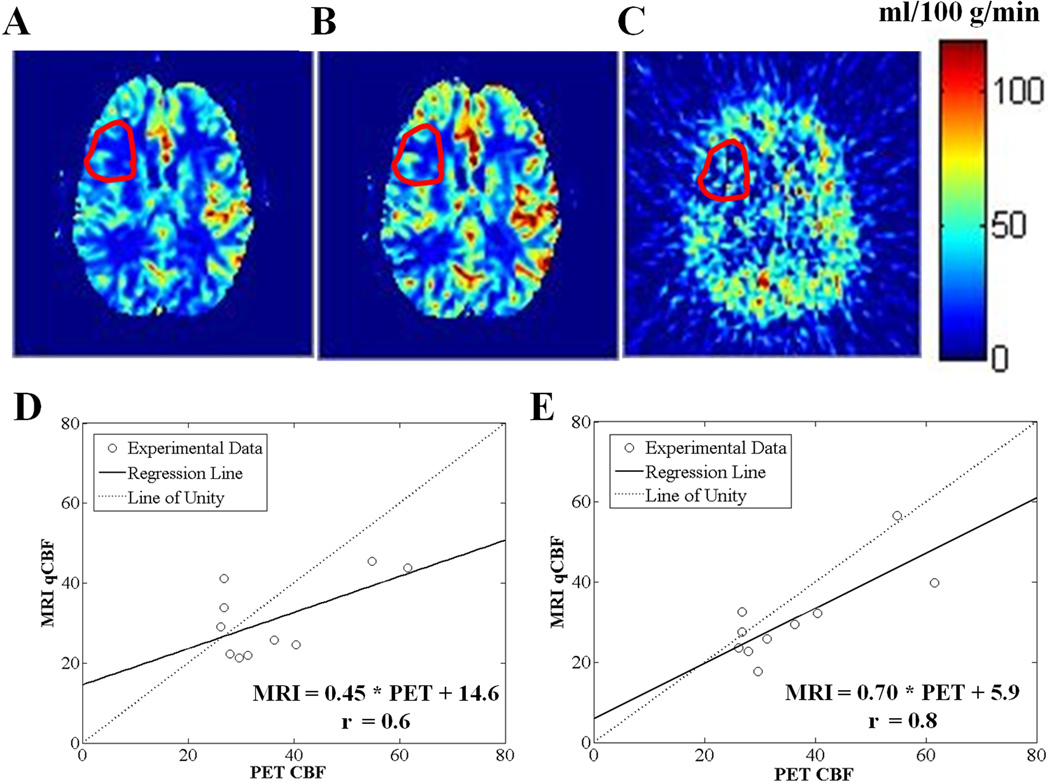
The MR-PET qCBF correlations in ROIs with well-defined delays improved due to the correction (Figure 8). Before correction (SVD): slope = 0.45, r = 0.60, and intercept =14.6, and after correction (bSVD): slope = 0.70, r = 0.79, and intercept = 5.9. The measured MR qCBV values were not significantly affected by the correction for all ROIs.

Figure 8.

A and B are MR qCBF maps before (SVD) and after (bSVD) applying the delay-dispersion correction, respectively, and C is the corresponding PET CBF map, for a representative patient with cerebrovascular occlusive disease. Mean CBF values in the ROIs with delayed arrival (shown in red) are: 21.9 ± 9.2, 25.8 ± 13.8, and 30.7 ± 17.8 ml/100 g/min, for A, B, and C, respectively. D and E are MR-PET correlation plots for the patients’ ROIs at 3.0T, before (SVD) and after (bSVD) applying the delay-dispersion correction, respectively: the regression line (solid line) and the line of unity (dotted line) are shown.

DISCUSSION

We have developed a comprehensive method using SVD deconvolution for the correction of experimental and physiological ATD effects on the quantification of cerebral perfusion measurements.

Experimental AIF Re-sampling Correction

We found that the proposed correction method (eSVD) for eliminating the experimental ATD artifact had a significant effect on the computed qCBF and MTT map (Table 1). The size of the error measured in vivo (Figure 6) was consistent with the expectations from the computer simulations (up to 35%) in Figure 3. Although rSVD and cSVD appeared to follow the same correction trend (Figure 3), its perfusion estimates remained influenced by other artifacts that are larger for smaller MTT (< 12 s) (5). eSVD minimized the MTT dependence (Figure 3), and eliminated the intrinsic SVD artifact with short MTT.

Although the same AIF signal was used to compute CBV (15), the absence of correction effect on the qCBV maps confirmed that the artifact under question was inherent to the SVD deconvolution used to compute the qCBF maps. MTT was computed as the ratio of CBV to CBF following the central volume theorem (29). This explains the consistency in the correction effects observed in the MTT and qCBF maps in the representative subject (see Figure 6). In all of the cases studied, the size of the error measured depended on the AIF slice location, and extended up to 30%, which agreed with the simulations. In fact, physicians rely to a great extent on the qCBF and MTT values for an accurate diagnosis. A 30% error can overlap with the amount of possible deviation due to diseases and pathologies, and may be greatly misleading in a clinical setting. Therefore, the eSVD correction reduces the bias in patient diagnosis.

Fitting the AIF C-T curve prior to applying the correction provided the additional advantage of smoothing the AIF. This made the deconvolution operation, which is very sensitive to noise, more successful. However, any failure in fitting the AIF would invoke a bias in the quantification of MTT and CBF. Therefore, it is important to use a robust fitting algorithm.

Physiological ATD and Dispersion Correction

We found that the proposed correction (bSVD), which combines both the experimental and physiological ATD and dispersion effects, had a significant effect on the computed qCBF and MTT maps as compared to standard SVD, cSVD, and rSVD methods (p < 0.05). Similarly to wSVD, the effect was not as significant on the qCBV maps, since the correction was inherent to the SVD deconvolution used to compute the CBF maps in the DSC phase of the quantitative perfusion method.

The results of the simulations presented in Figures 4 and 5 were expected since the existing standard SVD, rSVD, and cSVD techniques did not account or correct for dispersion, but merely for the ATD itself.

Figure 5.

The ratio of CBF/True CBF is compared for SVD, rSVD, cSVD, and bSVD methods, for a range of representative β values with ATD = 5 s at different MTT values: A and D correspond to MTT = 6 s, B and E correspond to MTT = 12 s, and C and F correspond to MTT = 24 s, for SNR = 5 and 20, respectively. TR = 1 s and N = 13 were assumed, and P_SVD = 0.2 was applied for all SVD methods. bSVD outperformed rSVD and cSVD for all MTT and β values.

In general, the correction fixed an underestimation of cerebral perfusion values in regions with positive delay, as it was expected from the simulations and previous literature (2,3,5,7,8,10,18). The correction was observed in both severely ischemic (or infarcted) and contralateral, normal ROIs. This confirms that delay and dispersion effects affect the accuracy of quantitative perfusion measurements in all regions suffering from ATD, not only diseased or hypoperfused ones. This is shown in the simulations (Figures 4 and 5), which suggest that all existing SVD deconvolution techniques for DSC analysis are in need of correction to mitigate up to a 60% inaccuracy in the computed CBF values due to delay and dispersion effects. This effect is substantial over the entire range of physiologically relevant ATD and dispersion amounts, which increases the cohort of subjects who can benefit from this technique.

The bSVD method can be applied in all DSC-MRI perfusion methods to correct for the effects of delay and dispersion in the relative cerebral perfusion measurements. However, the SCALE-PWI sequence used in this study to acquire the perfusion scans offers the advantage of absolute quantification of cerebral perfusion measurements, based on the Bookend technique. Identifying ischemic, yet salvageable, tissue would be more accurate if this technique were implemented along with the SCALE-PWI sequence in a clinical setting. Furthermore, quantifying perfusion changes between original and follow-up examinations can be made more accurate with the proposed correction (4).

Physiological ATD can essentially be characterized following the same time scale as the experimental ATD, i.e. integer multiples of fractions of TR. This would require voxel-by-voxel least-squares fitting of the C-T curve in order to compute the BATs of individual voxels more accurately (7). Since voxel-by-voxel fitting is a time-consuming procedure, we limited the determination of BAT values for individual voxels to increments of TR.

We have demonstrated the reproducibility of our perfusion measures obtained with the Bookend technique in a previous test-retest reliability study in 8 healthy subjects (ICC/COV = 0.90/0.09) and 25 patients (ICC/COV = 0.81/0.14)(17). We expect a similar reproducibility for the perfusion measures obtained with the delay and dispersion correction being applied, since the same fully-automatic perfusion post-processing code was used and the suggested model has been shown robust and insensitive to noise. A comprehensive reproducibility study shall be performed in the future to confirm our expectations.

The improvement in MR-PET correlational slope (0.45 to 0.7) and coefficient (0.4 to 0.8) due to the bSVD correction in regions with well-defined ATDs was manifested as a reduction in the spread of the overall brain perfusion value prior to correction (Figure 8). A perfect agreement was not expected (post-correction slope = 0.7) due to major differences in the nature of the PET and MR measurements. While perfusion DSC-MRI measurements rely mainly on the presence of an intact blood brain barrier and magnetic field inhomogeneity effects, PET perfusion measurements assume diffusible tracer kinetic models for the diffusable radiolabled water.

This work is not without limitations. The first group of patients was scanned with SCALE-PWI at 1.5T, while the PET validation was provided through a 3.0T study with the conventional Bookend protocol. We understand this could act as a confounding factor with regard to the results of this analysis. Future work shall involve the direct validation of the SCALE-PWI sequence measurements with gold standard PET at both magnetic field strengths.

Finally, the AIF signal can still be affected by partial volume effects due to the relatively low resolution of the perfusion scan (30–32). However, this is beyond the scope of the proposed correction, and shall be studied separately in the future to further improve the accuracy of the quantitative cerebral perfusion measurements.

CONCLUSION

In this study, we proposed a correction algorithm that eliminated an artifact due to the slice acquisition scheme, as well as errors in the perfusion measurements due to the delay of arrival of the contrast bolus to different regions in the brain, in DSC-MRI perfusion imaging. The efficiency of the algorithm was demonstrated in healthy subjects and patients scanned with the SCALE-PWI pulse sequence and conventional Bookend for absolute perfusion quantification, at 1.5 and 3.0T. No other work has reported on the correction of delay and dispersion effects in absolute quantitative DSC-based cerebral perfusion measurements using the Bookend technique. This correction is not only needed for SCALE-PWI perfusion images, but for all DSC images when postprocessed using SVD, and will greatly reduce the bias in patient diagnosis due to the existing errors and artifacts.