Characterization of a hyper-viscoelastic phantom mimicking biological soft tissue using an abdominal pneumatic driver with Magnetic Resonance Elastography (MRE)

Abstract

The purpose of this study was to create a polymer phantom mimicking the mechanical properties of soft tissues using experimental tests and rheological models.

Multifrequency Magnetic Resonance Elastography (MMRE) tests were performed on the present phantom with a pneumatic driver to characterize the viscoelastic (μ, η) properties using Voigt, Maxwell, Zener and Springpot models. To optimize the MMRE protocol, the driver behavior was analyzed with a vibrometer. Moreover, the hyperelastic properties of the phantom were determined using compressive tests and Mooney-Rivlin model.

The range of frequency to be used with the round driver was found between 60 Hz and 100 Hz as it exhibits one type of vibration mode for the membrane. MRE analysis revealed an increase in the shear modulus with frequency reflecting the viscoelastic properties of the phantom showing similar characteristic of soft tissues. Rheological results demonstrated that Springpot model better revealed the viscoelastic properties (μ = 3.45 kPa, η = 6.17 Pa.s) of the phantom and the Mooney-Rivlin coefficients were C10 = 1.09.10-2 MPa and C01 = −8.96.10-3 MPa corresponding to μ = 3.95 kPa.

These studies suggest that the phantom, mimicking soft tissue, could be used for preliminary MRE tests to identify the optimal parameters necessary for in vivo investigations. Further developments of the phantom may allow clinicians to more accurately mimic healthy and pathological soft tissues using MRE.

I. INTRODUCTION

Non-invasive imaging technologies such as ultrasound-based and Magnetic Resonance-based Elastography techniques have been developed, since a decade, to characterize the mechanical properties of soft tissues (liver, muscle, and breast) and are increasingly used in clinical practice for diagnostic purposes. In parallel to imaging methods, emergence of simulating tools has required improved knowledge of the mechanical properties of soft tissues (Nava et al., 2008; Marchesseau et al., 2010). The development of these technologies will be enhanced by the creation of phantoms that realistically simulate the mechanical properties of soft tissues. Thus, the originality of the present study was to develop a phantom with mechanical properties that adequately reflect those of biological soft tissue.

In the literature, various phantoms have been reported, consisting of media such as wirosil, agar, or bovine gels, in order to cross validate the magnetic resonance elastography (MRE) technique with ultrasound technique (Oudry et al., 2009a), dynamic mechanical analysis (Ringleb et al., 2005; Chen et al., 2005) and compression tests (Hamhaber et al., 2003). The feasibility of the MRE technique to depict tumors was estimated with the use of inclusions added to the phantom media to mimic tumors (Mariappan et al., 2009a). Moreover, MRE experimental parameters such as frequency, geometry, and boundary conditions (Chen et al., 2006), as well as specific MRE sequences to image dynamic organ (heart) (Kolipaka et al., 2009), were previously tested on phantoms to achieve in vivo MRE tests. The mechanical properties of biological tissues were further characterized with soft tissue models using in vivo and in vitro experiments. Liver behavior was characterized with numerical model reflected by a porous, visco-hyperelastic model using in vitro dynamic mechanical analysis (Marchesseau et al., 2010). In vivo aspiration experiments have also been modeled (Nava et al., 2008) using quasi-linear viscoelastic and non-linear elastic-viscoplastic models (Mazza et al., 2008) to determine the mechanical properties of the liver. In addition, constitutive modelling of brain tissue was done with mathematical (Miller and Chinzei, 1997) and numerical (Miller, 2000) models to simulate neurosurgical procedures. The viscoelastic parameter was further analyzed using multifrequency MRE technique and rheological models. Thus, standard rheological models such as Maxwell, Voigt, Zener, Jeffreys and Springpot models were applied to liver (Klatt et al., 2007; Asbach et al., 2008, 2010), muscle (Klatt et al., 2010) and brain (Klatt et al., 2007) tissues, allowing for a better assessment of disease. In addition to MRE, supersonic shear imaging was also performed to measure the viscoelastic properties of muscle (Gennisson et al., 2010) and liver (Muller et al., 2009) tissue using Voigt's model.

The purpose of this present study was to create a new generation of phantom mimicking the mechanical properties of biological soft tissue using specific multifrequency magnetic resonance elastography (MMRE) and compressive tests.

II. MATERIALS AND METHODS

2.1 Phantom preparation

Two homogeneous cylindrical phantoms of different sizes (Diameter: 25 cm with a thickness of 5 cm and diameter: 2.6 cm with a height of 3.8 cm) were created with an elasticity similar to that of muscle tissue (Bensamoun et al., 2006). The cylindrical phantoms analyzed in the present study were composed of 45% softener and 55% liquid plastic (LureCraft, LaGrande, USA), or plastisol, which is a suspension of PVC particles in a plasticizer. The mixture was heated to 177°C, poured into cylindrical silicone molds and left to cool at room temperature (23°C) until the phantoms solidified. The reproducibility of the phantom process induced a variability of the elastic properties (μ) about 10%. Then, the phantoms were stocked and preserved at room temperature (23°C).

2.2 Abdominal driver behavior

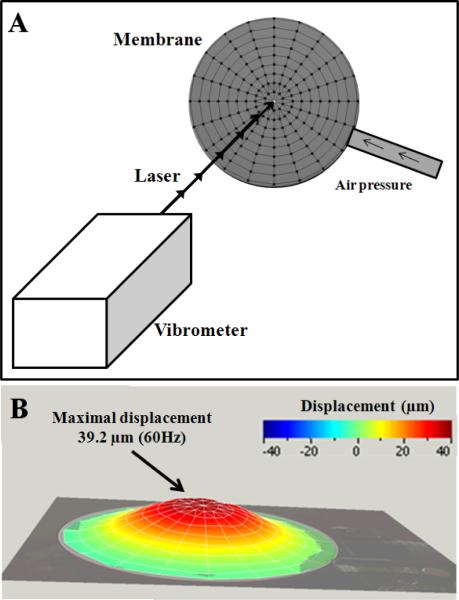
A laser doppler vibrometer (PSV 400, Polytec, France) was used to determine the accurate displacement of the membrane induced by the round driver at 60 Hz. Figure 1a shows the fixation of the driver placed to a distance of 74.3 cm from the vibrometer. Tests were performed from 0 Hz to 300 Hz to observe the magnitude of the membrane's deformation. A laser scaled the entire membrane with an angular resolution of approximately 0.002°, providing a mesh of the membrane composed of 171 nodes (Fig. 1a). The maximal displacement of membrane (D) was recorded for a frequency range of 60 Hz to 100 Hz, representing values typically applied to biological soft tissue (liver, muscle) using MRE.

Fig. 1.

Characterization of the membrane deformation, from 0 to 300 Hz, with a laser doppler vibrometer. Mesh of the membrane composed of 171 nodes where each displacement was acquired (A). Visualization of the entire shape of the membrane at 60Hz where the maximal displacement (39.2μm) was measured (B).

2.3 Multifrequency Magnetic Resonance Elastography (MMRE) tests

MMRE experiments were performed on the larger phantom inside a 1.5T (General Electric Signa HDx) MRI machine. The phantom was placed inside a head coil (Fig. 2a), resting on a round pneumatic driver, connected to a large active loudspeaker. The driver generates shear waves through the phantom at three frequencies (60 Hz, 70 Hz, 80 Hz), representing values typically applied to biological soft tissue (liver, muscle) using MRE. This driver is currently used for studying the liver (Yin et al., 2007), and consists of a thin flexible membrane (10–20 μm) made of polycarbonate enclosed by rigid walls, with a resonance frequency of 30 Hz. To avoid extraneous motion of the phantom during the MRE test, a support cushion was placed under the phantom.

Fig. 2.

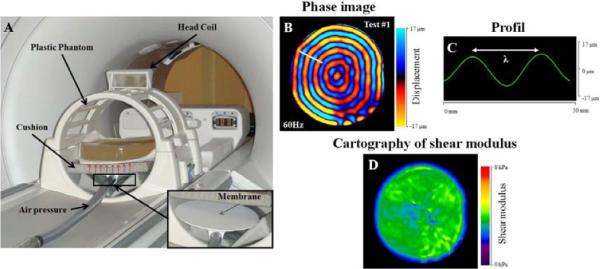
Experimental setup for Magnetic Resonance Elastography (MRE) tests performed at 60 Hz on the phantom (A). Acquisition of the phase image (B), placement of the profile (C) and elastograms (D) obtained with LFE algorithm.

MRE phase images (Fig. 2b) were collected using a motion sensitizing gradient echo sequence, a flip angle of 45°, a 30 × 30 cm field of view and a 256 × 64 acquisition matrix. Phase images composed of four offsets were recorded for each different frequency, with a TE corresponding to the minimum echo time allowing for motion encoding, and a TR equal to 50 ms, 43 ms and 38 ms at 60 Hz, 70 Hz and 80 Hz, respectively. Multifrequency MR Elastography tests allow for the characterization of the elastic properties of the phantom for each frequency. Moreover, the variation of the wavelengths as a function of the frequency will allow an analysis of the viscoelastic behavior. Thus, elastic properties were characterized, assuming that the media was linear elastic, isotropic and homogeneous, leading to the shear modulus (μ) using the following equation: μ = ρ (fλ)², where ρ is the density of the phantom (1000 kg/m³), f is the frequency (Hz) and λ is the shear wavelength (m). The wavelengths (Fig. 2c) were measured from the phase images (Fig. 2b) with a 1D profile drawn along the radial direction of the propagation of the shear wave and located in the same area for each phase image. Then, the shear modulus was calculated for each frequency. From the phase images, the corresponding cartography of the shear modulus (Fig. 2d) was generated using the local frequency estimate (LFE) algorithm (Manduca et al., 2001), providing a spatial distribution of the elastic properties.

The larger phantom underwent the first MRE test (test #1) one month after its development, and a follow up of the phantom behavior was done every month with reproducibility tests. Tests #2 and #3 corresponding to MRE tests performed at 5 and 11 months will be presented.

2.4 Viscoelastic modelling

The viscoelastic behavior being represented by an elastic (shear modulus: μ) and a viscous (the viscosity: η) components, four different rheological models (Voigt, Maxwell, Zener and Springpot) were used. These models are composed of springs and dashpots (Klatt et al., 2007), reflecting a complex shear modulus (G*, kPa) related to shear stiffness (μ, kPa), viscosity (η, Pa.s), and excitation pulsation (ω, Hz). To quantify the rheological coefficients (μ, η), an identification method was performed using a mean squared analysis with Matlab R2008b software (The Matworks, Inc., Natick, MA), based on a cost function composed of experimental velocities from the multifrequency MRE tests and theoretical velocities from Helmholtz equation (Bourbie et al., 1986) applied to rheological models.

2.5 Mechanical tests

Compression tests were performed on the smaller cylindrical phantom with a texture analyzer machine (Fig. 3a) (XT Plus, Stable Micro Systems, England). The samples were placed between a load cell and a heavy duty platform while a compressive force until 3 N was applied with a velocity of 0.5 mm/s. Then, the displacement (mm) as a function of the force (N) was recorded and normalized by the sample surface in order to obtain the representative stress-strain curve of the behavior of the phantom (Fig. 3b). The mechanical test was repeated twice on the sample.

Fig. 3.

Compression test performed on the phantom with a texture analyzer (A) with the non-linear stress-strain recorded curve (B).

2.6 Hyperelastic characterization

As expected by the composition of the phantom, a non-linear curve reflecting the phantom behavior was obtained. The stress-strain curve was computed with ABAQUS 6–9.1 Standard (Simulia Dassault Systems) in order to further characterize the non-linear properties of the phantom. As it is well known that non-linear behavior is represented by a hyperelastic model, the Mooney-Rivlin model was used, assuming that the material was isotropic and incompressible. This model is based on the strain energy function with a polynomial development of first order. In case of uniaxial compression, the relationship between engineering stress and strain is defined by the following equation (Miller and Chinzei, 1997):

$$\sigma =2\cdot \left({\lambda }^2-\frac{1}{\lambda }\right)\cdot \left(C_{10}+\frac{C_{01}}{\lambda }\right)\text{with}\lambda =\frac{L}{L_0}$$

where σ is the engineering stress (MPa), λ is the deformation, L is the length of phantom during the mechanical test (mm) and L₀ the initial length of sample (3.8 cm). The coefficients C₁₀ and C₀₁ are the Mooney-Rivlin's parameters (MPa). In addition, the shear stiffness (μ, MPa) was also calculated using the following equation (Miller and Chinzei, 1997):

$$\mu =2\cdot (C_{10}+C_{01})$$

III. RESULTS

3.1 Characterization of the elastic properties using MMRE tests

Phase images obtained as a function of time (1, 5 and 11 months) and frequency (60 Hz, 70 Hz and 80 Hz) represent the propagation of shear waves inside the larger phantom. A more uniform shape of the wave was observed at 60 Hz (Fig. 4a, d and g) as compared to 80 Hz (Fig. 4c, f, and i), where gaps begin to occur. This result reveals that 60 Hz is the optimal frequency to use for the characterization of the elastic properties of the present phantom. Moreover, it can be noted that the phantom exhibited a range of shear modulus between 3.3 and 4.3 kPa, whatever the frequency and the time are.

Fig. 4.

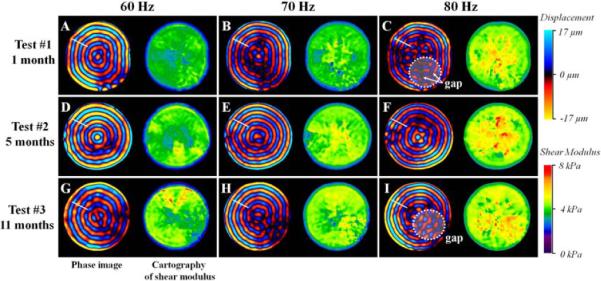
Representation of the phase images and the corresponding cartography of shear modulus obtained through MRE tests performed at 1 (test #1), 5 (test #2) and 11 (test #3) months at three different frequencies 60 Hz, 70 Hz and 80 Hz.

Test #1 showed a quasi-elastic behavior of the phantom, reflected by a homogeneous spatial distribution of stiffness (Fig. 4a) and by a slight increase of the shear modulus (0.10 kPa) as a function of the frequency. However, test #2 and #3 revealed a higher increase in the shear modulus measured from 60 Hz to 80 Hz (Δμ__test2 = 0.18 kPa, Δμ__test3 = 0.19 kPa), indicating an increase of the viscoelastic behavior with time. In addition, for each frequency, the cartographies of stiffness showed a slight stiffening of the phantom media from 1 to 11 months, reflected by an increase in the elastic properties of Δμ__60Hz = 0.82 kPa, Δμ__70Hz = 0.80 kPa, Δμ__80Hz = 0.91 kPa. The reproducibility tests showed a variation of the shear modulus measurement about 1.7%.

3.2 Characterization of abdominal driver behavior

Figure 5 shows the eigenfrequencies of the membrane characterized from 0 Hz to 300 Hz, where the resonant frequency of the loudspeaker was observed to be around 30 Hz. Between 60 Hz and 100 Hz, the flexible membrane exhibited only one type of vibration mode, represented by a unique antinode. After 100 Hz, the deformation of the membrane contained different shapes composed of another eigenmode, representing a non-uniform deformation of the membrane. For instance, at 110 Hz, two distinct antinodes were identified indicating that different areas of the membrane are vibrated at this frequency. Thus, the range of frequencies to be used with this round driver is between 60 Hz and 100 Hz.

Fig. 5.

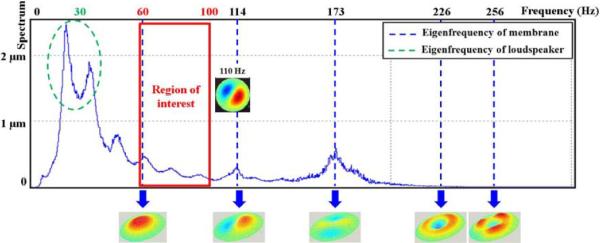
Illustration of the entire membrane displacement obtained with a laser doppler vibrometer from 0 to 300 Hz associated to the frequency response spectrum. The round pneumatic driver showed the same vibration mode for the membrane only between 60 Hz and 100 Hz.

The results showed a higher magnitude of displacement for 60 Hz and 80 Hz (D_60Hz = 39.2 μm, D_80Hz = 40.2 μm) compared to 70 Hz (D_70Hz = 31.5 μm), 90 Hz (D_90Hz = 31.0 μm) and 100 Hz (D_100Hz = 25.9 μm).

3.3 Characterization of the viscoelastic and hyperelastic properties

Table 1 shows the rheological parameters (shear modulus: μ and viscosity: η) at 1, 5 and 11 months obtained using the four models. The comparison of the elastic properties obtained with MMRE and rheological models showed similar values of the shear modulus as a function of time. The viscoelastic parameters for test #1 revealed lower viscosities (from 1.18 to 6.17 Pa.s) for the solid models (Voigt, Zener and Springpot) compared to the fluid model (Maxwell) which showed a higher viscosity (18.09 Pa.s) due to its property to reflect the viscous component. This result attested that the identification method is capable of differentiating solid and fluid behaviors. All models demonstrated a slight increase of the viscoelastic parameters over time. It can be noted that the Springpot model revealed the highest increase in the viscoelastic parameters compared to the other models. Hyperelastic properties were determined from the nonlinear stress-strain curves (Fig. 3b) that were obtained with the compressive tests, allowing for the measurement of the Mooney-Rivlin coefficients (C₁₀ = 1.09.10⁻² MPa and C₀₁ = −8.96.10⁻³ MPa). The corresponding shear stiffness was 3.95 kPa, which is in the same range as the previous elastic properties obtained with the multifrequency MRE tests.

Table 1.

Shear modulus (μ) obtained with the multifrequency MRE tests as well as rheological models allowing also for the characterization of the viscosity (η) with its proportional coefficient (α) for the phantom.

	Elastic case	Voigt	Maxwell	Zener	Springpot
Test #1 1 month	μ60Hz = 3.34 kPa	μ = 3.24 kPa η = 1.84 Pa.s	μ = 4.48 kPa η = 18.09 Pa.s	μ1 = 3.23 kPa	μ = 3.45 kPa
	μ70Hz = 3.41 kPa			μ2=2.44 kPa	α = 0.088
	μ80Hz = 3.44 kPa			η = 1.18 Pa.s	η = 6.17 Pa.s
Test #2 5months	μ60Hz = 4.09 kPa	μ = 3.85 kPa η = 2.84 Pa.s	μ = 4.48 KPa η = 17.79 Pa.s	μ1 = 3.82 kPa	μ = 3.97 kPa
	μ70Hz = 4.14 kPa			μ2 = 3.38 kPa	α = 0.138
	μ80Hz = 4.27 kPa			η = 1.97 Pa.s	η = 11.57 Pa.s
Test #3 11 months	μ60Hz = 4.16 kPa	μ = 3.89 kPa η= 4.62 Pa.s	η = 4.62 kPa η = 17.02 Pa.s	μ1 = 3.88 kPa	μ = 4.17 kPa
	μ70Hz = 4.21 kPa			μ2 = 9.98 kPa	α = 0.156
	μ80Hz = 4.35 kPa			η = 2.56 Pa.s	η = 9.60 Pa.s

IV. DISCUSSION

Magnetic resonance elastography (MRE) has been extensively developed to characterize the elastic properties of biological soft tissue such as liver (Rouvière et al., 2006) or muscle (Bensamoun et al., 2008). Thus, the purpose of this study was to demonstrate that the present phantom could be used for future MRE tests to mimic the mechanical properties of healthy human soft tissue. In the literature, different types of phantoms (wirosil, agar, bovine gel) were also developed to validate the MRE technique before performing in vivo tests. Indeed, elastic properties of agarose gel were characterized with MRE, in a range of 4 kPa to 130 kPa for different concentrations and excitation frequencies (from 100 to 400 Hz) (Ringleb et al., 2005, Chen et al., 2005, and Hamhaber et al., 2003). Another kind of phantom in a range of 1 kPa to 8 kPa, composed of copolymer-in-oil and B-gel, was analyzed with MRE tests using the same mechanical frequency (60 Hz) as the present study (Oudry et al., 2009a).

Elastic properties of healthy skeletal muscle at rest are represented by a shear modulus in a range of 2–4 kPa (Bensamoun et al., 2006), which is similar to the present phantom behavior. In the literature, the viscoelastic properties of skeletal muscle and liver tissues were quantified with Voigt and Zener's models (Klatt et al., 2007; Gennisson et al., 2010) and the use of these models to the present phantom demonstrated a quasi-constant viscosity (maximum of increase about 1 Pa.s at 5 months and 2 Pa.s at 11 months) as a function of time. To our knowledge, the present phantom is the first one to reflect both the elastic and viscoelastic properties of healthy biological tissue when testing with the MRE technique. Moreover, this new generation of phantom has the advantage to keep approximately the same viscoelastic properties over time unlike organic phantoms (agarose or bovine gel) which are unstable (Oudry et al., 2009b).

To better characterize the viscoelastic behavior of the phantom, a fractionary solid model (Springpot) was used, composed of a third parameter (coefficient α) allowing acquisition of information about the viscous component of the model. Indeed, when α tends to 1, the model is purely viscous represented by only one dashpot, and when α tends to 0, the model becomes purely solid represented by only one spring. The Springpot model demonstrated the highest increase in viscosity, which was also observed through MRE tests. Therefore, it was concluded that this model is the most adapted rheological model to quantify the viscoelastic properties of the phantom. Furthermore, the viscosity obtained in this present study at one month (6.17 Pa.s) was in agreement with the viscosity fixed for the liver tissue (7.30 Pa.s) by Asbach et al. (2010), as well as the viscosities fixed for quadriceps muscles (1–10 Pa.s) by Klatt et al. (2010) using MRE. In addition to the viscoelastic parameter, the elastic properties measured with the same Springpot model at one month (3.45 kPa) was similar to the one measured using MRE (μ_60Hz = 3.34 kPa, μ_80Hz = 3.44 kPa). The Springpot model seems to be more adapted to representing the mechanical properties (μ, η) of the biological soft tissues, and the present study confirmed the feasibility of the phantom to reflect the elastic (μ) and viscoelastic (η) properties of soft tissues.

During the last decade, drivers were optimized with new designs such as the assemblage of mechanical drivers for heart tissue (Mariappan et al., 2009b), a pneumatic tube for muscle tissue (Bensamoun et al., 2006) or a round pneumatic driver for the liver (Yin et al., 2007). In addition to the design, drivers were also further developed to improve the quality of shear wave propagation by sending longitudinal vibrations, (Yin et al., 2008) leading to an improvement in the measurement of elastic properties measurement. However, none of the previous studies have analyzed the mechanical behavior of the used driver. The present study showed the importance of this characterization to optimize the range of frequency to apply to each driver. We demonstrated that the range of frequency to be used with the round driver was between 60 Hz and 100 Hz as it exhibits one type of vibration mode for the membrane. However, MRE tests demonstrate a better propagation at 60 Hz, explaining why in the literature in vivo stiffness of biological soft tissues was characterized at 60 Hz using MRE with the same round pneumatic driver.

Magnetic Resonance Elastography is a clinical tool already implemented in the United States and Europe for liver tissue, and many other tissues as well as organs are under investigation with this non-invasive technique. The present study demonstrated the necessity to characterize the driver properties in order to set up specific MRE test's protocols. This new phantom, mimicking the mechanical properties of biological soft tissue, could be the first step to define optimal MRE parameters before in vivo investigations. It will be of interest to further develop the phantom behavior to more accurately mimic healthy and pathological soft tissues using MRE.