BiHelix: Towards de novo Structure Prediction of an Ensemble of G-Protein Coupled Receptor Conformations

Abstract

G-Protein Coupled Receptors (GPCRs) play a critical role in cellular signal transduction pathways and are prominent therapeutic targets. Recently there has been major progress in obtaining experimental structures for a few GPCRs. Each GPCR, however, exhibits multiple conformations that play a role in their function and we have been developing methods aimed at predicting structures for all these conformations. Analysis of available structures shows that these conformations differ in relative helix tilts and rotations. The essential issue is, determining how to orient each of the 7 helices about its axis since this determines how it interacts with the other 6 helices. Considering all possible helix rotations to ensure that no important packings are overlooked, and using rotation angle increments of 30° about the helical axis would still lead to 12⁷ or 35 million possible conformations each with optimal residue positions. We show in this paper how to accomplish this. The fundamental idea is to optimize the interactions between each pair of contacting helices while ignoring the other 5 and then to estimate the energies of all 35 million combinations using these pair-wise interactions. This BiHelix approach dramatically reduces the effort to examine the complete set of conformations and correctly identifies the crystal packing for the experimental structures plus other near-native packings we believe may play an important role in activation. This approach also enables a detailed structural analysis of functionally distinct conformations using helix-helix interaction energy landscapes and should be useful for other helical transmembrane proteins as well.

1. Introduction

The G protein-coupled receptors (GPCRs) form the largest superfamily of integral membrane proteins and comprise of seven transmembrane (TM) α-helices. The GPCRs are activated by a variety of bioactive molecules, like biogenic amines, peptides, lipids, nucleotides, proteins, tastants, odorants and non-molecular sensory signals like light, touch etc, making them essential for a range of physiological processes (e.g. neurotransmission, cellular metabolism, secretion, cell growth, immune defense, and differentiation).^1,2 Besides G proteins, these receptors couple to β-arrestins for signaling.³ The receptors have also been shown to couple exclusively to β-arrestins^4-6 (in a G protein independent manner) and hence are also referred to as 7TM proteins.

It is well established that the process of GPCR activation^7-11 involves a sequence of conformational changes that enable the cell to convert extracellular signals into physiological responses and is at the heart of their pleiotropic nature as nicely reviewed recently by Kenakin and Miller.¹² GPCR activation also occurs spontaneously in the absence of any signal (called constitutive activity) due to inherent conformational flexibility of these receptors.¹³ Kenakin has provided a conceptual framework to think about these signal-induced and signal-independent conformational changes in terms of shifting energy landscapes and transforming ensemble of conformations.^14,15 Strong experimental evidence for this flexibility includes fluorescence lifetime measurements that have identified distinct ligand-induced conformational states for the β₂-Adrenergic Receptor (β2AR) along the activation pathways¹⁰, as well as the recently crystallized agonist-bound conformation of β2AR stabilized by a G protein mimicking nanobody.¹⁶ Single point mutations have also been shown to induce constitutively more-active conformations.^17,18 Thus, to fully gain structural insight into the pleiotropic function of GPCRs will require the functional characterization of their multiple conformations to highlight how different ligands or mutations modulate (stabilize and/or induce) conformations to cause their effects.^12,19-22

In the last few years there has been a rapid increase in the solution of crystal structures for many GPCRs^16,23-31 due mainly to a technological revolution in membrane protein structure determination methods.³² The topological comparison of these crystal structures and their implications for GPCR activation has been reviewed extensively^33-37. All GPCR conformations observed so far have corresponded to the inactive state of the respective receptor, except for bovine opsin²⁸ and nanobody stabilized human β2AR bound to an agonist¹⁶. Structure determination efforts are moving towards the stabilization of GPCRs in different functional conformations (e.g., bound to agonists, G proteins or β arrestins), and structural computational biology can help by mapping the energy landscape sampled by GPCRs during their life-cycle and characterizing the critical conformations along the way to link with those that are observed in experimental structures.

Homology based computational methods have had successes with soluble proteins where there may be experimental structures for a variety of similar proteins, particularly where the homology is above 30%,³⁸ although it is not clear whether such structures are sufficiently accurate for drug design, though they may be accurate enough to be helpful in virtual ligand screening (VLS) efforts^39,40, in addition to those obtained from de novo methods, which have been successful in VLS efforts as well as in correctly predicting structure-activity relationships^41,42. The homology methods do not appear to be a viable alternative (yet) for predicting multiple GPCR conformations due to the very limited conformational sampling (if any) that is done to predict structures and will require significant modifications to be able to predict multiple diverse conformations for a GPCR. Homology models may be good for obtaining structures of very closely related receptors (like dopamine D2 from dopamine D3) and that too only for the same functional form (inactive form or one of many active GPCR forms) as that of the template, but homology modeling doesn’t provide a recipe to obtain multiple low-energy conformations, which the BiHelix approach is targeting and which is essential to describe GPCR activation and function.

The conformational flexibility associated with GPCRs can, however, be targeted by structure prediction methods that sample and identify all low energy (physiologically important) conformations for a GPCR. The lipid bilayer environment of the plasma membrane forces specific boundary conditions on these structures and how they fold. In contrast to the almost immeasurable ways of sampling tertiary conformations of soluble proteins, the tertiary structure of GPCRs with seven almost-parallel TM α-helices allows one to quantify the conformational space available to these TM bundles as will be shown in the next section. Molecular events like the binding of ligands or G proteins or β arrestins to GPCRs as well as point mutations in GPCRs will cause a different sampling of this available space and stabilize different sets of conformations. Methods based mainly on molecular dynamics (MD) are ill-positioned to sample all relevant conformations due to the large dimensionality of the energy landscape and high energetic barriers to access a diverse set of conformations. MD simulations are ideal to test the stability of GPCR structures (predicted or crystal structures) in their local minima, though it takes a long time and lot of effort to establish convergence⁴³.

Knowledge-based methods have been developed to predict GPCR structures^44-46 and their ability to predict structures for GPCRs distant from the templates remains to be seen. The Membstruk^47,48 and PREDICT⁴⁹ methods tried to sample TM helix bundles as well but do very coarse sampling. The Membstruk method sampled helix rotation angles on a 5° grid but didn’t sample anyway near the complete conformational space of the BiHelix approach presented here, because when a helix underwent rotation from 0° to 360°, the other 6 helices were held at 0°. So, the conformational space sampled in Membstruk was 72 × 7 ~ 504 conformations compared to the ~35 million or ~4.5 billion conformations sampled by the BiHelix approach in this work. The PREDICT method sampled and refined structures obtained from templates/decoys generated by placing the 7 helices as 7 discs on a 2-D plane in different possible topologies. The decoys sampled a highly unrealistic helix packing space as evidenced by the fact that their most stable helix packing for dopamine D2 receptor (Fig. 3 in ref.⁴⁹) shows TM7 in the middle which is at odds with all the GPCR crystal structures observed so far (including the very closely related one for dopamine D3 receptor²⁹) all of which show TM3 in the middle.

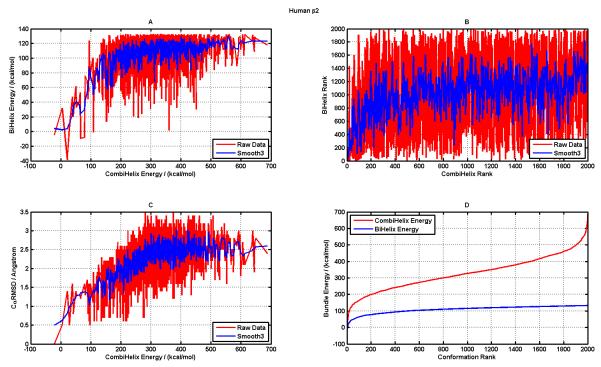
Figure 3.

A. Correlation between CombiHelix energies and BiHelix energies of the predicted helix bundle conformations, raw data (in red) and smoothed data using ±1 data points (in blue); B. Correlation between CombiHelix Rank and BiHelix Rank of the predicted conformations (colors same as in panel A); C. Correlation between CombiHelix energies and the corresponding Ca-RMSD of those conformations relative to the conformation observed in the crystal structure (PDBid: 2rh1) (colors same as in panel A); D. BiHelix (Blue) and CombiHelix (Red) energies as a function of Conformation Rank.

Monte carlo (MC) type methods have the best chance to sample the conformational space allowed to GPCRs by the lipid-bilayer of the membranes as long as they can ensure a complete sampling of this available conformational space because MC methods cannot guarantee the complete sampling of this space. If we take, as an example, the space of helix rotations in the TM bundles of GPCRs, our previous approaches to predict the structures of GPCRs indicated that one needs to sample rotations of each helix at increments no larger than 30° to identify important helical packings. Since we want to make sure that we sample all possible conformations in this space, this suggests that we should consider 12⁷ ~ 35,000,000 possible packings (using a 30° grid in the full rotational space from 0° to 360° for all seven helices). Packing such a huge number of conformations into 7-helix bundles, optimizing the side chains for each, and evaluating the energy after removing bad contacts would be an enormous undertaking. This paper introduces the BiHelix method that enables a complete sampling of this huge conformational space at a very modest computational cost. We illustrate this approach with a demonstration of the efficiency of a complete sampling of the helical rotational degree of freedom (DOF) using six of the available GPCR crystal structures. It will also be shown how this sampling can begin to identify other functionally important GPCR conformations and also enable an analysis of the functionally distinct conformations through helix-helix energy potential landscapes.

The efficiency of the BiHelix method will become even more critical when we sample helix tilts (see next section for definitions) in addition to helix rotations, which increases the available conformational space to > 10 trillion conformations. Even though this method has been demonstrated for GPCRs, it is directly applicable to helical membrane proteins in general and also has the potential to assist with some of the challenges associated with the TM helix cores that lie ahead for the prediction of membrane protein structures.⁵⁰

2. Materials and Methods

2.A Coordinate System

To characterize the conformational space available to GPCRs, we need to define a reference frame (relative to the plasma membrane) and a set of coordinates that uniquely define the orientation of each of the seven α-helices in the TM bundle. As crystal structures don’t provide absolute membrane orientation of GPCRs, we use their orientation as predicted by the OPM (Orientation of Proteins in Membrane) database,⁵¹ which aligns each newly deposited membrane protein structure to an implicit membrane. During this alignment, it optimizes the membrane width as well as tilt of the whole protein relative to the membrane middle to maximize the free energy of protein’s insertion into the membrane. The middle of the membrane corresponds to the z=0 plane and will be called the hydrophobic plane.

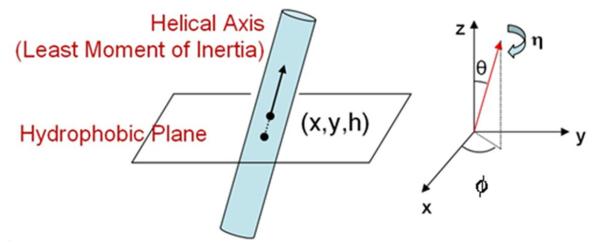
Each GPCR structure can then be characterized by the six orientation parameters of the seven α-helices relative to this plane. Figure 1 shows how the helix position and tilt are defined. Helix position (R) on the hydrophobic plane is given by x and y. The h value for a helix refers to the hydrophobic center residue of the helix and specifies the helix residue that intersects with the z=0 or hydrophobic plane described above. Two angles, θ and ϕ specify the tilt angles of the as yet undefined helical axis and the angle η corresponds to the helix rotation angle about this axis. The two tilt angles (θ,ϕ) and the rotation angle (η) require a unique definition of the helical axis which also account for the reality of bent helices caused mainly by Proline residues in the middle of TM helices. We use a helical axis that corresponds to the least moment of inertia vector for the helix, obtained by diagonalizing the moment of inertia matrix for the helix using only heavy backbone atoms.

Figure 1.

Coordinates specifying the orientation of a TM helix in a membrane.

In this coordinate system, each GPCR conformation will be represented by 42 numbers (6 orientation parameters defined above for each of the seven helices). In a GPCR structure prediction problem, two scenarios typically arise:

1. Structure for one conformation is available for a GPCR, usually in the inactive form from solving the crystal structure. This will be an ideal starting template for sampling to characterize the conformational changes possible in this GPCR as part of its function and ligand binding properties. During this sampling, it is likely that only a small subset of orientation parameters (out of 42) may need to be sampled locally around the starting template.

2. Structure is available for one conformation of a GPCR closely related to the target GPCR. That template conformation, mutated to reflect the residues in the target GPCR, becomes the starting template for sampling to characterize the potential conformational changes in the target GPCR. During this sampling, probably a larger subset of orientation parameters (compared to the previous case) may need to be sampled over a bigger range locally around the starting template.

2.B Starting TM Bundle

The BiHelix method, described in the next section, predicts the lowest energy structures in the conformational space being sampled. As mentioned in the previous section, the starting structure for sampling can be obtained either from a known conformation (e.g., from crystal structure) or from a homology structure based on a related protein structure. To demonstrate the BiHelix method, we use 6 of the available GPCR structures: bovine rhodopsin (PDB ID: 1u19)⁵², hβ2-AR (2rh1)²⁴, hA2AR (3eml)²⁵, turkey β1-AR (2vt4)²⁶, bovine opsin (3cap)²⁸, and squid rhodopsin (2z73)²⁷. The PDB structures aligned to the membrane from the OPM database⁵¹, are minimized using the Dreiding force-field (FF)⁵³ and their loop regions are removed leaving the GPCR bundles with only full length TM helices. These TM bundles serve as starting structures for the BiHelix sampling that is to be described next.

2.C BiHelix Sampling

The BiHelix sampling method deals with the optimization of the TM helix bundles and implicitly assumes that this optimization is not affected by the loops that connect the TM regions, although the effect of this assumption remains to be seen. This is a reasonable assumption as the loop regions are flexible compared to the TM regions and can potentially adapt to any TM bundle conformation that has strong TM bundle interactions. We anticipate that in the full sampling of all helix orientation angles (θ,ϕ,η) for the seven helices (conformational space ~10 trillion) loop closure condition can potentially eliminate the disallowed TM bundle packings by restricting the sampling space and make it computationally tractable.

For each of the starting templates mentioned in the previous section, we will need to determine the optimum orientation parameters (x, y, h, θ, ϕ, η) for the packing of each of the 7 helices into a 7-helix bundle. Complete sampling of these 42 parameters is neither practical nor the most efficient. The availability of many starting templates provides a good initial sampling of the x,y space. The parameter h or the hydrophobic center can be obtained from the starting template or from the estimation of the buoyant center of a TM helix from a hydrophobic profile (part of a new TM helix prediction algorithm to be covered in a forthcoming publication). So, one would need to sample helix orientation angles (θ, ϕ, η) for each of the 7 helices. The BiHelix sampling methodology will now be described and demonstrated using the helix rotation angle (η) as the DOF being sampled. The sampling method is independent of the number of DOFs being sampled.

Consider a 30° sampling of the η angle (keeping θ and φ fixed) for each of the 7 helices over full 360°, which leads to (12)⁷ ~ 35 million conformations, for each of which the side chains must be optimized. This number reaches trillions of conformations if all three angles (θ, ϕ, η) were being sampled. To make such a huge sampling computationally tractable, we devised the BiHelix sampling procedure. A typical class A GPCR template is shown in Figure 2A. It has 12 nearest-neighbor helix pairs shown by double arrows in Figure 2B. Since helix pairs 1-3, 1-4, 1-5, 1-6, 2-5, 2-6, etc don’t interact with each other, such pairs of helices don’t need to be sampled. In the BiHelix procedure, the seven-helix bundle is split into 12 two-helix bundles comprising of nearest-neighbor helices shown explicitly in Figure 2C, whose conformational space can be sampled completely, during which other five helices are not present.

Figure 2.

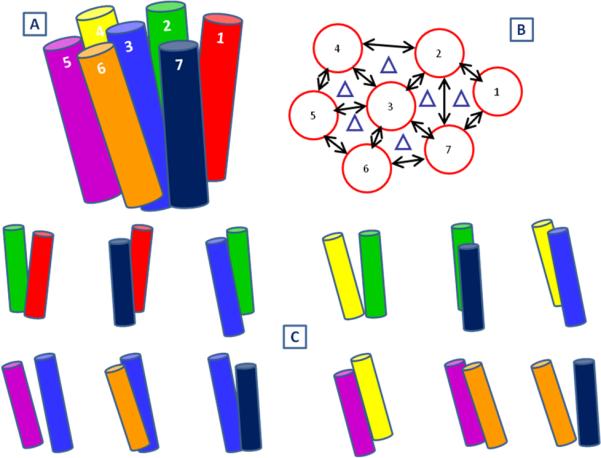
A. Typical seven-helix bundle. B. Nearest-neighbor helix pairs highlighted by double arrows; C. The 12 helix pairs shown explicitly.

Using the sampling of rotational angle η as an example, each two-helix bundle will sample (12)² = 144 conformations (using a 30° grid over full 360°). Each of these conformations is built for which the side chains need to optimized now. We use the SCREAM method⁵⁴ that uses an updated DREIDING force field (FF)⁵³ (referred to as DREIDING-III or D3FF). The energy functions based on D3FF don’t include the effects of the nonpolar environment because we have found (data not shown) that accounting of this environment only reorders the protein conformations locally and doesn’t affect the overall conformational preference of the structures.

SCREAM uses a library of residue conformations ranging from a CRMS diversity of 0.4Å to 1.6Å in conjunction with a Monte Carlo sampling using full valence, hydrogen bond and electrostatic interactions from D3FF, but with a special flat bottom van der Waals (vdW) potentials that reduces the penalty for contacts that are slightly too short while retaining the normal attractive interactions at full strength. To benefit from this penalty, the two-helix bundle with SCREAM optimized side-chains is minimized for 10 steps using a conjugate gradient (CG) method. The resulting D3FF energy is accurate enough to correctly select the best cases (without separate considerations of valence, electrostatic, hydrogen bond and vdW terms) as will be seen in the results.

This sampling is done for all 12 nearest-neighbor helix pairs mentioned earlier resulting in (12)×(144) =1728 energies, which can be combined to estimate the energy of all possible ~35 million (12)⁷ conformations in our sampling demonstration as follows. Each of the 1728 energies corresponds to a specific helix pair i-j, for a specific combination of η_i and η_j and is reported in the form of three energy components:

1. $e_{\mathit{ij}}^{\mathrm{int}\mathit{er}}({\eta }_i,{\eta }_j)$ (η_i,η_j): This component corresponds to interhelical energy of the helix pair that describes the total interaction energy between the helices. It is calculated by subtracting the internal energy of individual helices from the total energy of the two interacting helices and captures sidechain-sidechain, sidechain-backbone, backbone-backbone interactions across the two helices.

2. $e_{\mathit{ij}}^{\mathit{i},\mathrm{int}\mathit{ra}}({\eta }_i,{\eta }_j)$ (η_i,η_j): This component refers to the intrahelical energy of helix i while it is interacting with helix j in the i-j pair.

3. $e_{\mathit{ij}}^{\mathit{j},\mathrm{int}\mathit{ra}}({\eta }_i,{\eta }_j)$ (η_i,η_j): This component refers to the intrahelical energy of helix j while it is interacting with helix i in the i-j pair.

The interhelical component of the energy is additive and can be summed to give the total interhelical energy of a seven-helix bundle. The intrahelical component of helix 3, for example, in the 2-3 helix pair will in general be different from that in the 3-4 helix pair. To accommodate this, the intrahelical energy of a helix in the seven-helix bundle is approximated as the average of that energy from all helix-pairs involving that helix. Using this “mean-field” approximation, the energy of the ~35 million conformations for the seven-helix bundle can be estimated. The corresponding equations are shown in Equations (1) through (3). where N_i is the number of helix pairs involving helix i, and J₁ through J_Ni are the helix partners of helix i in those N_i pairs. The ordering of the energies of all ~35 million conformations can be used to select top M (typically 1000 or 2000) seven-helix conformations to be built explicitly and reordered using more accurate energies in the next step (as will be described), because until this point, only two-helix bundles have been optimized in the absence of other five helices.

$$e_{\mathit{total}}^{\mathrm{int}\mathit{ra}}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5,{\eta }_6,{\eta }_7)=\sum _{i=1}^7\frac{1}{N_i}\sum _{j=J_1}^{J_{N_i}}\left[e_{ij}^{i,\mathrm{int}\mathit{ra}}({\eta }_i,{\eta }_j)\right]$$ (1)

$$e_{\mathit{total}}^{\mathrm{int}\mathit{er}}({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5,{\eta }_6,{\eta }_7)=\sum _{i=1}^6\sum _{j=J_1}^{J_{N_i}}\left[e_{ij}^{i,\mathrm{int}\mathit{er}}({\eta }_i,{\eta }_j)\right]$$ (2)

$$E({\eta }_1,{\eta }_2,{\eta }_3,{\eta }_4,{\eta }_5,{\eta }_6,{\eta }_7)=e_{\mathit{total}}^{\mathrm{int}\mathit{ra}}+e_{\mathit{total}}^{\mathrm{int}\mathit{er}}$$ (3)

2.D CombiHelix Rotational Sampling

In the CombiHelix step, the top M structures from the BiHelix analysis are built explicitly using the rotations specified for each helix in the combination. The helical axis for rotation is identical to the one used in BiHelix. For each bundle, the side chains are optimized using SCREAM⁵⁴ as described in the previous section. This is followed by 10 steps of CG minimization.

The energy function in this CombiHelix stage refers to the energy of the full seven-helix bundle whose residue side-chains were optimized and the resulting structure minimized. The energy function in the BiHelix stage estimated the energy of the seven-helix bundle by combining the energies of the nearest-neighbor two-helix bundles (with optimized side-chains) using Equations (1) through (3). So, the energy of a seven-helix bundle at the CombiHelix stage is expected to be more accurate than at the BiHelix stage. The resulting energies are reordered to provide a new thermodynamic ranking of the M structures taken from BiHelix and the resulting lowest energy conformations can be analyzed in the context of the conformational space that was sampled, (e.g., η for all seven helices).

In the next section, this BiHelix/CombiHelix procedure will be applied to six of the GPCR crystal templates, to show that the complete sampling scheme works and that the energies are reliable enough to produce near-native GPCR conformations as ones with the lowest energy. Rhodopsin has been crystallized in ligand-free form (Opsin)²⁸ which has a different TM helix packing. These two systems will be used in the next section to analyze the results of the BiHelix methodology in terms of understanding their functional differences on the basis of structure. The methodology also lends itself to analyzing helix-helix interactions using potential energy landscapes that can provide additional insights into the function of these receptors.

3. RESULTS and DISCUSSION

3.A Validation of BiHelix/CombiHelix Sampling and Energy Function

For validation, we have applied this procedure to six of the available GPCR crystal structures: bovine rhodopsin (PDB ID: 1u19)⁵², hβ2-AR (2rh1)²⁴, hA2AR (3eml)²⁵, turkey β1-AR (2vt4)²⁶, bovine opsin (3cap)²⁸, squid rhodopsin (2z73)²⁷. The TM seven-helix bundles for the application of the computational procedure were obtained as described in section 2.B.

In the first demonstration of BiHelix, we compared energies obtained for three-helix bundles extracted from hβ2-AR and hA2AR using the BiHelix approximation and the corresponding exact energies from a full sampling of three-helix (trihelix) conformations. These energies were obtained for all possible rotations of 3 helices at 30° increment (12^3=1728 conformations) for the following six trihelices: H1-H2-H7, H2-H3-H4, H2-H3-H7, H3-H4-H5, H3-H5-H6, and H3-H6-H7. The trihelix energies are compared to those obtained by a BiHelix mean-field approximation utilizing three BiHelix pairs and the results are shown in three supplementary Figures S1, S2, and S3. Figure S1 has results for the hβ2-AR system and Figure S2 has results for the hA2AR system. The correlation between bihelix mean-field and trihelix energies holds for most of the trihelix energy range. Big deviations are seen between the two energies only in the very high energy (> 500kcal/mol) conformational space, seen especially in Figure S1.E for hβ2-AR and Figures S2.B and S2.D for hA2AR. Figure S3 shows these three cases with a focus on the lowest 1000 kcal/mol range, which shows that the correlation between these two energies holds in the relevant low energy range. Next we will look at the BiHelix energies at the seven-helix bundle level.

In the next demonstration of BiHelix, each of the seven-helix bundles was taken through a complete sampling of the conformational space using helix rotation angle η as a sampling variable. The angle was sampled over full 360° using two grids, a 30° grid and a 15° grid. The 30° grid samples ~35 million conformations and the 15° grid samples ~ 4.5 × 10⁹ conformations. After BiHelix sampling, the top 2000 conformations were taken through CombiHelix to produce a final ranking of lowest energy conformations. The results for all six systems are summarized in Table 1, which lists the rank of the crystal conformation (XTAL Rank) at the BiHelix level and at the CombiHelix level. It also lists the worst BiHelix ranked structure that shows up in the top 10 conformations after CombiHelix.

Table 1.

Summary of BiHelix/CombiHelix Results for all tested systems.

GPCR Combi 2000	360° Sampling of η Angle on 30° Grid			360° Sampling of η Angle on 15° Grid
	XTAL Rank		Worst BiHelix Rank in Top 10 CombiHelix	XTAL Rank		Worst BiHelix Rank in Top 10 CombiHelix
	BiHelix	CombiHelix		BiHelix	CombiHelix
A2A	1	1	88	1	1	789
Beta2	4	1	96	19	1	636
Beta1	2	1	82	6	2	1065
BovRhod	1	1	335	1	1	1278
BovOpsin	1	1	131	1	1	533
SquRhod	1	1	79	1	1	363

As can be seen from Table 1, the crystal conformation is ranked “first” for all cases in 30° sampling and all but one case in 15° sampling. The exception in the 15° sampling mode is for the turkey β₁ case, where the crystal conformation is ranked second. These results show that the energies used are reliable enough that, upon complete sampling of the conformational space they can still identify the lowest energy conformation assumed to be the crystal conformation. Since the crystal ligand is absent during sampling (except for Bovine Opsin case which is the ligand-free form of Rhodopsin), these results indicate that the predicted low-energy GPCR conformations in the absence of ligands are identical to or close to those observed experimentally at least in the helix rotation angle η space.

Table 1 also shows the worst BiHelix Rank for the top 10 conformations after the CombiHelix step, which is a function of the sampled conformational space as evident by higher worst ranks for the 15 degree sampling. Since CombiHelix energies are more accurate than those at the BiHelix level, this worst BiHelix Rank also provides a qualitative estimate of the accuracy of BiHelix energies for top 10 conformations after CombiHelix. Next, we will look at results for some GPCR systems to understand their implications and specific correlations between BiHelix/CombiHelix energies and Cα-RMSD of conformations to the crystal conformation.

3.B Conformational and Correlation Analysis

First we will look at the top 10 conformations for Bovine Rhodopsin after the application of BiHelix/CombiHelix procedure using 30° sampling of helix rotation angle. The top 2000 conformations from BiHelix were taken through CombiHelix. Table 2 shows the top 20 conformations after CombiHelix, along with their energy (SCH-Energy) in kcal/mol, BiHelix rank (SBHRnk), and BiHelix energy (SBH-Energy) also in kcal/mol. Since the starting template was the crystal conformation, that conformation corresponds to all seven η angles being “zero” and according to the Table 2 (green cells), it is ranked at the top after conformational sampling using BiHelix/CombiHelix. This is a validation of the energies being used to rank/score the conformations as well as additional validation of the side-chain placement program SCREAM.⁵⁴ Even though only helix rotation angle was sampled during this procedure, the top 20 conformations provide signatures for additional conformations that may be important as part of the function of Rhodopsin. First thing that is evident is the high conformational flexibility of TM5 in the helix rotational space, which is not inconsistent with flexibility associated with TM5 for class A GPCRs. In addition, we see counterclockwise 30° rotations in TM3 and TM6 as shown in Table 2 by red cells, which is consistent with the helix rotations observed in the Bovine Opsin (the retinal-free form of Bovine Rhodopsin) crystal structure, as characterized by the comparison of their templates shown in Table S1 in the supplementary information, which shows the Opsin TM3 and TM6 rotated by −28° and −31° respectively relative to Rhodopsin.

Table 2.

Top 20 Bovine Rhodopsin conformations after BiHelix/CombiHelix. The conformation observed in the bovine rhosopsin crystal structure (1u19) is shown in green cells. The helix rotation angles for TM3 and TM6 as observed in opsin crystal structure (2z73) are shown in pink cells.

SCHRNK	SCH-Energy	SBHRNK	SBH-Energy	Eta1	Eta2	Eta3	Eta4	Eta5	Eta6	Eta7	CRmsd
1	250	1	211	0	0	0	0	0	0	0	0.0
2	252	3	246	0	0	0	0	0	330	0	0.7
3	268	12	267	0	0	0	0	150	0	0	1.6
4	284	4	250	0	0	0	0	60	0	0	0.9
5	285	20	275	0	0	0	0	180	0	0	1.7
6	287	11	267	0	0	0	0	300	0	0	0.9
7	292	335	338	0	0	330	0	0	0	0	0.6
8	293	2	241	0	0	0	0	90	0	0	1.2
9	302	5	253	0	0	0	0	330	0	0	0.5
10	305	7	255	0	0	0	0	0	90	0	1.7
11	306	22	275	0	0	0	0	0	300	0	1.2
12	318	71	302	0	0	0	0	180	330	0	1.8
13	320	720	358	0	0	330	30	0	0	0	0.7
14	320	8	262	0	0	0	0	0	270	0	1.7
15	324	37	286	0	0	0	0	210	0	0	1.6
16	325	134	314	0	0	0	0	180	90	0	2.4
17	329	10	264	0	0	0	0	0	0	330	0.5
18	332	13	267	0	0	0	0	0	0	30	0.5
19	332	16	272	0	0	0	0	330	330	0	0.8
20	333	30	282	0	0	0	0	90	90	0	2.0

We don’t see a single conformation in the top 2000 that shows both TM3 and TM6 with this rotation, because these rotations are also associated with changes in helix tilts (Δϕ column in Table S1) which were not sampled. The results for Bovine Rhodopsin show that: a. BiHelix/CombiHelix procedure can identify the crystal conformation to be the lowest energy conformation; b. The procedure has the potential to identify multiple GPCR conformations that may have a physiological role in their function. These results for other 5 systems are included in the supplementary information (Tables S2 through S6).

Next we will use human β2 adrenergic receptor system to highlight different correlations that are present in the BiHelix/CombiHelix procedure. Figure 3A shows the correlation between BiHelix and CombiHelix energies as raw (red) and smoothened (blue) data (obtained by using a traveling window average of three points: i−1, i, and i+1, in the y-axis). This correlation is good for conformations ranked up to ~200, as expected due to less noise in the low-energy regions for both BiHelix and CombiHelix energies. Beyond that range of conformations, BiHelix energies flatten out, whereas CombiHelix energies continue to rise.

This is also clear from Figure 3D, which shows BiHelix/CombiHelix energies as a function of conformation rank, with BiHelix energies flattening at higher energies (presumably due to lack of steric clash in BiHelix) and CombiHelix energies rising steeply at high energies. Figure 3B shows the rank correlation between BiHelix and CombiHelix ranks. The raw data (in red) fluctuates a lot but the underlying behavior can be extracted by smoothening the raw data by a traveling window average using a window size of three points (i−1, i, and i+1) shown in blue. The rank correlation of Figure 3B qualitatively mimics the energy based correlation in Figure 3A. The correlation between Cα-RMSD of predicted conformations (relative to the crystal conformation) versus CombiHelix energy is shown in Figure 3C, as this energy determines the final rank of the conformations. It shows a good correlation and all high energy conformations have a high Cα-RMSD as well. This correlation should breakdown at high Cα-RMSD values as these can have potentially similar energies. The corresponding results for other 5 GPCR systems are included in the supplementary information (Figures S4 through S8). For predicting multiple GPCR conformations the energy and rank correlations of Figures 3A and 3B provide good signatures to assign confidence to the predictions.

3.C Helix-Helix interaction potential energy landscapes from BiHelix

The bihelix energies presented in the previous sections can also be used to look at the potential energy landscapes that describe helix-helix interactions. This is especially useful for the following two related applications: a. It can provide snapshots of energy landscapes that these receptors will encounter during the protein folding process, which for all membrane proteins is still not very well understood, except for evidence for a “two-stage” model for α-helical membrane protein folding⁵⁵ which suggests that helix formation takes place before helix-helix associations can take place in the membrane; b. It can also provide vital information about the flexibility in helix-helix packings (in terms of the degree of freedom being sampled and accessible conformational space) which when compared across related systems with different functional signatures can begin to provide useful insight into the structural implications of those functional differences. These implications will now be demonstrated using Bovine Rhodopsin and Bovine Opsin as examples bearing in mind that the ultimate fate of these observations is determined by the sum of all BiHelix energies.

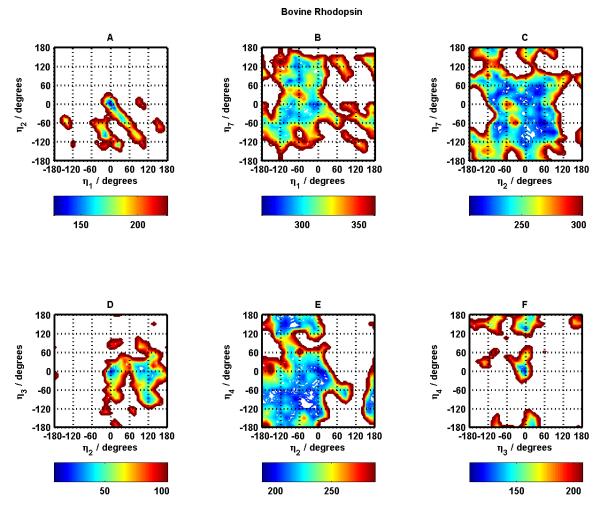
Figures 4 and 5 display the potential energy surfaces for all nearest neighbor helix-helix interactions as a function of the rotation angles of the corresponding helices for Bovine Rhodopsin. Panels A through F in Figure 4 show these surfaces for helix pairs 1-2, 1-7, 2-7, 2-3, 2-4, and 3-4. Panels A through F in Figure 5 show these surfaces for helix pairs 3-5, 3-6, 3-7, 4-5, 5-6, and 6-7. These figures only display data for BiHelix conformations that are within 100 kcal/mol of the lowest energy conformation in each case. The empty conformational space in the figures then refers to high energy conformations, which will be assumed to be inaccessible for the current discussions.

Figure 4.

Bovine Rhodopsin potential energy surfaces for helix pairs TM1-TM2 (A), TM1-TM7 (B), TM2-TM7 (C), TM2-TM3 (D), TM2-TM4 (E), and TM3-TM4 (F) as a function of helix rotation angles for corresponding helices. The energies are in kcal/mol, where the colorbar under each panel shows the lowest 100 kcal/mol energy range.

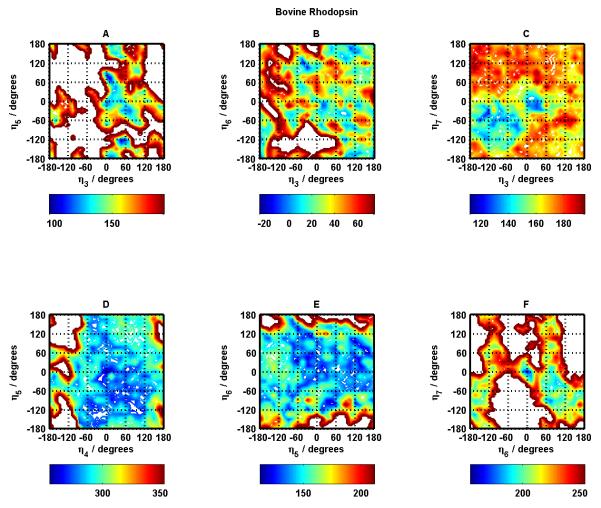
Figure 5.

Same as Figure 4 for helix pairs TM3-TM5 (A), TM3-TM6 (B), TM3-TM7 (C), TM4-TM5 (D), TM5-TM6 (E), and TM6-TM7 (F).

The darkest blue regions correspond to the most stable/favorable regions for the involved helix pairs. The center point in each panel refers to the (0°, 0°) conformation corresponding to the crystal structure. For majority of the helix pairs, the native (crystal structure) conformation and near-native conformations fall in the most stable (dark blue) regions. The exceptions appear to be helix pairs 3-5 and 3-6 (Figure 5 panels A and B). Helix pairs 4-5 and 5-6 (Figure 5 panels D and E) have the largest blue area in terms of conformational space in helix rotation angles suggesting a flatter energy landscape as compared to all other helix pairs.

Helix pairs 1-2, 2-3, and 3-4 (Figure 4 panels A, D, F) have the most inaccessible conformational space, which might be due to the necessity to restrict available conformations during the protein-folding process given the fact that these helix pairs involve the first four helices of the 7-helix bundle. This, however, remains to be verified. This observation about large inaccessible conformational space for these helix pairs is also seen in the corresponding helix pairs in most of the other GPCR systems studied in this work, suggesting something unique or unusual about these helix pairs requiring future investigation.

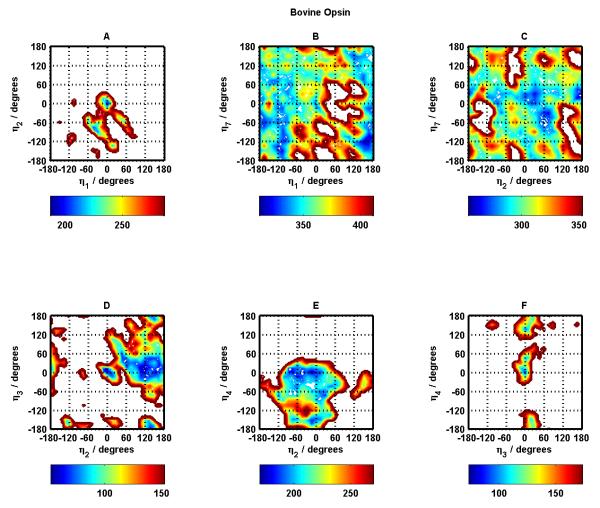
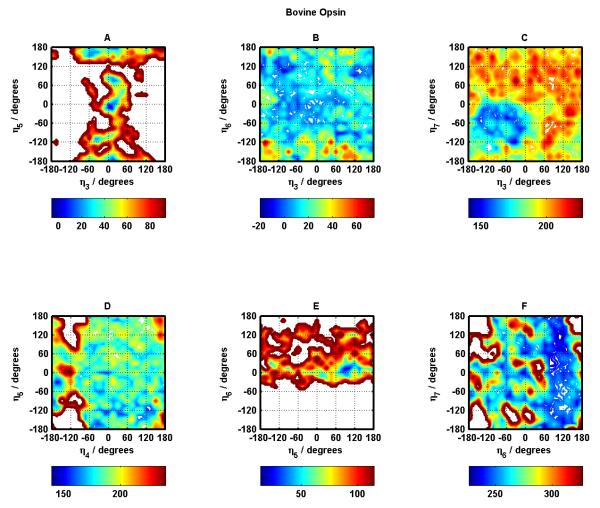
Figures 6 and 7 show the corresponding potential energy surfaces for Bovine Opsin, considered to be the near-active GPCR conformation. Figure 6 contains these surfaces for helix pairs 1-2, 1-7, 2-7, 2-3, 2-4, and 3-4. Figure 7 contains these surfaces for helix pairs 3-5, 3-6, 3-7, 4-5, 5-6, and 6-7.

Figure 6.

Same as Figure 4 for Bovine Opsin.

Figure 7.

Same as Figure 5 for Bovine Opsin.

Here also, for majority of the helix pairs, the native (crystal structure) conformation and near-native conformations fall in the most stable (dark blue) regions. The exceptions appear to be helix pairs 3-7 and 5-6 (Figure 7 panels C and E). Helix pairs 4-5 and 3-6 (Figure 7 panels D and B) have the largest blue area in terms of conformational space in helix rotation angles suggesting a flatter energy landscape as compared to all other helix pairs.

The critical helix-helix contact in Rhodopsin crystal structure appears to be the TM3-TM6 salt bridge which gets broken upon activation and Opsin (one of the near-active conformations downstream of meta Rhodopsin II) displays a TM5-TM6 salt bridge. Energy landscapes corresponding to these helix pairs for Rhodopsin and Opsin can provide some useful insight. It is curious that crystal conformations for TM5-TM6 Opsin BiHelix pair (Figure 7 panel E) and TM3-TM6 Rhodopsin BiHelix pair (Figure 5 panel B) are not in their lowest energy regions (dark blue), so interactions with other helices play a dominant role in making the crystal conformation more stable and attain lowest energy. Since the BiHelix method implicitly takes into account the effect of non-nearest-neighbor helices when we combine all the two-helix energies to get seven-helix bundle energies, the BiHelix/CombiHelix energies are able to correct this curious observation at the seven-helix bundle level. This is a testament to the strength of the BiHelix/CombiHelix method. In addition, the TM3-TM6 BiHelix pair exhibits a flat energy landscape in Opsin (Figure 7 panel B), consistent with its crystal structure which as described above shows that the TM3-TM6 Rhodopsin contact is broken in Opsin. It is the TM5-TM6 BiHelix pair that exhibits this flat energy landscape for Rhodopsin (Figure 5 panel E) consistent with its crystal structure showing a TM3-TM6 salt-bridge and a broken TM5-TM6 contact. This same BiHelix pair (TM5-TM6) exhibits a restricted landscape for Opsin (Figure 7 panel E), not inconsistent with its crystal structure showing stronger coupling between helices 5 and 6. This doesn’t appear to be the case for the analogous case in Rhodopsin (TM3-TM6, Figure 5 panel B), suggesting a stronger involvement of other helices (compared to Opsin) in restricting TM3-TM6 to the crystal conformation. These analyses suggest that connecting the energy landscapes with functional information about different receptors can begin to provide valuable mechanistic insight into the function of these receptors.

Opsin also displays Helix pairs 1-2, 2-3, and 3-4 (Figure 7 panels A, D, F) with the most inaccessible conformational space like Rhodopsin. The supplementary information contains the corresponding potential energy surfaces for other 4 systems studied: β2, β1, A2AR, SquidRhod (see Figures S9 through S16), which also share this observation. There is a wealth of information in all these landscapes which is currently being investigated. So, in addition to structure prediction, the BiHelix methodology can help rationalize functional behavior with structural insights and may even be helpful in protein folding studies of GPCRs.

In terms of computational resources consumed by BiHelix and Combihelix, the BiHelix sampling of 1728 two-helix conformations (on the η grid of 30°) is fast and takes about 2 hours on 12 Xeon 2.33GHz processors, whereas the CombiHelix sampling of top 2000 conformations (from the BiHelix step) takes about 16 hours on 12 processors, as this step now involves the optimization of residue side-chains on all seven helices along with minimization.

4. CONCLUSIONS

We have presented the BiHelix/CombiHelix methodology aimed towards de novo structure prediction of multiple conformations of helical membrane proteins using GPCRs as the example applications. The methodology efficiently performs a complete sampling of the available conformational space by breaking the full helix bundle into multiple pairs of interacting helices, whose energies are pooled together to get the energies of all conformations of the full helix bundle. Application of this approach to six of the available GPCRs is able to identify native and near-native conformations as the top conformations by energy. These results validate the sampling method as well as the scoring energy for assessing the best bundle conformations. The demonstrated sampling of helix rotation angles for Bovine Rhodopsin showed that the methodology can identify other physiologically important conformations for a GPCR. We expect that several of the best 10 or 20 predicted structures from BiHelix/CombiHelix conformational sampling might play a role in differential binding of agonists, antagonists and inverse agonists or in activation pathways. The BiHelix energy landscapes are also capable of providing structural insights into functionally different receptors as demonstrated for Rhodopsin vs Opsin comparisons.