Literal and figurative interpretations are computed in equal time

Abstract

The time courses for constructing literal and figurative interpretations of simple propositions were measured with the response signal, speed–accuracy tradeoff procedure. No differences were found in comprehension speed for literal and figurative strings in a task that required judging whether a string of words was meaningful. Likewise, no differences were found in processing speed for nonsense and figurative strings in a task that required judging whether a string of words was literally true. Figurative strings were less likely to be judged meaningful than were literal strings and less likely to be rejected as literally true than were nonsense strings. The absence of time-course differences is inconsistent with approaches to figurative processing that contend that a figurative interpretation is computed after an anomalous literal interpretation. The time-course profiles suggest that literal and figurative interpretations are computed in equal time but that the meaning of the latter is less constrained than that of the former.

The construction of a figurative interpretation for a string like Some surgeons are butchers (Gildea & Glucksberg, 1983) has been traditionally viewed as subordinate to the construction of a literal interpretation. What Cacciari and Glucksberg (1994) refer to as the standard view of figurative processing—a view that largely stems from Searle (1979) and Grice (1975)—contends that a figurative interpretation is signaled by the failure to construct a plausible literal interpretation. According to this serial approach to figurative comprehension, listeners/readers first attempt to construct a literal interpretation for a figurative string, seeking a figurative interpretation only after a literal reading is found to be implausible.

Cacciari and Glucksberg (1994; see also Gibbs, 1994) outline several problems with the traditional view. First, specifying the grounds on which readers reject a literal interpretation in favor of a figurative interpretation has proved to be difficult. Clear counter examples can be found to proposals that readers detect syntactic and semantic anomalies (e.g., Matthews, 1971), detect literal falsehood (Grice, 1975; Searle, 1979), or seek to determine the truth value of an interpretation with respect to a mental model (see, e.g., Miller, 1979). Often, as Black (1979) notes, a nonliteral reading is signaled simply by the banality of the literal reading. Second, readers may not fully derive a literal interpretation in all circumstances. For familiar idioms and indirect requests, readers appear to truncate a literal interpretation when the figurative (or indirect) interpretation is salient (Cacciari & Tabossi, 1988; Gibbs, 1980). Finally, when both literal and figurative readings are contextually appropriate, Keysar (1989) has argued that readers compute both interpretations. On the traditional view, processing should be restricted to a literal interpretation, since it provides a sufficient interpretation of the string.

More direct tests of the traditional view are provided by on-line measures of the time needed to compute literal and figurative interpretations. A figurative interpretation should be associated with longer processing times, if its construction depends on first deriving an anomalous literal interpretation. Unfortunately, extant results are somewhat mixed. Several studies have found comparable reading times for figurative and literal strings when the prior context sufficiently cues the appropriate interpretation, but reliably longer reading times for figurative strings when contextual support is minimal (Inhoff, Lima, & Carroll, 1984; Ortony, Schallert, Reynolds, & Antos, 1978; Shinjo & Myer, 1987). However, Gerrig and Healy (1983) found slower processing times for figurative strings, even when an informative context preceded a required metaphoric reading (for a review, see Cacciari & Glucksberg, 1994).

Reading times (eye movement tracking or various self-paced reading measures) provide a relatively natural and unintrusive measure of processing time. However, reading time differences can result from a confluence of factors, only a subset of which may reflect true underlying differences in processing speed (McElree, 1993; McElree & Griffith, 1995, 1998). The fact that language comprehension is mediated by a set of largely automatic, highly overlearned mental procedures does not entail that language performance is error free. A reading time difference can reflect differences in the probability that certain forms of information are retrieved and successfully processed, rather than an intrinsic difference in the time it takes to retrieve and process that information. For example, McElree (1993) demonstrated that reading time differences for a verb in a frequent versus an infrequent syntactic environment reflect the probability that each syntactic form is retrieved from the verb’s lexical representation, and not from a serial architecture in which parsing operations first attempt to compute the most frequent structure associated with the verb (Ford, 1986; Holmes, 1987; Shapiro, Brookins, Gordon, & Nagel, 1991).

Reading time differences between figurative and literal interpretations (when observed) may simply reflect the fact that readers are less likely to successfully retrieve and integrate the semantic and pragmatic information that is necessary to construct a figurative interpretation. If a reader fails to recover and process key information, some portion of the string may need to be reprocessed in order to construct the intended interpretation. Indeed, such an account provides a ready explanation for why contextual information often reduces or eliminates differences between reading times for figurative and literal strings (Inhoff et al., 1984; Ortony et al., 1978; Shinjo & Myers, 1987): An appropriate context may provide cues that are sufficient to recover information that otherwise would be difficult to recover.

TIME-COURSE MEASURES

The experiments reported here used the response signal, speed–accuracy tradeoff (SAT) procedure (Reed, 1973) to derive separate measures of the probability that readers converged on either a literal or a figurative interpretation, and the time course for computing each type of interpretation. In our application of the task (see, also, McElree, 1993; McElree & Griffith, 1995, 1998), the participants were required to judge whether figurative (Example 1: Some mouths are sewers), literal (Example 2: Some tunnels are sewers), or nonsense (Example 3: Some lamps are sewers) strings were either meaningful (Experiment 1A) or literally true (Experiment 1B). The strings were presented one word at a time, at a rate that approximated fast reading (250 msec/word). The final word in each string (e.g., sewers in Examples 1–3) forced either a literal, a figurative, or a nonsensical interpretation. We measured how each interpretation unfolds over time by requiring the participants to respond at varying times after the onset of the crucial, final word. The participants were trained to respond within a 100–300 msec window after the presentation of a response signal (a tone). The response signal occurred (randomly across trials) at one of six times, ranging from 28 to 2,500 msec after the onset of a final word.

The range of times across which the response signal was presented served to sample the full time course of processing, from times when performance was at or near chance, to times when performance had reached an asymptotic level. The asymptote of the time course function provides a measure of the probability (across trials and materials) that the reader succeeded in arriving at an interpretation sufficient to support either type of judgment. The point at which the time course function departs from chance, the intercept, and the rate at which the function grows to asymptote provide joint measures of processing speed. The SAT intercept measures the minimum time needed to compute an interpretation that is sufficient to support either a literal or a meaningful response. The SAT rate reflects either the rate of continuous information accrual or the distribution of finishing times if processing is discrete.

A strong test of the traditional view of figurative processing was provided by Experiment 1A, in which participants judged whether the strings were meaningful. This task directly contrasted the speed and accuracy of processing figurative and literal strings. A prediction of the serial model is that figurative strings should be associated with a delayed intercept and/or a slower rate than literal strings. (See McElree, 1993, for a detailed treatment of serial predictions for this type of task; see, also, McElree & Dosher, 1989, 1993, and McElree & Carrasco, in press, for predictions of serial models in other domains.) This follows from the assumption that a figurative interpretation is not attempted until an anomalous literal interpretation has been computed. A delay in the availability of the figurative interpretation will engender a corresponding delay in the time in which a figurative string is judged meaningful, providing there is no alternative literal interpretation. How this delay is expressed in SAT dynamics depends on the mean and variance of the difference in the times to compute a literal and a figurative interpretation. If the variability in processing time (across trials and materials) is small relative to the mean difference, most of the temporal differences will be evident in the SAT intercepts. Modest differences in variability can engender differences in SAT rate.¹ Crucially, these dynamics or speed differences are predicted independently of potential differences in asymptotic accuracy. That is, the intercepts and rates of the SAT function measure the speed of processing for just the proportion of cases in which the reader has successfully computed a plausible interpretation.

Judgments of the meaningfulness of a string contrast figurative and literal strings, using nonsense strings (to which participants should respond no) as a baseline estimate of the false alarm rate for the judgment. In a second task, we followed on the work of Glucksberg and colleagues (Gildea & Glucksberg, 1983; Glucksberg, Gildea, & Bookin, 1982) in using a literal judgment task (Is the string literally true?) to contrast the time courses of figurative and nonsense strings. Glucksberg and colleagues used a reaction time task to document that metaphors such as Example 1 above induced a Stroop-like effect, being rejected more slowly than nonsense strings, such as Example 3. The inflated rejection times for figurative strings suggest that some, but not all (Gildea & Glucksberg, 1983), metaphors are processed automatically.

The automaticity of metaphoric processing is orthogonal to the issue of whether figurative strings are processed by a serial process that first seeks to compute a literal interpretation. However, if the serial model is correct and figurative processing is indeed automatic, figurative strings should be associated with a slower (rejection) time course than nonsense strings, since the metaphoric interpretation will interfere with a no response when it becomes available. The interference effect will engender a time-course function for figurative strings with either a delayed intercept or a slower rate of rise, depending on the point in time at which the metaphoric interpretation is available.

METHOD

Participants

Thirteen native English speakers from the New York University community participated in three approximately 1-h sessions (two experimental sessions and one practice session). All the participants were paid for serving in the experiment.

Apparatus, Stimuli, and Procedure

Stimulus presentation, timing, and response collection were all carried out on a personal computer, using software with millisecond timing, synchronized to the vertical retrace interrupt. A trial began with a fixation point (a small filled square) presented for 500 msec in the center of an otherwise clear screen. The words of a string were presented one after another in the center of the screen in a normal mixture of uppercase and lowercase characters. Each word remained on the screen for 250 msec. A period was appended to the final word of the string, to clearly indicate to the participants that the presentation of the string was complete. At one of six response lags—either 28, 200, 400, 600, 800, or 2,500 msec after the onset of the final word in the string—a 50-msec, 1000-Hz tone was presented. The participants were instructed and trained to respond yes or no at the tone by pressing one of two designated keys on the keyboard. After a response was recorded, visual feedback on the latency to respond to the tone was displayed to the participant. The participants were informed that responses longer than 300 msec were unacceptably long and that responses shorter than 100 msec should be regarded as anticipations. All the participants had an initial 1-h practice session that served as training in the SAT procedure. Both the sentences and the response lags were randomized within a session.

In Experiment 1A, the participants were instructed to read the strings as they would normally read any text and, when the tone sounded, to judge whether the string was a meaningful statement. In Experiment 1B, the participants were asked to judge whether the string was literally true when the tone sounded. Seven participants performed the meaningful judgment task first, whereas the remaining participants performed the literal task first.

Materials

All the strings were of the form Some Xs are Ys. The primary contrasts consisted of 240 triples that shared a common final noun (e.g., stone). Literal, figurative, and nonsense strings were created by selecting different subject nouns (e.g., Some temples are stone, Some hearts are stone, and Some clouds are stone, respectively). The set of materials was carefully reviewed by four individuals, to verify the status of each member of the triple.²

All 240 triples were presented in both the meaningful and the literal judgment tasks. One hundred and five additional nonsense strings (e.g., Some artists are staplers; Some grocers are batteries; Some turnips are curtains) were included in the meaningful judgment task to increase the proportion of no responses to 41.7%. Fifty additional literal strings were added to the literal judgment task (e.g., Some mechanisms are staplers; Some implements are batteries; Some fabrics are curtains), to increase the proportion of yes responses to 37.8%.

Data Analysis

A d′ measure was used for each task, in order to derive time-course functions that were not influenced by response biases. In the meaningful task, the z scores for the hit rates for literal and figurative strings were scaled against the z scores for the false alarm rate for nonsense strings at each response lag for each participant. In the literal task, the z scores for the hit rate for literal strings were scaled against the z scores for the false alarm rates for figurative and nonsense strings at each response lag for each participant. Perfect performance at any lag was adjusted by a minimum-error correction (Macmillan & Creelman, 1991), to ensure that, given the sample size, the d′ values were measurable.

To estimate asymptotic accuracy and processing dynamics (speed), the empirical SAT functions were fit with an exponential approach to a limit:

$$d^{\prime }(t)=\lambda (1-e^{-\beta (t-\delta )}),\mathrm{for}t>\delta ,\mathrm{else}0.$$ (1)

Equation 1 describes the growth of accuracy over processing time, using three parameters: (1) λ, an asymptotic parameter reflecting the overall accuracy with maximal processing time; (2) δ, an intercept parameter reflecting the discrete point in time at which accuracy departs from chance (d′ = 0); and (3) β, a rate of rise parameter that describes the rate at which accuracy grows from chance to asymptote. Differences in processing speed or dynamics are reflected in the intercept (δ) and/or the rate of rise to asymptote (β) parameters. Numerous studies have found that Equation 1 provides a precise quantitative summary of the shape of a full time-course SAT function (Dosher, 1976, 1979, 1981, 1982, 1984; McElree, 1993, 1996; McElree & Dosher, 1989, 1993; McElree & Griffith, 1995; Reed, 1973, 1976; Wickelgren, 1977; see, also, Ratcliff, 1978, for an alternative three-parameter equation derived from the random-walk (diffusion) model, and McElree & Dosher, 1989, for a comparison of the two equations).

All the analyses were performed on the individual participants’ data. Consistent patterns across participants are summarized with analyses and graphs of the average (over participants) data. Differences among the SAT functions were quantified by fitting the exponential in Equation 1 with an iterative hill-climbing algorithm (Reed, 1976), similar to STEPIT (Chandler, 1969). This fitting procedure minimized the squared deviations of predicted values from observed data. A hierarchical model-testing scheme was used to determine the best-fitting exponential model. The functions were fit with sets of nested models that systematically varied the three parameters of Equation 1. These models ranged from a null model, in which all the functions were fit with a single asymptote (λ), rate (β), and intercept (δ), to a fully saturated model, in which each function was fit with a unique asymptote, rate, and intercept. The quality of the fit was assessed by using three criteria. The first was the value of an R² statistic,

$$R^2=1-\frac{\sum _{i=1}^n{(d_i-{\widehat{d}}_i)}^2/(n-k)}{\sum _{i=1}^n{(d_i-\overline{d})}^2/(n-1)},$$ (2)

where d_i represents the observed data values, d̂_i indicates the predicted values, d̄ is the mean, n is the number of data points, and k is the number of free parameters (Reed, 1973). This R² statistic is the proportion of variance accounted for by the fit, adjusted by the number (k) of free parameters (Judd & McClelland, 1989). The second criterion was evaluation of the consistency of the parameter estimates across the participants. The third was evaluation of whether the fit yielded systematic (residual) deviations that could be accommodated by allocating more (i.e., separate) parameters to various conditions.

It is important to acknowledge one limitation of the SAT procedure. This procedure is designed to derive time-course functions for individual participants. It is important to measure time course on an individual basis, since the variances in asymptote, rate, and intercept of the time-course functions between participants often exceed the variance between conditions. However, a typical SAT study does not have a sufficient number of cross-item replications for an item-based analysis. To partially compensate for this deficiency, the assignment of strings to a response lag was randomized in our design. This ensures that any systematic difference across participants in one or another component of the SAT function (e.g., asymptote) was not due to a few extreme items.

RESULTS

Experiment 1A

The top panel of Figure 1 presents the average (over participants) time-course functions (in d′ units) for judgments of the literal and figurative strings when the task required an assessment of meaningfulness. Performance at the longest response signal (2.5 sec) provides an empirical measure of asymptotic performance. Asymptotic levels of performance were higher for literal than for figurative strings by, on average, 0.5 d′ units [F(1,12) = 13.2, MS_e = 0.1295, p = .003]. This difference indicates that our figurative strings were less meaningful than the comparable literal strings. This may be the case if, in general, the meaning of a metaphor is less constrained than the meaning of a literal string or if, in the more limiting case, the metaphors used here were less semantically constrained than the literal strings.

Figure 1.

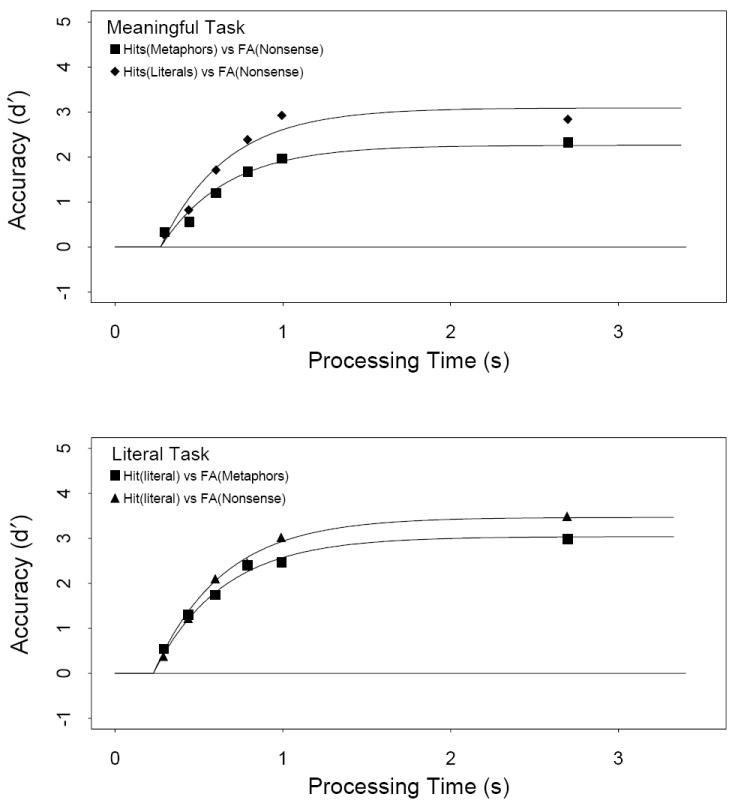
Average d′ accuracy (symbols) as a function of processing time (lag of the response cue plus latency to respond to the cue). Top panel: accuracy in the meaningfulness task for literal strings (filled diamonds) and figurative strings (filled squares). Bottom panel: accuracy in the literal task for nonsense strings (filled triangles) and figurative strings (filled squares). Smooth curves in each panel show the fits of exponential model (Equation 1), using the (average) parameters listed in Table 1.

Fits of the full time-course functions with Equation 1 enable one to determine whether a figurative interpretation was available later than a literal interpretation on the proportion of trials on which each interpretation was computed. Adequate fits of time-course data required a separate asymptotic parameter (λ in Equation 1) for figurative and literal strings, consistent with the analysis above. In the average data and across individual participants, all the fits of the two functions with a single asymptotic parameter produced systematic residuals at the late processing times and, consequently, yielded relatively low adjusted R² values (.888 to .916 in the average data). In contrast, a 2λ−1β−1δ fit produced a substantially higher adjusted R² value (.948 in the average data). Moreover, the estimated λ parameters for all 13 participants showed a consistent advantage for literal strings [F(1,12) = 34.7, MS_e = 0.1337, p < .001].

Beyond these asymptotic differences, however, there was no evidence to suggest that time course, estimated by the intercept (δ) or the rate (β) parameters, differed for figurative and literal strings. First, allocating additional β or δ parameters (viz., 2λ−2β−1δ, 2λ−1β−2δ, or 2λ−2β−2δ models) reduced the overall adjusted R² from those observed with the 2λ−1β−1δ model, indicating that the additional dynamics parameters were not accounting for systematic variance across conditions. Second, when the rate and intercept parameters were allowed to vary, no systematic differences in the parameter estimates emerged across participants. For example, with a 2λ−2β−2δ model, 6 participants showed a rate (β) advantage for figurative strings, whereas 7 participants showed a rate advantage for literal strings. The average 1/β estimates across participants were 348 ± 68 msec (M ± SE) for figurative strings and 332 ± 54 msec for literal strings [t(12) = 0.84, p = .42]. With respect to the intercept parameter, 7 participants showed an advantage for figurative strings, and 6 participants showed an advantage for literal strings. The average intercepts across participants were 310 ± 45 msec for figurative strings and 319 ± 30 msec for literal strings [t(12) = −0.31, p = .75]. (The β and δ estimates from the 2λ−2β−2δ model are listed in the Appendix.) When rate and intercept were combined into a composite measure of processing speed (δ + β ⁻¹) to avoid parameter tradeoffs, there was a nonsignificant 7-msec advantage for literal over figurative strings [t(12) = 0.3, p = .77]. Of course, with only 13 participants, there is little power to detect a difference this small in magnitude [power(α = .05) = .089]. However, differences of this size, even if reliable, provide little ground to motivate a serial processing model. As will be described more fully below, McElree (1993) and McElree and Griffith (1995) demonstrated that other types of reanalysis processes yield time-course differences on the order of 100–200 msec in this type of judgment task. The present study has sufficient power to detect differences of this size (power is .93 for a 100-msec difference and .61 for a 50-msec difference).

The absence of systematic time-course differences between figurative and literal strings is inconsistent with a serial model that argues that a figurative interpretation is computed after an anomalous literal interpretation. The similar β and δ estimates for figurative and literal strings and, crucially, the random manner in which the differences are ordered across participants (approximately half favoring figurative strings and half favoring literal strings) suggests that there were no substantial differences in processing speed for the two types of strings. The time-course data indicate that, contra the traditional view, figurative and literal interpretations are computed in comparable time. Parameter estimates for the best-fitting 2λ−1β−1δ model are shown in Table 1. The smooth functions in the top panel of Figure 1 show the model fits to the average data.

Table 1.

Exponential Parameter Estimates

Participants	Parameters for Meaningful Task					Parameters for Literal Task
	λ Literal	λ Figurative	β Common	δ Common	Adjusted R2	λ Nonsense	λ Figurative	β Common	δ Common	Adjusted R2
Average	3.09	2.26	2.56	0.272	.948	3.47	3.04	2.43	0.229	.985
S1	2.38	2.15	4.56	0.273	.844	3.27	3.09	4.02	0.258	.902
S2	2.73	1.94	1.98	0.262	.820	3.19	2.93	3.26	0.153	.752
S3	4.30	2.69	1.72	0.352	.879	3.59	3.47	3.51	0.146	.704
S4	3.35	2.27	2.85	0.226	.773	2.80	2.56	6.46	0.374	.921
S5	3.16	2.58	5.77	0.372	.771	3.69	3.23	11.8	0.245	.884
S6	2.69	1.84	3.87	0.364	.823	3.67	3.34	3.08	0.249	.699
S7	2.59	2.27	3.41	0.065	.682	4.57	4.31	11.1	0.107	.965
S8	3.87	2.01	2.11	0.297	.869	2.95	2.38	5.92	0.254	.815
S9	2.29	2.18	3.21	0.447	.909	3.35	2.69	1.94	0.403	.928
S10	2.98	2.41	3.08	0.516	.937	3.55	3.21	1.89	0.253	.700
S11	2.60	1.89	7.58	0.421	.872	3.36	2.41	1.79	0.263	.908
S12	3.58	2.48	3.61	0.383	.899	3.70	4.59	2.21	0.185	.859
S13	3.71	2.53	2.69	0.241	.750	3.35	3.04	2.09	0.247	.923

Experiment 1B

The bottom panel of Figure 1 presents the average (over participants) time-course functions (in d′ units) for judgments of the nonsense and figurative strings when the task required an assessment of whether the strings were literally true. Again, performance at the longest response signal (2.5 sec) provides an empirical measure of asymptotic performance. Asymptotic rejection rates were higher for nonsense than for figurative strings by, on average, 0.51 d′ units [F(1,12) = 12.4, MS_e = 0.1362, p = .004]. This difference is consistent with the notion that, on a proportion of trials, the metaphors were misinterpreted as literally true statements.

Fits of the full time-course functions displayed a pattern similar to judgments of meaningfulness. A 2λ−1β−1δ model was required to fit the asymptotic differences in performance in the average data and the data from 8 of the 13 participants, since fits with a single asymptotic parameter produced lower adjusted R² values and left systematic residuals. For the remaining 5 participants, however, the adjusted R² values for a 2λ−1β−1δ model were either similar or slightly lower than those for the 1λ−1β−1δ model. Nevertheless, when each participant was fit with the 2λ−1β−1δ model, the estimated λ parameters showed an advantage for nonsense over figurative strings [F(1,12) = 34.2, MS_e = 0.035, p < .001].

Beyond these differences in asymptote, there was no evidence that judgments of nonsense and figurative strings differed in time course. As before, more embellished models reduced adjusted R² values, and there were no systematic differences across participants in either the resulting rate (β) or intercept (δ) estimates when the two strings were allotted separate parameters. In fits of a 2λ−2β−2δ model, for example, 6 participants showed slower rate estimates for figurative than for nonsense strings, while the remaining 7 participants showed the opposite pattern. The average rate estimates (1/β) across participants were 460 ± 85 msec for figurative strings and 452 ± 78 msec for nonsense strings [t(12) = 0.09, p = .92]. The differences in intercept were more systematic, although nonsignificant and in a direction opposite to what was predicted: Nine of the 13 subjects had earlier intercept estimates for figurative than for nonsense strings (see the Appendix), with average estimates of 251 ± 23 msec for figurative strings and 270 ± 29 msec for nonsense strings. This modest advantage for figurative strings, however, was not significant [t(12) = −1.02, p = .37]. When rate and intercept are combined into a composite measure of processing speed (δ + β⁻¹), there is a non-significant 11-msec advantage for figurative over nonsense strings [t(12) = 0.15, p = .87]. Here again, the power to detect a difference this small is low [power(α = .05) = .068; power is .45 for a 50-msec difference and .64 for a 100-msec difference]; but the difference, even if reliable, is in the direction opposite to what would be predicted by a model that argued that a figurative interpretation is delayed, relative to a literal interpretation. Parameter estimates for the best-fitting 2λ−1β−1δ model are shown in Table 1. The smooth functions in the bottom panel of Figure 1 show the model fits to the average data.

The lower asymptotic rejection rates for figurative strings suggest that readers fail to differentiate metaphors from literal strings on a proportion of trials. However, the similar time-course profiles for figurative and nonsense strings are inconsistent with the notion of a late-accruing figurative interpretation that interferes with the rejection of the figurative strings as nonliteral. If such were the case, the dynamics portion of the SAT function for figurative strings should have been delayed (e.g., delayed intercept or slower rate), relative to the function for nonsense strings, which lack this potential source of interference.

Examination of the intercept estimates in Table 1 suggests that the intercepts are longer for the meaningful task (325 ± 32 msec) than for the literal task (241 ± 23 msec), and this difference was significant [t(12) = 2.64, p = .02]. The smaller difference in rate, 329 ± 36 and 323 ± 47 (respectively) in 1/β msec units, was not significant. However, if one combines rate and intercept into a composite measure, to avoid parameter tradeoffs (e.g., an earlier intercept, but a slower rate), the time-course difference between tasks is not significant [t(12) = 1.48, p = .16; power (α = .05) = .41]. Consequently, this apparent dynamics advantage for the literal task should be viewed with caution and should be replicated before any general conclusions concerning the two tasks are drawn. Nevertheless, we note that it is not surprising to find that different tasks engender different time-course profiles, since it is likely that they require participants to adopt different decision processes and criteria.

Prima facie, it may be surprising to find faster processing dynamics for literal than for meaningful judgments. However, it is possible that literal judgments can be reliably based on a subset of the information that is required for an accurate assessment of meaningfulness. Here, such judgments may have been, in part, determined by an assessment of the degree of relatedness or similarity of the subject and predicate phrases (e.g., metal–iron, in Some metals are iron; birds–parrots, in Some birds are parrots). Similarity information would have limited value in the meaningfulness task, since it would not reliably differentiate figurative and nonsense strings. Crucially, Ratcliff and McKoon (1982) found that a general assessment of the similarity of constituents in simple propositions such as A robin is a bird is available before detailed relational information. If participants used similarity information as a heuristic for literal truth early in processing, initial d′ values would be higher in the literal than in the meaningful judgment task.

DISCUSSION

Time Course of Figurative Interpretation

We found no evidence to indicate that figurative strings, such as Some mouths are sewers, take longer to understand than literal strings, such as Some tunnels are sewers, despite the fact that figurative strings are less likely to be judged meaningful. The comparable temporal dynamics for interpreting figurative and literal strings are incompatible with any viable formulation of a serial processing model in which figurative processing is delayed until the string has been interpreted in a literal fashion. To the contrary, the data suggest that both types of interpretations were computed in equal time.

The literal judgment task provided convergent support for the claim that figurative processing is not contingent on first computing a literal representation. Glucksberg and colleagues (Gildea & Glucksberg, 1983; Glucksberg et al., 1982) have argued that figurative processing is automatic, on the basis of the finding of Stroop-like interference effects in a literal judgment task. If a figurative interpretation accrues later than a literal interpretation, the dynamics of the time-course function for figurative strings should have been slowed, relative to the function for nonsense strings, as a consequence of the late-accruing interference from the metaphor interpretation.³ Although figurative strings were less likely to be rejected than nonsense strings, we found that, to the contrary, the temporal dynamics for rejecting figurative strings were indistinguishable from the dynamics for nonsense strings.

Some caution is always in order when arguing from a null result. Of particular concern is whether the task has the requisite sensitivity to detect potential time-course differences. In this regard, it is important to note that dynamics differences of less than 50 msec in both intercept (δ) and rate (β⁻¹) have been documented in other SAT tasks with nearly identical experimental procedures. McElree and Griffith (1995; see, also, McElree & Griffith, 1998), for example, contrasted unacceptable strings, such as Some students amuse exams, in which there is a thematic (semantic) mismatch between the verb and the direct object, and unacceptable strings, such as Some students laugh exams, in which the direct object violated the (intransitive) syntactic requirements of the verb. Thematic violations were associated with slower dynamics, which were well fit by a serial (or cascade) model, in which syntactic relations are computed before semantic relations. Similarly, McElree (1993) documented time-course differences arising from syntactic “garden paths.” After reading strings like While John rushed Mary …, judgments of fragments like started work were associated with a slower time course than were judgments of fragments like around work. Here, the time-course difference tracked the time taken to reanalyze the second noun (Mary) as being the subject of a main clause, following an initial preference to analyze it as being a direct object of the subordinate clause. The clear time-course differences documented in these studies demonstrate that the SAT procedure is well suited to detecting temporal differences arising from various types of reanalysis processes. The lack of time-course differences in the present study suggests that there is little empirical content to the claim that figurative processing is contingent on an initial assessment of literal plausibility.

Toward a Model of Figurative Interpretation

The time-course data indicate that literal and figurative interpretations are computed in equal time or in parallel. Time-course profiles do not, of course, uniquely specify the types of mental processes that underlie the construction of a figurative or a literal interpretation. However, similar time-course profiles are consistent with the contention that both types of interpretation are computed by similar, if not identical, processes. Cacciari and Glucksberg (1994; see, also, Glucksberg & Keysar, 1993) suggest that metaphoric statements of the sort examined here can be regarded as class inclusion statements, in which properties of the predicate (the metaphoric vehicle) are attributed to the subject (metaphoric topic). Figurative statements like Some mouths are sewers differ from literal statements like Some tunnels are sewers, in that sewer as a metaphoric vehicle refers to the class of things that it typifies (e.g., dirty and foul things), whereas sewer as a literal predicate refers to tokens of the type (in this case, token of the class of subterranean conduits). The interpretative process in both cases can be viewed as an attributive process in which properties retrieved from the predicate are ascribed to the subject phrase.

In such an account, time course should not differ for interpreting the two types of strings, unless retrieving the relevant properties associated with the predicate requires fundamentally different types of operations. Current time-course evidence suggests, however, that different types of semantic relations are retrieved with comparable temporal dynamics. Corbett and Wickelgren (1978) found that retrieval dynamics (SAT intercept and rate) were equivalent for category instances with high and low dominance (A robin is a bird vs. A chicken is a bird), although the latter were associated with lower asymptotic levels (see, also, Casey & Heath, 1990). More relevant to the present issue, Ratcliff and McKoon (1982) found similar time-course profiles for the verification of synonym relations (A carpet is a rug), category membership (A color is purple), and descriptions (A razor is sharp). Although none of these relations directly maps onto what a class inclusion approach contends is the fundamental difference between literal and figurative strings, current data indicate that many different types of semantic properties are retrieved with similar dynamics.

Although we found no evidence for temporal differences in computing literal and figurative interpretations, asymptotic accuracy was lower for figurative strings. This suggests that the meaning of our figurative strings was less constrained than that of comparable literal strings. We cannot determine whether this is generally true of metaphoric statements or is just true of our particular sample. Nevertheless, we note that, within a class inclusion framework (Cacciari & Glucksberg, 1994), this effect follows from an assumption that readers fail, on a proportion of trials, either to recover the necessary semantic properties from the metaphoric vehicle (e.g., the class of things that sewers typify) or to properly ascribe those properties to the metaphoric topic (e.g., mouths). We suspect that reading-time differences between figurative and literal strings, when observed (e.g., Gerrig & Healy, 1983; Inhoff et al., 1984; Ortony et al., 1978; Shinjo & Myer, 1987), also reflect the difficulty of recovering key semantic properties associated with the metaphoric vehicle and ascribing those properties to the topic (for the latter, see Glucksberg, McGlone, & Manfredi, 1997). An enriched context may attenuate these differences by providing a set of retrieval cues that increases the probability of recovering the key semantic properties that serve as the foundation for the figurative expression.

APPENDIX

Rate (β) and Intercept (δ) Estimates (in Milliseconds) From the 2λ−1β−1δ Model

Participants	Meaningful Task				Literal Task
	Figurative 1/β	Literal 1/β	Figurative δ	Literal δ	Figurative 1/β	Nonsense 1/β	Figurative δ	Nonsense δ
S1	180	181	207	299	268	240	245	265
S2	403	436	236	273	390	226	271	213
S3	1,111	909	94	372	222	289	254	231
S4	305	315	187	240	100	310	401	303
S5	233	293	340	252	641	1,219	246	215
S6	280	202	336	376	263	396	243	255
S7	240	292	49	104	1,123	751	54	148
S8	456	418	297	289	100	235	269	244
S9	331	298	565	426	699	446	322	434
S10	289	256	535	516	892	401	172	286
S11	125	133	507	403	473	588	184	303
S12	270	244	393	379	370	243	393	379
S13	303	341	283	221	434	531	235	254