Growth rates of protein crystals

Abstract

Protein crystallization is important for structural biology. The rate at which a protein crystallizes is often the bottleneck in determining the protein’s structure. Here, we give a physical model for the growth rates of protein crystals. Most materials crystallize faster under stronger growth conditions, however, protein crystallization slows down under the strongest conditions. Proteins require a crystallization slot of ’just right’ conditions. Our model provides an explanation. Unlike simpler materials, proteins are orientationally asymmetrical. Under strong conditions, protein molecules attempt to crystallize too quickly, in wrong orientations, blocking surface sites for more productive crystal growth. The model explains the observation that increasing the net charge on a protein increases the crystal growth rate. The model predictions are in good agreement with experiments on the growth rates of tetragonal lysozyme crystals as a function of pH, salt concentration, temperature, and protein concentration.

The growth of diffraction-quality crystals is the major obstacle in determining the atomic structure of folded proteins.^1-4 Of the proteins purified through the Protein Structure Initiative, fewer than a third are crystallized, and only 15% yield diffraction-quality crystals.⁵ The difficulty stems from the fact that proteins will only crystallize in a small range of solution conditions. Under such conditions the second virial coefficient of the protein lies in a narrow range of values, called the “crystallization slot”.⁶ With a better understanding of the the physical mechanism, we might be able to go beyond current trial-and-error protocols for protein crystallization. Here we present a theory describing the kinetics of protein crystal growth as a function of protein concentration, pH, temperature, and salt. We show that crystallization rates depend on pH, temperature, salt and protein concentration in a way that can be explained if strong growth conditions drive proteins to stick so fast to the growing crystal that they bind incorrectly, blocking further crystallization. Thus, while protein crystals are not stable if the crystallization solution conditions are too weak, protein crystals will also not form if conditions are too strong.

It is well established that protein crystals grow by extending 2D clusters on the surface of the crystal.^7,8 We define J as the rate that clusters form and v_step = d(r₊ − r₋) as the rate they grow, where r₊ is the rate of addition of monomers (here, individual protein molecules binding to a step edge), r₋ is the rate of monomer dissociation, and d is the diameter of the protein. We model the formation rate J using classical nucleation theory in which the growth of clusters is treated as a diffusion process on a free energy landscape defined by a bulk term favoring growth and a surface tension opposing growth. For a two dimensional cluster of radius r this free energy is ΔF(r) = −π(r/d)²Δμ + 2rγ/d, where γ is the surface tension of the cluster and Δμ = k_BT lnc/c_s is the chemical potential difference that drives the protein to crystallize, where T is the temperature, k_B is Boltzmann’s constant, c is the protein concentration and c_s is the concentration of soluble protein after the solution has reached equilibrium with the crystals. The nucleation rate is the net flux of clusters that diffuse over the peak in the free energy. This is given by⁹

$$J=wZ{e}^{-\Delta F^{‡}∕k_{B}T},$$ (1)

where, F^‡ is the activation barrier given by the maximum in ΔF(r), and Z is the Zeldovich factor, which is the probability that a supercritical cluster continues to grow without dissolving back to subcritical size. The factor w is the rate at which a critical cluster grows to supercritical size; it is given by r₊ times the number of addition sites on the perimeter of the critical cluster.

The perpendicular growth rate ν for adding one new layer of protein onto the crystal is v = d/t, where t = (3/πJ(r₊ − r₋)²)^1/3 is the time required to lay down a layer of protein.¹⁰ The 1/3 exponent arises from the fact that the area covered by the growing clusters is proportional the number of clusters (which is proportional to t) and the area of the individual clusters (proportional to t²). Overall, the classical expression for the crystal growth velocity is¹⁰

$$\nu =r_{+}d{\left(\frac{\pi }{3}\right)}^{1∕3}{\left(1-\frac{r_{-}}{r_{+}}\right)}^{2∕3}{\left(\frac{\Delta \mu }{k_{B}T}\right)}^{1∕6}{e}^{-\frac{\pi {\gamma }^2{d}^2}{3\Delta \mu k_{B}T}}.$$ (2)

A more detailed derivation of Eq. (2) is given in the Supporting Material.

Here, in order to explain how proteins differ from simpler molecules, we modify this classical approach in two ways. First, we account for the nonproductive binding of protein in wrong orientations to the crystal. Unlike crystals of small molecules, like NaCl, proteins have orientation-dependent interactions; proteins can bind in incorrect ways. Secondly, protein solutions always contain small-molecule salts. We account for the intercalation of the companion small-molecule salt component throughout the proteins in the crystal. Our approach is based on recent theory for the thermodynamic stabilities of protein crystals.¹¹

A protein from bulk solution adds to the edge of a growing layer on the crystal face with rate r₊. A protein dissociates from the crystal with rate r₋ (Figure 1a). We assume the protein binds to the protein in either of two ways: productively (in the correct crystal orientation and alignment, called P), or non-productively (in a non-crystalline orientation, called NP); see Figure 1b. The crystal only grows when a protein binds productively. And a protein can only bind to a site productively if that site is not already occupied by an unproductively bound bound protein. The probability that a site is not occupied by an NP protein is P_free = (1 + ce^−f/k_BT)⁻¹, where 1 represents the Boltzmann weight of empty sites and cexp(−f/k_BT) represents the weight of sites occupied by NP proteins that bind with free energy f(f ≥ 0; see Figure 1a,b). In other words, e^−f/k_BT is the partition function of all the rotational and translational ways that the protein can bind to the crystal that are not consistent with the correct P state.

Figure 1.

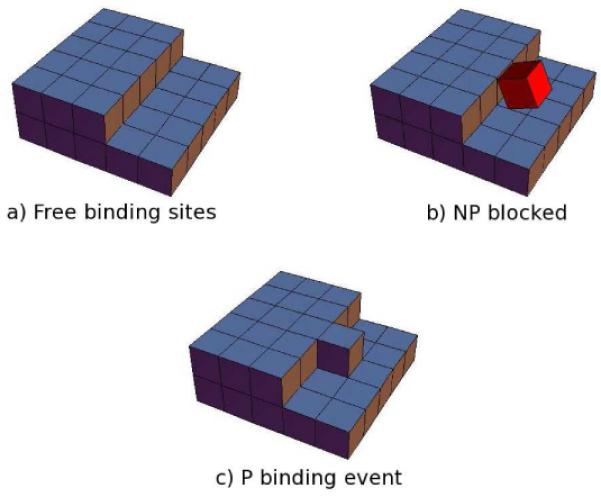
Schematic representation of: (a) row of free binding sites, (b) one site is blocked by a protein molecule in a nonproductive (NP) configuration, and (c) crystallization advances when one protein molecule binds productively (P).

The growth rate at a given site will be

$$r_{+}=kc{P}_{\text{free}}=\frac{kc}{1+c{e}^{-f∕k_{B}T}}$$ (3)

where c is the protein concentration in solution and kc is the rate of successful attachment of a protein in the productively bound state to a site that is not blocked by a NP protein. This approach assumes that the population of NP proteins equilibrates on the time scale of P binding. This assumption is is justified by the high entropy and marginal stability of the NP ensemble.^12,13 The site partition function does not include a term for P binding. The justification for this is that when a P binding event occurs, the binding site vanishes and is replaced by a new binding site at the newly advanced edge of the growing layer, Figure 1c. However, the previous binding site may be re-created if the protein detaches, which occurs at a rate r₋. At equilibrium, the addition and removal rates must be equal r₊ = r₋, so

$$r_{-}=\frac{k{c}_s}{1+c_s{e}^{-f∕k_{B}T}}$$ (4)

where c_s is the solubility of the protein in equilibrium with the crystal. The net attachment rate per site is r = r₊ − r₋.

Now, we decompose the free energy f of non-productive binding into a non-electrostatic attractive component, f_b, and an electrostatic repulsion, Δf_es, f = f_b + Δf_es. This factorization of the electrostatic component from the NP ensemble free energy is possible for proteins where the charge distribution is sufficiently homogenous that the monopole repulsion dominates over higher order terms. The dominant contribution to Δf_es has been shown to be the entropic cost of confining counterions within the crystal,^11,14 which we compute within the Poisson-Boltzmann approximation as follows. First, we calculate the net signed number of charges per protein q using average protein pKa values. ¹⁵ The entropic cost per unit volume to perturb the ion concentration from the bulk value c₀ to a final value c_f is $s_f={\int }_{c_0}^{c_f}\ln (c∕c_0)dc$. The final concentrations are given by the Boltzmann distribution c_± = c₀e^∓ψ where ψis the dimensionless electrostatic potential. Accounting for both the coion and counterion terms the entropy per unit volume is

$$s∕k_B=s_{+}+s_{-}=2c_0[-\psi \sinh \psi +\cosh \psi -1].$$ (5)

Previous work has shown that it is an excellent approximation to replace Ψ with its spatial average $\stackrel{‒}{\psi }$ within the protein crystal.¹¹ This approximation is likely to fail for larger proteins where the aqueous cavities are much larger than the Debye length. In these cases a linearized¹⁶ or numerical treatment may be more appropriate. The average potential can be determined from the charge neutrality condition for the crystal

$$q=-{\nu }_w(c_{+}-c_{-})=2{\nu }_w{c}_0\sinh \stackrel{‒}{\psi }.$$ (6)

Combining Eq. (5) and Eq. (6) and using Δf_es = −ν_wTs we have

$$\Delta f_{\mathrm{es}}=k_B{T}_q\left({\sinh }^{-1}\frac{q}{2{\nu }_w{c}_0}-\sqrt{1+{\left(\frac{2{\nu }_w{c}_0}{q}\right)}^2}+\frac{2{\nu }_w{c}_0}{q}\right),$$ (7)

where q is the protein charge and v_w is the solvent volume per protein in the crystal (11.7nm³ for tetragonal lysozyme crystals¹⁷).

The protein crystal growth rates are given by Eq. (2), Eq. (3), Eq. (4), and Eq. (7) with f = f_b + Δf_es.

We are interested in the growth rate as a function of pH, temperature, salt and protein concentration. Because the surface tension γ has been shown experimentally to vary weakly with these quantities,¹⁸ we treat it as a constant. We compute the driving force Δμ from,¹¹ which gives c_s as a function of pH, salt concentration, and temperature. The two fitting parameters are k and f_b. The best fit value of f_b is −26 kJ/mol, which is within ~2k_BT of the binding energy in the crystals¹¹ suggesting that there is a large entropic component stabilizing the NP ensemble. The values we find for k are on the order of 10⁵ sec⁻¹ Mol⁻¹ (see Figure 2). This is to be compared with ~10⁹ sec⁻¹ Mol⁻¹ that would be expected for a diffusion-limited collisions between non-interacting 3 nm spheres. This 10⁻⁴ reduction is comparable to the 10⁻⁵ factor found in previous work on larger proteins.¹³

Figure 2.

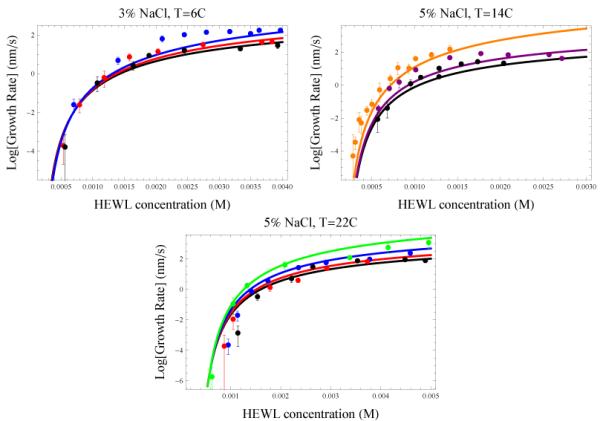
Growth rates of the (110) face of tetragonal lysozyme crystals^18,19 compared to Eq. (2). Colors indicate different pH conditions as follows: 4.0 (orange), 4.2 (green), 4.6 (blue), 4.8 (purple), 5.0 (red), 5.4 (black). Error bars show one s.d. Fitting parameters: f_b = −26 kJ/mol, k_3% = 1.2 × 10⁵ sec⁻¹ Mol⁻¹, and k_5% = 6.8 × 10⁵ sec⁻¹ Mol⁻¹. a) 3% NaCl, 6°C, b) 5% NaCl, 14°C, c) 5% NaCl, 22°C.

Figure 2 shows how lysozyme crystal growth rates depend on bulk protein concentration. These plots show the well-known general features that increasing protein concentration speeds up crystallization, but the rate reaches a saturating value at high concentrations. At concentrations just above the solubility limit (≈ 10⁻⁴M), the driving force Δμ is small, so the sizes of transition-state clusters are large, and thus costly in free energy. Therefore, such systems grow only slowly. This is the 2D-nucleation-limited regime.¹⁰ At higher concentrations, above ≈ 10⁻⁴M, 2D-cluster formation becomes appreciable and the growth rate increases exponentially with further increases in concentration. At the highest protein concentrations, the growth rate reaches a plateau and, in some cases, declines with further increases in concentration. This is due to blocking of binding sites by NP proteins. The concentration at which the plateau occurs depends strongly on the solution pH. Proteins having higher net charge (lower pH) plateau at higher protein concentration. Previous work explains the plateaus as a change in the growth mechanism: first, layer nucleation and growth, then random deposition of proteins on the surface.¹⁹ The present model is simpler: the plateau arises because the NP proteins block the growth surface for productive binding. In the Supporting Materials, we show the small errors can be reduced further by accounting for the cooperativity in binding of NP proteins to the growth step.

Figure 3 shows the dependence of protein-crystal growth rates on temperature. At high temperatures, the growth rate decreases with increasing temperature due to the decreased driving force Δμ (see the Arrhenius factor in Eq. (2)). At colder temperatures, crystallization conditions are stronger, causing substantial binding of NP proteins, which become kinetically trapped, inhibiting further growth.

Figure 3.

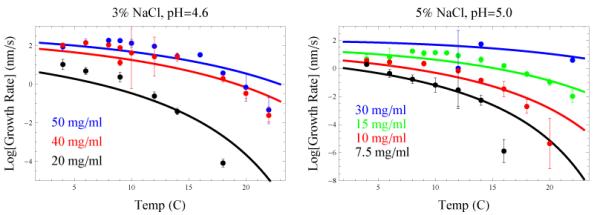
Growth rates of the (110) face of tetragonal lysozyme crystals^18,19 plotted against Eq. (2) as a function of temperature and concentration. Parameters taken from Figure 2. a) 3% NaCl, pH 4.6, b) 5% NaCl, pH 5.0.

The present work provides an explanation for the crystallization slot identified by George and Wilson.⁶ George and Wilson measured the second virial coefficients of proteins, a measure of their strength of interaction under different conditions. They found that for proteins to crystallize, the solution crystallization conditions must be neither too strong nor too weak. It is well understood that proteins should not crystallize if the thermodynamic driving force is too weak. But it has not been so clear why strong crystallization conditions can also reduce protein crystallization. We explain this as a kinetic effect. Under strong-growth conditions, proteins stick to the crystal-growth surface rapidly in incorrect orientations, “self-poisoning” the sites from more productive binding.¹³ To see this, take the limit of large c in Eq. (3) to find the maximum monomer addition rate for a given set of conditions

$$r_{\max }=k{e}^{f∕k_{B}T},$$ (8)

where f ≥ 0 is the free energy of binding the NP proteins to the crystal. Two conclusions follow from this expression. First, it shows that stronger binding of NP proteins leads to slower crystallization rates. And, second, since f is predominantly an equilibrium binding affinity among two proteins, it shows why protein crystallization rates should be related to the second virial coefficient. To make this latter observation we observe that the ensemble of binding states described by f will bear a strong resemblance to the ensemble of collision states between two proteins in solution. Clearly, the presence of the crystal will perturb the ensemble somewhat, so the connection is only qualitative.

Previous explanations of the kinetic arrest under strong binding conditions have focused on the formation of non-crystalline precipitates. The appearance of such precipitates is expected to be a sharp transition, akin to a first order phase transition, signifying that cooperative density fluctuations drive the condensation. In the Supporting Information we explore the onset of such cooperative behavior, however, the primary finding of our theory is that the kinetic arrest begins when the interactions are sufficiently weak to be treated as independent events.

Although we have focused on electrostatic considerations, Eq. (3) can be used to predict the effect on crystal growth of other variables that affect protein-protein interactions. Consider, for example, the effect of denaturants like urea or GdnHCl at low concentrations (insufficient to denature a significant fraction of the proteins). At high protein concentrations (within the plateau regime) the addition of denaturant would be expected to accelerate crystal growth by destabilizing NP proteins. However, this acceleration would be diminished at lower concentrations where the primary effect would be to destabilize the crystal.

We expect that similar models may also be used to describe the initial appearance of crystals from a supersaturated solution.²⁰ In this case the nucleation rate J features a three dimensional cluster free energy with the same kinetic pre-factor given by Eq. (3). The increased dimensionality will result in a larger free energy barrier and, thus, exacerbate the problem of finding conditions strong enough to nucleate, but not so strong to self-poison the potential binding sites. We expect that crystal nucleation rates will follow the same trends as crystal growth, namely, increasing with protein charge, concentration, and salt concentration and decreasing with temperature. These trends are observed in lysozyme nucleation,²¹ however, due to factors not included in our model, like the presence of nearby phase transitions,²² the agreement is only qualitative (data not shown).

A key question is how to optimize conditions to maximize the chances for successful crystallization. In this regard Eq. (8) paints a bleak picture; attempts to promote nucleation by stabilizing the crystal will necessarily poison the kinetics. It would seem that efforts to promote crystallization are best spent optimizing k. Here we have seen that k is strongly perturbed by salt concentration and weakly by pH (see Supporting Information). Therefore, a combination of high salt to maximize k with a large protein charge to enhance binding/unbinding kinetics would seem to be the optimal scenario.¹⁶ More work is required to determine how other precipitation agents affect k.

In summary, we have developed a theory for the kinetics of protein crystallization. The theory begins from classical nucleation theory and the established observation that proteins deposit as 2-dimensional clusters on the surfaces of growing crystals. However, our treatment deviates from models of small-molecule crystallization in two respects: (1) we account for the fact that proteins, unlike small molecules, have different binding affinities in different orientations (proteins are not spherically symmetric). That is, some proteins bind nonproductively, poisoning the surface, while other proteins bind productively. And, (2) we treat the strong effects of small-molecule salts on protein crystallization rate. We treat the latter at the level of Poisson-Boltzmann theory.

The theory gives a good accounting of the experimental data on the crystallization of lysozyme as functions of protein concentration, temperature, pH, and salt concentration. In particular, we explain the counterintuitive observation that increasing the protein charge increases the growth rate. The model gives a microscopic explanation for the observation of George and Wilson and others that there are optimal conditions, called the’crystallization slot’. In short, under weak conditions proteins don’t crystallize because there is not sufficient thermodynamic driving force, and under strong conditions proteins don’t crystallize because unproductive binding is so strong that it prevents productive binding.