Diameter-dependent axial prestretch of porcine coronary arteries and veins

Abstract

The pressure-diameter relation (PDR) and the wall strain of coronary blood vessels have important implications for coronary blood flow and arthrosclerosis, respectively. Previous studies have shown that these mechanical quantities are significantly affected by the axial stretch of the vessels. The objective of this study was to measure the physiological axial stretch in the coronary vasculature; i.e., from left anterior descending (LAD) artery tree to coronary sinus vein and to determine its effect on the PDR and hence wall stiffness. Silicone elastomer was perfused through the LAD artery and coronary sinus trees to cast the vessels at the physiologic pressure. The results show that the physiological axial stretch exists for orders 4 to 11 (> 24 μm in diameter) arteries and orders −4 to −12 (>38 μm in diameter) veins but vanishes for the smaller vessels. Statistically, the axial stretch is higher for larger vessels and is higher for arteries than veins. The axial stretch λ_z shows a linear variation with the order number (n) as: λ_z = 0.062n + 0.75 (R² = 0.99) for artery and λ_z = −0.029n + 0.89 (R² = 0.99) for vein. The mechanical analysis shows that the axial stretch significantly affects the PDR of the larger vessels. The circumferential stretch/strain was found to be significantly higher for the epicardial arteries (orders 9–11), which are free of myocardium constraint, than the intramyocardial arteries (orders 4–8). These findings have fundamental implications for coronary blood vessel mechanics.

mechanics plays a pivotal role in the growth and remodeling of blood vessels in response to mechanical and biochemical stimuli in health and diseases (3, 17, 18, 23, 30, 31). Therefore, an accurate assessment of the mechanical properties of the coronary vasculature (arteries and veins) is important in understanding vasospasm, atherogenesis, and plaque stability or rupture. To understand the state of stress and strain in the cardiovascular system (13), our group has established a database of the morphometry and mechanical properties of the aorta and coronary arterial tree in a porcine model, including the diameters and lengths (20), wall thickness (4), opening angles (13, 22), and distensibility (14). Although the mechanical properties of the coronary and peripheral arteries in normal and pathologic state have received considerable attention (1, 7, 17, 25, 28), there are generally limited data on the coronary venous system.

The recent simulations of Algranati et al. (2) showed that the in vivo axial stretch along the coronary vasculature significantly affects the pressure-diameter relation (PDR) and the respective vessel compliance. Specifically, the shape of the PDR was shown to substantially affect the coronary flow transmural distribution and was hypothesized as an important determinant of subendocardial vulnerability (15). These observations highlight the need for data on the axial stretch ratio from the largest epicardial arteries (order 11) through the largest veins (order −12). Such data are clearly needed to increase the understanding of coronary blood flow distribution as well as vessel wall stress and strain, vessel compliance, wave reflection, atherogenesis, vascular growth and remodeling.

In this study, we provide a complete set of the physiological axial stretch data through the coronary arterial and venous trees. Based on these data, the PDR of the vessels was used to account for the constraint of myocardium on intramyocardial vessels. Furthermore, the effects of axial stretch on the predictions of the PDR and physiological state were analyzed. Finally, the longitudinal variations along both the arterial tree and venous tree and between the arteries and veins of the same size were evaluated.

METHODS

Animal Preparation

Ten male growing domestic (4- to 5-mo-old) Yorkshire pigs weighing 42.6 ± 3.3 kg (means ± SD) were used in this study. Surgical anesthesia was induced with ketamine (33 mg/kg) and atropine (0.05 mg/kg) and maintained with isoflourane (1–2%). Ventilation with 100% O₂ was provided with a respiratory pump and a midline sternotomy was performed. Anticoagulation was induced with heparin (100 U/kg) followed with the injection of pentobarbital (80 mg/kg iv) to ensure deep anesthesia. All animal experiments were performed in accordance with national and local ethical guidelines, including the Institute of Laboratory Animal Research guidelines, Public Health Service policy, the Animal Welfare Act, and were approved by Institutional Animal Care and Use Committee at University of Indiana-Purdue University, Indianapolis.

Preparation of Coronary Arteries and Veins

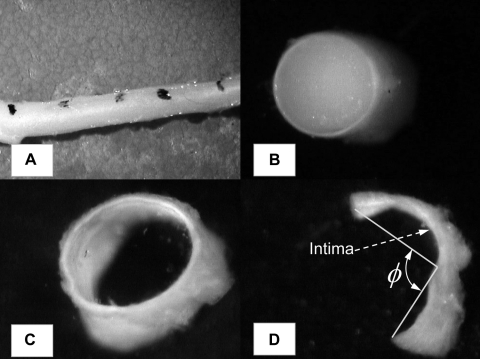
The heart was arrested with a saturated KCl solution, through the jugular vein with the animal deeply anesthetized. The heart was then excised and put into saline bath at room temperature. The isolated-heart preparations were identical to those described previously (13). The left common coronary artery was cannulated and perfused with saline. The blood was immediately flushed out of the heart. The left anterior descending (LAD) artery was then perfused with catalyzed silicone elastomer (Silicone SE4026 from General Electric). The arterial inlet perfusion pressure was maintained at 100 mmHg, and the venous outlet pressure was 5–6 mmHg (approximately equivalent to right atrial pressure). One hour was allowed for the elastomer to harden, and the LAD artery and the coronary sinusal veins were carefully dissected down to small branches with the diameters of ∼40–50 μm. Water-resistant carbon particles were used to mark the vessel segments to measure axial changes. Each marked segment was photographed to obtain axial length in the loaded state with the hardened elastomer maintained in the lumen (Fig. 1A). The vessels were then cut perpendicular to the longitudinal axis into segments as labeled with carbon particles. All segments were photographed from cross sections to obtain the inner and outer dimension and wall thickness in the physiologically loaded state. For the arterial segments, whose cross sections are circular, the inner and outer diameters were measured using an image analysis system (Sigma-Scan; Fig. 1B). The inner diameter was denoted as D_in in the foregoing analysis. For the vein segments, whose cross sections are approximately elliptical, the long and short principle axes were recorded (Fig. 1C).

Fig. 1.

Morphological measurements of coronary vessels at physiological state and zero-stress state. A: vessel segment dissected from myocardium, with hardened elastomer in the lumen. Water-resistant carbon particles were used to mark the vessel segments to measure axial changes before and after removal of the elastomer. B: cross section of a left anterior descending (LAD) arterial vessel segment at physiological state, with hardened elastomer in the lumen. Inner and outer dimension and wall thickness were measured. C: cross section of a vein segment with hardened elastomer in the lumen. D: cut-open vein segment at zero-stress state. Opening angle ϕ and midwall circumferential length were measured.

The elastomer was then pushed out of each segment, and a radial cut was made to reveal the zero-stress state (ZSS) similar to our previous studies (10, 29). The vessel segment opened into a sector and gradually approached a constant opening angle after ∼30 min. The segment was then photographed, and Sigma-Scan was used to measure the axial length, opening angle, and inner/outer circumferential length of the arteries (Fig. 1D). For venous vessels whose wall is thin, the midwall circumferential length was measured instead. The axial stretch ratio was calculated as the ratio of the segmental length between carbon marks in the loaded state to that in the cut-open ZSS. All the experimental protocols were completed within 6 h of euthanasia.

Data Analysis

Ordering of coronary arterial and venous branches.

We (21, 22) have previously developed and implemented an ordering system to classify various size vessels into orders based on a diameter-defined Strahler System. This results in a unique relationship between diameter and order number for the entire coronary arterial and venous tree. The relationship between the diameter range and order number obtained for LAD artery and coronary vein from the previous study is shown in Table 1. Since we determined the relationship among the axial stretch ratio, wall thickness, opening angle, and diameter throughout the coronary arterial and venous tree, the various parameters can be expressed as a function of order number (Table 1).

Table 1.

Inner diameters D_in of vessel segments in each order of vessels in LAD artery and coronary sinusal vein

LAD Artery		Sinus Vein
Order No. (n)	Din, μm	Order No. (n)	Din, μm
4	24.3–48.1	−4	38.1–80.5
5	48.2–101.5	−5	80.6–152.8
6	101.6–216.7	−6	152.9–253.2
7	216.8–384.2	−7	253.3–386.7
8	384.3–554.1	−8	386.8–600.2
9	554.5–986	−9	600.3–965.5
10	986.1–2,189.5	−10	965.6–1,322.5
11	>2,189.6	−11	1,322.6–3,148
		−12	>3,148.1

LAD artery, left anterior descending artery; D_in, inner diameter.

Statistical analysis.

Each vessel segment was considered as an independent statistical sample. The data in the figures with error bars denote means ± SD. The differences in LAD arterial and coronary venous order numbers were examined with one or two-way ANOVA. The results were considered significant when P < 0.05 (two way).

Biomechanical Analysis

The PDR of coronary vessels was determined by the residual deformation (opening angle), axial stretch, as well as the myocardial constraint. The mechanical analysis includes two steps: 1) determine the zero-pressure, axially stretched state (denoted as “no-load”), where the vessel is axially stretched by the measured physiological axial stretch λ_z, but without lumen pressure (see appendix, Stretched, Zero-Pressure State); and 2) calculate the PDR of the vessels (see appendix, PDR). To account for the perivascular constraint on intramyocardial arteries (orders 4–8), we surrounded the no-load vessel with an infinite myocardium with the myofiber orientation aligned with the axis of the vessel (24). This model reflects the difference between the physiological axial stretch of the vessels and the residual deformation of myocardium. Orders 9–11 arteries and order −12 to −9 veins are epicardial and were modeled without constraint. To investigate the effect of axial stretch, a comparison was made of the PDR with λ_z = 1 (no stretch) and λ_z = physiological stretch.

We also investigated the diameter distensibility of arteries defined at physiological pressure (10), as:

$$d=\frac{1}{D_{in}}\frac{d{D}_{in}}{dP}{|P=P}_{Phy}.$$ (1)

in which physiological pressure P_phy and inner diameter D_in were obtained as in the appendix, Physiological State, with use of the longitudinal pressure distribution formula previously determined by Kassab et al. (19) by least-square fit of the data (P_Phy in mmHg and D_in in μm):

$$P_{Phy}=6.7g^4-67.6g^3+231g^2-277g+132,\hspace{0.17em}g={\log }_{10}\left(D_{in}\right),$$ (2)

RESULTS

Morphological Measurements

Figure 2A shows the relation between the vessel wall thickness (WT) and the logarithm of the inner diameter for LAD artery and coronary sinus vein. In general, the arterial wall is thicker than the venous wall and the difference is more obvious for larger vessels. The data were grouped according to the order number, n, and are shown in Fig. 2B, as wall thickness-order number relation, of arterial (orders 4–11) and venous vessels (−12 to −4), respectively. The mean wall thickness was fitted with an exponential relation of the order number, as WT = 0.71exp[−0.38n] (4 ≤ n ≤ 11; R² = 0.99) for LAD arterial tree and WT = 1.04exp[−0.38n] (−12 ≤ n ≤ −4; R² = 0.99) for veins. This curve fit suggests that arterial wall is generally thicker than venous wall of the same order by ∼50%. The wall thickness-to-radius ratio (WTRR), however, increases toward the smaller diameter (P < 0.01) for both arteries and veins, as shown in Fig. 3A. This ratio is significant higher for the arteries than the veins of the same order (P < 0.01), and the difference is more obvious for the larger veins. The correlation between the thickness-to-radius ratio and the order number is plotted in Fig. 3B, which was fitted with second-order polynomial functions for artery and vein, as WTRR = 0.0038n² − 0.0774n + 0.48 (R² = 0.98, LAD artery) and WTRR = 0.0017n² + 0.039n + 0.29 (R² = 0.95, vein).

Fig. 2.

A: correlation between the logarithm wall thickness (WT, μm) and the logarithm of inner diameter (D_in, μm) along LAD arterial and coronary venous tree. B: variation of WT of the LAD artery and vein with order number (n). Solid line, least-square fit of the following form: LAD, WT = 0.71e^−0.38n (R² = 0.99); vein, WT = 1.04e^−0.38n (R² = 0.99). Statistical data are given in Supplemental Tables S1A (LAD) and S1B (coronary vein).

Fig. 3.

A: correlation between wall thickness-to-radius ratio (WTRR) and the logarithm of inner diameter (D_in, μm) along LAD arterial and coronary venous tree. B: variation of WTRR of the LAD artery and vein with order number (n). Solid line, least-square fit of the following form: LAD: WTRR = 0.0038n² − 0.0774n + 0.48 (R² = 0.98); vein, WTRR = 0.0017n² + 0.039n + 0.29 (R² = 0.95).

Figure 4 shows the relation between the physiological axial stretch ratio, λ_z, and the logarithm of the inner diameter D_in (Fig. 4A) and order number n (Fig. 4B) for LAD artery and coronary sinus vein. In general, the axial stretch ratio of LAD artery was significantly larger than that of vein (P < 0.01). There is also a significant increase of λ_z with the vessel diameter for both artery and vein (P < 0.01). As shown in Fig. 4B, λ_z increases from a mean value of 1.01 of order 4 arteries to 1.5 of order 11 and from 1.01 of order −4 veins to 1.23 of order −12 veins. The relation between λ_z and n is found to be nearly linear for arteries and veins, and can be fitted by a linear least-square fit, as λ_z = 0.062n + 0.75 (R² = 0.99) for LAD artery and λ_z = −0.029n + 0.89 (R² = 0.99) for the veins. Orders −4 and 4 vessels are nearly not axially stretched (λ_z ≈ 1) in vivo. Given this and that λ_z drops with vessel diameter, we verified that λ_z = 1 for smaller vessels (order −3 to 3), as shown by a dashed line in Fig. 4B. We also examined the relation between the WTRR and λ_z, individual data points (Fig. 5A) and the statistical data of each order number (Fig. 5B). For both LAD artery and vein, λ_z decreases as WTRR increases (P < 0.05) and the arteries have higher λ_z than the veins.

Fig. 4.

A: correlation between axial stretch ratio λ_z and the logarithm of inner diameter D_in (μm) along LAD arterial and coronary venous tree. B: variation of λ_z of the LAD artery and vein with order number, n. Solid line, least-square fit of the following form: LAD, λ_z = 0.062n + 0.75 (R² = 0.99); Vein, λ_z = −0.029n + 0.89 (R² = 0.99). Statistical values of λ_z are given in Supplemental Tables S1A (LAD) and S1B (coronary vein).

Fig. 5.

A: correlation between axial stretch ratio λ_z and WTRR along LAD arterial and coronary venous tree. B: data were classified into order numbers throughout the LAD and venous tree. Solid line, least-square fit of the following form: LAD, λ_z = 24.67WTRR² − 10.71WTRR + 2.17 (R² = 0.98); vein, λ_z = 22.44WTRR² − 7.06WTRR + 1.56 (R² = 0.97).

The opening angles of coronary veins are shown in Fig. 6. The opening angle decreases toward the smaller veins (P < 0.05). A linear least-square fit was used to describe the data, as ϕ = −11.67° n − 10.57° (R² = 0.98). Compared with the LAD arterial vessels, the veins have smaller opening angle that suggest lower residual deformation in the vessel wall.

Fig. 6.

Variation of the opening angle (ϕ) of the coronary venous tree with order number (n). Solid line, linear least-square fit ϕ = −11.67n − 10.57 (R² = 0.98).

The above numerical data of arteries and veins are also summarized in Supplemental Table S1 (Supplemental Material for this article is available online at the J Appl Physiol website).

PDR

The no-load state of LAD arteries (order 4–11) was first determined as described in the appendix, Stretched, Zero-Pressure State, and the numerical results are given in Supplemental Table S2. The PDR curve was then predicted (see appendix, PDR) with or without the constraint of myocardium. Figure 7, A–C, shows the representative PDR of the orders 5 (small intramyocardial arteries), 7 (midsize intramyocardial arteries), and 11 (large epicardial arteries), where the solid curves are with λ_z = physiological axial stretch ratio, and the dashed curves are with λ_z = 1.0. The physiological pressures and diameters were solved and plotted as symbols in Fig. 7, and the detailed data including transmural strain are given in Supplemental Table S3.

Fig. 7.

Representative pressure-diameter curves of LAD arteries. Solid line: λ_z = measured physiological axial stretch; dashed line: λ_z = 1.0 (vessel is free of axial stretch); ♦: calculated physiological state (see Supplemental Table S3 for the values). A: order 11 epicardial vessels. B: order 7 intramyocardial vessels. C: order 5 intramyocardial vessels. D: diameter distensibility (×100% × mmHg⁻²) of LAD arteries at physiological pressure with and without consideration of physiological axial stretch.

The mechanical analysis (Fig. 7) shows that the physiological axial stretch stiffens the vessel wall and reduces the lumen diameter and the cross-sectional area (CSA). The reduction is greatest for the large arteries whose physiological axial stretch is higher, and becomes less towards the smaller vessels with lower axial stretch. At no-load state (λ_z physiological axial stretch, pressure = 0), for example, the difference in CSA, is 20.8% of order 11 artery (λ_z = 1.446) and 17.9% of order 7 (λ_z = 1.206) and reduces to 5.5 and 1.2%, respectively for orders 5 (λ_z = 1.05) and 4 (λ_z = 1.01) (see Supplemental Table S2 for details). At physiological state where vessels are under the pressure, the difference in CSA is estimated at 11.8, 17.7, 2.8, and 0.06% for these respective vessels. Figure 7D shows that the axial stretch reduces the diameter distensibility (Eq. 1), most significantly for midsize vessels in terms of relative difference. The higher circumferential stretch of larger arteries, due to higher pressure and less perivascular constraint, further stiffens these vessels such that the distensibility is relatively lower.

DISCUSSION

The major finding is that the physiological axial stretch nearly vanishes for the vessels (arteries and veins) smaller than ∼40 μm and varies approximately linearly with the order number for the larger vessels. The stretch was also found to be higher in the arteries than the veins of the same order or diameter. Although it is not clear which strain component affects vascular regulation and remodeling, the epicardial arteries tend to be atherosclerosis-prone and have a relatively higher circumferential and axial strain.

Axial Prestretch

The length of vessel is constrained by vessel branches and surrounding tissue and the vessel is axially prestretched (9). The axial stretch is small in the young and increases with postnatal growth and development as the vessels are stretched by body growth (8, 34). Our data show that the physiological axial stretch λ_z is not uniform along the coronary vasculature, i.e., it decreases from large vessels toward smaller ones, for both arteries and veins. The axial stretch for the vessels smaller than order 4 (artery) or order −4 (vein) was found to be negligible, and can be considered as λ_z = 1. On the other hand, the veins show consistently lower axial stretch than the arteries of comparable diameter or of the same order (Fig. 4).

In our previous computational study (34) on large LAD artery (corresponding to order 11 in the present study), we confirmed the experimental observation that the axial stretch increases the circumferential stiffness of a blood vessel and thus decreases the PDR (6, 16, 33). Here, we evaluated coronary vessels down to order 4 arteries, which have previously not been studied, and showed significant effect of the axial stretch on vessel diameter at both the no-load (axially stretched but not pressurized) and physiological loaded states (Fig. 7). This result is significant for the study of coronary blood flow, as the flow resistance in a vessel segment is proportional to L × (D_in)⁻⁴ (L = length) and has significant effect on coronary blood flow (2). The present measurements provide a database to reduce ad hoc assumptions and increase the realism in future coronary flow simulation.

The vulnerability of subendocardium to hypoperfusion has been well documented (15). Several hypotheses have been proposed for the transmural distribution of coronary blood flow (2, 26). The difference in subendocardial and subepicardial vessel compliance has been proposed as an important determinant of the heterogeneous transmural blood distribution and the potential subendocardial vulnerability during hypoperfusion. This study underscores the significance of axial stretch on PDR (Fig. 7) and vessel diameter (Fig. 4) and hence the potential effect on transmural flow distribution. Future studies are needed to determine the myocardial transmural distribution of axial stretch since the present data were largely obtained from the epicardial surface and subepicardium.

Myocardial Constraint

Finite-element simulations (24, 34) showed that the constraint from the surrounding myocardium significantly reduces the PDR curve of large LAD artery and thus reduces the circumferential stretch/strain. The present analysis provides consistent results that the circumferential stretch of epicardial LAD artery (orders 9–11) is clearly higher than that of intramyocardial vessels (orders 4–8), i.e., λ_θ = 1.70 ± 0.04 vs. λ_θ = 1.39 ± 0.04, with details given in Supplemental Table S3. Since the axial stretch reduces the PDR (Fig. 7) and that the λ_θ at no-load state of all arteries are very similar (Supplemental Table S2), a reduction of the circumferential stretch must be contributed by the myocardial constraint. As an example, the circumferential stretch λ_θ shows an abrupt drop from 1.67 (corresponding to circumferential Green strain E_θ = 0.89) at order 9 (epicardial) to 1.39 (E_θ = 0.46) at order 8 (intramyocardial), which must be explained by the myocardial constraint, because these vessels have very similar axial stretch (1.25 vs. 1.30, Supplemental Table S1) and no-load λ_θ (Supplemental Table S2) and only a small difference in physiological pressure as calculated by Eq. 2 (19).

Silicone elastomer was used to perfuse the coronary vasculature to mimic physiological loading. Since silicone elastomer has a higher viscosity than blood (19) and the viscosity changes over time as the polymer hardens, the actual distribution of pressure along the LAD arterial tree may be different than the physiological distribution presented in formula Eq. 2, which was based on the in vivo viscosity of blood (22). In the appendix, Physiological State, we estimated P_phy with two approaches: 1) solve for (P_phy, D_in) from coupled Eq. 2 and PDR curve (Eq. A6); and 2) calculate P_phy from the experimentally measured D_in when the vessel was filled with elastomer. Interestingly, these two approaches yield very similar physiological diameter D_in (see Supplemental Tables S1A and S3) and pressure P_phy (data not shown). This comparison suggests that the pressure imposed by silicone elastomer along the coronary vasculature is similar to that given by formula Eq. 2 and is hence a good approximation to the actual physiological pressure. This is not surprising since the inlet and outlet pressures were physiological (100 and 5–6 mmHg, respectively).

In calculation of the PDR, the mean data of the opening angle, ZSS circumferential lengths, and axial stretch were used for each order of arteries, instead of individual values. Correspondingly, the material parameters in the constitutive model were statistical values previously obtained for large LAD arteries (32), rather than vessel specific. Furthermore, we assumed that the arterial wall is homogenous and used a one-layer model, instead of the more realistic two-layer model (32). These simplifications were made due to the lack of mechanical parameters for each order of the arteries. The model predictions of the physiological pressure, diameter, and deformation were similar to the measurements, indicating that the simplified model is reasonable and is statistically representative. The lack of constitutive model and material parameters of the veins prevented a similar analysis of PDR of these vessels.

The constraint from myocardium was also simplified by aligning the vessel axis with the myofiber orientation, such that intramyocardial vessels deform axisymmatrically in the analysis. While this is a good approximation for most smaller vessels and capillaries, it is not always true for larger vessels such as order 8 artery. The residual strain in myocardium was also not taken into account. For epicardial vessels, the assumption of lack of perivascular constraint was idealized, since these vessels are tethered to the heart by connective tissue to some extent.

The present results were obtained under passive state of the vessel and myocardium, i.e., without consideration of the muscle tone, pulsatile coronary blood pressure, and deformation of myocardium. Among these factors, myocardial deformation imposes additional axial stretch to the coronary vasculature and changes the stiffness of radial constraint on intramyocardial vessels and consequently PDR. The coronary blood pressure also affects the stress and strain in the myocardium, and hence, a detailed analysis of in vivo deformation of coronary vessels should be conducted in an interactive vessel-myocardium system (27).

Significance of the Study

This study provides a systematic and complete set of morphological measurement of coronary arterial and venous trees (the ZSS opening angle and inner/outer circumferences, physiological diameter, wall thickness, and axial stretch). These data represent the first measurements of axial stretch down to small coronary arteries and veins (40–50 μm). The data are important for accurate vascular mechanical analysis such as myocardial-vessel interaction in the coronary circulation, wave reflection, atherogenesis, and mechanotransduction in response to the change in mechanical stimuli (e.g., hypertension or flow overload). This database will serve as a foundation for additional realistic mechanical analysis that reduces ad hoc assumptions.

DISCLOSURES

No conflicts of interest, financial or otherwise, are declared by the author(s).

APPENDIX

Stretched, Zero-Pressure State

In cylindrical coordinate, the deformation gradient at material point with present radial coordinate r in the vessel wall is given by Wang et al. (32):

$$\text{F}\left(r\right)=\text{diag}\left(\frac{R}{\chi {\lambda }_{z}r},\frac{{\chi }^r}{R},{\lambda }_z\right)=\text{diag}\left({\lambda }_r,{\lambda }_{\theta },{\lambda }_z\right),\chi =\frac{180°}{180°-\phi °}R=\sqrt{\chi {\lambda }_z\left(r^2-r_{in}^2\right)+R_{in}^2}$$ (A1)

where R_in and ϕ are the inner radius and opening angle at ZSS of the vessel and r_in is the current inner radius. The Green strain components are E_* = $\frac{1}{2}$(λ_*×λ_* − 1) with * = r, θ, and z, respectively. Here, we used anisotropic hyperelastic model to describe the mechanics of LAD arterial wall (5):

$$W=\frac{c_0}{2}\left[\exp \left(Q\right)-1\right],Q=c_1{E}_r^2+c_2{E}_z^2+c_3{E}_{\theta }^2+2\left(c_4{E}_r{E}_z+c_5{E}_{\theta }{E}_z+c_6{E}_{\theta }{E}_r\right)$$ (A2)

where the parameters are (34) c₀ = 13.7 kPa, {c₁ ∼ c₆} {5.7, 3.1, 0.87, 2.7, 0.66, 0.41}. The radial and circumferential Cauchy stress components are:

$$\left(\begin{array}{c}{\sigma }_r\\ {\sigma }_{\theta }\end{array}\right)=-H+c_0\exp \left(Q\right)\left[\begin{array}{c}\left(1+2E_r\right)\left(c_1{E}_r+c_4{E}_z+c_6{E}_{\theta }\right)\\ \left(1+2E_{\theta }\right)\left(c_6{E}_r+c_5{E}_z+b_3{E}_{\theta }\right)\end{array}\right],$$ (A3)

where H is the hydrostatic pressure. By integrating the equilibrium equation in the radial direction (32), we obtained a relation between lumen pressure P_in, epivascular pressure P_out, and r_in, as:

$$P_{in}-P_{out}={\displaystyle {\int }_{r_{out}}^{r_{in}}\left({\sigma }_r-{\sigma }_{\theta }\right)r^{-1}dr,r_{out}=\sqrt{-r_{in}^2+A/\left(\pi {\lambda }_z\right)}}$$ (A4)

We assumed at no-load state that the vessel is free of lumen pressure and epivascular constraint, so that the inner radius of no-load state, denoted as r_in^nl, is the solution of 0 = ${\displaystyle {\int }_{r_{out}}^{r_{in}}\left({\sigma }_r-{\sigma }_{\theta }\right)r^{-1}\text{d}r}$. Obviously, the solution depends on the axial stretch λ_z of the vessel. To investigate the effect, we prescribed λ_z physiological axial stretch and λ_z= 1, respectively.

PDR

For epicardial arterials (orders 9–11) that are modeled as free of epivascular constraint, P_out equals to zero, and the lumen pressure P_in is determined by the inner radius r_in through Eq. A4.

To model the mechanical environment of intramyocardial arteries (orders 4–8), we imposed the stretch (by λ_z) but not pressurized vessel, as described above, into a infinite myocardium, whose myofibral orientation was assumed to align with the axis of the vessel. The inner radius of myocardium is the outer radius of stretched no-load vessel, r_out^nl = $r_{out}^{nl}=\sqrt{-{\left(r_{in}^{nl}\right)}^2+A/\left(\pi {\lambda }_z\right)}$. The myocardium was assumed free of stress and strain in the far field. Given a lumen blood pressure P_in, the vessel radius deforms from r_in^nl to r_in, and the outer radius changes from r_out^nl to r_out = $\sqrt{-r_{in}^2+A/\left(\pi {\lambda }_z\right)}$. Thus, a myocardial point with radial coordinate R displaces to radius r, and the deformation field was computed by the incompressibility condition, as

$$\text{F}\left(r\right)=\text{diag}\left(\frac{R}{r},\frac{r}{R},1\right)=\text{diag}\left({\lambda }_r,{\lambda }_{\theta },{\lambda }_z\right),R=\sqrt{r^2{\left(r_{out}\right)}^2+{\left(r_{out}^{nl}\right)}^2}$$ (A5)

We employed the transversely isotropic hyperelastic model of myocardium (12) in the form of Eq. A2, but with parameters {c₀ ∼ c₆} replaced by b₀ = 0.383 kPa and {b₁ ∼ b₆} {11.8, 40.6, 11.8, 0, 0, 0}. Thus the radial and circumferential Cauchy stress components were computed as in Eq. A3 with the same replacement of parameters. Finally, the relation between the pressure P_in and inner radius r_in, PDR, is given by:

$$P_{in}=\underset{\text{vessel}\hspace{0.17em}\text{wall}}{\underbrace{{\displaystyle {\int }_{r_{out}}^{r_{in}}\left({\sigma }_r-{\sigma }_{\theta }\right)r^{-1}\text{d}r}}}+\underset{\text{myocardium}}{\underbrace{{\displaystyle {\int }_{+\infty }^{r_{out}}\left({\sigma }_r-{\sigma }_{\theta }\right)r^{-1}\text{d}r}}},$$ (A6)

where the second integrate is the load supported by the myocardium.

Physiological State

The physiological pressure P_Phy and inner diameter D_in were obtained by solving coupled nonlinear Eqs. 2 and A6. A standard Quasi-Newton method is used. The results are given in Supplemental Table S3. An alternative approach was to calculate P_Phy by Eq. 2 using the measured inner diameter at the loaded state (filled with silicon elastomer, as described in Preparation of Coronary Arteries and Veins. Data are given in Supplemental Table 1A).