Abstract
Studying neural activity during natural viewing conditions is not often attempted. Isolating the neural response of a single saccade is necessary to study neural activity during natural viewing; however, the close temporal spacing of saccades that occurs during natural viewing makes it difficult to determine the response to a single saccade. Herein, a general linear model (GLM) approach is applied to estimate the EEG neural saccadic response for different segments of the saccadic main sequence separately. It is determined that, in visual search conditions, neural responses estimated by conventional event-related averaging are significantly and systematically distorted relative to GLM estimates due to the close temporal spacing of saccades during visual search. Before the GLM is applied, analyses are applied that demonstrate that saccades during visual search with intersaccadic spacings as low as 100–150 ms do not exhibit significant refractory effects. Therefore, saccades displaying different intersaccadic spacings during visual search can be modeled using the same regressor in a GLM. With the use of the GLM approach, neural responses were separately estimated for five different ranges of saccade amplitudes during visual search. Occipital responses time locked to the onsets of saccades during visual search were found to account for, on average, 79 percent of the variance of EEG activity in a window 90–200 ms after the onsets of saccades for all five saccade amplitude ranges that spanned a range of 0.2–6.0 degrees. A GLM approach was also used to examine the lateralized ocular artifacts associated with saccades. Possible extensions of the methods presented here to account for the superposition of microsaccades in event-related EEG studies conducted in nominal fixation conditions are discussed.
Keywords: saccades, EEG, visual search, microsaccades, artifact removal
eeg is well suited for the study of fast neural dynamics, and a variety of EEG studies have successfully explored saccadic planning (Everling et al. 1997; Richards 2003) and postsaccadic neural responses (Bellebaum et al. 2005; Ossandón et al. 2010). However, most EEG studies of saccadic eye movements are conducted with sparse synthetic visual targets and/or temporally well separated saccades in conditions that do not resemble those that are involved in natural viewing conditions. A variety of fMRI studies of saccadic eye movements, most of which were conducted in more controlled conditions than those associated with natural viewing, have identified various sites of neural activation likely involved in saccadic eye movements (Connolly et al. 2002; Corbetta et al. 1998). However, the low temporal resolution of fMRI makes the study of fast temporal neural dynamics during natural viewing conditions impractical.
Past research such as Bahill et al. (1975), Henderson (2003), and Hooge and Erkelens (1999) has demonstrated that, in natural viewing conditions and in visual search tasks, saccades and microsaccades are often closely spaced, with periods of fixation sometimes lasting 200 ms or less. Otero-Millan et al. (2008) determined that the average rate of all saccades executed in a visual search task was 3.3 Hz. Similarly, the average frequency of microsaccades even during periods of nominal fixation has been measured to be as high as 2.6 Hz (Martinez-Conde et al. 2004). Therefore, if the standard evoked potential (EP) paradigm is used to estimate the response to a single saccade, the EP of a single saccade is expected to be corrupted by linear summation and possibly nonlinear interactions from the EEG activity associated with closely temporally spaced, temporally adjacent saccades and microsaccades. (Note that the functional significance of microsaccades in vision is still an unresolved question; see Collewijn and Kowler 2008.) As described in Dimigen et al. (2011), the overlap of temporally adjacent EEG saccadic responses is also a problem in studies of normal reading (in which average fixations typically last only 200–250 ms).
A general linear least squares or general linear model (GLM) approach is proposed to estimate the neural response to a single saccade in the presence of other temporally close eye movements and other events of interest. The method presented here has a similar goal to the methods to correct for the overlap of multiple temporally adjacent EPs described in Hansen (1983) and Woldorff (1993) and also resembles methods used to correct for overlap of adjacent responses in event-related fMRI studies such as those methods described in Dale (1999). The method that has most commonly been applied to correct for overlap in EEG studies, the ADJAR (adjacent response) method of Woldorff (1993), applies an iterative convolution and subtraction technique to compensate for temporal overlap, differing substantially in the method of implementation from the approach presented here. Of the three references pertaining to temporal overlap compensation listed above, the regression-based approach that is applied here most closely matches the methods developed for event-related fMRI presented in Dale (1999).
In the work presented here, the GLM framework is applied to determine the response to a single saccade during the natural viewing conditions of a visual search. The GLM that is applied herein is designed to estimate multiple neural responses, with each estimated neural response being associated with a different segment of the saccadic main sequence. As will be seen in results, real visual-search eye-position data were used in a simulation to quantify the expected performance of regression and more standard EP-based neural response estimation techniques. Real visual-search eye-position data were used to take into account the actual temporal distribution of saccades in visual search. The simulation results indicated that the use of a GLM-based approach provides a significantly more accurate separation of the neural responses to single saccades in visual search conditions than is possible using standard event-related averaging methods. Furthermore, even for long data recordings (∼30 min of visual search data per subject averaged across all subjects), it was found that GLM results differed significantly from simple time-locked averaging results, with EP results being significantly and systematically distorted by the overlap of temporally adjacent saccades.
Also in results, it was determined that, for temporal intersaccadic spacings as low as 100–150 ms during visual search, there are no significant refractory effects on the neural saccadic response time locked to saccade onset. As a result of this finding, saccades in the same amplitude and velocity range but with different temporal intersaccadic spacings could be modeled using a single regressor, greatly simplifying the GLM approach.
The methods presented here use different regressors for saccades with different amplitudes, with a different EEG response function estimated for saccades of each size. Different sizes of eye movements might be expected to play different functional roles during eye-movement tasks (Martinez-Conde et al. 2004). Furthermore, work examining postsaccadic neural responses using EPs has demonstrated that the amplitude of the EEG saccadic λ-response increases in proportion to saccade size (Armington and Bloom 1974; Thickbroom et al. 1991). The GLM-based approach was therefore applied here to test the hypothesis that different sizes of eye movements are associated with different neural activity during visual search. In agreement with past event-related studies (Kazai et al. 2005; Kurtzberg et al. 1979; Takeda et al. 2001), it was found by applying the GLM approach that the saccade onset-triggered neural responses that were observed during a visual search task had a dominant occipital component.
Finally, the GLM approach was applied to examine the laterality of ocular artifacts associated with saccades, and the possibility of using a GLM approach to account for ocular artifacts in nominal fixation conditions is discussed. Note that it has been shown in past research that eye movements cause two main EEG artifacts. One artifact is direct current (DC) offsets and drifts attributable to change of the positions of the cornea-retinal dipoles during saccades. The second saccade-related artifact is an ocular muscle-related spike artifact that is caused by muscle contraction that is approximately time locked to the onset of an eye movement (Keren et al. 2010; Thickbroom and Mastaglia 1985; Yuval-Greenberg et al. 2008).
MATERIALS AND METHODS
Data collection.
Data were collected from eight subjects: five women and three men with normal vision. Before experiments were conducted, all subjects signed informed consent forms and experiments were approved by the Committee for the Protection of Human Subjects of the University of California, Berkeley. Right eye horizontal and vertical eye positions were recorded using a video-based infrared eye tracker (Eyelink SR 1000, Tower Mount with stabilized head) that sampled eye position at 1,000 Hz. EEG data were collected using an Active Two EEG System with DC recording (Biosemi). Details pertaining to the Biosemi method of referencing during data collection can be found at http://www.biosemi.com/faq/cms&drl.htm. The standard Biosemi head cap layout of 64 EEG electrodes was used to collect EEG data at 512 Hz. To synchronize the data, analog eye-position signals from the Eyelink were fed into the Biosemi input box and sampled along with the EEG at 512 Hz. The Biosemi system also recorded stimulus event markers generated by the stimulus presentation system (WinVis psychophysical and physiological testing toolbox).
Visual search task.
EEG and eye-position data were collected while subjects completed a visual search task involving eye movements. Data for the task were collected in a single EEG session per subject.
Images from the I Spy series of children's books (Wick and Marzollo 1997; Wick and Marzollo 2003) that were designed with visual search in mind were presented on a cathode ray tube monitor for 30 s each. Each visual search image subtended 23 degrees of visual angle vertically and 17 degrees of visual angle horizontally and was presented on a black background that was 26 by 35 degrees. All of the images consisted of cluttered scenes that required close scrutiny and many successive saccades to perform a visual search. An example search task for one of the images was: “Find how many vehicles are present in the image in 30 s.” Twenty such images were presented for 30 s each with 5 different search targets per image for 100 image-search trials total. Presentation order of the images and the associated search targets were randomized. The luminance of the background visual search images varied from image to image and also varied within a single image. The maximum luminance recorded within any one of the images was 70 cd/m2, and the minimum luminance measured was 0.5 cd/m2.
Preprocessing of EEG.
EEG data were digitally average referenced after data collection. Some of the merits of an average reference are discussed in Nunez and Srinivasan (2006). A modified average reference was applied that excluded the eight electrodes on the scalp located closest to the eyes. We adopted the modified average-referencing scheme to minimize ocular artifact amplitudes at the electrodes in which we were most interested (occipital electrodes). The decision to use the modified reference was made by comparing the results of standard average referencing and the modified referencing method at occipital electrodes. It was found that the amplitude of the saccadic spike in evoked potentials time locked to saccade onset was higher in magnitude at occipital electrode Oz when using the traditional average reference relative to the magnitude of the saccadic spike that resulted when the modified average reference was applied. We therefore decided to apply the modified average reference. Note that the eight electrodes closest to the eyes had the same modified average reference applied to them as the rest of the electrodes on the scalp and were retained for all analyses. No high-pass filter was applied; linear detrending using the Matlab detrend algorithm (MathWorks) with a detrend window of 10 s with intermediate breakpoints spaced at 1-s increments was used instead to lessen the effects of slow drifts and DC offsets on the EEG. (Importantly, some form of drift and offset correction is necessary before application of the GLM. Note that, as an alternative to detrending, a high-pass filter could have been used for removal of drift and DC artifacts. We repeated the analyses described here with a 1-Hz high-pass filter with zero-phase distortion attributable to forward and reverse filtering of the data and obtained very similar results to the results with detrending.) Data were then processed with an infinite impulse response low-pass filter with a 50-Hz cutoff, zero-phase distortion attributable to forward and reverse filtering of the data, a transition bandwidth of 1 Hz, and order 12 from the EEGlab toolbox (Delorme and Makeig 2004). Subjects 2, 3, and 8 had one of the 64 electrodes excluded from the analyses, and subject 7 had two of the 64 electrodes excluded from the analyses because it was noted during data collection that the electrodes in question failed to remain in good contact with the scalp during the course of the recording, likely attributable to localized looseness of the electrode cap. The electrodes that were excluded from analyses were electrode PO4 for subjects 2 and 3, electrodes Fpz and Fp2 for subject 7, and electrode AF8 for subject 8. (To view locations of the aforementioned electrodes, see http://www.biosemi.com/pics/cap_64_layout_medium.jpg.) All 64 electrodes were retained for individual subject analyses for all other subjects. However, only the 60 electrodes at which all subjects had usable data were retained for cross-subject analyses.
Eye-movement detection.
Saccades were detected by finding peaks in eye velocity. Peaks in velocity were located by finding acceleration zero crossings. Saccades were defined as occurring within the window between the acceleration and deceleration containing the velocity peak. Saccade onset was defined as the start of acceleration, and saccade offset was defined as the end of deceleration. Saccade amplitude was calculated as the change in position in the time period between the onset of acceleration and the end of deceleration. Eye velocities were determined using a similar formula to the moving average velocity estimate proposed in Engbert and Kliegl (2003). The formula proposed in Engbert and Kliegl (2003) was applied with the modification that the number of data samples from which eye velocity was estimated was increased from five samples to nine. Only peak velocities greater than 6 degrees/s were registered as saccades, and only potential saccades with amplitudes of >0.2 degrees were registered as saccades. Other past studies (Bosman et al. 2009; Martinez-Conde et al. 2006) have used similar thresholds for saccade detection.
Following Otero-Millan et al. (2008), a minimum temporal spacing of 20 ms was enforced between adjacent saccades to prevent eye-position overshoots associated with a single saccade from being classified as additional saccades. Eye-movement detection regressors consisted of time series with unit pulses placed at times of the start of eye acceleration with zeros at all other times.
Different regressors for different portions of the saccadic main sequence.
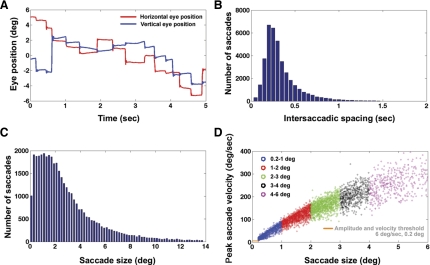
The close temporal spacing between adjacent saccades in natural viewing has been demonstrated in various other studies (Henderson 2003; Hooge and Erkelens 1999; Otero-Millan et al. 2008). The close temporal spacing of adjacent eye movements was also observed in the visual search task (Fig. 1A). Figure 1A is a plot of horizontal and vertical eye position of a representative subject. As can be seen from Fig. 1A and a pooled histogram across all subjects of intersaccadic spacings observed during the visual search task (Fig. 1B), eye movements often occur within short durations of one another. The goal was to estimate the neural activity associated with different amplitudes of eye movements separately. It was therefore necessary to examine the distribution of saccade amplitudes observed during the visual search task for all eight subjects (Fig. 1C). From saccade amplitude histograms, it was determined that, for all subjects, on average 88 ± 1.6% (all results presented in form of means ± SE) of the saccades were below 6 degrees. As can be observed in Fig. 1C, the upper 12% of eye-movement amplitudes were spread thinly over a range of eye movements above 6 degrees extending to 14 degrees and higher, making it difficult to define a single regressor for the broad range. GLM analyses were therefore restricted to saccades below 6 degrees in amplitude. A plot of the amplitude and peak velocity saccadic main sequence (Zuber and Stark 1965) for all saccades made by a representative subject involved in the visual search task is shown in Fig. 1D. (Note that the term “main sequence” can also refer to the relationship between saccade amplitude and duration.) The well-established relationship between saccade amplitude and peak velocity suggests that the neural responses associated with different amplitude/velocity ranges could be examined separately.
Fig. 1.
A: example plot of eye position vs. time in the visual-search task. Note the short periods of fixation and the closely spaced saccades of multiple sizes. B: pooled histogram across subjects of intersaccadic spacings observed during visual search. C: pooled histogram across subjects of saccade amplitudes during visual search. D: saccadic main sequence for a subject performing a visual search. The amplitude range is split up into 5 different regressors: 0.2–1.0-degree saccades, 1–2-degree, 2–3-degree, 3–4-degree, and 4–6-degree saccades. The minimum velocity and amplitude thresholds for a detected change in eye position to be classified as a saccade are indicated by the orange lines.
The possibility that different amplitudes and velocities of saccades have different neural responses was examined by assigning different regressors to different portions of the main sequence. Five different amplitude ranges that were used for binning saccades are plotted in five colors in Fig. 1D, with each amplitude range corresponding to a different regressor. The ranges for the five saccade regressors (0.2–1.0, 1–2, 2–3, 3–4, and 4–6 degrees) were decided based on examination of the histogram of Fig. 1C and dividing up the saccade range below 6 degrees, roughly equally such that each regressor had an adequate number of saccades falling in its range. The degree bins of 0.2–1.0, 1–2, 2–3, 3–4, and 4–6 degrees contained, on average across subjects, 20%, 24%, 19%, 12%, and 13% of the total eye movements made during visual search, respectively.
Saccade response determination methods.
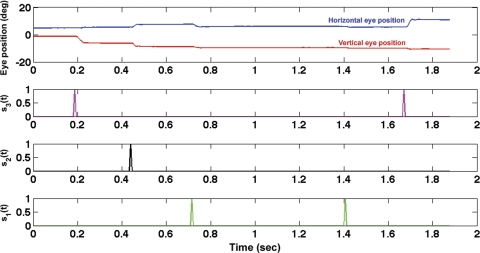
Regressor vectors derived from saccades detected in the eye-tracker data are plotted in Fig. 2. It can be seen that each regressor vector (sr) consists of unit pulses at the start of eye acceleration in a certain amplitude range. The most standard method of determining the neural saccadic response associated with each saccade range is to determine a time-locked average associated with each saccade event in sr as shown below in Eq. 1.
Fig. 2.
Example plot of regressors and eye position vs. time for a segment of visual-search data. Horizontal eye position is plotted in blue, and vertical eye position is plotted in red (top). Each regressor (sr) plotted in a different color (top-middle, bottom-middle, bottom), corresponds to saccades detected in a different amplitude range. Each sr consists of unit pulses at times of saccade onset.
The expression for a standard event-related average method (known in the single-unit recording literature as a spike-triggered average) to determine the average response to saccades in a single amplitude range (r) can be written as:
| (Eq.1) |
where L is the number of time samples in the EEG signal. Each τ at which the event-related average is calculated is a single delay measured relative to the saccade events of interest that are indicated by unit pulses in the saccade detection vector, sr. For any given saccade-amplitude range, one can divide the result of Eq. 1 by the number of saccades detected in the saccade detection vector sr for that saccade amplitude range (r) to obtain an event-related average.
For the GLM/regression approach to saccade neural response estimation, each saccade regression vector, sr, is associated with a neural saccadic response, hr, for the corresponding saccade amplitude range. The subscript r denotes a particular regressor associated with the specific saccade amplitude range. Assuming that the EEG data at any time t can be approximated as the linear superposition of the pre- and postsaccadic effects of all saccades occurring within ±Nt time samples of time t, and if Nr denotes the number of regressor categories (number of saccadic sizes), then:
| (Eq.2) |
Saccade detection events in the regressors are of unit amplitude so that the magnitude of the response is encoded in the size of the response time function, hr. Equation 2 is in the form of a GLM. The noise term in Eq. 2 accounts for spontaneous EEG activity that is not time locked to the saccade events that occur at the times of unit pulses in sr. The sum of convolutions of Eq. 2 can also be expressed in matrix form as shown in Eq. 3.
| (Eq.3) |
The individual elements of the matrices of Eq. 3 are shown in Eq. 4. The matrix E is composed of a single column of EEG data of length L, where L is the number of time samples of EEG data. H contains the as yet unknown EEG saccadic responses for each saccade size. H is a column vector with (2Nt + 1) × Nr elements. The unknown saccadic responses hr are concatenated vertically in H. The notation hr1 refers to the saccadic response associated with the first regressor, and the notation hrNr refers to the saccadic response associated with the last regressor of Nr total regressors. It can be observed in Eq. 4 that the points at which the response for each hr will be calculated range from τ-Nt to τ+Nt for each of the regressors, yielding estimates Nt samples before and Nt samples after the saccade event of interest. The neural responses stored in H were calculated at 84 delays before and after the start of eye acceleration (i.e., Nt = ±84), with a spacing between adjacent delays of 5.9 ms. This yielded saccade response estimates for ±492 ms relative to the start of eye acceleration. S in Eq. 3 is composed of the saccade regressors (sr ranging from sr1 to srNr), with the appropriate time segments of each sr arranged in S as specified in Eq. 4.
| (Eq.4) |
Equations 2, 3, and 4 can be solved for H by minimizing the sum-squared error between the left and right sides in a standard linear regression (Press 1986). The solution for H can be written as:
| (Eq.5) |
Note that the ST·E term of Eq. 5 is simply the matrix form of the right-hand side of Eq. 1 that is used for the calculation of the standard event-related potential. As discussed, the standard saccade time-locked averaging implemented in Eq. 1 is expected to be contaminated by the effects of temporally adjacent saccades. Note that the only difference between the GLM solution and the event-related average solution is the inverse of the covariance of the S matrix that appears in Eq. 5 but not in Eq. 1. The inverse of the covariance matrix takes into account the temporal overlap of adjacent neural responses. It is for this reason that, for example, in the fMRI literature, such as in Dale (1999), the author refers to the equivalent of the ST·E term in Eq. 5 as a “selective averaging term”, whereas the inverse of the covariance matrix is referred to as an “overlap correction term”. The size of the ST·S matrix was N x N, where N = (2 × 84 +1) × 5. (Note there were 5 total regressors.) The same general framework was also used with six regressors (3 amplitudes and 2 saccade directions, left and right) in another GLM that took into account saccade direction as described in detail in results.
Saccade regressor vectors and EEG data were subsampled by a factor of three before the regressor covariance matrix calculation. The original data were sampled with 1.95-ms spacing. Subsampling therefore resulted in estimates of H with 5.86-ms spacing. Subsampling was performed to reduce temporal correlation between adjacent time points in the data, to reduce noisiness of the estimated covariance matrix, and to reduce processing time.
EEG artifact rejection via zeroing of regressor vectors.
Preprocessing was necessary to ensure that GLM results were not contaminated by inclusion of noisy periods or blinks. Artifacts were prevented from corrupting GLM results by zeroing out time periods adjacent to artifacts in the saccade detection regressors. Blinks were detected by applying a blink detection algorithm described in the Eyelink eye tracker user manual to pupil data recorded by the Eyelink. Time windows adjacent to blinks corresponding to ±Nt samples (number of samples in the saccadic response to be estimated, see previous section) were zero padded in the regressors. This procedure prevented the EEG data recorded at the times of blinks from being included in the regression results.
In addition, the same zero-padding procedure of the saccade detection regressors was performed around time samples in which a saccade larger than 6 degrees was detected. This effectively zeroed 12% of the total visual-search eye movements. (The rationale for exclusion of saccades with amplitudes that were larger than 6 degrees was discussed in detail in Different regressors for different portions of the saccadic main sequence.)
Determining neural regions contributing to saccadic response.
To determine topographies and time functions associated with the neural response for each saccade size separately, the singular value decomposition (SVD) procedure below was applied to the GLM results for each saccade size, hr, separately for every subject. The rationale for performing a single, separate SVD for every subject and saccade regressor (i.e., saccade size) was that it was unknown whether the same cortical region or regions could be expected to be involved in saccades of different sizes.
It was found that, if SVD was applied over the entire EEG saccadic response, the components accounting for the most variance had electrode weightings predominantly near the eyes consistent with ocular muscle contraction artifacts (Keren et al. 2010; Thickbroom and Mastaglia 1985; Yuval-Greenberg et al. 2008). The dominance of ocular artifacts was not surprising because of the large magnitude of ocular muscle potentials relative to neural signals. Therefore, to examine components more likely to be neural in origin, SVD was applied to portions of the saccadic responses corresponding to 90 to 200 ms after the start of eye acceleration.
The subset of the GLM-determined saccadic response to which the SVD is applied is denoted as ht(e, τ) where the t subscript indicates the time-truncation window. Electrode is denoted as e, and time relative to saccadic onset is denoted as τ.
| (Eq.6) |
Application of Eq. 6 results in a single E (electrode weighting) and time component (T) for each SVD component (c).
After the finding of the SVD components in the truncated time window used in Eq. 6, the untruncated time courses Tfull associated with each SVD component over the entire duration of h (±492 ms relative to saccadic onset) could be determined by projecting the electrode weightings found in Eq. 6 onto the untruncated EEG saccadic response [hfull (e, τ)] as shown below, where pinv denotes the psuedoinverse.
| (Eq.7) |
It should be noted that the application of Eq. 7 to time-truncated GLM results (ht) rather than hfull results in the identical Tt as determined in Eq. 6.
RESULTS
Comparing event-related averaging to GLM methods: simulations.
GLM-based methods for neural saccadic response estimation were compared with traditional event-related potential methods via simulations using real visual-search eye-position data from all subjects. Real eye-position data were used to take into account the actual temporal distribution of eye movements when quantifying the expected differences in GLM and EP solutions.
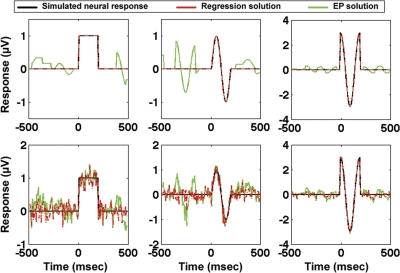
Saccade detection/regressor vectors, sr, were determined from 1-min segments of real eye-position data from all subjects collected during the visual-search task. Three different saccade regressor vectors that corresponded to the saccades of degree bins of 0.2–1.0, 1–2, and 2–6 degrees were determined from the real eye-position data. Three different simulated neural response functions, hr (shown in black in Fig. 3) were assumed for each of the different eye-movement sizes. Assuming that the EEG data can be modeled as the linear superposition of the responses to various saccade sizes, Eq. 2 was applied to create simulated EEG data sets with varying levels of noise. (See the following section for a validation and discussion of the assumptions of Eq. 2).
Fig. 3.
Simulation results comparing evoked potential (EP) to general linear model (GLM) methods, using real visual-search eye-movement data for simulation as described in the text. In black are the 3 simulated neural saccadic response functions (hr). In green are the results of event-related averaging, and in dashed red are the results of applying GLM methods. Row 1 is a simulation without added noise, and row 3 contains added noise with a signal-to-noise ratio of 1:1 as defined in the text.
Figure 3 compares the results of estimating the simulated neural response functions using event-related average methods and GLM methods for one representative subject. As expected, in the no-noise simulation, the GLM-based regression results (in dashed red) perfectly recover the three simulated neural response functions with zero residual. However, even with no additive noise, the event-related potential (in green) is distorted by the superposition of the effects of multiple saccades. The GLM solution was compared with event-related averaging both in a situation with no added noise (Fig. 3, top) as well as a situation with a signal-to-noise ratio (SNR) of 1:1 (Fig. 3, bottom). The SNR in the noise simulation was determined by computing the ratio of the root mean square (RMS) power of the simulated neural response functions to the RMS power of the added noise.
The noise and no-noise simulations described above were repeated for all subjects using 1-min segments extracted from each subject's visual-search eye-position data. To quantify the similarity between the simulated neural response functions and the estimated neural response functions determined using GLM and EP solutions, Pearson correlation coefficients were calculated between the simulated neural response functions and the GLM and EP solutions. As expected, in the no-noise simulation, the GLM results perfectly matched the neural response functions and therefore were perfectly correlated with the neural response functions for all subjects. In contrast, the EP approach resulted in mean correlation coefficients across subjects of 0.95 ± 0.01 in the no-noise simulation. In the additive white-noise simulation, the mean correlation of GLM solutions with the simulated neural response functions for all subjects was 0.96 ± 0.01. The corresponding mean correlation coefficient using an EP approach on the additive white-noise simulation for all subjects was 0.92 ± 0.01.
In both the no-noise and additive white-noise simulations using real visual-search data from all subjects, the GLM results produced significantly higher correlation coefficients with the neural response functions than the corresponding correlations of the EP solutions with the simulated neural response functions [significant difference in no-noise simulation: t(7) = 6.5, P < 0.001; significant difference in additive white-noise simulation: t(7) = 7.4; P < 0.001].
Effects of changing intersaccadic temporal spacing on saccadic neural response.
An assumption of the general linear least squares framework presented in Eq. 2–4 is that the neural response to any given saccade does not depend on the spacing between that saccade and the saccade immediately preceding it. In other words, it was assumed that saccades in the same amplitude range but with different intersaccadic intervals (ISIs) could be modeled by a single neural response function. Before testing the aforementioned assumption, the variability in ISIs was examined (Fig. 1B). The variability observed in ISI during the visual-search task is plotted in Fig. 1B as a histogram pooled across subjects. As can be observed in Fig. 1B, the majority of saccades in the visual-search task (82% across all subjects) were spaced between 0.1 and 0.5 s following the preceding saccade. To test whether ISI had an effect on the neural response, the evoked potentials of saccades with two different ranges of ISIs lying on the two extreme ends of the most commonly observed ISIs were compared. The two ranges of ISIs chosen for comparison were 0.1–0.15 s and 0.45–0.5 s. These ranges were chosen because of the wide temporal spacing between the two ranges, and, importantly, as can be observed in the histogram in Fig. 1, both of these ISIs had an adequate number of saccades in their respective time ranges to estimate saccade-related evoked potentials (3.4% and 4.7% of the total number of saccades observed across subjects, respectively). 38,887 total saccades were observed across subjects.
EPs for both ISIs were calculated separately for all five saccade sizes. To determine whether there were any significant differences between the short-ISI EPs and the long-ISI EPs, a standard nonparametric statistical method commonly applied to both fMRI (Nichols and Holmes 2002) and EEG/MEG data (Maris and Oostenveld 2007; Medendorp et al. 2007) was applied using Fieldtrip software for EEG/MEG analysis (see http://www.ru.nl/fcdonders/fieldtrip, Donders Institute for Brain, Cognition and Behavior, Radbound University, Nijmegen, the Netherlands.) This permutation-cluster analysis accounts for both the multiple-comparisons problem and the correlated-noise problem that make significance testing difficult. A brief description of the application of nonparametric statistics follows.
For each subject at each electrode, an event-related potential time locked to saccade onset was calculated for both saccades with long ISIs and saccades with short ISIs. This yielded EP estimates for the two ISI conditions at every electrode for every subject. Cross-subject EPs for the two conditions were determined by averaging the individual subject EPs at every electrode. To determine the probability that the differences observed in the cross-subject averages for the two ISIs were attributable to chance alone, a null distribution of cross-subject average EP differences was created as follows. Within each subject, the definition of the long-ISI EP and the short-ISI EP was swapped for all 28 (where 8 is the number of subjects) possible permutations of the eight subjects' long-ISI EPs and short-ISI EPs. (Note that the permutations were pairwise and occurred within single subjects only.) For every possible permutation, cross-subject grand average EP differences were determined sample by sample at all electrode-time pairs.
In both the permuted and the original data, samples whose t values corresponded to P < 0.05 (two-sided test) were selected and “clustered” with other adjacent samples also meeting the P < 0.05 criterion. Clustering was done based on adjacency in time and adjacency in position on the scalp (i.e., adjacent electrodes). Finally, “cluster-level statistics” were determined by summing all of the t values associated with each cluster. For the permuted data, a null distribution of cluster-statistic maxima was created by recording the maximum cluster statistic observed on each of the 28 permutations of the pairs of EPs.
The significance of clusters observed in the real data could be obtained via comparison to the null distribution of cluster-statistic maxima. The P values that are reported in this section are therefore the proportion of null-distribution cluster statistics that exceeded the cluster statistics associated with clusters of differences between the two conditions observed in the real data.
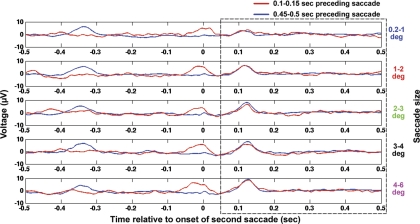
EP waveforms corresponding to both the long (0.45–0.50) and short (0.10–0.15) ISIs as averaged across all subjects for the five saccade-amplitude ranges are shown in the five panels of Fig. 4. Figure 4 consists of the EP for both ISIs calculated at electrode Oz. Importantly, note that the nonparametric statistical test was applied across all electrodes, but for simplicity we show the averages across all subjects only at electrode Oz to examine possible visual refractory effects.
Fig. 4.
Comparison of the saccadic neural response when the preceding saccade occurred shortly (100–150 ms prior) before the current saccade to the neural response observed when the preceding saccade occurred relatively long (450–500 ms prior) before the current saccade. The EP responses shown are averaged over all subjects at electrode Oz for 5 saccade sizes as labeled. Note that nonparametric statistics were applied at all electrodes for a time window extending from 50–500 ms after the current (second) saccade to test for significant differences; this time window is marked with a dashed box. No significant differences were found.
The nonparametric cluster statistics were applied to test for significant differences at all electrodes over a time window ranging from 50–500 ms after saccade onset. Differences in the two ISI conditions between 0 and 50 ms after the onset of the current saccade were expected as a result of the continued persistence of the neural effects of the immediately preceding saccade in the short-ISI case but not in the long-ISI case. In addition, the two large responses visible before time zero in the short-ISI and long-ISI cases were expected as well and are attributable to the neural responses of the prior saccade occurring at 0.10–0.15 s and 0.45–0.50 s before the current saccade, respectively (see Fig. 4).
For all five saccade sizes, no significant differences were found between the neural responses to the long and short ISIs over any region of the scalp between 50 and 500 ms after saccade onset. In fact, no significant differences between the long- and short-ISI neural responses with P < 0.3 were found. Therefore, saccades with different ISIs that were in the same amplitude range could be modeled using a single regressor.
Comparing event-related averaging to GLM methods: visual-search data.
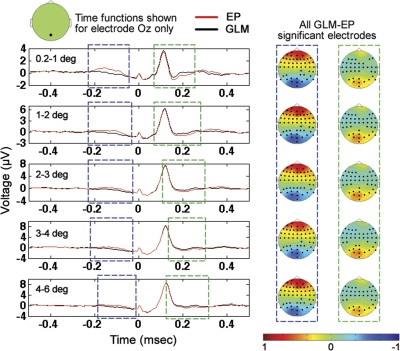
GLM and standard event-related averaging methods were applied to estimate the EEG response associated with each saccade size for all visual-search data for each of the eight subjects. There was ∼30 min of visual-search data per subject. The same methods for nonparametric comparison of multiple subject data in two conditions that were applied in the previous section (to compare long-ISI and short-ISI EPs for every saccade size separately) were applied here to determine significant clusters of difference between EP and GLM results for each saccade size separately. As was the case in the previous section, the methods were applied at all electrodes. Significant clusters (P < 0.05) of difference between the GLM and EP results were found for all saccade sizes. Occipital cross-subject averages at electrode Oz with periods of significant positive and negative differences highlighted are shown in Fig. 5. For all saccade sizes, there is a cluster of significant difference between EP and GLM results ranging from approximately −200 to −50 ms relative to saccade onset in which the occipital GLM results are significantly smaller than the corresponding EP results. The significant negativity of the GLM results in the −200 to −50-ms range relative to the EP results is likely attributable to the superposition of the positive peaks associated with the preceding occipital responses onto the EP waveforms. Note that the topographies associated with the −200 to −50-ms periods of significant difference have a significant cluster of positivity in occipital regions. In addition, for all saccade sizes, there is a cluster of significant difference between EP and GLM results ranging from ∼100 to 300 ms relative to saccade onset in which the occipital GLM results are significantly larger than the corresponding EP results. The 100–300-ms significant differences are likely due to the superposition of presaccadic negativity of the occipital responses from saccades occurring after the current saccade on the EP results. The presaccadic negativity of the occipital response is most visible in the cross-subject averages at electrode Oz shown in Figs. 6 and 10, in which it can be seen that, at electrode Oz, for all saccade sizes, there is a negativity in the occipital response before saccade onset from approximately −150 to 0 ms (with time 0 being saccade onset). Note that the significant differences between the EP and GLM results were not confined to only electrode Oz but were observed across all electrodes as marked in the topographies of Fig. 5. Furthermore, in addition to the two temporal periods of significant difference that included electrode Oz shown in Fig. 5, for all five saccade sizes, there were periods of significant difference (P < 0.05) between EP and GLM results from −50 to 100 ms (not shown in Fig. 5), in which electrodes other than electrode Oz, but not including electrode Oz, displayed significant EP vs. GLM differences. For example, at time zero, across saccades sizes, there were on average 27 ± 1.5 electrodes belonging to significant clusters of electrodes at which significant (P < 0.05) EP vs. GLM differences were observed.
Fig. 5.
Comparison of the cross-subject average of GLM and EP results for all 5 saccade sizes. Note that, for all saccade sizes, the EP results were significantly different (P < 0.05) from the GLM results as a result of the superposition of temporally adjacent saccades. Topographies shown are GLM minus EP differences from the 2 time periods of significant difference shown, with electrodes included in the significant clusters highlighted in bold. In addition to the significant clusters in the 2 highlighted time windows shown that included electrode Oz, there were also significant differences in the −50 to 100-ms window for all saccade sizes at electrodes on the scalp not including electrode Oz.
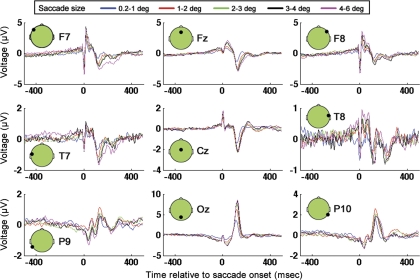
Fig. 6.
GLM results for electrodes F7, Fz, F8, T7, Cz, T8, P9, Oz, and P10 for 5 saccade amplitudes.
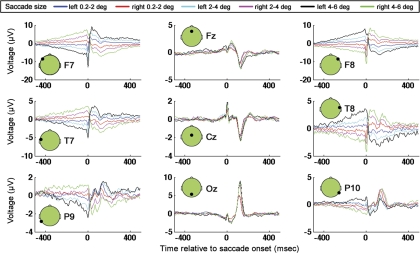
Fig. 10.
GLM results for electrodes F7, Fz, F8, T7, Cz, T8, P9, Oz, and P10 for leftward and rightward saccades of 3 sizes.
Importantly, note that all of the significant clusters of difference between the EP and GLM results were remarkably similar across the five saccade-amplitude ranges. For example, as described in greater detail above, for all saccade sizes, there was a negativity in occipital regions of GLM results relative to EP results from approximately −200 to −50 ms relative to saccade onset and a positivity in occipital regions of GLM results relative to EP results from ∼100 to 300 ms, with the scalp topographies of the GLM minus EP differences being very similar across saccade size (see Fig. 5). The similarity in the differences between GLM and EP results across saccade size in the cross-subject averages suggests that the significant differences between GLM and EP results were not random but instead were systematic distortions of the EP results relative to the GLM results attributable to systematic patterns of temporal saccadic spacing (and, as a result, systematic patterns of superposition of temporally adjacent EEG waveforms) that were consistent across saccade size and likely largely consistent across subjects to appear in the cross-subject average. The consistent nature of the distortions across saccade size that were observed in the cross-subject average suggests that, even if more data were collected and averaged, the EP results would likely still show the same systematic distortions relative to the GLM results.
GLM results: neural responses to saccades of different amplitudes during visual search.
Saccadic responses were determined at all electrodes by applying the GLM methods described in materials and methods. Cross-subject averages of GLM results at nine electrodes distributed across the scalp at locations F7, Fz, F8, T7, Cz, T8, P9, Oz, P10 are shown in Fig. 6. Note that the sharp peak visible in the vicinity of the start of eye movement (approximately time 0) in most of the plots in Fig. 6 is likely attributable to extraocular muscle contraction associated with the onset of the current saccade (Keren et al. 2010; Thickbroom and Mastaglia 1985; Yuval-Greenberg et al. 2008). As expected on the basis of aforementioned past studies, the saccadic muscle-related spike has the highest magnitude amplitude at frontal and lateral locations on the scalp (note that F7 and F8 are the two most frontal and lateral electrodes shown), with a smaller spike with opposite polarity visible at posterior electrodes (i.e., Oz, P10). In addition to saccadic spike artifacts, saccades are also associated with DC step artifacts, attributable to rotation of the corneo-retinal dipoles. Reverse polarity of DC step artifacts is associated with leftward and rightward saccades. Note that DC step artifacts are not readily apparent in Fig. 6, likely because the GLM used to determine the saccade responses for Fig. 6 grouped leftward and rightward saccades together in the same regressors, and the DC step artifacts therefore were cancelled out in the GLM as a result of there being a roughly equal number of leftward and rightward saccades. As will be seen in the next section, in contrast, when leftward and rightward saccades are solved for separately in the GLM, step-like artifacts become more apparent in the GLM solutions.
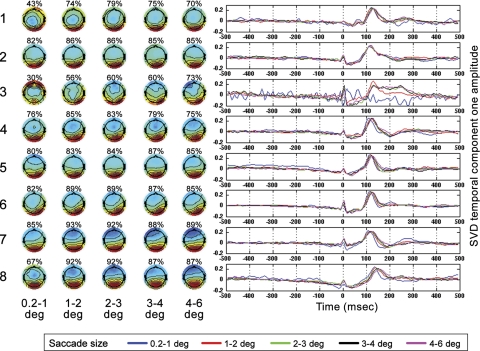
The results of applying SVDs to saccade GLM results for all subjects according to procedures described in materials and methods are shown in Fig. 7. Results from the eight subjects are the eight rows of Fig. 7. The five topographies plotted per subject are the SVD topographies that accounted for the most variance when SVD was applied to the GLM results for every saccade size for every subject in the time window 90–200 ms after saccade onset. Across all subjects and saccade sizes, (with the one exception of subject 3 for the smallest saccade size), the dominant topography was an electrode weighting indicating that the SVD component accounting for the most variance was occipital in origin. On average across all eight subjects for the five saccade sizes, the first SVD component accounted for 79 percent of the total variance with a standard error of 2%. On the basis of the high-frequency noise present in some of subject 3's GLM results (see, for example, SVD results for smallest saccade size of subject 3 in Fig. 7), and the association of high-frequency artifacts with muscle-related artifacts in the literature (Nunez and Srinivasan 2006), we hypothesize that the reason for the relatively poor performance of the GLM on subject 3 is attributable to, at least in part, muscle artifacts, possibly from neck muscles in the vicinity of occipital electrodes or facial muscles.
Fig. 7.
Singular value decompositions (SVDs) were applied to the GLM results for each saccade size for each subject in the time window 90–200 ms following saccade onset as described in the text. Each row contains the SVD component 1 results for 1 subject for all 5 saccade regressor sizes, with labels on the left indicating subject number. The percentage over each topography indicates the percent variance accounted for by SVD component 1 in the 90–200-ms window. Saccade size is shown at the bottom of each column. Time functions for all saccade sizes are plotted in the rightmost panels according to the legend shown. Time is relative to saccade onset.
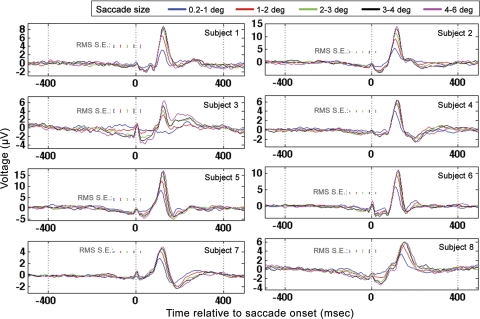
The GLM results at electrode Oz for all subjects are shown in Fig. 8. The RMS error shown for each saccade size was determined by performing the GLM three times for each subject on three separate, nonoverlapping segments of visual-search data for each subject. The three segments were derived from each subject's data by taking all of the data from every subject and segmenting the length of the total time course into three, nonoverlapping segments of time of approximately equal length. The RMS standard error was therefore determined across the three separate GLM results per subject.
Fig. 8.
Occipital electrode (Oz) GLM results for all subjects when time locked to saccade onset. Results for all saccade sizes are plotted according to the legend at top. Root mean square (RMS) standard errors were determined from repeated applications of the GLM to distinct, nonoverlapping temporal segments of data as described in the text.
The amplitudes and latencies of the occipital Oz response for the largest and smallest saccade sizes were tested for significant differences. Because subject 3 did not exhibit a clear positive peak in occipital response for the smallest saccade size, subject 3 was excluded from these analyses. For all other subjects, the largest regressor category had a significantly higher peak in the occipital response than the smallest saccade regressor category: 4.7 μV ± 0.7 for 0.2–1.0-degree regressor and 9.7 μV ± 1.7 for the 4–6-degree regressor (paired t-test; P < 0.05, t = −4.5). The scaling of the magnitude of the λ-response with saccade size is consistent with past research (Armington and Bloom 1974; Thickbroom et al. 1991). In addition, the largest saccade regressor category had a significantly larger latency to 90% of highest peak value (paired t-test; P < 0.05, t = −6) than the smallest regressor category (mean latency for 0.2–1.0-degree saccades 111 ± 4.4 ms; mean latency for 4–6-degree saccades 121 ± 5.4 ms).
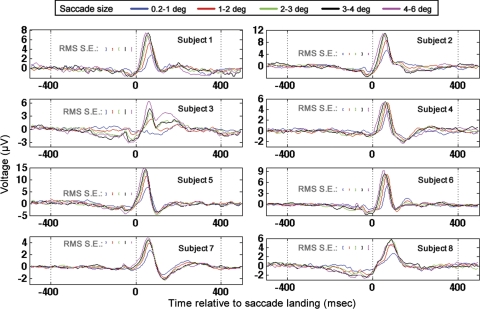
The GLM was also run on the identical regressors but time locked to saccade landing (Fig. 9). In contrast to the saccade-onset GLM results described above (in which small-amplitude saccades had significantly smaller latencies than large saccades), small-amplitude saccades had significantly longer latencies to peak than large-amplitude saccades in the saccade-landing-locked response (paired t-test; P < 0.05, t = 8.3, mean latency to 90% of highest peak for 0.2–1.0-degree saccades 65 ± 4.7 ms, mean latency to 90% of highest peak for 4–6-degree saccades 44 ± 2.8 ms). In addition, in the saccade-onset-locked response, the magnitude of the latency difference between the occipital response associated with small-amplitude saccades and large-amplitude saccades was significantly smaller than the magnitude of the difference in occipital response peak latency observed when the same comparison was done in the saccade-landing-locked GLM results (absolute value of difference between 0.2–1.0- and 4–6-degree saccades in time to 90% of highest peak in saccade-onset-locked response, 10 ± 4.4 ms; for saccade-landing-locked response 21 ± 6.6 ms; P < 0.05, t = −4.6). Finally, when time locked to saccade landing, the latency of the highest peak of the occipital response was inversely correlated with saccade amplitude (r = −0.49, P < 0.002). The aforementioned GLM results replicate event-related potential results in Thickbroom et al. (1991) in which the authors found that the latency of the peak in the occipital response time locked to saccade onset was ∼100 ms across all saccade sizes. Furthermore, in Thickbroom et al. (1991), the absolute value of the latency difference in the occipital peaks between small and large saccades was significantly smaller in the saccade-onset-locked event-related potentials than the same latency difference observed in the saccade-landing-locked event-related potentials. In addition, the GLM results discussed above replicate the results of Thickbroom et al. in which the authors found that the latency of the occipital peak in the saccade-landing-locked response was inversely correlated with saccade duration/amplitude. The latency of the saccade-onset- locked component is therefore more consistent across saccade size than the latency of the saccade-landing-locked component. The aforementioned findings led Thickbroom et al. to conclude that the peak ∼100 ms after saccade onset is more closely locked to saccade onset than landing.
Fig. 9.
Occipital electrode (Oz) GLM results for all subjects when time locked to saccade landing. Results for all saccade sizes are plotted according to the legend at top. RMS standard errors were determined from repeated applications of the GLM to distinct, nonoverlapping temporal segments of data as described in the text.
Although the dominant peak appearing ∼100 ms after saccade onset in the GLM results was therefore likely more tightly locked to saccade onset than to saccade offset, as discussed in Thickbroom et al., the occipital response observed after saccades likely has both onset- and offset-locked components. It was found in Thickbroom et al. that there is a second peak in the occipital λ-response that is more tightly locked to saccade landing than to saccade onset, with the peak in the offset-locked response becoming more widely temporally spaced from the onset-locked component for very large saccades (∼10 degrees or greater). Because the saccades modeled in the visual-search task described here were no larger than 6 degrees, the saccade-onset and saccade-landing responses likely overlapped rather than producing two distinct occipital peaks, which is consistent with the predictions of Thickbroom et al. for saccades less than ∼10 degrees.
GLM results: lateralized saccade artifacts.
Saccade artifacts have been shown to be lateralized (Keren et al. 2010; Thickbroom and Mastaglia 1985; Yuval-Greenberg et al. 2008). Furthermore an unresolved question is whether the main sequence is direction dependent (Boghen et al. 1974; Kaminiarz et al. 2009). Here, the same GLM methods described in materials and methods are applied to leftward and rightward saccades separately. The six regressor categories were left and right 0.2–2.0–degree, left and right 2–4-degree, and left and right 4–6-degree saccades. Note that the left and right categorizations were coarse, with all saccades (even saccades which had larger vertical than horizontal components) being grouped into “left” and “right” categories based on whether the landing position of any given saccade was leftward or rightward of the position of saccade onset. The main purpose of the GLM analysis presented here was to examine lateralized ocular muscle and corneo-retinal artifacts, and therefore only a coarse left and right separation was used. Importantly, note that, to determine directional differences in saccade artifacts in more detail or to examine the laterality of neural responses associated with saccades, one would likely need to separate saccades into more finely tuned direction categories than was done here.
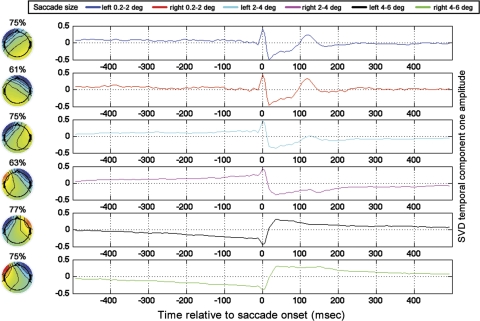
Figure 10 is a plot of the GLM results for the lateralized regressors. Comparing Fig. 10 to Fig. 6 (in which the GLM did not include lateralized regressor categories), one can observe that both figures contain the saccadic-spike artifact, which is most pronounced in frontal, laterally positioned electrodes. In Fig. 10, unlike in Fig. 6, however, there are prominent, step-like artifacts (most prominent in lateral electrodes). Note that the step artifacts in Fig. 10 go in opposite directions (from low to high vs. from high to low) for leftward and rightward saccades, consistent with the step artifacts being associated with corneo-retinal dipole rotation in opposite directions for left and right saccades. In contrast, the absence of step-like artifacts in the nonlateralized GLM (Fig. 6) is likely due to the fact that left and right saccades were grouped into the same category, and therefore the corneo-retinal step artifacts with opposite signs cancelled out. Recall that detrending was applied during preprocessing to minimize DC and low-frequency drift contributions to the EEG. The somewhat triangular shape of the step artifact that is visible in Fig. 10 (rather than the more rectangular step-like appearance that one might expect given the DC shift expected due to cornea-retinal dipole rotation) is likely due to the detrending during preprocessing. Note that, as an alternative to detrending, we tried filtering the data with a high-pass filter before application of the GLM. A 1-Hz high-pass filter with zero phase distortion attributable to forward and reverse filtering of the data had a very similar effect on the DC step artifact as the detrending (data not shown).
To examine the topographies of the saccade artifacts, GLM results from all subjects were averaged for every saccade size. Next, for every saccade size, a windowed SVD was performed ±35 ms around the time of saccade onset in the cross-subject average. With the use of the SVD topographies from the truncated window, an untruncated time course was derived via the projection procedure as described in materials and methods. It can be seen that, for the two smallest saccade sizes, the dominant topographic component contains the saccadic muscle artifact (Fig. 11). In agreement with past work (Keren et al. 2010; Thickbroom and Mastaglia 1985; Yuval-Greenberg et al. 2008), the saccadic muscle artifact is highly lateralized, with the highest magnitude of the muscle-related spike being recorded at the front of the head on the side ipsilateral to the eye movement. For the largest saccade size, likely because the displacement of the cornea-retinal dipoles are greater for larger saccades than smaller saccades, the component explaining the most variance is, instead of the saccadic spike, the step artifact associated with cornea-retinal dipole rotation. As could be seen in the single electrode plots, it can be seen in the SVD results that the step artifact goes in opposite directions for leftward and rightward saccades.
Fig. 11.
SVDs of cross-subject averages of lateralized GLM results. The percentage over each topography indicates the percent variance accounted for by SVD component 1 in the ±35-ms window around saccade onset. Time functions for all saccade sizes are plotted in the rightmost panels according to the legend shown. Time is relative to saccade onset.
Although we did not attempt to examine neural lateralization of the saccadic response, note that, if one were interested in comparing the neural responses of leftward and rightward saccades, one would need to remove the step artifact from the rightward and leftward GLM results to keep the step artifact from obscuring differences in neural activity. A simple way to reduce the effect of the step artifact would be to apply the Matlab detrend algorithm to the results of the GLM with breakpoints specified around the saccade, or (alternatively or in addition to the detrending) apply a method such as independent-components analysis to remove saccade-related artifacts before application of the GLM. Note also, if one were interested in applying GLM methods to examine the laterality of the neural saccadic response, one would likely need to restrict the analysis to saccades with a dominant horizontal component, which, as mentioned previously, was not the case for the regression shown in Figs. 10–11.
In discussion, it will be further discussed how compensation for the variance introduced by microsaccades in conditions in which subjects are nominally fixating can be accomplished by using a GLM consisting of regressors at the time of microsaccades and regressors associated with experimental events of interest, such that the microsaccade activity is prevented from superimposing on the neural activity associated with experimental events of interest. Microsaccades have a much smaller range in saccade amplitude than the saccades in visual search, and thus one could assign more regressor categories for different saccade directions than was done in the coarse “left and right” separation shown here. Saccadic spikes, step artifacts, and the neural activity associated with microsaccades could thus be prevented from superimposing on other neural time courses of interest. Note that, if such a scheme were applied, unless one were interested in the neural responses associated with microsaccades, one would not need to remove the step artifacts from the EEG responses associated with microsaccades recovered by the GLM.
DISCUSSION
GLM-based methods were applied to determine the EEG responses associated with saccades of various sizes in a visual search task. The performance of GLM-based methods relative to EP methods was quantified via a simulation using real visual-search eye-position data from all subjects as well as tests on real GLM and EP results from visual-search data. In both cases, GLM results were found to be significantly more accurate estimates of neural response functions than EP solutions during visual-search conditions. Importantly, even for long data recordings that were averaged across all subjects, the EP results were distorted relative to the GLM results as a result of the close temporal spacing of eye movements in visual search. Therefore, temporally adjacent EEG responses systematically overlapped in time and distorted EP results (Fig. 5). Past research that has relied on EP estimates to model the saccadic response in conditions in which saccades are closely temporally spaced (such as in Ossandón et al. 2010) could therefore be improved by employing GLM-based estimates.
It was found that there is no significant refractory behavior for saccades with intersaccadic spacings as low as 100–150 ms (see results and Fig. 4). To the best of our knowledge, this is a new result, and it allowed for simplification of the GLM approach by allowing saccades with different intersaccadic spacings to be assigned to the same regressor. The finding is consistent with past research examining the electrophysiological visual refractory period in humans in fixation conditions, such as in Shagass and Schwartz (1964). In Shagass and Schwartz, it was found that the visual evoked-potential (VEP) waveform observed in response to the second of two closely temporally spaced flashed stimuli recovered to approximately the same VEP waveform observed for a single flash when the two flashed stimuli had ∼100–120 ms or greater spacing. Importantly, the 100–150-ms saccade spacing that was examined for refractory effects relative to the 450–500 ms spacing was commonly observed during the visual search for all subjects (see histogram of ISIs, Fig. 1B). One might reason that the finding of no significant refractory behavior for the 100–150-ms saccade spacing makes sense because it seems reasonable that an intersaccadic spacing that is commonly observed in visual search should exceed the temporal window during which past studies using rapid flashes have found refractory visual responses.
Using GLM-based methods, it was observed that there are occipital responses time-locked to saccade onsets for all saccade sizes during visual search. This general finding agrees with past research using event-related averaging in more controlled viewing conditions (Dimigen et al. 2009; Gaarder et al. 1964; Jagla et al. 2007) that has demonstrated that there is a saccade-onset-triggered occipital response, often referred to as the λ-response. It was also found, in agreement with past work (Thickbroom et al. 1991), that the magnitude of the λ-response is saccade amplitude dependent. Note that this finding is also in agreement with past research involving reading in which the saccade-amplitude dependence of the λ-response has been demonstrated (Dimigen et al. 2011). It has been hypothesized (see Dimigen et al. 2009) that the saccade-onset-triggered occipital response is due to image motion across the retina caused by the saccade. In addition, various groups such as Ossandón et al. (2010) have found evidence that the magnitude of the λ-response is dependent on the difference in luminance between the image at saccade onset and the image at saccade offset. One might speculate that the significant difference in the magnitude of the occipital response observed across saccade size discussed in results could therefore at least be partially attributable to the fact that larger saccades are likely associated with a larger difference in luminance between the image at saccade onset and saccade landing than the luminance difference between saccade onset and offset expected for smaller saccades.
In Otero-Millan et al. (2008), the authors hypothesized that there is a common saccadic generator across saccade size during visual search based on their finding of similar temporal intersaccadic interval characteristics/refractory periods for microsaccades and saccades made in a visual search task. As was quantified here via application of SVD, the dominant component time locked to saccade onset for all saccade sizes during natural viewing was occipital, which could indicate that there are common regions of neural response across saccade size during visual search as well (Fig. 7). Note that the finding of dominant occipital sources during visual search agrees with past event-related potential work that has associated the saccadic λ-response during conditions of visual search (or conditions resembling visual search) with an occipital source (Kazai et al. 2005; Kurtzberg et al. 1979; Takeda et al. 2001).
Importantly, even saccades of less than a degree have an occipital neural response. In Dimigen et al. (2009), the authors also demonstrate the presence of microsaccadic neural effects and discuss how the P300 can be corrupted by microsaccades. More generally, the authors make the point that microsaccades are a source of variability that is almost never addressed in EEG and fMRI studies conducted in nominal fixation conditions. In addition to application in studies of neural processing during natural viewing, the methods presented here could be applied to address the problem of the ocular muscle (Yuval-Greenberg et al. 2008) and neural (Dimigen et al. 2009) contributions of microsaccades to the event-related EEG conducted in nominal fixation conditions. Recall that the GLM results recovered the neural occipital responses associated with saccades, as well as the ocular muscle artifact expected in the vicinity of the time of saccade onset, and the step artifacts associated with saccades when the lateralized GLM was run. As demonstrated with simulations and GLM and EP results from the EEG visual-search data, GLM methods will perfectly recover the responses to closely temporally spaced events whose associated EEG effects overlap, whereas event-related averaging will exhibit distortions in the case of closely temporally spaced events.
Therefore, in experiments conducted during fixation, rather than applying traditional methods to estimate responses to time-locking events (i.e., performing a simple time-locked average), we propose estimating the neural responses to the time-locking events by applying a GLM, which includes as regressors both experiment-related time-locking events as well as regressors consisting of unit pulses at times of fixational microsaccade detection. Such neural-response estimation techniques could prove particularly beneficial in experimental paradigms in which microsaccade-related activity might be expected to superimpose on the event-related average attributable to a characteristic pattern of microsaccade rate modulation relative to image presentation or other experimental events used for time locking (Dimigen et al. 2009; Engbert and Kliegl 2003). Importantly, the fact that saccadic spikes, step artifacts, and the neural activity associated with saccades appeared in GLM results (see results) would allow the GLM to effectively minimize or prevent all of these features from superimposing on the neural activity associated with experimental events of interest. In addition, the methods presented here could be applied to reduce the effects of microsaccades on time-frequency analyses (for a description of the time-frequency artifacts introduced by microsaccades, see Keren et al. 2010; Yuval-Greenberg et al. 2008). Before the application of time-frequency analyses, a GLM could be applied to estimate the EEG responses associated with microsaccades, ideally using different regressor vectors for different microsaccade directions. The microsaccade GLM solutions could then be convolved with the corresponding regressor vectors and the results of these convolutions subtracted from the raw EEG signal before application of time-frequency analyses.
Natural viewing is a challenging situation to model, and the neural saccadic response is undoubtedly dependent on a variety of factors not included in the simple GLM that only takes into account saccade amplitude that is presented here. For example, as discussed earlier, the occipital saccadic response has been found to be dependent on a variety of factors, including saccade amplitude (Armington and Bloom 1974; Thickbroom et al. 1991), direction, and change in luminance between images at saccade onset and offset (Ossandón et al. 2010). Adequately modeling all of the factors that contribute to the neural responses during natural viewing is therefore a challenge that will undoubtedly require some extensions and modifications of the basic framework presented here. However, with some basic extensions of the GLM framework presented here, one can address a variety of hypotheses pertaining to neural activity during natural viewing.
For example, one question that arises from the present work is what factors contribute to the significant differences in occipital-response amplitude that were observed for different saccade sizes. One hypothesis is that the amplitude differences were primarily attributable to the different saccade amplitudes causing varying degrees of retinal image motion at saccade onset that were proportional to saccade size. A second hypothesis is that the difference in occipital response across saccade size was instead primarily attributable to large saccades being more likely to be associated with a larger change in image luminance between the image at saccade onset and the image at saccade offset than the same onset minus offset luminance difference associated with smaller saccades. (Note that, with the present data, we were not able to test the hypothesis that large saccades are associated with a larger change in luminance than small saccades, and it would also be necessary to test that hypothesis.) To quantify the relative contributions of retinal slip and change in image luminance between saccade onset and offset on the magnitude of the occipital saccade response, one could run two GLMs using the same basic framework presented here. The first would be the current GLM in which each regressor is associated with a different size range of eye movements. The second could be a GLM in which different regressor categories could be defined for different magnitudes of luminance difference between the image at saccade onset and the image at saccade offset. After solving for the EEG saccadic response in both cases, one could determine (by convolving the GLM solutions with the corresponding regressor vectors and subtracting these convolution results from the raw data) the percentage variance accounted for by the amplitude- and luminance-based GLMs. Furthermore, on the basis of running preliminary GLMs to determine the relative contributions of saccade size and luminance, one might be able to determine template response functions for these parameters that could be fixed in subsequent applications of the GLM so that one might solve for other parameters of interest that would likely have an impact on the residual variance.
Further experiments using a similar framework to the one presented here could use separate regressors for saccades that have different functions or different landing sites. For example, separate regressors could be used for those saccades that land on targets that a subject is searching for in a visual search vs. those saccades that land on objects that are not targets. Past work has indicated that late, cognitive components of EEG such as the P300 (Cooper et al. 1977; Dimigen et al. 2011) and N400 (Dimigen et al. 2011) can be observed in natural viewing scenarios. Note that, because these cognitive components in the EEG occur later than sensory components, and because cognitive EEG components such as the P300 display more temporal persistence than sensory EEG components, cognitive EEG components are likely to be distorted to an even greater extent by temporal overlap during free viewing than the significant distortions in the sensory responses during free viewing that were observed here. Therefore, to accurately observe cognitive EEG components in free viewing scenarios, the GLM approach may be even more crucial than demonstrated here. Applying the framework presented here with more functionally distinct regressors could reveal neural differences between saccades that are mechanically identical but cognitively distinct.
GRANTS
Funding for this research was provided by DARPA grant B8U556562 and NIH grant RO1 EY04776.
DISCLOSURES
No conflicts of interest, financial or otherwise, are declared by the authors.
REFERENCES
- Armington JC, Bloom MB. Relations between the amplitudes of spontaneous saccades and visual responses. J Opt Soc Am A 64: 1263–1271, 1974 [DOI] [PubMed] [Google Scholar]
- Bahill AT, Bahill KA, Clark MR, Stark L. Closely spaced saccades. Invest Ophthalmol 14: 317–321, 1975 [PubMed] [Google Scholar]
- Bellebaum C, Hoffmann KP, Daum I. Post-saccadic updating of visual space in the posterior parietal cortex in humans. Behav Brain Res 163: 194–203, 2005 [DOI] [PubMed] [Google Scholar]
- Boghen D, Troost BT, Daroff RB, Dell'Osso LF, Birkett JE. Velocity characteristics of normal human saccades. Invest Ophthalmol 13: 619–623, 1974 [PubMed] [Google Scholar]
- Bosman CA, Womelsdorf T, Desimone R, Fries P. A microsaccadic rhythm modulates gamma-band synchronization and behavior. J Neurosci 29: 9471–9480, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Collewijn H, Kowler E. The significance of microsaccades for vision and oculomotor control. J Vis 8: 20.1–21, 2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Connolly JD, Goodale MA, Menon RS, Munoz DP. Human fMRI evidence for the neural correlates of preparatory set. Nat Neurosci 5: 1345–1352, 2002 [DOI] [PubMed] [Google Scholar]
- Cooper R, Mccallum W, Newton P, Papakostopoulos D, Pocock P, Warren W. Cortical potentials associated with detection of visual events. Science 74–77, 1977 [DOI] [PubMed] [Google Scholar]
- Corbetta M, Akbudak E, Conturo TE, Snyder AZ, Ollinger JM, Drury HA, Linenweber MR, Petersen SE, Raichle ME, Van Essen DC, Shulman GL. A common network of functional areas for attention and eye movements. Neuron 21: 761–773, 1998 [DOI] [PubMed] [Google Scholar]
- Dale AM. Optimal experimental design for event-related fMRI. Hum Brain Mapp 8: 109–114, 1999 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Delorme A, Makeig S. EEGLAB: an open source toolbox for analysis of single-trial EEG dynamics including independent component analysis. J Neurosci Methods 134: 9–21, 2004 [DOI] [PubMed] [Google Scholar]
- Dimigen O, Sommer W, Hohlfeld A, Jacobs AM, Kliegl R. Coregistration of eye movements and EEG in natural reading: Analyses and review. J Exp Psychol Gen 140: 552–572, 2011 [DOI] [PubMed] [Google Scholar]
- Dimigen O, Valsecchi M, Sommer W, Kliegl R. Human microsaccade-related visual brain responses. J Neurosci 29: 12321–12331, 2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Engbert R, Kliegl R. Microsaccades uncover the orientation of covert attention. Vision Res 43: 1035–1045, 2003 [DOI] [PubMed] [Google Scholar]
- Everling S, Krappmann P, Flohr H. Cortical potentials preceding pro- and antisaccades in man. Electroencephalogr Clin Neurophysiol 102: 356–362, 1997 [DOI] [PubMed] [Google Scholar]
- Gaarder K, Krauskopf J, Graf V, Kropfl W, Armington JC. Averaged brain activity following saccadic eye movement. Science 146: 1481–1483, 1964 [DOI] [PubMed] [Google Scholar]
- Hansen JC. Separation of overlapping waveforms having known temporal distributions. J Neurosci Methods 9: 127–139, 1983 [DOI] [PubMed] [Google Scholar]
- Henderson JM. Human gaze control during real-world scene perception. Trends Cogn Sci 7: 498–504, 2003 [DOI] [PubMed] [Google Scholar]
- Hooge IT, Erkelens CJ. Peripheral vision and oculomotor control during visual search. Vision Res 39: 1567–1575, 1999 [DOI] [PubMed] [Google Scholar]
- Jagla F, Jergelová M, Riecanský I. Saccadic eye movement related potentials. Physiol Res 56: 707–713, 2007 [DOI] [PubMed] [Google Scholar]
- Kaminiarz A, Königs K, Bremmer F. Task influences on the dynamic properties of fast eye movements. J Vis 9: 1.1–11, 2009 [DOI] [PubMed] [Google Scholar]
- Kazai K, Abe Y, Yagi A, Nakano T, Higuchi K, Yamamoto S. Eye-fixation related potential to stimuli simulating the vision of an older adult. Psychoanal Q 48: 120–126, 2005 [Google Scholar]
- Keren AS, Yuval-Greenberg S, Deouell LY. Saccadic spike potentials in gamma-band EEG: characterization, detection and suppression. Neuroimage 49: 2248–2263, 2010 [DOI] [PubMed] [Google Scholar]
- Kurtzberg D, Vaughan HG, Kreuzer J. Task-related cortical potentials in children. In: Cognitive Components in Cerebral Event-Related Potentials and Selective Attention, edited by Desmedt JE. Basel: Karger, 1979 [Google Scholar]
- Maris E, Oostenveld R. Nonparametric statistical testing of EEG- and MEG-data. J Neurosci Methods 164: 177–190, 2007 [DOI] [PubMed] [Google Scholar]
- Martinez-Conde S, Macknik SL, Hubel DH. The role of fixational eye movements in visual perception. Nat Rev Neurosci 5: 229–240, 2004 [DOI] [PubMed] [Google Scholar]
- Martinez-Conde S, Macknik SL, Troncoso XG, Dyar TA. Microsaccades counteract visual fading during fixation. Neuron 49: 297–305, 2006 [DOI] [PubMed] [Google Scholar]
- Medendorp WP, Kramer GF, Jensen O, Oostenveld R, Schoffelen JM, Fries P. Oscillatory activity in human parietal and occipital cortex shows hemispheric lateralization and memory effects in a delayed double-step saccade task. Cereb Cortex 17: 2364–2374, 2007 [DOI] [PubMed] [Google Scholar]
- Nichols TE, Holmes AP. Nonparametric permutation tests for functional neuroimaging: a primer with examples. Hum Brain Mapp 15: 1–25, 2002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nunez PL, Srinivasan R. Electric Fields of the Brain: the Neurophysics of EEG. Oxford: Oxford University, 2006, pp. xvi, 611 [Google Scholar]
- Ossandón JP, Helo AV, Montefusco-Siegmund R, Maldonado PE. Superposition model predicts EEG occipital activity during free viewing of natural scenes. J Neurosci 30: 4787–4795, 2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Otero-Millan J, Troncoso XG, Macknik SL, Serrano-Pedraza I, Martinez-Conde S. Saccades and microsaccades during visual fixation, exploration, and search: foundations for a common saccadic generator. J Vis 8: 21.21–18, 2008 [DOI] [PubMed] [Google Scholar]
- Press WH. Numerical Recipes: the Art of Scientific Computing. Cambridge: Cambridge University, 1986, pp. xx, 818 [Google Scholar]
- Richards JE. Cortical sources of event-related potentials in the prosaccade and antisaccade task. Psychophysiology 40: 878–894, 2003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shagass C, Schwartz M. Recovery functions of somatosensory peripheral nerve and cerebral evoked responses in man. Electroencephalogr Clin Neurophysiol 17: 126–135, 1964 [DOI] [PubMed] [Google Scholar]
- Takeda Y, Sugai M, Yagi A. Eye fixation related potentials in a proof reading task. Int J Psychophysiol 40: 181–186, 2001 [DOI] [PubMed] [Google Scholar]
- Thickbroom G, Knezevic W, Carroll W, Mastaglia F. Saccade onset and offset lambda waves—relation to pattern movement visually evoked-potentials. Brain Res 551: 150–156, 1991 [DOI] [PubMed] [Google Scholar]
- Thickbroom GW, Mastaglia FL. Presaccadic ‘spike’ potential: investigation of topography and source. Brain Res 339: 271–280, 1985 [DOI] [PubMed] [Google Scholar]
- Wick W, Marzollo J. I Spy Super Challenger: a Book of Picture Riddles. New York: Scholastic, 1997, p. 31 [Google Scholar]
- Wick W, Marzollo J. I Spy Ultimate Challenger!: a Book of Picture Riddles. New York: Scholastic, 2003, p. 31 [Google Scholar]
- Woldorff MG. Distortion of ERP averages due to overlap from temporally adjacent ERPs: analysis and correction. Psychophysiology 30: 98–119, 1993 [DOI] [PubMed] [Google Scholar]
- Yuval-Greenberg S, Tomer O, Keren AS, Nelken I, Deouell LY. Transient induced gamma-band response in EEG as a manifestation of miniature saccades. Neuron 58: 429–441, 2008 [DOI] [PubMed] [Google Scholar]
- Zuber BL, Stark L. Microsaccades and the velocity-amplitude relationship for saccadic eye movements. Science 150: 1459–1460, 1965 [DOI] [PubMed] [Google Scholar]